1 Zahlen, Gleichungen und Gleichungssysteme

Gleichungssysteme

Zahlen und Mengen geh¨oren zu den wichtigsten Grundbegriffen der Mathematik, auf denen alle weiteren Gebilde und Konstruktionen aufbauen. In diesem Kapitel werden die Grundlagen sowohl ¨uber Mengen als auch ¨uber die nat¨urlichen Zahlen gelegt. Zur Be- schreibung der nat¨urlichen Zahlen werden die Peanoschen Axiome eingef¨uhrt und das Prinzip der vollst¨andigen Induktion an vielen Beispielen demonstriert. Die reellen Zahlen und elementaren Rechengesetze werden angegeben; die Grundgesetze zu den Potenzen und Logarithmen werden wiederholt.

Zu den elementaren Aufgaben der Mathematik geh¨ort das L¨osen von Gleichungen. In diesem Kapitel werden auch einfache Gleichungen sowie die f¨ur die Anwendungen wichti- gen linearen Gleichungssysteme behandelt und der Gauß-Algorithmus eingef¨uhrt. Da nur wenige Typen von Gleichungen explizit l¨osbar sind, werden wir nicht systematisch auf das L¨osen von Gleichungen eingehen, sondern exemplarisch zeigen, wie man grundlegen- de Gleichungen bearbeitet.

Hinweis: Auf der Homepage befindet sich ein zus¨atzlicher Abschnitt ¨uber elementare mathematische Beweismethoden.

1.1 Mengen

”Unter einerMengeM verstehen wir jede Zusammenfassung von bestimm- ten wohlunterschiedenen Objekten unserer Anschauung oder unseres Den- kens zu einem Ganzen”; diese Festlegung (=Definition) des Mengenbegriffs stammt von G. Cantor (1895). Diese Definition des Mengenbegriffs reicht f¨ur unsere Zwecke vollst¨andig aus. Mengen bezeichnen wir im Folgenden immer mit Großbuchstaben. Die Objekte einer MengeAheißenElemente vonA und werden mit Kleinbuchstaben bezeichnet.

a∈A heißt:aist Element der MengeA.

a /∈A heißt:aist nicht Element der MengeA.

Mengen werden ¨ublicherweise angegeben durch

das Auflisten der Elemente in einer Mengenklammer {a₁, a₂, a₃, a₄, . . .},

eine Aussageform

{a∈A:a hat die Eigenschaft E}.

Die leere Menge ∅bzw. {}enth¨alt keine Elemente. B heißtTeilmenge von A (B⊂A), wenn jedes Element vonB auch Element vonAist.

Beispiele 1.1 (Mengen):

IN = Menge der nat¨urlichen Zahlen ={1,2,3,4, ...}. IN₀ = Menge der nat¨urlichen Zahlen mit Null ={0,1,2,3,4, ...}. ZZ = Menge der ganzen Zahlen ={0,±1,±2,±3, ...}. QI = Menge der rationalen Zahlen ={^p_q :p∈ZZ, q∈IN}. IR = Menge der reellen Zahlen

Es gilt: IN⊂ZZ⊂Q^I ⊂IR.

Bemerkungen:

(1) Die Reihenfolge der Elemente einer Menge spielt keine Rolle. Es ist daher {a, b, c, d}={d, c, a, b}.

(2) Jedes Element einer Menge wird nur einmal aufgez¨ahlt, d.h.

{a, a, a, b, d, d}={a, b, d}.

Mengenoperationen

F¨ur zwei MengenAundB sind derDurchschnittA∩B,dieVereinigungA∪B und dasKomplementA\B definiert durch

A∩B:={x:x∈A und x∈B}, A∪B:={x:x∈A oder x∈B},

A\B:={x:x∈A und x /∈B}.

Hierbei bedeutet”:=”, dass das Symbol auf der linken Seite durch die rechte Seite der Gleichung festgelegt (= definiert) wird. ¨Ahnlich ist das Zeichen ”:⇐⇒” zu lesen, als logische ¨Aquivalenz nach Definition dessen, was auf Seiten des Doppelpunktes steht.

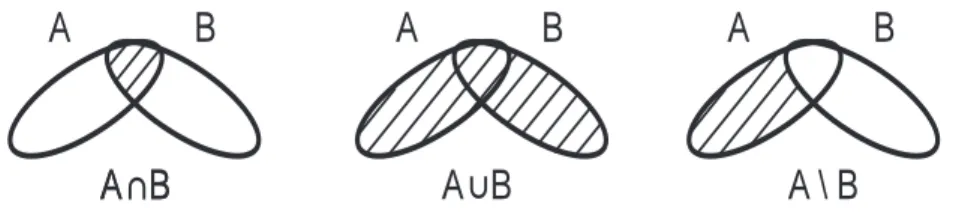
Abb. 1.1.Venn-Diagramme

Durch die sog.Venn-Diagramme(siehe Abb. 1.1) lassen sich Mengen und Men- genoperationen schematisch darstellen. Links ist der Schnitt zweier Mengen A∩B, in der Mitte die Vereinigung der MengenA∪B und rechts das Komple- ment der MengeAzur MengeB aufgezeigt. Mit den Venn-Diagrammen lassen sich die folgenden Rechenregeln f¨ur Mengen leicht veranschaulichen:

1. A∪B=B∪A 2. A∪A=A

3. A∪(B∪C) = (A∪B)∪C 4. A∪(B∩C) = (A∪B)∩(A∪C) 5. (A\B)\C= A\(B∪C)

6. A⊂B⇔A∩B=A⇔A∪B=B⇔A\B=∅

Daskartesische Produktvon zwei MengenM₁ undM₂ist die Menge, die aus allen Paaren(x, y)besteht, wobei x∈M₁ undy∈M₂:

M₁×M₂:={(x, y) :x∈M₁ und y∈M₂}.

Beispiel 1.2: IR×IR besteht aus allen Paaren von reellen Zahlen. Dies ist nichts anderes als die Zahlenebene;(x, y)ist jeweils ein Punkt in dieser Ebene.

Statt IR×IR schreibt man kurz IR².

1.2 Nat¨ urliche Zahlen

Zu den einfachsten Gegenst¨anden der Arithmetik geh¨oren die nat¨urlichen Zah- len. Sie bilden das Fundament unseres Zahlengeb¨audes. Die Gesamtheit aller nat¨urlichen Zahlen nennen wir die ”nat¨urliche Zahlenmenge” IN. Der Ausdruck

”nat¨urliche” Zahlen f¨ur IN={1,2,3, . . .}ist sicherlich gut gew¨ahlt, denn Kin- der beginnen so zu z¨ahlen und in allen Kulturen beginnt das mathematische Denken mit diesen Zahlen. Die Null wurde erst sehr sp¨at, n¨amlich etwa 870 n. Chr. von den Indern erfunden und wird heute zu den nat¨urlichen Zahlen hinzugenommen: IN₀.

Erst durch die Entdeckung der Zahl Null war die indische Mathematik erstmals in der Lage, ein heutzutage in der ganzen Welt ¨ubernommenes Stellenwertsys- tem zu schaffen, das nur mit zehn Ziffern (einschließlich der Null) auskommt.

Das Stellenwertsystem ist schon bei A. Ries (1492-1559) in seinem zweiten Re- chenbuch 1522 beschrieben. Darin befindet sich auch die W¨urdigung der Zahl Null! Das Fundamentalprinzip der nat¨urlichen Zahlen geht auf den Mathema- tiker Peano (1858-1939, 1889) zur¨uck.

1.2.1 Peanosche Axiome

(1) 1 ist eine nat¨urliche Zahl.

(2) Zu jeder nat¨urlichen Zahl n existiert genau ein Nachfolger n, der ebenfalls der nat¨urlichen Zahlenmenge angeh¨ort.

(3) Es gibt keine nat¨urliche Zahl, deren Nachfolger 1 ist.

(4) Die Nachfolger zweier verschiedener nat¨urlicher Zahlen sind voneinan- der verschieden.

(5) Eine Teilmenge der nat¨urlichen Zahlen enth¨alt alle nat¨urlichen Zahlen, wenn 1 zur Menge geh¨ort und mit einer nat¨urlichen Zahlnstets auch der Nachfolgern zur Menge geh¨ort.

Mit den Peanoschen Axiomen ist man in der Lage, die nat¨urliche Zahlenmen- ge aufzubauen, denn man erh¨alt sofort die folgenden Konsequenzen aus den Axiomen:

Folgerungen:

(1) Die nat¨urliche Zahlenmenge hat unendlich viele verschiedene Elemente:

Wegen (A1) gibt es mindestens eine nat¨urliche Zahl: 1. Wegen (A2) gibt es zu 1 einen Nachfolger, der nach (A3) = 1: 2. Wegen(A2) gibt es zu 2 einen Nachfolger, der= 1 (A3)und= 2 (A4): 3. usw.

(2) Die Elemente der nat¨urlichen Zahlenmenge lassen sich in einer bestimmten Reihenfolge anordnen, wobei schrittweise alle nat¨urlichen Zahlen erfasst werden:

1; 2; 3; 4; 5;..., n;n+ 1;...

Hierbei bedeutetn+ 1der Nachfolger vonn. Durch diese Reihenfolge wird auf nat¨urliche Weise die Addition von nat¨urlichen Zahlen festgelegt.

(3) Jede Teilmenge M der nat¨urlichen Zahlen M ⊂IN, welche die 1 und mit n∈M auch stets den Nachfolger n+ 1enth¨alt, ist gleich der Menge aller nat¨urlichen Zahlen.

Aus der Folgerung (3) erhalten wir ein Beweisprinzip, welches zu den wichtigs- ten Beweismethoden der Analysis geh¨ort, n¨amlich dievollst¨andige Induktion.

1.2.2 Vollst¨andige Induktion

Um eine AussageA(n)f¨ur alle nat¨urlichen Zahlen zu beweisen, gen¨ugt es nach Folgerung (3) zu zeigen:

(I) Induktionsanfang: F¨urn= 1 ist die Aussage richtig.

(II) Induktionsschlussvonn₀aufn₀+1: Ist die Aussage f¨ur eine belie- bige nat¨urliche Zahln₀g¨ultig, dann muss sie auch f¨ur den Nachfolger n₀+ 1 richtig sein.

K¨onnen beide Schritte durchgef¨uhrt werden, dann gilt die Aussage f¨ur alle n ∈ IN. Denn nach (I) ist die Aussage f¨ur 1 richtig. Nach (II) ist dann die Aussage auch f¨ur den Nachfolger 2 richtig. Nach (II) ist dann die Aussage auch f¨ur den Nachfolger, also 3, richtig. usw.

Beispiel 1.3. 1 + 2 +· · ·+n= n(n+ 1)

2 (n∈IN)

Beweismit vollst¨andiger Induktion. Der Induktionsanfang besteht darin, dass man explizit nachpr¨ufen muss, dass die Formel f¨urn= 1 richtig ist.

Wir setzen dahern= 1sowohl in die linke wie auch rechte Seite der Glei- chung ein: F¨ur n= 1 ist die linke Seite der Gleichung 1 und die rechte Seite ¹₂^·2 = 1.Damit stimmt die Formel f¨urn= 1.

Induktionsschluss vonn₀ aufn₀+ 1: Sein₀∈IN beliebig und die Formel sei richtig f¨ur diesesn₀, d.h. es gilt 1 + 2 +· · ·+n₀ = ⁿ⁰⁽ⁿ₂⁰⁺¹⁾. Unter dieser Voraussetzung m¨ussen wir zeigen, dass die Formel dann f¨urn₀+ 1 gilt. Wir starten mit der linken Seite der Gleichung; die Summe geht nun bis n₀+ 1. Wir setzen die Induktionsvoraussetzung ein und formen den Term so lange um, bis die rechte Seite f¨urn₀+ 1 heraus kommt:

1 + 2 +· · ·+n₀+ (n₀+ 1) = (1 + 2 +· · ·+n₀) + (n₀+ 1)

= n₀(n₀+ 1)

2 + (n₀+ 1)

= n₀(n₀+ 1) + 2(n₀+ 1) 2

= (n₀+ 1)(n₀+ 2)

2 .

Dies ist die zu beweisende Formel f¨urn₀+ 1.

Anmerkung:Man sagt, dass diese Summenformel auf F. Gauß (1777-1855) zur¨uck geht, der einer Anekdote zufolge die Summe der ersten 100 Zahlen dadurch berechnete, dass er die Summe der ersten mit der letzten, der zweiten mit der zweitletzten, der dritten mit der drittletzten usw. bildete:

1 + 2 + 3 +· · ·+ 98 + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) +· · ·. Somit erh¨alt man von den 100 Summanden nur noch ¹⁰⁰₂ , jeder mit dem Wert 101, also1 + 2 + 3 +· · ·+ 100 = ¹⁰⁰₂^·101.Tats¨achlich war sowohl die Formel als auch der Rechenweg schon Adam Ries (1492-1559; 1522) bekannt.

Als Abk¨urzung f¨ur Summen und Produkte f¨uhrt man folgende Notationen ein:

Definition:

(1)Summen: F¨ur die Summe der Zahlena_l, a_l+1,. . . , a_n ∈IR schreibt man n

k=l

a_k :=a_l+a_l+1+. . .+a_n.

(2)Produkt: F¨ur das Produkt vona_l, a_l+1,. . . , a_n∈IR schreibt man n

k=l

ak:=al·a_l+1·. . .·an.

(3)Fakult¨at: Zu jedemn∈IN definiert man

n! := 1·2·. . .·n (Fakult¨atvon n) und 0! := 1.

Ubrigens w¨¨ achst n!sehr schnell. Z.B. 13!≈6·10⁹; um diese Zahl zu z¨ahlen, ben¨otigte man 100 Jahre, wenn man in einer Minute bis 100 z¨ahlen k¨onnte!

Beispiele 1.4.

1

10 i=5

i²= 5²+ 6²+ 7²+ 8²+ 9²+ 10²= 355.

2

5 i=1

1 2i = 1

2·1+ 1 2·2 + 1

2·3+ 1 2·4 + 1

2·5 = 137 120. 3

6 i=3

(2i−1)²= 5²·7²·9²·11²= 12006225.

4 5! = 1·2·3·4·5 = 120.

Beispiel 1.5. 1 + 3 + 5 +· · ·+ (2n−1) = n k=1

(2k−1) =n² (n∈IN) Beweis mit vollst¨andiger Induktion. Wir beginnen beim Induktionsan- fangn= 1, indem wirn= 1sowohl in die linke wie auch rechte Seite der Gleichung einsetzen:1 = 1². Damit ist die Formel richtig f¨urn= 1.

Induktionsschluss vonnauf n+ 1: Seinbeliebig und die Formel richtig f¨ur dieses n, dann ist zu zeigen, dass die Formel auch f¨urn+ 1gilt:

1 + 3 + 5 +· · ·+ (2n−1) + (2n+ 1) = [1 + 3 +· · ·+ (2n−1)] + (2n+ 1)

=n²+ 2n+ 1 = (n+ 1)². Dies ist die Formel f¨urn+ 1.

Achtung: Zum Beweisprinzip der vollst¨andigenInduktion geh¨oren so- wohl der Induktionsanfang als auch der Induktionsschluss. Fehlt einer die- ser beiden Beweisteile, ist der Beweis nicht vollst¨andig und die Aussage nicht bewiesen, wie die beiden folgenden Beispiele zeigen:

f¨ur n = 1,2,3, . . . ,40 Primzahlen, n¨amlich p = 41,43,47, . . . ,1601 wie man durch Einsetzen explizit nachrechnet. Dies reicht aber nicht f¨ur einen allge- meinen Beweis aus. F¨ur n= 41folgt p= 41²−41 + 41 = 41².Dies ist keine Primzahl. Die Primzahlberechnung ist zwar f¨ur viele einzelnenrichtig; sie gilt abernichtallgemein!

2 + 1

(vgl. Beispiel 1.3) und zeigen, dass dennoch der Induktionsschluss durchf¨uhrbar ist: Wir nehmen also an, die Formel sei f¨ur ein nrichtig und zeigen, dass sie dann auch f¨urn+ 1 g¨ultig ist.

1 + 2 + 3 +· · ·+n+ (n+ 1) = ⁿ⁽ⁿ⁺¹⁾₂ + 1 + (n+ 1)

= n(n+1)+2(n+1)

2 + 1

= ^(n+1)(n+2)₂ + 1.

Dies ist die Formel f¨urn+ 1. Obwohl der Induktionsschluss durchf¨uhrbar ist, gibt es keinenat¨urliche Zahln, f¨ur welche die Formel richtig ist. Der Induk- tionsschluss verliert also seinen Sinn, wenn der Nachweis f¨ur n = 1 oder f¨ur einen anderen festen Zahlenwert nicht erbracht werden kann.

1.2.3 Geometrische Summenformel

F¨ur viele Anwendungen wichtig ist die geometrische Summenformel:

Satz (Geometrische Summenformel)

F¨ur jede reelle Zahlq= 1gilt:

n i=0

qⁱ= 1−qⁿ⁺¹

1−q (n∈IN₀)

Beweis durch vollst¨andige Induktion.

Induktionsanfangn= 0:

0 i=0

qⁱ=q⁰= 1 = 1−q¹ 1−q .

Induktionsschluss vonn auf n+ 1: Sein beliebig und die Formel richtig f¨urn, dann gilt f¨urn+ 1:

n+1

i=0

qⁱ= n i=0

qⁱ+qⁿ⁺¹=1−qⁿ⁺¹ 1−q +qⁿ⁺¹

= 1−qⁿ⁺¹+ (1−q)qⁿ⁺¹

1−q = 1−qⁿ⁺² 1−q .

1.2.4 Permutationen

Als Permutation einer Menge versteht man alle m¨oglichen Anordnungen der Elemente der Menge. IstA={a₁, a₂, a₃, . . . , a_n}, so kommt auf jede Position in der Menge genau ein Element. Eine andere Anordnung der Menge ist z.B.

{a₂, a₁, a₃, . . . , an}.

Der folgende Satz gibt Aufschluss dar¨uber, wie groß die Anzahl aller verschie- dener Anordnungen einern-elementigen Menge ist:

Satz:Die Anzahl aller m¨oglichen Anordnungen einern-elementigen Men- gea₁, . . . , a_n ist gleich n! = 1·2·3·. . .·n.

Beweis durch vollst¨andige Induktion. Der Induktionsanfang ist wieder bei n= 1: Die Anzahl aller Anordnungen der 1-elementigen Menge{a₁} ist 1. Wegen 1! = 1gilt die zu beweisende Formel also f¨urn= 1.

Induktionsschluss vonnaufn+ 1: Gesucht ist die Anzahl aller Anordnun- gen einer(n+ 1)-elementigen Menge{a₁, a₂, a₃, . . . , a_n+1}.Dazu betrach- ten wir das Element a₁ und dessen Pl¨atze (Positionen) in dieser Menge.

a₁ kann an 1. Stelle stehen; dann gibt es nach Induktionsvoraussetzung f¨ur die restlichen n Elemente n! Anordnungen.a₁ kann auch an 2. Stel- le stehen; dann gibt es nach Induktionsvoraussetzung f¨ur die restlichenn Elementen!Anordnungen.a₁kann auch an 3. Stelle stehen; wieder gibt es dann f¨ur die restlichennElementen!Anordnungen. usw.a₁ kann also an n+ 1verschiedenen Positionen stehen, und die verbleibendennElemente haben dann noch n! unterschiedliche m¨ogliche Anordnungen. Insgesamt gibt es alson!·(n+ 1) = (n+ 1)!M¨oglichkeiten.

Folgerung: Die Anzahl der k-elementigen Teilmengen einer n-elementigen Menge{a₁, . . . , a_n}ist gleich

n!

k!(n−k)!.

Begr¨undung:Allek-elementigen Teilmengen der MengeM ={a₁, . . . , an} findet man, indem aus allen n! Anordnungen nur die ersten k Elemente genommen werden. Dabei tritt jede k-elementige Teilmenge k!-mal auf und die verbleibenden (n−k)!-mal. Damit sind die k-elementigen Teil- mengen gleich _k!(n^n!_−k)!.

Anwendung:Die Chance, beim Lotto-Spiel ”6 aus 49” die richtige Kombina- tion zu erraten, ist etwa 1:14 Millionen. Denn die Anzahl der 6-elementigen Teilmengen einer 49-elementigen Menge ist gleich _{6! 43!}^49! = ^44·45_1·^·₂⁴⁶_·3^·_·⁴⁷_4·5^·48_·6^·49 = 13.983.816.

1.2.5 Der binomische Lehrsatz

F¨ur zwei nat¨urliche Zahlennundkmit0≤k≤nbezeichnet man die Zahl n

k

:= n!

k!(n−k)! =n(n−1). . .(n−k+ 1) k!

(man spricht nuber¨ k) als Binomialkoeffizient. Die Binomialkoeffizienten be- stimmen sich entweder durch die obige Formel oder durch das nach Pascal benannte Schema, dem sog.Pascalschen-Dreieck: Beginnend mit 1 wird die unten angegebene Pyramide in jeder Stufe um eine 1 rechts und links erwei- tert. Die Zahlen im Schema ergeben sich aus der Summe der beiden dar¨uber stehenden Zahlen.

₀

k

: 1 ₁

k

: 1 1 ₂

k

: 1 2 1 ₃

k

: 1 3 3 1 ₄

k

: 1 4 6 4 1 ₅

k

: 1 5 10 10 5 1 ₆

k

: 1 6 15 20 15 6 1 ...

Bemerkung:Mit den Binomialkoeffizienten k¨onnen wir die letzte Folgerung kurz formulieren: Es gibt

n k

M¨oglichkeiten ausnObjekten genaukauszu- w¨ahlen. Aus dieser Aussage erhalten wir die binomische Formel:

Satz:(Binomischer Lehrsatz). F¨ur beliebige Zahlena, b∈IR und jede nat¨urliche Zahl n≥0 gilt:

(a+b)ⁿ= n k=0

n k

a^n−k b^k

Beweis:Multipliziert man die rechte Seite aus, so kommt der Termb^k so oft vor, wie mankFaktoren ausnFaktoren w¨ahlen kann, also

n k

-mal (siehe obige Bemerkung). Die restlichen(n−k)Faktoren tragen zua^n−k bei.

Beispiele 1.8.

1 (x+y)⁰= 1 (x+y)¹=x+y

(x+y)²=x²+ 2xy+y²

(x+y)³=x³+ 3x²y+ 3xy²+y³

2 Wir berechnen den Wert der Potenz(104)³mit dem Lehrsatz:

(104)³= (100 + 4)³= 100³+ 3·100²·4 + 3·100·4²+ 4³

= 1 000 000 + 120 000 + 4 800 + 64 = 1.124.864.

1.3 Reelle Zahlen

Wir stellen uns auf den Standpunkt, dass uns die reellen Zahlen zur Verf¨ugung stehen und gehen nicht auf den axiomatischen Aufbau ein. F¨ur physikalische Messungen w¨urden die rationalen Zahlen ausreichen, f¨ur die h¨ohere Analysis weisen die rationalen Zahlen ”zu viele L¨ocher” auf. Erst ihre Erweiterung zu den reellen Zahlen macht die Differenzial- und Integralrechnung m¨oglich.

1.3.1 Zahlenmengen und Operationen

Auf den nat¨urlichen Zahlen IN gibt es als Grundrechenarten + und ·. Die Gleichung x+ 1 = 0 ist innerhalb IN formulierbar, aber nicht l¨osbar. Man erweitert daher den Zahlenbereich um all die L¨osungen der Gleichungen

x+n= 0,

wenn n ∈IN₀. Die L¨osungen sind 0,−1,−2,−3,· · · und der erweiterte Zah- lenbereich nennt man ZZ, die ganzen Zahlen. In ZZ l¨asst sich f¨ur jedesn ∈ZZ die Gleichung x+n = 0 l¨osen. Nicht l¨osbar ist die Gleichung 2x = 1. Man erweitert nun ZZ um all die L¨osungen von Gleichungen der Form

q·x=p

mit p, q ∈ZZ und q = 0. Somit erh¨alt man die Zahlenmenge der rationalen ZahlenQ. In diesem Zahlenbereich sind alle Gleichungen obiger Form l¨^I osbar.

Aber die Gleichung

x²= 2

besitzt in Q keine L¨^I osung. Also erweitert man die rationalen Zahlen um all die L¨osungen von Gleichungen obiger Bauart und kommt so zu den reellen Zahlen IR. In den reellen Zahlen sind noch die sog.transzendentenZahlen, wie eundπenthalten, die wir im Kapitel ¨uber Folgen noch genauer untersuchen.

In Tabelle 1 sind die Zahlenbereiche mit den zugeh¨origen Rechenoperationen nochmals aufgelistet.

Tabelle 1: Zahlenmengen und Grundrechenoperationen Mengen Grundoperationen nicht l¨osbar IN0 nat¨urliche Zahlen + · x+ 1 = 0

ZZ ganze Zahlen + − · 2·x= 1

Q rationale ZahlenI + − · \ x²= 2 IR reelle Zahlen + − · \ x²+ 1 = 0

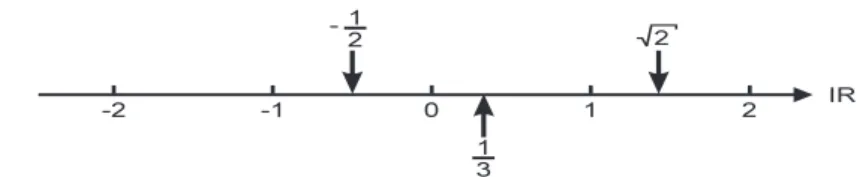
Darstellung reeller Zahlen.Zur Veranschaulichung der reellen Zahlen dient die bekannte von−nach+gerichteteZahlengerade. Jeder Punkt auf der Zah- lengeraden entspricht genau einer reellen Zahl.

Abb. 1.2.Reelle Zahlengerade

1.3.2 Die Rechengesetze f¨ur reelle Zahlen

In IR sind zwei Verkn¨upfungen gegeben, n¨amlich+und·. Addition und Mul- tiplikation zweier reeller Zahlen liefern wieder reelle Zahlen. Formal hat man hiermit zwei Abbildungen+und·definiert:

+ :IR×IR−→IR mit (x, y)−→x+y

·: IR×IR−→IR mit (x, y)−→x·y.

Es gelten dieRechengesetze der Addition

(A1) x+ (y+z) = (x+y) +z Assoziativgesetz

(A2) x+y=y+x Kommutativgesetz

(A3) x+ 0 =x Existenz der Null

(A4) Zu jedem x gibt es ein (−x)∈IR mit

x+ (−x) = 0 Inverses Element

Es gelten dieRechengesetze der Multiplikation

(M1) x·(y·z) = (x·y)·z Assoziativgesetz

(M2) x·y=y·x Kommutativgesetz

(M3) Es gibt eine Zahl1∈IR mit1= 0, so dass

1·x=x Existenz der Eins

(M4) Zu jedemx∈IR\{0}gibt es einx⁻¹∈IR mit

x·x⁻¹= 1 Inverses Element

Es gilt dasDistributivgesetz (D) x·(y+z) =x·y+x·z

Alle weiteren Rechengesetze der reellen Zahlen lassen sich auf diese elementaren Gesetze zur¨uckf¨uhren. Da diese Rechengesetze nicht nur f¨ur die Menge der reellen Zahlen gelten, sondern auch f¨ur andere Konstruktionen, f¨uhrt man den Begriffs des K¨orpers ein und verallgemeinert: Eine Menge K zusammen mit

zwei Verkn¨upfungen

+ :K×K−→K mit (x, y)−→x+y

· : K×K−→K mit (x, y)−→x·y,

die den Axiomen(A1)-(A4), (M1)-(M4), (D)gen¨ugen, nennt manK¨orper.

Beispiele 1.9:

1 Sowohl (IR,+,·)als auch(Q,^I +,·)bilden K¨orper.

2 (ZZ,+,·)ist kein K¨orper, da(M4)verletzt ist: z.B.2∈ZZ besitzt bez¨uglich der Multiplikation kein Inverses, so dass2·x= 1.

3 (IN,+,·)ist kein K¨orper, da z.B.(A4)verletzt ist.

4 (F₂,+,·)mitF₂={0,1} und den Verkn¨upfungen

+ 0 1

0 0 1

1 1 0

· 0 1

0 0 0

1 0 1

ist ein K¨orper. Man rechnet die Rechengesetze direkt nach. F₂ ist der kleinste K¨orper; denn jeder K¨orper muss mindestens zwei Elemente ent- halten: 0 und 1.

1.3.3 Potenzrechnen

Wir definieren zu jeder reellen Zahla∈IR die Potenzvonadurch a⁰:= 1, a¹:=a, aⁿ:=a ·. . .·a

n−mal

(n∈IN).

Definition:Dien-te Wurzel einer Zahla≥0 b:= √ⁿ

a:=aⁿ¹ (n∈IN)

ist definiert als diejenige positive reelle Zahlbmit der Eigenschaftbⁿ=a.

Mit der Schreibweise √ⁿ

a = aⁿ¹ lassen sich die n-ten Wurzeln einer Zahl als Potenzen mit rationalem Exponenten interpretieren. F¨ur die Potenzen von Pro- dukten bzw. Quotienten von reellen Zahlen gelten die allgemeinen Potenzre- chenregeln, die in der folgenden ¨Ubersicht zusammengestellt sind:

Es gelten diePotenzrechenregeln

(1)aⁿ·bⁿ = (a·b)ⁿ (2) aⁿ bⁿ =

a b

n

f¨ur(b= 0)

(3) aⁿ

a^m =a^n−m f¨ur(a= 0) (4)(a^m)ⁿ=a^n·m (5) √ⁿ

a^m=a^m/n f¨ur (a≥0) (n, m∈IN)

Beispiele 1.10.

1 a^5x−2y

b^6m−1 : a^4x+y

b^m−2 =a^{5x−2y−4x−y}

b^6m−1−m+2 = a^x−3y b^5m+1. 2 (a²b)²

2a√

ab =a⁴b^{2 1}₂a⁻¹a⁻¹2b⁻¹2 = ¹₂a⁵2 b³2. 3 (8a³b⁻³)⁻²

(12a⁻²b⁻⁴)⁻³ = 8⁻²a⁻⁶b⁶ 12⁻³a⁶b¹² = 3³

a¹²b⁶.

1.3.4 Logarithmen

Definition:Gegeben ist die Gleichunga=b^x (a, b >0).Gesucht ist bei gegebenemaundbder Exponent x. Wir nennen

x=logba denLogarithmus von azur Basis b.

F¨ur feste Basis bgelten dieLogarithmenrechenregeln (1)log(u·v) =log(u) +log(v) (u, v >0)

(2)log(^u_v) =log(u)−log(v) (u, v >0) (3)log(uⁿ) =n·log(u) (u >0)

Spezielle Logarithmen sind der Logarithmus zur Basis 10 lg a:=log₁₀a, der Logarithmus zur Basis 2 (Logarithmus dualis) ld a:=log₂a,

und der Logarithmus zu Basise(nat¨urlicher Logarithmus) ln a:=log_ea.

Zwischen unterschiedlichen Logarithmen besteht der Zusammenhang

log_by=log_cy

log_cb (b , c, y >0).

Dadurch ist es ausreichend einen Logarithmus (z.B. den nat¨urlichen Logarith- mus) berechnen zu k¨onnen. Die Logarithmen zu anderen Basen ergeben sich dann durch obige Formel.

Beweisder Logarithmenformel: Ausb^x=yfolgt per Definition des Loga- rithmus zur Basisb, dassx=log_by. Andererseits gilt f¨ur den Logarithmus zur Basisc nach der Logarithmusregel (3):

log_cy=log_cb^x=x·log_cb⇒x=log_cy logcb. Hieraus folgt die behauptete Formel.

Beispiele 1.11:

1 2^x= ¹₈ ⇒x=log₂¹₈ =−log₂8 =−3.

2 10^x= 0.0001⇒x=log₁₀10⁻⁴=−4 log₁₀10 =−4.

3 ln ^√√₃^ab−2

cd⁻³ = ln√

a+ lnb⁻²−lnc¹3−lnd⁻³= ¹₂lna−2 lnb−¹₃lnc+ 3 lnd.

4 log

3

a²b√⁴

a c²= log((a²b a¹⁴c¹²)¹³)¹² = loga¹³b¹⁶a²⁴¹c¹²¹

= ₂₄⁹ loga+¹₆logb+₁₂¹ logc.

1.3.5 Anordnung der reellen Zahlen

Unter den reellen Zahlen herrscht eine bestimmteAnordnung: Zwei reelle Zah- lena, b∈IR stehen stets in genau einer der drei folgenden Beziehungen zuein- ander:

a < b (aliegt links von b), a=b (aidentisch mit b), a > b (aliegt rechts vonb).

Unter demBetrageiner reellen Zahlawird der Abstand vonazum Nullpunkt verstanden. Er wird durch das Symbol|a|gekennzeichnet:

|a|:=

⎧⎨

⎩

a f¨ur a >0 0 f¨ur a= 0

−a f¨ur a <0

Beispiele 1.12: |3|= 3 ;|−5|= 5 ;−¹₂= ¹₂;√2=√ 2.

DerAbstand zweier Zahlenxundaauf der Zahlengerade ist|x−a|.

Abb. 1.3.Abstand zweier Zahlen

Nach der Definition des Betrags ist also

|x−a|=x−af¨urx−a≥0bzw.x≥a,

|x−a|=−(x−a)f¨urx−a <0bzw.x < a.

Diese Fallunterscheidung wird beim L¨osen von Betragsgleichungen und Be- tragsungleichungen eine wichtige Rolle spielen.

Es gelten dieGesetze:

(1) x >0, y >0⇒x+y >0.

(2) x >0, y >0⇒x·y >0.

(3) Sindx >0, y >0,dann gibt es immer eine nat¨urliche Zahln∈IN mit n x > y (Archimedes Axiom).

Folgerung:(Bernoullische Ungleichung)

(1 +x)ⁿ≥1 +n x (x≥ −1undn∈IN)

Beweisdurch vollst¨andige Induktion. F¨urn= 1gilt sogar die Gleichheit.

Induktionsschluss vonnaufn+ 1: Wegen1 +x >0folgt durch Multipli- kation der Induktionsvoraussetzung (1 +x)ⁿ≥1 +n x mit(1 +x):

(1 +x)ⁿ⁺¹≥(1 +nx)(1 +x) = 1 + (n+ 1)x+nx²≥1 + (n+ 1)x.

Intervalle: Teilmengen der reellen Zahlen nennt man Intervalle. Dabei un- terscheidet man zwischen den endlichen und den unendlichen Intervallen. Zur Beschreibung dieser Teilmengen von IR f¨uhren wir folgende Notationen ein:

(1) Endliche Intervalle(a < b)

[a, b] := {x:a≤x≤b} abgeschlossenes Intervall [a, b)

(a, b]

:=

:=

{x:a≤x < b} {x:a < x≤b}

halb offene Intervalle (a, b) := {x:a < x < b} offenes Intervall

(2) Unendliche Intervalle

IR_≥a := [a,∞) :={x:a≤x <∞}

IR>a := (a,∞) :={x:a < x <∞}

IR_≤a := (−∞, a] :={x:−∞< x≤a} IR_<a := (−∞, a) :={x:−∞< x < a}

1.4 Gleichungen und Ungleichungen

Die L¨osungsmethoden beim L¨osen von Gleichungen sind so Vielf¨altig wie es Gleichungs- typen gibt. Wir zeigen exemplarisch, wie einfache Gleichungen und Ungleichungen zu l¨osen sind. Allerdings werden wir nicht systematisch auf das L¨osen von Gleichungen und Ungleichungen eingehen, da sie in vielen F¨allen nicht exakt gel¨ost werden k¨onnen und man daher auf numerische Verfahren angewiesen ist (siehe z.B. das Bisektionsverfahren

§6.4 oder das Newton-Verfahren§7.8 ).

Hinweis:Auf der Homepage befindet sich ein zus¨atzliches Kapitel ¨uber das numerische L¨osen von Gleichungen.

1.4.1 Gleichungen

Jede Beziehung zwischen (reellen) Gr¨oßen, in der ein Gleichheitszeichen auf- tritt, nennt manGleichung. Treten die Gr¨oßen der Gleichung nur als Summen und Produkte von Potenzen auf, so spricht man von algebraischen Glei- chungen. Die gr¨oßte Summe aller Exponenten eines Terms gibt denGradder Gleichung an.