distribution amplitudes Integrability of the evolution equations for heavy–light baryon Physics Letters B

Contents lists available atScienceDirect

Physics Letters B

www.elsevier.com/locate/physletb

Integrability of the evolution equations for heavy–light baryon distribution amplitudes

V.M. Braun

^a

^,

^∗

, S.E. Derkachov

^b

^,

^c

, A.N. Manashov

^a

^,

^d

aInstitutfürTheoretischePhysik,UniversitätRegensburg,D-93040Regensburg,Germany bSt.PetersburgDepartmentofSteklovMathematicalInstitute,191023St.Petersburg,Russia cSt.PetersburgStatePolytechnicUniversity,195251St.Petersburg,Russia

dDepartmentofTheoreticalPhysics,St.PetersburgUniversity,199034St.Petersburg,Russia

a r t i c l e i n f o a b s t ra c t

Articlehistory:

Received4June2014

Receivedinrevisedform22September 2014

Accepted29September2014 Availableonline2October2014 Editor:B.Grinstein

We consider evolution equations describing the scale dependence of the wave functionof a baryon containingan infinitelyheavyquark and apairoflightquarks atsmalltransverse separations,which is the QCD analogueofthe helium atom. Theevolution equations depend onthe relative helicityof the lightquarks.Forthealignedhelicities,wefindthatthe equationis completelyintegrable,that is, it hasanontrivialintegralofmotion,and obtainexactanalyticexpressionsfortheeigenfunctionsand theanomalousdimensions.Theevolutionequationforanti-alignedhelicitiescontainsanextratermthat breaksintegrabilityandcreatesa“boundstate”withtheanomalousdimensionseparatedfromtherest ofthespectrumbyafinitegap. Thecorresponding eigenfunctionisfoundusingnumericalmethods.It describesthemomentumfractiondistributionofthelightquarksin,e.g.,Λb-baryonatlargescales.

©^{2014TheAuthors.PublishedbyElsevierB.V.ThisisanopenaccessarticleundertheCCBYlicense} (http://creativecommons.org/licenses/by/3.0/).FundedbySCOAP³.

1. PrecisiontestsoftheflavorsectoroftheStandardModelmay revealnewphysicsandremainhighontheagenda.Mainattention hasbeensofarfocusedonB-mesonsbutinterestisdevelopingto theheavy baryon decaysaswell. Such baryonsare produced co- piouslyattheLHCand,asmoredataarecollected,studiesofrare b-baryon decays involving flavor-changingneutral current transi- tionshavebecomequantitativeinordertomakeanimpactonthe field.Inparticular, the

Λ

_b→

Λ μ

⁺

μ

⁻ decaysarereceivingalotof attention,seee.g.Ref.[1]andreferencestherein.

Theoreticaldescriptionoftheb-hadrondecaysisbasedonfac- torizationtheoremsthatmakeuseofthelargemassoftheb-quark inordertoseparate calculableeffectsofshortdistancesfromthe nonperturbativelargedistancephysics.The correspondingformal- ismis similar butmuch lessdevelopedfor baryonsascompared tomesons.ArecentdiscussionusingSCETformalismcanbefound in Ref. [2]. For the exclusive decays involving large energy re- lease in the final state, the relevant nonperturbative quantities arebaryonwavefunctionsatsmalltransverseseparations,dubbed light-conedistributionamplitudes (DA).Theirstudywasstartedin Refs. [3–5]where thecompleteclassification andrenormalization groupequations (RGE)that governthe scale-dependencearepre- sented.

*

Correspondingauthor.

In this work we point out that these equations have a hid- densymmetryandcompletelyintegrableinthecasethatthelight quarkshavethesamehelicity.Inotherwords,we identifya non- trivial quantum number that distinguishes heavy baryon states with different scale dependence and obtain exact analytic solu- tion of the evolution equations. This phenomenon is similar to integrabilityofRGEsforthelightbaryons[6,7]and,inamoregen- eralcontext,tointegrabilityinhigh-energyQCD[8–10]andinthe N=4 supersymmetric Yang–Mills theory [11–13] that attracted hugeattentionasatooltochecktheAdS/CFTcorrespondence.The integrablemodelthat weencounterinthepresentcontextisdif- ferent;ithasbeendiscussedrecentlyin[17].

The similar equation for the case that the two light quarks haveopposite helicitycontainsan extratermthat breaksintegra- bilityandcreates a“bound state”withtheanomalous dimension separatedfromthe restofthespectrum bya finitegap.Thecor- responding eigenfunction is found numerically. It describes the momentum fractiondistributionofthelightquarks in,e.g.

Λ

b,at large scales andcan be called“asymptoticDA” inanalogy to the acceptedterminologyforhadronsbuiltoflightquarks.

2. Consideratfirsttheleading-twistDAofabaryoncontaining an infinitelyheavy quark anda transverselypolarized “diquark”:

a pair of light quarks with aligned helicities. It can be defined as[4]

http://dx.doi.org/10.1016/j.physletb.2014.09.062

0370-2693/©^{2014TheAuthors.PublishedbyElsevierB.V.ThisisanopenaccessarticleundertheCCBYlicense}(http://creativecommons.org/licenses/by/3.0/).Fundedby SCOAP³.

0

_q^T₁

(

z1n

)

C

/

n

γ

_⊥^μq2

(

z2n

)

hv

(

0

)

_B^j=1

(

v

)

= √

¹

3

_⊥^μu

(

v

)

f_B⁽²⁾

( μ )Ψ

_⊥

(

z₁

,

z₂

; μ ).

(1) Hereq1,2=^u

,

d

,

sarelightquarksseparatedbyalightlikedistance, hv

(

0

)

is theeffectiveheavy quark field withfour-velocity v,C is the charge conjugation matrix, u

(

v

)

is the Diracspinor

/

v u

(

v

)

= u

(

v

)

, and

^μ is the diquark polarization vector, vμ

μ=^{0. The} transverseprojections are definedwithrespect tothe two auxil- iary light-like vectorsn and ⁿ¯ ^{whichwe choose such that v}μ=

(

nμ+ ¯ⁿμ

)/

2, v·ⁿ=^1,n· ¯ⁿ=^2:

_⊥^μ

=

g^μν_⊥

_ν

,

g^μν_⊥

=

g^μν

−

n^μn

¯

^ν

+

n^νn

¯

^μ

/(

n

· ¯

n

),

(2)

andsimilar for

γ

_⊥^μ.The Wilson linesconnecting thequark fields arenot shownforbrevity. The heavyquark field hv canitself be relatedtotheWilsonlineas[18]

0

h_v

(

0

)

h

,

v

=

^{Pexp ig}

0

−∞

d

α

v_μA^μ

( α

v

)

,

(3)

so that the operator in Eq.(1) can be viewed as a pair of light quarks(adiquark), attachedto the Wilsonlinewith acusp con- tainingone lightlike and one timelike segment. Finally,the cou- pling f_B⁽²⁾ is definedasthe matrixelement ofthe corresponding localq1q2hv operator;itisinsertedfornormalization[4].Thepa- rameter

μ

is the renormalization(factorization) scale. We tacitly implyusingM S scheme.

The product

_⊥^μu

(

v

)

on the right-hand-side (r.h.s.) of Eq. (1) can be expanded in irreducible representations corresponding to physical baryon states with J^P =¹

/

2⁺ and J^P =³

/

2⁺ using suitable projection operators, see [4]. These (ground) statesform the SU

(

3

)

F multiplets (sextets),

Σ

b

, Ξ

b

, Ω

b and

Σ

_b^∗

, Ξ

_b^∗

, Ω

_b^∗, re- spectively, whichare degenerate inthe heavy b-quark limit. The double-strange

Ω

b baryon is ofspecial interest forflavor physics asitonlydecays throughweak interaction.The DA

Ψ

_⊥

(

z1

,

z2;

μ )

iswrittenusuallyintermsofitsFouriertransform

Ψ

_⊥

(

z

; μ ) =

∞

0

d

ω

1

∞

0

d

ω

2e^{−i(ω1z1+ω2z2)}

Ψ

_⊥

( ω

1

, ω

2

; μ )

=

∞ 0

ω

d

ω

1

0

due^{−iω(uz2+¯uz1)}

Ψ

_⊥

( ω ,

u

; μ ),

(4)

where z= {^z1

,

z2} ^{and in the second line we redefine}

ω

1=^u

ω

,

ω

2= ¯^u

ω

withu¯ =¹−^{u.The variables}

ω

1 and

ω

2 correspondto theenergies(uptoafactortwo)oflightquarksinthebaryonrest frame.TheDA(4)isthemostimportantnonperturbativeinputin QCDcalculationsofexclusive heavy baryon decaystothe leading poweraccuracyintheheavyquarkmass.

Thescaledependenceof

Ψ

_⊥

( ω ,

u

, μ )

or,equivalently,

Ψ

_⊥

(

z;

μ )

, isgovernedbytherenormalizationgroupequation[3,4]

μ ^∂

∂ μ ^{+ β(} α

s

) ∂

∂ α

s

+

²

α

s

3

π ^H

f_B⁽²⁾

( μ )Ψ

_⊥

(

z

; μ ) =

⁰

.

(5)

Theevolution kernel H ^{is an integral operatorwhich can be de-} composedas

H =

H12

+

H^h₁

+

H^h₂

−

⁴

.

(6) ThekernelsH^h_k^areduetoheavy–lightquarkinteractions,

H^h₁f

(

z

) =

1

0

d

α α

f

(

z

) − ¯ α

f

( α ¯

z1

,

z2

)

+

^ln

(

iz1

μ )

f

(

z

),

H^h₂^f

(

z

) =

1

0

d

α α

f

(

z

) − ¯ α

f

(

z₁

, α ¯

z₂

)

+

^ln

(

iz₂

μ )

f

(

z

).

(7)

Theyare identicalto theLange–Neubert kernels[19–21].The re- mainingcontribution

H12f

(

z

) =

1

0

d

α α

2f

(

z

) − ¯ α

f

z^α₁₂

,

z2

− ¯ α

f

z1

,

z^α₂₁

(8)

takesinto account theinteraction betweenthelight quarks; itis similartothestandardEfremov–Radyushkin–Brodsky–Lepageevo- lutionkernelforthepionDA.Hereandbelowweusethenotation

z^α₁₂

= ¯ α

z1

+ α

z2

, α ¯ =

1

− α .

(9) Theevolutionkernels(7),(8)canbewrittenintermsofthegen- eratorsofthecollinearsubgroupofconformaltransformations

S₊

=

^z2

∂

z

+

^2jz

,

S0

=

^z

∂

z

+

^j

,

S₋

= − ∂

z

,

(10) where j=^{1 istheconformal spinofthelightquark.The genera-} torssatisfythestandardSL

(

2

)

commutationrelations

[

^S+

,

S₋

] =

^2S0

, [

^S0

,

S_±

] = ±

^S±

.

(11) Onecanshowthat[23]

H^h₁

=

ln

i

μ

S⁽₊¹⁾

− ψ (

1

),

H^h₂

=

ln

i

μ

S⁽₊²⁾

− ψ (

1

),

where S⁽₊¹⁾, S₊⁽²⁾actonthefirst,z1,andthesecond,z2,light-cone coordinate,respectively.The last kernel(8)iswritten intermsof thetwo-particleCasimiroperator S²₁₂[24]

H12

=

²

ψ (

J12

) − ψ (

1

)

,

(12)

where S²₁₂=^S+S₋+^S0

(

S0−¹

)

= ^J12

(

J12−¹

)

, S₊=^S(₊¹⁾+^S(₊²⁾ etc.,and

ψ(

x

)

is Euler’sdigammafunction.Thus,thecompleteevo- lutionkerneltakesaverycompactform

H =

^ln

i

μ

S⁽₊¹⁾

+

^ln

i

μ

S⁽₊²⁾

+

²

ψ (

J₁₂

) −

⁴

ψ (

2

).

(13) The evolution equation for the DA in momentum space,

Ψ

_⊥

(

w1

,

w2;

μ )

, is given by the same expression with the SL

(

2

)

generatorsinthemomentumspacerepresentation[22].Eigenfunc- tions of H ^{correspond to the statesthat have autonomousscale} dependenceandthe corresponding eigenvaluesdefine anomalous dimensions.

3. Ourmainresultisthatthisevolutionequationcanbesolved explicitly.Tothisendweconsiderthefollowingoperators

Q

1

=

ⁱ

S⁽₊¹⁾

+

^S(₊²⁾

, Q

2

=

^S(₀^1)S(₊²⁾

−

^S(₀^2)S(₊¹⁾

.

(14) It ispossibleto show that Q1 andQ2 commutewitheach other andwiththeevolutionkernelH^:

[Q

1

, Q

2

] = [Q

1

, H] = [Q

2

, H] =

⁰

.

(15) Thefirsttworelationsaretrivial,thelastonecanbeverifiedusing theexplicitexpressionsforQ2 andH^.

If H ^is interpreted as a Hamiltonian of a certain quantum- mechanical model, the operators Q1 and Q2 correspond to the conservedcharges.Intheformalismofthequantuminversescat- teringmethod(QISM)thechargesQ1

,

Q2appearintheexpansion

oftheelementC

(

u

)

ofthemonodromymatrix,

C

(

u

) =

^u

Q

1

+ Q

2

.

The commutation relation [^C

(

u

),

H]=^{0, and its} generalization to more degrees offreedom then follow directly from the QISM [14–16]. Note that in classical applications of integrable models one encounters Hamiltonians that commute with the sumof di- agonal elements, A

(

u

)

+^D

(

u

)

, of the monodromymatrix. In our casetheHamiltoniancommuteswithC

(

u

)

,which correspondsto anew,nonstandardintegrablemodel.

The conserved chargesQ1, Q2 are self-adjoint operators with respecttotheSL

(

2

,

R

)

invariantscalarproduct

Φ|Ψ =

¹

π

²

C−

d²z₁

C−

d²z₂

Φ(

z

)

_∗

Ψ (

z

),

(16)

where the integration goes over the lower complex half-plane, Imzi

<

0. The eigenfunctions of C

(

u

)

provide the basis of the so-calledSklyanin’srepresentationofSeparatedVariablesandare knowninexplicitform[25].Theyarelabeled,forthepresentcase, bytworealnumbers:s

>

0 andx∈R^suchthat

C

(

u

)φ

s,x

(

z1

,

z2

) =

s

(

u

−

x

)φ

s,x

(

z1

,

z2

),

(17) with

φ

s,x

(

z

) =

^s z²₁z²₂

1

0

d

α α

¯ α

ix

exp

is

( α ¯ /

z₁

+ α /

z₂

)

=

^s

ρ (

x

)

^e

is/z1

z²₁z²₂¹F₁

1

+

^ix

,

2

,

is

z⁻₂¹

−

^z−₁¹

,

(18)

where

ρ (

x

) = π

x

/

sinh

( π

x

).

(19) Theeigenfunctions

φ

s,x

(

z

)

forma completesysteminthe Hilbert spacedefinedbythescalarproduct(16)

φ

_s,x

| φ

_s,x

=

²

π

s

δ

s

−

^s

δ

x

−

^x

.

(20)

SincetheconservedchargesQ1andQ2commutewiththeHamil- tonianH^{,theysharethesamesetof}eigenfunctions,

Hφ

s,x

(

z

) = γ (

s

,

x

)φ

s,x

(

z

).

(21) The simplestway to calculate the eigenvalues is to comparethe large-z asymptotics of the expressions on the both sides of this equation.Inthiswayoneobtainstheanomalousdimensions

γ (

s

,

x

; μ ) =

^{2 ln}

( μ

s

/

s₀

) +

E

(

x

),

E

(

x

) = ψ (

1

+

^ix

) + ψ (

1

−

^ix

) +

²

γ

E (22) wheres0=^{e2−γE.GoingbacktotheRGEequation(5),weexpand} theDA

Ψ

_⊥

(

z

, μ )

overtheeigenfunctionsofH

Ψ

_⊥

(

z

, μ ) =

∞

0

ds s

∞

−∞

dx

2

π η

_⊥

(

s

,

x

; μ )φ

s,x

(

z

).

(23)

The expansion coefficients

η

_⊥

(

s

,

x;

μ )

=

φ

s,x|

Ψ

_⊥ ^{evolve au-} tonomously,

f_B⁽²⁾

( μ ) η

_⊥

(

s

,

x

; μ ) =

^f_B⁽²⁾

( μ

0

) η

_⊥

(

s

,

x

; μ

0

) μ

μ

0

_−3β⁸

0

× μ

0s

s₀

₃⁸_β

0lnL

L^{34β0[E(x)− 4}

π β₀αs(μ₀)]

,

(24)

where L=

α

s

( μ )/ α

s

( μ

0

)

,

β

0=¹¹₃^Nc−²₃ⁿf. For large scales, the coefficients

η

_⊥

(

s

,

x;

μ )

slowlydrifttowardssmallervaluesofboth parameters:s→^{0,thankstothefactors8 lnL/3β0,and}|^x|→^0,tak- ingintoaccountthat

ψ(

1+^ix

)

∼^ln|^x|^forx→ ±∞^.

GoingovertotheDAinmomentumspace,

Ψ

_⊥

( ω ,

u;

μ )

,wede- finethecorrespondingeigenfunctionsas

φ

s,x

( ω ,

u

) =

e^{−iω(¯uz1+uz2)}

φ

s,x

(

z₁

,

z₂

)

.

(25)

Usingthat^e−ikz|^z−2eis/z= −

(

1

/

√

ks

)

J1

(

2√

ks

)

[23]oneobtains

φ

s,x

( ω ,

u

) =

¹

ω ^√

u^u

¯

1

0

d

α

√ α α ¯ α

^ix

α ¯

^−ix

×

^J1

(

2

√

ws

α ¯

u

¯ )

J₁

(

2

√

ws

α

u

).

(26)

Theeigenfunctions

φ

s,x

( ω ,

u

)

areorthogonalandformacomplete set:

s 2

π

∞ 0

ω

³d

ω

1

0

du uu

¯ φ

_s,x

( ω ,

u

) φ

^∗_s,x

( ω ,

u

) = δ

s

−

^s

δ

x

−

^x

,

(27)

ω

³u^u

¯

∞

0

sds

∞

−∞

dx

2

π ^φ

^s,x

⁽ ω ,

u

) φ

_s^∗_,x

ω

,

u

= δ

ω − ω

δ

u

−

^u

.

(28) Making useof Bateman’s expansionfortheproductoftwo Bessel functionsweobtainaseriesrepresentation

φ

s,x

( ω ,

u

) =

¹

ω

∞ n=0

iⁿ

_n⁻¹C_n^3/2

(

1

−

^2u

)

Hn

(

x

) √

¹

s

ω

^J2n+3

⁽

²

√

s

ω ).

(29) Here C_n^3/2

(

x

)

aretheGegenbauerpolynomials, J2n+³

(

x

)

areBessel functions,and

n

= (

n

+

¹

)(

n

+

²

)

4

(

2n

+

³

) .

(30)

ThefunctionsH_n

(

x

)

aregivenbythecontinuousHahnpolynomials uptotheprefactor

ρ (

x

)

:

H_n

(

x

) =

ⁱⁿ

1

0

du

u

¯

u

ix

C_n^3/2

(

1

−

^2u

)

= (

n

+

¹

)(

n

+

²

)

2 iⁿ

ρ (

x

)

3F₂

−

ⁿ

,

n

+

³

,

1

+

^ix 2

,

2

¹

,

(31) e.g.

ρ

⁻¹

(

x

)

H₀

(

x

) =

¹

, ρ

⁻¹

(

x

)

H₁

(

x

) =

^3x

,

ρ

⁻¹

(

x

)

H₂

(

x

) =

^5x2

−

¹

,

(32) etc. Hahn polynomials are real functions, have the symmetry Hn

(

x

)

=

(−

¹

)

ⁿHn

(−

^x

)

,andformacompleteorthogonalsystem.In ournormalization

∞

−∞

dx

2

π

^Hn

⁽

^x

⁾

^Hm

⁽

^x

^{) =}

ⁿ

^δ

^mn

^.

⁽³³⁾

Collectingeverythingweobtainthefinalresult:

Ψ

_⊥

( ω ,

u

; μ ) = ω

²uu

¯

∞

−∞

dx 2

π

∞

0

sds

φ

s,x

( ω ,

u

) η

_⊥

(

s

,

x

; μ ),

(34)

wherethescaledependenceof

η

_⊥

(

s

,

x;

μ )

isgiveninEq.(24).The expansioncoefficients of

η

_⊥

(

s

,

x;

μ )

in Hahnpolynomialsare re- latedto theexpansion coefficientsof

Ψ

_⊥

( ω ,

u;

μ )

inGegenbauer polynomials,

η

_⊥

(

s

,

x

; μ ) =

n

iⁿ

η

_n^⊥

(

s

; μ )

Hn

(

x

) →

Ψ

_⊥

( ω ,

u

; μ ) =

^uu

¯

n

ψ

_n^⊥

( ω ; μ )

C_n^3/2

(

2u

−

¹

),

(35) bytheBesseltransform(cf.Eq. (30)inRef.[23])

ψ

_n^⊥

( ω _; μ ) =

∞ 0

ds

√

s

ω

J2n+³

(

2

√

s

ω ) η

^⊥_n

(

s

; μ ).

(36)

Making use of the asymptotic expansion for the Bessel function onefindsthatthesmall-sbehavior

η

_n^⊥

(

s

)

∼^{spn translatesintothe} large-

ω

asymptoticsofthefunction

ψ

_n^⊥

( ω )

∼

ω

^−1−pn unlessthere issomecancellation,seebelow.

Theexpansion coefficientsat thereference(low) scale can be calculatedfromagivenmodeloftheDAas

η

_⊥

(

s

,

x

; μ

0

) =

∞ 0

ω

d

ω

1

0

du

φ

_s^∗_,x

( ω ,

u

) Ψ

_⊥

( ω ,

u

; μ

0

).

(37)

Intheexisting studies itis usually assumedthat

Ψ

_⊥

( ω ,

u;

μ

0

)

is decreasingexponentiallyatlargeenergies

ω

.Forarather general modelofthistype

Ψ

_⊥

( ω ,

u

; μ

0

) = ω

²uu

¯

n

cn

ω

n

κne^−ω/n

_n^{4 C}

3/2

n

(

2u

−

1

)

(38)

oneobtains

η

_⊥

(

s

,

x

; μ

0

) =

^s

n

iⁿcn

(

s

n

)

ⁿHn

(

x

)

× Γ (

n

+

⁴

+ κ

n

) Γ (

2n

+

⁴

)

^1F1

n

+

⁴

+ κ

n

2n

+

4

−

^s

n

.

(39)

In particular, for the simplest phenomenologically acceptable model[3–5]

Ψ

_⊥

( ω ,

u

; μ

0

) = ω

²uu

¯

e^−ω/0

₀⁴

^→ η

_⊥

(

s

,

x

; μ

0

) = ρ (

x

)

se^−s0

.

(40) Exponentialdecrease ∼^{e−ω/n ofeach Gegenbauerharmonics in} (38)amounts,fromtheviewpointoftherelationinEq.(36),tothe finetuning such that all leading powerterms inthe asymptotics

ω

→ ∞^{drop out. This finetuning is, however,destroyed by the} evolutionsothatapower-likeasymptoticsisalwaysgenerated.

Toseethis, considerthesimplestmodelin(40)corresponding tothetermn=^{0 in(38)asanexample.Astheresultoftheevo-} lution(24)allharmonicswithn

>

0 becomeexcited

η

_n^⊥

(

s

, μ ) =

cn

( μ )

s

( μ

0s

)

^−δe^−s0 (41) where

δ

= −⁸

/

3

β

0lnLand

cn

( μ ) ∼

dx H0

(

x

)

L^4/3β0E(x)Hn

(

x

).

(42)

For the corresponding coefficients in the Gegenbauer expansion (35)oneobtainsusing(36)

ψ

_n^⊥

( ω , μ ) =

^cn

( μ )

₀⁻²

₀

μ

0

δ

ω

0

n+²

× Γ (

n

+

⁴

− δ) Γ (

2n

+

⁴

)

^1F1

n

+

⁴

− δ

2n

+

⁴

− ω

0

.

(43)

The confluenthypergeometricfunction 1F1

(

a

,

b|

ω )

decreases asa powerof

ω

at

ω

→ ∞^{,cf.Eq.(62)below,unlessa}−^bisanonneg- ativeinteger,inwhichcasetheasymptoticbehaviorisexponential.

Thus,unless

δ

=^{0 andn}=^0,weobtain

ψ

_n^⊥

( ω , μ ) ∼ ( ω /

0

)

^−2+δ

.

(44) Notethattheasymptoticbehavioristhesameforanyn.

4. Next,weconsiderheavybaryonswiththelightquarkshav- ing opposite helicity. The scale dependence of the leading twist DAs does not depend on the spin ofthe light quark pair andis thesame forthe j^P=^{0+ SU}

(

3

)

F triplet andall longitudinalDAs ofheavybaryonsinthe j^P=^{1+ sextets,see[4].For}definiteness, considerthe

Λ

b-baryonDA[3,4]definedas

0

u^T

(

z1n

)

C

γ

5nd

/ (

z2n

)

hv

(

0

)Λ(

v

)

=

^f_Λ⁽¹⁾

( μ )Ψ

Λ

(

z₁

,

z₂

; μ )

u_Λ

(

v

).

(45) The evolution equation for

Ψ

Λ

(

z₁

,

z₂;

μ )

contains an additional term corresponding to the gluon exchange between the light quarks(inFeynmangauge)

H12

→

H12

− δ

H12

, δ

H12f

(

z

) =

1

0

d

α

¯

α

0

d

β

f

z^α₁₂

,

z^β₂₁

(46) thatcorrespondstoH→H−¹

/

J₁₂

(

J₁₂−¹

)

intheSL

(

2

)

-invariant representation of the evolution kernel in Eq. (13). Expanding

Ψ

Λ

(

z1

,

z2;

μ )

intermsoftheeigenfunctions(18)oftheintegrable Hamiltonian(13)

Ψ

_Λ

(

z

, μ ) =

∞ 0

dss

∞

−∞

dx

2

π η

_Λ

(

s

,

x

; μ )φ

s,x

(

z

)

(47)

one obtains the RGE equation for the expansion coefficients

η

Λ

(

s

,

x

, μ )

μ ^∂

∂ μ ^{+ β(} α

s

) ∂

∂ α

s

+

²

α

s

3

π

2 ln

μ

s

s0

+

E

(

x

)

×

^f_Λ⁽¹⁾

( μ ) η

Λ

(

s

,

x

, μ )

=

²

α

s

3

π

^f

(1) Λ

( μ )

∞

−∞

dxV

x

,

x

η

Λ

s

,

x

, μ ,

(48)

whereE

(

x

)

isdefinedinEq.(22)andthekernel V

(

x

,

x

)

isgiven bythematrixelement

φ

_s,x

| δ

H12

| φ

_s,x

= δ

s

−

^s

V

x

,

x

.

(49)

Weobtain V

x

,

x

=

¹ 2

π

∞ n=⁰

_n^{−1 H}

∗n

(

x

)

H_n

(

x

) (

n

+

¹

)(

n

+

²

)

=

¹

2 sinh

π (

x

−

^x

)

x

−

^x

xx

− π

sinh

π (

x

−

^x

)

sinh

π

xsinh

π

x

.

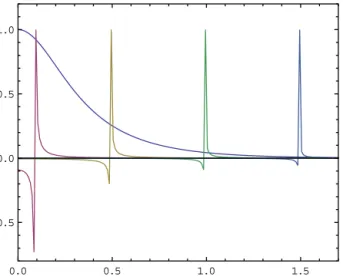
(50)

Fig. 1.ThespectrumofeigenvaluesE(xn)≡^EnofthediscretizedversionofEq.(51) x→^xn=(2n+¹)/200,n=⁰,1,. . . ,99 (bluedots)comparedtothe“unperturbed”

spectrumE(xn)(redsolidcurve).Inordernottooverloadtheplot,onlyeverysec- ondeigenvalueisshown.(Forinterpretationofthereferencestocolorinthisfigure legend,thereaderisreferredtothewebversionofthisarticle.)

Fig. 2.Thex-eveneigenfunctionsη_k⁺(xn)=η⁺_k(−xn)fork=0 (thegroundstate), andk=¹⁰,50,100,150 (fromlefttoright),forL=^{5 andN}=^500.Normalization isarbitrary.

Itiseasytoseethat V

(

x

,

x

)

∼¹

/(

2

π

x²

)

forlarge x,anddecreases exponentiallyin|^x−^x|^.

Inorder tosolve (48)one needs tofindthe eigenfunctionsof theintegralequation

E

(

x

) η

_E

(

x

) − [

^V

η

_E

_] (

x

) =

^E

η

_E

(

x

).

(51) If V →^{0,obviously all} eigenfunctions are localizedin x,

η

a

(

x

)

∼

δ(

x−^a

)

.Thespectrumofeigenvaluesiscontinuous, Ea=E

(

a

)

≥^0, and double degenerate since E(^a

)

=E

(−

^a

)

. In order to under- stand the effect of the “perturbation” V we consider the dis- cretizedversionofthisequation:x→^xn=

(

n+¹

/

2

)

x,

x=^L

/

N, n = −^N

, . . . ,

N −^{1. The} unperturbed eigenfunctions,

η

k

(

xn

)

=

δ

nk, correspond to local excitations at the k-th site. Discretiz- ing the integral in (48) one replaces the original eigenvalue problem (51) by the eigenvalue problem for the matrix Vnk=

δ

nkE

(

xn

)

−

xV

(

xn

,

xm

)

.SinceV

(

x

,

x

)

=^V

(

−^x

,

−^x

)

,alleigenstates have definite parity with respect to x→ −^{x; the double degen-} eracy is lifted and one can study x-even and x-odd eigenstates separately.Diagonalizing thismatrixnumericallywefindthatthe shiftof eigenvaluesas comparedto theunperturbed spectrumis surprisinglysmall,

δ

E=^E−E≤⁰

.

003, forall eigenstates except forthelowestone,cf.Fig. 1,andthecorrespondingeigenfunctions

η

k

(

xn

)

remainwelllocalizedaroundthepointx_k,seeFig. 2.Atthe sametimethelowestx-eveneigenstatechangesdrastically:Itbe- comes delocalized, seeFig. 2,andseparatedfrom therestof the spectrumbyafinitegap¹

E

=

^E0

−

⁰

.

3214

.

(52)

Inthecontinuumlimit

(

x→⁰

,

L→ ∞)^{thisphenomenoncanbe} understoodascreationofaboundstateinadditiontothecontin- uum spectrumthatremainstobe largelyunperturbed.The“wave function”ofthis(lowest)statecanbeapproximatedtoagoodac- curacy(betterthat1%for|^x|

<

3)bythefollowingexpression:

η

0

(

x

)

√

2E0

√

2

+

^x2

ρ (

x

)

[

E0

−

E

(

x

)] , η

0

(

0

) =

1

.

(53) ItcanbeconvenienttoexpandthisfunctioninHahnpolynomials

η

0

(

x

) =

^∞

n=⁰,2,...

χ

nH_n

(

x

),

(54)

wherethefirstfewcoefficientsread

χ

0

⁰

.

612

, χ

2

−

⁰

.

126

, χ

4

⁰

.

0574

,

χ

6

−

⁰

.

0338

, χ

8

⁰

.

0226

, χ

10

−

⁰

.

0163

.

(55) Thenormalizationisgivenby

∞

−∞

dx

2

π η

₀²

(

x

) =

^∞

n=⁰

n

χ

_n²

⁰

.

0758

.

(56)

Coming backtotherepresentationoftheDAintheform(47)we canseparatethecontributionofthediscrete(lowest)levelas

η

_Λ

(

s

,

x

, μ ) = ξ

0

(

s

, μ ) χ

₀⁻¹

η

0

(

x

) + η

_Λ

(

s

,

x

, μ ).

(57) wherethefunction

η

_Λ

(

s

,

x

, μ )

accountsforthecontributionofthe continuumspectrumandmustbeorthogonalto

η

0

(

x

)

,

dx

η

0

(

x

) η

_Λ

(

s

,

x

, μ ) =

0

.

(58)

Goingovertothemomentumspaceweobtainforthecontribution oftheloweststate(asymptoticDA)

f_Λ⁽¹⁾

( μ ) Ψ

_Λ⁽⁰⁾

( ω ,

u

; μ )

=

^f_Λ⁽¹⁾

( μ

0

) χ

₀⁻¹

ω

²uu

¯ μ

μ

0

₋₃⁸_β

0L

4

3β₀[^E0−_β0α⁴_s^π(μ₀)]

∞

−∞

dx 2

π η

0

(

x

)

×

∞ 0

sds

φ

s,x

( ω ,

u

)ξ

0

(

s

, μ

0

) μ

0s

s0

_3β⁸

0lnL

,

(59)

cf. Eq. (24). Note that the restriction to the contribution of the discrete level impliesa certain relation betweenthe momentum fractiondistribution betweenthe twolight quarksandtheir total momentum

ω

, the remaining freedom is encodedin the “profile function”

ξ

0

(

s

, μ

0

)

atthereferencescale,which canbe arbitrary.

Forthesimplestansatz

ξ

₀

(

s

, μ

₀

) =

^se−s0

,

(60)

1 Thesizeofthegapcoincideswiththegapinthespectrumofanomalousdimen- sionsofthree-light-quarkoperatorsinthelarge-Nlimit[7],indicatingthatthese problemsarerelated.Unraveling thisconnectiongoesbeyondthetasksofthislet- ter.