violation in baryon octet light-cone distribution amplitudes

JHEP05(2015)073

Published for SISSA by Springer Received: February 12, 2015 Accepted: April 23, 2015 Published:May 14, 2015

Model-independent calculation of SU(3)

violation in baryon octet light-cone distribution amplitudes

Philipp Wein and Andreas Sch¨afer

Institut f¨ur Theoretische Physik, Universit¨at Regensburg, Universit¨atsstraße 31, D-93040 Regensburg, Germany E-mail: philipp.wein@physik.uni-regensburg.de, andreas.schaefer@physik.uni-regensburg.de

Abstract: In this work we present a minimal parametrization of the light-cone distribu- tion amplitudes of the baryon octet including higher twist contributions. Simultaneously we obtain the quark mass dependence of the amplitudes at leading one-loop accuracy by the use of three-flavor baryon chiral perturbation theory (BChPT), which automatically yields model-independent results for the leading SU(3) flavor breaking effects. For that purpose we have constructed the nonlocal light-cone three-quark operators in terms of baryon octet and meson fields and have carried out a next-to-leading order BChPT calculation. We were able to find a minimal set of distribution amplitudes (DAs) that do not mix under chiral extrapolation towards the physical point and naturally embed the Λ baryon. Additionally they are chosen in such a way that all DAs of a certain symmetry class have a similar quark mass dependence (independent of the twist of the corresponding amplitude), which allows for a compact presentation. The results are well-suited for the extrapolation of lattice data and for model building.

Keywords: Higher Twist Effects, Effective field theories, Chiral Lagrangians ArXiv ePrint: 1501.07218

JHEP05(2015)073

Contents

1 Introduction 1

2 Fundamental definitions 4

3 Operator construction 5

3.1 Symmetry properties 6

3.2 Low energy operators 7

3.3 Symmetry under exchange of quark fields 10

3.4 Elimination of linearly dependent structures 12

4 Calculation at leading one-loop order 13

4.1 Meson masses and the Z-factor 13

4.2 Baryon-to-vacuum matrix elements of three-quark operators 15

4.3 Projection onto standard DAs 18

5 Results 19

5.1 General strategy and choice of distribution amplitudes 19 5.2 Minimal parametrization of baryon octet distribution amplitudes 22

5.3 Example of application 25

5.4 Dependence on the mean quark mass 31

6 Summary 32

A Loop contributions 33

B Handbook of distribution amplitudes 34

C Matching to other definitions in the literature 36

D Some construction details 36

E Matching relations 37

1 Introduction

Due to the unstable nature of the weakly decaying hyperons there are no scattering experi- ments with hyperons in the initial state. However, they naturally occur in the final state, for instance in baryon-antibaryon pair production via electron-positron annihilatione⁺e⁻ −→

BB, in deeply virtual exclusive meson electroproduction¯ γ^∗p −→ K⁺Λ, K⁺Σ⁰, K⁰Σ⁺, and in decays of heavy quarkonia to baryon-antibaryon pairs like J/Ψ, Υ −→ BB. The¯

JHEP05(2015)073

standard way to parametrize the nonperturbative information contained in such exclusive processes are (transition) generalized parton distributions or ordinary form factors. At high momentum transfer the contributions from Fock states containing more than the minimal number of partons are power-suppressed and the process can be approximated by a con- volution of the involved distribution amplitudes (DAs) with the process-dependent hard scattering kernel. The requirement of large momentum transfer, the instability of the final state hadrons and the fact that distribution amplitudes only occur in convolutions require high luminosity and high granularity detectors to extract information on the hyperon DAs from experiment.

Another type of process where hyperon DAs are involved are the exclusive rare decays of b-baryons, like Ξ_b, Λ_b, Σ_b and Ω_b, into octet baryons (plus γ, l⁺l⁻, . . . ). Due to the large mass difference one can hope that higher order Fock states are sufficiently suppressed to allow for a description by three-quark DAs. Since the bottom baryons are produced with increasing rates at LHC and at B-factories worldwide, we have to expect that ever more precise experimental results will be available in future, even for rare decays containing flavor-changing neutral currents, which are sensitive to new physics. Notwithstanding the fact that b-baryons are produced at much lower rates than b-mesons, they are not less interesting since they allow for an examination of the helicity structure of the b −→ s transition and thus complement the measurements in the meson sector [1]. As shown in refs. [2, 3] there are possible scenarios where deviations from the standard model are not seen in the branching ratio of Λ_b −→ Λl⁺l⁻ but only in the Λ baryon polarization. It is therefore mandatory to establish a theoretical basis for the description of such decays, and the knowledge of hyperon DAs is one important ingredient. Even the higher twist components can yield relevant contributions [4]. Note that constraining the shape of wave functions by calculating the moments of the DAs with lattice QCD plays an even more important role for hyperons than for nucleons, since experimental bounds are less strict than in the nucleon sector.

A first parametrization of the leading twist contributions in hyperon wave functions was already presented in ref. [5]. A complete parametrization (including all contributions from higher twist) of baryon-to-vacuum matrix elements was first performed for the case of the nucleon in ref. [6], where it turned out that higher twist contributions can yield substantial effects in the baryon sector, since the corresponding normalization constantsλ^N₁ andλ^N₂ are large compared to the leading twist wave function normalization constant f^N. The same procedure has later on been reused in refs. [7,8] to give similar parametrizations for matrix elements of the hyperons in the baryon octet, namely Σ^±, Σ⁰, Ξ⁻, Ξ⁰ and Λ. Our work unifies these different approaches and we find relations between the distribution amplitudes for different baryons even if SU(3)_f symmetry is broken. The obtained relations are exact including terms up to first order in the quark masses. In this sense we call our results model-independent. However, one should keep in mind that higher order contributions which lie beyond the accuracy of our analysis are model-dependent indeed, since they are affected by the neglection of higher order terms during operator construction and by the choice of the regularization scheme.

JHEP05(2015)073

As shown in refs. [7, 8] one has to introduce six additional DAs if one extends the formalism from the nucleon doublet to the complete baryon octet. Our results show that these additional DAs are determined by the eight independent DAs already known from the nucleon sector. I.e., if one knows the eight standard DAs (and their dependence on the mass splitting between light and strange quarks) for the Λ and for at least two types of octet baryons with nonzero isospin, one can predict all the rest. Using the parametrization given in refs. [9–11], where contributions of Wandzura-Wilczek type [12] are taken into account, and applying the approximation advocated in ref. [9], where contributions that can mix with four-particle operators are systematically neglected, we need only 43 parameters to describe the complete set of baryon octet DAs, including their dependence on the splitting between light and strange quark mass. For details see section 5.3. This amounts to a significant reduction of parameters compared to an ad hoc linear extrapolation without the knowledge of SU(3)_f symmetry breaking, which would require 72 parameters for the given setup. Therefore our results are useful for the extrapolation of lattice data. In a first step it can be checked whether the nontrivial relations between the different DAs that we have obtained are realised in lattice simulations. If this is the case to a satisfactory degree, one can perform a simultaneous fit to all DAs, which, owing to the significant reduction of parameters mentioned above, has much higher precision. Note that the parameters occurring in the approximation described above are determined by the zeroth, first and second moments of the leading twist DAs and by the zeroth and first moments of twist 4 DAs, which are, apart from the first moments of the higher twist amplitudes, within reach of state of the art lattice simulations (see ref. [13]).

Let us note that SU(3)_f breaking effects can be of considerable strength: e.g. sum rule estimations of the symmetry breaking for leading twist wave function normalization constants range from ∼ 10%, see ref. [5], to ∼ 50%. The latter is obtained if one takes the values for f^Σ and f^Ξ from refs. [7,8]. In ref. [5] it is stated that the impact on the shape of the wave function is even larger (at a scale of 1 GeV). One therefore has to expect substantial effects also at intermediate scales which are relevant for phenomenolog- ical computations. We expect lattice QCD calculations to provide quantitative results for SU(3)_f breaking effects at physical mean quark mass in the near future. These will provide the means to determine the strength of the symmetry breaking terms in our formalism, allowing us to draw more definite conclusions.

At this point we want to highlight a conclusion that can be drawn from our results, which is of conceptual importance and also affects the nucleon sector: we find that the nonanalytic chiral behaviour of moments of DAs does not depend on the twist of the amplitude. Instead, the leading chiral logarithms in the chiral-odd sector are determined by the type of amplitude to which the corresponding moment contributes. The ones occurring in Φ^B_+,i(Φ^B_−,i) amplitudes, which will be defined in eq. (5.7), have the same chiral logarithms asf^B (λ^B₁). The odd moments of the leading twist DA therefore behave likeλ^B₁ instead of f^B, which is quite contrary to the intuitional expectation. The shape parameters occurring in ref. [9] can all be assigned uniquely to one of the two classes, which means that the destinction between moments described above is to some extent already present in currently used parametrizations.

JHEP05(2015)073

This work is organized as follows: in section2we present some fundamental definitions to lay the base for the parametrization of the nonlocal three-quark operators in terms of baryon and meson fields, which is performed in section3. A sketch of the leading one-loop baryon chiral perturbation theory (BChPT) calculation is given in section 4, where we also explain how we have matched our results to the standard DAs given in ref. [6]. In section 5 we present our main results. We provide a definition for DAs that do not mix under chiral extrapolation and naturally embed the Λ baryon. The result section is to the most part self-contained such that the reader can skip the details of the derivation at will.

We summarize in section 6.

2 Fundamental definitions

There exist various possible realizations of chiral symmetry, which all lead to equal results.

In the following we only present the definitions we use in this work. For a detailed treatment of the effective field theory framework we refer to [14–19]. The pseudoscalar fields are contained in

u=√

U = exp i

2F₀λ^aφ^a

= exp i

2F₀φ

, (2.1)

where λ¹, . . . , λ⁸ are Gell-Mann matrices and F0 is the pion decay constant in the three- flavor chiral limit, which corresponds to the convention whereF_π =F₀+O(m²_π, m²_K, m²_η)≈ 92 MeV. The matrixφcan be written in terms of meson fields

φ=√ 2







√1

2π⁰+ ^√1

6η π⁺ K⁺

π⁻ −^√1₂π⁰+^√1

6η K⁰ K⁻ K⁰ −^√2₆η





 . (2.2)

The 3×3 matrix B contains the baryon octet:

B =







√1

2Σ⁰+√¹

6Λ Σ⁺ p

Σ⁻ −^√1₂Σ⁰+√¹

6Λ n

Ξ⁻ Ξ⁰ −^√2₆Λ







≡κ_pp+κ_nn+κ_Σ⁻Σ⁻+κ_Σ⁰Σ⁰+κ_Σ⁺Σ⁺+κ_Ξ⁻Ξ⁻+κ_Ξ⁰Ξ⁰+κ_ΛΛ,

(2.3)

where the second line defines the matricesκ_B. Let us from now on useX ∈ {L, R}and, as a convenient notation, ¯L=R and ¯R =L. Where they are not used as an index, Land R are meant to be elements of SU(3)_L/R. Defining u_R =u and u_L= u^† the transformation properties of meson and baryon fields under chiral rotations read

u_X −→^χˆ Xu_XK^†=Ku_XX¯^†, (2.4a)

B −→^χˆ KBK^†, (2.4b)

with the so-called compensator fieldK, which is a common, nonlinear realization of chiral symmetry [17,20]. The covariant derivative acting on a baryon field is defined as

D_µB =∂_µB+ [Γ_µ, B], (2.5)

JHEP05(2015)073

Γ η_Γ^P η^C_Γ η_Γ^h η_Γ⁵

1 1 −1 1 1

γ₅ −1 −1 −1 1

γ_µ (−1)_µ 1 1 −1

γ_µγ₅ −(−1)_µ −1 1 −1 σµν (−1)µ(−1)ν 1 1 1

Table 1. The constantsηΓ^P,η^CΓ,η^hΓ andη⁵Γcharacterizing the symmetry properties of the elements of the Clifford algebra, where (−1)µ is 1 forµ= 0 and−1 forµ= 1,2,3.

where Γµis called the chiral connection and is given by Γ_µ= 1

2 u^†∂_µu+u∂_µu^†

. (2.6)

The chiral vielbein u_µ and the quark mass insertionsχ_± are defined as u_µ=i u^†∂_µu−u∂_µu^†

, (2.7a)

χ_±=u^†χu^†±uχ^†u , (2.7b)

whereχ= 2B₀Mincludes the quark mass matrix, and transform under chiral rotations as follows:

u_µ−→^χˆ Ku_µK^†, (2.8a)

χ_±−→^χˆ Kχ_±K^† . (2.8b)

Finally we define for the elements of the Clifford algebra in a unitary representation

Γ =η^P_Γγ₀Γγ₀, (2.9a)

Γ^T =η^C_ΓCΓC , (2.9b)

Γ^†=η^h_Γγ0Γγ0, (2.9c)

Γ =η⁵_Γγ₅Γγ₅, (2.9d)

whereC=iγ²γ⁰is the charge conjugation matrix. The differentη’s are collected in table1.

3 Operator construction

In this section we will construct the light-cone (n is a lightlike four-vector) three-quark operator

q_α^a(a1n)q^b_β(a2n)q^c_γ(a3n), (3.1) in terms of baryon octet and meson octet fields. The antisymmetrization in color indices (which makes the operator a color singlet) and the Wilson lines connecting the quark fields (providing gauge invariance) are not written out explicitly. a, b, c are flavor and α, β, γ

JHEP05(2015)073

Dirac indices. Note that there are many possible parametrizations owing to the freedom of choice one has by neglecting higher order effects. The task is therefore not only to find a parametrization, but to find one that is most convenient for the loop calculation to be performed and can be easily matched to the standard decomposition given in ref. [6]. For the parametrization of the nonlocal operator one needs functions, where the moments of the functions play the role of low energy constants (LECs). For the parametrization presented below these functions can be easily matched to standard distribution amplitudes.

3.1 Symmetry properties

To perform the construction of an operator within the effective theory we have to know its symmetry properties. To make use of chiral symmetry it is convenient to split the quark fields in left- and right-handed parts

q^a_α(a1n)q_β^b(a2n)q_γ^c(a3n) =ORR,αβγ^abc (a1, a2, a3) +O^abcLL,αβγ(a1, a2, a3) +O^abcRL,αβγ(a1, a2, a3) +OLR,αβγ^abc (a1, a2, a3) +O^cabRL,γαβ(a₃, a₁, a₂) +OLR,γαβ^cab (a₃, a₁, a₂) +O^bcaRL,βγα(a₂, a₃, a₁) +OLR,βγα^bca (a₂, a₃, a₁),

(3.2)

where the operators OXY forX,Y ∈ {L, R}are given by

O^abcXY,αβγ(a1, a2, a3) =q_X,α^a (a1n)q^b_X,β(a2n)q_Y,γ^c (a3n), (3.3) where the left-/right-handed quark fields are defined as q_L/R=γ_L/Rq with the projection matricesγ_L/R= (1∓γ₅)/2. These operators can be characterized by their transformation properties under parity transformation (ˆp), charge (ˆc) and hermitian (†) conjugation and chiral rotations ( ˆχ):

O^abcXY,αβγ(a₁, a₂, a₃)−→^pˆ (γ₀)_αα^′(γ₀)_ββ^′(γ₀)_γγ^′OX^abc¯Y ,α¯ ^′β^′γ^′(a₁, a₂, a₃), (3.4a) O^abcXY,αβγ(a₁, a₂, a₃)^ˆc−→ −^†pˆ C_αα^′C_ββ^′C_γγ^′OXY,α^{abc ′}β^′γ^′(a₁, a₂, a₃), (3.4b) O^abcXY,αβγ(a₁, a₂, a₃)−→^χˆ X_aa^′X_bb^′Y_cc^′O^aXY,αβγ^′b′c′ (a₁, a₂, a₃), (3.4c) where in eq. (3.4b) charge conjugation is performed first. Additionally we know that each operator transforms under a translation in n-direction as

OXY,αβγ^abc (a1+δa, a2+δa, a3+δa) = expn

i δa n·Pˆo

OXY,αβγ^abc (a1, a2, a3) expn

−i δa n·Pˆo , (3.5) where ˆP is the momentum operator which acts as a generator of translations. Another symmetry of the three-quark operators defined in eq. (3.3) is the invariance under the exchange of the quark in the first and the second position or even an invariance under exchange of all three quarks in case of the operators containing right-handed or left-handed fields exclusively. On top of this the operator is invariant if one simultaneously rescales ai−→λai and nµ−→nµ/λ, which we will call scaling property.

JHEP05(2015)073

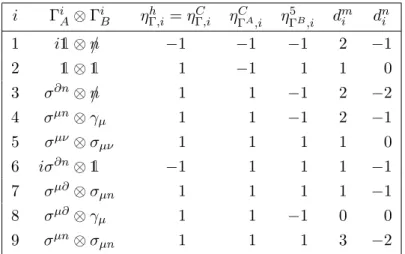
i Γⁱ_A⊗Γⁱ_B η_Γ,i^h =η^C_Γ,i η_Γ^CA,i η_Γ⁵B,i d^m_i dⁿ_i

1 i1⊗n/ −1 −1 −1 2 −1

2 1⊗1 1 −1 1 1 0

3 σ^∂n⊗n/ 1 1 −1 2 −2

4 σ^µn⊗γ_µ 1 1 −1 2 −1

5 σ^µν⊗σµν 1 1 1 1 0

6 iσ^∂n⊗1 −1 1 1 1 −1

7 σ^µ∂⊗σµn 1 1 1 1 −1

8 σ^µ∂⊗γ_µ 1 1 −1 0 0

9 σ^µn⊗σ_µn 1 1 1 3 −2

Table 2. List of Γⁱ_A⊗Γⁱ_B. η^PΓ,i = 1 by choice (see comment in the text). We have multiplied structures 1 and 6 with a factor ofi such thatη^hΓ,i =ηΓ^C,i for all structures and, thus,ηΓ^{hP C},i = 1.

In cases where four-vectors are used in the place of Lorentz indices the notation means that the corresponding Lorentz index is contracted with the index of the vector; e.g.σ^∂n=σ^µν∂µnν.

3.2 Low energy operators

Using the previously defined fields u_R and u_L we can write down the operators, which contribute to baryon-to-vacuum matrix elements of three-quark currents at leading one- loop level and have correct transformation properties under chiral rotations in the following compact form:

OXY,αβγ^abc (a₁, a₂, a₃) = Z

[dx]X

i,j kj

X

k=1

FXY^i,j,k(x₁, x₂, x₃) Γ^i,XXY_αβγδ B_δ,abc^j,k,XXY(z), (3.6) where the correct transformation behaviour under translations inn-direction is ensured by z_µ=n_µP

x_ia_i and the constraint that x₁+x₂+x₃ = 1 in Z

[dx] = Z

dx₁dx₂dx₃δ 1−X x_i

, (3.7)

where the integrations run from 0 to 1. The F’s are functions ofx1,x2,x3 only and kj is given in table 3. The Γ’s are defined as

Γ^{i,XY Z}_αβγδ = (γXΓⁱ_AγYC)αβ(γZΓⁱ_B(i /∂)^dmi )γδ(n·∂)^dni , (3.8) where Γⁱ_A, Γⁱ_B,d^m_i and dⁿ_i can be taken from table 2. The occurring derivatives act on the B’s. We have introduced adequate powers ofi /∂ to have functionsF of mass dimension 2, which is compatible with the standard mass dimension of distribution amplitudes. Using i /∂ (which leads to a factor m_B in the final result) instead of the baryon mass in the chiral limitm₀ (which would be the standard choice) has the advantage that it allows for a straightforward matching of our parametrization to the general decomposition given in ref. [6] and to refs. [7,8] (see also section4.3). The power of (n·∂) is chosen such that the scaling property is fulfilled. Note that in the chiral-odd sector one can actually write down

JHEP05(2015)073

j B^j_1,δ B₂^j B₃^j trace^j kj

1 B_δ 1 1 1 3

2 B_δ 1 1 tr{χ₊}m⁻₀² 3

3 B_δ χ˜+m⁻₀² 1 1 6

Table 3. In this table we list only terms which contribute to the one-loop calculation of baryon- to-vacuum matrix elements of the operator. ˜χ+ is defined asχ+−tr{χ+}/3. This is a convenient choice since this combination (in a leading one-loop calculation) vanishes along the symmetric line, wheremu=md=ms.

more structures, which have the form Γ^{i,XY X}_βγαδ or Γ^{i,Y XX}_γαβδ . However, these structures are not independent. They can be rewritten in terms of Γ^i,XXY_αβγδ using Fierz transformation.

In order to reduce the Γ’s to the minimal set given in table 2 one has to use the identity σ^µνγ₅ = ₂ⁱε^µνρσσ_ρσ and the fact that it is sufficient to construct structures of positive parity (see explanation below eq. (3.15)). Additionally one has to use that multiplying both structures Γⁱ_Aand Γⁱ_B with aγ₅ does not lead to a new, independent structure owing to the projection withγ_L/R in eq. (3.8).

The B’s in eq. (3.6) are defined as

B_δ,abc^{j,k,XY Z} = (u_X)_aa^′(u_Y)_bb^′(u_Z)_cc^′B_δ,a^j,k′b^′c^′, (3.9) where

B_δ,abc^j,1 = (B^j_1,δ)_aa^′(B₂^j)_bb^′(B₃^j)_cc^′ε_a^′_b^′_c^′×trace^j, (3.10a) B_δ,abc^j,2 = (B^j₃)_aa^′(B_1,δ^j )_bb^′(B₂^j)_cc^′ε_a^′_b^′_c^′×trace^j, (3.10b) B_δ,abc^j,3 = (B^j₂)_aa^′(B₃^j)_bb^′(B^j_1,δ)_cc^′ε_a^′_b^′_c^′×trace^j, (3.10c) B_δ,abc^j,4 = (B^j₂)_aa^′(B_1,δ^j )_bb^′(B₃^j)_cc^′ε_a^′_b^′_c^′×trace^j, (3.10d) B_δ,abc^j,5 = (B^j_1,δ)_aa^′(B₃^j)_bb^′(B₂^j)_cc^′ε_a^′_b^′_c^′×trace^j, (3.10e) B_δ,abc^j,6 = (B^j₃)_aa^′(B₂^j)_bb^′(B^j_1,δ)_cc^′ε_a^′_b^′_c^′×trace^j . (3.10f) For cases whereB₂^j =B₃^jwe only useB_δ,abc^j,1 ,B_δ,abc^j,2 andB^j,3_δ,abcand thuskj = 3. The different possible combinations ofB’s can be taken from table3. All baryon and meson fields which are connected to each other (by a summation over a shared flavor index) have to be at the same spacetime position, owing to the fact that the compensator field K is a local transformation. However, chiral symmetry actually also allows for the possibility that the trace term inB is situated at a different spacetime position as the rest of the operator. We consider this possibility in appendixDand show that such a parametrization only differs in higher order terms. Note that no structures of the form [B_δ,χ˜₊], {B_δ,χ˜₊}, or tr{B_δχ˜₊} occur in table 3, since they can be reexpressed in terms of the third structure, which means that we have only one second order structure (j= 3) that is responsible for SU(3)_f breaking. Also the operators which describe the behaviour along the SU(3)_f symmetric line (j = 1,2) are not linearly independent, but the situation is more complicated in this

JHEP05(2015)073

case: since operators of the same class (i.e. samejbut differentk) are related to each other (see eq. (3.30)) one has to take care that the symmetry properties of the operator under quark exchange are respected. Therefore, we postpone this discussion to section 3.4.

There are no covariant derivatives acting on the baryon field within the B’s. In ap- pendix D we show that they can always be traded for derivatives acting on the whole structure plus higher order contributions, which can be neglected. This fact will turn out to be very convenient for calculating loop contributions, since the derivatives acting on the complete structure do not lead to additional loop momenta in the integrals.

The effective operator given in eq. (3.6) already transforms correctly under chiral ro- tations and translations along the light-cone vectorn. It also fulfills the scaling property.

The remaining symmetry properties given in section 3.1will now be implemented by con- straining the functionsF. We consider

B_δ,abc^{j,k,XY Z} −→^pˆ (γ0)_δδ^′B^j,k,_δ′,abc^X¯Y¯Z¯, (3.11a) B_δ,abc^{j,k,XY Zˆc}−→ −^†pˆ C_δδ^′B_δ^{j,k,XY Z}′,abc , (3.11b) and

Γ^{i,XY Z}_αβγδ −→ −^pˆ η_Γ,i^P (γ0)_αα^′(γ0)_ββ^′(γ0)_γγ^′ Γ^i,_α^X′^¯β^Y′¯γ^Z′¯δ^′ (γ0)_δ^′_δ, (3.12a) Γ^{i,XY Z}_αβγδ ^ˆc−→ −^†pˆ η_Γ,i^{hP C} C_αα^′C_ββ^′C_γγ^′ Γ^{i,XY Z}_α′β^′γ^′δ^′ C_δ^′_δ . (3.12b) Eqs. (3.11b) and (3.12b) yield (together with eqs. (3.4b) and (3.6) and since η_Γ^{hP C} = 1)

FXY^i,j,k

_∗

=FXY^i,j,k, (3.13)

which would mean that the F’s are real-valued. However this argument relies on the assumption that one gets no additional phases from charge conjugation of quarks and baryons, which is not necessarily true. If we allow for such additional phases the above equation has to be generalized to

F_XY^i,j,ke^iθ_∗

=F_XY^i,j,ke^iθ, (3.14)

where we have an additional overall phase which is equal for all distribution amplitudes.

However, this additional phase is unphysical and can be dropped. Eqs. (3.11a) and (3.12a) yield (together with eqs. (3.4a) and (3.6) and sinceη_Γ^P = 1)

FX^i,j,k¯Y¯ =−F_XY^i,j,k . (3.15) Therefore we only have to differentiate between chiral-even F_RR^i,j,k = −F_LL^i,j,k ≡ Feven^i,j,k and chiral-oddF_LR^i,j,k =−F_RL^i,j,k ≡ F_odd^i,j,k. Notice that we have chosen to only construct structures Γ_A⊗Γ_B which have positive parity. The negative parity structures, which one can obtain by multiplying all Γ_B with a γ₅, would lead to the same operators since eq. (3.15) then would yield an extra minus sign.

JHEP05(2015)073

3.3 Symmetry under exchange of quark fields

In this section we use the symmetry of the original three-quark operators under exchange of quark fields with the same handedness to reduce the number of amplitudes. Using the constraint that the operators have to be equal under exchange of the first and the second quark yields

j= 1,2: FXY^i,j,1(x1, x2, x3) =−η_Γ^CA,iFXY^i,j,2(x2, x1, x3), (3.16a) F_XY^i,j,3(x₁, x₂, x₃) =−η_Γ^CA,iF_XY^i,j,3(x₂, x₁, x₃), (3.16b) j= 3: FXY^i,3,1(x₁, x₂, x₃) =−η_Γ^CA,iFXY^i,3,4(x₂, x₁, x₃), (3.16c) F_XY^i,3,2(x₁, x₂, x₃) =−η_Γ^CA,iF_XY^i,3,5(x₂, x₁, x₃), (3.16d) F_XY^i,3,3(x₁, x₂, x₃) =−η_Γ^CA,iF_XY^i,3,6(x₂, x₁, x₃) . (3.16e) In the chiral-odd sector one now uses these relations to eliminate FXY^i,j,2 (if j = 1,2) and FXY^i,3,4/5/6. Additionally we can use that

(γ_YΓ_Aγ_XC)_γβ(γ_XΓ_B)_αδ = 0, ifX 6=Y and Γ_A∈ {1, γ₅, σ_µν} . (3.17) Using Fierz transformation this leads to

Γ^3,XXY_αβγδ = Γ^4,XXY_αβγδ + 1

2Γ^9,XXY_αβγδ , (3.18a)

Γ^5,XXY_αβγδ = 0, (3.18b)

Γ^6,XXY_αβγδ = Γ^4,XXY_αβγδ −Γ^7,XXY_αβγδ , (3.18c) ifX6=Y. Therefore we have the freedom to choose

Fodd^3,j,k(x1, x2, x3) =Fodd^5,j,k(x1, x2, x3) =Fodd^6,j,k(x1, x2, x3) = 0 . (3.19) In the chiral-even sector the projection with γ_L/R leads to similar constraints. The coun- terpart of eq. (3.17) reads

(γ_XΓ_Aγ_XC)_γβ(γ_XΓ_B)_αδ = 0, if Γ_A∈ {γ_µ, γ_µγ₅} . (3.20) With a Fierz transformation one obtains

Γ^7,XXX_αβγδ =−Γ^4,XXX_αβγδ +1

2Γ^5,XXX_αβγδ + Γ^6,XXX_αβγδ , (3.21a) Γ^8,XXX_αβγδ =−1

4Γ^5,XXX_αβγδ , (3.21b)

Γ^9,XXX_αβγδ = 0 . (3.21c)

Therefore, we can choose

Feven^7,j,k(x₁, x₂, x₃) =Feven^8,j,k(x₁, x₂, x₃) =Feven^9,j,k(x₁, x₂, x₃) = 0 . (3.22)

JHEP05(2015)073

The operators containing left-/right-handed quarks exclusively also have to be invariant under an exchange of the first and the last quark. Performing a Fierz transformation and using the identities given above we find

Γ^i,XXX_γβαδ =

6

X

i^′=1

Γⁱ_αβγδ^′,XXXc^i′i . (3.23)

The matrix cis given by

c=



















1

2 0 −¹₂ −³₂ 0 −¹₂ 0 ¹₂ 0 0 6 −¹₂

0 0 1 0 0 0

−¹₂ 0 −¹₂ −¹₂ 0 −¹₂ 0 ¹₈ 0 0 −¹₂ ¹₈

0 0 0 0 0 1



















. (3.24)

By the use of this relation the symmetry property of the operator under exchange of the first and the last quark translates to the following constraints on the amplitudes:

j= 1,2: F_XX^i,j,1(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,j,3(x₃, x₂, x₁), (3.25a)

FXX^i,j,2(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′FXX^i′,j,2(x₃, x₂, x₁), (3.25b)

F_XX^i,j,3(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,j,1(x₃, x₂, x₁), (3.25c)

j= 3: F_XX^i,3,1(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,3,6(x₃, x₂, x₁), (3.25d)

FXX^i,3,2(x1, x2, x3) =−

6

X

i^′=1

c^ii′FXX^i′,3,4(x3, x2, x1), (3.25e)

F_XX^i,3,3(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,3,5(x₃, x₂, x₁), (3.25f)

FXX^i,3,4(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′FXX^i′,3,2(x₃, x₂, x₁), (3.25g)

F_XX^i,3,5(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,3,3(x₃, x₂, x₁), (3.25h)

FXX^i,3,6(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′FXX^i′,3,1(x₃, x₂, x₁) . (3.25i)

JHEP05(2015)073

Using these equations one finds for the operator with j = 3 that one can eliminate all amplitudes apart fromFXX^i,3,1, by using the following relations recursively:

FXX^i,3,2(x1, x2, x3) =η^C_ΓA,i 6

X

i^′=1

c^ii′FXX^i′,3,3(x3, x1, x2), (3.26a)

F_XX^i,3,3(x₁, x₂, x₃) =η^C_ΓA,i 6

X

i^′=1

c^ii′F_XX^i′,3,1(x₃, x₁, x₂), (3.26b) FXX^i,3,4(x1, x2, x3) =−η_Γ^CA,iFXX^i,3,1(x2, x1, x3), (3.26c) F_XX^i,3,5(x₁, x₂, x₃) =−η_Γ^CA,iF_XX^i,3,2(x₂, x₁, x₃), (3.26d) FXX^i,3,6(x₁, x₂, x₃) =−η_Γ^CA,iFXX^i,3,3(x₂, x₁, x₃), (3.26e) For the operators withj = 1,2 we can eliminate

FXX^i,j,2(x₁, x₂, x₃) =−η_Γ^CA,iFXX^i,j,1(x₂, x₁, x₃), (3.27a) F_XX^i,j,3(x₁, x₂, x₃) =−

6

X

i^′=1

c^ii′F_XX^i′,j,1(x₃, x₂, x₁), (3.27b)

and additionally

F_XX^1,j,1(x₁, x₂, x₃) =F_XX^3,j,1(x₁, x₂, x₃) +F_XX^4,j,1(x₁, x₂, x₃)−2F_XX^4,j,1(x₁, x₃, x₂) +FXX^6,j,1(x1, x2, x3),

(3.28a) F_XX^2,j,1(x₁, x₂, x₃) =−4F_XX^5,j,1(x₁, x₂, x₃) + 8F_XX^5,j,1(x₁, x₃, x₂) +F_XX^6,j,1(x₁, x₂, x₃), (3.28b) FXX^3,j,1(x1, x2, x3) =−FXX^3,j,1(x1, x3, x2), (3.28c) F_XX^6,j,1(x₁, x₂, x₃) =−F_XX^6,j,1(x₁, x₃, x₂) . (3.28d) From the fact that the local operator at the origin, where a₁ = a₂ = a₃ = 0, is indepen- dent of the light-cone vector n one can deduce constraints for the zeroth moments of the distribution amplitudes

Z

[dx]FXY^i,j,k(x1, x2, x3) = 0, fori= 1,3,4,6,7,9 . (3.29) 3.4 Elimination of linearly dependent structures

To avoid overparametrization we will now annihilate linearly dependent structures of those given in table 3. Considering all possible three-quark operators and all baryons from the octet, one finds (for j = 1,2) that only two out of the three structures B_δ,abc^j,1 , B_δ,abc^j,2 and B_δ,abc^j,3 are linearly independent, since one has

0 =B_δ,abc^j,1 +B_δ,abc^j,2 +B_δ,abc^j,3 . (3.30)

JHEP05(2015)073

In the chiral-odd sector we can use this relation to replaceB_δ,abc^j,3 =−B_δ,abc^j,1 −B_δ,abc^j,2 , which is equivalent to the replacement

F_odd^i,j,1(x₁, x₂, x₃)−→F˜_odd^i,j,1(x₁, x₂, x₃)≡ F_odd^i,j,1(x₁, x₂, x₃)− F_odd^i,j,3(x₁, x₂, x₃), (3.31a) Fodd^i,j,2(x₁, x₂, x₃)−→F˜odd^i,j,2(x₁, x₂, x₃)≡ Fodd^i,j,2(x₁, x₂, x₃)− Fodd^i,j,3(x₁, x₂, x₃), (3.31b) F_odd^i,j,3(x₁, x₂, x₃)−→F˜_odd^i,j,3(x₁, x₂, x₃)≡0 . (3.31c) Using eqs. (3.16a) and (3.16b) one finds that the new functions have the same symmetry properties as the old ones. Therefore we can choose

F_odd^i,j,3(x₁, x₂, x₃) = 0, j= 1,2, (3.32) in accordance with symmetry properties and without loss of generality. In the chiral- even sector the situation is different since the amplitudes are already constrained by the symmetry under exchange of the first and the third quark. An elimination of one structure in favor of the two others would therefore not lead to a simplification. Instead one just obtains a reparametrization of the problem for which it would be hard to implement the symmetry properties under exchange of the first and the last quark.

4 Calculation at leading one-loop order

In this section we describe the leading one-loop calculation. In section4.3 we explain how we have matched to the standard DAs defined in ref. [6].

4.1 Meson masses and the Z-factor

We work in the limit of exact isospin symmetry, wherem_u=m_d≡m_l. Using the standard leading order meson Lagrangian (see e.g. [16, 21]) one finds for the meson masses the standard Gell-Mann-Oakes-Renner relations

m²_π = 2B₀m_l=m²_i=1,2,3 = 2B₀( ¯m_q−δm_l), (4.1a) m²_K =B₀(m_l+m_s) =m²_i=4,...,7=B₀(2 ¯m_q+δm_l), (4.1b)

m²_η = B₀

3 (2m_l+ 4m_s) =m²_i=8= 2B₀( ¯m_q+δm_l), (4.1c) where

¯ m_q = 1

3(2m_l+m_s), (4.2a)

δm_l = ¯m_q−m_l, (4.2b)

and B0 is the LEC proportional to the quark condensate in the chiral limit. As additional ingredient we need the first order meson-baryon Lagrangian, which we take from ref. [22]

(this version differs from refs. [18,21] by a minus sign in the terms containingD andF in order to be consistent with the standard sign convention gA≈D+F >0):

L⁽¹⁾

M B = trBγ¯ _µiD^µB −m₀trBB¯ +D

2 trBγ¯ _µγ₅{u^µ, B} +F

2 trBγ¯ _µγ₅[u^µ, B] . (4.3)

JHEP05(2015)073

p p

2

(a)

p p

1 1

p−q q

(b)

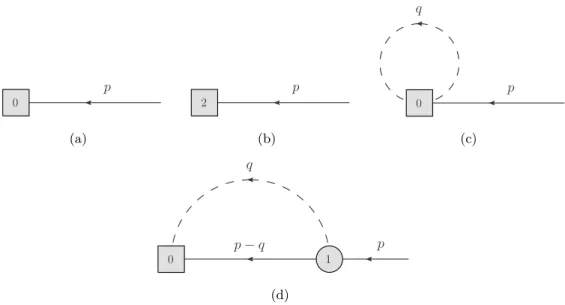
Figure 1. Feynman diagrams needed for the calculation of the self-energy.

For our calculation we need the baryon-meson-baryon vertex for an incoming baryon B, an outgoing baryon B^′ and an incoming meson (the k-th one in the Cartesian basis) with momentum q, which is given by

−1

2F0/qγ5trn

κ^T_B′(D{λ^k, κ_B}+F[λ^k, κ_B])o

. (4.4)

The self-energy to third chiral order is given by the sum of the irreducible diagrams shown in figure1(where external legs are to be amputated) multiplied with ani. The contribution of diagram(b)(in figure1), which is relevant for the calculation of theZ-factor is given by i×(b)= 3gB,πf(mπ, m0, /p) + 4gB,Kf(mK, m0, /p) +gB,ηf(mη, m0, /p), (4.5) where

f(m, m₀, /p) = −1

4F₀² (p²−m²₀)/pI₁₁⁽¹⁾(m, m₀, /p) + (/p+m₀) I₀₁(m₀, /p)−m²I₁₁(m, m₀, /p) . (4.6) The loop functionsI_kl and I_kl⁽¹⁾ are defined as in ref. [23] and the coefficients are given by

g_N,π = (D+F)², g_N,K = 5

6D²−DF +3

2F², g_N,η= 1

3(D−3F)², g_Σ,π= 4

9(D²+ 6F²), g_Σ,K =D²+F², g_Σ,η= 4 3D², g_Ξ,π= (D−F)², g_Ξ,K = 5

6D²+DF +3

2F², g_Ξ,η= 1

3(D+ 3F)², gΛ,π= 4

3D², gΛ,K = 1

3(D²+ 9F²), gΛ,η= 4

3D² . (4.7) These constants fulfill the constraints that the sums

3gB,π+ 4gB,K+gB,η= 4

3(5D²+ 9F²), (4.8a) 2g_N,M + 3g_Σ,M+ 2g_Ξ,M+g_Λ,M = 4

3(5D²+ 9F²), (4.8b) are independent of the baryon/meson species. This yields similar baryon masses and Z- factors along the line of equal quark masses and is a consequence of SU(3)_f symmetry. For