MARTIN-LUTHER-UNIVERSITÄT HALLE-WITTENBERG
Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Statistik
Prof. Dr. Claudia Becker
Wintersemester 2005/06 1. Termin
Klausur Anwendungsprojekte
über
Regressionsanalyse
„Einflussgrößen auf den Benzinverbrauch“
08.02.2006
Name: ...
Matrikelnummer: ...
Inhaltsverzeichnis
1. Einleitung ... 1
2. Problemstellung ... 1
3. Theoretische Grundlagen der statistischen Verfahren ... 3
3.1 Deskriptive Verfahren ... 3
3.2 Zusammenhangsanalyse / Regressionsanalyse ... 5
4. Statistische Auswertung ... 10
Abkürzungsverzeichnis ... 19
Literaturverzeichnis ... 20
Anhang ... 21
1. Einleitung
Vor dem Hintergrund einer Vielzahl von Naturkatastrophen in den letzten Jahren und einer zunehmenden ökologischen Sensibilisierung der Bevölkerung gewinnt der Begriff Nachhaltigkeit in der Ökonomie eine immer größere Bedeutung. Bei vielen Unternehmen stellt Nachhaltigkeit mittlerweile einen Bestandteil des Zielsystems und den Ausgangspunkt der Planungen dar. Demnach müssen nachhaltige Produktionsprozesse und Produkte so beschaffen sein, dass der Ressourcenverbrauch und die mit der Produktion/Nutzung verbundenen Emissionen den Lebensstandard bzw. die Existenz nachfolgender Generationen nicht beeinflussen.
Insbesondere die Automobilindustrie hat daher in den letzten Jahren eine Vielzahl von Anstrengungen unternommen, um den Kraftstoffverbrauch und den Abgasausstoß ihrer Produkte zu reduzieren. Einen der ersten Ausgangspunkte dieser Nachhaltigkeitsbemühungen der Automobilindustrie könnte die in diesem Bericht zu analysierende Studie aus den 70er Jahren dargestellt haben. Aufgabe dieser Arbeit ist es, auf Basis dieser Studie die wesentlichen Einflussfaktoren auf den Benzinverbrauch zu ermitteln. Ebenso wird geklärt, wie stark sich diese Faktoren auf den Verbrauch auswirken und wie sich der Verbrauch ändert, wenn die Ausprägungen dieser Faktoren variiert werden. Folglich besteht das Ziel darin, ein Regressionsmodell zu erstellen, welches den funktionalen Zusammenhang zwischen den Faktoren und dem Verbrauch beschreibt. Dazu werden in den folgenden Kapiteln die Grundlagen der Regression erläutert und die Studie mit diesem Instrumentarium ausgewertet.
2. Problemstellung
Um den Zusammenhang zwischen den möglichen Einflussfaktoren und dem Benzinverbrauch zu ermitteln, wurden im Jahr 1975 für den US- amerikanischen PKW-Markt durch das Unternehmen „Motor Trend“
markenübergreifend folgende Fahrzeugdaten von den 30 populärsten bzw.
meistverkauften Automodellen erhoben:1 a) Benzinverbrauch [Gallonen/Meile],
1 Vgl. Peck, E.A. (1982): Introduction to Linear Regression Analysis.
b) Hubraum [Kubikzoll], c) Leistung [PS],
d) Länge [Zoll], e) Gewicht [Pfund].
Über die Art und Dauer der Datenerhebung werden keine Angaben gemacht.
Es ist aber davon auszugehen, dass die Variablen b)-e) über Sekundärerhebungen ermittelt wurden, die Erhebung der Variable a) jedoch über groß angelegte und standardisierte Fahrzeugtests der betreffenden Automodelle erfolgte. Letztendlich wurden die Daten soweit verdichtet, dass je Automodell nur noch 5 Merkmale mit je einer (durchschnittlichen) Ausprägung zu analysieren sind. Die Genauigkeit der Merkmalserhebung kann allerdings nicht beurteilt werden. Der Datensatz weist keine fehlenden Werte auf.
Die Variablen verfügen alle über metrisches Skalenniveau. Da die mögliche Bildung von Quotienten je Merkmal zu keinen interpretierbaren Ergebnissen führt, liegt intervallskaliertes Datenmaterial zu Grunde.
Obwohl sich diese Studie auf die 30 meistverkauften PKW-Typen mit Ottomotor beschränkt2 und die Dieselmodelle unberücksichtigt bleiben, kann die Studie als repräsentativ für das Jahr 1975 angesehen werden.
Die Daten konnten unter Anwendung der folgenden amtlichen Umrechnungsregeln in europäische Maßeinheiten umgewandelt werden:
• 1 Gallone = 3.78609 Liter,
• 1 Meile = 1.609344 km,
• 1 Zoll = 2.54 cm,
• 1 Pfund = 0.4536 kg.
Damit erfolgt die Analyse der Variablen im Bericht in folgenden Einheiten:
a) Benzinverbrauch [Liter/100km],
b) Hubraum [1000 Kubikzentimeter; 1000 ccm ],
2 Diese 30 PKW-Typen sind: Apollo, Omega, Nova, Monarch, Duster, Jenson, Skyhawk, Monza, Scirocco, Corolla SR-5, Camaro, Datsun B210, Capri II, Pacer, Bobcat, Granada, Eldorado, Imperial, Nova LN, Valiant, Starfire, Cordoba, Corolla E-5, Mark IV, Celica GT, Charger SE, Cougar, Elite, Matador, Corvette.
c) Leistung [PS], d) Länge [Meter m], e) Gewicht [Tonnen t].
Die Auswertungen wurden mit dem Programm SPSS 12.0 für Windows vorgenommen.
3. Theoretische Grundlagen der statistischen Verfahren 3.1 Deskriptive Verfahren
Bevor die eigentliche Analyse der Daten mit Hilfe der Regressionsanalyse erfolgt, ist es ratsam, den Datensatz durch Berechnung von deskriptiven Maßzahlen zu charakterisieren. Damit wird das Ziel verfolgt, einen globalen Überblick über die Daten zu erlangen, indem die Eigenschaften eines Datensatzes durch die Ermittlung statistischer Kennzahlen zusammenfassend beschrieben werden. In der Regel analysiert man isoliert für jedes Merkmal so genannte Lage-, Streuungs- und Gestaltmaße.
Mit der Berechnung von Lagemaßen wird die Größenordnung der Merkmalswerte charakterisiert, indem die Lage des Zentrums des Datensatzes oder ein typischer Wert dafür angegeben wird. Der Modus stellt dabei die am häufigsten berechnete Größe dar. Er ist definiert als der Wert, der die geordnete Datenreihe in zwei Hälften teilt. Damit repräsentiert er die Mitte der Verteilung, da sich etwa genauso viele Untersuchungseinheiten oberhalb bzw. unterhalb dieses Wertes befinden. Da nur der mittlere Wert des Datensatzes bestimmt wird, wird der Modus durch außergewöhnlich hohe/niedrige Beobachtungen (Ausreißer) kaum verzerrt.
Ein ebenso populäres Lagemaß stellt das arithmetische Mittel dar. Es errechnet sich, in dem die Merkmalssumme des Datensatzes durch die Anzahl der Merkmalsträger dividiert wird und entspricht somit jenem Wert, den jeder Merkmalsträger erhält, wenn die Merkmalssumme auf alle N Merkmalsträger zu gleichen Teilen aufgeteilt wird:
x s
=v.
Je nachdem, wie stark die Beobachtungswerte um den Mittelwert x streuen, kann der Datensatz mehr oder weniger gut durch den Mittelwert repräsentiert
werden. Aus diesem Grund ist die Berechnung von Streuungsmaßen angezeigt, die der Charakterisierung der Ausbreitung und Homogenität einer statistischen Masse dienen. Bei geringer Streuung ist der Mittelwert x eher ein typischer Wert der Verteilung als bei hoher Variabilität. Als Streuungsmaß wird in diesem Projekt die Varianz untersucht, welche die positive Quadratwurzel der durchschnittlichen quadratischen Abweichung der Merkmalsausprägungen vom arithmetischen Mittel x beschreibt:
N
2 i
2 i 1
(x x)
s N
=
−
=
∑
.
Da die Varianz dieselbe Maßeinheit wie die Beobachtungswerte besitzt, ist sie insbesondere gut für einen Vergleich der Streuungen zwischen unterschiedlichen Datensätzen geeignet. Hierbei hat die Varianz insbesondere Vorteile gegenüber dem Variationskoeffizient, der als dimensionsloses Streuungsmaß kaum für solche Vergleiche geeignet ist.
Daher soll er im Weiteren nicht betrachtet werden.
Häufigkeitsverteilungen können bei gleichem Mittelwert x und gleicher Varianz eine unterschiedliche Gestalt besitzen. Wenn sich die Merkmalswerte gleichförmig zu beiden Seiten um den Mittelwert x verteilen, liegt eine symmetrische Häufigkeitsverteilung vor. Anderenfalls ist die Häufigkeitsverteilung asymmetrisch bzw. schief. Mit Hilfe eines Schiefemaßes (hier der Schiefekoeffizient g nach Pearson) kann die Richtung und das Ausmaß der Wölbung (Kurtosis) beurteilt werden. Die Berechnungsformel stellt sich wie folgt dar:
N
3 i i 1
3
N 2
2 i i 1
1 (x x)
g N
1 (x x)
N
=
=
−
=
⎛ − ⎞
⎜ ⎟
⎝ ⎠
∑
∑
.
Konzentrieren sich die Merkmalswerte auf der rechten Seite, heißt die Häufigkeitsverteilung rechtssteil und das Schiefemaß wird negativ. Wenn sich die Merkmalswerte mehrheitlich auf der linken Seite der Verteilung konzentrieren, spricht man von einer linksschiefen Verteilung und das Schiefemaß nimmt negative Werte an. Im Falle einer symmetrischen Verteilung errechnet sich für das Schiefemaß der Wert 0.
Eine Visualisierung der grundlegenden Struktur (Lage, Variabilität, Schiefe) eines Datensatzes kann durch die Konstruktion eines Boxplots erfolgen.
Dabei werden die mittleren 75% der Beobachtungsobjekte durch einen Kasten dargestellt, der durch den Modus und den Median begrenzt wird. Das arithmetische Mittel teilt die Box in zwei Hälften mit jeweils 37.5% der Werte.
Der kleinste bzw. der größte Wert des Datensatzes wird durch einen Stern bzw. Kreis dargestellt.
3.2 Zusammenhangsanalyse / Regressionsanalyse
Nachdem der Datensatz mit Hilfe der deskriptiven Statistik charakterisiert wurde, sollte der nächste Schritt darin bestehen, die möglichen Beziehungen zwischen den Variablen in einem Streudiagramm zu untersuchen. Dabei wird das bei einem Untersuchungsobjekt i erhobene Beobachtungspaar (xi,yi) zweier Merkmale X und Y durch einen Punkt in einem Koordinatensystem abgetragen und dies insgesamt für alle N Beobachtungsobjekte durchgeführt. Die Abszisse repräsentiert die Werte des Merkmals X, die Ordinate die Werte des Merkmals Y. Nun können Aussagen über die Richtung und Art der Beziehung zwischen den betrachteten Merkmalen getroffen werden. Ebenso ist es möglich, potenzielle Ausreißer zu erkennen, die Einfluss auf die Lage der Regressionsfunktion nehmen können.
Ausreißer können die Regressionsanalyse insoweit verzerren, dass die Regressionsfunktion dann nicht mehr die Beziehung zwischen der Masse der Beobachtungen widerspiegelt, sondern durch die Ausreißer dominiert wird.
Sind im Streudiagramm Zusammenhänge zwischen Variablen aufgedeckt worden, kann die Stärke und Richtung der Beziehung zwischen diesen Merkmalen durch eine statistische Maßzahl quantifiziert werden. Dies leistet der so genannte Korrelationskoeffizient nach Bravais-Pearson, welcher jedoch nur für qualitative Daten berechnet werden kann. Die Korrelation nach Bravais-Pearson zwischen zwei Merkmalen X und Y wird nach folgender Formel berechnet:
N
i i
i 1 XY
X Y
1 (x x)(y y)
r N
s s
=
− −
=
∑
.
Der Korrelationskoeffizient stellt eine dimensionslose Größe mit einem festen Wertebereich von − ≤1 rXY ≤1 dar. Je größer |rXY|, desto stärker ist der
monotone Zusammenhang der Merkmale X und Y. Ist |rXY|=1, so liegt ein perfekter monotoner Zusammenhang vor, bei dem alle Beobachtungspaare (xi,yi) auf einer Geraden liegen würden. Das Vorzeichen des Korrelationskoeffizienten gibt Auskunft darüber, in welcher Abhängigkeit bzw.
Ursache-Wirkungsbeziehung (Kausalität) die Merkmale X und Y zueinander stehen. Ist rXY > 0, so ist X ursächlich für das Zustandekommen der Werte von Y (X beeinflusst Y). Sollte rXY < 0 sein, wird Y als Ursache für die Werte von X angesehen (Y beeinflusst X). Bei rXY = 0 streuen die Beobachtungspaare unsystematisch. Folglich beeinflussen sich hier X und Y gegenseitig oder es liegen lineare Zusammenhänge zwischen X und Y vor.
Mit den bisherigen Verfahrensschritten können nur Aussagen über die Art, Stärke und Richtung des Zusammenhanges von Variablen getroffen werden, aber es nicht möglich, aus den Werten der einen Variablen auf die Werte der anderen Variable zu schließen. Daher beschäftigt sich die Regressionsanalyse mit der Spezifizierung einer funktionalen Beziehung zwischen einer abhängigen (Regressand) und einer oder mehreren unabhängigen Variablen (Regressoren), um so die Werte der abhängigen Variable schätzen bzw. prognostizieren zu können. Eine Grundvoraussetzung der Regressionsanalyse ist das metrische Skalenniveau der Variablen. Weiterhin muss vor der Durchführung der Regressionsanalyse durch sachlogische Überlegung eine eindeutige Richtung der Abhängigkeit zwischen den Variablen festgelegt werden.
Unabhängige Variablen xj stellen hierbei die Ursache für das Entstehen der Werte der abhängigen Variable y dar.
Insgesamt wird eine Regressionsfunktion gesucht, welche die Abhängigkeit zwischen den Merkmalen möglichst gut widerspiegelt:
1 2 k
y=F(x , x ,..., x , )ε .
Im vorliegenden Bericht wird nur der Fall linearer Regressionsfunktionen analysiert. Eine multiple lineare Regressionsfunktion (mit mindestens 2 unabhängigen Variablen) kann wie folgt formuliert werden:
0 1 1 2 2 k k ˆ
y= β + βx + β x + + β... x + ε bzw. ˆy=b0+b x1 1+b x2 2+ +... b xk k.
Dabei stellen ˆy die mit Hilfe der Regressionsfunktion geschätzten Werte der unabhängigen Variable, y die tatsächlich beobachteten Werte der unabhängigen Variable und x1,...,xk die abhängigen Variablen dar. Die unbekannten und zu schätzenden Größen β0 und βj heißen Regressionskoeffizienten: β0 ist hierbei das Absolutglied und legt den Schnittpunkt der Regressionsfunktion mit der Ordinate fest, wenn alle xj = 0 sind. Die Parameter βj erfassen den Einfluss der Variable xj auf die abhängige Variable und beschreiben dabei, wie sehr sich y ändert, wenn sich xj um eine Einheit ändert. Zudem werden β0 und βj als die „wahren“
Regressionskoeffizienten in der Grundgesamtheit bezeichnet. Die (auf Basis einer Stichprobe) geschätzten Regressionskoeffizienten b0 und bj können als Realisationen der Koeffizienten der Grundgesamtheit β0 und βj verstanden werden. Die senkrechte Abweichung zwischen yi und ˆyi für dieselbe Beobachtungseinheit i wird als Residuum εi bezeichnet:
i i i
ˆ y yˆ
ε = − .
Das Residuum entsteht, wenn die Regressionsfunktion die empirisch beobachteten Werte y nicht vollständig erklären kann, weil nicht alle beeinflussenden Variablen berücksichtigt wurden bzw. Messfehler oder Beobachtungsfehler aufgetreten sind. Das Ziel der Regressionsanalyse besteht nun darin, die Regressionskoeffizienten b0 und bj so zu bestimmen, dass die mit Hilfe der Regressionsfunktion geschätzten Werte ˆy möglichst adäquat den empirischen Werten der abhängigen Variable y entsprechen.
Dies ist dann der Fall, wenn die Residuen „klein“ sind. Ein in diesem Zusammenhang häufig verwendetes Verfahren stellt die Methode der
„Kleinsten Quadrate“ dar, welche die Residuenquadratsumme durch geeignete Wahl der Regressionsparameter minimiert:
0 j
N N
2 2
i i i
i 1 i 1 b ,b
ˆ (y y )ˆ min
= =
ε = − →
∑ ∑
.Da häufig nur eine Stichprobe analysiert wird, die Bestandteil einer größeren, unbekannten Grundgesamtheit ist, muss die Regressionsanalyse einen Zusammenhang zwischen der abhängigen und den unabhängigen Variablen auf Grundlage der empirischen Werte der Stichprobe schätzen und danach
überprüfen, ob das so ermittelte Modell für die Grundgesamtheit als gültig angesehen werden kann. Dazu wird in einem ersten Schritt die Regressionsfunktion als Ganzes überprüft und dabei ermittelt, wie gut y insgesamt durch die unabhängigen Variablen erklärt wird. Als Instrumente dieses Schrittes dienen das Bestimmtheitsmaß R² und der F-Test. In einem zweiten Schritt werden die Regressionskoeffizienten einzeln überprüft, um festzustellen, ob die einzelnen Variablen xj einen Erklärungsbeitrag für y liefern. Durchzuführen sind hierbei t-Tests. In einem letzten Schritt muss die Erfüllung der grundlegenden Annahmen der Regressionsanalyse geprüft werden.
Die im ersten Schritt geforderte globale Einschätzung der Anpassungsgüte der Regressionsfunktion an die empirischen Daten kann über das Bestimmtheitsmaß R² erfolgen. Durch einen festen Wertebereich von
9 . 0 1
.
0 ≤R2 ≤ ist dieses Maß einfach interpretierbar und ermöglicht einen Vergleich der Anpassung von Regressionen unterschiedlicher Datensätze.
Dabei gibt R² den prozentualen Anteil der durch die Regression erklärten Varianz an der gesamten Varianz der abhängigen Variablen an:
N
2 i
2 i 1 2
N YYˆ
2 i i 1
(yˆ y)
R r
(y y)
=
=
−
= =
−
∑
∑
.Je größer R² ist, desto höher fällt die Anpassungsgüte der Regressionsfunktion an die empirischen Daten aus. Erreicht R² den Wert 1, stimmen die Werte von y und ˆy überein. Die gesamte Streuung von y wird folglich vollständig durch die unabhängigen Variablen erklärt. Für den Fall, dass R² den Wert 0 annimmt, kann der Zusammenhang zwischen y und den unabhängigen Variablen nicht durch die unterstellte Regressionsfunktion dargestellt werden. Es können nur andere – bisher unberücksichtigte – unabhängige Variablen y erklären, aber nicht die in der Regressionsfunktion aufgenommenen Merkmale.
Der sich an die Ermittlung von R² anschließende F-Test dient der Überprüfung, ob das geschätzte Modell für die Grundgesamtheit Gültigkeit besitzt. Besteht in der Grundgesamtheit ein funktionaler Zusammenhang
zwischen y und den unabhängigen Variablen, müssen die Regressionsparameter der Grundgesamtheit βj statistisch gesichert (signifikant) von 0 verschieden sein. Der Test erfolgt auf Basis der in der Stichprobe ermittelten Regressionsparameter bj über die Hypothesen:
0 j
H :β = ∀ =0 j 1,..., k vs. H :1 β ≠j 0 (Für mindestens ein j).
H0 besagt, dass zwischen y und den unabhängigen Variablen keine Abhängigkeit besteht und daher die Regressionskoeffizienten null sind (lediglich das Absolutglied wird nicht überprüft). Ob H0 beibehalten werden kann oder zu verwerfen ist, wird durch die Berechnung einer Prüfgröße Femp
entschieden:
2
emp 2
R / k F =(1 R ) /(N k 1)
− − − .
Gilt H0, wird Femp null oder nahe null sein. Weicht Femp jedoch stark von null ab und überschreitet einen kritischen Wert, so ist es unwahrscheinlich, dass H0 gilt. Folglich ist diese Hypothese zu verwerfen und H1 anzunehmen. Dies bedeutet, dass nicht alle Regressionskoeffizienten null sind und der Zusammenhang zwischen y und den unabhängigen Variablen als signifikant zu erachten ist. SPSS entscheidet den Test über einen Vergleich des realisierten p-Wertes mit einer vorher festgelegten Irrtumswahrscheinlichkeit
α (auch als Signifikanzniveau bezeichnet). Der Wert α beschreibt die vom Anwender maximal tolerierbare Wahrscheinlichkeit für einen Irrtum, den man begeht, wenn H0 abgelehnt wird, obwohl die Nullhypothese angenommen wird. Im Bericht wird, wie allgemein üblich, α = 0.05 gesetzt. Dies besagt, dass der Test in 95% der Fälle zu einer Ablehnung von H0 führen wird, wenn diese korrekt ist und sich der Anwender in maximal 5% der Fälle täuschen wird, wenn er von H1 ausgeht. Die Wahl von α ist vom Ausmaß der Unsicherheit im Untersuchungsbereich abhängig, ebenso von den Konsequenzen einer Fehlentscheidung. Der realisierte p-Wert kann als das kleinste Signifikanzniveau interpretiert werden, zu dem H0 gerade noch abgelehnt werden kann.
Gilt p<α, ist H1 zu verwerfen und H0 anzunehmen. Dies bedeutet, dass die Regressionsbeziehung nicht signifikant ist und empirisch nicht bestätigt werden kann. Die Ursachen dafür könnten unberücksichtigte Variablen sein
oder ein zu geringer Stichprobenumfang. Wenn α ≥ p ist, muss H1
angenommen werden.
Zeigt sich im F-Test, dass das Gesamtmodell einen Erklärungswert für y hat, sind in einem zweiten Schritt die Regressionskoeffizienten (auch das Absolutglied) einzeln mit Hilfe von t-Tests zu überprüfen. Für jeden Koeffizienten j=0,1,...,k kann auf Basis der Stichprobe folgendes Hypothesenpaar über den entsprechenden Regressionskoeffizienten der Grundgesamtheit getestet werden:
j
0 j
H :β β =0 vs. H :1βj β ≠j 0.
H0 besagt, dass der jeweilige Regressor keinen statistisch gesicherten Einfluss auf y hat und daher der Regressionskoeffizient null ist (bzw. das Absolutglied nicht signifikant von 0 verschieden ist). Ob H0 beibehalten werden kann oder zu verwerfen ist, wird wiederum durch die Berechnung einer Prüfgröße temp für jeden Koeffizienten entschieden:
j
j
j emp
b
t b s
β = .
Gilt H0, wird temp null oder nahe null sein. Weicht |temp| jedoch stark von null ab und überschreitet einen kritischen Wert, so ist es unwahrscheinlich, dass H0 gilt. Folglich ist diese Hypothese zu verwerfen und H1 anzunehmen. Dies bedeutet, dass der Regressor einen signifikanten Einfluss auf y hat (bzw. das Absolutglied signifikant von null abweicht). SPSS entscheidet den Test ebenfalls über einen Vergleich des realisierten p-Wertes mit der vorher festgelegten Irrtumswahrscheinlichkeit α. Die Testentscheidung ist analog zum F-Test. Ein nicht signifikanter Regressor ist aus der Regressionsfunktion zu entfernen.
4. Statistische Auswertung
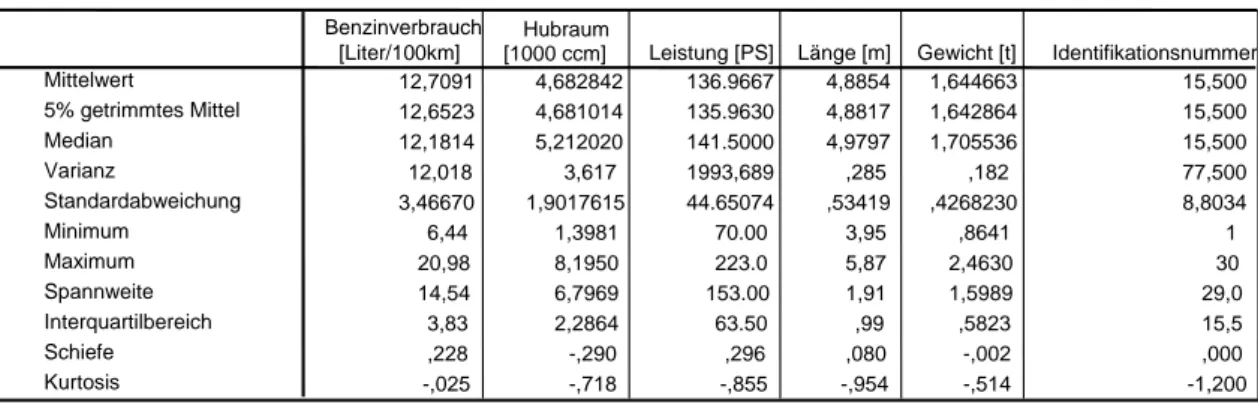
Den Ausgangspunkt der statistischen Analyse stellt die Ermittlung von deskriptiven Kennzahlen für jedes der 6 Merkmale dar (vgl. Tabelle 1).
Durchschnittlich verbrauchen die 30 PKW 12.18 Liter/100 km, haben einen Hubraum von 5212 Kubikzentimeter, eine Leistung von 141.5 PS bei einem Gewicht von rund 1.71 Tonnen und sind rund 4.98 m lang.
Tabelle 1: Deskriptive Kennzahlen
Für alle Variablen können hinsichtlich der Varianz keine besonderen Erkenntnisse gewonnen werden. Die größte Varianz weist die Variable Leistung auf (1993.69 PS), gefolgt von der Variable Identifikationsnummer.
Nur bei diesen beiden Variablen ist die Varianz größer als der Mittelwert.
Soll die Schiefe der einzelnen Häufigkeitsverteilungen beurteilt werden, ist zuerst zu betrachten, ob es einen Unterschied zwischen Median und Mittelwert gibt. Bei allen Variablen ist jedoch diese Abweichung unbedeutend, so dass relativ symmetrische Verteilungen vorliegen werden.
Auch aus den Werten des Schiefemaßes kann dies abgelesen werden. Nur der Wert für das Schiefemaß der Variable Identifikationsnummer zeigt mit –1.2 eine rechtssteile Verteilung an. Diese Aussagen zur Schiefe lassen sich auch an den Boxplots ablesen (vgl. Abbildung 1 und Abbildung 2). Boxplots können auch zur Identifikation von Ausreißern genutzt werden. Jedoch stellt man bei allen Variablen in Abbildung 1 keine solchen Werte fest.
Da die Variable Benzinverbrauch die wichtigste Betrachtungsgröße in diesem Bericht ist, werden ihre Boxplots alleine ohne die anderen Variablen dargestellt (vgl. Abbildung 2). Aus diesen Darstellungen ist eine leicht rechtssteile Verteilung für den Benzinverbrauch erkennbar. Das Schiefemaß für die Variable Benzinverbrauch hatte jedoch eine leicht linksschiefe Verteilung festgestellt (vgl. Tabelle 1). Auch aus diesen Boxplots für den Benzinverbrauch können keine Anzeichen für Ausreißer gewonnen werden.
Univariate Statistiken
12,7091 4,682842 136.9667 4,8854 1,644663 15,500
12,6523 4,681014 135.9630 4,8817 1,642864 15,500
12,1814 5,212020 141.5000 4,9797 1,705536 15,500
12,018 3,617 1993,689 ,285 ,182 77,500
3,46670 1,9017615 44.65074 ,53419 ,4268230 8,8034
6,44 1,3981 70.00 3,95 ,8641 1
20,98 8,1950 223.0 5,87 2,4630 30
14,54 6,7969 153.00 1,91 1,5989 29,0
3,83 2,2864 63.50 ,99 ,5823 15,5
,228 -,290 ,296 ,080 -,002 ,000
-,025 -,718 -,855 -,954 -,514 -1,200
Mittelwert
5% getrimmtes Mittel Median
Varianz
Standardabweichung Minimum
Maximum Spannweite Interquartilbereich Schiefe Kurtosis
Benzinverbrauch [Liter/100km]
Hubraum
[1000 ccm] Leistung [PS] Länge [m] Gewicht [t] Identifikationsnummer
,8641 ,9113 1,0319 1,0524 1,1499 1,2043 1,2247 1,3699 1,3835 1,4424 1,5264 1,5309 1,5921 1,6602 1,7509 1,7622 1,7645 1,7736 1,9119 1,9278 1,9822 2,0593 2,1387 2,3519 2,3995 2,4630
Gewicht [t]
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
6,44 6,77 7,37 7,73 9,83 9,98 10,62 10,93 10,95 11,58 11,71 11,75 11,91 11,93 12,43 12,88 13,20 13,82 14,24 14,32 15,78 16,33 16,91 17,07 17,71 20,98
Benzinverbrauch [Liter/100km]
0,0%
1,0%
2,0%
3,0%
4,0%
5,0%
6,0%
7,0%
Prozent
Abbildung 1: Boxplots
Ident ifikat
ions num
mer Hubr
aum [ccm
] Lei
stung [ PS]
Länge [m]
Ge wicht
[t]
0,0000 50,0000 100,0000 150,0000 200,0000 250,0000
Ident ifikat
ions num
mer Hubr
aum [1000
ccm ] Lei
stung [ PS]
Länge [m]
Ge wicht
[t]
0,0000 50,0000 100,0000 150,0000 200,0000 250,0000
Ident ifikat
ions num
mer Hubr
aum [ccm
] Lei
stung [ PS]
Länge [m]
Ge wicht
[t]
0,0000 50,0000 100,0000 150,0000 200,0000 250,0000
Ident ifikat
ions num
mer Hubr
aum [1000
ccm ] Lei
stung [ PS]
Länge [m]
Ge wicht
[t]
0,0000 50,0000 100,0000 150,0000 200,0000 250,0000
Abbildung 2: Boxplots der Variable Benzinverbrauch
Bevor die Regressionsanalyse durchgeführt werden kann, müssen die Modellspezifikationen festgelegt werden. Entsprechend den Zielen dieses Berichts ist der Benzinverbrauch als abhängige Variable festzulegen. Die Variablen Hubraum, Leistung, Länge und Gewicht sind im Regressionsmodell als ursächliche Einflussfaktoren auf den Benzinverbrauch anzusehen. Diese Einstufungen der Variablen erscheinen sachlogisch gerechtfertigt, da tatsächlich sogar von einem Kausalzusammenhang dieser
Variablen und dem Benzinverbrauch auszugehen ist. Ob die abhängige Variable durch die berücksichtigten Regressoren vollständig beschrieben werden kann, ist jedoch anzuzweifeln, da andere Faktoren (z.B.
Außentemperatur, Fahrtstrecke usw.) unberücksichtigt bleiben. Wie stark diese Auswirkungen auf die Anpassungsgüte der Regression sind, kann im Verlauf der Analyse festgestellt werden.
Welche Form des Zusammenhangs zwischen einem einzelnen Regressor und der abhängigen Variable vorliegt, kann durch Streudiagramme beurteilt werden (im Bericht nicht abgebildet). In allen Streudiagrammen zwischen dem jeweiligen Regressor und dem Benzinverbrauch können lineare Zusammenhänge festgestellt werden. Weiterhin ist in den Streudiagrammen nicht davon auszugehen, dass Ausreißer vorliegen. Das Bestehen von linearen Zusammenhängen wird durch die Berechnung von Korrelationskoeffizienten zwischen den Regressoren und der abhängigen Variable Benzinverbrauch gestützt (vgl. Tabelle 2).
Tabelle 2: Korrelationen nach Bravais-Pearson mit Benzinverbrauch
Für alle 4 Regressoren ergibt sich eine Korrelation von genau 0.000 mit der abhängigen Variablen, so dass eindeutig lineare Zusammenhänge vorliegen.
Nach diesen Vorüberlegungen kann nun ein multiples lineares Regressionsmodell aufgestellt und geschätzt werden:
Geschätzter Verbrauch = b0 + b1·Hubraum + b2·Leistung + b3·Länge + b4·Gewicht.
Die Schätzergebnisse sind Tabelle 3 zu entnehmen. Insgesamt stellt sich die geschätzte Regressionsfunktion wie folgt dar:
Geschätzter Verbrauch = 5.819 + 0.750·Hubraum + 0.019·Leistung + 2.137·Länge + 4.444·Gewicht.
Korrelationen
1 ,867 ,846 ,716 ,846
,000 ,000 ,000 ,000
30 30 30 30 30
Signifikanz (2-seitig) N Benzinverbrauch [Liter/100km]
Benzinverbrauch [Liter/100km]
Hubraum
[1000 ccm] Leistung [PS] Länge [m] Gewicht [t]
Die Regressionsparameter weisen die erwarteten positiven Vorzeichen auf.
Dies bedeutet, dass eine Veränderung der unabhängigen Variablen um eine Skaleneinheit den Benzinverbrauch um den Wert des Regressionsparameters verändert.
Tabelle 3: Schätzergebnisse der Regression mit 4 unabhängigen Variablen
Bereits dieses erste Modell zeigt eine erstaunliche Anpassungsgüte an die empirischen Daten. Denn 90.9% der Streuung der abhängigen Variablen können erklärt werden. Auch der F-Test bestätigt, dass das Gesamtmodell statistisch gesichert ist und die Regressoren einen Erklärungswert für y haben. Somit können die Ergebnisse aus der Stichprobe verallgemeinert werden.
Der zweite Schritt der Modellbewertung enthält den in Kapitel 3.2 erläuterten t-Test der einzelnen Regressionsparameter. Hier zeigt sich allerdings für die Variablen Länge und Gewicht, dass diese keinen signifikanten Erklärungsbeitrag für y liefern, da bei ihnen α <0.05. Somit müssen diese
Koeffizientena
19,679 5,819 3,382 ,002
-,224 ,750 -,123 -,299 ,768
,023 ,019 ,291 1,181 ,249
-6,315 2,137 -,973 -2,955 ,007
13,274 4,444 1,634 2,987 ,006
(Konstante) Leistung [PS]
Länge [m]
Gewicht [t]
Modell 1
B
Standardf ehler Nicht standardisierte
Koeffizienten
Beta Standardisie
rte Koeffizienten
T Signifikanz
Abhängige Variable: Benzinverbrauch [Liter/100km]
a.
Hubraum [1000 ccm]
ANOVAb
287,857 4 71,964 29,656 ,000a
60,665 25 2,427
348,522 29
Regression Residuen Gesamt Modell
1
Quadrats
umme df
Mittel der
Quadrate F Signifikanz
Einflußvariablen : (Konstante), Gewicht [t], Leistung [PS], Länge [m], Hubraum a.
Abhängige Variable: Benzinverbrauch [Liter/100km]
b.
Modellzusammenfassung
,909a ,826 ,798 1,55776
Modell 1
R R-Quadrat
Korrigiertes R-Quadrat
Standardf ehler des Schätzers
Einflußvariablen : (Konstante), Gewicht [t], Leistung [PS], Länge [m], Hubraum [1000 ccm]
a.
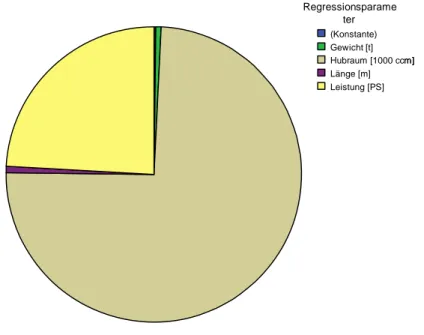
Variablen aus der Analyse ausgeschlossen werden. Auch Abbildung 3 bestätigt diese Schlussfolgerung. Hier sind alle Signifikanzniveaus der t- Tests aller Regressionsparameter abgetragen. Man erkennt, dass nur die Variablen Hubraum und Leistung wegen ihres hohen Signifikanzniveaus einen Erklärungsbeitrag für y liefern und die anderen Variablen Länge und Gewicht nur einen minimalen Erklärungsanteil besitzen.
Abbildung 3: Signifikanzniveaus der Regressionsparameter (t-Test)
Regressionsparame ter (Konstante) Gewicht [t]
Hubraum [1000 ccm]
Länge [m]
Leistung [PS]
Fälle gewichtet nach Signifikanzniveau
Regressionsparame ter (Konstante) Gewicht [t]
Hubraum [1000 ccm]
Länge [m]
Leistung [PS]
Fälle gewichtet nach Signifikanzniveau
Deswegen wird im Folgenden ein zweites Modell ohne die Variablen Länge und Gewicht geschätzt. Die Ergebnisse können in Tabelle 4 abgelesen werden. Es ergibt sich folgende Regressionsfunktion:
Geschätzter Verbrauch = 1.129 + 0.506·Hubraum + 0.022·Leistung.
Tabelle 4: Schätzergebnisse der Regression mit 2 unabhängigen Variablen
Die Nichtberücksichtigung der zwei Variablen Länge und Gewicht führt zu einem dramatischen Abfall des Bestimmtheitsmaßes. Jetzt können nur noch 74.2% der Varianz von y durch die Regression erklärt werden. Auch der F- Test zeigt ein ernüchterndes Ergebnis: H0 muss auf Grund des Signifikanzniveaus verworfen werden. Dies bedeutet, dass das Gesamtmodell keinen signifikanten Erklärungsbeitrag für y liefert. Folglich ist dieses zweite Modell vollständig zu verwerfen und letztendlich dem ersten Modell, welches alle vier möglichen Einflussfaktoren berücksichtigte, der Vorzug zu geben. Alle Schätzungen des Benzinverbrauches sollten daher mit diesem ersten Modell erfolgen, wenn die grundlegenden Annahmen des Regressionsmodells erfüllt sind. So wird vorausgesetzt, dass die Residuen heteroskedastisch, autokorreliert und normalverteilt sind, da bei Nichterfüllung die Güte der Schätzung sinkt bzw. die Regressionskoeffizienten der Stichprobe verzerrt geschätzt werden. Daher wird zum Abschluss der Regressionsanalyse die Erfüllung dieser grundlegenden Annahmen für das erste Regressionsmodell mit den 4 unabhängigen Variablen geprüft. Dabei kann die graphische Inspektion auf
Koeffizientena
4,629 1,129 4,100 ,000
1,135 ,506 ,623 2,242 ,033
,020 ,022 ,260 ,935 ,358
(Konstante) Leistung [PS]
Modell 1
B
Standardf ehler Nicht standardisierte
Koeffizienten
Beta Standardisie
rte Koeffizienten
T Signifikanz
Abhängige Variable: Benzinverbrauch [Liter/100km]
a.
Hubraum [1000 ccm]
Modellzusammenfassung
,872a ,760 ,742 1,76040
Modell 1
R R-Quadrat
Korrigiertes R-Quadrat
Standardf ehler des Schätzers Einflußvariablen : (Konstante), Leistung [PS], Hubraum [1000 ccm]
a.
ANOVAb
264,849 2 132,424 42,731 ,000a
83,674 27 3,099
348,522 29
Regression Residuen Gesamt Modell
1
Quadrats
umme df
Mittel der
Quadrate F Signifikanz
Einflußvariablen : (Konstante), Leistung [PS], Hubraum [1000 ccm]
a.
Abhängige Variable: Benzinverbrauch [Liter/100km]
b.
0 10 20 30
Beobachteter Wert
-2 -1 0 1 2
Erwarteter Normalwert
Q-Q-Diagramm von Identifikationsnummer
7,20 7,30 7,40 7,50 7,60 7,70 7,80 7,90
Benzinverbrauch [Liter/100km]
0,0 0,2 0,4 0,6 0,8 1,0
Häufigkeit
Mean = 7,5485 Std. Dev. = 0,25703 N = 2
von Hubraum_x2= 1,5882 Histogramm
Autokorrelation unterbleiben, da hier eine Zeitreihe vorliegt und ein Autokorrelations-Check nur bei Querschnittsdaten vorgenommen werden muss. Zur Überprüfung auf Heteroskedastie kann Abbildung 2 herangezogen werden. Da dort weder eine steigende noch eine fallende Varianz zu erkennen ist, wird die Eigenschaft der Heteroskedastie erfüllt.
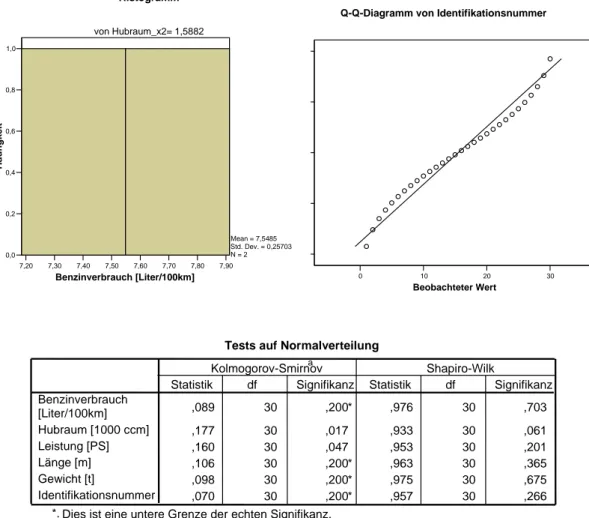
Abschließend ist die Normalverteilung der Residuen zu überprüfen. Dazu sind in Abbildung 4 ein Histogramm und ein PP-Plot der Residuen dargestellt. Es ist zu erkennen, dass die Abweichungen von der Winkelhalbierenden im PP-Plot gering sind und daher von hinreichend normalverteilten Residuen auszugehen ist. Auch im Histogramm kann eine Normalverteilung der Residuen angenommen werden.
Abbildung 4: Überprüfung der Normalverteilung der Residuen
Zusammenfassend kann festgestellt werden, dass das erste Regressionsmodell mit allen vier unabhängigen Variablen in überzeugender
Tests auf Normalverteilung
,089 30 ,200* ,976 30 ,703
,177 30 ,017 ,933 30 ,061
,160 30 ,047 ,953 30 ,201
,106 30 ,200* ,963 30 ,365
,098 30 ,200* ,975 30 ,675
,070 30 ,200* ,957 30 ,266
Benzinverbrauch [Liter/100km]
Hubraum [1000 ccm]
Leistung [PS]
Länge [m]
Gewicht [t]
Identifikationsnummer
Statistik df Signifikanz Statistik df Signifikanz Kolmogorov-Smirnova Shapiro-Wilk
Dies ist eine untere Grenze der echten Signifikanz.
*.
Signifikanzkorrektur nach Lilliefors a.
Art und Weise zur Erklärung der abhängigen Variablen Benzinverbrauch herangezogen werden kann. Es erfüllt die grundsätzlichen Annahmen der Regression und hat ein hohes Bestimmtheitsmaß von 90.9%. Daher kann es uneingeschränkt zur Prognose des Benzinverbrauches verwendet werden.
Abkürzungsverzeichnis
o.V. ohne Verfasser
Literaturverzeichnis
Eckey, H.F. / Kosfeld, R. / Dreger, C. (2002): Statistik – Grundlagen, Methoden, Beispiele, 3. Auflage, Gabler Verlag, Wiesbaden.
Backhaus, K. / Erichson, B. / Plinke, W. / Weiber, R. (2000): Multivariate Analysemethoden – Eine anwendungsorientierte Einführung, 9. Auflage, Springer Verlag, Berlin.
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
50,00 100,00 150,00 200,00
Leistung [PS]
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
4,00 4,50 5,00 5,50 6,00
Länge [m]
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
1,0000 1,5000 2,0000 2,5000
Gewicht [t]
Anhang
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
2,0000 4,0000 6,0000 8,0000
Hubraum [1000 ccm]
6,00 9,00 12,00 15,00 18,00 21,00
Benzinverbrauch [Liter/100km]
2,0000 4,0000 6,0000 8,0000
Hubraum [1000 ccm]