HALLE-WITTENBERG
Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Statistik
Prof. Dr. Claudia Becker
Wintersemester 2004/05 1. Termin
Klausur Anwendungsprojekte
über
Regressionsanalyse
„Prognose der Anzahl von Neuimmatrikulationen“
15.02.2005
Inhaltsverzeichnis
1. Einleitung ... 1
2. Problemstellung ... 2
3. Erklärung der Methoden und Verfahren ... 3
3.1 Deskriptive Statistik ... 3
3.2 Korrelationsanalyse ... 5
3.3 Multiple Regression ... 7
4. Auswertung des Datensatzes... 10
4.1 Deskriptive Statistik ... 10
4.2 Korrelationsanalyse ... 13
4.3 Multiple Regression ... 17
5. Zusammenfassung... 21
Literaturverzeichnis ... 22
1. Einleitung
In den USA besteht schon seit langem die Tradition, dass die Studenten für ihre Ausbildung an einer Universität Studiengebühren zahlen müssen. Insbesondere stellt sich daher für die Universitäten das Problem, optimale Studienbedingungen für jeden einzelnen Studenten garantieren zu können. So erscheint es besonders wichtig, schon frühzeitig vor Beginn der Einschreibefrist den Raumbedarf, den Bedarf an Lehrkräften und die Einnahmen aus den Studiengebühren zu planen. Dazu ist es nötig, die Anzahl der Neuimmatrikulationen auf einer statistisch gesicherten Basis abschätzen zu können.
Das Ziel dieses Berichtes besteht darin, ein aussagefähiges und gesichertes Prognosesystem für die Neuimmatrikulationen von Studenten an Hand von Zeitreihen früherer Jahre aufzustellen. Dazu müssen in einem ersten Schritt Variablen ermittelt werden, die im Zusammenhang mit der Zahl der Neuimmatrikulationen stehen und für eine Vorhersage der Neuimmatrikulationen geeignet erscheinen.
Dies wird durch die Verwendung der Korrelationsanalyse ermöglicht.
In einem zweiten Schritt muss die Beziehung zwischen den gefundenen Variablen und der Anzahl der Neuimmatrikulationen funktional spezifiziert werden. Hierbei kommt die Regressionsanalyse zur Anwendung. Wenn davon ausgegangen werden kann, dass die Regressionsbeziehung statistisch gesichert ist, können mit Hilfe der Variablen Prognosen der Anzahl der Neuimmatrikulationen vorgenommen werden. Im Bericht zeigt sich, dass 2 unterschiedliche Regressionsmodelle sehr gut zur Prognose geeignet sind.
Der Bericht gliedert sich in 5 Kapitel. Das folgende Kapitel 2 widmet sich der Diskussion der Problemstellung und es werden Angaben zur Datenqualität gemacht, aus denen Einschränkungen bei der Ergebnisinterpretation resultieren könnten. Im Kapitel 3 werden die verwendeten Verfahren und Methoden – vor allem die Korrelations- und Regressionsanalyse – näher erläutert. Kapitel 4 beschäftigt sich
mit der Analyse der Ausgangsdaten und dem Auffinden des besten Regressionsmodells. Das letzte Kapitel gibt einen abschließenden und zusammenfassenden Überblick über die Untersuchung.
2. Problemstellung
Ende 1989 stellte sich für das „Office of Institutional Research“ der Universität New Mexico in Albuquerque das Problem, die Anzahl der Neuimmatrikulationen zum Wintersemester für die gesamte Universität aus organisatorischen Gründen genauer planen zu müssen. Mit Hilfe von Vergangenheitsdaten sollte versucht werden, Variablen zu erkennen, welche die Prognose der Neuimmatrikulationen ermöglichen (=Ziel der Korrelationsanalyse).
Denn mit diesen Variablen soll ein funktionaler Zusammenhang beschrieben werden, der in späteren Jahren zu Prognosezwecken genutzt werden kann (=Ziel der Regressionsanalyse). Dazu konnte man auf einen Datensatz der amtlichen Statistik zurückgreifen, der aus folgenden 5 Variablen für die Zeitpunkte (t=1,..., T) von 1961 bis 1989 besteht (vgl. Tabelle 1).
Tabelle 1: Überblick über die Variablen des Datensatzes
Variablenbezeichnung Skalenniveau
Jahr ordinal Anzahl von Immatrikulationen im Herbst an
der Universität of New Mexico metrisch Arbeitslosenrate im Januar in New Mexico metrisch Anzahl der Abiturienten im Juni in New
Mexico metrisch Reales Pro-Kopf-Einkommen in Albuquerque metrisch
Im Datenmaterial befinden sich keine fehlenden Werte. Ebenso handelt es sich um amtlich ermittelte Zahlen für T=30 Zeitpunkte, woraus keine Einschränkungen bei der Verwendung der Daten für die Korrelations- und Regressionsanalyse und insbesondere für die Prognose resultieren. Die Problemstellung wurde mit Hilfe des Softwarepaketes SPSS 12.0 bearbeitet.
3. Erklärung der Methoden und Verfahren 3.1 Deskriptive Statistik
Die Anwendung der deskriptiven Statistik verfolgt das Ziel, Eigenschaften eines Datensatzes durch die Ermittlung von statistischen Kennzahlen zusammenfassend und verdichtend zu beschreiben. Maßzahlen erleichtern die Interpretation und den Vergleich zu anderen statistischen Massen. In der Regel analysiert man Lagemaße, Streuungsmaße und Gestaltmaße.
Mit der Berechnung von Lagemaßen wird versucht, das Niveau der Merkmalswerte zu charakterisieren. Zu den Lagemaßen werden Mittelwerte und Quantile gezählt. Quantile sind allgemeine Werte xp, welche die geordnete Datenreihe x(t) in 2 beliebig große Anteile p und 1-p aufteilen. Unterhalb des p-Quantils xp befinden sich mindestens p•100% der Merkmalswerte, oberhalb von xp befinden sich mindestens (1-p) •100% der Merkmalswerte. Aus den Abständen von Quantilen lassen sich Anhaltspunkte über die Ausbreitung und Form einer Häufigkeitsverteilung gewinnen. Dem gegenüber wollen Mittelwerte (z.B. Modus, Median, arithmetisches Mittel) die Lage des Zentrums des Datensatzes bzw. einen typischen Wert angeben. Der Modus lokalisiert dabei genau den Gipfel der Dichtefunktion einer Variablen, also den häufigsten Wert einer Häufigkeitsverteilung. Da im vorliegenden Datenmaterial alle Merkmalsausprägungen eines Merkmals dieselbe Häufigkeit besitzen, soll auf seine Berechnung verzichtet werden. Die Verwendung des Median scheint daher plausiblere Ergebnisse zu liefern. Er stellt einen Merkmalswert dar, welcher die geordnete Datenreihe in 2 Hälften gleichen Umfangs teilt. Jedoch ist der Median extrem ausreißerempfindlich und soll daher auch keine Anwendung finden. In der Regel wird aus diesen Gründen nur das arithmetische Mittel berechnet. Es errechnet sich, in dem die Merkmalssumme durch die Anzahl der Merkmalsträger dividiert wird und entspricht somit jenem Wert, den jeder Merkmalsträger erhält, wenn die Merkmalssumme auf alle T Merkmalsträger zu gleichen Teilen aufgeteilt wird.
Je nachdem, wie stark die Beobachtungswerte um einen Mittelwert streuen, kann der Datensatz mehr oder weniger gut durch den Mittelwert repräsentiert werden. Aus diesem Grund ist die Berechnung von Streuungsmaßen angezeigt, die der Charakterisierung der Ausbreitung und Homogenität einer statistischen Masse dienen. Bei geringer Streuung ist ein Mittelwert eher ein typischer Wert der Verteilung als bei hoher Variabilität. Als Streuungsmaße sollen die Spannweite, die Standardabweichung und der Variationskoeffizient untersucht werden. Die Spannweite ist die Differenz zwischen dem größten und kleinsten Beobachtungswert und gibt somit den Variationsbereich der Daten wieder, kann aber durch extreme Werte beeinflusst werden. Die Standardabweichung s beschreibt die durchschnittliche quadratische Abweichung der Merkmalsausprägungen vom arithmetischen Mittel. Erschwerend wirkt bei ihrer Interpretation, dass sie die quadrierte Maßeinheit der Merkmalswerte besitzt. Deshalb sollte immer die Quadratwurzel der Standardabweichung interpretiert werden. Ein Vergleich der Variabilität der Häufigkeitsverteilungen verschiedener Merkmale auf Grundlage der Standardabweichungen ist ebenso nur bedingt möglich. Dazu ist eine Relativierung unter Verwendung eines Mittelwertes erforderlich. Die gebräuchlichste Maßzahl hierfür stellt der Variationskoeffizient V dar, der als Quotient aus der Standardabweichung s und dem arithmetischen Mittel definiert ist:
∑
∑
=
= n=
i i i n
i i i
n x
n x V
1 0 0 1
0 1
.
Häufigkeitsverteilungen können bei gleichem Mittelwert und gleicher Streuung eine unterschiedliche Gestalt besitzen. Wenn sich die Merkmalswerte gleichförmig um den Mittelwert verteilen, liegt eine symmetrische Häufigkeitsverteilung vor. Anderenfalls ist die Häufigkeitsverteilung asymmetrisch. Mit Hilfe eines Schiefemaßes (hier der Schiefekoeffizient nach Pearson) kann die Richtung und das Ausmaß der Schiefe beurteilt werden. Wenn sich die
Merkmalswerte mehrheitlich auf der linken Seite der Verteilung konzentrieren, spricht man von einer linkssteilen Verteilung und das Schiefemaß nimmt positive Werte an. Konzentrieren sich die Merkmalswerte auf der rechten Seite, heißt die Häufigkeitsverteilung rechtsschief und das Schiefemaß wird negativ. Im Falle einer symmetrischen Verteilung nimmt ein Schiefemaß den Wert 0 an.
Mit Hilfe eines Boxplots möchte man einen visuellen Eindruck über die Lage, Variabilität und Schiefe eines Datensatzes vermitteln sowie potentielle Ausreißer ausweisen. Er stellt dabei eine komprimierte graphische Darstellung unter Verwendung robuster Maßzahlen dar.
Die mittleren 50% der Beobachtungen werden durch einen Kasten dargestellt, welcher durch das 25%- und das 75%-Quantil begrenzt wird. Die Box wird durch das arithmetische Mittel in 2 Hälften mit jeweils 25% der Beobachtungswerte geteilt. Ebenso werden sogenannte Zäune festgelegt, die extreme Beobachtungen ausgrenzen sollen. Die Zäune umfassen dabei ein Intervall des 1,5fachen Interquartilsabstandes (Differenz des 75%- und des 25%- Quantils) über- bzw. unterhalb des 75%- bzw. 25%-Quantils.
Jenseits der Zäune liegende Beobachtungen stellen potentielle Ausreißer dar.
3.2 Korrelationsanalyse
Die Aufgabe der Korrelationsanalyse besteht darin, die Stärke, die Art und die Richtung der Beziehung zwischen 2 Variablen durch eine statistische Maßzahl zu quantifizieren. Dabei stellt das Streudiagramm den Ausgangspunkt jeder Zusammenhangsmessung dar, denn aus ihm geht die Form der Beziehung zwischen den beiden Variablen hervor, deren Kenntnis in der Korrelations- und Regressionsanalyse hilfreich ist. Ebenso werden Ausreißer erkenntlich. Zum Zwecke der Messung der Stärke und Richtung des linearen Zusammenhanges zwischen 2 metrischen Merkmalen X und Y wird der Korrelationskoeffizient nach Bravais-Pearson rXY nach folgender Rechenvorschrift berechnet:
Y X
XY
XY s s
r = s
mit sXY = Kovarianz zwischen X und Y,
sX bzw. sY =Standardabweichung der Variable X bzw. Y.
Er verfügt über einen normierten Wertebereich von −1≤rXY ≤1. Je größer | rXY |, desto stärker ist der lineare Zusammenhang zwischen den beiden Variablen. Die Richtung des Zusammenhanges ist aus dem Vorzeichen des Korrelationskoeffizienten ersichtlich: Ist rXY>0, verläuft die Beziehung zwischen X und Y gleichläufig (positiver Zusammenhang), ist rXY<0, spricht man von einer gegenläufigen Beziehung (negativer Zusammenhang).
Eine alternative Kennzahl stellt der Korrelationskoeffizient nach Spearman rsp dar. Auch er quantifiziert die Stärke und Richtung des linearen Zusammenhanges zwischen 2 Merkmalen X und Y:
2 1
6 1 ( ² 1)
T t t sp
d
r T T
= − =
−
∑
mit dt =rg(xt)−rg(yt).
Er verfügt über den gleichen Wertebereich wie rXY und ist bezüglich Stärke und Richtung der Beziehung zwischen X und Y identisch zu interpretieren.
Um einen Zusammenhang zwischen 2 Merkmalen abschließend beurteilen zu können, wird die Durchführung eines statistischen Tests empfohlen. Dieser beurteilt, ob der Korrelationskoeffizient signifikant von 0 verschieden ist und somit von einem statistisch gesicherten Zusammenhang zwischen den beiden Merkmalen auszugehen ist. Getestet werden die Hypothesen
H0: rXY = 0 (bzw. rsp = 0) vs. H1: rXY ≠ 0 (bzw. rsp ≠ 0). H0 wird verworfen, wenn das realisierte Signifikanzniveau über der gedachten Irrtumswahrscheinlichkeit α (im ganzen Bericht α=0,05) liegt.
3.3 Multiple Regression
Mit Hilfe der Korrelationsanalyse ermittelt man, ob zwischen 2 Merkmalen ein Zusammenhang besteht. Jedoch ist damit noch keinerlei Aussage darüber getroffen, ob ein Merkmal als ursächlich für das andere Merkmal angesehen werden kann. Oft ist aber genau die Kenntnis einer funktionalen Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen von Belang. Die Regressionsanalyse beschäftigt sich mit der Spezifizierung der Form einer Beziehung zwischen metrischen Merkmalen.
Bei der einfachen linearen Regressionsanalyse wird die Beziehung zwischen einer abhängigen Variable Y (Regressand, zu erklärende Variable) und einer unabhängigen Variable (Regressor, erklärende Variable) quantifiziert. Dabei wird eine Regressionsfunktion
t t
t a bx u
y = + +
gesucht, welche die Abhängigkeit zwischen den Variablen möglichst gut widerspiegelt. Die unbekannten Größen a und b heißen Regressionskoeffizienten, wobei a den Ordinatenabschnitt darstellt (konstantes Glied) und b der Steigungsparameter der Funktion ist.
Die Größe ut gibt die nicht durch die Regressionsbeziehung erklärten Teile der Beobachtungswerte der abhängigen Variable Y wieder und wird als Residuum bezeichnet. Sie wird berechnet, in dem die senkrechten Abweichungen der Beobachtungswerte yt von den korrespondierenden Schätzwerten yˆt der Regressionsbeziehung gebildet werden:
ˆt t ˆt u = −y y
mit yˆt = +a bxˆ ˆ t .
Die Regressionskoeffizienten a und b werden nun so festgelegt, dass die Summe der quadrierten Residuen
∑
= T
t
ut 1
2 minimal wird und somit die Regressionsfunktion optimal an die Tendenz der Punktewolke angepasst wird. Dieses Vorgehen wird als Methode der Kleinsten Quadrate (auch bekannt als KQ-Methode, Maximum-Likelihood- Schätzung oder GLS-Methode) bezeichnet. Stehen für die Ermittlung
der Regressionskoeffizienten nicht die gesamten Daten der Grundgesamtheit sondern nur eine Stichprobe daraus zur Verfügung, stellen die mit der KQ-Methode ermittelten Regressionskoeffizienten aˆ und bˆ nur Schätzungen für die wahren Parameter a und b der Grundgesamtheit dar. Die Anwendung der KQ-Methode führt zu erwartungstreuen bzw. effizienten Ergebnissen, wenn die Residuen folgende Anforderungen erfüllen:
- der Erwartungswert der Residuen soll 0 betragen (d.h. alle relevanten erklärenden Variablen sind im Regressionsmodell berücksichtigt),
- die Varianz der Residuen soll konstant sein, - die Residuen sollen normalverteilt sein und
- es soll keine Autokorrelation der Residuen existieren.
Daher ist die Analyse der Residuen unerlässlich, muss aber in diesem Bericht unterbleiben.
Des Weiteren dürfen die unabhängigen Variablen nicht mit den Residuen korreliert sein und selber untereinander nicht stark korreliert sein. Die Existenz von Ausreißern im Datenmaterial beeinflusst die Lage und den Verlauf der geschätzten Regressionsfunktion, weshalb ihr Einfluss bei der Aufstellung der Funktion berücksichtigt werden muss.
Treten in der Beziehung zwischen 2 Variablen Nichtlinearitäten auf, lassen sich diese durch geeignete Transformationen der abhängigen und unabhängigen Variable beseitigen und die Regressionsparameter mit Hilfe der KQ-Methode schätzen, so lange die Regressionsfunktion linear in den Parametern bleibt.
Um den Aussagegehalt einer Regressionsanalyse zu steigern, erscheint es oft zweckmäßig, mehrere unabhängige Variablen xi mit i=1,...,n zur Erklärung der abhängigen Variable heranzuziehen (multiple Regression). Die in der gesuchten Regressionsgleichung
t n
i it i
t a bx u
y = +
∑
+=1
unbekannten Parameter a und bi werden auch hier mit Hilfe der KQ- Methode geschätzt.
Im Anschluss daran ist es wünschenswert, eine globale Einschätzung über die Güte der Anpassung der Regression zu erhalten. Ein geeignetes Maß ist das Bestimmtheitsmaß R², welches über einen normierten Wertebereich 0≤R²≤1 verfügt und zum Vergleich der Güte der Anpassung genutzt werden kann. R² gibt dabei das Verhältnis der durch die Regression erklärten Varianz der unabhängigen Variable und der Gesamtvarianz der unabhängigen Variable an:
∑
∑
=
=
−
−
= T
t t T
t t
y y
y y R
1
2 1
2
) (
ˆ ) (
² .
Die Güte der Anpassung erhöht sich mit größerem R². Ist R² = 1, so kann mit Hilfe der Regressionsbeziehung keinerlei Aussage über Y getroffen werden. Ist R² = 0, liegen alle Beobachtungswerte auf der Regressionsebene.
Um zu überprüfen, ob das Regressionsmodell statistisch gesicherte Ergebnisse liefern kann, werden sowohl der F-Test für das Gesamtmodell als auch t-Tests für jede unabhängige Variable durchgeführt. Dabei überprüft der F-Test, ob das aufgestellte Regressionsmodell gesichert ist. Dies ist dann nicht der Fall, wenn die unabhängigen Variablen keinen Einfluss auf die abhängige Variable haben (also die Parameterschätzwerte der unabhängigen Variablen bˆi nur zufallsbedingt von 0 verschieden sind) und man für die Grundgesamtheit nicht auf einen gesicherten Zusammenhang schließen kann. Somit wird folgendes Testproblem aufgestellt:
H0: bi = 0 für alle i = 1,...,n vs.
H1: bi ≠ 0 für mindestens ein i.
H0 wird verworfen, wenn die gedachte Irrtumswahrscheinlichkeit α das realisierte Signifikanzniveau überschreitet.
Mit Hilfe des t-Tests kann für jede unabhängige Variable separat geprüft werden, ob sie über einen statistisch gesicherten Einfluss auf die abhängige Variable verfügt (also ihr Regressionsparameter bˆi signifikant von 0 abweicht). Für eine beliebige unabhängige Variable xi lautet das Testproblem:
H0: bi = 0 vs.
H1: bi ≠ 0 .
Die Testentscheidung ist analog zum F-Test zu treffen.
Erst wenn durch Anwendung der Tests festgestellt ist, dass das Regressionsmodell statistisch gesicherte Ergebnisse liefert, kann es für Prognosezwecke genutzt werden. Stehen gleichzeitig mehrere statistisch gesicherte Regressionsmodelle zur Prognose zur Verfügung, sollte dasjenige mit dem größten Bestimmtheitsmaß genutzt werden.
4. Auswertung des Datensatzes 4.1 Deskriptive Statistik
Durch Anwendung von deskriptiven Maßzahlen soll nun die Lage, Variabilität und Schiefe jeder einzelnen Ausgangsvariablen ermittelt werden. Eine Übersicht darüber gibt Tabelle 2 und eine kurze graphische Zusammenfassung des Datensatzes ist in Abbildung 1 ersichtlich.
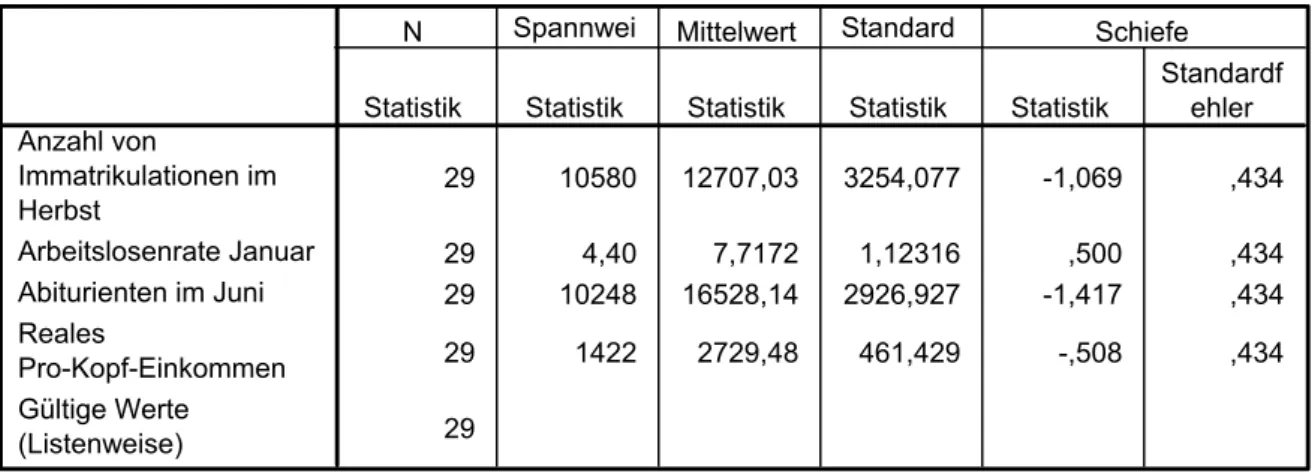
Tabelle 2: Deskriptive Auswertungen der Ausgangsvariablen
Deskriptive Statistik
29 10580 12707,03 3254,077 -1,069 ,434
29 4,40 7,7172 1,12316 ,500 ,434
29 10248 16528,14 2926,927 -1,417 ,434
29 1422 2729,48 461,429 -,508 ,434
29 Anzahl von
Immatrikulationen im Herbst
Arbeitslosenrate Januar Abiturienten im Juni Reales
Pro-Kopf-Einkommen Gültige Werte (Listenweise)
Statistik Statistik Statistik Statistik Statistik
Standardf ehler
N Spannwei Mittelwert Standard Schiefe
Für die Anzahl der Immatrikulationen kann über alle Zeitpunkte hinweg festgestellt werden, dass sich im Durchschnitt 10580 Studenten jedes Wintersemester neu eingeschrieben haben. Dabei streuen die Neuimmatrikulationen im Durchschnitt mit 3254 Studenten² relativ stark um den Mittelwert. Wie auch aus dem Boxplot erkenntlich ist, konzentriert sich die obere Hälfte der Verteilung auf einen engen Wertebereich. Das Schiefemaß ist negativ und daher ist die Variable Neuimmatrikulationen als rechtsschief anzusehen.
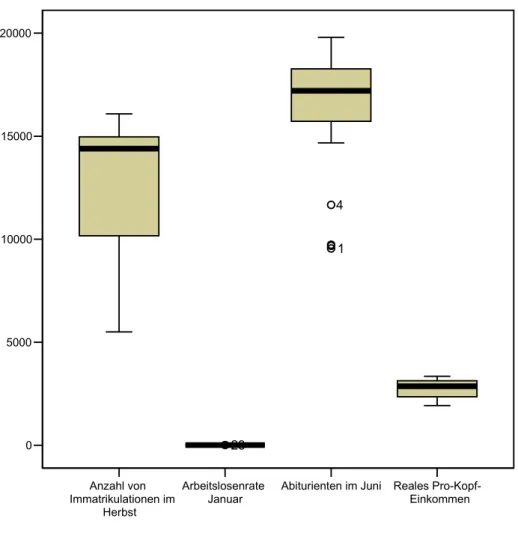
Abbildung 1: Boxplots der Ausgangsvariablen
Anzahl von Immatrikulationen im
Herbst
Arbeitslosenrate Januar
Abiturienten im Juni Reales Pro-Kopf- Einkommen 0
5000 10000 15000 20000
23
1 4
Über den Zeitraum 1961-1989 beträgt die durchschnittliche Arbeitslosenrate 4,4%. Die Standardabweichung ist gering und liegt bei 1,123%². Das Schiefemaß ist positiv und deutet auf eine leicht linksschiefe Verteilung hin.
Im Gegensatz dazu muss man bei der Zahl der Abiturienten von einer rechtsschiefen Verteilung ausgehen, da das Schiefemaß
negativ ist. Im Boxplot ist dies durch ein in der oberen Hälfte der Box liegendes arithmetisches Mittel ersichtlich. Weiterhin sind im Boxplot potentielle Ausreißer ausgewiesen. Dabei handelt es sich um die ersten 4 Zeitpunkte. Bei der Betrachtung des Streudiagramms muss entscheiden werden, ob diese 4 Werte aus der Analyse zu entfernen sind. Durchschnittlich bestehen 10248 Studenten ihr Abitur im Juni.
Damit ist die Zahl der Abiturienten geringfügig niedriger als die Zahl der Neuimmatrikulationen, was darauf hindeutet, dass auch Studenten aus anderen Bundesstaaten an der Universität ihr Studium beginnen.
Für das reale Pro-Kopf-Einkommen kann ein Durchschnitt von 1422 $ ermittelt werden. Die Standardabweichung liegt bei 461,43 $² und die Häufigkeitsverteilung ist leicht rechtsschief.
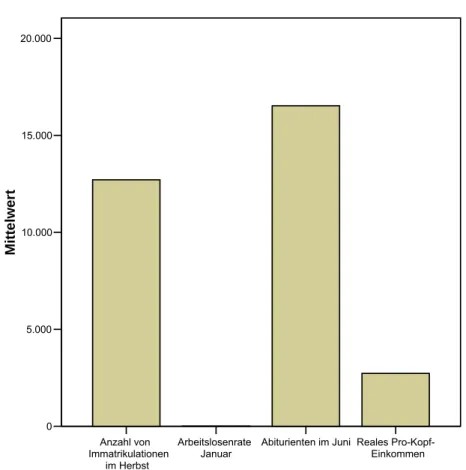
Zur zusammenfassenden Darstellung des Größenverhältnisses zwischen den Mittelwerten der einzelnen Variablen dient Abbildung 2.
Abbildung 2: Größenverhältnis der Mittelwerte (I)
Anzahl von Immatrikulationen
im Herbst
Arbeitslosenrate
Januar Abiturienten im Juni Reales Pro-Kopf- Einkommen 0
5.000 10.000 15.000 20.000
Mittelwert
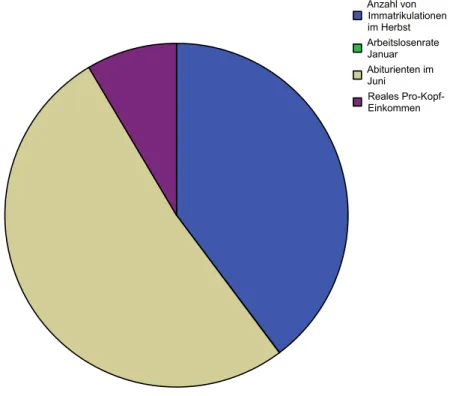
Einen besonderen Aspekt der Herkunft der Studenten beleuchtet Abbildung 3. Hier ist deutlich ersichtlich, dass der Großteil der Abiturienten aus dem Bundesstaat New Mexico stammt, aber kleiner als die Zahl der Neuimmatrikulationen ist.
Abbildung 3: Größenverhältnis der Mittelwerte (II)
Anzahl von Immatrikulationen im Herbst Arbeitslosenrate Januar Abiturienten im Juni
Reales Pro-Kopf- Einkommen
4.2 Korrelationsanalyse
Die Anwendung der Korrelationsanalyse verfolgt das Ziel, aus den vorliegenden Variablen diejenigen auszuwählen, die mit der Anzahl der Neuimmatrikulationen korrelieren und die somit für die Aufnahme in ein Regressionsmodell in Frage kommen.
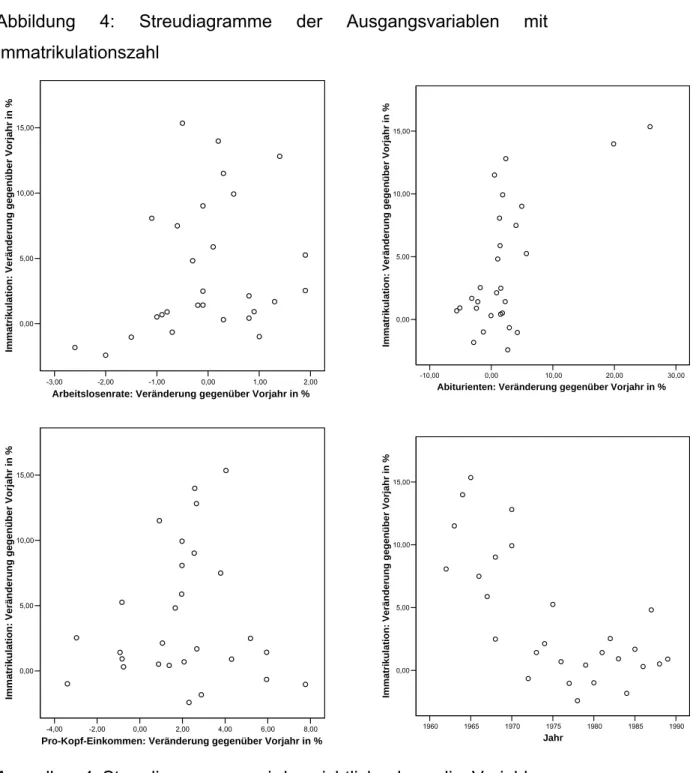
Dazu werden in einem ersten Schritt alle Streudiagramme ausgewertet, die den Streuungsverbund der Variablen Arbeitslosenrate, Abiturientenzahl, reales Pro-Kopf-Einkommen und Jahr mit der Variable Immatrikulationszahl zeigen. Anschließend werden die Korrelationsmatrizen nach Bravais-Pearson und Spearman berechnet, um die in den Streudiagrammen deutlich werdenden Zusammenhänge mit der Variable Immatrikulationen zu quantifizieren.
-10,00 0,00 10,00 20,00 30,00
Abiturienten: Veränderung gegenüber Vorjahr in %
0,00 5,00 10,00 15,00
Immatrikulation: Veränderung gegenüber Vorjahr in %
1960 1965 1970 1975 1980 1985 1990
Jahr
0,00 5,00 10,00 15,00
Immatrikulation: Veränderung gegenüber Vorjahr in %
Abbildung 4: Streudiagramme der Ausgangsvariablen mit Immatrikulationszahl
-3,00 -2,00 -1,00 0,00 1,00 2,00
Arbeitslosenrate: Veränderung gegenüber Vorjahr in % 0,00
5,00 10,00 15,00
Immatrikulation: Veränderung gegenüber Vorjahr in %
-4,00 -2,00 0,00 2,00 4,00 6,00 8,00
Pro-Kopf-Einkommen: Veränderung gegenüber Vorjahr in % 0,00
5,00 10,00 15,00
Immatrikulation: Veränderung gegenüber Vorjahr in %
Aus allen 4 Streudiagrammen wird ersichtlich, dass die Variablen einen deutlich positiven und somit gleichläufigen Zusammenhang zur Zahl der Immatrikulationen haben. Die in Kapitel 4.1 beschriebenen 4 potentiellen Ausreißer bei der Variable Abiturienten werden im Streudiagramm nicht ersichtlich bzw. unterstützen den positiven Zusammenhang mit der Variable Neuimmatrikulationen und müssen daher nicht ausgeschlossen werden.
Demzufolge sollten die Korrelationsmatrizen positive Korrelationskoeffizienten mit der Variable Neuimmatrikulationen
ausweisen. Wie in Tabelle 3 zu sehen ist, wurden auch nur positive Korrelationskoeffizienten berechnet. Mit den Variablen Abiturienten und reales Pro-Kopf-Einkommen korreliert die Anzahl der Neuimmatrikulationen hochsignifikant und nahezu perfekt linear (rXY=0,890 bzw. rXY=0,950). Nur die Korrelation mit der Variable Arbeitslosenrate ist gering (rXY=0,391). Auch die Nullhypothese kann für den Korrelationskoeffizienten zwischen Arbeitslosenrate und Anzahl der Immatrikulationen bei einem realisierten Signifikanzniveau von 36% nicht verworfen werden. Somit dürfte die Variable Arbeitslosenrate nicht in die Regressionsanalyse einbezogen werden.
Tabelle 3: Korrelationsmatrix nach Bravais-Pearson
Korrelationen
1 ,391* ,890** ,950**
,036 ,000 ,000
29 29 29 29
,391* 1 ,177 ,282
,036 ,357 ,138
29 29 29 29
,890** ,177 1 ,820**
,000 ,357 ,000
29 29 29 29
,950** ,282 ,820** 1
,000 ,138 ,000
29 29 29 29
Korrelation nach Pearson Signifikanz (2-seitig) N
Korrelation nach Pearson Signifikanz (2-seitig) N
Korrelation nach Pearson Signifikanz (2-seitig) N
Korrelation nach Pearson Signifikanz (2-seitig) N
Anzahl von Immatrikulationen im Herbst
Arbeitslosenrate Januar
Abiturienten im Juni
Reales
Pro-Kopf-Einkommen
Anzahl von Immatrikulatio nen im Herbst
Arbeitslosen rate Januar
Abiturienten im Juni
Reales Pro-Kopf- Einkommen
Die Korrelation ist auf dem Niveau von 0,05 (2-seitig) signifikant.
*.
Die Korrelation ist auf dem Niveau von 0,01 (2-seitig) signifikant.
**.
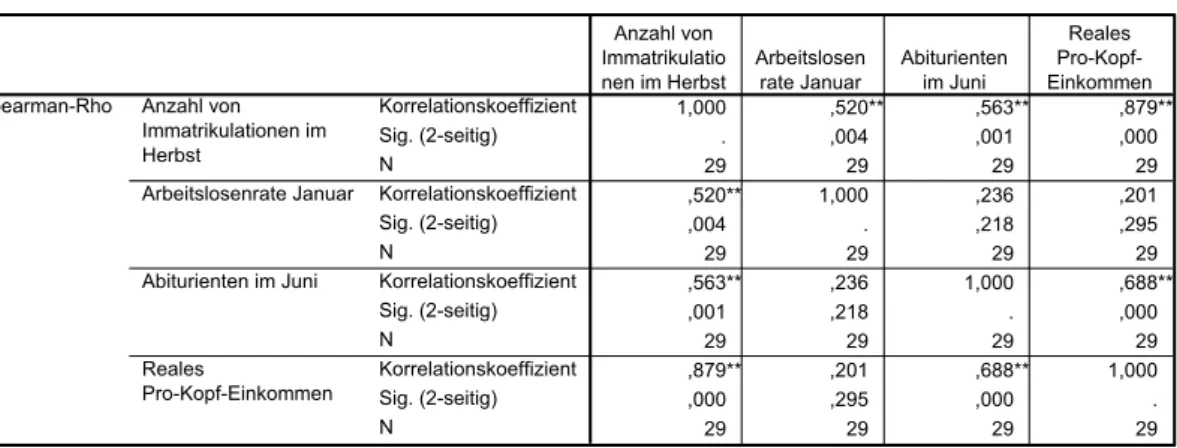
Tabelle 4: Korrelationsmatrix nach Spearman
Korrelationen
1,000 ,520** ,563** ,879**
. ,004 ,001 ,000
29 29 29 29
,520** 1,000 ,236 ,201
,004 . ,218 ,295
29 29 29 29
,563** ,236 1,000 ,688**
,001 ,218 . ,000
29 29 29 29
,879** ,201 ,688** 1,000
,000 ,295 ,000 .
29 29 29 29
Korrelationskoeffizient Sig. (2-seitig) N
Korrelationskoeffizient Sig. (2-seitig) N
Korrelationskoeffizient Sig. (2-seitig) N
Korrelationskoeffizient Sig. (2-seitig) N
Anzahl von Immatrikulationen im Herbst
Arbeitslosenrate Januar
Abiturienten im Juni
Reales
Pro-Kopf-Einkommen Spearman-Rho
Anzahl von Immatrikulatio nen im Herbst
Arbeitslosen rate Januar
Abiturienten im Juni
Reales Pro-Kopf- Einkommen
Die Korrelation ist auf dem 0,01 Niveau signifikant (zweiseitig).
**.
Berechnet man allerdings für Kontrollzwecke die Korrelationsmatrix nach Spearman (vgl. Tabelle 4), wird die Stärke des linearen Zusammenhanges zwischen der Arbeitslosenrate und der Anzahl der Immatrikulationen (rsp=0,520) wieder als hochsignifikant eingestuft.
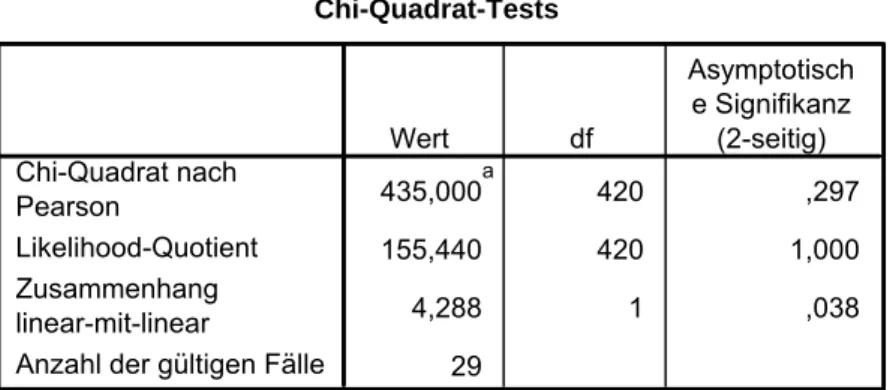
Für die übrigen Variablen ergeben sich keine gravierenden Abweichungen. Um nun abschließend beurteilen zu können, ob die Variable Arbeitslosenrate in die Regressionsanalyse aufgenommen werden kann, wurde ein Chi-Quadrat-Unabhängigkeitstest zwischen den Variablen Arbeitslosenrate und Neuimmatrikulationen vorgenommen. Das Ergebnis in Tabelle 5 zeigt, dass von einem signifikanten Zusammenhang zwischen den beiden Variablen auszugehen ist und somit die Variable Arbeitslosenrate für die Regressionsanalyse berücksichtigt werden kann.
Tabelle 5: Chi-Quadrat-Unabhängigkeitstest zwischen Arbeits- losenrate und Immatrikulationszahl
Chi-Quadrat-Tests
435,000a 420 ,297
155,440 420 1,000
4,288 1 ,038
29 Chi-Quadrat nach
Pearson
Likelihood-Quotient Zusammenhang linear-mit-linear
Anzahl der gültigen Fälle
Wert df
Asymptotisch e Signifikanz
(2-seitig)
464 Zellen (100,0%) haben eine erwartete Häufigkeit kleiner 5. Die minimale erwartete Häufigkeit ist ,03.
a.
Insgesamt ist festzustellen, dass alle Variablen mit der Anzahl der Neuimmatrikulationen korreliert sind und somit für die Regressionsanalyse geeignet sind. Es zeigt sich in den Korrelationsmatrizen, dass die Korrelationen der Variablen Arbeitslosenrate, Abiturienten und reales Pro-Kopf-Einkommen untereinander erfreulich niedrig sind, so dass keine Verletzungen der Annahmen der KQ-Methode zu befürchten sind.
4.3 Multiple Regression
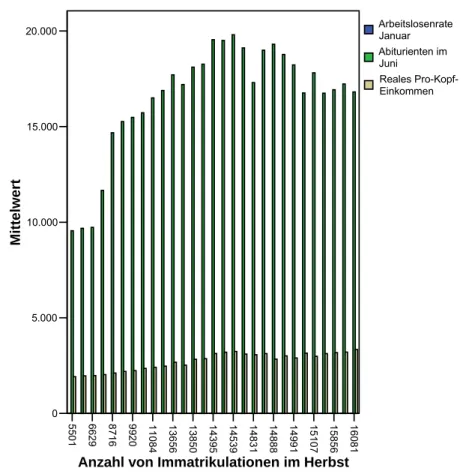
Durch die Anwendung der Regressionsanalyse soll nun der funktionale Zusammenhang zwischen der abhängigen und mehreren unabhängigen Variablen ermittelt werden. Da die Zahl der Immatrikulationen zu prognostizieren ist, stellt diese Variable die unabhängige Variable dar. Als erklärende Variable können die Arbeitslosenrate, die Abiturienten, das reale Pro-Kopf-Einkommen und das Jahr herangezogen werden. Das Histogramm in Abbildung 5 stellt das Zusammenwirken aller erklärenden Variablen bzgl. der zu erklärenden Variable Neuimmatrikulationen dar.
Abbildung 5: Histogramm
5501 6629 8716 9920 11084 13656 13850 14395 14539 14831 14888 14991 15107 15856 16081
Anzahl von Immatrikulationen im Herbst
0 5.000 10.000 15.000 20.000
Mittelwert
Arbeitslosenrate Januar Abiturienten im Juni
Reales Pro-Kopf- Einkommen
Im Folgenden werden 2 Regressionsmodelle mit verschiedenen erklärenden Variablen aufgestellt und mittels der in Kapitel 3.3 beschriebenen Vorgehensweise bewertet.
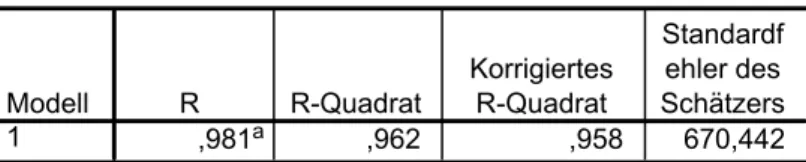
Das erste Modell berücksichtigt als unabhängige Variable die Arbeitslosenrate, die Abiturientenzahl und das reale Pro-Kopf- Einkommen. Tabelle 6 gibt die notwendigen Kennzahlen zur Bewertung des Regressionszusammenhanges an. Es ist zu
erkennen, dass mit diesem Modell bereits 96,2% der Streuung der Variable Neuimmatrikulationen durch die Regression erklärt werden kann. Dem zu Folge bestätigt der F-Test das aufgestellte Gesamtmodell.
Tabelle 6: SPSS-Output des Regressionsmodells 1
Modellzusammenfassungb
,981a ,962 ,958 670,442
Modell
1 R R-Quadrat
Korrigiertes R-Quadrat
Standardf ehler des Schätzers Einflußvariablen : (Konstante), Reales
Pro-Kopf-Einkommen, Arbeitslosenrate Januar, Abiturienten im Juni
a.
Abhängige Variable: Anzahl von Immatrikulationen im Herbst
b.
ANOVAb
2,9E+08 3 95085055 211,539 ,000a
1,1E+07 25 449492,51
3,0E+08 28
Regression Residuen Gesamt Modell
1
Quadrats
umme df
Mittel der
Quadrate F Signifikanz
Einflußvariablen : (Konstante), Reales Pro-Kopf-Einkommen, Arbeitslosenrate Januar, Abiturienten im Juni
a.
Abhängige Variable: Anzahl von Immatrikulationen im Herbst b.
Koeffizientena
-9153,254 1053,181 -8,691 ,000
450,125 118,168 ,155 3,809 ,001
,406 ,076 ,366 5,347 ,000
4,275 ,495 ,606 8,642 ,000
(Konstante)
Arbeitslosenrate Januar Abiturienten im Juni Reales
Pro-Kopf-Einkommen Modell
1
B
Standardf ehler Nicht standardisierte
Koeffizienten
Beta Standardisie
rte Koeffizienten
T Signifikanz
Abhängige Variable: Anzahl von Immatrikulationen im Herbst a.
Die auf Grund der KQ-Schätzung ermittelte Regressionsfunktion lautet:
1 2 3
ˆt 9153, 254 450,125 4, 06 4, 275
y = − + x + x + x
mit yt = Anzahl der Immatrikulationen, x1 = Arbeitslosenrate,
x2 = Abiturienten,
x3 = Reales Pro-Kopf-Einkommen.
Durch die Analyse der Ergebnisse des t-Tests kann man davon ausgehen, dass jede Variable isoliert einen Einfluss auf die abhängige Variable hat. Auch die Koeffizienten erscheinen plausibel.
Steigt die Zahl der Abiturienten um eine Person, so steigt die Anzahl der Neuimmatrikulationen durchschnittlich um 4,06 Personen. Auch der Einfluss der Studiengebühren auf das Studierverhalten wird ersichtlich: Sinkt das Pro-Kopf-Einkommen um 1$, so ist mit 4,275 Studenten weniger bei der Neueinschreibung zu rechnen.
Erklärungsbedürftig ist der Koeffizient für die Arbeitslosenrate: Steigt sie um 1%, schreiben sich rund 450 Studenten mehr ein. Dies kann damit erklärt werden, dass die Chancen auf eine Arbeit bei hoher Arbeitslosigkeit für Nicht-Akademiker geringer sind. Einzig das Absolutglied entzieht sich einer Interpretation.
In einem zweiten Modell geht man von der Überlegung aus, dass auch ein zeitlicher Trend in den Daten zu berücksichtigen sein könnte. Daher werden als unabhängige Variable die Arbeitslosenrate und Abiturienten berücksichtigt. Die Variable reales Pro-Kopf- Einkommen wird durch die Variable Jahr ersetzt. Die Outputs sind in Tabelle 7 enthalten.
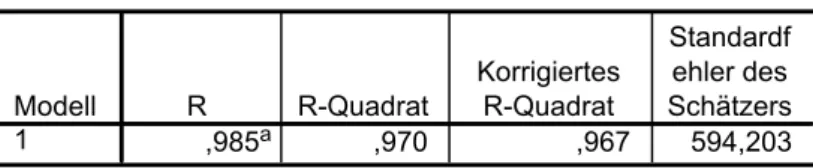
Durch die Substitution der Variable reales Pro-Kopf-Einkommen mit der Variablen Jahr können nun bereits 98,5% der Varianz der abhängigen Variable erklärt werden. Der F-Test weist analoge Werte zum Modell 1 aus. Die ermittelte Regressionsgleichung lautet:
1 2 3
ˆt 1096,157 108, 678 0, 052 19, 011
y = + x + x + x
mit yt = Anzahl der Immatrikulationen, x1 = Arbeitslosenrate,
x2 = Abiturienten, x3 = Jahr.
Mit der neuen Variablen Jahr ist ein deutliches Abweichen der Regressionskoeffizienten vom Modell 1 bemerkbar. Das Absolutglied ändert sein Vorzeichen und lässt sich nun als autonome (von den Merkmalsausprägungen der anderen Variablen unabhängige) Immatrikulationszahl beschreiben. Der Einfluss der Arbeitslosenrate
und der Abiturientenzahl sinkt im Vergleich zu Modell 1. Der Regressionskoeffizient für die Variable Jahr muss wie folgt interpretiert werden: Jedes Jahr schreiben sich durchschnittlich 19,011 Studenten mehr an der Universität New Mexico ein. Die Ergebnisse des t-Testes sind allerdings ernüchternd. Nur für das Absolutglied kann die Alternativhypothese verworfen werden (denn nur hier ist das realisiertes Signifikanzniveau > α). Damit scheint das Modell 2 für Prognosezwecke ungeeignet.
Tabelle 7: SPSS-Output des Regressionsmodells 2
Modellzusammenfassungb
,985a ,970 ,967 594,203
Modell 1
R R-Quadrat
Korrigiertes R-Quadrat
Standardf ehler des Schätzers Einflußvariablen : (Konstante), Jahr, Arbeitslosenrate Januar, Abiturienten im Juni
a.
Abhängige Variable: Anzahl von Immatrikulationen im Herbst
b.
ANOVAb
2,9E+08 3 95888514 271,579 ,000a
8826935 25 353077,40
3,0E+08 28
Regression Residuen Gesamt Modell
1
Quadrats
umme df
Mittel der
Quadrate F Signifikanz
Einflußvariablen : (Konstante), Jahr, Arbeitslosenrate Januar, Abiturienten im Juni a.
Abhängige Variable: Anzahl von Immatrikulationen im Herbst b.
Koeffizientena
-2380,397 1096,157 -2,172 ,040
308,593 108,678 ,107 2,839 ,009
,595 ,052 ,535 11,430 ,000
191,913 19,011 ,502 10,095 ,000
(Konstante)
Arbeitslosenrate Januar Abiturienten im Juni Jahr
Modell
1 B
Standardf ehler Nicht standardisierte
Koeffizienten
Beta Standardisie
rte Koeffizienten
T Signifikanz
Abhängige Variable: Anzahl von Immatrikulationen im Herbst a.
5. Zusammenfassung
Im vorliegenden Bericht sollte ein Regressionsmodell für die Vorhersage der Anzahl von Neuimmatrikulationen aufgestellt werden. Dazu konnten die mit den Immatrikulationen korrelierenden Variablen Arbeitslosenrate, Abiturientenzahl, reales Pro-Kopf- Einkommen und Jahr in verschiedenen Regressionsansätzen untersucht werden. Es stellte sich heraus, dass ein Regressionsansatz mit den unabhängigen Variablen Arbeitslosenrate, Abiturientenzahl und reales Pro-Kopf-Einkommen allen anderen Modellen überlegen ist und 98,1% der Gesamtstreuung der abhängigen Variable beschreibt. Nur er kann für die Prognose der Immatrikulationszahlen des aktuellen Wintersemesters verwendet werden, in dem in die Regressionsgleichung die aktuellen Merkmalsausprägungen der unabhängigen Variablen eingesetzt werden.
Eine Überprüfung des Regressionszusammenhanges in regelmäßigen zeitlichen Abständen erscheint trotzdem zweckmäßig.
Literaturverzeichnis
Eckey, H. F. / Kosfeld, R. / Dreger, C. (2002): Statistik - Grundlagen, Methoden, Beispiele, 3. Auflage, Gabler Verlag, Wiesbaden.
Bücker, R. (1997), Statistik für Wirtschaftswissenschaftler, 3. Aufl., Oldenbourg, München.
Backhaus, K. / Erichson, B. / Plinke, W. / Weiber, R. (2004):
Multivariate Analysemethoden – Eine anwendungsorientierte Einführung, 9. Auflage, Springer Verlag, Berlin.
1960 1965 1970 1975 1980 1985 1990
Jahr
5000 7500 10000 12500 15000 17500
Anzahl von Immatrikulationen im Herbst
Anhang
8000 10000 12000 14000 16000 18000 20000
Abiturienten im Juni
5000 7500 10000 12500 15000 17500
Anzahl von Immatrikulationen im Herbst
2000 2500 3000
Reales Pro-Kopf-Einkommen
5000 7500 10000 12500 15000 17500
Anzahl von Immatrikulationen im Herbst
Jahr Neuimma- trikulationen
Arbeistlosen-
rate Abiturienten
reales Pro- Kopf- Einkommen 1 5501 8,1 9552 1923 2 5945 7 9680 1961 3 6629 7,3 9731 1979 4 7556 7,5 11666 2030 5 8716 7 14675 2112 6 9369 6,4 15265 2192 7 9920 6,5 15484 2235 8 10167 6,4 15723 2351 9 11084 6,3 16501 2411 10 12504 7,7 16890 2475 11 13746 8,2 17203 2524 12 13656 7,5 17707 2674 13 13850 7,4 18108 2833 14 14145 8,2 18266 2863 15 14888 10,1 19308 2839 16 14991 9,2 18224 2898 17 14836 7,7 18997 3123 18 14478 5,7 19505 3195 19 14539 6,5 19800 3239 20 14395 7,5 19546 3129 21 14599 7,3 19117 3100 22 14969 9,2 18774 3008 23 15107 10,1 17813 2983 24 14831 7,5 17304 3069 25 15081 8,8 16756 3151 26 15127 9,1 16749 3127 27 15856 8,8 16925 3179 28 15938 7,8 17231 3207 29 16081 7 16816 3345