1.3. GRENZEN DER KLASSISCHEN PHYSIK. QUANTENEFFEKTE

1.3. GRENZEN DER KLASSISCHEN PHYSIK. QUANTENEFFEKTE 21 freien Elektron gestreut werden. In dieser Photonen-Hypothese ist der Compton-Effekt also ein Stoßprozess.

Abbildung 1.15: Lichtstreuung an freien Elektronen

Wir benutzen also die Energieerhaltung, wobei wir das Elektron als relativistisches Teilchen betrachten m¨ussen. Mit β =v/c gilt:

Eph =E_ph^′ +E_e^′ −Ee

~ω =~ω^′ +m0c² 1− 1 p1−β²

!

Außerdem benutzen wir die Impulserhaltung und setzen die Geschwindigkeit des Elektrons vor dem Stoß gleich 0.

~k =~k^′+ m0v^′ p1−β² Das Resultat ist:

λ^′ =λ+λC(1−cosϑ) (1.11)

fest. Hierbei istλC die sogenannte Compton-Wellenl¨ange f¨ur die gilt:

λC = h mc

Der Compton-Effekt ist also eine direkte Best¨atigung f¨ur die Photonen-Hypothese von Planck und Einstein.

Wir k¨onnen damit folgendes Fazit aus den Ph¨anomen A), B) und C) ziehen:

1. Die klassische Elektrodynamik erkl¨art makroskopische Ph¨anomene, wie Brechung oder Reflexion.

2. Mikroph¨anomene (Wechselwirkung Licht-Atom/Elektron) erfordern Annahmen ¨uber die Quanten-Natur (Photonen).

Moderne Theorie: Die moderne Theorie des elektromagnetischen Feldes ist die Quanten- elektrodynamik (2. Quantisierung). Hier ersetzt man die elektrodynamischen Potenziale (A,Φ) durch die Operatoren ( ˆA,Φ), welche die Maxwell-Gleichungen erf¨ullen, mit den Kommutati-ˆ onsregeln f¨ur bosonische Operatoren.

22 KAPITEL 1. EINLEITUNG

1.3.2 Quanteneigenschaften der Atome

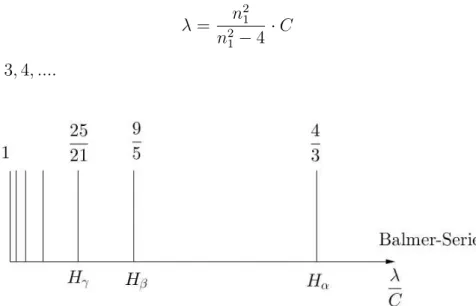
Jedes Atom hat ein charakteristischen Linienspektrum. 1885 stellteBalmerf¨ur die experimentell bestimmten Emissionsspektren von Wasserstoff eine Formel auf. Diese Formel beschreibt die Abst¨ande einiger gemessener Emissionslinien.

λ= n²₁ n²₁−4·C Hierbei ist n1 = 3,4, ....

Abbildung 1.16: Abst¨ande der Balmer-Serie des Emissionsspektrums von Wasserstoff Die Quantenmechanik liefert hierf¨ur die Erkl¨arung. Im Atom liegen die Energie-Niveaus gem¨aß ihrer Hauptquantenzahl in ebensolchen Abst¨anden. Eine Emissionslinie entspricht jetzt ei- nem ¨Ubergang von einem Energie Niveau auf ein anderes. Die Balmer-Serie beschreibt alle Uberg¨ange auf die Hauptquantenzahl¨ n = 2. F¨ur die anderen Quantenzahlen gibt es entspre- chende analoge Serien (s. Kapitel 5).

Abbildung 1.17: Diskrete Energie-Niveaus gem¨aß der Hauptquantenzahl n

1913 gelang Franck und Hertz der experimentelle Nachweis diskreter Niveaus durch Stoßan- regung von Atomen. Das klassische Atommodell von Rutherford und Thomson besagte, dass das Atom insgesamt neutral ist und einen kleinen positiven Kern besitzt. Diese Vorstellung gestattete die korrekte Beschreibung der Streuung von α-Teilchen an einer d¨unnen Goldfolie (Rutherford-Formel). Nach diesem Ergebnis m¨ussen nun negative Ladungen im Atom existie- ren, damit dieses neutral ist. Offen blieb die Frage, wie diese Ladungen (Elektronen) im Kern verteilt sind, wobei man wusste, dass das Atom weitgehend “leer” ist.

Die naheliegende Idee war, dass sich die Elektronen analog zu Planeten auf Kreisbahnen (auf Ellipsen um die Sonne) um den Kern bewegen. Das Problem an diesem Modell ist, dass ein sol- ches Atom aber instabil ist. Dies sehen wir im Folgenden ein. Ein rotierendes Elektron vollf¨uhrt

1.3. GRENZEN DER KLASSISCHEN PHYSIK. QUANTENEFFEKTE 23 eine beschleunigte Bewegung ( ¨Anderung der Richtung). Es stellt einen elektromagnetischen Di- pol, welcher Strahlung emittiert, dar. Der Energieverlust ergibt sich nach der Elektrodynamik zu:

dE

dt =− 2 3c³|¨p|²

Mit diesem Energieverlust ist das Planeten-Modell instabil. Betrachte nun:

|F_Z|=|F_{COU L}| mv²

r = Ze·e 4πǫ0r²

Mit Hilfe dieses Kr¨aftegleichgewichtes einer Kreisbahn ohne Strahlung kann man die charak- teristische Lebensdauer eines Atoms nach diesem Modell absch¨atzen. Es ergeben sich Zeiten von:

t≈10⁻¹¹s· 1 Z⁴

Dieses Ergebnis widerspricht nat¨urlich den Erkenntnissen der Stabilit¨at der Atome. N. Bohr versuchte, dies in seinem Atommodell zu “begr¨unden” durch folgende Postulate.

1. Es existieren stabile (strahlungsfreie) Bahnen. Die Auswahl erfolgt gem¨aß:

rn·pn

| {z }

Ln

=n·~ (1.12)

Hierbei istn ∈Zund Ln der Betrag des Drehimpulses. Es existieren also nur bestimmte Bahnen, da der Drehimpuls nur bestimmte diskrete Werte annehmen kann.

2. Der ¨Ubergang zwischen Bahnen geschieht nicht allm¨ahlich, sondern durch Emission eines Photons:

~ωm,n =Em−En

Dies erkl¨art die Balmer-Serie sowie das komplette Spektrum wasserstoff¨ahnlicher Atome.

3. Die klassisch stabilen Bahnen sind bestimmt durch:

mev²

r = Ze² 4πǫ0r² Mit dem ersten Postulat ergibt sich

p²r² = Ze²mer 4πǫ0

=n²~²

mit n= 1,2, .... Hiermit lassen sich die erlaubten Radien berechnen:

rn =ab

n²

Z (1.13)

Hierbei ist aB der Bohr-Radius:

aB = ~² me

4πǫ₀

e² (1.14)

Die Energie auf der n-ten Bahn wird dann zu:

En =−1 2

e² 4πǫ0aB

Z² n²

Das Bohr’sche Atommodell erkl¨art zwar die Grundz¨uge des Linienspektrums, enth¨alt aber nur einen kleinen Teil der m¨oglichen elektronischen Zust¨ande im Atom. Außerdem ist der Charakter der Elektronen“bahnen” falsch. Die Quantenmechanik ergibt hingegen, dass das Elektron kein Punktteilchen, sondern r¨aumlich ausgedehnt ist.

24 KAPITEL 1. EINLEITUNG

1.3.3 Beugung freier Elektronen

1927 machten Davisson und Germer Versuche zur Elektronenbeugung am Kristallgitter.

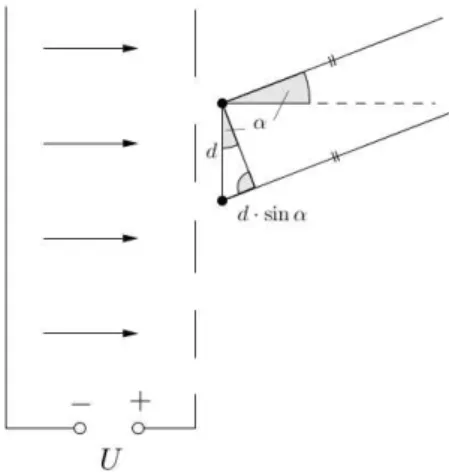
Abbildung 1.18: Versuchs-Skizze zur Beugung von Elektronen am Kristallgitter Mit der Spannung U kann, gem¨aß

m

2v² =e·U ,

die Energie der Elektronen berechnet werden. Auf dem Schirm sieht man ein Interferenzmuster, wenn man die Intensit¨at auftr¨agt. Hierbei sind x die ganzen Zahlen, bei denen ein Maximum auftritt.

Abbildung 1.19: Intensit¨atsverteilung der Elektronenbeugung

Die Geschwindigkeit der Elektronen kann durch die Spannung eingestellt werden. Man stellt fest, dass die Lage der Maxima bei unterschiedlichen Geschwindigkeiten bei unterschiedlichen x liegen und kann folgende Beziehung herleiten:

x= me·U

h ·dsinα. (1.15)

Dies ist typisch f¨ur Beugung. Bei Licht erh¨alt man die Formel f¨ur die Maxima zu:

dsinα =xλ

Hierbei sind wiederx die Maxima. Man kann also auch Elektronen eine Wellenl¨ange zuordnen, wenn man beide Gleichungen vergleicht und erh¨alt:

λe= h

me·v = h pe

(1.16) Dies geht auf DeBroglie (1924) zur¨uck. Indem man Elektronen eine Wellenl¨ange zuordnet, erkl¨art man die beobachteten Interferenzeffekte am Kristallgitter.

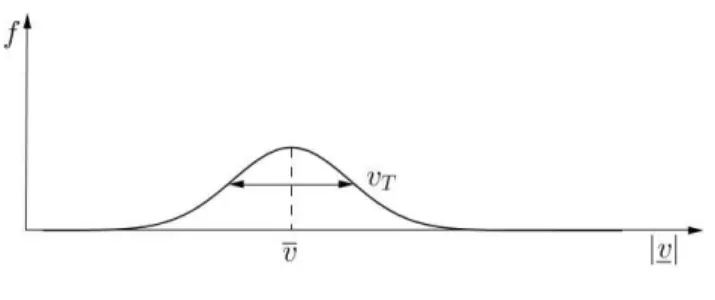
1.3. GRENZEN DER KLASSISCHEN PHYSIK. QUANTENEFFEKTE 25 Beispiel: Betrachten wir ein Elektronengas im Gleichgewicht. Die Geschwindigkeiten sind dann um einen Mittelwertv herum Maxwell-verteilt.

Abbildung 1.20: Maxwell-verteilte Geschwindigkeit Hieraus l¨asst sich mit der Beziehung

vT ≈

r2πkT m

f¨ur die charakteristische thermische Geschwindigkeit diethermische DeBroglie-Wellenl¨ange be- rechnen:

λT = h

√2πmkT.

Dies ist wichtig etwa f¨ur die Behandlung von dichten Gasen oder Plasmen, insbesondere f¨ur die Beschreibung von Sternen und Planeten. Der Entartungsparameter, den wir in Glg. (1.1) eingef¨uhrt hatten, sagt uns nun, dass quantenmechanische Eigenschaften wichtig werden, wenn

nλ³_T &1

gilt. Diese Beziehung l¨asst sich ¨ubertragen auf einen Zusammenhang zwischen Dichte und Tem- peratur, und sie trennt klassische von Quanten-Vielteilchensystemen [Bonitz, 2016].

Grenzen der klassischen Physik: Fazit

Dualismus von Welle und Teilchen bedeutet, dass Licht und Teilchen beide sowohl Licht- als auch Teilcheneigenschaften besitzten.

1. Licht

• Welleneigenschaften: ω, k

• Teilcheneigenschaften (Photonen): E =~ω, p=~k 2. Teilchen

• Teilcheneigenschaften: E, p

• Welleneigenschaften: λ= ^2π_k = _mv^h

Hiermit k¨onnen wir Quanteneffekte durch diese “naive Theorie” beschreiben und erkl¨aren. Eine strenge Erkl¨arung bzw. Ableitung geschah allerdings erst durch die Quantenmechanik, die vor allem von 1926-1928 vonHeisenberg, Schr¨odinger, Born, Dirac, Pauli, Jordan, Bohrund vielen anderen gepr¨agt wurde.

26 KAPITEL 1. EINLEITUNG

Kapitel 2

Grundlagen der Quantenmechanik

2.1 Doppelspaltexperiment mit klassischen Teilchen

Nehmen wir eine Quelle, die klassische Teilchen in zuf¨alliger Richtung aussendet. Diese gehen durch einen Doppelspalt und werden auf einem dahinter liegenden Detektor registriert. Wir f¨uhren N unabh¨angige Sch¨usse durch. Wir untersuchen drei Versuchsreihen mit:

1. Spalt 2 ist geschlossen. Spalt 1 ist offen.

2. Spalt 1 ist geschlossen. Spalt 2 ist offen.

3. beide Spalte sind ge¨offnet.

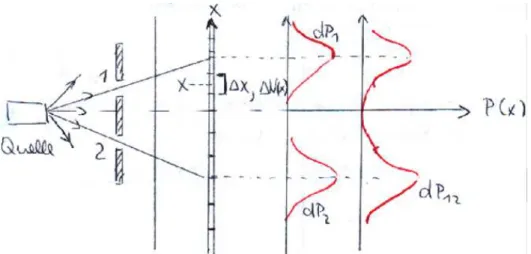
In untenstehender Abbildung ist der Versuchsaufbau sowie die gemessene Auftreff-H¨aufigkeitsverteilung skizziert.

Abbildung 2.1: Schema des Doppelspaltexperiments mit klassischen Teilchen. dP₁ ist die Auf- treffwahrscheinlichkeit (Mittel ¨uber N → ∞ Versuche) bei geschlossenem Spalt 2, dP2 das entsprechende Resultat bei geschlossenem Spalt 1. Wenn beide Spalte ge¨offnet sind, ergibt sich dP₁₂.

Das Einzelereignis (Auftreff-Ort x) ist nicht vorhersagbar. Aus der vom Detektor gemessenen absoluten Auftreff-H¨aufigkeit ∆N(x) gewinnen wir eine Wahrscheinlichkeitsverteilung durch Erh¨ohung der Zahl der Durchf¨uhrungenN des Versuchs und Mittelung ¨uber die Messwerte. Es ergibt sich f¨ur die drei Versuchsdurchf¨uhrungen:

27

28 KAPITEL 2. GRUNDLAGEN DER QUANTENMECHANIK 1. Die Wahrscheinlichkeit, dass das Objekt am Ort xauftrifft und durch den Spalt 1 gegan-

gen ist, betr¨agt:

dP1(x) = lim

N→∞

∆N₁(x) N

2. Die Wahrscheinlichkeit, dass das Objekt am Ort xauftrifft und durch den Spalt 2 gegan- gen ist, betr¨agt:

dP2(x) = lim

N→∞

∆N₂(x) N

3. In diesem Versuch geht das Objekt entweder durch Spalt 1 oder durch Spalt 2. Das Experiment zeigt:

dP1,2 =dP1(x) +dP2(x) (2.1)

= lim

N→∞

∆N1(x) + ∆N2(x) N

Wir halten also fest, dass die Gesamtwahrscheinlichkeit f¨ur klassische Teilchen die Summe der Einzelwahrscheinlichkeiten ist. Außerdem ist die relative Auftreff-H¨aufigkeit (Wahrscheinlich- keit) vorhersagbar. Dies macht Wahrscheinlichkeitstheorie zur Beschreibung n¨otig.

2.2 Einschub: Wahrscheinlichkeits-Theorie

A. Allgemeiner diskreter stochastischer Prozess

Sei unser System charakterisiert durch die zuf¨alligen m¨oglichen Ereignissex1, ..., xk; man nennt x={x1, ..., xk}auch dasEreignisfeld. Nach dem Beispiel von oben registriern wir jedes Ereignis in einer eigenen Spaltex1bisxk vorstellen. Eine Messung ist nun eine wiederholte Registrierung von Einzelereignissen mit anschließender Mittelung

Nr. n der Messung x1 x2 ... xk

1 x

2 x

...

n...

N x

Summe N1 N2 Nk

Tabelle 2.1: Messtabelle f¨ur das Ereignisfeld x (k verschiedene M¨oglichkeiten) bei N un- abh¨angigen Wiederholungen.

Offensichtlich gilt folgende Normierung:

N = Xk

i=1

Ni

2.2. EINSCHUB: WAHRSCHEINLICHKEITS-THEORIE 29 Die Wahrscheinlichkeit pi des i-ten Ereignisses erh¨alt man durch:

N→∞lim Ni

N =pi (2.2)

Jetzt folgt:

Xk i=1

pi = 1, (2.3)

wobei f¨ur jedes 1≤i≤k gilt:

0≤pi ≤1 (2.4)

Hierbei nennt manp= 0 ein unm¨ogliches Ereignis und p= 1 ein sicheres Ereignis.

Mittelwerte physikalischer Gr¨oßen: Nehmen wir an, jedes Ereignisxiist mit der Messung einer EnergieEi verkn¨upft. Der Erwartungswert f¨ur die Energie ist dann:

hEi= 1 N

XN n=1

En.

Dabei tritt jedes der k Ereignisse i.a. mehrmals (Ni-mal) auf. Sortieren wir dies nach den m¨oglichen verschiedenen Ereignissen um, so erhalten wir:

hEi= 1 N

Xk i=1

EiNi = Xk

i=1

Ei

Ni

N

F¨ur den Grenzwert N → ∞ erhalten wir dann mit (2.2):

hEi= Xk

i=1

Eipi (2.5)

Der Satz der Wahrscheinlichkeiten{pi}gen¨ugt also zur Berechnung beliebiger Erwartungswerte des stochastischen Prozesses.

B. Kontinuierliches Ereignisfeld

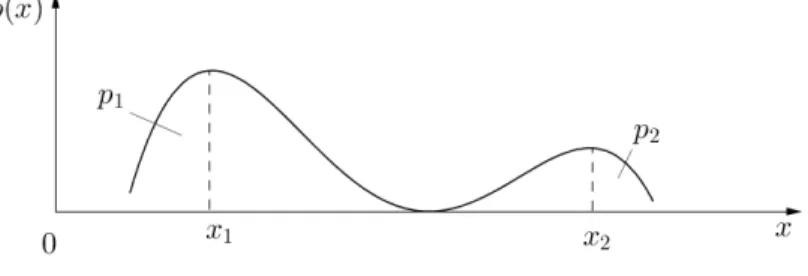
Nun betrachten wir nicht mehr endlich viele diskrete Ereignisse, sondern eine kontinuierliche Verteilung. In obigem Beispiel k¨onnte man sagen, dass es immer mehr immer kleinere Spalte gibt, wobei die Gesamtl¨ange Lunver¨andert bleibt.

Abbildung 2.2: Kontinuierliche Wahrscheinlichkeitsdichte als Grenzwert einer diskreten Vertei- lung.

30 KAPITEL 2. GRUNDLAGEN DER QUANTENMECHANIK Mit der Wahrscheinlichkeitsdichteρ(x) wird die Wahrscheinlichkeit bezeichnet, einen Messwert im Intervall [x1, x2] zu registrieren:

P(x1 ≤x≤x2) =

x₂

Z

x₁

ρ(x)dx

Die Wahrscheinlichkeit des Ereignissesx ist dann:

P(x) = Zx

0

ρ(x^′)dx^′

Differenziert man dies nach der oberen Grenze, so erh¨alt man eine alternative Definition der Wahrscheinlichkeitsdichte:

ρ(x) = dP(x) dx

Ist die Zufallsgr¨oße x verteilt von 0 bisL, so erfolgt die Normierung ¨uber:

1 = ZL

0

dP(x) = ZL

0

ρ(x)dx.

Der Mittelwert berechnet sich analog zur Summe, im diskreten Fall, nun ¨uber das Integral zu:

hEi= ZL

0

E(x)ρ(x)dx

C. Abh¨angige Einzelereignisse

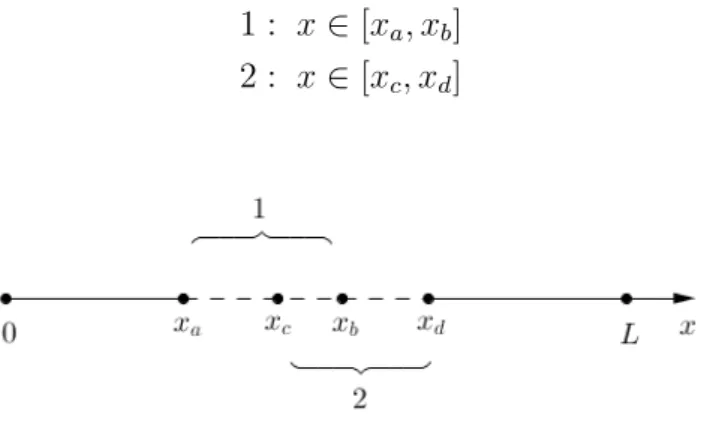
Wir betrachten jetzt eine allgemeinere Situation nicht unabh¨angiger Ereignisse. Stellen wir uns zwei ¨uberlappende Elemente auf dem Detektor vor:

1 : x∈[xa, xb] 2 : x∈[xc, xd]

Abbildung 2.3: Zwei sich ¨uberlappende Ereignisse (z.B. Detektor-Elemente) Die Wahrscheinlichkeit, dass das Ojekt auf Element 1 trifft, ist:

P⁽¹⁾=P(xa≤x≤xb), sowie auf Element 2:

P⁽²⁾=P(xc ≤xd).

2.3. DOPPELSPALTEXPERIMENT MIT WELLEN 31 Die WahrscheinlichkeitP^1,2, dass das Objekt entweder auf Element 1 oder Element 2 trifft, ist nun:

P^(1,2) =P⁽¹⁾+P⁽²⁾−P(1∪2)

=P⁽¹⁾+P⁽²⁾−P(xc ≤x≤xb) Die ¨Uberlapp-Menge der Ereignisse ist:

xc ≤x≤xb

Diese Doppelz¨ahlung muss inP^(1,2) ber¨ucksichtigt werden.

Frage: Wie ¨andert sich die Normierungsbedingung?

2.3 Doppelspaltexperiment mit Wellen

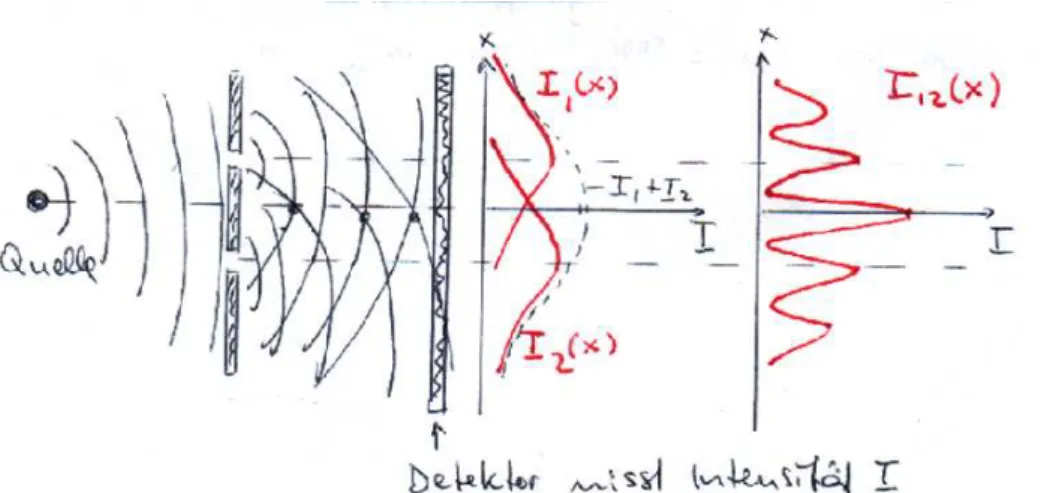
Nun betrachten wir das Doppelspalt-Experiment, welches wir zuvor f¨ur klassische Makroteilchen behandelt haben, f¨ur Wellen. Der Versuchsaufbau ist wieder derselbe, s. Abb. 2.4.

Abbildung 2.4: Doppelspaltexperiment mit Wellen und die gemessenen ortsabh¨angigen Inten- sit¨aten (schematisch)

Wir betrachten, wie oben in der Abbildung schon angedeutet, wieder:

1. Spalt 2 ist geschlossen. Spalt 1 ist offen. Wir messen die Intensit¨at I1(x).

2. Spalt 1 ist geschlossen. Spalt 2 ist offen. Wir messen die Intensit¨at I2(x).

3. Die Spalte 1 und 2 sind ge¨offnet. Offensichtlich gilt hier keine Additivit¨at:

I1,2 6=I1(x) +I2(x)

Die Intensit¨at I1,2 kann sogar 0 werden, obwohl die Einzelintensit¨aten ungleich Null sind.

Man beobachtet hier also Interferenz.

Die Erkl¨arung der Elektrodynamik wollen wir an dieser Stelle noch einmal besprechen. Die Maxwell-Gleichungen im Vakuum besitzen eine Wellenl¨osung f¨ur das elektrische (und das ma- gnetische) FeldE(r, t). Außerdem sind die Maxwell-Gleichungen linear. Also gilt das Superposi- tionsprinzip f¨ur ihre L¨osungen. Sind alsoE₁(x) undE₂(x) L¨osungen der Maxwell-Gleichungen, so ist auch

E1,2(x) = E1(x) +E2(x)

32 KAPITEL 2. GRUNDLAGEN DER QUANTENMECHANIK L¨osung der Maxwell-Gleichungen. Die Koeffizienten der Linearkombination wurden hier zur Vereinfachung gleich 1 gesetzt.

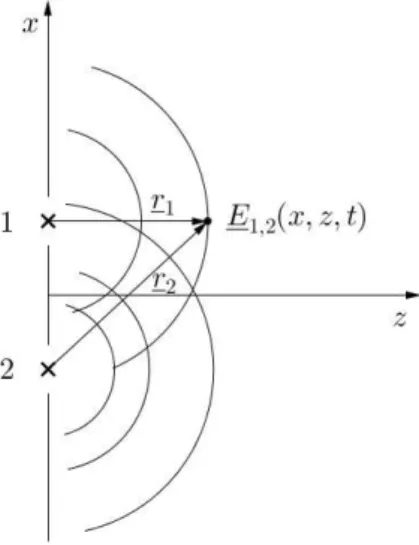
Abbildung 2.5: Superposition und Interferenz zweier Kreiswellen

Setzen wir an

E₁(x, z, t) = E₁₀e^iϕ1(x,z,t), E₂(x, z, t) = E₂₀e^iϕ2(x,z,t),

mit den AmplitudenE10,E20∈Cund den reellen Phasenϕ1 und ϕ2, so gilt f¨ur das elektrische Feld bei (x, z, t) die Superposition:

E_1,2(x, z, t) =E₁(x, z, t) +E₂(x, z, t).

Man beachte, dass hier keine Interferenz ablesbar ist. Die physikalische Messgr¨oße ist aber nicht die Feldst¨arke, sondern die Intensit¨at I, die proportional zu |E|² ist. Berechnen wir diese [CGS-System], so gilt mit der Abk¨urzung ∆ϕ=ϕ1(x, z, t)−ϕ2(x, z, t):

4π

c I1,2(x, z, t) = (E₁+E₂)(E₁+E₂)^∗

=|E₁|²+|E₂|²+E₁·E^∗₂+E^∗₁·E₂

=|E₁₀|²+|E₂₀|²+E₁₀E₂₀^∗ e^i∆ϕ+E₂₀E₁₀^∗ e^−i∆ϕ

=|E₁₀|²+|E₂₀|²+ 2· ℜ

E₁₀E₂₀^∗ e^i∆ϕ

= I1+I2

| {z }

klass. Teilchen

+ 2|E10| · |E20| ·cos ∆ϕ

| {z }

Interferenzterm

.

Man erkennt, dass die Intensit¨at Maxima hat f¨ur¹ ∆ϕ = n · π, wobei n gerade ist (Gang- unterschied von Vielfachen der Wellenl¨ange). Minima der Intensit¨at findet man hingegen f¨ur

∆ϕ =n·π f¨ur n ungerade. Komplette Ausl¨oschung sowie maximale Verst¨arkung sind nur f¨ur E10=E20 m¨oglich.

1Das gefundene Ergebnis gilt f¨ur reelle AmplitudenE¹⁰ undE²⁰. F¨ur komplexe Amplituden ist die Phasen- differenz durch die Argumente vonE¹⁰ undE²⁰zu modifizieren.

34 KAPITEL 2. GRUNDLAGEN DER QUANTENMECHANIK 2. ρ2(x) = ^dP_dx², Wahrscheinlichkeitsdichte bei geschlossenem Spalt 1.

3. Sind beide Spalte offen, so misst man:

dP1,2 6=dP1+dP2

Hier gilt also offensichtlich keine Additivit¨at, sondern Interferenz (dies basiert auf der Beobachtung im Experiment, s. Abb. 2.6). Es liegt also eine gegenseitige Beeinflussung der beiden Spalte vor, unddP_1,2verh¨alt sich wie die Intensit¨atI_1,2bei der elektromagnetischen Welle.

Das Experiment zeigt also sowohl diskrete Teilcheneigenschaften – wie Masse oder Elemen- tarladung – als auch Inteferenzeffekte, welche den Welleneigenschaften zuzuordnen sind. Die Vermutung ist nun, dass die Wahrscheinlichkeitsdichte ¨ahnliche Eigenschaften hat wie die In- tensit¨at des elektromagnetischen Feldes. In Analogie zur Interferenz der Intensit¨at muss auch hier ein analoger Zusammenhag bestehen, der zur beobachteten Interferenz f¨uhrt:

ρ1,2 =ρ1+ρ2+ 2|ψ1| · |ψ2|cos ∆ϕ,

wobei die Funktionψad hoc als “Wahrscheinlichkeitsamplitude”, in Analogie zur Feldamplitude der elektromagnetischen Welle eingef¨uhrt wurde. Hieraus lassen sich dann weitere Analogien ableiten, die wir in folgender Tabelle zusammenstellen.

EM-Welle Mikroteilchen

Darstellung E(r, t) = E₀e^iϕ(r,t) ψ(r, t) = ψ0e^iϕ(r,t) Messgr¨oße αI(r, t) =E(r, t)·E^∗(r, t) ρ(r, t) = ψ(r, t)·ψ^∗(r, t)

Normierung R

I(r)dr∝Wel

R ρ(r, t)dr =R

dP = 1 Superposition E₁₂(r, t) =E₁(r, t) +E₂(r, t) ψ₁₂(r, t) = ψ₁(r, t) +ψ₂(r, t) Addition der Messgr¨oßen I12=I1+I2+ 2√

I1√

I2cos ∆ϕ ρ12=ρ1+ρ2+ 2|ψ1| · |ψ2|cos ∆ϕ Tabelle 2.2: Analogie zwischen den Grundgr¨oßen zur Beschreibung von Mikroteilchen und EM- Wellen. α=c/4π

Also ersetzt eine elementare Beschreibung der Welleneigenschaften von Mikroteilchen mit einer Wahrscheinlichkeitsamplitude ψ(r, t) die klassischen Trajektorien. Wir haben also im Gegen- satz zur klassischen Mechanik eine r¨aumliche Delokalisierung vorliegen. Offen ist nun noch die Bewegungsgleichung f¨ur ψ(r, t). Diese finden wir im Abschnitt 2.5.

Vorher diskutieren wir aber noch einmal die Analogie zwischen dem Verhalten elektromagneti- scher Strahlung und von Mikroteilchen. Die Beobachtung von Interferenz in derkontinuierlichen Messgr¨oße Intensit¨at,I ist nur auf den ersten Blick qualitativ verschieden von der Wahrschein- lichkeitsbetrachtung bei den Mikroteilchen. Wenn wir uns an Plancks Lichtquanten-Hypothese erinnern, bedeutet das, dass auch bei der Beobachtung von Interferenz ein diskreter Teilchen- strom zugrunde liegt. Die Intensit¨at ist dann proportional zur Anzahl der Photonen pro Fl¨ache und Zeit, I ∼N~ω, wenn monochromatische Strahlung vorliegt. Wenn man jetzt die Zahl der Photonen kontinuierlich reduziert, sollte – wie im Fall der Mikroteilchen – das Interferenzbild unscharf werden und der zuf¨allige Charakter einzelner Photonen deutlich werden. Genau das ist experimentell zu beobachten, wie in Abbildung 2.7 gezeigt. Die Abbildung zeigt die Fotografie ein und desselben Objekts bei sechs verschiedenen Belichtungszeiten, was einer Variation der Photonenzahl entspricht.

2.5. DIE SCHR ¨ODINGERGLEICHUNG 35

Abbildung 2.7: Teilchencharakter des Lichts bei der Fotografie. Das Foto wurde mit unterschiedlicher Belichtungszeit durchgef¨uhrt. Dadurch nahm die Zahl der Photonen von 3,000 (links oben) auf 30,000,000 (rechts unten) zu. Quelle: https://www.uni- ulm.de/fileadmin/website uni ulm/nawi.inst.251/

2.5 Die Schr¨ odingergleichung

Nach den vorigen Ergebnissen ist die Aufenthaltswahrscheinlichkeit eines Mikroteilchens am Ort r im Volumen ∆V bestimmt durch die Wahrscheinlichkeitsdichte ρ(r, t) = |ψ(r, t)|². Die Wahrscheinlichkeit, das Teilcheni im Volumen ∆V ⊂ V zu finden, ist dann:

P(i∈∆V) = Z

∆V

|ψ(r, t)|²dr. (2.6)

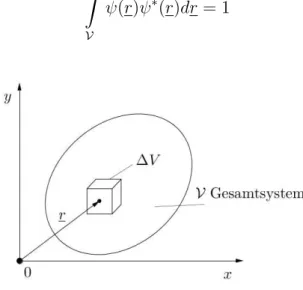
F¨ur die Aufenthaltswahrscheinlichkeit im GesamtvolumenV (sicheres Ereignis) gilt dann:

Z

V

ψ(r)ψ^∗(r)dr= 1

Abbildung 2.8: Volumen ∆V im Gesamtsystem V. Die Wahrscheinlichkeit, ein Teilchen im Volumen ∆V zu finden, ist durch Formel (2.6) gegeben.

Wir versuchen nun, die Bewegungsgleichung f¨ur ψ(r, t) zu finden. Dies werden wir wieder in Analogie zur Elektrodynamik tun. Nehmen wir zun¨achst den eindimensionalen Fall einer ebenen

36 KAPITEL 2. GRUNDLAGEN DER QUANTENMECHANIK monochromatischen Welle f¨ur das elektrische Feld³:

E(x, t) =E₀e^−iωt+ikx. (2.7) Diese Funktion l¨ost die Wellengleichung, die aus den Maxwellgleichungen folgt:

∂²E

∂t² =c²∂²E

∂x². (2.8)

Die Bedingung daf¨ur, dass der Ausdruck (2.7) die Wellengleichung l¨ost, ist gegeben duch die sogenannte Dispersionsrelation, welche man durch Einsetzen findet:

ω(k) =c·k. (2.9)

Das heißt, f¨ur elektromagnetische Wellen existiert zwingend ein linearer Zusammenhang zwi- schen Frequenz und Wellenzahl.

Jetzt erfolgt die ¨Ubertragung dieser Ergebnisse auf Mikroteilchen. Da wir hier analoge Interferenz- Effekte beobachtet haben, ist die L¨osung durch die selbe monochromatische ebene Welle ge- geben. Aus den bereits besprochenen Experimenten zu den Eigenschaften von Mikroteilchen wissen wir, dass Frequenz und Wellenzahl mit der Energie bzw. dem Impuls verkn¨upft sind:

ω= E

~, k = p

~. Setzen wir dies ein, so erhalten wir ψ f¨ur ein Mikroteilchen:

ψ(x, t) =ψ₀e^−iE~t+ip~x. (2.10) Wir wissen jedoch auch, dass die Dispersion f¨ur nicht-relativistische Teilchen quadratisch ist:

E(p) = p²

2m. (2.11)

Dies ist ein grundlegender Unterschied zur elektromagnetischen Welle. Die Bewegungsgleichung f¨ur ψ muss also von der Wellengleichung f¨ur das elektromagnetische Feld abweichen. Um diese Bewegungsgleichung zu finden, berechnen wir aus der Wellenl¨osung (2.10):

∂ψ

∂t =−i

~E·ψ,

∂²ψ

∂x² =− 1

~²p²·ψ =−2mE

~² ·ψ,

wobei wir in der letzten Zeile die Dispersionsrelation (2.11) verwendet haben. Formen wir die linken Seiten so um, dass wir die rechten Seiten gleichsetzen k¨onnen so erhalten wir die von E. Schr¨odinger 1926 gefundene Gleichung. Wir verallgemeinern sofort auf dreidimensionale Probleme:

Schr¨odingergleichung (SGL) f¨ur ein freies Teilchen:

i~∂ψ

∂t(r, t) =− ~²

2m∇²ψ(r, t) (2.12)

3Das ist keine Einschr¨ankung, denn wegen der Linearit¨at der Maxwell-Gleichungen l¨asst sich eine beliebige L¨osung durch Superposition solcher Funktionen darstellen.

2.5. DIE SCHR ¨ODINGERGLEICHUNG 37 Die L¨osung dieser Gleichung kennen wir ja bereits. Zur vollst¨andigen L¨osung brauchen wir nun noch Anfangsbedingungen [ψ(r, t = 0)] und Randbedingungen [ψ(r, t)|^Γ, ∇ψ(r, t)|^Γ]. Hierbei ist Γ der Rand des dem Teilchen zur Verf¨ugung stehenden Volumens. Die obige Gleichung ist—anders als f¨ur elektromagnetische Wellen—von 1.Ordnung in t. Sie ¨ahnelt damit der Dif- fusionsgleichung, und wir werden in der Tat sp¨ater ein Auseinanderlaufen der Wellenfunktion mit der Zeit sehen.

Die Schr¨odingergleichung ist in ihrer Analogie zur Elektrodynamik gut begr¨undbar aber nicht ableitbar im strengen Sinne⁴. Sie ist das Grundpostulat der Quantenmechanik, so wie die New- tonschen Gleichungen die Grundpostulate f¨ur die klassische Mechanik darstellen.

Von der obigen L¨osung dieser Gleichung k¨onnen wir den Zeitanteil zum ParameterE separieren:

ψ(r, t) =e^−~iE·t·ψE(r)

Setzen wir dies in die Schr¨odingergleichung ein, so erhalten wir eine Bestimmungsgleichung f¨ur die station¨are L¨osung:

i~

−i

~E

e^−~iE·tψE(r) =− ~²

2m∇²ψE(r)e^−~iE·t EψE(r) =− ~²

2m∇²ψE(r) Die station¨are Schr¨odingergleichung ist gegeben durch:

EψE(r) = −~²

2m∇²ψE(r) (2.13)

Bisher haben wir nur freie Teilchen betrachtet. Jetzt wollen wir die Schr¨odinger-Gleichung auf Teilchen in einem externen Feld erweitern. Diezentrale Hypothese ist, dass man die Energie, welche bisher nur durch die kinetische Energie gegeben war, durch die Gesamtenergie ersetzt:

E →E+V(r). Dabei ist, nach Glg. (2.13), die kinetische Energie offenbar durch den Ausdruck

−_2m^~2∇² gegeben,

Die station¨are Schr¨odingergleichung f¨ur ein Teilchen im externen Potential V(r) ist:

−~²

2m∇²+V(r)

ψE(r) =EψE(r) (2.14)

Die zeitabh¨angige Schr¨odingergleichung f¨ur ein Teilchen im externen Potential V(r) ist:

i~∂

∂tψ(r, t) =

− ~²

2m∇²+V(r)

ψ(r, t) (2.15)

Die obigen Gleichungen sind lediglich Postulate. Diese sind aber sehr gut durch Experimente best¨atigt und sind auch f¨ur k¨unftige Anwendungen weiter zu ¨uberpr¨ufen.

4Daf¨ur w¨urde man noch grundlgendere Postulate ben¨otigen.