⋅µ)⋅v für alle , µ∈K und v∈V, (V3) 1⋅v=v für allev∈V, (V4) Distributivgesetze ( +µ)⋅v= ⋅v+µ⋅v ⋅(v+w)= ⋅v+ ⋅w für alle , µ∈K und v, w∈V

(1)

eine MengeV zusammen mit zwei Verknüpfungen V ×V �→ V (Addition)

(v, w) �→ v+w

K×V �→ V (Skalarmultiplikation) ( , v) �→ ⋅v

die folgenden Axiomen genügen:

(V1) (V,+) ist eine abelsche Gruppe, (V2) Assoziativgesetz

⋅(µ⋅v)=( ⋅µ)⋅v für alle , µ∈K und v∈V,

(V3) 1⋅v=v für allev∈V, (V4) Distributivgesetze

( +µ)⋅v= ⋅v+µ⋅v

⋅(v+w)= ⋅v+ ⋅w für alle , µ∈K und v, w∈V.

Die Elemente eines Vektorraums nennen wir auchVektoren.

Man beachte, dass hier + sowohl für die Addition in K als auch in V verwendet wird, und ⋅ sowohl für die Multiplikation inK als auch die Skalarmultiplikation. Welche der beiden Mög- lichkeiten gemeint ist, ist aber aus dem Typ der verknüpften Elemente klar.

Beispiel 5.3.2 SeiKein Körper. Beispiele vonK-Vektorräumen sind:

(2)

1) Kⁿ={(a₁, ..., a_n)�a_i∈K} mit

(a₁, ..., a_n)+(b₁, ..., b_n)∶=(a₁+b₁, ..., a_n+b_n) (a₁, ..., a_n)∶=( a₁, ..., a_n)

wobei man Elemente vonKⁿauch als Spaltenvektoren schreibt, d.h. als

��

� a1

⋮ an

��

�∈Kⁿ,

Das neutrale Element der Addition von Kⁿ ist der Null- vektor

0=�

�� 0⋮ 0

��

� 2) der Polynomring K[x],

3) die Menge der Folgen in K

K^N={a∶N�→K} mit

(a+b)(m)∶=a(m)+b(m) ( ⋅f)(m)∶= ⋅f(m) für m∈N.

Bemerkung 5.3.3 Sei V ein K-Vektorraum. Dann gilt:

1) 0_K⋅v=0_V für allev∈V,

⋅0V =0V für alle ∈K, 2) (−1)⋅v=−v für alle v∈V,

3) ⋅v=0�⇒ =0oder v=0 für alle ∈K, v∈V.

Dabei bezeichnet0_Kdas Neutrale von(K,+)und0_V das Neu- trale von (V,+). Ist aus dem Kontext klar, ob die Konstante 0_K oder der Nullvektor0_V gemeint ist, schreiben wir einfach0.

(3)

v=1⋅v=( ⁻¹ )v= ⁻¹( v)= ⁻¹0V =0V.

Beispiel 5.3.4 Wir geben Beispiele für die Aussagen in Bemer- kung 5.3.3:

1)

0⋅� ¹₂ �=� ⁰₀ � 2⋅� ⁰₀ �=� ⁰₀ � 2)

� ¹₂ �+(−1)� ¹₂ �=� ¹₂ �+� ⁻₋¹₂ �=� ⁰₀ � 3)

⋅� ^x_x¹

2 �=� ^x_x¹

2 �=� ⁰₀ �

genau dann, wenn x1 =0 und x2=0, d.h. genau dann, wenn =0oder x1=x2=0.

Bemerkung 5.3.5 Man könnteKin der Definition vonV durch einen kommutativen Ring R mit 1 ersetzen (z.B. Z oder einen Polynomring). Dann spricht man von einemR-Modul. Die Struk- turtheorie von Moduln ist wesentlich komplizierter als die von Vektorräumen. Ein wesentlicher Grund hierfür liegt darin, dass die Aussage(3)in Bemerkung 5.3.3 im Allgemeinen nicht mehr korrekt ist. Beispielsweise ist Z�2 ein Z-Modul mit der Skalar- multiplikation

Z×Z�2 → Z�2

(n, a) � n⋅a=a+...+a

��_n =n⋅a und es gilt

2⋅1=2=0,

(4)

obwohl2≠0 und1≠0.

Wir bemerken noch: Ein Z-Modul ist das gleiche wie eine abelsche Gruppe, denn genau wie beiZ�2 können wir einer abel- schen Gruppe durchn-fache Addition

Z×G → G

(n, g) � n⋅g=g+...+g

��_n eineZ-Modulstruktur geben.

Summen und Vielfache von Lösungen von homogenen linearen Gleichungssystemen sind wieder Lösungen. Deshalb definieren wir:

Definition 5.3.6 SeiV einK-Vektorraum. Eine nichtleere Teil- menge U⊂V heißt Untervektorraum, wenn

u₁, u₂∈U�⇒u₁+u₂∈U

∈K, u∈U �⇒ ⋅u∈U.

Bemerkung 5.3.7 1) U mit der von V induzierten Additi- on und Skalarmultiplikation ist ein K-Vektorraum (siehe Übung 5.1).

2) Jeder Untervektorraum U enthält die 0 ∈V (denn es gibt ein u∈U und 0=0⋅u∈U).

Satz 5.3.8 Die Lösungsmenge eines homogenen linearen Glei- chungssystems für x1, ..., xn über dem Körper K ist ein Unter- vektorraum vonKⁿ.

Beweis.Betrachte das System

a_1,1x₁+...+a_1,nx_n=0

⋮

a_r,1x₁+...+a_r,nx_n=0

über einem KörperK. Sindx, y∈Kⁿ Lösungen, dann auchx+y und ⋅xfür alle ∈K:

(5)

∑j=1 ( + )=∑j=1 +∑j=1 = und ∑ⁿj=1ai,j( ⋅xj)= ⋅∑ⁿj=1ai,jxj=0.

Die Lösungsmengen von inhomogenen linearen Gleichungssy- stemen (also mit einem konstanten Term ≠0 in einer der Glei- chungen) sind dagegen keine Untervektorräume, denn sie enthal- ten nicht die0∈Kⁿ.

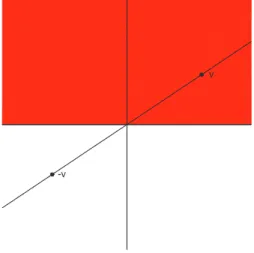
Beispiel 5.3.9 Eine Gerade L ⊂ Rⁿ ist ein Untervektorraum genau dann, wenn0∈L(siehe Abbildung 5.2).

Abbildung 5.2: Geraden im R², die Untervektorräume sind

Beweis.Die Notwendigkeit von 0∈L ist klar. Falls0∈L, dann L={ v� ∈R}

mit0≠v∈L. Somit ist

1v+ ²v=( ¹+ ²)v∈L

1( 2v)=( 1 2)v∈L

(6)

für alle i∈R.

Beispiel 5.3.10 1) Untervektorräume von R³ sind {0}, die Geraden durch 0, die Ebenen durch 0 (Übung) und R³ selbst. Dass dies alle möglichen Untervektorräume sind, werden wir später zeigen.

2) K[x]_≤d ={f∈K[x]�degf ≤d}⊂K[x] ist ein Untervek- torraum.

3) Die Mengen

U₁=�(x, y)∈R²�y≥a� mit a∈R (siehe Abbildung 5.3 für a=0) und

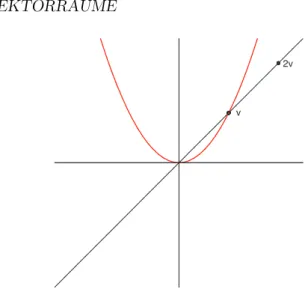
U2=�(x, y)∈R²�y=x²�

(siehe Abbildung5.4) sind keine Untervektorräume vonR². Warum?

-v

v

Abbildung 5.3: Halbebene

4) Sind a₁ , ...a_n∈K, dann ist die Hyperebene

H ={(x₁, ..., x_n)∈Kⁿ�a₁x₁+...+a_nx_n=0}

ein Untervektorraum. Dies haben wir schon allgemeiner in Bemerkung5.3.8für Lösungsmengen von homogenen linearen Gleichungssystemen beobachtet.

(7)

v

Abbildung 5.4: Parabel

Definition und Satz 5.3.11 SeiV einK-Vektorraum undv1, ..., vn∈ V. Ein Vektorv∈V ist eine Linearkombinationvonv₁, ..., v_n, wenn es i∈K gibt mit

v= 1v₁+...+ nv_n. Die Menge aller Linearkombinationen

�v1, ..., vn�∶={ ¹v1+...+ ⁿvn� ⁱ∈K}⊂V

ist ein Untervektorraum, dervon v₁, ..., v_naufgespannte Un- tervektorraum.

Beweis.Sindv, w∈�v₁, ..., v_n�alsov=∑ⁿⁱ=1 iv_iundw=∑ⁿⁱ=1µ_iv_i mit i, µ_i∈K, dann

v+w=�ⁿ

i=1( i+µ_i)v_i∈�v₁, ..., v_n� und

v=�ⁿ

i=1( ⋅ i)v_i∈�v₁, ..., v_n�.

(8)

Beispiel 5.3.12 1) Die Vektoren

v1=�

�� 1 0 0

��

�, v2=�

�� 0 1 0

��

�∈R³

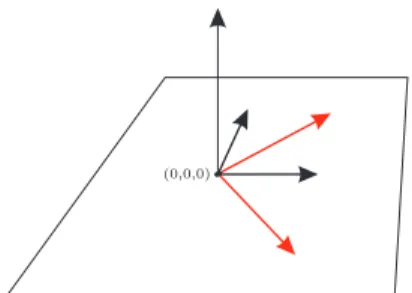
spannen die Ebene E={z=0} auf, denn für jeden Vektor in der Ebene gilt

E∋�

��

1 2

0

��

�= 1v₁+ 2v₂. Die Vektoren

w1=�

�� 1 1 0

��

�, w2=�

��

−11 0

��

�∈R³ spannen ebenfalls die Ebene auf, d.h.

E=�v1, v2�=�w1, w2� dennw1=v1+v2 und w2=v1−v2 also

�w₁, w₂�⊂�v₁, v₂� undv₁=¹₂w₁+¹₂w₂ und v₂=¹₂w₁−¹₂w₂, also

�v₁, v₂�⊂�w₁, w₂�. Siehe auch Abbildung 5.5.

2) Die Polynome1, x, ..., x^d∈K[x] spannen K[x]≤d auf.

Definition 5.3.13 Sei V ein K-Vektorraum.

1) Vektoren v₁, ..., v_n ∈ V heißen ein Erzeugendensystem vonV, wenn

V =�v1, ..., vn�.

(9)

Abbildung 5.5: Zwei Erzeugendensysteme der Ebene{z=0}⊂R³

2) Vektoren v₁, ..., v_n ∈ V heißen linear unabhängig, wenn aus

1v1+...+ ⁿvn=0 folgt, dass

1=...= n=0, anderenfallslinear abhängig.

3) Ein Erzeugendensystem v₁, ..., v_n von V aus linear unab- hängigen Vektoren heißtBasis vonV.

Algorithmus 5.3.14 Vektoren v₁, ..., v_n ∈ K^m sind linear un- abhängig genau dann, wenn das homogene lineare Gleichungs- system

x1v1+...+xnvn=0 nur die Lösung

��

� x1

⋮ x_n

��

�=�

�� 0⋮ 0

��

�

hat. Dies können wir mit dem Gaußalgorithmus entscheiden.

Beispiel 5.3.15 1) Die Vektoren

v1=� ¹₀ �,v2=� ⁰₁ �, v3=� ¹₁ �∈R² sind linear abhängig, denn das Gleichungssystem

x₁� ¹₀ �+x₂� ⁰₁ �+x₃� ¹₁ �=� ⁰₀ �

(10)

d.h. x₁ + x₃ = 0 x₂ + x₃ = 0 hat den Lösungsraum

��

�

��

�

−x3

−x₃ x3

��

��x3∈R��

��≠��

��

� 0 0 0

��

�

��

�

Das heißt, die Vektorenv1, v2, v3 erfüllen die (bis auf Viel- fache eindeutige) Relation

−v1−v2+v3=0.

Die Vektorenv₁ und v₂ bilden dagegen eine Basis von R². Allgemeiner:

2) Die Einheitsvektoren

e₁=

��

�� 1 0⋮ 0

��

, ..., e_n=

��

�� 0⋮

0 1

��

��∈Kⁿ

bilden eine Basis vonKⁿ, die sogenannteStandardbasis:

Jeder Vektor inKⁿ lässt sich schreiben als

��

� a₁

⋮ an

��

�=a₁e₁+...+a_ne_n unde₁, ..., e_n sind linear unabhängig, denn

a₁e₁+...+a_ne_n=0�⇒a₁=...=a_n=0

3) Die Polynome 1, x, ..., x^d bilden eine Basis von K[x]≤d, denn

a₀⋅1+...+a_d⋅x^d=0�⇒a₀=...=a_d=0. Siehe auch Übungsaufgabe5.4.

Mit Hilfe einer Basis kann man den Lösungsraum eines homogenen linearen Gleichungssystems wesentlich kompakter schreiben. Die Basis liest man von der reduzierten Zeilenstufenform ab:

(11)

sungsmenge aus Bemerkung 5.2.10für die freien Variablen eine Einheitsbasis einsetzen.

Beweis.Sei

l1=xi1+ti1(xj1, ..., xj_n−r)=0

⋮

lr=xir+tir(xj1, ..., xj_n−r)=0

mitl_i∈K[x₁, .., x_n] homogen linear in reduzierter Zeilenstufen- form mitLeitvariablen

xi1, ..., xir

undfreien Variablen

x_j₁, ..., x_j_n₋_r

(also{j1, ..., jn−r}={1, ..., n}�{i1, ..., ir}). Mit

g_i∶=� −t_i(x_j₁, ..., x_j_n₋_r) fallsx_i eine Leitvariable x_i fallsx_i eine freie Variable können wir die Lösungsmenge schreiben als

L=��

��

�

g1(xj1, ..., xj_n−r)

⋮

g_n(x_j₁, ..., x_j_n₋_r)

��

��x_j₁, ..., x_j_n₋_r∈K��

��

Da die g_i homogene lineare Polynome in x_j₁, ..., x_j_n₋_r sind und somit

��

�

g₁(x_j₁, ..., x_j_n₋_r)

⋮

gn(xj1, ..., xjn−r)

��

�=x_j₁⋅�

��

g₁(1,0, ...,0)

⋮ gn(1,0, ...,0)

��

�+...+x_j_n₋_r⋅�

��

g₁(0, ...,0,1)

⋮ gn(0, ...,0,1)

��

� erhalten wir ein Erzeugendensystem

L=��

��

g1(1,0, ...,0)

⋮ gn(1,0, ...,0)

��

�, ...,�

��

g1(0, ...,0,1)

⋮ gn(0, ...,0,1)

��

(12)

Da in den Koordinaten x_j₁, ..., x_j_n₋_r der Erzeuger eine Ein- heitsbasis vonKⁿ⁻^r steht, sind diese linear unabhängig und bilden somit eine Basis vonL.

Siehe auch Aufgabe5.2.

Beispiel 5.3.17 Das System

l₁ = x₁ + 2x₂ − 2x₅ = 0

l₂ = x₃ + x₅ = 0

l₃ = x₄ + 2x₅ = 0

in Q[x] ist schon in reduzierter Zeilenstufenform, also die Lö- sungsmenge

V =��

��

�

��

�

−2x2+2x5

x2

−x5

−2x5

x₅

��

�

�x2, x5∈Q

��

und somit erhalten wir mit(x₂, x₅)=(1,0) und (x₂, x₅)=(0,1) eine Basis:

V =�

��

�

−2 1 0 0 0

��

� ,

��

�

−2

−01

−2 1

��

�

Wir überprüfen nochmals in diesem Spezialfall, dass es sich tatsächlich um eine Basis handelt: Jedes Element von V lässt sich als eindeutige Linearkombination darstellen

��

�

−2x2+2x5

x2

−x₅

−2x5

x5

��

�

=x2⋅

��

�

−2 1 0 0 0

��

� +x5⋅

��

�

−2

−01

−2 1

��

� und die Vektoren sind linear unabhängig, denn

x2⋅

��

�

−2 1 0 0 0

��

� +x5⋅

��

�

−2

−01

−2 1

��

�

=

��

� 0 0 0 0 0

��

�

�⇒ x2=0 x₅=0

Für weitere Beispiele siehe auch die Aufgaben 5.16.1 und 5.16.2.

(13)

sen eines Vektorraums gleich viele Elemente haben. Diese Zahl ist eine wichtige Invariante des Vektorraums, genannt Dimen- sion. Damit werden wir dann Vektorräume im darauﬀolgenden Abschnitt klassifizieren: Jedern-dimensionaleK-Vektorraum ist isomorph zuKⁿ.

Satz 5.4.1 Sei V ein K-Vektorraum und ⌦ = (v1, ..., vn) eine Liste von Vektoren in V. Dann sind äquivalent:

1) ⌦ist eine Basis von V.

2) ⌦ist ein unverkürzbares Erzeugendensystem von V. 3) ⌦ist ein unverlängerbares System linear unabhängiger Vek-

toren inV.

4) Jeder Vektor in V lässt sich eindeutig als Linearkombina- tion von⌦ darstellen.

Beweis.(1⇒2): Angenommen

v1, ..., vi−1, vi+1, ..., vn

sind auch ein Erzeugendensystem vonV. Dann ist insbesondere vi= ¹v1+...+ ⁱ−1vi−1+ ⁱ+1vi+1+...+ ⁿvn

eine Linearkombination mit j∈K, also

1v1+...+ ⁱ−1vi−1−vi+ ⁱ+1vi+1+...+ ⁿvn=0, ein Widerspruch zur linearen Unabhängigkeit vonv₁, ..., v_n.

(2⇒3): Wir zeigen zunächst, dassv₁, ..., v_n linear unabhän- gig sind. Angenommen

1v₁+...+ nv_n=0 und i≠0. Dann ist

vi= 1

i( ¹v1+...+ ⁱ−1vi−1+ ⁱ+1vi+1+...+ ⁿvn)

(14)

alsov₁, ..., v_i−1, v_i+1, ..., v_nein kürzeres Erzeugendensystem vonV (d.h. eines mit weniger Elementen), ein Widerspruch zu(2).

Da nach (2) die Vektoren v1, ..., vn den Vektorraum V erzeugen, wäre jedes weitere v ∈ V eine Linearkombination von v₁, ..., v_n und somitv₁, ..., v_n, vlinear abhängig.

(3⇒4): Wir zeigen, dass v₁, ..., v_n ein Erzeugendensystem vonV sind: Seiv∈V beliebig. Nach Voraussetzung sindv1, ..., vn, v linear abhängig, also gibt es i, ∈K, nicht alle 0, mit

1v₁+...+ nv_n+ v=0.

Angenommen =0. Dann ist 1v₁+...+ nv_n=0, wegenv₁, ..., v_n linear unabhängig also auch 1 =... = n =0, ein Widerspruch.

Somit lässt sichvdarstellen als

v= ¹v1+...+ ⁿvn.

Zum Beweis der Eindeutigkeit nehmen wir an, dass

1v1+...+ ⁿvn=v=µ1v1+...+µnvn

also ( ¹−µ1)v1+...+( ⁿ−µn)vn=0. Dav₁, ..., v_n linear unabhängig sind, folgt i=µ_i ∀i.

(4⇒1): Nach Voraussetzung ist v₁, ..., v_n ein Erzeugenden- system. Wären die Vektoren linear abhängig, dann gäbe es zwei unterschiedliche Darstellungen der0

1v₁+...+ nv_n=0=0v₁+...+0v_n.

Bemerkung 5.4.2 Mit Hilfe von Satz5.4.1 können wir Vekto- ren einesK-VektorraumsV im Computer darstellen: Dazu wäh- len wir eine Basis ⌦= (v1, ..., vn) von V. Da jedes v ∈ V eine eindeutige Darstellung

v=a1v1+...+anvn

mit a_i∈K hat, können wir v im Computer durch

��

� a1

⋮ an

��

�∈Kⁿ

(15)

lc⌦∶ Kⁿ �→ V

��

� a1

⋮ an

��

� �→ a₁v₁+....+a_nv_n ist bijektiv. Ihre Umkehrabbildung

co⌦=lc⁻_⌦¹∶V �→Kⁿ

bezeichnen wir alsKoordinatendarstellung bezüglich ⌦. Vom praktischen Standpunkt können wir uns co⌦ als Parser und lc⌦

als Ausgaberoutine vorstellen.

Beispiel 5.4.3 Wählen wir für den VektorraumV =K[x]≤2 der Polynome vom Grad≤2die Basis ⌦=(1, x, x²), so erhalten wir die Bijektion

lc⌦∶ K³ �→ K[x]≤2

��

� a0

a1

a2

��

� �→ a₀+a₁x+a₂x²

Somit ist z.B. die Koordinatendarstellung des Polynoms 3x²+x

co_⌦(3x²+x)=�

�� 0 1 3

��

�

Wie aber findet man eine Basis? Auch dieses Problem wir von Satz5.4.1gelöst, dann wir können aus einem Erzeugendensystem durch sukzessives Weglassen von Erzeugern ein unverkürzbares Erzeugendensystem, d.h. eine Basis, erhalten:

Corollar 5.4.4 (Basisauswahlsatz) Ist V ein K-Vektorraum undv1, ..., vmein Erzeugendensystem vonV, dann gibt esi1, ..., in∈ {1, ..., m}, sodass vi1, ..., vin eine Basis von V bilden.

Siehe auch Übungsaufgabe5.7.

(16)

Beispiel 5.4.5 Die Vektoren

v1=�

�� 1 0 0

��

�, v2=�

�� 0 1 0

��

�, v3=�

�� 1 1 0

��

�, v4=�

�� 0 0 1

��

�

erzeugen R³. Der Lösungsraum des Gleichungssystems ∑ⁱ ⁱv_i= 0, d.h.

1 + ³ = 0

2 + 3 = 0

4 = 0

ist

V =�

��

−1

−1 1 0

��

�

also gilt die Relation

−v1−v2+v3=0

d.h. wir können einen der drei Vektoren streichen. Da es keine weiteren Relationen zwischen denv1, ..., v4 gibt, erhalten wir dann linear unabhängige Vektoren und somit eine Basis. Die möglichen Basisauswahlen sind also

v1, v2, v4

v1, v3, v4

v₂, v₃, v₄

Im Allgemeinen haben Vektorräume viele verschiedene Ba- sen: Sowohl

� ¹₀ �,� ⁰₁ � als auch

� ¹₁ �,� ₋¹₁ �

bilden eine Basis vonR². Für jedes b∈Rsind die Polynome 1,(x−b),(x−b)², ...,(x−b)^d

(17)

Basis unabhängig. Dies werden wir im folgenden Satz zeigen.

Definition 5.4.6 Ein Vektorraum heißtendlichdimensional, wenn er ein endliches Erzeugendensystem besitzt.

Bemerkung 5.4.7 Mit dem Basisauswahlsatz 5.4.4 hat jeder endlichdimensionale Vektorraum dann auch eine (endliche) Ba- sis.

Definition und Satz 5.4.8 (Hauptsatz über Vektorräume) Sei V ein endlichdimensionaler K-Vektorraum. Dann haben je zwei Basen dieselbe Anzahl von Elementen.

Diese Anzahl bezeichnen wir als die Dimension dim_KV von V über K. Ist V nicht endlichdimensional, so setzen wir dim_KV = ∞. Ist aus dem Zusammenhang klar, über welchem Körper wirV betrachten, so schreiben wir auch kurz dimV. Beispiel 5.4.9 Mit Satz5.4.8und den Basen aus Beispiel5.3.15 folgt:

1) dimKⁿ=n, 2) dimK[x]≤d=d+1,

3) dimK[x]=∞, denn jede endliche Menge von Polynomen erzeugt nur einen Untervektorraum, da sie nur Polynome beschränkten Grades enthält.

4) R ist ein Q-Vektorraum unendlicher Dimension (hätte R Dimension nüber Q, dann gäbe es wie oben eine bijektive Abbildung Qⁿ → R. Somit wäre mit Q auch R abzählbar, ein Widerspruch). Alsodim_QR=∞ (aber dim_RR=1 mit der Basise1=1).

Der Beweis von Satz5.4.8beruht auf folgendem Lemma:

Lemma 5.4.10 (Austauschlemma) Sei v1, ..., vn eine Basis von V und 0 ≠ w ∈ V ein weiterer Vektor. Dann existiert ein i∈{1, ..., n}, sodass auch v1, ..., vi−1, w, vi+1, ..., vn eine Basis von V bilden.

(18)

Beweis.Dav₁, ..., v_nein Erzeugendensystem sind, gibt es 1, ..., _n∈ K mit

w= ¹v1+...+ ⁿvn.

Hier muss ein i≠0sein, da w≠0. Nach Umnummerieren kön- nen wir 1≠0 annehmen. Also ist

v₁= 1

1(w−( 2v₂+...+ nv_n))

eine Linearkombination vonw, v2, ..., vnund somit diese Vektoren Erzeuger von V. Hier verwenden wir essentiell die Körpereigen- schaft vonK. Über einem Ring würde ¹₁ im Allgemeinen nicht existieren.

Zur linearen Unabhängigkeit: Angenommen µw+µ₂v₂+...+µ_nv_n=0, also

µ ₁v₁+(µ₂+µ ₂)v₂+...+(µ_n+µ _n)v_n=0. Dav₁, ..., v_n linear unabhängig sind, gilt

µ ₁=µ₂+µ ₂=...=µ_n+µ _n=0 Aus 1≠0folgtµ=0und somitµ₂=...=µ_n=0.

Beispiel 5.4.11 Die Einheitsvektorene₁, e₂, e₃∈R³ bilden eine Basis. Da

w=�

��

−21 0

��

�=2⋅�

�� 1 0 0

��

�+(−1)⋅�

�� 0 1 0

��

�+0⋅�

�� 0 0 1

��

�

können wir sowohl e₁ als auche₂ durch w ersetzen und erhalten die Basenw, e₂, e₃ bzw. e₁, w, e₃.

Mit dem Austauschlemma folgt durch Induktion:

Satz 5.4.12 (Austauschsatz) SeiV einK-Vektorraum,v₁, ..., v_n eine Basis von V und w₁, ..., w_s linear unabhängig. Dann gilt

s≤n.

Weiter gibt esi₁, ..., i_n₋_s∈{1, ..., n}, sodass w₁, ..., w_s, v_i₁, ..., v_i_n₋_s eine Basis von V bilden.

(19)

w₁... , w_s₋₁, v_s, ... , v_n eine Basis vonV. Somit existieren i∈K mit

w_s= 1w₁+...+ s−1w_s−1+ sv_s+...+ nv_n.

Wären s = ... = ⁿ = 0, dann w1, ... , ws linear abhängig, ein Widerspruch. Es gibt also eini≥smit i≠0, und damit können wirv_i mit Lemma 5.4.10gegen w_s austauschen.

Insbesondere erhalten wir:

Corollar 5.4.13 (Basisergänzungssatz) Ist V ein endlichdi- mensionalerK-Vektorraum undv1, ... , vmlinear unabhängig. Dann gibt esvm+1, ..., vn∈V, sodass v1, ..., vn eine Basis bilden.

Beweis. Nach Corollar 5.4.4 hat V eine Basis und nach Satz 5.4.12lassen sich in der Basis Vektoren durch v₁, ... , v_m austauschen.

Der Austauschsatz impliziert auch direkt Satz5.4.8:

Beweis. Satz 5.4.12 angewendet auf zwei Basen der Länge n undsliefert sowohls≤nals auchn≤s.

Wir demonstrieren den Austauschsatz an einem Beispiel:

Beispiel 5.4.14 Die Polynome

x²+1, x²+x, x+1∈Q[x]≤2

bilden eine Basis: In der Standardbasis 1, x, x² können wir x² durch x²+1 austauschen, denn

x²+1= 1

≠0⋅x²+1⋅1, und wir erhalten die Basis

1, x, x²+1.

Weiter lässt sichx durch x²+x austauschen, denn x²+x=1⋅(x²+1)+1

≠0⋅x+(−1)⋅1,

(20)

und wir erhalten die Basis

1, x²+x, x²+1.

Schließlich kann man1 durch x+1 ersetzen, denn x+1= 2

≠0⋅1+1⋅�x²+x�+(−1)⋅�x²+1�. Aus dem Austauschsatz folgt auch:

Corollar 5.4.15 Sei U ⊂V ein Untervektorraum. Dann gilt dimU≤dimV.

FallsdimU=dimV, so ist U=V.

Beweis. Für dimV = ∞ ist die erste Behauptung trivial. Ist v₁, ..., v_neine Basis vonV undw₁, ..., w_s eine Basis vonU, so gilt s≤nmit Satz5.4.12.

Für s = n lassen sich v₁, ..., v_n mit Satz 5.4.12 vollständig gegenw1, ..., wn austauschen. Somit bildenw1, ..., wn eine Basis.

Bemerkung 5.4.16 Sei V ein Vektorraum der Dimensionn<

∞ undv1, ..., vn∈V. Dann sind äquivalent:

1) v₁, ..., v_n bilden eine Basis, 2) v₁, ..., v_n sind linear unabhängig,

3) v₁, ..., v_n sind ein Erzeugendensystem von V.

Beweis.Seienv1, ..., vn linear unabhängig. Dann bildenv1, ..., vn

eine Basis vonU=�v1, ..., vn� und somit ist dimU =n=dimV also mit Corollar5.4.15U =V.

Seienv₁, ..., v_n ein Erzeugendensystem vonV. Somit können wir v1, ..., vn mit Corollar 5.4.4 zu einer Basis verkürzen. Wäre die Basis echt kürzer, dann wäre dimV < n, ein Widerspruch.

Also sind v1, ..., vn ein unverkürzbares Erzeugendensystem, d.h.

nach Satz5.4.1 eine Basis.

(21)

beliebigen endlichdimensionalen Vektorraums im Computer darstellen lassen. Dazu wählen wir eine Basis⌦=(v1, ..., vn)vonV. Da jedesv∈V eine eindeutige Darstellung

v=a1v1+...+anvn

mitai∈K hat, können wirvdurch den Vektor der Koeﬃzienten a_irepräsentieren. Die Linearkombinationsabbildung bezüglich⌦

lc_⌦∶ Kⁿ �→ V

��

� a1

⋮ a_n

��

� �→ a1v1+....+anvn

ist also bijektiv, wobei wir die Umkehrabbildung, die Koordina- tendarstellung bezüglich⌦, mit

co⌦=lc⁻¹_⌦ ∶V �→Kⁿ bezeichnen.

Soll die Darstellung von Elementen vonV durch Vektoren in Kⁿvon Nutzen sein, müssenlc_⌦undco_⌦die Vektorraumstruktu- ren vonKⁿ undV respektieren, d.h. es darf keine Rolle spielen, ob wir Rechnungen inV oder mit den Koordinatendarstellungen inKⁿ durchführen. Dies ist tatsächlich der Fall, denn

lc⌦

��

�

��

� a1

⋮ an

��

�+�

�� b1

⋮ bn

��

�

��

�=lc⌦

��

� a1+b1

⋮ an+bn

��

�=�ⁿ

i=1(ai+bi)vi

=�ⁿ

i=1

aivi+�ⁿ

i=1

bivi=lc⌦

��

� a1

⋮ an

��

�+lc⌦

��

� b1

⋮ bn

��

� und

lc⌦

��

� ⋅�

�� a1

⋮ an

��

�

��

�=lc⌦

��

� a1

⋮ an

��

�=�ⁿ

i=1( ai)vi

= �ⁿ

i=1

aivi= ⋅lc⌦

��

� a1

⋮ an

��

�.

Das heißt, dasslc_⌦ ein Homomorphismus von Vektorräumen ist:

(22)

Definition 5.5.1 Ein K-Vektorraumhomomorphismus ist eineK-lineare AbbildungF ∶V →W zwischenK-Vektorräumen, d.h.

F(v₁+v₂)=F(v₁)+F(v₂) für allevi∈V und

F( v)= F(v) für allev∈V und ∈K.

Die Begriﬀe Mono-, Epi- und Isomorphismus werden analog wie bei Gruppen und Ringen verwendet.

Beispiel 5.5.2 1) Analog können wir die Linearkombinati- onsabbildunglc⌦ auch für eine beliebige Liste⌦=(v1, ..., vn) von Vektoren inV definieren, nach unserem obigen Beweis ist sie immer noch ein Homomorphimus, aber i.A. weder injektiv noch surjektiv. Es gilt oﬀenbar:

lc⌦ Epimorphismus ⇔⌦Erzeugendensystem vonV lc⌦ Monomorphismus⇔⌦linear unabhängig

lc_⌦ Isomorphismus ⇔⌦Basis von V

Man zeigt wie üblich, dass mit lc⌦ auch co⌦=lc⁻_⌦¹ ein Iso- morphismus ist.

2) Insbesondere ist z.B.

lc_(1,x,...,xd)∶ K^d⁺¹ �→ K[x]≤d

��

� a₀

⋮ ad

��

� �→ a₀+a₁x+...+a_dx^d ein K-Vektorraumisomorphismus.

Die Klassifikation von endlichdimensionalen Vektorräumen bis auf Isomorphie ist sehr einfach, die Dimension ist dafür schon ausreichend:

Satz 5.5.3 (Klassifikationssatz für Vektorräume) SeiV ein K-Vektorraum der Dimension n<∞. Dann ist V isomorph zu Kⁿ. Schreibe

V ≅Kⁿ.

(23)

lc_⌦∶Kⁿ→V ein Isomorphismus.

Definition und Satz 5.5.4 Eine n×m-Matrix A über K ist eine Tabelle

A=�

��

a_1,1 � a_1,m

⋮ ⋮

a_n,1 � a_n,m

��

�=(a_i,j)ⁱ=1,...,n j=1,...,m

Die Menge dern×m-Matrizen bezeichnen wir mitKⁿ^×^m. Durch die Matrixmultiplikation

��

�

a11 � a1,m

⋮ ⋮

an,1 � an,m

��

�⋅�

�� x1

⋮ xm

��

�∶=�

��

�∑^mj=1a_1,jx_j�

�∑^mj=1a⋮n,jxj�

��

� ist ein Vektorraumhomomorphismus

K^m→Kⁿ, x�A⋅x

gegeben, den wir wieder mit A bezeichnen. Das Bild von x ist also einfach die xj-Linearkombination der Spalten Ai ∈Kⁿ von A=(A₁�...�A_m), d.h.

(A₁�...�A_m)⋅�

�� x1

⋮ x_m

��

�=�^m

j=1

x_j⋅A_j.

Beweis.Die Abbildung A=lc₍_A₁_,...,A_m₎, sie ist also eine Linear- kombinationsabbildung und somit wie oben bemerkt ein Homo- morphismus.

Beispiel 5.5.5 Es gilt

� ¹₄ ²₅ ³₆ �⋅�

�� 1 2 3

��

�=� ¹₄^⋅_⋅¹₁⁺₊²₅^⋅_⋅²₂⁺₊³₆^⋅_⋅³₃ �=� ¹⁴₃₂ �

(24)

mit der Multiplikationsformel. Alternativ mit der Interpretation als Linearkombinationsabbildung erhalten wir dasselbe Ergebnis:

� ¹₄ ²₅ ³₆ �⋅�

�� 1 2 3

��

�=1⋅� ¹₄ �+2⋅� ²₅ �+3⋅� ³₆ �=� ¹⁴₃₂ �

Beispiel 5.5.6 Die Ableitung

d

dx ∶ R[x] �→ R[x] ist einR-Vektorraumhomomorphismus, da

d

dx�∑^dⁱ=0aixⁱ�=∑^dⁱ=1iaixⁱ⁻¹

also das Bild linear von den Koeﬃzienten a_i des Polynoms ab- hängt (überprüfen Sie das). Sie ist kein Monomorphimus, denn

z.B. d

dx0= d dx1, aber ein Epimorphismus, denn

d dx�∑^di=0

a_i

i+1xⁱ⁺¹�=∑^di=0a_ixⁱ, d.h. jedes Polynom besitzt eine Stammfunktion.

Lemma 5.5.7 Sei F ∶ V → W ein Vektorraumhomomorphis- mus. Dann sind Ker(F)⊂V und Bild(F)⊂W Untervektorräu- me. Die Dimension des Bildes bezeichnen wir auch als Rang vonF

rk(F)∶=dim Bild(F).

Beweis.Für den Kern: Ist F(v1)=0undF(v2)=0, dann auch F(v₁+v₂)=F(v₁)+F(v₂)=0

und

F( ⋅v1)= ⋅F(v1)=0 für alle ∈K.

Die Aussage für das Bild zeigt man analog.

(25)

F Monomorphismus ⇐⇒ Ker(F)={0}, wobeiKer(F)={v∈V �F(v)=0}.

In Verallgemeinerung von5.5.2.(1) haben wir:

Bemerkung 5.5.9 Sei F ∶V →W ein Homomorphismus, ⌦= (v₁, ..., v_n)eine Basis vonV und =(F(v₁), ..., F(v_n))das Bild von⌦unter F. Dann gilt

F Epimorphismus ⇔ Erzeugendensystem vonW F Monomorphismus ⇔ linear unabhängig

F Isomorphismus ⇔ Basis vonW

Beweis.Jeder Vektor inV ist von der Form∑ⁿⁱ=1 iv_imit i∈K. Es gilt also

Bild(F)={F(∑ⁿⁱ=1 iv_i)� i∈K}

={∑ⁿⁱ=1 iF(v_i)� i∈K}.

Somit ist Bild(F)=W genau dann, wenn die F(v_i) ein Erzeu- gendensystem bilden.

Weiter ist

Ker(F)={∑ⁿⁱ=1 iv_i�F(∑ⁿⁱ=1 iv_i)=0, i∈K}

={∑ⁿⁱ=1 iv_i�∑ⁿⁱ=1 iF(v_i)=0, i∈K}

Somit ist Ker(F)={0} genau dann, wenn die F(v_i) linear un- abhängig sind.

Insbesondere sehen wir da ein Erzeugendensystem minde- stens so viele Elemente hat wie eine Basis und eine linear un- abhängige Familie höchstens so viele Vektoren:

F Epimorphismus ⇒ dimV ≥dimW F Monomorphismus ⇒ dimV ≤dimW F Isomorphismus ⇒ dimV =dimW