Friedrich U. Mathiak

Friedrich U. Mathiak

Ebene Flächen- tragwerke II

Grundlagen der Plattentheorie

Ebene Flächentragwerke II

Grundlagen der Plattentheorie

Copyright Neubrandenburg 2008 / Friedrich U. Mathiak

Der Nachdruck oder das Kopieren dieses Skriptes ist auch auszugsweise nur mit Genehmi- gung des Autors erlaubt.

1. Auflage Neubrandenburg 2008

Hochschule Neubrandenburg Prof. Dr.-Ing. Friedrich U. Mathiak Fachbereich:

Bauingenieur- und Vermessungswesen

Postanschrift:

Brodaer Straße 2

D-17033 Neubrandenburg Tel.: (0395) 5693-(0)-301

Inhaltsverzeichnis

Inhaltsverzeichnis ...I

1 Einleitung... 1

2 Einführung in den Tensorkalkül ... 5

2.1 Skalar... 5

2.2 Vektor... 5

2.3 Der Tensor zweiter Stufe... 5

2.3.1 Der transponierte Tensor... 6

2.3.2 Der symmetrische Tensor... 6

2.3.3 Der antimetrische Tensor ... 7

2.3.4 Der Einheitstensor... 7

2.3.5 Der Kugeltensor ... 7

2.4 Summationsvereinbarung... 8

2.5 Das Kronecker δ-Symbol... 8

2.6 Das ε - Symbol... 9

2.7 Vektor- und Tensoralgebra... 10

2.7.1 Das Skalarprodukt zweier Vektoren... 10

2.7.2 Das Vektorprodukt zweier Vektoren... 10

2.7.3 Das Spatprodukt dreier Vektoren ... 11

2.7.4 Das doppelte Vektorprodukt ... 11

2.7.5 Skalarprodukt Vektor-Tensor... 12

2.7.6 Skalarprodukt Tensor-Tensor... 13

2.7.7 Doppelskalarprodukt Tensor-Tensor... 13

2.8 Vektor- und Tensoranalysis... 14

2.8.1 Der Nabla-Operator... 14

2.8.2 Der Gradient eines Skalarfeldes ... 14

2.8.3 Die Divergenz eines Vektorfeldes... 14

2.8.4 Der Rotor eines Vektorfeldes... 15

2.8.5 Der Gradient eines Vektorfeldes ... 15

2.8.6 Die Divergenz eines Tensorfeldes... 15

2.8.7 Der Delta-Operator... 16

2.8.8 Der Rotor eines Tensorfeldes... 16

2.8.9 Allgemeine Beziehungen für die Operatoren ... 17

3 Grundgleichungen der klassischen Plattentheorie ... 19

3.1 Voraussetzungen... 19

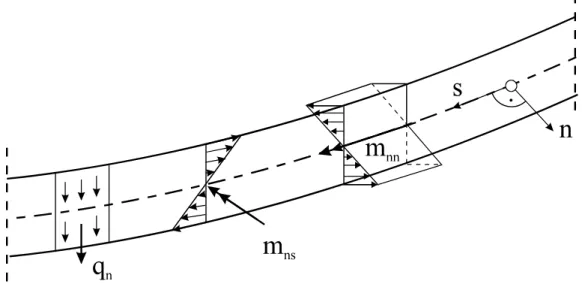
3.2 Plattenschnittlasten... 19

3.3 Transformationsgleichungen für die Schnittmomente... 21

II Inhaltsverzeichnis

3.3.1 Hauptbiegemomente... 21

3.3.2 Hauptdrillmomente ... 23

3.4 Gleichgewicht am Plattenelement... 25

3.5 Das Verschiebungsfeld w(x,y)... 26

3.6 Die Plattendifferenzialgleichung... 28

3.7 Die Plattengleichung in Zylinderkoordinaten... 28

3.8 Randbedingungen... 32

3.8.1 Kartesische Koordinaten ... 33

3.8.2 Zylinderkoordinaten... 34

3.8.3 Der eingespannte Rand... 34

3.8.3.1 Der eingespannte Rand x = x0 = konst. in kartesischen Koordinaten... 34

3.8.3.2 Der eingespannte Rand y = y0 = konst. in kartesischen Koordinaten... 35

3.8.3.3 Der eingespannte Rand r = r0 = konst. in Zylinderkoordinaten... 35

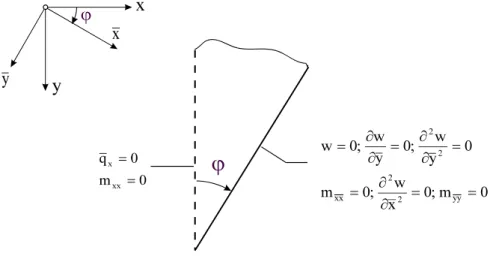
3.8.3.4 Der eingespannte Rand ϕ = ϕ₀ = konst. in Zylinderkoordinaten... 36

3.8.4 Der gelenkig gelagerte Rand ... 37

3.8.4.1 Der gelenkig gelagerte Rand x = x0 = konst. in kartesischen Koordinaten ... 37

3.8.4.2 Der gelenkig gelagerte Rand y = y0 = konst. in kartesischen Koordinaten ... 38

3.8.4.3 Der gelenkig gelagerte Rand r = r0 = konst. in Zylinderkoordinaten ... 38

3.8.4.4 Der gelenkig gelagerte Rand ϕ = ϕ0 = konst. in Zylinderkoordinaten ... 39

3.8.5 Der freie Rand ... 40

3.8.5.1 Der freie Rand x = x0 = konst. in kartesischen Koordinaten ... 40

3.8.5.2 Der freie Rand y = y0 = konst. in kartesischen Koordinaten ... 41

3.8.5.3 Der freie Rand r = r0 = konst. in Zylinderkoordinaten ... 41

3.8.5.4 Der freie Rand ϕ = ϕ₀ = konst. in Zylinderkoordinaten ... 42

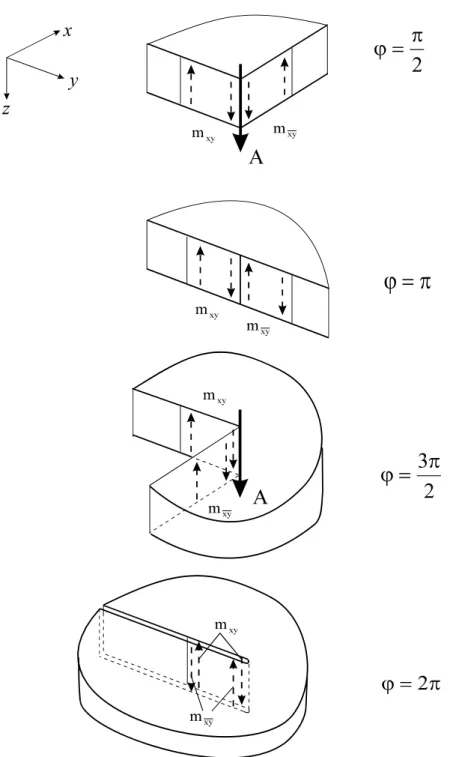
3.9 Das Verhalten der Platten an Ecken... 42

4 Die elastisch gebettete Platte ... 47

4.1 Lösung der homogenen Plattengleichung der elastisch gebetteten Platte in kartesischen Koordinaten49 4.2 Die elastisch gebettete Platte in Zylinderkoordinaten... 52

4.2.1 Die Kelvin-Funktionen... 59

4.2.2 Rotationssymmetrie... 60

5 Lösungsmethoden der Plattendifferenzialgleichung ... 65

5.1 Allgemeines... 65

5.2 Lösungen der homogenen Plattendifferenzialgleichung in kartesischen Koordinaten... 66

5.2.1 Potenzen in x und y ... 66

5.2.2 Potenzialfunktionen... 67

5.2.3 Potenzialfunktionen in Produktform ... 68

5.2.4 Logarithmische Funktionen... 69

5.2.5 Bipotenzialfunktionen ... 69

5.2.6 Direkte Produktlösungen von ΔΔw(x,y) = 0 ... 70

5.3 Lösungen der homogenen Plattendifferenzialgleichung in Zylinderkoordinaten... 71

5.3.1 Rotationssymmetrie... 71

5.3.2 Der Fall w = w(ϕ) ... 72

5.3.3 Potenzialfunktionen... 72

5.3.4 Rotationssymmetrische Lösung von ΔΔw... 73

5.3.5 Direkte Produktlösung... 74

5.3.6 Lösungen der Form w(r,ϕ) = f(r) cosϕ... 75

5.3.7 Lösungen der Form w(r,ϕ) = f(r) cos2ϕ... 76

5.4 Untersuchung einfacher Biegeflächen... 76

5.4.1 Lineare Verschiebungen... 76

5.4.2 Zylindrische Biegeflächen... 77

5.4.3 Parabolische Biegeflächen ... 78

5.4.4 Hyperbolische Biegeflächen ... 79

Inhaltsverzeichnis III

5.4.5 Reine Torsion... 80

5.5 Partikularlösungen der Plattendifferenzialgleichung in kartesischen Koordinaten... 81

5.5.1 Partikuläre Lösungen für Flächenlasten ... 81

5.5.1.1 Flächenlast p = p0... 82

5.5.1.2 Flächenlast p(ξ) = p₀ ξ... 82

5.5.1.3 Flächenlast p(x,y) = p0 η... 82

5.5.1.4 Flächenlast p(x,y) = p0(ξ + η) ... 82

5.5.1.5 Flächenlast p(x,y) = p0 ξ η... 83

5.5.1.6 Flächenlast p(x,y) = p0 sin(nπξ) ... 83

5.5.1.7 Flächenlast p(x,y) = p0 sin(nπξ) sin(kπη)... 83

5.6 Partikularlösungen der Plattendifferenzialgleichung in Polarkoordinaten... 83

5.6.1 Flächenlast p(r,ϕ) = p0... 83

5.6.2 Flächenlast p(r,ϕ) = p₀ ρ... 83

5.6.3 Flächenlast p(r,ϕ) = p₀ ρ²... 83

5.7 Die Fundamentallösung der klassischen Plattentheorie... 83

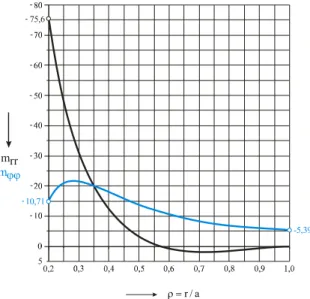
5.7.1 Die singuläre Lösung Einzelkraft... 84

5.7.2 Die singuläre Lösung Einzelmoment M, Drehung um die y-Achse... 86

5.7.3 Die singuläre Lösung EinzelmomentM, Drehung um die x-Achse ... 88

5.8 Rotationssymmetrische Kreis- und Kreisringplatten... 89

5.9 Die eingespannte Kreisplatte unter Gleichlast... 92

5.10 Die drehbar gelagerte Kreisplatte unter Gleichlast... 95

5.11 Die eingespannte Kreisplatte unter konstanter Teilflächenbelastung... 98

5.12 Die eingespannte Kreisplatte unter mittiger Einzelkraft... 102

5.13 Die eingespannte Kreisplatte mit Mittelstütze unter Gleichlast... 103

5.14 Die drehbar gelagerte Kreisplatte unter mittiger Einzelkraft... 107

5.15 Die innen eingespannte Kreisringplatte unter Gleichlast... 110

5.16 Die Kreisringplatte mit gelenkig gelagertem Außenrand unter Gleichlast... 114

5.17 Die Kreisringplatte mit eingespanntem Außenrand unter Gleichlast... 119

5.18 Die Kreisringplatte mit gelenkiger Lagerung unter Linienlast... 122

5.19 Die Kreisringplatte unter konstanter Linienlast längs eines Kreises... 128

6 Rechteckplatten... 133

6.1 Der unendlich lange Plattenstreifen... 133

6.2 Der Plattenhalbstreifen... 140

6.2.1 Der Plattenhalbstreifen mit gelenkiger Lagerung des kurzen Randes... 147

6.2.2 Der Plattenhalbstreifen mit Einspannung des kurzen Randes ... 156

6.2.3 Der Plattenhalbstreifen mit freiem kurzen Rand ... 158

6.3 Die allseits gelenkig gelagerte Rechteckplatte unter Gleichlast... 162

6.4 Die auf vier Eckstützen gelagerte Rechteckplatte unter konstanter Flächenlast... 169

7 Die schubelastische Platte... 177

7.1 Allgemeines... 177

7.2 Die Grundgleichungen einer schubelastischen Platte... 177

7.3 Plattenkinematik... 178

7.4 Die statischen Grundgleichungen... 180

7.5 Das Stoffgesetz... 183

7.6 Die Differenzialgleichungen... 184

IV Inhaltsverzeichnis

7.7 Die Grundgleichungen der flächenlastfreien Platte in kartesischen Koordinaten... 189

7.8 Die Grundgleichungen der flächenlastfreien Platte in Polarkoordinaten... 190

7.9 Ein Vergleich mit der klassischen Lösung... 191

7.10 Die isotherme Formänderungsenergie... 193

7.11 Der Satz von Betti... 193

7.12 Die Randwerte einer schubelastischen Platte... 194

7.13 Die eingespannte schubelastische Kreisplatte unter konstanter Teilflächenbelastung... 195

8 Näherungsverfahren ... 203

8.1 Das Streifenkreuzverfahren nach Markus... 203

8.2 Die drillweiche Platte... 205

9 Fourierreihen... 213

9.1 Einfache Fourierreihen... 213

9.2 Fourierdoppelreihen... 218

Index... 221

Literatur... 225

1 Einleitung

Eine Platte ist ein dünnes ebenes Flächentragwerk, das nur Lasten senkrecht zur Plattenmittel- fläche aufnimmt. Ihre Plattendicke h soll dabei als konstant vorausgesetzt werden. Die im Folgenden vorgestellte Theorie der dünnen Platte gehen in ihren theoretischen und experi- mentellen Grundlagen auf Arbeiten von

- Jakob II Bernoulli¹, 1759-1789

- Ernst Florens Friedrich Chladni, Physiker, 1756-1827

- Leonhard Euler, schweiz. Mathematiker, 1707-1783

- Sophie Germain, 1776-1831

- Joseph Louis Comte de Lagrange, frz. Mathematiker, 1736-1813

- Claude Louis Marie Henri Navier, frz. Physiker, 1785-1836

- Simeón Dénis Poisson, frz. Physiker und Mathematiker, 1781-1840

- Gustav Robert Kirchhoff, 1824-1887

Ein Jahr vor seinem Tode legte Jakob II Bernoulli der Petersburger Akademie seine Platten- theorie² vor. Die Anregung zur Aufstellung einer Plattentheorie erhielt der junge hoffnungs- volle Wissenschaftler aus der Arbeit von Chladni, der seine Entdeckungen über die Theorie des Klanges der Petersburger Akademie vortrug. Basis für Bernoullis Untersuchungen war die Arbeit von Leonhard Euler über die Transversalschwingungen von Stäben, deren Theorie Bernoulli auf die Platte übertrug, indem er eine rechteckige Platte als eine Doppelschicht von senkrecht zueinander angeordneten und miteinander fest verbundenen Stäben ansieht. Ber- noulli kommt zu der Differenzialgleichung

4 4 4 4 4

c z y

z x

z =

∂ + ∂

∂

∂

Mit z wird die Auslenkung und mit x und y die Achsenkoordinaten der Ersatzstäbe angege- ben. c⁴ ist eine Konstante. Bernoulli räumt selbst Schwächen seiner Theorie ein. In seiner Ar- beit Neue Beiträge zur Akustik macht Chladni auf die Diskrepanz zwischen Theorie und Ex-

1 Enkel des großen Johann I Bernoulli, ertrank beim Baden in der Newa

2 Essai théoretique sur les vibrations des plaques élastiques, rectangulaires et libres

2 1 Einleitung

periment aufmerksam. Nachdem Chladni am Ende des Jahres 1808 der Französischen Aka- demie in Anwesenheit des regierenden Kaisers Napoleon seine Arbeiten zum Klang vortrug, setzte diese auf Empfehlung Napoleons einen außerordentlichen Preis für die mathematische Theorie der Flächenschwingungen aus. Die Aufgabe wurde in den Pariser Akademieberichten für das Jahr 1808 abgedruckt. Die Aufgabe lautete¹:

Die mathematische Theorie von Schwingungen elastischer Flächen ist aufzustellen und mit dem Experiment zu vergleichen.

Da zunächst keine annehmbaren Arbeiten eingereicht wurden, musste die Bewerbungsfrist zweimal verschoben werden (1. Abgabetermin 1.10.1811, 2. Abgabetermin 1.10.1813, 3. Ab- gabetermin 1.10.1815). Von Sophie Germain wurden insgesamt drei Arbeiten eingereicht. Die 1. Denkschrift war fehlerhaft. Sie wurde von Lagrange, der Mitglied der Prüfungskommission war, berichtigt. In dieser Arbeit kommt sie zu der Differenzialgleichung

y 0 x

z y

x z t

z

4 2

6 2

4 6 2 2

2 ⎟⎟⎠=

⎜⎜ ⎞

⎝

⎛

∂

∂ + ∂

∂

∂ λ ∂

∂ +

∂

Lagrange erhält nach Korrektur der Arbeit die Differenzialgleichung

y 0 z y

x 2 z x k z t

z

4 4 2 2

4 4

4 2 2

2 ⎟⎟⎠=

⎜⎜ ⎞

⎝

⎛

∂ + ∂

∂

∂ + ∂

∂ + ∂

∂

∂

die von der ersten stark abweicht. Das ist aber die noch heute bestehende Form der Platten- gleichung, wobei die Bedeutung von k zur damaligen Zeit noch nicht gegeben werden konnte.

Zum 1. Oktober 1813 reichte Sophie Germain ihre neue Denkschrift ein, die von der Kom- mission "ehrenvoll erwähnt" wurde. Den ausgesetzten Preis erhielt sie dafür aber nicht. Das gelang ihr erst im Jahre 1816, obwohl auch diese Arbeit in den Augen der Gutachter noch immer nicht befriedigte. Es folgten dann Navier und Poisson, die weitere Grundlagen der heu- tigen Plattentheorie legten.

Mit den Arbeiten von Kirchhoff kam die Entwicklung der klassischen Plattentheorie zu einem vorläufigen Ende, weshalb auch von der Kirchhoffschen Plattentheorie gesprochen wird.

Erweiterte Theorien, die eng mit den Namen E. Reissner und R.D. Mindlin verbunden sind, versuchen die Diskrepanz der klassischen Plattentheorie zwischen zwei möglichen Randbe- dingungen für die Biegefläche und den dort vorhandenen drei Schnittlasten zu beseitigen. Das führt bei Reissner auf eine partielle Differenzialgleichung 6. Ordnung für die Biegefläche w und bei Mindlin auf ein Differenzialgleichungssystem zweier Differenzialgleichungen, die in

1 Donnez la théorie des surfaces élatiques et la comparez à l'expérience

1 Einleitung 3

der Summe ein Integrationsproblem 6. Ordnung darstellen und somit, wie bei Reißner, die Erfüllung dreier Randbedingungen am Rand ermöglichen

2 Einführung in den Tensorkalkül

2.1 Skalar

Ein Skalar¹ ist eine von der Wahl eines Koordinatensystems unabhängige und damit gegen- über einer Koordinatentransformation invariante Größe, die durch Angabe einer Zahl charak- terisiert ist. Skalare werden auch als Tensoren nullter Stufe bezeichnet.

Beispiel: Die Temperatur T

2.2 Vektor

Ein Vektor² ist eine Größe, die außer einem bestimmten Betrag eine bestimmte Richtung hat.

Ein Vektor kann im Raum auch als geordnetes Zahlentripel definiert werden, das gewissen Transformationsgesetzen genügt. Vektoren werden auch als Tensoren erster Stufe bezeichnet.

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

= +

+

=

z y x z z y y x x

v v v v

v

v e e e

v ;

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

= +

+

=

3 2 1 3 3 2 2 1 1

v v v v

v

v e e e

v

2.3 Der Tensor zweiter Stufe

Ein Tensor³ zweiter Stufe ist eine extensive Größe höherer Ordnung, die durch 9 Zahlenanga- ben festgelegt ist.

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

=

⊗ +

+

⊗ +

⊗

=

zz zy zx

yz yy yx

xz xy xx z

z zz y

x xy x x xx

T T T

T T T

T T T T

T

T e e e e e e

T K

1 zu lat. scalaris ›zur Leiter, Treppe gehörig‹

2 von lat. vector ›Träger‹, ›Fahrer‹, zu vehere ›fahren‹

3 zu lat. tendere, tensum ›spannen‹

6 2 Einführung in den Tensorkalkül

oder

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

=

⊗ +

+

⊗ +

⊗

=

33 32 31

23 22 21

13 12 11 3 3 33 2

1 12 1 1 11

T T T

T T T

T T T T

T

T e e e e e e

T K

Tjk: Koordinate des Tensors T

k

j e

e ⊗ : Basisdyaden

k j

Tjke ⊗e : Komponente des Tensors T

ϕ: 1 = 3⁰ Tensor 0.ter Stufe (Skalar im ѳ) v: 3 = 3¹ Tensor 1.ter Stufe (Vektor im ѳ) T: 9 = 3² Tensor 2.ter Stufe

27 = 3³ Tensor 3.ter Stufe 81 = 3⁴ Tensor 4.ter Stufe 3ⁿ Tensor n.ter Stufe

Hinweis: Die dyadischen Produkte der Basisvektoren e_x ⊗e_x oder e₁⊗e₁ usw. sind nicht weiter zerlegbar. Für lineare Dyaden gelten die folgenden Rechenregeln

a b b a

c b a c b a

c b a c b a

⊗

≠

⊗

⋅

=

⋅

⊗

⋅

=

⊗

⋅

) ( )

(

) ( ) (

2.3.1 Der transponierte Tensor

Aus T entsteht T^T durch spiegeln der Elemente an der Hauptdiagonalen.

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

1 5 2

0 2 4

1 3 1

1 0 1

5 2 3

2 4 1

TT

T

2.3.2 Der symmetrische Tensor

T

T^T = und damit T_jk =T_kj.

2.3 Der Tensor zweiter Stufe 7

Beispiel:

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

6 1 4

1 3 2

4 2 1 T

Der symmetrische Tensor ist durch sechs Zahlenangaben festgelegt.

2.3.3 Der antimetrische Tensor

T

T^T =− und damit T_jk =−T_kj

Beispiel:

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

−

−

−

=

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

−

−

−

=

0 1 4

1 0 2

4 2 0

0 1 4

1 0 2

4 2 0

TT

T

Der antimetrische Tensor ist durch drei Zahlenangaben festgelegt.

2.3.4 Der Einheitstensor

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

1 0 0

0 1 0

0 0 1 I

2.3.5 Der Kugeltensor

I

T S

1 0 0

0 1 0

0 0 1 S S 0 0

0 S 0

0 0 S

=

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

Der Kugeltensor ist durch eine Zahlenangabe festgelegt.

8 2 Einführung in den Tensorkalkül

2.4 Summationsvereinbarung

In der Tensorrechnung wird zwischen freien und gebundenen Indizes unterschieden.

Freie Indizes:

⎪⎩

⎪⎨

⎧

ϕ

=

ϕ

= ϕ

=

→ ϕ

=

3 3

2 2

1 1

j j

cos a x

cos a x

cos a x cos

a x

oder

⎪⎩

⎪⎨

⎧

ϕ

=

ϕ

= ϕ

=

→ ϕ

=

3 3

2 2

1 1

r r

cos a x

cos a x

cos a x cos

a x

Gebundene Indizes: (sie kommen doppelt vor):

33 22 11

jj α α α

α = + +

33 22 11

kk β β β

β = + +

3 3 2 2 1 1 k

ky x y x y x y

x = + +

3 3 33 2 3 32 1 3 31

3 2 23 2 2 22 1 2 21

3 1 13 2 1 12 1 1 11 k

k

β β α + β β α + β β α +

β β α + β β α + β β α +

β β α + β β α + β β α

= β β α _{l l}

2.5 Das Kronecker δ-Symbol

⎩⎨

⎧

≠

= =

δ 0 für k

k für 1

k l

l

l

1 0

0

0 1

0

0 0

1

33 32

31

23 22

21

13 12

11

= δ

= δ

= δ

= δ

= δ

= δ

= δ

= δ

= δ

mit δkl : Kronecker-Symbol¹

Einheitstensor: _{jk j k}

1 0 0

0 1 0

0 0 1

e e

I =δ ⊗

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

Es gilt: δ_kl =δ_lk

1 Leopold Kronecker, Mathematiker, 1823-1891

2.6 Das ε - Symbol 9

sowie δ_jlδ_lk =δ_j1δ_1k +δ_j2δ_2k +δ_j3δ_3k =δ_jk

Beispiel: x_kδ_kl =x_l, denn x_kδ_kl =x₁⋅δ_1l +x₂⋅δ_2l +x₃⋅δ_3l

2.6 Das ε - Symbol

Das ε-Symbol wird im Zusammenhang mit der Bildung des Vektorproduktes bei Vektoren und Tensoren benutzt. Es gilt:

⎪⎩

⎪⎨

⎧

=

−

=

= ε

sonst 0

. zykl und 1 2 3 m k für 1

. zykl und 3 2 1 m k für 1

m

k l

l

l

0 1

0

1 0

0

0 0

0

133 123

113

132 122

112

131 121

111

= ε +

= ε

= ε

−

= ε

= ε

= ε

= ε

= ε

= ε

0 0

1

0 0

0

1 0

0

233 223

213

232 222

212

231 221

211

= ε

= ε

−

= ε

= ε

= ε

= ε

+

= ε

= ε

= ε

0 0

0

0 0

1

0 1

0

333 323

313

332 322

312

331 321

311

= ε

= ε

= ε

= ε

= ε +

= ε

= ε

−

= ε

= ε

l l

lm mk mk

k =ε =ε

ε (zyklisch vertauscht)

Entwicklungssatz der Tensor- und Vektorrechnung

kn km k

jn jm j

in im i mn ijk

δ δ δ

δ δ δ

δ δ δ

= ε ε

l l l

l

n = k:

km 3

k

jk jm j

ik im i mk ijk

δ δ

δ δ δ

δ δ δ

= ε ε

l l l l

Entwicklung nach der letzten Zeile:

10 2 Einführung in den Tensorkalkül

l l

l l

l l

l l

l l

l l

l l

l l

l l

l

j im i jm

im j jm i im j jm i i jm j im

im j jm i ik j km jk i km ik jm k jk im k

im j jm i ik

j jk i km ik jm jk im k

3 3

3 3

) (

3 ) (

) (

δ δ

− δ δ

=

δ δ

− δ δ + δ δ + δ δ

− δ δ

− δ δ

=

δ δ

− δ δ + δ δ δ + δ δ δ

− δ δ δ

− δ δ δ

=

δ δ

− δ δ + δ δ

− δ δ δ

− δ δ

− δ δ δ

=

und damit:

jm j

im i im j jm i mk

ijk δ δ

δ

= δ δ δ

− δ δ

= ε

⋅ ε

l l l

l l

m = j: ε_ijkε_ljk =δ_ilδ_jj−δ_jlδ_ij =3δ_il−δ_il =2δ_il m = i ε_ijkε_ijk =2δ_ii =6

2.7 Vektor- und Tensoralgebra

Die Basisvektoren werden aus schreibtechnischen Gründen umbenannt: e_x;e_y;e_z ⇒e₁;e₂;e₃

r k

j

3 2

1 z

z y y x

e e

e

e e

e e

e e

v

r k

j

3 2

1 x

v v

v

v v

v v

v v

=

=

=

+ +

= +

+

=

2.7.1 Das Skalarprodukt zweier Vektoren

3 3 2 2 1 1 j j jk k j k

j k

j b a b a b a b a b a b a b

a ⋅ = ⋅ = δ = = + +

=

⋅b e_j e_k e_j e_k a

Herausfiltern einer Koordinate: v⋅e_j =v_ke_k ⋅e_j =v_kδ_kj =v_j

2.7.2 Das Vektorprodukt zweier Vektoren

d e e

e e e

e b

a× =a_{j j}×b_{k k} =a_jb_{k j}× _k =a_jb_kε_{jkl l} =d_{l l} =

l l ajbk jk

d = ε ist nur von Null verschieden, wenn

2.7 Vektor- und Tensoralgebra 11

⎩⎨

⎧

−

→ ε

ε ε

+

→ ε

ε

= ε

ε ; ; 1

1

;

;

132 213 321

312 231 123 jkl

und damit

3 2

1

2 3

1 2

1 3

e e

e

e e

e e

e e

b a

) b a b a ( ) b a b a ( ) b a b a (

b a b a b a b a b a b a

1 2 2 1 3

1 1 3 2

3 3 2

3 1 1 2 2 3 1 3 3 2 2

1

− +

− +

−

=

−

−

− +

+

=

×

oder symbolisch:

3 2 1

3 2 1

b b b

a a a

3 2

1 e e

e b a× =

Behauptung: )(a×b)⋅(c×d)=^! (a⋅c)(b⋅d)−(a⋅d)(b⋅c

) )(

( ) )(

(

c b d a d b c a d c b a d c b a

d c b a d

c b a ) (

d c b a

d c b a d

c b a

) d

c ( ) b

a ( ) d (c ) b (a

k k j j k k j j j k k j k j k j

jm k m k j km j m k j jm k km j m k j

mn jkn m k j np mp jkn m k j

p mp m n

jkn k j m m k

k j j

c b d a d b c a

e e

e e

e e d) (c b) (a

⋅

⋅

−

⋅

⋅

=

−

=

−

=

δ δ

− δ δ

= δ δ

− δ δ

=

ε ε

= δ ε ε

=

ε

⋅ ε

=

×

⋅

×

=

=

×

⋅

×

l l l

l l

l l

l l

l l

l l l

l

q.e.d.

2.7.3 Das Spatprodukt dreier Vektoren

3 2 1

3 2 1

3 2 1 2 3 1 3 1 2 1 2 3 2 1 3 1 3 2 3 2 1

k j jk j k k j m

k k j m

k k j

c c c

b b b

a a a c b a c b a c b a c b a c b a c b a

c b a c

b a c

b a ) c

b ( a

=

−

−

− +

+

=

ε

= ε

=

⋅ ε

= ε

⋅

=

×

⋅

≡a (b c) e_{j l l} e_{m l l} e_j e_{m l l l l} [abc]

2.7.4 Das doppelte Vektorprodukt

Behauptung: a×(b×c)=(a⋅c)b−(a⋅b)c

Zwischenrechnung: b×c=b_rc_sε_rske_k =d_ke_k =d

12 2 Einführung in den Tensorkalkül

b)c (a c)b (a

e e

e e

e

e e

e e e

e c) (b

a _{j k j k}

⋅

−

⋅

=

−

=

δ δ

− δ δ

= δ δ

− δ δ

=

ε ε

= ε

=

×

=

×

=

×

×

l l l

l

l l l

l l

l l

l l l

l

c b a c b a

c b a c

b a ) (

c b a

c b a d

a d

a d

a

j j j j

s rj s r j sj r s r j s

rj sj r s r j

jk rsk s r j jk

k j k

j k

j

q.e.d.

2.7.5 Skalarprodukt Vektor-Tensor

w e e

e e

e e

e e e e

e e T v

=

=

=

=

⋅

=

⊗

⋅

=

⊗

⋅

=

⋅

l l l l l

l l

l

l l

l l

w T

v δ

T v ) ( T v

) (

T v T

v

j j jk

k j k

j k j

k j k j k

k j j

3 2 1

e e e e

w

) T v T v T v (

) T v T v T v (

) T v T v T v ( T

v

33 3 23 2 13 1

32 3 22 2 12 1

31 3 21 2 11 1 j

j

+ +

+

+ +

+

+ +

=

= _{l l}

nun:

j j j k jk j k jk

j k jk k

j jk k

j jk

v T v

T δ

v T

) ( v T )

( v T v

) (

T

e e

e

e e e e

e e e

e e v

T

l l l

l

l l l

l l

l

=

=

=

⋅

=

⋅

⊗

=

⋅

⊗

=

⋅

Vergleich der obigen Ergebnisse zeigt:

v T T v⋅ = ^T⋅

Ist T der Einheitstensor, dann folgt:

v e e

e e

e e

e e e e

e e I v

=

= δ

= δ δ

=

⋅ δ

=

⊗

⋅ δ

=

⊗ δ

⋅

=

⋅

j j j

j jk

k j k

j k j

k j k j k

k j j

v v

v ) ( v

) (

v v

l l l

l l

l

l l

l l

oder: I⋅v= v⋅I=v

Die Koordinaten eines Tensors erhält man durch entsprechende Skalarmultiplikation

jk mk j m k m m

j k

j⋅T⋅e =e ⋅T_l (e_l ⊗e )⋅e =T_l δ_lδ =T e

2.7 Vektor- und Tensoralgebra 13

2.7.6 Skalarprodukt Tensor-Tensor

) (

) (

T S

T S

m jk

m jk

m k

j

m k

j

e e e e

e e e

e T S

⊗

⋅

⊗

=

⊗

⋅

⊗

=

⋅

l l

l l

Def.: (a⊗b)⋅(c⊗d)=(b⋅c)(a⊗d)

R e e

e e T S e e T S e e e e T

S

m j

m j km jk m j m jk m j k

=

⊗

=

⊗

=

⊗

=

⊗

⋅

=

⋅

jm

k m

jk

R

δ )

)(

( T

S _{l l l l}

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

+ +

+ +

+ +

+ +

+ +

+ +

+ +

+ +

+ +

=

⋅

33 33 23 32 13 31 32 33 22 32 12 31 31 33 21 32 11 31

33 23 23 22 13 21 32 23 22 22 12 21 31 23 21 22 11 21

33 13 23 12 13 11 32 13 22 12 12 11 31 13 21 12 11 11

T S T S T S T S T S T S T S T S T S

T S T S T S T S T S T S T S T S T S

T S T S T S T S T S T S T S T S T S T S

nun I statt T

S e e e

e

e e e e e

e e e

e e e e e

e e

e I

S

k j j

j k k

j

m k

j m

k j

=

⊗

=

⊗ δ

=

⊗

⋅

⋅

=

⊗

⋅

⊗

=

⊗

⋅

⊗ δ

=

⊗ δ

⋅

⊗

=

⋅

jk m

jk

j jk

jk

m jk m

jk

S ) (

S

) (

) ( S ) (

) (

S

) (

) (

S ) (

) (S

l l

l l

l

l l

l l

I I I T;

I T T I S;

T T

S⋅ ≠ ⋅ ⋅ = ⋅ = ⋅ =

Das Ergebnis ist wieder ein Tensor.

2.7.7

Doppelskalarprodukt Tensor-Tensor

) (

) (

S

) (

T ) (

S

jk

m jk

m k

j m

m k

j

e e e e T

e e e

e T

S

⊗

⋅⋅

⊗

=

⊗

⋅⋅

⊗

=

⋅⋅

l l

l l

Def.: )(a⊗b) ⋅⋅(c⊗d)=(b⋅c)(a⋅d

33 33 23 32 13 31 32 23 22 22 12 21 31 13 21 12 11 11

kj jk jm km jk jm k m jk

m jk

T S T S T S T S T S T S T S T S T S

T S T

S δ

T S

) )(

( T S

+ +

+ +

+ +

+ +

=

= δ

= δ

=

⋅

⋅

=

⋅⋅

l l

l

l ek e ej em

T S

14 2 Einführung in den Tensorkalkül

T e e e

e I

T

Spur : T T T

T T

T δ T

) (

T

33 22 11

m m mj j m k mj jk m

k j jk m m

= + +

=

=

= δ

= δ δ

= δ δ

=

⊗ δ

⋅⋅

⊗

=

⋅⋅

ll l l l

l l l

l l

S T T

S ⋅⋅ = ⋅⋅ ; T ⋅⋅I=I ⋅⋅T=SpurT; I ⋅⋅I=3

2.8 Vektor- und Tensoranalysis

2.8.1 Der Nabla-Operator

Der Nabla-Operator ist ein symbolischer Vektor.

j 3

2

1 x x x

x z

y

x ∂

= ∂

∇

∂ → + ∂

∂ + ∂

∂

= ∂

∂ + ∂

∂ + ∂

∂

= ∂

∇ e_x e_y e_z e₁ e₂ e₃ e_j

2.8.2 Der Gradient eines Skalarfeldes

j 3

2

1 x

F F x x

F x

F ∂

= ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ + ∂

∂ + ∂

∂

= ∂

∇

= e₁ e₂ e₃ e_j

grad

Das Ergebnis ist ein Vektorfeld.

2.8.3 Die Divergenz eines Vektorfeldes

3 3 2 2 1 1 j j jk j k k k j

j x

v x v x v x v x

v v div x

∂ +∂

∂ +∂

∂

= ∂

∂

= ∂

∂ δ

= ∂

∂ ⋅

= ∂

⋅

∇

= v e e

v

Das Ergebnis ist ein skalares Feld.

2.8 Vektor- und Tensoranalysis 15

2.8.4 Der Rotor eines Vektorfeldes

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂

− ∂

∂

∂

∂

−∂

∂

∂

∂

−∂

∂

= ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ + ∂

∂

− ∂

∂ + ∂

∂ +∂

∂

= ∂

∂ ε

= ∂

∂ ×

= ∂

∂ ×

= ∂

×

∇

=

2 1 1 2 1 3 3 1 3 2 2 3

2 1 3 3 2 1 1 3 2 2

3 1 1 2 3 3 1 2

jk j k k j j k k

j

x v x

; v x v x

; v x v x v

x v x

v x

v x

v x

v x

v

x v x

v v x

e e

e e

e e

e e

e e

e v v

rot _{j k l l}

Das Ergebnis ist ein Vektorfeld.

Beispiel:

) 1 e

; 1

; 1 ( ) 1

; 8

; 0 (

) 1 e

; x cos 0

; 1 0 ( )

x sin x

; x e

; x x (

8

x x 1 1

3 3 x x 2

1 ^{1 2 1 2}

−

−

−

=

−

−

−

=

→ +

+ +

= ^{+ +}

v rot

v rot v

2.8.5 Der Gradient eines Vektorfeldes

k j j k k k j

j x

v v

grad v v e x e e ⊗e

∂

= ∂

∂ ⊗

= ∂

⊗

∇

=

⎟⎟

⎟⎟

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜⎜

⎜⎜

⎜

⎝

⎛

∂

∂

∂

∂

∂

∂ ∂

∂

∂

∂

∂

∂ ∂

∂

∂

∂

∂

∂

=

3 3 3 2 3 1

2 3 2 2 2 1

1 3 1 2 1 1

x v x v x v

x v x v x v

x v x v x v gradv

Das Ergebnis ist ein Tensorfeld

2.8.6 Die Divergenz eines Tensorfeldes

3 3 33 2

23 1

13 2

3 32 2

22 1

12 1

3 31 2

21 1

11

j j jk

j k k

j j k k

k j j

x T x

T x T x

T x

T x

T x

T x

T x T

x δ T

x ) T x (

T T div x

e e

e

e e

e e e e

e e

T T

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂ + ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂ + ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂

= ∂

∂

= ∂

∂

= ∂

⊗

∂ ⋅

= ∂

⊗

∂ ⋅

= ∂

⋅

∇

= _{l l} ^l _l ^l _l ^l _l

16 2 Einführung in den Tensorkalkül

2.8.7 Der Delta-Operator

2 3 2 2 2 2 2 1 2

3 3 2 2 1 1 3 3 2 2 1 1

x x

x

x x

x x

x grad x

div

∂ + ∂

∂ + ∂

∂

= ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ + ∂

∂ + ∂

∂

⋅ ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ + ∂

∂ + ∂

∂

= ∂

∇

⋅

∇

=

=

Δ e e e e e e

2 3

2 2

2 2 2

1 2

x F x

F x

F F

∂ + ∂

∂ + ∂

∂

= ∂ Δ

(

) (

)

Δ

=

Δv e e e

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

Δ Δ

Δ

Δ Δ

Δ

Δ Δ

Δ

= Δ

33 32

31

23 22

21

13 12

11

T T

T

T T

T

T T

T T

2.8.8 Der Rotor eines Tensorfeldes

Def.: a×(b⊗c)=(a×b)⊗c

⎥⎥

⎥⎥

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎢

⎣

⎡

∂

−∂

∂

∂

∂

−∂

∂

∂

∂

−∂

∂

∂ ∂

−∂

∂

∂

∂

−∂

∂

∂

∂

−∂

∂

∂ ∂

−∂

∂

∂

∂

−∂

∂

∂

∂

−∂

∂

∂

=

∂ ⊗

= ∂

⊗

∂ ×

= ∂

⊗

∂ ×

= ∂

×

∇

=

2 13 1

23 2

12 1

22 2

11 1

21

1 33 3

13 1

32 3

12 1

31 3

11

3 23 2

33 3

22 2

32 3

21 2

31

m jkm j k k

j j k k

k j j

x T x T x

T x

T x

T x T

x T x T x

T x

T x

T x T

x T x

T x

T x

T x

T x

T rot

x ε ) T

x T T

rot x

T

e e e

e (e e

e e

T

T _{l l} ^l _l ^l _l

2.8 Vektor- und Tensoranalysis 17

2.8.9 Allgemeine Beziehungen für die Operatoren

) F ( grad grad )

F grad grad (

) F ( grad )

F grad (

) (grad Δ ) (Δ grad

) (grad Δ ) (Δ grad

div grad )

grad ( div

) grad ( div

F grad )

F ( div

) div ( ) ( div

T T

T

Δ

= Δ

Δ

= Δ

=

=

= Δ

=

= Δ

= Δ

v v

v v

v v

v v I

v v