11 Integralrechnung bei Funktionen mit mehreren Variablen
In diesem Kapitel wird der Begriff des bestimmten Integrals auf Doppel-, Dreifach- und Kurvenintegrale sowie auf Oberfl¨achenintegrale erweitert. Bei jedem dieser Be- griffe wird die Berechnung des Integralwertes auf die eines bestimmten Integrals zu- r¨uck gespielt. Zun¨achst f¨uhren wir in 11.1 Doppelintegrale z.B. zur Beschreibung von Volumina, Schwerpunkten von ebenen Fl¨achen und Fl¨achenmomenten ein. Anschlie- ßend ¨ubertragen wir in 11.2 die Vorgehensweise auf Dreifachintegrale, um Schwer- punkte und Massentr¨agheitsmomente von K¨orpern zu berechnen.
Hinweis:Eine weitere Notwendigkeit, den Integralbegriff auf Funktionen mit meh- reren Variablen zu erweitern, besteht in der Integration entlang einer Linie. Dies f¨uhrt auf den Begriff derLinienintegrale, die in der Elektrodynamik und Thermo- dynamik zur Berechnung der Energie herangezogen werden. Neben den Linieninte- gralen werden in einem weiteren Web-AbschnittOberfl¨achenintegralediskutiert.
Die hierzu notwendigen Substitutionsregeln und Koordinatentransformationen wer- den ebenfalls auf der Homepage zur Verf¨ugung gestellt.
11.1 Doppelintegrale (Gebietsintegrale)
11.1Wir besch¨aftigen uns in diesem Abschnitt mit zweidimensionalen Integralen. Die ¨Uber- tragung vom eindimensionalen auf den mehrdimensionalen Fall bereitet im Prinzip keine Schwierigkeiten, wird von seiner Konstruktion her aber aufw¨andiger, da nicht ein Intervall sondern nun ein zweidimensionales Gebiet aufgeteilt werden muss.
Hinweis: Die Anwendungsbeispiele werden durch Maple-Prozeduren erg¨anzt, die sich zus¨atzlich auf der Homepage befinden.
11.1.1 Definition
Das bestimmte Integral einer positiven Funktionf(x)
Abb. 11.1.
im Intervall[a, b] repr¨asentiert die Fl¨ache, welche die Kurve f(x) mit der x-Achse im Bereich [a, b] ein- schließt. Definiert wird das bestimmte Integral
Z b
a
f(x)dx
als Grenzwert ¨uber die Summe aller Rechteckfl¨achen(xk−xk−1)f(ξk), wenn die Intervallbreite4xk = (xk−xk−1)der Unterteilung des Intervalls
a=x0< x1< . . . < xn−1< xn=b f¨urn→ ∞gegen Null strebt (siehe Abb. 11.2).
454 11. Integralrechnung bei Funktionen mit mehreren Variablen
Abb. 11.2.Summe der Rechteckfl¨achen
Um diesen Integralbegriff auf zweidimensionale Gebiete zu ¨ubertragen, reicht es f¨ur unsere Zwecke vollkommen aus, nur einen beschr¨ankten, einfach zusam- menh¨angenden BereichG⊂IR2 in der(x, y)-Ebene zu betrachten, der einen
”glatten” Rand besitzt. Diesen Bereich nennen wir im Folgenden einGebiet.
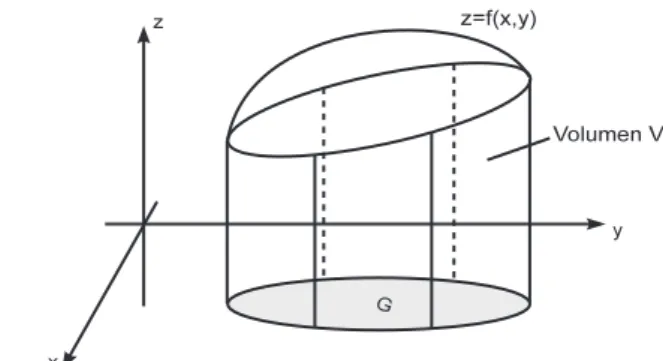
Es seiz=f(x, y)eine auf dem GebietGstetige, positive Funktion. Gesucht ist das Volumen zwischen dem Funktionsgraphen undG:
Abb. 11.3. Funktionf(x, y) ¨uber einem zweidimensionalen GebietG
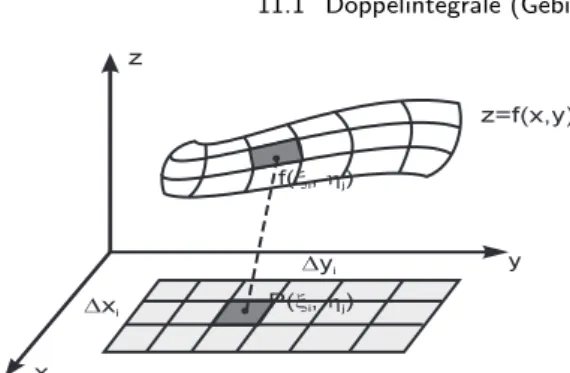
Zur Bestimmung des VolumensV zerlegen wir das GebietGin Rechteckfl¨achen der L¨ange4xi und Breite4yj. Die Anzahl der Unterteilungen inx-Richtung sein, die Anzahl der Unterteilungen iny-Richtungm. D.h.ivariiert zwischen 1 und n, j variiert zwischen 1 und m. F¨ur jedes Rechteck mit Index (i, j) w¨ahlen wir einen beliebigen Punkt P(ξi, ηj) und bestimmen den zugeh¨ori- gen Funktionswertf(ξi, ηj). Das Zylindervolumen ¨uber dem Rechteck betr¨agt Grundfl¨ache mal H¨ohe:
Vij =f(ξi, ηj) ∆xi∆yj .
Anschließend bildet man die Summe aller Zylindervolumen ¨uber dem Gebiet G. (F¨ur Rechtecke außerhalb von G setze man das Volumen auf Null.) Die Zwischensumme aller Zylindervolumen bildet eine N¨aherung f¨ur das zu be-
11.1 Doppelintegrale (Gebietsintegrale) 455
Abb. 11.4.Zur Konstruktion des Doppelintegrals
rechnende Volumen V ≈
m
X
j=1 n
X
i=1
f(ξi, ηj) ∆xi∆yj .
Je feiner die Unterteilung des GebietesGausf¨allt, umso genauer ist diese N¨a- herung. Wir lassen daher die Anzahl der Unterteilungen inx- undy-Richtung anwachsen. Strebt beim Grenz¨ubergangn→ ∞, m→ ∞die Zwischensumme gegen einen Grenzwert, so bezeichnet man ihn alsDoppelintegralbzw. alsGe- bietsintegral.
Definition: (Doppelintegral, Gebietsintegral).Der Grenzwert
Z Z
(G)
f(x, y)dG:= lim
m→∞ lim
n→∞
m
X
j=1 n
X
i=1
f(ξi, ηj) ∆xi∆yj
wird (falls er existiert) als Doppelintegral bzw. Gebietsintegral vonf uber¨ Gbezeichnet. Man nennt dannf ¨uber Gintegrierbar.
Bemerkungen:
(1) Oftmals wird die symbolische Schreibweise Z
(G)
f(x, y)dGnur mit einem Integralzeichen benutzt.
(2) Man nennt
(x, y) die Integrationsvariablen f(x, y) den Integrand
dG das Fl¨achenelement (G) den Integrationsbereich.
(3) F¨ur stetige Funktionen ist das Doppelintegral immer definiert.