1 Ein Modell f¨ ur Zufallsexperimente

Inhaltsverzeichnis

1 Ein Modell f¨ur Zufallsexperimente 2

2 Laplace-Experimente, elementare Kombinatorik 3 3 Bedingte Wahrscheinlichkeiten und Unabh¨angigkeit 4

3.1 Bedingte W’keiten . . . 4

3.2 Unabh¨angigkeit . . . 4

4 Diskrete Zufallsgr¨oßen 5 4.1 Allgemeines . . . 5

4.2 Einige wichtige Verteilungen . . . 5

4.2.1 BinomialverteilungX∼bin(n, p) . . . 5

4.2.2 Hypergeometrische VerteilungX ∼Hyp(M, m, n) (LOTTO) 5 4.2.3 geometrische VerteilungX ∼geom(p) . . . 6

4.2.4 PoissonverteilungX ∼pois(λ) . . . 6

4.3 Erwartungswert und Momente . . . 6

5 Stetige Zufallsgr¨oßen 9 5.1 Allgemeines . . . 9

5.2 Einige wichtige stetige Verteilungen . . . 9

5.2.1 Gleichverteilung . . . 9

5.2.2 Exponentialverteilung . . . 9

5.2.3 Normalverteilung . . . 10

5.3 Erwartungswerte und Momente . . . 11

6 Mehrdimensionale Zufallsgr¨oßen und Unabh¨angigkeit 12 6.1 Faltung vonPX undPY . . . 14

6.2 Transformationssatz f¨ur W’-Dichten . . . 14

7 Erzeugende Funktionen 15 7.1 w’erzeugende Funktion . . . 15

7.2 momenterzeugende Funktion . . . 15

Tabellenverzeichnis

1 Urnenmodelle – (Kom sind Per, wobei die Elemente geordnet sind ) 3 2 Tabelle mit EW und Var diskreter Verteilungen . . . 8

3 Tabelle mit Verteilungsfunktionen und Dichten der stetigen Vertei- lungen . . . 10

Abbildungsverzeichnis

1 Gleichverteilung (Verteilungsfunktion, Dichtefunktion) . . . 9

2 Normalverteilung (Dichtefunktion) . . . 10

1 Ein Modell f¨ ur Zufallsexperimente

Ω: Ergebnisraum, enth¨alt die m¨oglichen Ergebnisse des Zufallsexperimentes A: System der EreignisseA⊂Ω

P : ω → [0,1]: Abbildung, die jedem Ereignis A seine Wahrscheinlichkeit P(A) zuordnet. Es gilt: P(A)≥0,P(ω) = 1 und

F¨ur alleA₁, A₂,· · · ∈ωmitA_i∩A_j=∅f¨uri6=j(Folge von paarweise disjunkten Ereignissen) gilt:

P(

∞

[

i=0

A_i) =

∞

X

i=1

P(A_i) (σ−Additivit¨at)

Satz 1 erste Folgerungen 1. P(∅) = 0

2. P(A)≤1

3. P(A^c) = 1−P(A)

4. A⊂B⇒P(A)≤P(B)Homogenit¨at

5. P(A1+· · ·+Ak) =P(A1) +. . . P(Ak)endliche Additivit¨at Satz 2 weitere Folgerungen

1. boolesche Ungleichung:P(A₁∪ · · · ∪A_k)≤P(A₁) +· · ·+P(A_k)wichtig hierbei ist, dass nicht vorrausgesetzt wird, das A₁, ..., A_k paarweise disjunkt sind.

2. Formel von Sylvester-Poincarr´e, Siebformel

P(

n

[

i=1

A_i) =

n

X

k=1

(−1)^k+1· X

H⊂{1,...,n}

P(\

i∈H

A_i) (Siebformel)

P(

3

[

i=1

A_i) : P(A₁∪A₂∪A₃) =P(A₁) +P(A₂) +P(A₃)

−P(A1∩A2)−P(A1∩A3)−P(A2∩A3) +P(A₁∩A₂∩A₃)

P(

2

[

i=1

Ai) : P(A1∪A2) =P(A1) +P(A2)−P(A1∩A2)

2 Laplace-Experimente, elementare Kombinatorik

Ein Laplace-Experiment liegt vor, wenn 1. #Ω<∞(endlicher Ergebnisraum)

2. A=R(Ω) (alle Teilmengen von Ω kommen als Ergebnis in Frage) 3. P(A) =#A

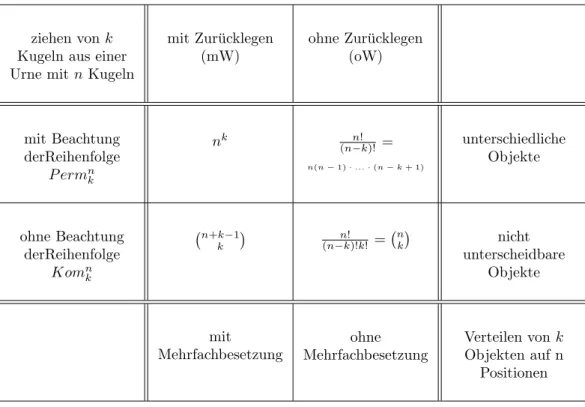
#Ω =Anzahl der g¨unstigen M¨oglichkeiten Anzahl der M¨oglichkeiten isg Urnenmodelle und passende Formeln:

ziehen vonk Kugeln aus einer Urne mitnKugeln

mit Zur¨ucklegen (mW)

ohne Zur¨ucklegen (oW)

mit Beachtung derReihenfolge

P ermⁿ_k

n^k _(n−k)!^n! =

n(n−1)·...·(n−k+ 1)

unterschiedliche Objekte

ohne Beachtung derReihenfolge

Komⁿ_k

n+k−1 k

n!

(n−k)!k! = ⁿ_k nicht

unterscheidbare Objekte

mit

Mehrfachbesetzung

ohne Mehrfachbesetzung

Verteilen vonk Objekten auf n

Positionen

Tabelle 1: Urnenmodelle – (Kom sind Per, wobei die Elemente geordnet sind )

Erinnerung:

n! = 1·2·3·. . .·nFakult¨at

n k

=_(n−k)!k!^n! ”n ¨uber k” oder ”k aus n”, Binomial-Koeffizient

3 Bedingte Wahrscheinlichkeiten und Unabh¨ angig- keit

3.1 Bedingte W’keiten

Es seien A und B Ereignisse in einem Zufallsexperiment. Welche Wahrscheinlichkeit hat B, wenn bekannt ist, dass A eintrit?

Definition 1 Es sei A ein Ergebnis mitP(A)>0. Die bedingte Wahrscheinlichkeit von B unter A wird definiert durch

P(B|A) =P(A∩B) P(A) Satz 3 (einige Definitionen)

1. Multiplikationsregel

SindA₁, ..., A_n Ereignisse mit P(A₁∩...∩A_n)>0, so gilt

P(A₁∩...∩A_n) =P(A₁)·P(A₂|A₁)·P(A₃|A₁∩A₂)·...·P(A_n|A₁∩...∩A_n−1) 2. Gesetz der totalen Wahrscheinlichkeit = Zerlegung

IstA1, ..., AneineEreignispartitionvonΩ, d.h.A1∩...∩An = Ω, Ai∩Aj =

∅ f¨ur i6=j, so gilt f¨ur alle Ereignisse B

P(B) =

n

X

i=1

P(B|Ai)P(Ai)

Hierbei istP(Ai) = 0zugelassen, der Summand wird dann als 0interpretiert.

3. Formel von Bayes

Es seien A₁, ...A_n und B wie oben und P(B)>0. Dann ist P(Ai|B) = P(Ai)P(B|Ai)

Pn

k=1P(B|Ak)P(A_k)

3.2 Unabh¨ angigkeit

Einer der zentralen Begriffe der Stochastik ist der , der (stochastischen)Unabh¨angig- keit.

B ist von A unabh¨angig, wenn die Information ”A ist eingetreten” die W’keit f¨ur B nicht ¨andert⇒P(B|A) =P(B) ^P(B∩A)_P(A) =P(B).

Definition 2 (Unabh¨angigkeit)

Zwei Ereignisse A und B heissen stochastisch unabh¨angig, wenn P(A∩B) = P(A)·P(B)gilt.

P(A∩B) =P(A)·P(B)⇒A, B unabh¨angig Aus einer paarweisen Unabh¨angigkeit in einer Ereignisfamilie

P(A_i∩A_j) =P(A_i)P(A_j), f¨ur allei, j∈I, i6=j folgt nichtdie totale Unabh¨angigkeit.

4 Diskrete Zufallsgr¨ oßen

4.1 Allgemeines

Oft interessiert man sich nicht f¨ur das Ereignisωeines Zufallsexperimentes, sondern nur f¨ur einen hiervon abh¨angigen Wert X(ω).

Definition 3 (ZV, Verteilung, WMF, Verteilungsfunktion)

1. Eine diskrete Zufallsvariable (ZV) ist eine Abbildung X : Ω → R mit endlich vielen oder abz¨ahlbar unendlich (N,Z,Q) vielen Werten.

2. Die Verteilung einer diskretenZV X ist die AbbildungA→P(X ∈A) (=

P(ω∈Ω :X(ω))∈A), diese ist ein W’Maß.

3. Die Wahrscheinlichkeitsmassenfunktion (WMF) P^X einer diskreten ZV X wird definiert durch

P^X :R→[0,1], P^X(x) =P(X=x)

4. Die VerteilungsfunktionFX einer diskretenZV X wird definiert durch FX :R→[0,1], FX(x) =P(X≤x)

Massenfunktionen k¨onnen beispielsweise durch ein Stabdiagramm illustriert werden.

Bem.:

i) Zu jeder ZV geh¨ort eine Verteilung und verschiedene ZV k¨onnen durchaus die gleiche Verteilung haben.

ii) Da durch die Abbildung X in der Regel unterschiedlich viele Argumentwerte ω zu einem Bildwert X(ω) zusammengefasst werden, sind in der Regel selbst bei einem Laplace-Experiment die WerteP(X =x) nicht gleichgroß.

4.2 Einige wichtige Verteilungen

4.2.1 BinomialverteilungX ∼bin(n, p)

X heißt binomialverteilt mit Parameternnundp, wenn gilt P(X =k) =

n k

p^k(1−p)^n−k f¨ur k= 0,1, ..., n

Man erh¨altBin(n, p) als Verteilung der Anzahl X der Erfolge beinunabh¨angigen Versuchswiederholungen mit Erfolgswahrscheinlichkeitp.

4.2.2 Hypergeometrische VerteilungX ∼Hyp(M, m, n) (LOTTO) Eine ZV heißt hypergeometrisch verteilt mit Parametern M,m,n (alles nat¨urliche Zahlen), wenn gilt

P(X =k) =

m k

M−m n−k

M n

Typische Fragestellung ist nach der W’keit f¨ur zwei Richtige im Zahlenlotto ”6 aus 49”: (⁶2)(⁴⁹⁻⁶6−2)

(⁴⁹₆)

Die Verteilung taucht bei Stichproben ohne Zur¨ucklegen auf.

F¨ur große M;Binomialverteilung

4.2.3 geometrische Verteilung X ∼geom(p)

Eine Art ”Wartezeitverteilung”: ”Angenommen, ein W¨urfel wird solange geworfen, bis eine sechs erscheint...”

X heißt geometrisch verteilt mit Parameterp, wenn gilt P(X =n) = (1−p)ⁿ⁻¹·p, f¨urn∈N

Diese Verteilung taucht immer dann auf, wenn ein Zufallsexperiment solange wie- derholt wird, bis ein bestimmtes Ereignis eintritt, der Parameter ist die W’keit des Ereignisses, auf das gewartet wird.

Z¨ahlt man stattdessen die Anzahl der Misserfolge, so erh¨alt man eine andere Version der geometrischen Verteilung:

P(X=n) = (1−p)ⁿ·p, f¨ur n∈N 4.2.4 Poissonverteilung X ∼pois(λ)

Die ZV Xheißt poisson-verteilt, mit Parameter λ(λ >0), wenn gilt P(X=k) =e^−λ·λ^k

k!, k∈N⁰ Satz 4 (”Das Gesetz der seltenen Ereignisse”)

Ist (pn)_n∈N⊂[0,1]eine Nullfolge mit lim

n→∞n pn =λ, so gilt f¨ur allek∈N0 n→∞lim

n k

p^k_n(1−pn)^k=e^−λλ^k k!

W’keit f¨ur kErfolge bei nWiederholungen mit Erfolgswahrscheinlichkeit p.

Bekannt ist: limn→∞(1 +^x_n)ⁿ=e^x

4.3 Erwartungswert und Momente

In diesem Abschnitt werden einige Verteilungsparameter eingef¨uhrt. Dies sind Zah- len, die bestimmte Aspekte einer Verteilung, wie beispielsweise die Lage oder die Streuung, beschreiben.

Definition 4 (ErwartungswertE(X))

SeiXeine diskrete Zufallsvariable mit WMFPX. Dann wird derErwartungswert E(X)vonX defniniert durch

E(X) =X

x∈N

x·P(X =x)

Hierbei wird vorrausgesetzt, dass die Reihe absolut konvergiert, d.h. P

|x|px(x)<

∞. Ist dies nicht der Fall, so sagt man, dass der Erwatungswert nicht existiert.

Beobachtungen:

• Der Erwartungswert einer Poissonverteilung mit Parameterλist geradeλ.

Erwartungswert von Funktionen von Zufallsvariablen

Oft kann man die interessierende Zufallsvariable Y als Funktiongeiner anderen ZV schreiben

Ω ^X_→R ^g→R Y =:g(x).

Satz 5 Es gilt E g(X) =P

x∈Rg(X)·PX(x) = P

x∈R g(X)·P(X =x), vorraus- gesetzt, die Summen konvergieren absolut.

Satz 6 (Rechenregeln f¨ur Erwartungswerte) Seien X,Y diskrete ZV und c∈R.

Vorrausgesetzt, dass die beteiligten Summen absolut konvergieren, dann gilt:

1. E(X) =E(E(X))

2. E(X+Y) =E(X) +E(Y)

E(X₁+X₂+...+X_n) =E(X₁) +E(X₂) +...+E(X_n) 3. E(cX) =c·E(X)

4. X≤Y ⇒E(X)≤E(Y) Definition 5 (k-te Moment)

Das k-te Moment von X ist definiert als E(X^k), vorrausgesetzt, die Reihe ist absolut konvergent(P

x|x|^kP(X=x)<∞).

DieVarianz von X ist definiert als

var(X) =E(X−EX)² (Maß f¨ur die Streuung)

(Vorraussetzung ist, dass EX²<∞, sonst sagt man, die Varianz existiert nicht) Schließlich heißt σ(X) =p

var(X) dieStandardabweichung von X.

Die Varianz ist ein Maß f¨ur die Streuung einer ZV um ihren Erwartungswert.

Rechenregeln:

1.

var(X) =E(X−EX)² = E(X²−2X(EX) + (EX)²)

= E(X²)−E(2X(EX)) +E((E(X))²)

= E(X²)−2E(X)·E(X) + (E(X))²

= E(X²)−(E(X))² also var(X) =E(X²)−(E(X))²

2. Seic∈R, dann

var(X+c) = E((X+c)−E(X+c))²=E(X+c−EX−c)²

= E(X−EX)²=var(X)⇒ var(X+c) =var(X) 3.

var(cX) = E(c²X²)−(E(cX))²

= c²(E(X²))−c²(EX)²

= c²(E(X²)−(EX)²) =c²var(X)⇒ var(cX) =c²var(X) damit klar:

σ(X+c) =σ(x) undσ(cX) =|c| ·σ(X).

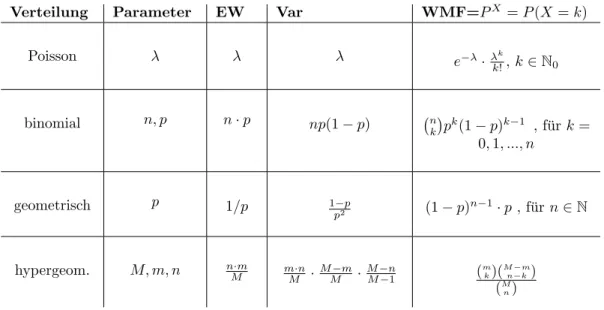
Tabelle mit Erwartungswerten und Varianzen der bisher genannten Verteilun- gen:

Verteilung Parameter EW Var WMF=P^X =P(X =k)

Poisson λ λ λ e^−λ·^λ_k!^k, k∈N0

binomial n, p n·p np(1−p) ⁿ

k

p^k(1−p)^k−1 , f¨urk= 0,1, ..., n

geometrisch p 1/p ^1−p

p² (1−p)ⁿ⁻¹·p, f¨urn∈N

hypergeom. M, m, n ^n·m_M ^m·n

M ·^M_M^−m·^M_M⁻ⁿ₋₁ (^mk)(^M−mn−k) (^M_n)

Tabelle 2: Tabelle mit EW und Var diskreter Verteilungen

5 Stetige Zufallsgr¨ oßen

5.1 Allgemeines

Viele Zufallsgr¨oßen k¨onnen ein Kontinuum von Werten annehmen: Lebensdauer, Messfehler, Proportionen, etc.

Definition 6 (Dichte, stetig verteilt)

Eine ZVX heißtabsolut stetig verteilt(kurz stetig) mitWahrscheinlichkeits- dichtefunktion fX (kurz Dichte), wenn gilt

P(X≤x) =

x

Z

−∞

f_X(y)dy ∀x∈R

Die Funktion FX : R→ R,FX(x) =P(X ≤x), heißt die Verteilungsfunktion zu X.

Im diskreten Fall ist FX vom reinen Sprungtyp. Im stetigen Fall ist FX ”glatt”.

Grob ist f_x die Ableitung von F_X, insbesondere alsoF_X stetig. Insbesondere gilt P(X =x) = 0 ∀x∈Rbei stetigen ZV.

5.2 Einige wichtige stetige Verteilungen

5.2.1 Gleichverteilung

Eine Zufallsvariable ZV heißtgleichverteiltauf dem Intervall (a,b), kurz:L(X) = unif, X ∼unif(a, b), wenn X die Dichtefunktionf(x) =

( ₁

b−a , a < x < b

0 hat.

Die zugeh¨orifge Verteilungsfunktion istF(X) =

∞

R

−∞

f(y)dy

Abbildung 1: Gleichverteilung (Verteilungsfunktion, Dichtefunktion)

5.2.2 Exponentialverteilung

Die Exponentialverteilungmit Parameter λ(>0) wird durch die Dichte f(x) =

(λe^−λx , x≥0

0 , sonst}Stammfkt:1−e^−λx beschrieben; die zugeh¨orige Verteilungsfunktion ist

F(x) =

(1−e^−λx , x≥0 0 , x <0

Diese Verteilung taucht h¨aufig im Zusammenhang mit Wartezeiten und Lebens- dauern auf. In Beispielen sieht man, daß dann das Alter keine Rolle spielt, diese Tatsache nennt man auch dieGed¨achtnislosigkeit der Exponentialverteilung.

5.2.3 Normalverteilung

Die wichtigste stetige Verteilung ist dieNormalverteilungmit Parameternµ∈R undσ²>0, kurz:N(µ, σ²), mit der Dichtefunktion:

f(x) = 1

√

2πσ²exp(− 1

2σ²(x−µ)²), −∞< x <∞.

Dies ist die Gaußsche Glockenkurve mit ihren Wendepunkten in µ±σ Taucht oft Abbildung 2: Normalverteilung (Dichtefunktion)

im Zusammenhang mit Messfehlern auf (Zentraler Grenzwertsatz)

!Man findet keine Stammfunktion, deshalb gibt esTabellen!

F¨ur die zugeh¨orige Verteilungsfunktion gibt es keine einfache Formel. F¨ur die Werte µ= 0, σ² = 1 (Man nennt N(0,1) auchStandardnormalverteilung) sind die Werte der Verteilungsfunktion

Φ(x) = 1

√2π

∞

Z

−∞

e^−1/2y2 dy

vertafelt (Tabelle), beispielsweise gilt Φ(1,645) = 0.95.

Tabelle mit den behandelten stetigen Verteilungen

Verteilung kurz Vert.funktion Dichte

Gleich

unif(a, b) FX(x) =

∞

R

−∞

f(y)dy fX(x) =_b−a¹

Exponential exp(λ) FX(x) = 1−e^−λx f¨urx≥0, 0 sonst.

fX(x) =λe^−λx

f¨urx≥0, 0 sonst. Stammfkt:−e^−λx

Normal N(µ, σ²) Es gibt keine Funktion, f¨urN(0,1) sind Werte

vertafelt.

fX(x) =

√1 2π

∞

R

−∞

e^−1/2y2dy

fX(x) =^√1

2πσ²exp(−_2σ¹2(x−µ)²) , −∞< x <∞

Tabelle 3: Tabelle mit Verteilungsfunktionen und Dichten der stetigen Verteilungen Lemma 5.2

F¨ur alleβ∈R, α6= 0 giltX ∼N(µ, σ²)⇒αX+β ∼N(αµ+β, α²σ²)

5.3 Erwartungswerte und Momente

Definition 7 (Erwartungswert stetiger ZV)

Ist X eine stetige Zufallsgr¨oße mit Dichte f, so wird der Erwartungswert EX von X definiert durch

EX = Z

x f(x)dx , vorrausgesetzt, es gilt R

|x|f(x)dx < ∞ sont sagt man, dass der Erwartungswert nicht existiert.

Satz 7

E g(x) = Z

g(x)f(x)dx Satz 8 (Linearit¨at und Monotonie)

Unter der Vorraussetzung, dass die beteligten Erwartungswerte existieren, gilt 1. E(X+Y) =EX+EY,E(cX) =c EX c∈R (Linearit¨at)

2. X≤Y ⇒EX ≤EY (Monotonie) Definition 8 (Momente stetiger ZV)

Dasi-te Momenteiner (stetigen) ZVXist mitE(X^k), dieVarianzmitvar(X) = E(X−EX)² und die Standardabweichung mitσ(X) =p

var(X)gegeben.

Rechenregeln sind (f¨ur c∈R):

var(X) = EX²−(EX)² var(cX) = c²var(X) var(X+c) = var(X) Merke:

zur StandardnormalverteilungN(0,1) geh¨oren der Erwartungswert 0 und die Vari- anz 1.

im allgemeinen Fall X∼N(µ, σ²) giltEX =µundvar(X) =σ²

6 Mehrdimensionale Zufallsgr¨ oßen und Unabh¨ angig- keit

Hat man mehrere, von dem Ergebnisωeines Zufallsexperimentes abh¨angige Gr¨oßen X₁(ω), ..., X_n(ω)∈R, so kann man diese zu einem stochastischen VektorX zusam- menfassen: ω7→(X₁(ω), ..., X_n(ω)).

Definition 9 (gemeinsame Verteilungsfunktion von ZVektoren)

Die gemeinsame Verteilungsfunktion F_X,Y : R² → R zweier ZV X und Y, oder auch: die Verteilungsfunktion des Zufallsvektors(X, Y), wird definiert durch

FX,Y(x, y) =P(X ≤xundY ≤y) =P({ω∈Ω :X(ω)< x∧Y(ω)< y}).

Definition 10 (Unabh¨angigkeit von Zufallsvektoren)

Es seien X, Y ZV mit gemeinsamer Verteilungsfunktion FX,Y. Weiter seiFX die Verteilungsfunktion zu X und FY die Verteilungsfunktion zu Y. Dann heißen X und Y stochastisch unabh¨angig, wenn gilt:

F_X,Y(x, y) =F_X(x)·F_Y(y) f¨ur allex, y∈R speziell bei diskreten stetigen ZV setzt man:

Definition 11 (diskreter, stetiger Zufallsvektor)

1. Nehmen X und Y nur endlich viele oder h¨ochstens abz¨ahlbar viele Werte an, so nennt man(X, Y)einen diskreten ZufallsvektorundPX,Y(x, y) :=

P(X =x, Y =y)diegemeinsame Massenfunktion vonX undY. 2. Gibt es eine FunktionfX,Y :R²→R+ mit der Eigenschaft

FX,Y(x, y) =

x

Z

−∞

y

Z

−∞

fX,Y(s, t)ds dt ∀x, y∈R

so nennt man (X, Y) einen absolut stetig verteilten Zufallsvektor und fX,Y einegemeinsame Dichtefunktion vonX undY.

Satz 9 ()

Es seien X undY Zufallsvektoren und g:R²→R eine Funktion, dann gilt 1. Ist(X, Y)ein diskreter Zufallsvektor mit Massenfunktion PX,Y, so gilt

E g(x, y) =X

X

X

Y

g(x, y)PX,Y(x, y).

2. Ist(X, Y)ein stetiger Zufallsvektor mit DichtefunktionFX,Y, so gilt E g(x, y) =

Z Z

g(x, y)f_X,Y(x, y)dx dy.

Interpretation:

Wahrscheinlichkeiten als Volumina unter der durch die Dichte definierte Ober- fl¨ache.

Satz 10 (Zusammenhang zur Unabh¨angigkeit:)

1. Ist X, Y diskret mit Massenfunktion PX,Y, so sind X und Y genau dann unabh¨angig, wenn

pX,Y(x, y) =pX(x)·pY(y) f¨ur allex, y∈R gilt (konkret: P(X =x, Y =y) =P(X=x)·P(Y =y)).

Hierbei sindpX(x) =P(X =x) =P

YP(X =x, Y =y) =P

Y pX,Y(x, y) undpY(y) =P

XpX,Y(x, y)die Massenfunktionen zu X undY.

2. Ist X, Y stetig mit Dichtefunktion fX und fY, so sind sie genau dann un- abh¨angig, wennfX,Y mitfX,Y(x, y) =fX(x)·fY(y)eine Dichtefunktione zum Zufallsvektor (X, Y)ist.

Satz 11 (Multiplikationsregel f¨ur Erwartungewerte)

F¨ur unabh¨angige ZV X und Y gilt E(XY) = E(X)·E(Y) (vorrausgesetzt, die Erwartungswerte existieren)

Definition 12 (CoVarianz)

DieKovarianz cov(X, Y)zweier ZV X undY wird definiert durch cov(X, Y) =E(X−EX)·(Y −EY)).

als Korrelationskoeffizient ϕ(X, Y) berechnet man ϕ(X, Y) = _σ(X)σ(Y^cov(X,Y)₎ (vorr- ausgesetzt, die ZV haben eine endliche, von 0 verschiedene Varianz).

Es gilt

cov(X, Y) = E(XY −(EX)Y −X(EY) + (EX)(EY))

= E(XY)−(EX)(EY)−(EX)(EY) + (EX)(EY)

= E(XY)−(EX)(EY)

SindX, Y unabh¨angig giltcov(X, Y) = 0 und man sagt, X,Y sind unkorreliert.

Die Umkehrung gilt nicht.

cov undϕk¨onnen als Maß eier linearen Abh¨angigkeit angesehen werden.

Cauchy-Schwarz-Ungleichung

|E(X−EX)(y−EY)| ≤p

(E(X−EX)²)(E(Y −EY)²)

|cov(X, Y)| ≤p

var(X)·var(Y) =σ(X)σ(Y)

Insbesondere nimmt der Korrelationskoeffizient Werte im Intervall [−1,1] an.

Zwei ZufallsvariablenXundY sind unabh¨angig, wenn sich die gemeinsame (Massen- )Verteilungsfunktion also Produkt der marginalen (Massen-)Verteilungsfunktionen schreiben lassen.

Bei der Dichtefunktion ist zu beachten, dass man die marginalen Dichtefunktioen durch ”ausintegrieren” der anderen Komponente erhalten kann:

f_X(x) =

∞

Z

0

F_X,Y(x, y)dy=

∞

Z

0

e^−x−y=e^−x

Damit lassen sich W’keiten ausrechnen, die sich auf beide ZV beziehen, zum Beispiel:

P(X ≤2Y) = x

{(x,y):x≤2y, x,y≥0}

Z

fX,Y(x, y)dydx= Z

0^∞

∞

Z

x/2

e^−x−ydydx= 2/3

Satz 12 (Gleichheit von Bienaym´e)

SindX1, ..., Xnunabh¨angige Zufallsvektoren, mit endlicher Varianz, so giltvar(X1)+

...+var(Xn)

Ist die gemeinsame Verteilung zweier ZV X und Y bekannt, so l¨asst sich (im Prinzip) die Verteilung von Z :=g(X, Y) unter g: R² →R gegeben, bestimmen.

Besonders wichtig, Z=X+Y, alsog:R²→R, x= ^x_x¹

2

→x₁+x₂.

6.1 Faltung von P

_X

und P

_Y

Satz 13 1. SindX, Y unabh¨angige diskrete ZV mit Massenfunktionen pX, pY, so istX+Y wieder eine diskrete ZV mit Massenfunktion

PX+Y(z) = X

x

pX(x)pY(z−x)

= X

y

p_X(z−y)p_Y(y)

Terminologie: Man nenntPX+Y dieFaltungvonPX und PY

2. Sind X, Y unabh¨angige stetige ZV mit Dichtefunktionen fx, fy, so ist auch X+Y eine stetige ZV, und die Dichtefunktion lautet

f_X+Y(z) = Z

f_X(x)f_Y(z−x)dx= Z

f_X(z−y)f_Y(y)dy Terminologie: Man nenntfX+Y die FaltungvonfX undfY.

6.2 Transformationssatz f¨ ur W’-Dichten

Satz 14 (Transformationssatz f¨ur W’-Dichten)

Es seien U undV offene Teilmengen vonR^d undΨ :U →V eine bijektive, stetige diffbare Abbildung mit det((Ψ⁰(x))6= 0 f¨ur allex∈U.

Ist dann X ein Zufallsvektor mit DichtefX undP(X∈U) = 1, so hat Y := Ψ(x) die Dichte

fY(y) =|det(Ψ⁻¹)⁰(y)|fX(Ψ⁻¹(y)), y∈V.

7 Erzeugende Funktionen

In diesem Kapitel geht es um Transformationsmethoden, die in vielen Berei- chen der Mathematik von großer Bedeutung sind und eine starke Verbindung zur Analysis herstellen.

7.1 w’erzeugende Funktion

Die w’erzeugende Funktion im allgemeinen ist definiert durch gX(s) =

∞

X

k=0

fX(k)s^k =Es^X siehe hierzu ¨Ubung11

siehe Skript von Frau Prof. B¨auerle S.29 ff.

7.2 momenterzeugende Funktion

Die momenterzeugende Funktion zu einer Zufallsvariablen is definiert als:

ϕX(t) =Ee^tX = Z ∞

0

e^tx·fX(x)dx