Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind.

4 Differentialrechnung in einer Variablen

Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind.

Die Entwicklung erfolgte unabhängig voneinander durch Gottfried Wilhelm von Leibniz (1646-1716, links) und Sir Isaac Newton (1643-1727, rechts).

Die unabhängige Leistung gilt heute als gesichert, damals allerdings kam es zum bekanntesten Prioritätsstreit der Wissenschaftsgeschichte.

Differentialrechnung TU Bergakademie Freiberg

229

4.1 Differenzierbarkeit Grundidee

Diese ist sehr einfach: Ersetzt man eine Funktion f(x) nahe einer Stelle x

durch ihre Tangente t(x), so macht man nahe x

nur kleine Fehler.

t f

x0

Die Tangente ist dabei als lineare Funktion viel leichter zu handhaben, als die Funktion f selbst.

Differentialrechnung TU Bergakademie Freiberg

230

Definition 4.1 (Erste Ableitung).

Sei f : D

→ R eine reelle Funktion und x

∈ D

ein innerer Punkt von D

. Dann heißt f differenzierbar an der Stelle x

, wenn der Grenzwert

f

(x

) := lim

x→x0

f(x) − f(x

) x − x

= lim

h→0

f(x

+ h) − f (x

) h existiert. f

(x

) heißt erste Ableitung von f an der Stelle x

. Ist f an jeder Stelle x

∈ M ⊆ D

differenzierbar, so heißt f in M differenzierbar. Man nennt die Funktion

f : M →R, x 7→ f

(x),

dann die erste Ableitung von f.

Geometrische Interpretation

x0 x0+h f(x0)

f(x0+h) f(x)

t(x) s(x)

s(x) =f(x0)+^{f(x0+h)−f(x}_h ⁰⁾(x−x0)

t(x) =f(x0) +f⁰(x0)(x−x0)

| {z }

h→0

Für h → 0 geht die Sekante s(x) durch (x

, f(x

)) und (x

+ h, f(x

+ h)) in eine Tangente t(x) über.

Die erste Ableitung f

(x

) ist also der Anstieg der Tangente t an f im Punkt x

.

Differentialrechnung TU Bergakademie Freiberg

232

Ist zu einer Funktion f die erste Ableitung f

in x

ebenfalls differenzierbar, so heißt

f

(x

) := (f

)

(x

) die zweite Ableitung von f an der Stelle x

. Entsprechend wird (für n ∈ N) die n-te Ableitung

f

(x

) = (f

)

(x

)

von f an der Stelle x

definiert. (Dabei ist f

(x

) := f(x

) zu setzen.) Notation:

Für die ersten drei Ableitungen schreibt man f

, f

und f

. Ab n = 4 schreibt man zumeist f

.

Zudem sind in der Physik auch f(t) ˙ und f(t) ¨ für die ersten zwei Ableitungen üblich, wenn das Argument t eine Zeit darstellt.

Differentialrechnung TU Bergakademie Freiberg

233

Leibniz-Notation

Auf Leibniz geht die folgende Schreibweise für Ableitungen zurück:

f

(x

) = df

dx (x

) = d dx f(x

), f

(x

) = d

f

dx

(x

) = d

dx

f(x

) = df

dx (x

), ...

f

(x

) = d

f

dx

(x

) = d

dx

f (x

) = df

dx (x

).

Diese Schreibweise ist noch heute weit verbreitet, da man damit manche

Rechenregeln (z. B. Kettenregel) sehr eingängig fassen kann, und die

Variable, nach der man differenziert, eindeutig gekennzeichnet ist.

Leibniz hatte damals die vage Vorstellung, dass sich die erste Ableitung f

(x

) als Quotient “infinitesimal kleiner Elemente“ dy und dx schreiben lässt.

Er betrachtete dazu den Differenzenquotienten

∆y

∆x = y − y

x − x

= f (x) − f(x

) x − x

und machte gedanklich die Größen ∆y und ∆x “unendlich klein“.

In Anlehnung an den Differenzenquotienten verwendete er für die erste Ableitung den Ausdruck

.

Die lediglich formale Quotientenform der Leibniz-Notation lässt sich mit dem Differentialbegriff (siehe später) mathematisch unterlegen.

Manchmal nennt man die Ableitung daher auch Differentialquotient.

Differentialrechnung TU Bergakademie Freiberg

235

Beispiele

Die konstante Funktion f

(x) = c (c ∈ R ) ist differenzierbar mit f

(x) = 0, denn

f

(x + h) − f

(x)

h = c − c

h = 0 → 0 (h → 0).

Die Funktion f

(x) = ax (a ∈ R ) ist differenzierbar mit f

(x) = a, denn

f

(x + h) − f

(x)

h = a(x + h) − ax

h = ah

h = a → a (h → 0).

Die Funktion f

(x) = x

ist differenzierbar mit f

(x) = 2x, denn f

(x+h)−f

(x)

h = (x + h)

−x

h = 2hx+h

h = 2x + h → 2x (h → 0).

Differentialrechnung TU Bergakademie Freiberg

236

Weitere Beispiele

Ohne Beweis geben wir hier noch einige weitere Funktionen mit ihren Ableitungen an:

Für f

(x) = x

(n ∈ N ) gilt f

(x) = nx

. Für f

(x) = e

gilt f

(x) = f

(x) = e

. Für f

(x) = sin x gilt f

(x) = cos x.

Für f

(x) = cos x gilt f

(x) = − sin x.

Mit Hilfe der Ableitungsdefinition bestimme man die erste Ableitung

von f(x) =

.

Beispiel für eine nicht differenzierbare Funktion

Die Funktion f(x) = | x | ist in x

= 0 nicht differenzierbar, denn

h

lim

f(0+h)−f(0)

h

= lim

h→0+

h−0

h

= 1, aber

h

lim

f(0+h)−f(0)

h

= lim

h→0−

−h−0

h

= −1 6= 1.

Der Differenzenquotient besitzt also keinen Grenzwert für h → 0.

Der bei x

= 0 auftretende “Knick“ ist typisch für Funktionen, die stetig, aber nicht differenzierbar sind. Es ist offensichtlich, dass man in diesem Punkt keine eindeutig bestimmte Tangente finden kann.

Differentialrechnung TU Bergakademie Freiberg

238

Bezug zur Stetigkeit Satz 4.2.

Ist f : D

→ R in x

∈ D

differenzierbar, dann ist f in x

auch stetig.

Beweisidee:

f(x) − f(x

) = f(x) − f(x

) x − x

| {z }

→f⁰(x0)

(x − x

)

| {z }

→0

→ 0 (h → 0).

Achtung: Wie das Beispiel f(x) = | x | zeigt, gibt es sehr wohl stetige Funktionen, die nicht differenzierbar sind. Die Umkehrung von Satz 4.2 ist also falsch!

Differenzierbarkeit ist somit eine stärkere Eigenschaft als Stetigkeit.

Differentialrechnung TU Bergakademie Freiberg

239

Präzisierung des Linearisierungsgedankens

Wir wollen noch einmal den Bezug der Funktion f zu ihrer Tangente t nahe x

aufgreifen. Dabei hilft folgende alternative Charakterisierung der Differenzierbarkeit:

Satz 4.3.

Eine reelle Funktion f : D

→ R ist genau dann in x

∈ D

differenzierbar, wenn es eine Zahl a ∈ R und eine Funktion ϕ : D

→ R gibt mit

f(x) = f(x

) + a(x − x

) + ϕ(x) (1)

und

→ 0 für x → x

. In diesem Fall gilt a = f

(x

).

Mit der Tangentenfunktion t(x) = f(x

) + f

(x

)(x − x

) liest sich (1) für eine differenzierbare Funktion f als

f(x) = t(x) + ϕ(x) mit ϕ(x)

x − x

→ 0 für x → x

. Grob gesprochen: “Funktion = Tangente + Restterm, wobei der Restterm für x → x

schneller als linear gegen Null geht“.

Visualisierung:

x0 x f t

|ϕ(x)|

Überzeugen Sie sich, dass mit

→ 0 erst recht ϕ(x) → 0 für x → x

gilt.

Differentialrechnung TU Bergakademie Freiberg

241

4.2 Differentiationsregeln

Satz 4.4 (Regeln für die Ableitung).

Sind f, g : D → R differenzierbar in x

∈ D, dann sind auch cf(c ∈ R ), f ± g, f g und f /g (falls g(x

) 6 = 0) in x

differenzierbar.

Dabei gelten folgende Regeln:

(cf)

(x

) = cf

(x

) (für c ∈ R),

(f ± g)

(x

) = f

(x

) ± g

(x

) (Summenregel), (f g)

(x

) = f

(x

)g(x

) + f(x

)g

(x

) (Produktregel),

g

(x

) =

(Quotientenregel).

Differentialrechnung TU Bergakademie Freiberg

242

Beispiele

Finden Sie die Ableitungen von f

(x) = 7x

+ 4x − 8, f

(x) = (x + 1)e

, f

(x) =

,

f

(x) =

für n ∈ N, ausgehend von (x

)

= nx

.

Verkettete Funktionen Satz 4.5 (Kettenregel).

Ist f : D

→ R in x

∈ D

differenzierbar und g : D

→ R in f(x

) ∈ D

differenzierbar, dann ist (g ◦ f) ebenfalls in x

differenzierbar mit

(g ◦ f)

(x

) = g

(f(x

)) · f

(x

). (2) Die Multiplikation mit f

(x

) in (2) nennt man “Nachdifferenzieren“.

Außerdem sind für g

und f

die Begriffe “äußere“ und “innere“

Ableitung gebräuchlich.

In Leibniz-Notation schreibt man für (2) mitunter kurz

=

·

. Man bestimme die Ableitung von f (x) = e

.

Differentialrechnung TU Bergakademie Freiberg

244

Differentiation von Umkehrfunktionen Satz 4.6.

Die reelle Funktion f : D

→ W

sei in x

∈ D

differenzierbar und besitze die Umkehrfunktion f

: W

→ D

. Ist f

(x

) 6 = 0 und ist f

stetig in f(x

), dann ist f

in f(x

) differenzierbar mit

(f

)

(f(x

)) = 1

f

(x

) bzw. (f

)

(y

) = 1

f

(x

) für y

= f(x

).

Leibniz-Notation:

=

für y = f (x) bzw. x = f

(y).

Differentialrechnung TU Bergakademie Freiberg

245

Beispiel

Für y = f (x) = sin x, x ∈ ( −

,

), gilt f

(x) = cos x 6 = 0. Desweiteren ist f

(y) = arcsin(y) stetig. Damit gilt nach Satz 4.6:

arcsin

(y) = 1

sin

(x) = 1

cos x = 1

p 1 − sin

x = 1 p 1 − y

.

Bestimmen Sie die auf diese Weise die Ableitungen von f

(x) = ln x und f

(x) = √ x.

Wie lässt sich die Ableitung einer beliebigen Potenzfunktion

f(x) = x

(x > 0, r ∈ R ) bestimmen?

Logarithmisches Differenzieren

Die Kettenregel liefert für positive differenzierbare Funktionen f die Gleichung

(ln(f (x)))

= f

(x) f (x) bzw.

f

(x) = (ln(f(x)))

f(x).

Dieser “Trick“ erleichtert manchmal die Berechnung der Ableitung.

Beispiel: Für f(x) = x

(x > 0) gilt

(x

)

= (ln(x

))

x

= (x ln x)

x

= (1 + ln x)x

.

Man bestimme die Ableitung der Funktion f(x) = q

x−1 (x−2)(x−3)

.

Differentialrechnung TU Bergakademie Freiberg

247

4.3 Ableitungen elementarer Funktionen

Mit Hilfe von Definition und der Regeln aus Abschnitt 4.2 lassen sich zu vielen gebräuchlichen Funktionen Ableitungen gewinnen.

Die folgenden Tabellen (betrifft vor allem diese Seite) sollten Sie am besten auswendig lernen.

Potenz- und Exponentialfunktionen, Logarithmen f(x) x

(r ∈ R ) e

ln x a

(a > 0) log

(x) f

(x) rx

e

a

ln a

Trigonometrische Funktionen

f(x) sin x cos x tan x cot x f

(x) cos x − sin x

= 1 + tan

x −

Differentialrechnung TU Bergakademie Freiberg

248

Arkusfunktionen

f(x) arcsin x arccos x arctan x arccot x f

(x)

1−x²

−

1+x²

−

Hyperbelfunktionen

f(x) sinh x cosh x tanh x coth x f

(x) cosh x sinh x

−

Areafunktionen

f(x) arsinh x arcosh x artanh x arcoth x f

(x)

√ 1

x²−1

, x > 1

, |x| < 1

, |x| > 1

4.4 Extrema, Wachstum und Krümmung differenzierbarer Funktionen

Mit der Differentialrechnung steht uns nun ein sehr mächtiges Instrument zur Untersuchung reeller Funktionen zur Verfügung.

Wir beginnen mit etwas Begriffsbildung.

Definition 4.7 (Lokale Extrema).

Sei f : D

→ R eine reelle Funktion. Ein Punkt x

∈ D

heißt lokales Maximum [lokales Minimum] von f, wenn es ein ε > 0 gibt, so dass

f(x

) ≥ f(x) [f(x

) ≤ f(x)] für alle x ∈ D

∩ (x

− ε, x

+ ε). (3) x

heißt lokales Extremum von f, wenn x

ein lokales Maximum oder ein lokales Minimum von f ist.

Differentialrechnung TU Bergakademie Freiberg

250

Bei einem lokalen Extremum x

betrachtet man also nur das Verhalten der Funktion f sehr nahe bei x

.

Das Gegenstück sind globale Extrema, bei denen die Beziehung f(x

) ≥ f(x) bzw. f (x

) ≤ f(x) aus (3) für alle x ∈ D

gelten muss.

Zeichnen Sie die Graphen der Funktionen f : R → R , f(x) = 2 cos 2x,

g : [0, ∞) →R, g(x) =

cos x

(qualitativ reicht), und machen Sie sich den Unterschied zwischen

“global“ und “lokal“ auch graphisch klar.

Differentialrechnung TU Bergakademie Freiberg

251

Bei differenzierbaren Funktionen ist die Suche nach lokalen Extrema eher einfach:

Satz 4.8 (Notwendige Bedingung für lokale Extrema).

Ist x

ein lokales Extremum der differenzierbaren Funktion f : (a, b) → R, dann gilt

f

(x

) = 0. (4)

Mit Satz 4.8 kann man also die “Kandidaten“ finden, die für ein lokales Extremum überhaupt in Frage kommen.

Nur für diese wird man dann einen konkreten Nachweis versuchen.

Graphische Darstellung

x0

f t

An einem Extremalstelle x

besitzt die Funktion f aus Satz 4.8 eine horizontale Tangente.

Finden Sie die Beweisidee von Satz 4.8. Betrachten Sie dafür das Vorzeichen des Differenzenquotienten in x

für h > 0 und h < 0.

Differentialrechnung TU Bergakademie Freiberg

253

Hat man mittels Satz 4.8 Kandidaten für lokale Extrema gefunden, prüft man häufig folgende Bedingung:

Satz 4.9 (Hinreichende Bedingung für lokale Extrema).

Sei f : (a, b) →R zweimal differenzierbar mit f

(x

) = 0 für ein x

∈ (a, b). Dann ist x

Stelle eines lokalen Minimums, wenn f

(x

) > 0, Stelle eines lokalen Maximums, wenn f

(x

) < 0.

Bestimmen Sie die lokalen und globalen Extrema von f(x) = x

e

. Analysieren Sie das Verhalten von f(x) = x

(n = 2, 5, 6) im Hinblick auf die Sätze 4.8 und 4.9 und das tatsächliche Auftreten von Extrema.

Differentialrechnung TU Bergakademie Freiberg

254

Der Mittelwertsatz

Wir fahren mit einem Ergebnis fort, das für den Anwender eher den Charakter eines Lemmas hat, aber an vielen Stellen von zentraler Wichtigkeit ist.

Wir beginnen mit einem einfachen Spezialfall:

Satz 4.10 (von Rolle

).

Ist f : [a, b] → R stetig und in (a, b) differenzierbar, und gilt f(a) = f(b), dann gibt es ein ξ ∈ (a, b) mit f

(ξ) = 0.

∗)Michel Rolle, frz. Mathematiker, 1652-1719

Graphische Darstellung

a ξ b

f

Beweisidee

f nimmt auf [a, b] Maximum und Minimum an. (Warum?) Liegen Maximum und Minimum auf dem Intervallrand, so ist f (x) = 0 auf [a, b], d,˙h f

(x) = 0 für alle x ∈ (a, b)

Ansonsten gibt es ein lokales Extremum ξ ∈ (a, b). Für dieses gilt f

(ξ) = 0 nach Satz 4.8.

Differentialrechnung TU Bergakademie Freiberg

256

Die Voraussetzung f(a) = f(b) = 0 kann durch folgende Modifikation entfernt werden:

Satz 4.11 (Mittelwertsatz).

Ist f : [a, b] →R stetig und in (a, b) differenzierbar, dann gibt es ein ξ ∈ (a, b) mit

f

(ξ) = f(b) − f(a)

b − a . (5)

Beweisidee:

Anwendung des Satzes von Rolle auf F(x) := f(x) −

f(a) + f(b) − f(a) b − a (x − a)

| {z }

Sekante

.

Differentialrechnung TU Bergakademie Freiberg

257

Graphische Darstellung

a ξ ξ˜ b

f(a) f(b)

s f

Die Funktion nimmt an mindestens einer Zwischenstelle ξ den Anstieg der Sekante s durch (a, f (a)) und (b, f(b)) an.

Hat ein Autofahrer, der eine Tempo-30-Zone mit durchschnittlich

38 km/h durchfährt, eine Ordnungswidrigkeit begangen? Lässt sich

ggf. der exakte Ort der Tempoüberschreitung bestimmen?

Monotonie

Mit dem Mittelwertsatz lässt sich sofort ein Ergebnis zur Bestimmung des Monotonieverhaltens einer differenzierbaren Funktion herleiten:

Folgerung 4.12.

Sei f : [a, b] →R stetig und differenzierbar in (a,b).

Ist f

(x) = 0 für alle x ∈ (a, b), so ist f konstant.

Ist f

(x) ≥ 0 (bzw. f

(x) ≤ 0) für alle x ∈ (a, b), so ist f monoton wachsend (bzw. fallend).

Ist f

(x) > 0 (bzw. f

(x) < 0) für alle x ∈ (a, b), so ist f streng monoton wachsend (bzw. fallend).

Führen Sie den Beweis für einen Punkt Ihrer Wahl aus.

Differentialrechnung TU Bergakademie Freiberg

259

Ein altes Problem neu diskutiert

Die Funktion f(x) = x

ist, wie in Kapitel 3 diskutiert, streng monoton wachsend, da aus x < y immer x

< y

folgt.

Versuchen Sie sich an einem Nachweis mittels Folgerung 4.12.

Differentialrechnung TU Bergakademie Freiberg

260

Krümmungsverhalten Definition 4.13.

Eine reelle Funktion f : D

→ R heißt konvex [konkav] im Intervall I ⊂ D

, wenn für alle x, y ∈ I und alle λ ∈ (0, 1)

f(λx + (1 − λ)y) ≤ λf(x) + (1 − λ)f(y)

[f(λx + (1 − λ)y) ≥ λf(x) + (1 − λ)f(y)] (6) gilt.

Veranschaulichung: Die Sekante durch (x, f(x)) und (y, f (y)) verläuft in [x, y] oberhalb [unterhalb] des Graphen von f.

Machen Sie sich klar, warum diese Veranschaulichung korrekt ist.

Graphische Darstellung

Bild einer konvexen (links) und einer konkaven Funktion (rechts).

Die bei Bewegung “von links nach rechts“ auftretende Links- und Rechtskrümmung ist typisch; insbesondere wenn in (6) die strengen Ungleichungsrelationen gelten.

Finden Sie ein Beispiel für eine auf R konvexe [konkave] Funktion.

Differentialrechnung TU Bergakademie Freiberg

262

Wie folgende Sätze zeigen, wird die Untersuchung der Krümmung leichter, wenn man Ableitungen zur Verfügung hat.

Satz 4.14.

Ist die Funktion f : (a, b) → R differenzierbar, so definieren wir für jedes z ∈ (a, b) die „Tangentenfunktion“

t

: x 7→ f (z) + f

(z)(x − z).

f ist in (a, b) genau dann konvex [konkav], wenn f(x) ≥ t

(x) [f(x) ≤ t

(x)]

für alle z ∈ (a, b) und alle x ∈ (a, b) gilt.

Anschauung: Jede Tangente an f verläuft unterhalb [oberhalb] des Graphen von f.

Differentialrechnung TU Bergakademie Freiberg

263

Satz 4.15.

Ist die Funktion f : (a, b) → R differenzierbar, dann ist f genau dann konvex [konkav] in (a, b), wenn f

in (a, b) monoton wachsend [fallend]

ist.

Ist f zweimal differenzierbar, dann ist f in (a, b) genau dann konvex [konkav], wenn

f

(x) ≥ 0 [f

(x) ≤ 0]

für alle x ∈ (a, b) gilt.

Untersuchen Sie das Krümmungsverhalten der Funktionen

f

(x) = x

(n ∈ N ), f

(x) = e

, f

(x) = ln x und f

(x) = sin x mit

Hilfe von Satz 4.15.

Graphische Darstellung

f f

z tz

Situation der Sätze 4.14 und 4.15 am Beispiel einer konvexen (links) und einer konkaven Funktion (rechts).

Machen Sie sich die Aussagen von Satz 4.14 und 4.15 noch einmal anhand der Bilder plausibel.

Differentialrechnung TU Bergakademie Freiberg

265

Definition 4.16 (Wende- und Sattelpunkt).

Ein Punkt (x

, f(x

)) des Graphen, an dem sich das

Krümmungsverhalten einer Funktion f ändert, heißt Wendepunkt von f. Die Stelle x

heißt Wendestelle.

Die Tangente in einem Wendepunkt heißt Wendetangente. Einen Wendepunkt mit horizontaler Tangente nennt man auch Sattelpunkt.

f(x) = sinxmit Wendepunkt(0,0) g(x) =x³mit Sattelpunkt(0,0)

Differentialrechnung TU Bergakademie Freiberg

266

Ist Differenzierbarkeit gegeben, ist die Bestimmung von Wendepunkten wieder einfacher:

Satz 4.17.

Ist f : (a, b) → R zweimal differenzierbar und (x

, f(x

) ein Wendepunkt von f, dann ist f

(x

) = 0.

Ist f : (a, b) → R dreimal differenzierbar und gilt für ein x

∈ (a, b) sowohl f

(x

) = 0 als auch f

(x

) 6 = 0, dann ist (x

, f(x

)) ein Wendepunkt von f.

Man bestätige das Vorliegen eines Wende-/Sattelpunkts in den

Beispielen von Seite 266 mit Hilfe von Satz 4.17.

Zusammenfassende graphische Darstellung

0 1 2 3 4 5

−3

−2

−1 0 1 2 3

konkav konvex

monoton

wachsend monoton

fallend monoton

wachsend f

f’

f’’

Dargestellt ist eine Funktion f , ihre Ableitungen f

und f

, sowie die resultierenden Monotonie- und Krümmungsbereiche.

Differentialrechnung TU Bergakademie Freiberg

268

4.5 Verschiedene Anwendungen 4.5.1 Kurvendiskussion

Eine Kurvendiskussion setzt sich aus den folgenden Teilaufgaben zusammen:

Definitionsbereich. Auf welcher (möglichst großen) Menge D

ist die Funktion f definiert?

Wertebereich. Welche Werte kann f(x) (x ∈ D

) annehmen?

Symmetrien. Ist f gerade oder ungerade?

Nullstellen. Löse f(x) = 0.

Extrema. Bestimme die Lösungen x

von f

(x) = 0. Ist f

(x

) > 0, dann ist (x

, f(x

)) ein lokales Minimum von f. Ist f

(x

) < 0, dann ist (x

, f(x

)) ein lokales Maximum von f.

Differentialrechnung TU Bergakademie Freiberg

269

Wendepunkte. Bestimme die Lösungen x

von f

(x) = 0. Ist f

(x

) 6 = 0, dann ist (x

, f(x

)) ein Wendepunkt von f.

Verhalten an Polstellen. Ist f eine rationale Funktion, bestimme die Pole x

von f (Nullstellen des Nennerpolynoms) und berechne

x→

lim

f(x) sowie lim

x→xP+

f(x).

Verhalten im Unendlichen. Berechne lim

x→∞

f(x) sowie

x→−∞

lim f(x).

Monotoniebereiche. Untersuche Vorzeichen von f

(x).

Krümmungsverhalten. Untersuche Vorzeichen von f

(x).

Graphische Darstellung.

Führen Sie eine Kurvendiskussion für f (x) = e

durch. Erinnern Sie

sich an einen Geldschein, auf dem der Funktionsgraph zu finden war?

4.5.2 Newton-Verfahren

In Abschnitt 3.3 hatten wir das Intervallhalbierungsverfahren zur Lösung von Gleichungen der Form

f(x) = 0 (7)

kennengelernt.

Mit dem Newton-Verfahren behandeln wir nun ein Verfahren für differenzierbare Funktionen f, welches im Allgemeinen wesentlich schneller ist.

Ziel ist die Bestimmung einer Lösung x

von (7) – ausgehend von einem Startwert x

, der möglichst in der Nähe von x

liegt.

Differentialrechnung TU Bergakademie Freiberg

271

Idee:

x

x

x

x

f

Man berechnet im n−ten Schritt die Nullstelle x

der Tangente t an f in x

. Diese wird als neue Näherung für x

verwendet.

Natürlich wird man zu Beginn einen Startwert x

wählen müssen.

Differentialrechnung TU Bergakademie Freiberg

272

Herleitung der Verfahrensvorschrift

x^∗ xn

xn−1

f t

Wir stellen die Bedingung

t(x

) = f(x

) + f

(x

)(x

− x

) = 0.

Umstellen nach x

führt auf die Verfahrensvorschrift des Newton-Verfahrens:

x

= x

− f(x

)

f

(x

) (n = 1, 2, . . .). (8)

Numerisches Experiment

Für das Beispiel f(x) = x + e

aus Abschnitt 3.3 liefert (8) die Vorschrift

x

= x

− x

+ e

1 + e

.

Ausgehend vom Startwert x

= 0 liefert M

folgende Werte:

n xn |f(xn)|

1 −0.500000000000000 1.06·10⁻¹ 2 −0.566311003197218 1.30·10⁻³ 3 −0.567143165034862 1.96·10⁻⁷ 4 −0.567143290409781 4.55·10⁻¹⁵ 5 −0.567143290409784 1.11·10⁻¹⁶

Für 14 Nachkommastellen benötigt man gerade 4 Schritte. Das Intervallhalbierungsverfahren hätte dagegen 48 Schritte gebraucht!

Differentialrechnung TU Bergakademie Freiberg

274

Konvergenzeigenschaften

Wenn das Newton-Verfahren konvergiert, dann wesentlich schneller als das Intervallhalbierungsverfahren (Faustformel: in jedem Schritt Verdopplung der Anzahl korrekter Dezimalstellen).

Voraussetzung für Konvergenz ist aber, dass der Startwert x

“genügend nahe“ bei x

liegt (“lokal konvergentes Verfahren“).

Ist f : R → R dagegen zweimal stetig differenzierbar (d.h. f

ist stetig) sowie konvex, und besitzt f eine reelle Nullstelle, so konvergiert die Newton–Folge für jeden Startwert x

mit f

(x

) 6= 0.

Man mache sich die letzten beiden Aussagen an den Beispielen f

(x) = x

− 1 und f

(x) = x

e

graphisch klar.

Differentialrechnung TU Bergakademie Freiberg

275

4.5.3 Die Regeln von Bernoulli-l’Hospital Bei der Berechnung von Grenzwerten der Form lim

x→ξ f(x)

g(x)

waren wir bei unbestimmten Ausdrücken wie “

“ oder “

“ auf Probleme gestoßen.

Solche Probleme werden häufig leichter, wenn Differenzierbarkeit gegeben ist.

Das betreffende Ergebnis wurde von Johann Bernoulli (1667-1748, links)

entwickelt, und vom Marquis de l’Hospital (1661-1704, rechts) im ersten

Lehrbuch der Differentialrechnung (1696) veröffentlicht.

Satz 4.18 (Regeln von Bernoulli-l’Hospital).

Seien f, g : (a, b) → R differenzierbare Funktionen mit g

(x) 6 = 0 für alle x ∈ (a, b) und sei entweder

x→b−

lim f(x) = lim

x→b−

g(x) = 0 oder

x

lim

f(x) = lim

x→b−

g(x) = ±∞

Dann gilt

x

lim

f(x) g(x) = lim

x→b−

f

(x) g

(x) ,

wenn der zweite Grenzwert existiert. Hierbei ist b = ∞ erlaubt.

Entsprechende Aussagen gelten für rechtsseitige und beidseitige Grenzwerte.

Differentialrechnung TU Bergakademie Freiberg

277

Plausibilitätsargument zu Satz 4.18

Nahe einer Stelle x

mit f(x

) = g(x

) = 0 gilt f(x) ≈ f

(x

)(x − x

) und g(x) ≈ g

(x

)(x − x

). Damit also

≈

.

Beispiele

x

lim

x

= lim

x→0 cosx

1

= 1,

x→−∞

lim

x³

exp(−x)

= lim

x→−∞

3x²

−exp(−x)

= lim

x→−∞

6x

exp(−x)

= lim

x→−∞

6

−exp(−x)

= 0.

Man berechne die Grenzwerte lim

x→0 x−sin(x)

xsin(x)

und lim

x→∞

e^αx

x

für α > 0.

Wie kann man aus letzterem einem Aussage über lim

für α, β > 0 gewinnen?

Differentialrechnung TU Bergakademie Freiberg

278

Anmerkung

Die Bedeutung der l’Hospitalschen Regeln wird vom Anfänger oft überschätzt und endet in nervenaufreibenden Rechnungen ohne Ergebnis.

Betrachten Sie dazu zum Beispiel

x

lim

e

− e

e

+ e

= lim

x→∞

1 − e

1 + e

= 1

.

Häufig ist es günstiger, bei der Grenzwertberechnung für unbestimmte Ausdrücke wie “

“ oder “

“ auf Potenzreihen zurückzugreifen.

Doch diese Betrachtungen verschieben wir in das Modul HM 2.

4.5.4 Totales Differential und Fehlerfortpflanzung

Wir kommen noch einmal auf die Leibniz-Schreibweise y

(x

) =

(x

) zurück und wollen die Ausdrücke dx und dy näher fassen.

Definition 4.19 (Totales Differential).

Sei f : D

→ R eine in x

differenzierbare Funktion. Für eine beliebige Zahl dx = x − x

heißt

dy := f

(x

) dx = f

(x

)(x − x

) totales Differential von f bei x

.

Differentialrechnung TU Bergakademie Freiberg

280

Geometrische Deutung

x0 x f(x0)

f(x) f

dx

∆ydy

dy ist die Änderung der Funktionswerte der Tangente bei Änderung des Arguments um dx.

Idee für Fehlerfortpflanzung

Approximiert man f nahe x

durch die Tangente, so gilt näherungsweise f(x) − f(x

) =: ∆y ≈ dy = f

(x

) dx.

Differentialrechnung TU Bergakademie Freiberg

281

Praktische Anwendung

In Experimenten ist häufig der Einfluss des Fehlers ∆x einer Messgröße x auf den Fehler ∆y einer berechneten Zielgröße y = f(x) von Interesse.

Mit dem totalen Differential und der eben beschriebenen Idee ergibt sich die Näherungsformel

|∆y| ≈ |f

(x)| · |∆x|.

Durch Messung der Parallaxe p eines Fixsterns (in

) lässt sich mittels r(p) = 1/p

der Abstand des Sterns zu Erde errechnen (in Pc; 1 Pc ≈ 3.262 ly). Die erste Parallaxe wurde 1838 am Stern 61 Cyg von F. W. Bessel mit p = (0.3483 ± 0.0095)

gemessen.

Welcher Abstand zur Erde ergibt sich? Wie genau ist das Ergebnis?

4.6 Der Satz von Taylor

Mit der ersten Ableitung waren wir in der Lage, Funktionen nahe einer Stelle x

linear zu approximieren.

Statt linearer Funktionen kann man auch Polynome höherer Ordnung verwenden und damit ggf. noch bessere Ergebnisse erreichen.

Der betreffende Satz trägt den Namen des englischen Mathematikers Brook Taylor (1685-1731).

Differentialrechnung TU Bergakademie Freiberg

283

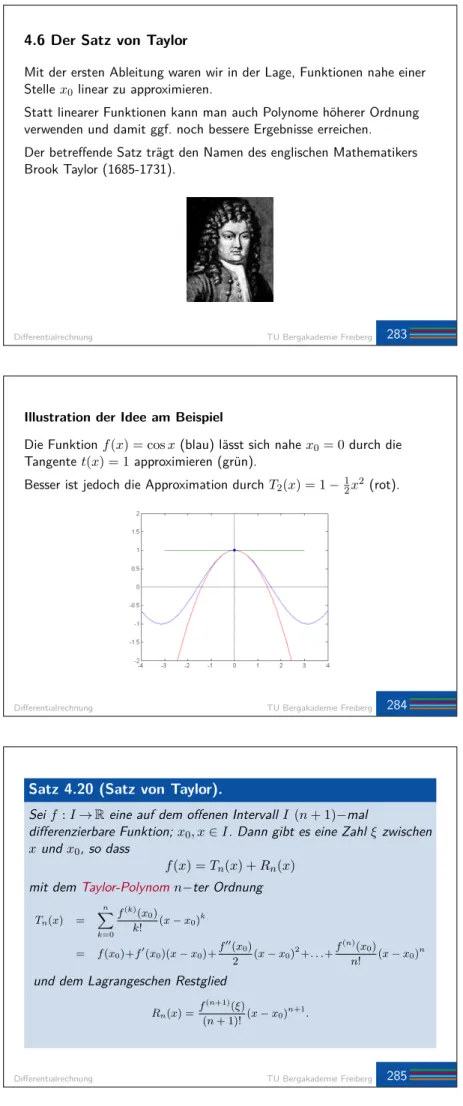
Illustration der Idee am Beispiel

Die Funktion f(x) = cos x (blau) lässt sich nahe x

= 0 durch die Tangente t(x) = 1 approximieren (grün).

Besser ist jedoch die Approximation durch T

(x) = 1 −

x

(rot).

Differentialrechnung TU Bergakademie Freiberg

284

Satz 4.20 (Satz von Taylor).

Sei f : I → R eine auf dem offenen Intervall I (n + 1) −mal

differenzierbare Funktion; x

, x ∈ I. Dann gibt es eine Zahl ξ zwischen x und x

, so dass

f(x) = T

(x) + R

(x) mit dem Taylor-Polynom n−ter Ordnung

Tn(x) = Xn k=0

f^(k)(x0) k! (x−x0)^k

= f(x0)+f⁰(x0)(x−x0)+f⁰⁰(x0)

2 (x−x0)²+. . .+f⁽ⁿ⁾(x0) n! (x−x0)ⁿ

und dem Lagrangeschen Restglied

Rn(x) =f⁽ⁿ⁺¹⁾(ξ)

(n+ 1)!(x−x0)ⁿ⁺¹.

Beispiel

Für f(x) = sin x und x

= 0 gilt f

(x) = cos x, f

(x) = − sin x, f

(x) = − cos x, f

= f, f

= f

,. . .

Somit ergibt sich

f(x

) = 0, f

(x

) = 1, f

(x

) = 0, f

(x

) = −1, f

(x

) = 0, . . . Die ersten 6 Taylor-Polynome lauten also

T

(x) = 0 + 1(x − 0) = x,

T

(x) = 0 + 1(x − 0) +

(x − 0)

= x,

T

(x) = 0 + 1(x − 0) +

(x − 0)

−

(x − 0)

= x −

x

, T

(x) = x −

x

,

T

(x) = T

(x) = x −

x

+

x

.

Differentialrechnung TU Bergakademie Freiberg

286

Bild zum Beispiel:

f(x) = sin x (blau) mit den Taylorpolynomen T

(x) = T

(x) (grün), T

(x) = T

(x) (rot) und T

(x) = T

(x) (türkis) im Entwicklungspunkt x

= 0.

Schätzen Sie den relativen Fehler

der “Physiker-Näherung“

sin x ≈ x (| x | klein) für | x | < 0.1 mit dem Lagrangeschen Restglied ab.

Differentialrechnung TU Bergakademie Freiberg

287

Taylor-Reihen

Verhält sich das Restglied “gutartig“, so approximieren die

Taylorpolynome T

die Funktion f mit größer werdendem n nahe x

immer besser.

Im günstigsten Fall lässt sich f in einer Umgebung von x

durch eine Taylor-Reihe darstellen:

f(x) = X

f

(x

)

n! (x − x

)

für alle x mit | x − x

| < ε.

Wichtige Taylor–Reihen:

(1−x)⁻¹ X∞ n=0

xⁿ |x|<1 arctan(x) X∞ n=0

(−1)ⁿx²ⁿ⁺¹ 2n+ 1 |x| ≤1

exp(x) X∞ n=0

xⁿ

n! x∈R sinh(x)

X∞ n=0

x²ⁿ⁺¹

(2n+ 1)! x∈R

sin(x) X∞ n=0

(−1)ⁿx²ⁿ⁺¹

(2n+ 1)! x∈R cosh(x) X∞ n=0

x²ⁿ

(2n)! x∈R

cos(x) X∞ n=0

(−1)ⁿx²ⁿ

(2n)! x∈R artanh(x) X^∞

n=0 x²ⁿ⁺¹

2n+ 1 |x|<1

ln(1 +x) X∞ n=1

(−1)ⁿ⁺¹xⁿ

n x∈(−1,1] (1 +x)^a X∞ n=0

a n

xⁿ |x|<1

mit ^a0

:= 1und ^an

:=^{a(a−1)···}_n!^(a−n+1)für allen∈Nund allea∈R.

Differentialrechnung TU Bergakademie Freiberg

289

Warnung

Es soll aber vor dem Trugschluss gewarnt werden, der Satz von Taylor garantiere die Entwickelbarkeit jeder unendlich oft differenzierbaren Funktion in eine Taylor-Reihe. Vielmehr gilt:

Es gibt Fälle, in denen die Taylor-Reihe für x 6 = x

überhaupt nicht konvergiert.

Es gibt Fälle, in denen die Taylor-Reihe für x 6 = x

konvergiert, aber mit der eigentlichen Funktion f nichts zu tun hat.

Zum Beispiel gilt für f(x) =

(

e

, x 6 = 0;

0, x = 0

die Beziehung T

(x) = 0 für alle n ∈ N.

Informationen über die Konvergenz erhält man mit Hilfe des Restglieds.

Dies soll hier aber nicht weiter diskutiert werden.

Differentialrechnung TU Bergakademie Freiberg

290

Ziele erreicht?

Sie sollten nun (bzw. nach Abschluss der Übungen/Tutorien):

den Ableitungsbegriff und die Idee der linearen Approximation tiefgreifend verstanden haben,

Funktionen sicher auf Differenzierbarkeit untersuchen und deren Ableitung mit Diffenzenquotient oder Ableitungsregeln sicher bestimmen können,

alle Punkte einer Kurvendiskussion sicher ausführen können, Taylor-Polynome sicher berechnen können und wissen was man unter einer Taylor-Reihe versteht,

über Newton-Verfahren und Fehlerfortpflanzung grob Bescheid wissen.

Sie sind sich nicht sicher oder meinen “nein“? Sie wissen schon. . .