Die Parameterdarstellung des Kreises im Raum

Die Parameterdarstellung des Kreises im Raum

D R . C ARSTEN O BACH 8/2010

In der analytischen Geometrie wird bei der Behandlung der Themen Kreis und Kugel der Kreis häufig nur im zweidimensionalen Koordinatensystem behandelt. Als Gebilde im dreidimensionalen Raum taucht der Kreis meist bei der Berechnung der Schnittmenge von Kugel und Ebene oder beim Schnitt zweier Kugeln auf. Hier findet häufig eine Beschränkung auf die Angabe von Mittelpunkt und Radius des Schnittkreises statt. Im Folgenden wird gezeigt, wie die Parameterdarstellung des Kreises im Raum gewonnen werden kann. Das Verfahren greift auf grundlegende Kenntnisse der Vektorrechnung zurück und hat sich deshalb im Leistungskurs wie auch im Grundkurs als für Schülerinnen und Schüler zugänglich herausgestellt. Mit der entwickelten Parameterdarstellung des Kreises lassen sich Lagebeziehungen zu anderen geometrischen Objekten ermitteln. Exemplarisch wird daher im Anschluss aufgezeigt, wie die Lage zwischen einem Kreis und einer Ebene im Unterricht untersucht werden kann.

Die Konstruktion der Parameterform des Kreises

Die Basis der Überlegungen bildet die Parameterdarstellung des Kreises in der Ebene. Spannen die orthonormalen Vektoren e₁

und e₂

die x-y-Ebene eines dreidimensionalen Koordinatensystems auf, so gilt entsprechend den Verhältnissen in einem ebenen Koordinatensystem für den Ortsvektor eines Kreises mit Mittelpunkt im Koordinatenursprung:

2

1 sin

cos 0

sin cos

e r e r r

r

x  

ϕ ϕ

ϕ ϕ

+

=

⎟

⎟⎟

⎠

⎞

⎜

⎜⎜

⎝

⎛

= (1).

Vorausgesetzt die Vektoren e₁

und e₂ sind Einheitsvektoren und orthogonal zu einander, beschreibt die Gleichung x rcos e₁ rsin e₂

ϕ ϕ +

= aber auch

unabhängig von der Lage von e₁

und e₂

einen Kreis im Raum mit dem Koordinatenursprung als Mittelpunkt. Mit dem Skalarprodukt und der Identität

sin

²

ϕ + cos

²

ϕ = 1

lässt sich nämlich leicht nachrechnen, dass für alle Ortsvektoren x

: x =r

gilt. Folglich liegen alle Punkte, die zu den Ortsvektoren x

gehören, auf einem Kreis in der von e₁

und e₂

aufgespannten beliebig orientierten Ebene.

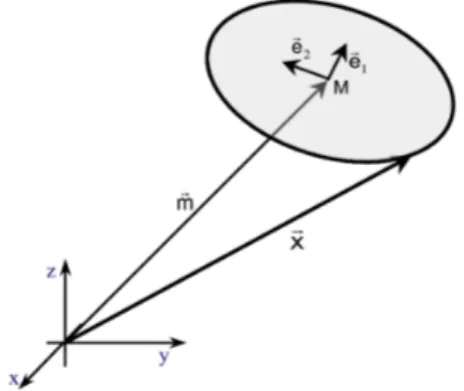
Um einen Kreis mit einem beliebigen Mittelpunkt M mit Ortsvektor m

in Parameterform darzustellen ist jetzt nur noch eine Translation m

durchzuführen (s. Abbildung 1).

Man erhält: x m rcos e₁ rsin e₂ ϕ ϕ + +

= (2) mit dem

Parameter

ϕ ∈ [ ^{0 ; 2} π ]

. Auch hier gilt natürlich r

m

x− = . Vorteil der Darstellung (2) ist, dass sie sich anschaulich leicht verstehen lässt, in dem man sich den Ortsvektor x

als Summe des Mittelpunktsvektors m und einem um den Mittelpunkt in einer Ebene rotierenden Vektor mit dem Winkelparameter ϕ vorstellt.

Abbildung 1: Der Ortsvektor x

eines Punktes des Kreises lässt sich als Summe aus dem Mittelpunktsvektor m

und der Linearkombination rcos e₁ rsin e₂

ϕ

ϕ + ^der

Vektoren e₁

und e₂

darstellen.

Die Bestimmung der Parameterform an einem Beispiel aus dem Unterricht

Im Unterricht hatten die Schülerinnen und Schüler für den Schnittkreis einer Kugel und der Ebene E: 4x+2y+z=2 den Mittelpunkt M(2|1|3) und den Radius r=2 bestimmt.

Nach der Besprechung der oben ausgeführten Überlegungen hatten sie die Aufgabe den Schnittkreis in Parameterform anzugeben. Die Schülerinnen und Schüler diskutierten, wie sie die Vektoren e₁

und e₂

bestimmen sollten und kamen darauf, dass der Vektor e₁

zunächst

als beliebiger zu dem Normalenvektor

⎟

⎟⎟

⎠

⎞

⎜

⎜⎜

⎝

⎛

= 1 2 4 n

der Ebene

senkrecht stehender Vektor festgelegt werden kann.

Dieser ist anschließend noch auf Eins zu normieren. Der gesuchte Vektor kann einfach mit der Bedingung, dass das Skalarprodukt der Vektoren e₁

und n

Null ist, bestimmt werden. Beispielsweise erfüllt der Vektor

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

−

= 0

2 1 3 1 e1

die geforderten Bedingungen. Der Vektor

e2

muss senkrecht auf e₁ und n

stehen. Mit Hilfe des Kreuzproduktes berechneten die Schülerinnen und

Schüler deswegen den Vektor

⎟

⎟⎟

⎠

⎞

⎜

⎜⎜

⎝

⎛

−

=

×

10 1 2 3 1 e1

n 

.

Alternativ hätte man auch über das Skalarprodukt und die Forderungen e₂∗e₁ =0

und e₂∗n=0

einen entsprechenden Vektor gewinnen können. Mit der Normierung erhält man für den Vektor e₂

:

⎟

⎟⎟

⎠

⎞

⎜

⎜⎜

⎝

⎛

−

=

10 1 2 105

1 e2

. Die gesuchte Parameterdarstellung

des Kreises lautet somit:

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

− +

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

− +

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

=

10 1 2 105sin

2 0

2 1 3cos 2 3 1 2

ϕ x ϕ

.

Der zugehörige Kreis ist in Abbildung 2 dargestellt.

Abbildung 2: Darstellung des ermittelten Kreises in einem dreidimensionalen Koordinatensystem

Lagebeziehung zwischen Kreis und Ebene

Mit der gewonnenen Parameterdarstellung des Kreises lassen sich Untersuchungen der Lagebeziehung eines Kreises zu den aus der analytischen Geometrie bekannten Objekten Gerade, Ebene und Kugel durchführen.

Exemplarisch soll hier die gegenseitige Lage von Ebene und Kreis betrachtet werden.

Mögliche Lösungen für diese Objekte sind, dass der Kreis und die Ebene keine gemeinsamen Punkte, einen gemeinsamen Punkt, zwei gemeinsame Punkte haben oder, dass der Kreis in der Ebene liegt.

Als Beispiel wurde den Schülerinnen und Schülern die Gleichungen des oben gefundenen Kreises und der Ebene

E mit E: 0

1 0 2 2 1 2

=

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

−

∗

⎥

⎥⎥

⎦

⎤

⎢

⎢⎢

⎣

⎡

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

x−

gegeben. Schnell war klar,

dass man eventuelle Schnittpunkte bestimmen kann, indem man den Ortsvektor der Parameterdarstellung des Kreises in die Ebenengleichung einsetzt. Den Schülerinnen und Schülern stand im Leistungskurs ein Computeralgebrasystem (CAS) zur Verfügung, was eine rasche Lösung der resultierenden Gleichung ermöglichte.

Damit das CAS nicht als reine Black box eingesetzt wurde, sollte die zugrundeliegende Gleichungsstruktur genauer analysiert werden. Für das Beispiel erhält man

die Gleichung 105sin 1

15 cos 4 3 3

4 ϕ+ ϕ = ^(3).

Allgemein liegt eine Gleichung der Form:

c b

acosϕ+ sinϕ= ^vor.

Die Formelsammlung hilft hier mit der Beziehung

⎟⎟⎠

⎞

⎜⎜⎝

⎛ ⎟

⎠

⎜ ⎞

⎝

− ⎛

+

=

+ a

b b a b

acosϕ sinϕ ^{2 2} cos ϕ arctan ⁽⁴⁾

weiter. Der Beweis dieser Formel bietet sich im Unterricht für stärkere Schülerinnen und Schüler mit geeigneter Hilfestellung z.B. als Binnendifferenzierung an. Vorgestellt werden sollen hier zwei Beweise, die für die Schülerinnen und Schüler entsprechend vorbereitet werden müssen.

Eine Beweisidee basiert hier bewusst kontextbezogen auf dem Skalarprodukt der Vektorrechnung. Es gilt:

⎟⎟⎠

⎞

⎜⎜⎝

∗⎛

⎟⎟⎠

⎞

⎜⎜⎝

=⎛

+ ϕ

ϕ ϕ

ϕ sin

sin cos

cos b

b a a

α α

ϕ

ϕ ^{sin cos cos}

cos^{2 2 2 2}

2

2 b a b

a + + = +

= ^.

Den Winkel α zwischen den Vektoren bestimmt man am anschaulichsten mit Hilfe einer Skizze (s. Abbildung 3).

Der Vektor ⎟⎟

⎠

⎞

⎜⎜⎝

⎛

ϕ ϕ sin

cos schließt mit der x-Achse den Winkel

φ ein. Der Winkel des Vektors ⎟⎟

⎠

⎞

⎜⎜⎝

⎛

b

a zur x- Achse ergibt

sich zu ⎟

⎠

⎜ ⎞

⎝

⎛

a

arctan b . Der Differenzwinkel ist somit gerade

⎟⎠

⎜ ⎞

⎝

− ⎛

= a

arctan b ϕ

α und damit identisch mit dem oben in der Formel angegebenen.

Abbildung 3: Der Winkel α zwischen den beiden Vektoren ist gleich der Differenz aus dem Winkel φ und

b arctana.

Ein alternativer und kürzerer Beweis stützt sich auf das folgende Additionstheorem:

(

ϕ β

)

cosβcosϕ sinβsinϕ

cos r r

r − = + ^(5).

Definiert man a=rcosβ und b=rsinβ, so erhält man

(

ϕ β

)

cosϕ sinϕ

cos a b

r − = + (6). Zwischen den Größen

bestehen folgende Zusammenhänge β

β β _tan cos sin =

=r r a b

bzw. ⎟

⎠

⎜ ⎞

⎝

= ⎛

a arctan b

β ^und r= a²+b² . Das Einsetzen von

β

und r in die Formel (6) führt zur Gleichung (4).

Ein weiterer Weg zur Lösung der Gleichung (3) wäre, dass man die Gleichung nach

^sin ϕ

^{oder cosϕ} umstellt, quadriert und mit der Identität

sin

²

ϕ + cos

²

ϕ = 1

ⁱⁿ

eine quadratische Gleichung transformiert. Nachteilig bei diesem Verfahren ist allerdings, dass man durch das Quadrieren eine größere Lösungsmenge erhält. Im Nachhinein müssten so entsprechende Lösungen aussortiert werden.

Mit Hilfe des CAS oder der Beziehung (4) erhält man schließlich als Lösungen für das obige Beispiel die Parameterwerte

ϕ

₁

≈ 2 , 157

^und ϕ2≈^5,865, d.h. der Kreis und die Ebene schneiden sich in zwei Punkten. Die beiden Schnittpunkte lassen sich durch Einsetzen in die Kreisgleichung gewinnen. Sie lauten S₁(1,687|2,440|1,374) und S₂(2,897|-1,190|3,793).

Fazit

Im vorliegenden Artikel wurde gezeigt, wie mit einfachen Mitteln der Vektorrechnung ein Kreis im Raum dargestellt werden kann. Alternativ könnte eine Kreisgleichung auch durch die Hinterausführung von Drehmatrizen gewonnen werden. Hier wurde ein anschaulicherer Weg gewählt, indem die Parameterdarstellung des Kreises in der Ebene auf den Raum übertragen wurde. Demonstriert wurde wie man bei der Bestimmung des Schnittkreises von Kugel und Ebene über die übliche Angabe von Mittelpunkt und Radius des Kreises hinaus die Parameterdarstellung des Kreises ermitteln kann. Die Lagebeziehung eines Kreises und einer Ebene wurde ebenfalls exemplarisch untersucht.

Dabei ermöglichte der Einsatz des CAS einen rechnerisch einfacheren Zugang. Die Lösung des Problems per Hand ist allerdings im Grund- wie Leistungskurs ebenfalls möglich. Hierbei kann der Umgang mit trigonometrischen Gleichungen vertieft werden. Resümierend erwies sich die Parameterdarstellung des Kreises im Raum als Schülerinnen und Schüler interessierende Vertiefung des Themengebiets Kreis und Kugel.