Klausur Aerodynamik II 08. 09. 2017 M U S T E R L

AERODYNAMISCHES INSTITUT der Rheinisch - Westf¨alischen Technischen Hochschule Aachen Univ.-Prof. Dr.-Ing. W. Schr¨oder

Klausur Aerodynamik II

08. 09. 2017

M U S T E R L ¨ O S U N G E I N S IC H T N A H M E

Hinweis:

Achten Sie darauf, ob Sie alle Aufgaben erhalten haben:

Klausur Aerodynamik II

Fragenteil, Skelett-Theorie und linearisierte Potentialtheorie, ¨Uberschallstr¨omung und numerische Verfahren

Integrale und Additionstheoreme

Additionstheoreme

• sin(x±y) = sin(x)·cos(y)±sin(y)·cos(x)

• cos(x±y) = cos(x)·cos(y)∓sin(x)·sin(y)

• sin²(x) + cos²(x) = 1

• sin(2x) = 2·sin(x)·cos(x)

• sin(x) = 2·sin(x/2)·cos(x/2)

• sin²(x) = 1

2(1−cos(2x))

• cos²(x) = 1

2(1 + cos(2x))

• cos(2x) = cos²(x)−sin²(x)

• tan(x 2) =

r1−cosx 1 + cosx

• tan(x

2)·sin(x) = 1−cos(x)

• sin(x)·sin(nx) =−1

2(cos[(n+1)x]−cos[(n−1)x])

• sin[(n+ 1)x]−sin[(n−1)x] = 2·cos(nx)·sin(x)

•

∞

X

n=1

1

nsin(nϕp)·sin(nϕ) = 1 4ln

1−cos(ϕ_p+ϕ) 1−cos(ϕp−ϕ)

Integrale

•

Z 1

ax+bdx= 1

a·ln(ax+b)

•

Z x

ax+bdx= x a− b

a² ·ln(ax+b)

• Z x²

Xdx= 1 a³

h1

2(X)−2b(X) +b²ln(X)i mitX =ax+b

• Z

sin(ax)dx=−cos(ax) a

• Z

cos(ax)dx= +sin(ax) a

• Z

sin²(ax)dx= x 2 − 1

4asin(2ax)

• Z

cos²(ax)dx= x 2 + 1

4asin(2ax)

• Z

sin³(ax)dx= cos³(ax)

3a −cos(ax) a

• Z

cos³(ax)dx=−sin³(ax)

3a + sin(ax) a

• Z

cos⁴(ax)dx= 3

8x+sin(2ax)

4a +sin(4ax) 32a

• Z

sin(ax) cos(ax)dx= sin²(ax) 2a

• Z π

0

cos(n·ϕ)·cos(p·ϕ)dϕ=

π/2 n=p 0 n6=p

• Z π

0

sin(n·ϕ)·sin(p·ϕ)dϕ=

π/2 n=p 0 n6=p

• Glauert-Integral Z π

0

cos(n·ϕ⁰)

cos(ϕ)−cos(ϕ⁰)dϕ⁰ =−π·sin(n·ϕ) sin(ϕ)

• Z

cos(ax)·cos(bx)dx= sin[(a−b)x]

2(a−b) +sin[(a+b)x]

2(a+b) ∀ |a| 6=|b|

1. Aufgabe: Fragenteil (14 Punkte)

1. Erkl¨aren Sie das d’Alembert’sche Paradoxon und den induzierten Widerstand im Rahmen der Poten- tialtheorie.

2. Mit welchem Berechnungsverfahren der Potentialtheorie l¨asst sich der induzierte Widerstand eines gepfeilten Fl¨ugels bestimmen? Erl¨autern Sie in eigenen Worten kurz das Verfahrensprinzip.

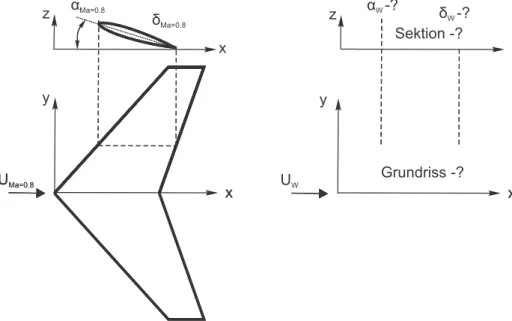
3. Zur experimentellen Untersuchung eines gepfeilten Fl¨ugels f¨ur eine Machzahl von M a∞ = 0.6 wird ein nach der Prandtl-Glauert ¨Ahnlichkeitsregel skalierter Modellfl¨ugel f¨ur den vorhandenen Wasser- schleppkanal ben¨otigt. ¨Ubertragen Sie in Ihre Aufgabenbl¨atter die unten stehende Skizze und erg¨anzen Sie diese sorgf¨altig f¨ur das entsprechende Versuchsmodell (rechts). Achten Sie dabei auf die Relation der geometrischen Abmaße zum originalen Fl¨ugel (links) und geben Sie quantitative Angaben, welche Gr¨oßen wie ver¨andert werden.

UMa=0.8

x U_W

UMa=0.8 x

α_Ma=0.8

x y

α_W-?

x y

Sektion -?

Grundriss -?

δMa=0.8

δ_W-?

x

z z

Abbildung 1.1: Grundriss und Profilschnitt eines gepfeilten Fl¨ugels.

4. Es wird im Folgenden ein Laminarprofil NACA 64₂-015 in einer inkompressiblen Anstr¨omung mit Null-Anstellwinkel betrachtet.

(a) Zeichnen Sie f¨ur das untersuchte Laminarprofil die zu erwartende Druckbeiwertverteilungc_p(X) bei der Reynoldszahl von Rec= 5·10⁵.

(b) Skizzieren Sie sorgf¨altig den dem Fall 4(a) entsprechenden Verlauf des Reibungsbeiwertes c_f entlang der Profiloberseite.

(c) Erweitern Sie Ihr Diagramm aus 4(a) mit dem zu erwartenden Druckbeiwertverlauf f¨ur das be- trachtete Profil bei der Reynoldszahl von Rec= 1·10⁶.

(d) Erg¨anzen Sie Ihr Diagramm aus 4(b) mit dem zu erwartenden Verlauf des Reibungsbeiwertes c_f entlang der Profiloberseite f¨ur das betrachtete Profil bei der Reynoldszahl von Rec= 1·10⁶. Hinweis:

Falls n¨otig, ¨ubertragen Sie die Skizzen in Ihre L¨osungsbl¨atter und zeichnen Sie die L¨osung dort ein!

2. Aufgabe: Skelett-Theorie und linearisierte Potentialtheorie (18 Punkte)

Im Rahmen eines Flugzeugvorentwurfs wird f¨ur die Skelettlinie eines Nurfl¨uglers das folgende Polynom dritten Grades untersucht. Das Profilskelett ist um den Winkel α angestellt und wird je nach Aufgabenteil f¨ur verschiedene Machzahlen untersucht.

Z(X) =X³−7

4X²+3

4X, 0≤X≤1.

1. Unter Anwendung der Skelett-Theorie f¨ur einen inkompressiblen Fall:

(a) Zeigen Sie, dass es sich um ein S-Schlag-Profil handelt und bestimmen Sie anschließend die zuge- h¨orige Zirkulationsverteilung nach dem Ansatz von Birnbaum-Ackermann unter der Angabe aller KoeffizientenA_n.

(b) Leiten Sie den Auftriebsbeiwert des untersuchten Profils in Abh¨angigkeit vom Anstellwinkel α her.

(c) Der Momementenbeiwert um die Profilnase kann i.a. nach der Formelc_m =−^π₄(2A₀+ 2A₁−A₂) berechnet werden.

Bestimmen Sie die Lage des Druckpunktes Xcp und diskutieren Sie kurz ihre Abh¨angigkeit vom Anstellwinkel α. Zeigen Sie anschließend, dass der Neutralpunkt des Profils bei X_N = ¹₄ liegt.

2. Nun wird dasselbe Profil im ¨Uberschall unter Anwendung der linearisierten Potentialtheorie untersucht.

Berechnen Sie die Lagen des Druckpunktes und des Neutralpunktes des Profils im ¨Uberschall.

Gegeben: Anstellwinkel α, Sehnenl¨ange l,V∞. Hinweise:

γ(ϕ) = 2V∞· A0·tan ϕ

2

+

N

X

n=1

An·sin(nϕ)

!

−w_a(ϕ) =− w V∞

=A₀+

N

X

n=1

A_n·cos(nϕ)

− w V∞

=α− dZ dX

u V∞

=±γ(X) V∞

c_p|_sup=± 2β pM a²_∞−1 X = x

l

3. Aufgabe: Numerische Verfahren (18 Punkte)

Das Str¨omungsfeld eines schlanken Doppelkeilprofils in einer ¨Uberschallstr¨omung (M a > 1) mit einem Anstellwinkel α >0 soll durch die numerische L¨osung der Euler-Gleichungen approximiert werden. Es wird von einer zweidimensionalen Str¨omung ausgegangen.

1. Skizzieren Sie sorgf¨altig das Rechengebiet sowie ein uniformes kartesisches Rechengitter um das Profil.

2. Erl¨autern Sie mittels der Charakteristikentheorie die Wahl der Ein- und Austr¨omrandbedingungen und geben Sie alle f¨ur die L¨osung des Problems notwendigen Randbedingungen f¨ur die Geschwindig- keitskomponenten in Hauptstr¨omungsrichtung und in Normalenrichtung u, van.

3. Beurteilen Sie die F¨ahigkeit des Verfahrens den Auftrieb bzw. den Widerstand bei verschiedenen An- stellwinkeln zu berechnen. Geben Sie hierbei insbesondere an, ob alle Ihnen bekannten Widerstands- anteile ber¨ucksichtigt werden.

Schlagen Sie anschließend gegebenenfalls ein alternatives Verfahren vor, mit dem die m¨oglicherweise nicht ber¨ucksichtigten Widerstandsanteile berechnet werden k¨onnten, und erl¨autern Sie, wie dabei das Rechengitter sowie die Randbedingungen angepasst werden m¨ussten.

4. Eine zweidimensionale ¨Uberschallstr¨omung wird nun durch die f¨ur kartesische Koordinaten formu- lierte partielle Differentialgleichung zweiter Ordnung des Geschwindigkeitspotentials, die sogenannte Wellengleichung, beschrieben:

−β²∂²φ

∂x² +∂²φ

∂y² = 0, β =p

M a²−1, M a >1. (1) Diese soll durch ein numerisches knotenzentriertes Differenzenverfahren gel¨ost werden. Entwickeln Sie aus der Taylorreihe

f(x) =

∞

X

m=0

1

!m

∂^mf(x₀)

∂x^m ·(x−x₀)^m (2)

eine zentrale Approximation f¨ur die zweite Ableitung einer Funktionf(x) eines ¨aquidistanten Gitters, die eine Genauigkeit von zweiter Ordnung in x besitzt. Geben Sie zudem den f¨uhrenden Term des Abbruchfehlers an.

5. Ersetzen Sie die r¨aumlichen Ableitungen der Wellengleichung durch zentrale Differenzen, welche den folgenden Differenzenstern enthalten. Dabei entspricht der Indexiderx-Richtung und der Indexjder y-Richtung.

j+1 j j-1

i-1 i i+1

Abbildung 3.1: Differenzenstern.

1. Aufgabe: (L ¨ OSUNG) Fragenteil (14 Punkte)

1. Das d’Alembertsche Paradoxon folgt aus der Potentialtheorie und besagt, dass in einer zweidimensio- nalen reibungsfreien Str¨omung ein geschlossener K¨orper keine Widerstandskraft erf¨ahrt.

In einem dreidimensionalen Fall eines Fl¨ugels endlicher Spannweite ist die Auftriebsverteilung ent- lang der Spannweite nicht konstant. An den Fl¨ugelspitzen kommt es zum Ausgleich. Aufgrund des variierenden Druckfeldes auf der Ober- und Unterseite unterscheiden sich die Stromlinienfelder, wes- halb sich hinter dem Fl¨ugel eine Wirbelfl¨ache ausbildet. Diese Wirbelfl¨ache induziert am Fl¨ugel eine nach unten gerichtete Geschwindigkeit, die zur Reduktion des geometrischen Anstellwinkels um den induzierten Anstellwinkel f¨uhrt. Die resultierende Luftkraft wird um den induzierten Anstellwinkel entgegen der Flugrichtung geneigt, so dass eine in Str¨omungsrichtung weisende Kraft entsteht, die einer Widerstandskraft entspricht.

2. Der induzierte Widerstand eines gepfeilten Fl¨ugels l¨asst sich mit der Trafl¨achentheorie bestimmen.

Hierzu wird eine fl¨achige Verteilung der Wirbeldichte entlang der Spannweite sowie der Fl¨ugeltiefe angenommen. Aus der kinematischen Randbedingung, dass die von der Wirbelfl¨ache induzierte Ge- schwindigkeit und die Normalkomponente der Anstr¨omung sich gegenseitg aufheben, erh¨alt man ein System von Integralgleichungen, das numerisch gel¨ost wird.

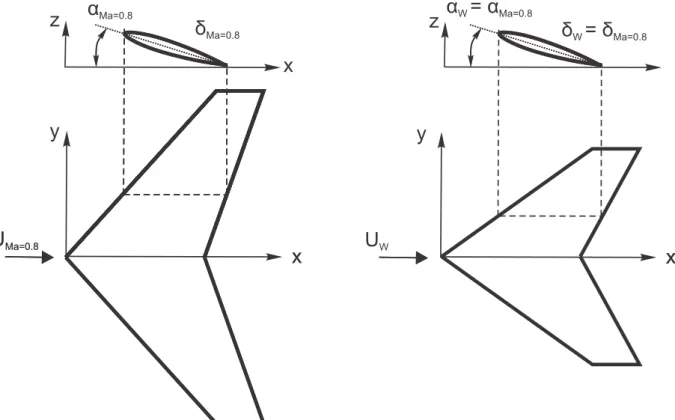
3. Ein Wasserschleppversuch stellt eine inkompressible Str¨omung dar, somit muss eine Kompressibilit¨ats- korrektur beim Modellbau ber¨ucksichtigt werden.

Die Anwendung einer Kompressibilit¨atskorrektur (z.B. der Prandtl-Glauert-Regel) auf den gepfeilten Fl¨ugel ergibt den rechts dargestellten Modellfl¨ugel f¨ur den Wasserschleppversuch.

Die x und zRichtungen bleiben unver¨andert: α_{M a=0.6} =α_{W asser},δ(X)_{M a=0.6}=δ(X)_{W asser}. Die y-Richtung wird mit p

1−M a²_∞ = √

1−0.6² = 0.8 skaliert (Spannweite sowie Vorder- und Hinterkantenpfeilungswinkel).

U

x U

U

x

α

x y

α

= α

x y

δ

δ

= δ

x

z z

Abbildung 1.1: Grundriss und Profilschnitt eines gepfeilten Fl¨ugels

4. (a) Die Druckbeiwertverteilung des NACA 64₂-015 beiα= 0 weist folgende Merkmale auf (siehe die durchgezogene Linie in der Skizze):

-Verl¨aufe auf der Ober- und Unterseite identisch (symmetrische Anstr¨omung und Profilform);

-Druckminimum bei X = 0.4 (2. Kennziffer);

(b) Da es sich um ein laminares Profil handelt und die Reynoldszahl vonRec= 5·10⁵relativ klein ist, erfolgt der laminar-turbulente Umschlag am Profil relativ sp¨at. Der Wandreibungsbeiwert nimmt im laminaren Bereich kontinuierlich ab, erh¨oht sich sprungartig im Bereich der Transition und nimmt dann im turbulenten Abschnitt wieder kontinuierlich ab.

(c) Aufgrund der h¨oheren Reynoldszahl sind zwei Effekte festzustellen (gestrichelte Linie):

-H¨ohere Saugspitze aufgrund der zun¨achst geringeren Grenzschichtdicke;

-Kleinerer cp-Wert im Bereich der der Hinterkante.

(d) Aufgrund der h¨oheren Reynoldszahl sind zwei Effekte festzustellen (gestrichelte Linie):

-Verschiebung der Transition stromauf;

-Zun¨achst niedrigererc_f-Beiwert.

0.4

x/l 1

-c

1

x/l 1

c

2. Aufgabe: (L ¨ OSUNG) Skelett-Theorie und linearisierte Potentialtheo- rie (18 Punkte)

1. (a)

Z(X) =X³−7

4X²+3

4X=X(X−3

4)(X−1)

Das Profil besitzt einen S-Schlag aufgrund der drei Nullstellen beiX= 0,X= ³₄,X= 1 innerhalb des Intervalls 0≤X≤1.

dZ(X)

dX = 3X²−7 2X+3

4

Aus der kinematischen Randbedingung und dem Ansatz von Birnbaum-Ackermann folgt:

α− dZ

dX =A0+

N

X

n=1

An·cos(nϕ)

Mit der Substitution X= ¹₂(cosϕ+ 1) ergibt sich:

α−3(1

2(cosϕ+ 1))²+7 2 ·1

2(cosϕ+ 1)−3

4 =A₀+

N

X

n=1

A_n·cos(nϕ)

α− 3

4cos²ϕ−3

2cosϕ−3 4 +7

4cosϕ+7 4 −3

4 =A0+

N

X

n=1

An·cos(nϕ)

α−3

4cos²ϕ+ 1

4cosϕ+1

4 =A₀+

N

X

n=1

A_n·cos(nϕ)

α− 3

8(1 +cos(2ϕ)) + 1

4cosϕ+1

4 =A₀+

N

X

n=1

A_n·cos(nϕ)

α−1 8 −3

8cos(2ϕ)) +1

4cosϕ=A0+

N

X

n=1

An·cos(nϕ)

Der Koeffizientenvergleich liefert die Konstanten A₀ bisA_n: A0=α−1

8; A1= 1

4; A2 =−3

8; An= 0 f¨ur n≥3 Der gesuchte Zirkulationsverteilung ergibt sich zu:

γ(ϕ) = 2V∞·

(α−1 8)·tan

ϕ 2

+1

4sin(ϕ)−3

8sin(2ϕ)

(b) Aus dem Satz von Kutta-Zhukhovski folgt f¨ur die zweidimensionale Auftriebskraft Lˆ =%V∞Γ =%V∞

Z l

0

γ(x)dx=%V∞l Z 1

0

γ(X)dX ,wobei X =x/l.

F¨ur den Auftriebskoeffizienten cl ergibt sich:

Lˆ 2R₁

γ(X)dX

Eingesetzt γ(ϕ) mit dX =−¹₂sinϕdϕaus der SubstitutionX = ¹₂(1 +cosϕ) ergibt c_l= 1

V∞

Z _π

0

γ(ϕ)sinϕdϕ= 2 Z _π

0

A₀tan(ϕ

2)sinϕ+A₁sin²ϕ+A₂sin(2ϕ)sinϕ dϕ

= 2 Z π

0

A0(1−cosϕ) +A1sin²ϕ+A2sin(2ϕ)sinϕ dϕ

=π(2A0+A1) Mit den berechneten Werten f¨ur An ergibt sich der Auftriebsbeiwert zu:

c_l= 2πα (c) F¨ur den Momentenbeiwert ergibt sich:

c_m =−π

4(2A₀+ 2A₁−A₂) =−π

2α−5π 32 Der Druckpunkt ergibt sich aus der Momentenbilanz um die Profilnase:

Xcp =−cm

c_l = 1 4 + 5

64α

F¨ur den Fallα→0 liegt der DP demnach weit hinter dem Profil. Mit zunehmendem Anstellwinkel wandert der DP in RichtungX = ¹₄, da sich das Verh¨altnis zwischen Nullmoment und auftriebs- abh¨angigem Moment immer mehr zu Gunsten des auftriebsabh¨angigen Moments verschiebt.

Aus der Momentenbilanz um die Profilnase und der Definition des Neutrapunktes (∂cm0/∂cl= 0) folgt:

cm =cm0−c_l·X_N ⇒ (abgeleitet nachc_l) ⇒ X_N =−∂cm

∂c_l =−∂cm

∂α

∂α

∂c_l =−−π/2 2π = 1

4 2. F¨ur die Bestimmung der Lagen des Druckpunktes und des Neutralpunktes m¨ussen zun¨achst der Auf-

triebsbeiwert cl2 und der Momentenbeiwert um die Profilnasecm2 im ¨Uberschall bestimmt werden.

Mit den absoluten lokalen Str¨omungs¨anderungswinkelnβi entlang des Profilskeletts und dem Hinweis c_p|_sup=±√ ^2βi

M a²∞−1 ergibt sich:

c_p,i|_sup=± 2β_i

pM a²_∞−1 ⇒∆c_p,i = 4(α−_dX^dZ) pM a²_∞−1 Aus der Integration ergibt sich der Auftriebsbeiwert zu:

c_l|_sup= Z 1

0

∆c_pdX =...(Nur Anstellung der Profilsehne relevant) = 4α pM a²_∞−1

c_m|_sup=− Z 1

0

∆c_pXdX =− 4 pM a²_∞−1

Z 1 0

(α−3X²+ 7 2X−3

4)XdX

=− 4

pM a²_∞−1(α 2 − 3

8−3 4 +7

6) =− 4

pM a²_∞−1(α 2 + 1

24) Somit ergibt sich f¨ur die Lagen des Druckpunktes und des Neutralpunktes im ¨Uberschall:

3. Aufgabe: Numerische Verfahren (18 Punkte) (L ¨ OSUNG)

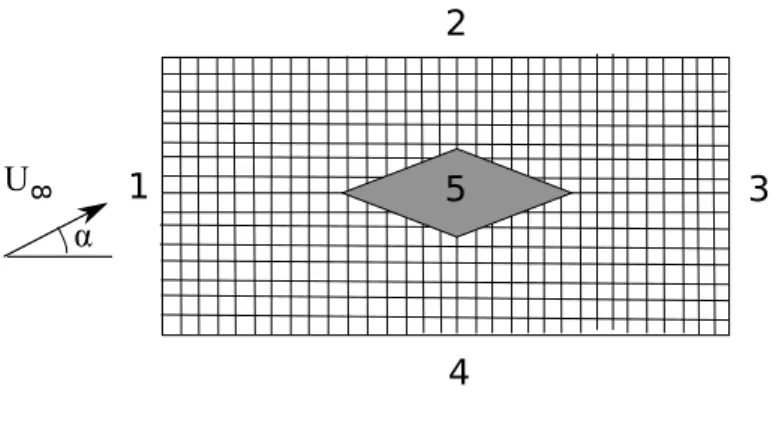
1. Kartesisches Rechengitter mit Berandungen 1-5.

1

2

3

4 U⁸ 5

α

Abbildung 3.1: Gitter.

2. Bestimmung der Randbedingungen ¨uber die charakteristischen Ausbreitungsgeschwindigkeiten (u− c, u, u+c).

Abbildung 3.2: Charakteristische Ausbreitungsgeschwindigkeiten.

1: Einstr¨omrand; u(y) =U∞cos(α), v(y) =U∞sin(α)

2: Ausstr¨omrand; muss nichts vorgegeben werden; alle Variablen k¨onnen aus dem Rechengebiet extra- poliert werden ^∂u_∂y = 0,^∂v_∂y = 0

3: Ausstr¨omrand; muss nichts vorgegeben werden; alle Variablen k¨onnen aus dem Rechengebiet extra- poliert werden ^∂u_∂x = 0,^∂v_∂x = 0

4: Einstr¨omrand; u(x) =U∞cos(α), v(x) =U∞sin(α) 5: K¨orperoberfl¨ache; ~u·~n= 0

3. Berechnung von Auftrieb und Widerstand:

- Auftrieb: kann aus dem Druckverlauf am K¨orperrand n¨aherungsweise berechnet werden.

-Wellenwiderstand: kann berechnet werden, da nur die Druckverteilung ben¨otigt wird.

-induzierter Wiederstand: nicht vorhanden, da ein zweidimensionales Problem betrachtet wird.

-Druckwiderstand: kein Druckwiderstand vorhanden, da eine reibungsfreie Str¨omung betrachtet wird (d’Alembertsches Paradoxon).

-Reibungswiderstand: kann nicht berechnet werden, da viskose Effekte in den Euler-Gleichungen ver- nachl¨assigt werden.

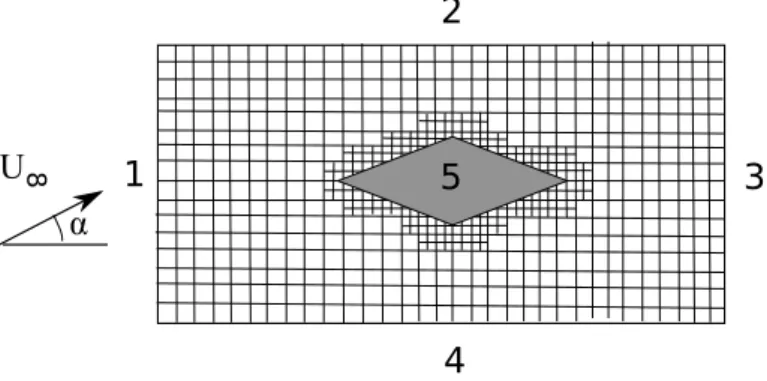
Um den Reibungswiderstand zu bestimmen, m¨ussen die Navier-Stokes Gleichungen verwendet wer- den. Dazu muss das Rechengitter in Wandn¨ahe eine h¨ohere Aufl¨osung besitzen, um die Geschwin- digkeitsgradienten, welche aufgrund der Haftbedingung (~u=0) entstehen, zu erfassen. Abh¨angig von der Reynoldszahl kann es an den Kanten, die die maximale Dicke des Profils definieren, zur Abl¨osung kommen. In diesem Fall is auch der Druckwiderstand zu berechnen.

1

2

3

4 U8 5

α

5

Abbildung 3.3: Gitter mit Randverfeinerung.

4. Taylorreihenapproximation f¨ur die zweite Ableitung:

I : φ_i+1=φ_i+∂φ_i

∂x∆x+1 2

∂²φ_i

∂x²∆x²+1 6

∂³φ_i

∂x³∆x³+ 1 24

∂⁴φ_i

∂x⁴∆x⁴+O(∆x⁵) (3)

II : φi−1 =φ_i− ∂φ_i

∂x∆x+ 1 2

∂²φ_i

∂x² ∆x²− 1 6

∂³φ_i

∂x³ ∆x³+ 1 24

∂⁴φ_i

∂x⁴ ∆x⁴+O(∆x⁵) (4) Addition von I undII ergibt:

φ_i+1+ φi−1 = 2φ_i+∂²φ_i

∂x²∆x²+ 1 12

∂⁴φ_i

∂x⁴ ∆x⁴ (5)

Damit ergibt sich f¨ur die zweite Ableitung:

∂²φi

∂x² = φi+1−2φi+φi−1

∆x² −

1 12

∂⁴φi

∂x⁴ ∆x²

Abbruchf ehler

(6)

5. Diskretisierte Wellengleichung:

−β²φi+1,j−2φi,j+φi−1,j

∆x² +φi,j+1−2φi,j+φi,j−1

∆y² = 0, i= 1, ..., j= 1, ... (7)