Kapitel 2 Funktion einer Ver¨anderlichen

Kapitel 2

Funktion einer Ver¨ anderlichen

2.1 Zum Begriff

Im Experiment wird oft eine Meßgr¨oße (z. B. die Konzentration K) in Abh¨angigkeit von einer anderen Gr¨oße (z. B. der Zeit t) gemessen. Dies ergibt eine Zuordnungsvorschrift oder Funktion:

Die Konzentration K wird als Funktion der Zeit t erfasst K =K(t)

t wird als Ver¨anderliche oder Variable bezeichnet.

Wir behandeln zun¨achst reelle Funktionen mit einer reellen Ver¨anderlichen.

Definition 2.1 Eine reelle Funktion (Abbildung) ist eine Vorschrift, durch die jedem Element x∈D⊂ in eindeutiger Weise eine reelle Zahl f(x) zugeordnet wird.

f : x#→f(x) Wir lesen: x wird abgebildet auff(x).

Die Menge Dist der Definitionsbereich von f,

die Menge W :={y ∈ , y =f(x) mitx∈D} ist der Wertebereich von f. Der Begriff Abbildung ist synonym mit dem Begriff Funktion.

Beispiel 2.1

x#→f(x) D W x+ 1

x^{2 +}₀

√x ⁺₀ ⁺₀

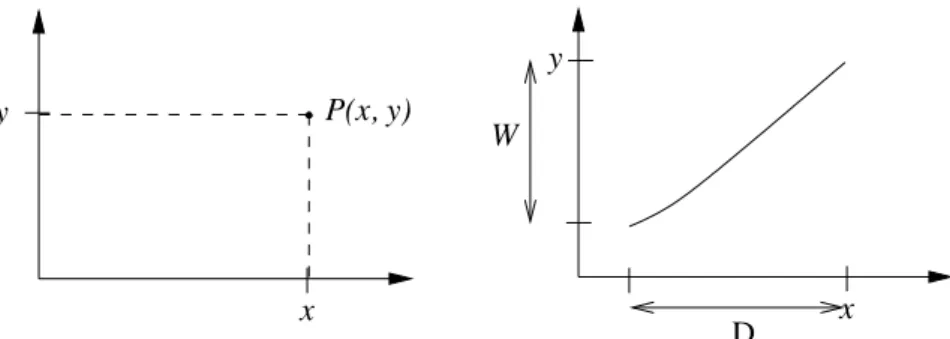
y W

x P(x, y)

D x y

Abbildung 2.1:karthesisches Koordinatensystem Graphische Darstellung

Kartesisches Koordinatensystem in der Ebene:

Der Graph einer Funktion f ist die Menge aller Punkte P(x, y) mit x∈D und y=f(x).

Beispiele:

1. lineare Funktion

f(x) =ax+b x, a, b∈ a, bbeliebig aber fest f¨ur allea = 0 ergibt sich eine konstante Funktion.

b

x y

−b/a

f(x)=b

Abbildung 2.2: lineare Funktionen

2. quadratische Funktion Normalparabel:

f(x) =x²

allgemein:

f(x) = ax²+bx+c (a̸= 0) y = a

!

x²+ 2b 2ax+

"

b 2a

#2

−

"

b 2a

#2$ +c

= a(x−x0)²+y0 mit x0=− b

2a, y0=−b² 4a +c d.h. Parabel mit Scheitel in (x₀, y₀).

x y=1/2 x² y=x² y=2x²

y=−x² y

Abbildung 2.3:quadratische Funktionen

3. Betragsfunktion

x y

Abbildung 2.4:Betragsfunktion f(x) =|x|=

% x : x≥ 0

−x : x <0

D= , W = ⁺₀

Die Funktion besitzt eine Spitze beix= 0.

4. Vorzeichenfunktion

1

x

−1 y

Abbildung 2.5: Vorzeichenfunktion

sgn(x) : x#→

⎧

⎨

⎩

−1 x <0 0 x= 0 1 x >0 D= , W ={−1,0,1}

Die Funktion besitzt eine Sprungstelle bei x= 0.

5. Hyperbel

x y

Abbildung 2.6: Hyperbelfunktion f(x) = 1

x

D=W = \{0}

x >0 : f(1) = 1, f(x→ ∞) = 0, f(x→0) = ∞ x <0 : f(−1) =−1, f(x→ ∞) = 0, f(x→0) = −∞

Die Funktion besitzt eine Polstelle beix= 0.

2.2 Eigenschaften von Funktionen

1. Symmetrieverhalten

Es gibt zwei Arten von Symmetrien:

(a) Achsensymmetrie

Die Funktionen sind symmetrisch zury-Achse:

y

x

y

x

Abbildung 2.7: Achsensymmetrie (linker Plot) Punktsymmetrie (rechter Plot)

f(−x) =f(x)

Solche Funktionen nennen wir geradeFunktionen. Beispiele daf¨ur sind f(x) = x²und f(x) =|x|.

(b) Punktsymmetrie

Diese Funktionen sind punktsymmetrisch zum Nullpunkt N = (0,0).

f(−x) =−f(x)

Punktsymmetrische Funktionen nennen wirungeradeFunktionen. Als Beispiel kennen wir f(x) = sgn(x) und f(x) = 1/x.

2. Periodizt¨at

f(x± p) =f(x)

Die Funktion f wiederholt sich periodisch mit der Periode p.

Als Beispiel betrachten wir sin(x± 2π) = sinx.

p y

x

Abbildung 2.8: periodische Funktion

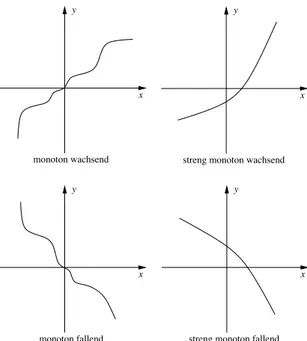
3. Monotonie

Sei a < b∈ : Dann heißt f

• monoton wachsend, wenn f(a)≤f(b)

• streng monoton wachsend, wenn f(a)< f(b)

• monoton fallend, wenn f(a)≥ f(b)

• streng monoton fallend, wenn f(a)> f(b) f¨ur jeweils alle a < b.

monoton fallend x y

x y

x y

x y

monoton wachsend streng monoton wachsend

streng monoton fallend

Abbildung 2.9: monotone Funktion

4. Nullstellen

f(x0) = 0 ↔ x0ist Nullstelle von f.

Nullstellen sind Schnitt- oder Ber¨uhrpunkte von f mit der x-Achse.

x y

Abbildung 2.10: Nullstellen einer Funktion

5. Extremstellen

Sei x∈[x₀−ϵ, x₀+ϵ] mit ϵ>0.

y

Maximum

Minimum x

Abbildung 2.11: Extremstellen einer Funktion f(x0)< f(x)→ x0ist (lokales) Minimum von f.

f(x0)> f(x)→ x0ist (lokales) Maximum von f.

Gelten die Bedingungen nicht nur f¨ur (kleine) Umgebungen, sondern f¨ur allex∈D, so spricht man von globalen Extrema.

2.3 Darstellung von Funktionen

Funktionen k¨onnen dargestellt werden durch

• Wertetabelle

• graph. Darstellung

• analytische Darstellung

Funktionen werden analytisch explizitoder impliziertdargestellt:

1. explizite Darstellung

y=f(x) Die Funktion ist nach y aufgel¨ost.

2. implizierte Darstellung

F(x, y) = 0 z. B. F(x, y) =y−f(x) = 0.

Aber: Es gibt Gleichungen F(x, y) = 0, die nicht auf eine Funktion reduziert werden k¨onnen:

Beispiel 2.2

F(x, y) = x²−y²= 0

→y = ±x

d.h. f¨ur jedes x̸= 0 haben wirzwei L¨osungen. Dies beschreibt keine Funktion.

Beispiel 2.3

F(x, y) = x²+y²−1 = 0

→y = ±√

1−x² |x|≤1

Es gibt also zwei L¨osungen f¨ur jedes x (außer x=±1), deshalb beschreibt die Gleichung keine Funktion. Allgemein wird dieser Gleichungstyp durch Pythagoras (x²+y²= r²) beschrieben.

y=x y

x y=−x

Abbildung 2.12: y=±x

x

r y

x y

Abbildung 2.13:^x2+y²=r²

2.4 Rechnen mit Funktionen

Zu den Funktionen f : D → und g : D → (mit gleichem D) k¨onnen folgende, elementare Verkn¨upfungen definiert werden:

Summe f +g Differenz f −g Produkt f ·g

“a-fache” a·f (a ∈ ) Spezialfall des Produnktes Quozient f /g f¨ur alle x∈ mit g(x)̸= 0

Wir k¨onnen also mit Funktionen ¨ahnlich wie mit reellen Zahlen rechnen, es gelten auch die analogen Rechenregeln, z. B.:

f +g =g+f Addition f ·g =g·f Kommutativgesetz der

Multiplikation

(f +g) +h=f+ (g+h) Addition

(f g)h=f(gh) Assoziationsgesetz der

Multiplikation

Aber: Es gibt auch Verkn¨upfungen von Funktionen, f¨ur die wir kein Analogen bei den Zahlen finden.

Komposition (Verkettung):

(f ◦g) =f(g(x)) Wir lesen “f nach g”, d.h. g wird in f eingesetzt.

D(f ◦g) ={x∈ , mitg(x)∈D(f)}.

Beispiel 2.4 Sei f(x) = √xmit dem Definitionsbereich D(f) = ⁺₀ und g(x) = 1−x²mit dem Definitionsbereich D(g) = .

Dann erhalten wir

(f ◦g)(x) =f(g(x)) =√

1−x² mit dem Definitionsbereich D(f◦g) = [−1,1].

F¨ur (g◦f) hingegen ergibt sich

(g◦f)(x) = 1−√

x²= 1−|x| mit D(g◦f) = ⁺₀. Daraus folgt: (g◦f)(x) = 1−x.

Die Reihenfolge der Verkettung ist also wesentlich, das Kommutativgesetz gilt nicht:

f ◦g ̸=g◦f

2.5 Umkehrfunktion

Ausgangsfragestellung: Ich messe Konzentration K als Funktion der Zeit t K =f(t)

Umkehrfragestellung: Zu welcher Zeit t erhalte ich die Konzentration K?

t =g(K)

Allgemein gilt: Indem die Gleichung nach xaufgel¨ost wird, erhalten wir dieUmkehrfunk- tion:

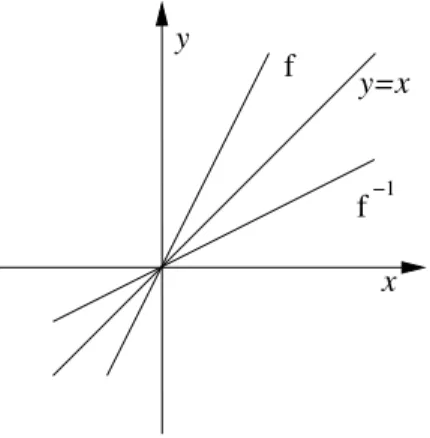
Funktion y=f(x) → Umkehrfunktion x=g(y)

Graphisch kann man entweder die Koordinatenachsen umbenennen oder die Funktion an der Geraden f(x) =y=x spiegeln.

Beispiel 2.5 Lineare Funktion:

y=f(x) =ax+b mit (a̸= 0) Die Umkehrfunktion ist ebenfalls eine lineare Funktion:

x=g(y) = y−b a = 1

ay− b a Beispiel 2.6 Quadratische Funktion:

y=f(x) =x² Die Umkehrgleichung ist jetzt keine Funktion:

x=±√y

Der Funktionswert y=a wird durch zwei verschiedene x erzeugt.

y=x² a

x y

Abbildung 2.14: ^y=x²

a =f(x=√

a) =f(x=−√ a)

Man sagt auch: Das Bildy =a wird durch zwei verschiedene Urbilder x=±√

a erzeugt.

Die Umkehrung ist also nicht eindeutig.

Abhilfe:

Einschr¨ankung des Definitionsbereichs D, z. B.

f(x) = x² mit D= ⁺₀ → x= g(y) = +√y D= ⁻₀ → x= g(−y) = −√y

Definition 2.2 1. Eine Funktionf heißt ein-eindeutig, wenn es zu jedem y∈W nur ein x∈D gibt mit y=f(x).

2. Streng monotone Funktionen sind ein-eindeutig.

3. Ein-eindeutige Funktionen sind immer umkehrbar, d.h. es existiert eine Umkehr- funktion

g : y→x=g(y) (2.1)

wobei y=f(x).

4. Die Umkehrfunktion von f wird oft mit f⁻¹ bezeichnet (nicht zu Verwechseln mit 1/f).

Es gilt

(f⁻¹)⁻¹ =f

d.h. die Umkehrung der Umkehrfunktion ist wieder die urspr¨ungliche Funktion.

Graphische Interpretation Beispiel 2.7 Identit¨atsfunktion

y=I(x) =x ↔ x=I⁻¹(y) =y Beispiel 2.8

y = f(x) = 2x x = f⁻¹(y) = 1

2y

Die Graphen der Funktionen f und f⁻¹ liegen spiegelbildlich bez¨uglich der Graphen von

f⁻¹ y=x

x

y f

Abbildung 2.15: f(x) und f⁻¹(x) im Koordinatensystem x =y.

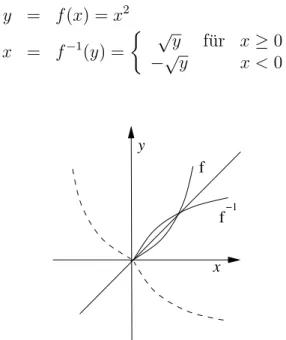
Beispiel 2.9

y = f(x) =x² x = f⁻¹(y) =

% √y f¨ur x≥ 0

−√y x <0

f⁻¹ y

x f

Abbildung 2.16: f(x) und f⁻¹(x) im Koordinatensystem

Satz 2.1 Ist die Funktionf streng monoton wachsend (fallend), so ist auchf⁻¹(x) streng monoton wachsend (fallend).