10.2 Numerische Lösung: D iskretisierung

10 Numerische Methoden

10.1 Mathematische K lassif iz ierung der D ifferentialgle i- chungen

Partielle Differentialgleichungen lassen sich klassifizieren anhand von

„charakteristischen Kurven“ oder „Charakteristiken“. Charakteristiken sind die K urven, entlang denen Information über die Lösung sich aus- breitet. Für quasilineare, homogene Differentialgleichungen zweiter Ord- nung in zwei V ariablen gibt es dazu eine exakte Theorie. Wir betrachten als Modellgleichung:

2 0

2 2

2

2 =

∂ + ∂

∂

∂ + ∂

∂

∂

y C u y x B u x

A u (10.1)

(ein beliebiges System von 2 quasilinearen, homogenen DGL erster Ordnung lässt sich auf die Form 10.1 transformieren).

Wir suchen Lösungen der Form )

(y mx f

u= + (10.2)

Die K urven

const.

= +mx y

sind dann die Charakteristiken der Gleichung.

m bestimmt sich als Lösung der quadratischen Gleichung

2+Bm+C=0

Am (10.3)

Wir unterscheiden die Fälle

- B²−4AC>0: es existieren zwei reelle Lösungen für m und damit zwei Kurvenscharen für die Charakteristiken. Die Differentialglei- chung heisst „hyperbolisch“.

- B²−4AC<0: die beiden Lösungen für m sind komplex. Die Diffe- rentialgleichung heisst „elliptisch“.

- B²−4AC=0: es existiert eine reelle Lösungen für m. Die Differen- tialgleichung heisst „parabolisch“.

Elliptische Gleichungen beschreiben Gleichgewichtszustände (B eispiel:

Laplace-Gleichung), hyperbolische Gleichungen Schwingungen und Ausbreitungszustände (B eispiel: Wellengleichung), der Grenzfall der pa- rabolischen Gleichungen beschreibt Diffusionsprobleme (Beispiel:

Wärmeleitungs- oder Diffusionsgleichung).

Je nach Typus der Differentialgleichung ändert sich der Typ der erlaub- ten Randbedingungen:

- Für elliptische Gleichungen müssen die Randbedingungen auf dem Rand eines geschlossenen Gebietes vorgegeben werden.

- für hyperbolische und parabolische Gleichungen dürfen Randbe- dingungen nur auf solchen K urven vorgegeben werden, von denen Charakteristiken ins Gebiet hineinführen

Wenn die K oeffizientenA, B, C keine Konstanten sind, ist der Typus der Gleichung im Raum variabel: je nach Gebiet ist die Gleichung elliptisch, parabolisch oder hyperbolisch.

Für Differentialgleichungen höherer Ordnung und solche in mehr als zwei unabhängigen Variablen existiert keine geschlossene Theorie mehr. Klassifizierung in die drei Typen ist aber nach wie vor möglich und sinnvoll.

Randbedingungen und Lösungsmethode müssen den Charakter der Dif- ferentialgleichung berücksichtigen.

10.2 Numerische Lösung: D iskretisierung

0 ) (u ,...,u',u,x =

F ⁽ⁿ⁾ (10.4)

wird die Funktion u durch ihre Werte an einer endlichen Anzahl von dis- kreten P unkten approximiert:

) (x_i u

u_i = (10.5)

Die P unkte x_iliegen auf einem (mehr oder weniger regelmässigen) Git- ter. Die Differentialausdrücke werden durch die Werte an den Gitterpunk- ten approximiert, und die Differentialgleichungen werden durch ein Sys- tem von algebraischen Differenzengleichungen ersetzt. Den A bstand von benachbarten Gitterpunkten bezeichnen wir als „Maschenweite“ des Git- ters (engl. „mesh size“).

Man unterscheidet zwischen Lösungsmethoden für „finite Elemente“, „fi- nite Differenzen“ und „finite V olumen“.

Finite Elem ente

Der B ereich wird in eine A nzahl Elemente, typischerweise Dreiecke oder Rechtecke (in 2D) beziehungsweise Tetraeder oder Quader (in 3D) auf- gelöst. Die Funktion wird durch ihre Werte auf den „K noten“ (Ecken der Elemente) dargestellt. Integrale über die Elemente werden als Funktio-

nen der Werte an den K noten mit Hilfe von Gewichtsfunktionen approxi- miert. Die Methode der finiten Elemente ist vor allem für mechanische Probleme sehr verbreitet.

Finite Differ enzen

Die Methode der finiten Differenzen verwendet ein räumliches Gitter und approximiert die Differentialoperatoren in den Gleichungen durch Diffe- renzen der Werte an den Gitterpunkten (Differenzengleichungen).

−1

xi x_i xi+1

yj +1

yj

∆x

∆y

Der Differentialoperator du/dx lässt sich in verschiedener Weise appro- ximieren, z.B.

x u u dxx

du _{i i}

i ∆

≈ − ⁻¹ , (10.6a)

x u u dxx

du _{i i}

i ∆

≈ ⁺¹− (10.6b)

x u u dxx

du _{i i}

i ∆

≈ ⁺ − ⁻ 2

1

1 , (10.6c)

je nachdem spricht man von linksseitiger, rechtsseitiger oder zentraler Differenz. In der Regel ist die A pproximation umso genauer, je höher die Ordnung der A pproximation (d. h. die Anzahl Punkte –1 , die dafür ver- wendet werden).

Für zweite A bleitungen verwendet man meist die A pproximation

2 1 1

2

2 2

x u u u x

u _{i i i}

∆ +

≈ −

∂

∂ + − (10.7)

Finite V olum en

Die Methode der finiten V olumen verwendet die E rhaltungssätze in In- tegralform. Der Lösungsbereich wird dabei aufgeteilt in endlich grosse Zellen bzw. Kontroll-V olumen. Jede Zelle bildet einen K noten, auf dem

die Werte der Lösung gegeben sind. Für die Lösung müssen V olumen- und Oberflächenintegrale approximiert werden.

∆x

∆y

j

ui_, u_i+1,j

j

vi_, 1 ,j+

vi

Beispielsweise wird die Gleichung ∇⋅u=0mit der Diskretisierung für das finite V olumen in obiger Figur (mit Höhe ∆z) zu

0 )

( )

(u_i+_1,j−u_i,j ∆y∆z+ v_i,j+₁−v_i,j ∆x∆z= (10.8) In unserem (einfachen) Fall ist dies formal dasselbe wie eine Formel, die wir durch finite Differenzen gewinnen würden

, 0

1 , , ,

1 =

∆ + −

∆

− ₊

+

y v v x

u

u_{i j ij ij ij}

(10.9) Die Methode der finiten V olumen hat den V orteil, dass sie Erhaltungs- sätze in natürlicher Weise respektiert.

Für lineare Differentialgleichungen sind die diskretisierten Differenzen- gleichungen ebenfalls linear. B ei nichtlinearen Differentialgleichungen werden auch die Differenzengleichungen nichtlinear. Um die Lösung zu finden, muss dann meist die Gleichung (bzw. das Gleichungssystem) linearisiert und iterativ gelöst werden.

10.3 Eigenschaften von Lösungsmethoden

• Konsistenz: die Differenzengleichungen sollen für kleine Gitterab- stände gegen die Differentialgleichungen konvergieren

• Stabilität: die Lösungsmethode soll numerische Fehler nicht ver- stärken

• Konvergenz: die numerische Lösung soll für kleine Gitterabstände gegen die exakte Lösung konvergieren

• Konservativität: Die numerische Lösung soll die E rhaltungssätze der unterliegenden Gleichungen respektieren

• Genauigkeit: die numerische Lösung unterscheidet sich von der exakten Lösung durch einen „Fehler“, der unterschieden werden kann nach

Modellfehler: Unterschied zwischen mathematischem Modell und Wirklichkeit

Diskretisierungsfehler: Unterschied zwischen numerischer Lö- sung auf endlich grobem Gitter und exakter Lösung

Konvergenzfehler: Unterschied zwischen iterativer und exakter Lösung

• Begrenztheit: viele physikalische Grössen haben natürliche Gren- zen, so müssen etwa Dichte, E nergiedichte oder (absolute) Tem- peratur immer positiv sein. Die Lösungsmethode soll solche B e- grenzungen respektieren.

• Geschwindigkeit: die Lösung sollte „innert nützlicher Frist“ berech- net werden können

Kritisch für jede Methode sind Stabilität und K onvergenz

10.4 Expliz ite Methoden

Als Beispiel betrachten wir die A dvektions-Diffusionsgleichung

2 2

x u x

t ∂

∂

=Γ

∂ + ∂

∂

∂ φ

ρ φ

φ (10.10)

Diese Gleichung dient uns als Modellgleichung für die Navier-Stokes- Gleichungen. Die Werte an den Gitterpunkten schreiben wir als

) , ( _{i n}

n

i φ x t

φ ≡ (10.11)

„Explizite“ Methoden verwenden zur Berechnung vonφ_iⁿ⁺¹in den Diffe- rentialoperatoren (ausser der Zeitableitung) nur die bekannten Werte zur Zeitt . Die explizite Euler Methode verwendet einen „V orwärtsschritt“ in_n der Zeitableitung:

( )

( )

1 1

1

1 2

2 x x

t u

n i n i n i n i n i n i n i

∆ +

− +Γ

∆

− −

∆ =

− + − + −

+ φ φ φ

ρ φ φ φ

φ (10.12)

Für beide Ortsableitungen (1. und 2. Ordnung) haben wir hier zentrale Differenzen verwendet. A ufgelöst nach der Unbekannten:

n i n

i n

i n

i

c

c d

d

d _{1 1}

1

2 ) 2

2 1

( _{+ −}

+ 



 



 +

 +



 



 − +

−

= φ φ φ

φ (10.13)

( )

d ∆

∆

≡Γ

ρ (10.14)

x t c u

∆

≡ ∆ (10.15)

Damit die Methode stabil und begrenzt ist, müssen die Koeffizienten von φ auf der rechten S eite von (10.13) positiv sein (eine positive Grösse behält ihr V orzeichen unter Diffusion und A dvektion), also

2 0 2 ,

1 ± >

< c

d

d (10.16)

Bei gegebener Maschenweite ∆x liefert dies B edingungen für den ma- ximal erlaubten Zeitschritt, z.B. aus (10.14)

( )²

2

1 x

t ∆

< Γ

∆ ρ (10.17)

Wenn A dvektion dominiert (Γ=0), ist die Methode (10.13) in jedem Fall instabil. Dann ist es von V orteil, die konvektive A bleitung auf der strom- aufwärts gelegenen Seite auszuwerten („upwind differencing“). Damit wird (füru > 0):

( )

i n i n

i⁺¹=(1−2d−c)φ +dφ₊₁+ d+c φ₋₁

φ (10.18)

Stabilität verlangt dann

( )

1 2

2 ⁻





+∆

∆

< Γ

∆ x

u t x

ρ (10.19)

oder für vernachlässigbare Diffusion (Γ=0):

u t<∆x

∆ (10.20)

Bedingung (10.20) heisst „Courant-B edingung“. Sie bedeutet auch, dass der Zeitschritt nicht länger sein darf als die Zeit, in der die Fl üssigkeit um eine Maschenweite vorwärts kommt.

10.5 Impliz ite Methoden

Explizite Methoden lassen – besonders auf feinen Gittern – nur kleine Zeitschritte zu (vgl. 10.17, 10.19, 10.20). Grössere Zeitschritte sind hin- gegen in „impliziten“ Methoden erlaubt. Hier werden die Differentialaus- drücke mit den „neuen“ (unbekannten) Werten ausgewertet. Für die im- plizite Euler-Methode mit zentralen Differenzen wird dann aus (10.10)

( )

( )

1 1 1 1 1 1

1 1 1

1 2

2 x x

t u

n i n i n i n

i n i n

i n i

∆ +

− +Γ

∆

− −

∆ =

− −⁺

+ + + +

− + +

+ φ φ φ

ρ φ φ φ

φ (10.21)

Dies gibt ein Gleichungssystem in den „neuen“ V ariablen

P n i W n i E n i

P A A Q

A + + −⁺ =

+ +

+ 1

1 1

1

1 φ φ

φ ^(10.22)

( )

2 x x

A_E u

∆

− Γ

= ρ∆ (10.23)

( )

2 x x

A_W u

∆

− Γ

− ∆

= ρ (10.24)

( )

A t A

A_{P E W}

+∆ +

−

= ρ (10.25)

n i

P t

Q ρ φ

=∆ (10.26)

(der Index P bezeichnet den P unkt, E steht für „east“, W für „west“).

Diese Methode ist für beliebige Zeitschritte stabil, für ∆t→∞ reduziert sie sich auf eine Methode für das zeitunabhängige P roblem

2 2

x u x

∂

∂

=Γ

∂

∂ φ

ρ

φ (10.27)

Der Nachteil impliziter Methoden ist, dass (sehr) grosse Gleichungssys- teme gelöst werden müssen. Allerdings sind diese Gleichungssysteme

„schwach besetzt“ (engl. „sparse“), d.h., die meisten Elemente in der Matrix sind identisch Null. Mit besonderen – in der Regel iterativen – Lö- sungsmethoden lässt sich diese Eigenschaft ausnutzen.

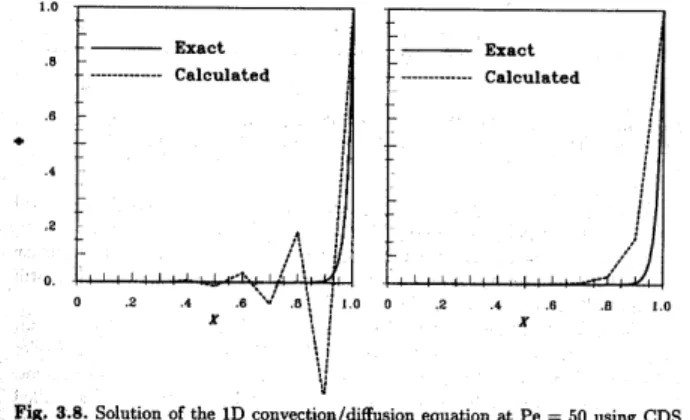
Weitere P robleme, die auch bei impliziten Methoden auftreten, sind Os- zillationen (bei Verwendung von zentralen Differenzen), und „numerische Diffusion“ bei Verwendung von „upwind-Differenzen“, vor allem auf gro- ben Gittern, vgl. die Figur aus (Ferzinger und P erič):

Figur aus Ferzinger und Perič,Pe=ρuL/Γ, stationäre Lösung von (10.27) mit impliziter Methode, links mit zentralen Differenzen, rechts mit „upwind“-Differenzen.

10.6 Beispie l: U mströmung e ines Würfels

Das Beispiel zeigt die (zeitlich gemittelte) Lösung für die turbulente Um- strömung eines auf eine Platte montierten Würfels (aus Ferzinger und Perič):

(Figur aus Ferzinger und Perič)

Deutlich erkennbar sind der „Hufeisenwirbel“ vor dem Würfel und seitlich davon, und die Wirbel, die durch A blösung der Strömung an den Würfel- kanten entstehen.

Weiter e Liter atur :

- Ferzinger und P erič(und Referenzen darin)

- Referenzen in White, Kap. 8.9 (Numerical Analysis)