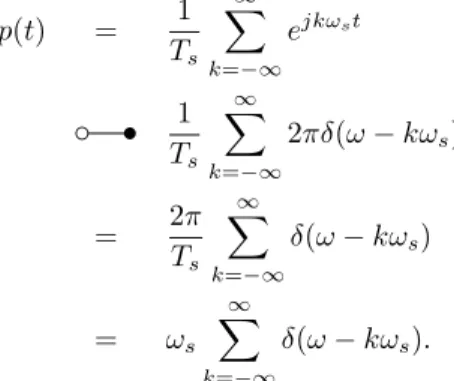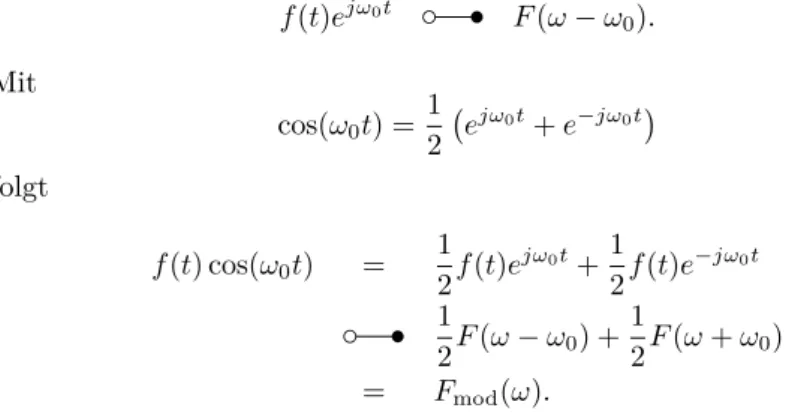Heilbronn, den 25.10.2021 Prof. Dr. V. Stahl WS 21/22
Übungen zu Digitale Signalverarbeitung und Mustererkennung mit Musterlösungen
Blatt 3
Aufgabe 1. In der Vorlesung wurde die Fourier Reihe für den Impulszugp(t) hergeleitet. Es gilt
p(t) =
∞
X
n=−∞
δ(t−nTs)
= 1
Ts
∞
X
k=−∞
ejkωst, ωs= 2π/Ts.
Berechnen Sie damit die Fourier TransformierteP(ω) vonp(t) und zeigen Sie, dass P(ω) wiederum ein Impulszug ist. Sie dürfen dabei verwenden, dass
ejωtˆ c s 2πδ(ω−ω).ˆ
Lösung von Aufgabe 1. Mit der Linearität der Fourier Transformation gilt p(t) = 1
Ts
∞
X
k=−∞
ejkωst
c s 1 Ts
∞
X
k=−∞
2πδ(ω−kωs)
= 2π
Ts
∞
X
k=−∞
δ(ω−kωs)
= ωs
∞
X
k=−∞
δ(ω−kωs).
Dies ist ein Impulszug, wobei die Impulse Abstandωsund Höheωshaben.
Aufgabe 2. In Bild 1 ist die Fourier TransformierteF(ω) eines bandbegrenzten Signalsf(t) mit Grenzfrequenz ˆωdargestellt.
−ωˆ ωˆ F(ω)
ω
Abbildung 1: Fourier Transformierte vonf(t).
1
Sei
f(t) cos(ω0t) c s Fmod(ω).
wobeiω0>ω.ˆ
• Skizzieren Sie den Verlauf von Fmod(ω). Benutzen Sie hierzu den Modulationssatz der Fourier Transformation.
• Welchen Zweck könnte es haben, dass man bei der Signalübertragung statt des eigentlichen Signalsf(t) lieber das Signalf(t) cos(ω0t) über- trägt?
• Was ist das Ergebnis, wenn man nochmal mit cos(ω0t) multipliziert und dann mit einem idealen Tiefpassfilter mit Fourier Transformier- ten
G(ω) =
2 falls −ˆω≤ω≤ωˆ 0 sonst
faltet?
Lösung von Aufgabe 2. Der Modulationssatz besagt f(t)ejω0t c s F(ω−ω0).
Mit
cos(ω0t) =1
2 ejω0t+e−jω0t folgt
f(t) cos(ω0t) = 1
2f(t)ejω0t+1
2f(t)e−jω0t c s 1
2F(ω−ω0) +1
2F(ω+ω0)
= Fmod(ω).
Anschaulich besteht somitFmod(ω) aus zwei Kopien vonF(ω) mit halber Amplitude um jeweilsω0 nach links und rechts verschoben, siehe Bild 2.
Daω0>ωˆ gilt, überlappen sich die Kopien nicht.
Fmod(ω)
−ω0 ω0
ω
−ωˆ ωˆ F(ω)
ω
Abbildung 2: Links: Fourier Transformierte vonf(t). Rechts: Fourier Transfor- mierte vonf(t) cos(ω0t).
2
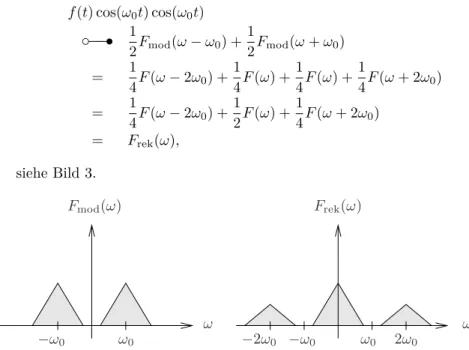
Nochmalige Multiplikation mit cos(ω0t) ergibt f(t) cos(ω0t) cos(ω0t)
c s 1
2Fmod(ω−ω0) +1
2Fmod(ω+ω0)
= 1
4F(ω−2ω0) +1
4F(ω) +1
4F(ω) +1
4F(ω+ 2ω0)
= 1
4F(ω−2ω0) +1
2F(ω) +1
4F(ω+ 2ω0)
= Frek(ω), siehe Bild 3.
Fmod(ω)
−ω0 ω0
ω
−2ω0 −ω0 ω0
ω 2ω0
Frek(ω)
Abbildung 3: Links: Fourier Transformierte von f(t) cos(ω0t). Rechts: Fourier Transformierte vonf(t) cos(ω0t) cos(ω0t).
Tiefpassfilterung mitG(ω) ergibt somit im Frequenzbereich wiederF(ω) bzw. im Zeitbereich das Originalsignalf(t). Das Verfahren heißt Ampli- tudenmodulation und wird angewandt, wenn man mehrere Signale über das selbe Medium übertragen möchte. Jedes Signal bekommt dann einen bestimmten Frequenzbereich (hier [ω0−ω, ωˆ 0+ ˆω]) zugeordnet.
3