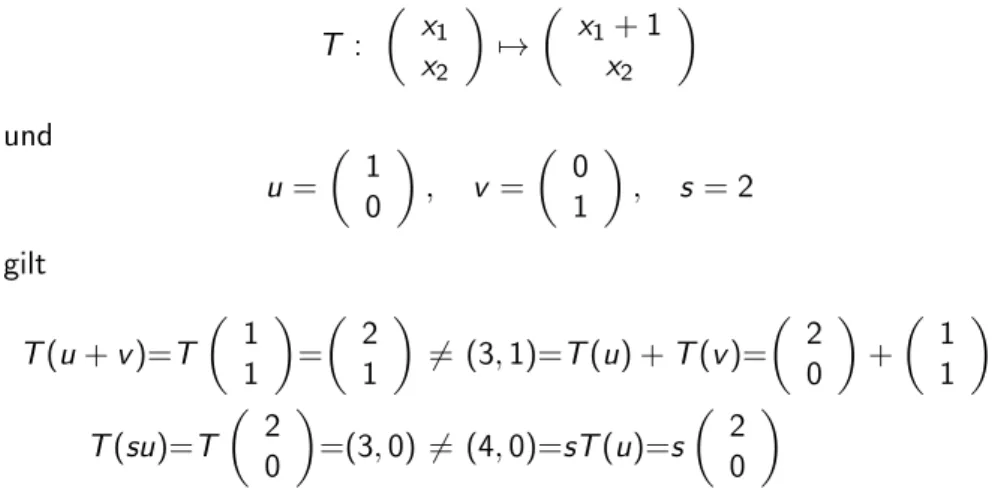Assoziativit¨ at: (a b) c = a (b c ) ∀a, b, c ∈ G

(1)

Gruppe

Unter einer Gruppe (G , ) versteht man eine Menge G , auf der eine bin¨ are Operation definiert ist:

: G × G 7−→ G ,

d.h. jedem Elementepaar (a, b) : a, b ∈ G ist ein Element a b ∈ G zugeordnet. Ferner m¨ ussen folgende Eigenschaften gelten:

Assoziativit¨ at: (a b) c = a (b c ) ∀a, b, c ∈ G

Neutrales Element: Es existiert ein eindeutig bestimmtes neutrales Element e ∈ G , d.h.

e a = a e = a ∀a ∈ G

Inverses Element: Zu jedem Element a ∈ G existiert ein eindeutig bestimmtes inverses Element a

⁻¹

∈ G mit

a a

⁻¹

= a

⁻¹

a = e

1 / 415

Man nennt eine Gruppe eine kommutative oder abelsche Gruppe, wenn die Operation kommutativ ist:

a b = b a ∀a, b ∈ G

Wenn aus dem Zusammenhang ersichtlich ist, welche Operation verwendet wird, schreibt man h¨ aufig statt (G , ) nur G .

2 / 415

Beispiel

Die bijektiven reellen Funktionen f : R → R bilden bez¨ uglich der Hintereinanderschaltung ◦ eine Gruppe.

Verifizierung der Gruppenaxiome Assoziativit¨ at:

((f ◦ g ) ◦ h)(x ) = f (g (h(x ))) = (f ◦ (g ◦ h))(x ) Neutrales Element: Identit¨ at

e : x 7→ x Inverses Element: Umkehrfunktion

f

⁻¹

: f (x ) 7→ x

3 / 415

Gegenbeispiel zur Kommutativit¨ at: f ◦ g 6= g ◦ f f¨ ur f : x 7→ 2x , g : x 7→ x + 1 f (g (x )) = 2(x + 1) 6= 2x + 1 = g (f (x ))

4 / 415

(2)

Beispiel

Abelsche Gruppe

Z

n

= Z mod n

der Restklassen {0, 1, . . . , n − 1} mit der Addition modulo n als Gruppenoperation

Illustration der Gruppenaxiome f¨ ur Z

4

= {0, 1, 2, 3}

Assoziativit¨ at

(1 + 2 mod 4) + 3 mod 4 = 3 + 3 mod 4 = 6 mod 4 = 2

1 + (2 + 3 mod 4) mod 4 = 1 + (5 mod 4) mod 4 = 1 + 1 mod 4 = 2 X Neutrales Element 0

3 + 0 mod 4 = 0 + 3 mod 4 = 3

5 / 415

Inverses Element

0 = 1 + 3 mod 4 = 2 + 2 mod 4 = 3 + 1 mod 4 Die Multiplikation modulo 4 definiert keine Gruppenstruktur, denn beispielsweise gilt

2 = 2 · 1 mod 4 = 2 mod 4

= 2 · 3 mod 4 = 6 mod 4

= ⇒ keine Eindeutigkeit des neutralen Elements (1 6= 3)

6 / 415

Gruppentafel

Die Operation auf einer endlichen Gruppe G = {g

₁

, . . . , g

_n

} kann durch die Verkn¨ upfungsmatrix A definiert werden:

A : a

_j,k

= g

_j

g

_k

F¨ ur eine abelsche (kommutative) Gruppe ist A symmetrisch:

g

_j

g

_k

= g

_k

g

_j

⇐⇒ A = A

^t

.

Die erste nicht-abelsche Gruppe hat 6 Elemente und kann mit den Permutationen von {1, 2, 3} identifiziert werden.

Beispiel

Gruppentafeln f¨ ur Gruppen mit ≤ 4 Elementen

e a e e a a a e

e a b e e a b a a b e b b e a

e a b c e e a b c a a e c b b b c e a c c b a e

e a b c

e e a b c

a a e c b

b b c a e

c c b e a

(3)

Untergruppe

F¨ ur eine Gruppe (G , ) bezeichnet man (U, ) als Untergruppe, wenn U eine Teilmenge von G ist, die selbst eine Gruppe bildet.

Um zu testen, ob (U , ) die Gruppenaxiome erf¨ ullt, gen¨ ugt es zu uberpr¨ ¨ ufen, dass U bez¨ uglich der Verkn¨ upfung und der Bildung von Inversen abgeschlossen ist:

a, b ∈ U = ⇒ a b ∈ U ∧ a ∈ U = ⇒ a

⁻¹

∈ U .

9 / 415

Beispiel

Gruppe der Kongruenzabbildungen eines Quadrates ABCD 7→ BCDA, ABCD 7→ ADCB, . . .

Untergruppe der Drehungen D

_α

: α = 0

^◦

, 90

^◦

, 180

^◦

, 270

^◦

0

^◦

: ABCD 7→ ABCD 90

^◦

: ABCD 7→ BCDA 180

^◦

: ABCD 7→ CDAB 270

^◦

: ABCD 7→ DABC abgeschlossen bzgl. Verkn¨ upfung und Invertierung

D

_α

◦ D

_β

= D

_α+β

, (D

_α

)

⁻¹

= D

_−α

10 / 415

Spiegelungen bilden keine Untergruppe:

Verkn¨ upfung Drehung, z.B. Komposition von Spiegelung an der Diagonale durch A und C ,

S

₁

: ABCD 7→ ADCB ,

und Spiegelung an der Mittelsenkrechten auf der Strecke von A nach B, S

₂

: ABCD 7→ BADC ,

D = S

₂

◦ S

₁

: ABCD 7→ BCDA

= Drehung um 90 b

^◦

F¨ ur Spiegelungen existiert ebenfalls kein neutrales Element.

11 / 415

Permutationen

F¨ ur eine endliche Menge M bilden die bijektiven Abbildungen p : M → M , versehen mit der Komposition von Abbildungen als Operation, die

symmetrische Gruppe von M.

F¨ ur M = {1, 2, . . . , n} bezeichnet man diese Gruppe mit S

_n

und die n!

Elemente p als Permutationen. Die Permutationsgruppe ist nur f¨ ur n = 2 kommutativ.

Man benutzt die Schreibweise p =

1 2 3 . . . n

p(1) p(2) p(3) . . . p(n)

zur Beschreibung einer Permutation. Ebenfalls gebr¨ auchlich ist die Zyklendarstellung. Ein Zyklus besteht aus einem Element und seinen Bildern bei wiederholter Ausf¨ uhrung der Permutation, bis wieder das urspr¨ ungliche Element erreicht wird. Aus den Elementen, die im ersten Zyklus nicht vorkommen, werden weitere Zyklen gebildet, bis alle Elemente

12 / 415

(4)

auftreten. Die Zyklen werden nach der Anzahl der Elemente absteigend sortiert und jeweils in runden Klammern hintereinander geschrieben.

Zyklen der L¨ ange 1 werden meist weggelassen.

Beispielsweise ist p =

1 2 3 4 5 6

4 3 2 6 5 1

≡ (1 4 6) (2 3) (5) bzw. p = (1 4 6) (2 3) .

13 / 415

Transposition und Signum einer Permutation Eine Transposition

τ = (j k )

ist eine Vertauschung von j und k . Durch Verkn¨ upfung dieser elementaren Permutationen l¨ asst sich jede Permutation p darstellen:

p = τ

₁

◦ · · · ◦ τ

_m

Die Parit¨ at (gerades oder ungerades m) ist eindeutig bestimmt, und man definiert

σ(p) = (−1)

^m

als Vorzeichen oder Signum der Permutation p.

F¨ ur eine zyklische Permutation p ist σ(p) = n − 1 mit n der L¨ ange des Zyklus. Der Exponent m kann damit aus der Zyklendarstellung einer Permutation als Summe der jeweils um 1 verminderten Zyklenl¨ angen bestimmt werden.

14 / 415

Beweis

(i) Wohldefiniertheit von σ:

Beweis durch Induktion

Induktionsanfang (n = 2):

S

₂

= {p, q} mit p = (1)(2) (Identit¨ at) und q = (1 2) (Transposition) in Zykelschreibweise

p = q ◦ q ◦ · · · ◦ q (gerade Anzahl) und q = q ◦ q ◦ · · · ◦ q (ungerade Anzahl)

= ⇒ eindeutig bestimmte Vorzeichen σ(p) = 1, σ(q) = −1 Induktionsschritt ((n − 1) → n):

betrachte

τ

₁

◦ · · · ◦ τ

_m

= p ∈ S

_n

definiere

q = (k n) ◦ p mit k = p(n)

q(n) = n und damit Identifikation von q mit einer Permutation

˜

q in S

n−1

mit

σ( ˜ q) = (−1)(−1)

^m

Induktionsvoraussetzung = ⇒ σ( ˜ q) eindeutig bestimmt

= ⇒ Exponent m eindeutig bestimmt

(ii) Vorzeichen von Zykeln:

p = (p

₁

p

₂

. . . p

_n

) = (p

₁

p

₂

. . . p

_n−1

) ◦ (p

_n−1

p

_n

)

| {z }

q

,

denn q(p

_n−1

) = p

_n

, q(p

_n

) = p(p

_n−1

) = p

₁

wiederholte Anwendung der Aufspaltung Darstellung von p als Komposition von n − 1 Transpositionen

(p

₁

p

₂

) ◦ (p

₂

p

₃

) ◦ . . . ◦ (p

_n−1

p

_n

)

= ⇒ σ(p) = n − 1

(5)

Beispiel

Bestimmung des Signums der Permutation p =

1 2 3 4 5 6 6 5 3 1 2 4

(i) Darstellung als Komposition von Transpositionen:

Uberf¨ ¨ uhrung von

(p(1), . . . , p(6)) = (6, 5, 3, 1, 2, 4)

durch Transpositionen sukzessive in die kanonische Reihenfolge:

(1 6) : (1, 5, 3, 6, 2, 4) (2 5) : (1, 2, 3, 6, 5, 4) (4 6) : (1, 2, 3, 4, 5, 6)

= ⇒

id = (4, 6) ◦ (2, 5) ◦ (1, 6) ◦ p, p = (1, 6) ◦ (2, 5) ◦ (4, 6) und σ(p) = (−1)

³

= −1

17 / 415

(ii) Alternative Bestimmung von σ mit Hilfe der Zyklenschreibweise:

p = (1 6 4) (2 5) (3) σ(τ ) = (−1)

^k−1

f¨ ur einen Zyklus τ der L¨ ange k, denn

(a b c . . . f ) = (a b) ◦ (b c) ◦ . . . ◦ (e f ) Anwendung auf das Beispiel

σ(p) = (−1)

(3−1)+(2−1)+(1−1)

= (−1)

³

= −1

18 / 415

K¨ orper

Eine Menge K , auf der eine Addition

” +“ und eine Multiplikation

” ·“

definiert sind, nennt man einen K¨ orper, wenn folgendes gilt:

Additive Gruppenstruktur: (K , +) ist eine abelsche Gruppe mit neutralem Element 0 (Nullelement), d.h. f¨ ur alle a, b ∈ K gilt

a + b = b + a (a + b) + c = a + (b + c)

a + 0 = a a + (−a) = 0 ,

wobei (−a) das inverse Element zu a bezeichnet.

19 / 415

Multiplikative Gruppenstruktur: (K \{0}, ·) ist eine abelsche Gruppe mit neutralem Element 1 (Einselement), d.h. f¨ ur alle a, b, c ∈ K \{0}

gilt

a · b = b · a (a · b) · c = a · (b · c)

a · 1 = a a · a

⁻¹

= 1 , wobei a

⁻¹

das inverse Element zu a bezeichnet.

Distributivgesetz:

a · (b + c ) = a · b + a · c f¨ ur alle a, b, c ∈ K .

20 / 415

(6)

Beispiel

K¨ orper der rationalen, reellen und komplexen Zahlen Q ⊂ R ⊂ C

Nullelement: 0, Einselement: 1

Inverses Element bez¨ uglich der Multiplikation einer komplexen Zahl z = x + iy 6= 0 :

w = x

x

²

+ y

²

+ i −y x

²

+ y

²

, denn

z · w = (x + iy ) x

x

²

+ y

²

+ i −y x

²

+ y

²

= x

²

− i

²

y

²

x

²

+ y

²

+ i −xy + yx

x

²

+ y

²

= 1 + i0 = 1

21 / 415

Beispiel

Gruppentafeln von Addition und Multiplikation f¨ ur den Galois-K¨ orper GF[2

²

] mit 4 Elementen

+ 0 1 a b

0 0 1 a b

1 1 0 b a

a a b 0 1

b b a 1 0

· 0 1 a b

0 0 0 0 0

1 0 1 a b

a 0 a b 1 b 0 b 1 a z.B: (a + 1) · b = b · b = 1, −b = b (⇐⇒ b + b = 0), 1/a = b

Die Konstruktion von K¨ orpern mit p

^`

Elementen, ` ∈ N , ist f¨ ur beliebige Primzahlen p durchf¨ uhrbar.

alle endlichen K¨ orper

22 / 415

Primk¨ orper

F¨ ur jede Primzahl p ist die Menge

Z

p

= {0, 1, . . . , p − 1}

ein K¨ orper unter der Addition und Multiplikation modulo p.

Allgemeiner existieren endliche K¨ orper mit p

^k

Elementen f¨ ur jedes k ∈ N , die sogenannten Galois-K¨ orper. Dies sind die einzigen K¨ orper mit endlich vielen Elementen.

Beweis

Rechenregeln f¨ ur Addition und Multiplikation in K¨ orpern gelten in den ganzen Zahlen

G¨ ultigkeit der Rechenregeln f¨ ur Z

p

noch zu zeigen: Existenz eines inversen Elementes a

⁻¹

f¨ ur a ∈ {2, . . . , p − 1}

betrachte dazu die Folge

a

^k

mod p, k = 0, . . . , p − 1 a

^k

6= 0 mod p ∀k ∈ N , denn

a

^k

= np = ⇒ p teilt a

^k

= ⇒

pPrimzahl

p teilt a = ⇒ Widerspruch zu a < p

= ⇒ mindestens ein Rest tritt zweimal auf:

a

^k¹

= a

^k²

mod p, k

₁

< k

₂

a

^k¹

a

^k²^−k¹

= a

^k¹

= ⇒

1 = a

^k²^−k¹

mod p = a

^k²^−k¹⁻¹

a mod p = ⇒ a

⁻¹

= a

^k²^−k¹⁻¹

mod p

(7)

Beispiel

Inverse Elemente im Primk¨ orper Z

5

2

⁻¹

mod 5 = 3, 3

⁻¹

mod 5 = 2, 4

⁻¹

mod 5 = 4 Uberpr¨ ¨ ufung durch Multiplikation, z.B.

2 · 2

⁻¹

mod 5 = 2 · 3 mod 5 = 6 mod 5 = 1 X Illustration anhand des Distributivgesetzes

(2 + 4) · 3

⁻¹

mod 5 = 6 · 2 mod 5

= 12 mod 5 = 2 2 · 3

⁻¹

+ 4 · 3

⁻¹

mod 5 = 2 · 2 + 4 · 2 mod 5

= 4 + 8 mod 5 = 12 mod 5 = 2

25 / 415

Beispiel

Paarungstabellen f¨ ur Sportturniere

In Stuttgart, M¨ unchen und Berlin soll an 4 Terminen ein Turnier unter 9 Mannschaften ausgetragen werden. Dabei soll

” jeder gegen jeden“ spielen.

Es sind also an jedem Termin 3 Gruppen aus je 3 Mannschaften zu bilden, die jeweils in einer der St¨ adte ihre Spiele untereinander austragen.

Mathematische Formulierung:

S

_0,k

∪ S

_1,k

∪ S

_2,k

= {1, . . . , 9}, k = 0, . . . , 3 ,

| S

_j,k

∩ S

_j⁰_,k⁰

|≤ 1,

mit drei-elementigen Mengen S

_j,k

, die jeweils der Dreiergruppe in der Stadt j am Termin k entsprechen. Die Bedingung an den Durchschnitt besagt, dass kein Mannschaftspaar doppelt vorkommt.

26 / 415

Konstruktion mit Hilfe des Primk¨ orpers Z

3

= {0, 1, 2}:

Identifikation der Mannschaften mit Punkten der Ebene Z

²₃

, d.h.

{1, 2, ..., 9} ↔ {(x , y ) : x , y ∈ Z

3

} und der Mengen S

_j_,k

mit den Geraden in Z

3

S

_j,k

= {(x , k · x + j mod 3) : x = 0, 1, 2}, ( Steigung k = 0, 1, 2) S

_j,3

= {(j , y ) : y = 0, 1, 2} ( senkrechte Geraden )

Durchschnittsbedingung trivialerweise erf¨ ullt: Geraden schneiden sich in h¨ ochstens einem Punkt

27 / 415

Paarungstabelle f¨ ur 16 Mannschaften, 4 St¨ adte und 5 Termine basierend auf 4-elementigen Galois-K¨ orper GF[2

²

]

Spielort 1 Spielort 2 Spielort 3 Spielort 4 1. Spieltag 1,2,3,4 5,6,7,8 9,10,11,12 13,14,15,16 2. Spieltag 1,6,11,16 5,2,15,12 9,14,3,8 13,10,7,4 3. Spieltag 1,10,15,8 5,14,11,4 9,2,7,16 13,6,3,12 4. Spieltag 1,14,7,12 5,10,3,16 9,6,15,4 13,2,11,8 5. Spieltag 1,5,9,13 2,6,10,14 3,7,11,15 4,8,12,16 Galois-K¨ orper GF [q] mit q einer Primzahlpotenz

Paarungstabelle f¨ ur q

²

Mannschaften und q St¨ adte

28 / 415

(8)

Euklidischer Algorithmus

Der gr¨ oßte gemeinsame Teiler zweier nat¨ urlicher Zahlen n

₁

> n

₂

kann durch sukzessive Division bestimmt werden. Man berechnet n

_k+1

, k = 2, 3, . . ., als Rest bei der Division n

_k−1

: n

_k

, d.h.

n

_k₋₁

= q

_k

n

_k

+ n

_k+1

, n

_k+1

< n

_k

,

und erh¨ alt GGT(n

₁

, n

₂

) = n

_K

f¨ ur den Index K mit n

_K+1

= 0 (Abbruch der Divisionskette: n

_K−1

= q

_K

n

_K

+ 0).

29 / 415

Beweis

(i) n

_K

teilt n

₁

und n

₂

:

n

_K−1

= q

_k

n

_K

= ⇒ n

_K

teilt n

_K−1

rekursive Definition, n

_k−1

= q

_k

n

_k

+ n

_k+1

, f¨ ur k = K − 1

= ⇒ n

_K

teilt n

_K−2

Iteration des Arguments f¨ ur k = K − 2, . . . , 3, 2

= ⇒ n

_K

teilt n

_K−3

, . . . , n

₂

, n

₁

(ii) n

_K

ist gr¨ oßter Teiler:

t teilt n

₁

und n

₂

, d.h. n

₁

= s

₁

t, n

₂

= s

₂

t, = ⇒ s

₁

t

|{z}

n1

= q

₂

s

₂

t

|{z}

n2

+n

₃

und folglich teilt t ebenfalls n

₃

, d.h. n

₃

= s

₃

t Wiederholung des Arguments:

n

_k₋₁

= q

_k

n

_k

+ n

_k+1

= ⇒ n

_k₊₁

= s

_k+1

t f¨ ur k = 3, 4, . . . , K − 1

= ⇒ n

_K

= s

_K

t ≥ t, d.h. n

_K

ist nicht kleiner als ein Teiler von n

₁

und n

₂

30 / 415

Beispiel

Gr¨ oßter gemeinsamer Teiler von n

₁

= 156 und n

₂

= 42 Euklidischer Algorithmus Divisionskette

n

_k−1

= q

_k

n

_k

+ n

_k+1

, n

_k+1

< n

_k

⇐⇒ n

_k−1

: n

_k

= q

_k

Rest n

_k+1

im konkreten Fall:

156 = 3 · 42 + 30 42 = 1 · 30 + 12 30 = 2 · 12 + 6 12 = 2 · 6

|{z}

n_K

+0 (K = 5)

= ⇒ GGT(156, 42) = n

₅

= 6

Beispiel

Berechnung der Inversen x von m = 81 modulo p = 64, d.h.

1 = x · m mod p ⇐⇒ 1 = x · m + y · p (m, p teilerfremd)

(i) Allgemeine Vorgehensweise:

Euklidischer Algorithmus

n

_k₋₁

= q

_k

n

_k

+ n

_k+1

, n

_k+1

< n

_k

mit n

₁

= m, n

₂

= p n

_K

= 1, da GGT(n

₁

, n

₂

) = 1, und die vorletzte Gleichung der Divisionskette hat somit die Form

n

_K₋₂

= q

_K₋₁

n

_K−1

+ 1 bzw. 1

|{z}

nK

= n

_K−2

− q

_K−1

n

_K−1

R¨ uckw¨ artseinsetzen von

n

_K₋₁

= n

_K₋₃

− q

_K−2

n

_K−2

, n

_K−2

= n

_K−4

− q

_K−3

n

_K₋₃

, . . .

(9)

(ii) Konkrete Werte n

₁

= m = 81, n

₂

= p = 64:

Euklidische Divisionskette

81 = 1 · 64 + 17

|{z}

n3

64 = 3 · 17 + 13 17 = 1 · 13 + 4 13 = 3 · 4 + 1

|{z}

nK

Auf¨ osen der Gleichungen jeweils nach der Zahl n

_j

mit dem h¨ ochsten Index und R¨ uckw¨ artseinsetzen

13 = 3 · 4 + 1 = ⇒ 1 = 13 − 3 · 4

4 = 17 − 1 · 13 = ⇒ 1 = 13 − 3 · (17 − 1 · 13) = 4 · 13 − 3 · 17 13 = 64 − 3 · 17 = ⇒ 1 = 4 · (64 − 3 · 17) − 3 · 17 = 4 · 64 − 15 · 17 17 = 81 − 1 · 64 = ⇒ 1 = 4 · 64 − 15 · (81 − 1 · 64) = 19 · 64 − 15 · 81

= ⇒ 1 = −15 · 81 mod 64 = 49 · 81 mod 64, d.h. x = 49 ist die gesuchte Inverse modulo 64 zu 81

33 / 415

Chinesischer Restsatz

F¨ ur teilerfremde nat¨ urliche Zahlen p

₁

, . . . , p

_n

besitzen die Kongruenzen x = a

₁

mod p

₁

. . .

x = a

_n

mod p

_n

genau eine L¨ osung x ∈ {0, . . . , P − 1}, P = p

₁

· · · p

_n

.

Bezeichnet Q

_k

eine zu P

_k

= P /p

_k

inverse ganze Zahl modulo p

_k

, d.h. ist Q

_k

P

_k

= 1 mod p

_k

,

so gilt

x =

n

X

k=1

a

_k

Q

_k

P

_k

mod P .

34 / 415

Beweis (i) Existenz:

Darstellung

x =

n

X

k=1

a

_k

Q

_k

P

_k

mod P

= ⇒

x mod p

_`

= a

_`

Q

_`

P

_`

mod p

_`

, da p

_`

Teiler von P

_k

f¨ ur k 6= `

Definition einer zu P

_`

inversen Zahl Q

_`

modulo p

_`

: Q

_`

P

_`

= 1 mod p

_`

= ⇒

x = a

_`

· 1 mod p

_`

= a

_`

mod p

_`

35 / 415

(ii) Eindeutigkeit:

zu zeigen:

x = x

⁰

mod p

_k

f¨ ur k = 1, . . . , n = ⇒ x − x

⁰

= mP sukzessives Betrachten der Kongruenzen

x = x

⁰

mod p

₁

= ⇒

x − x

⁰

= m

₁

p

₁

x = x

⁰

mod p

₂

= ⇒

m

₁

p

₁

= 0 mod p

₂

⇐⇒ m

₁

p

₁

= sp

₂

p

₁

, p

₂

teilerfremd = ⇒ p

₂

teilt m

₁

, d.h.

m

₁

= m

₂

p

₂

, x − x

⁰

= m

₂

p

₁

p

₂

weitere Kongruenzen

x − x

⁰

= m

₃

p

₁

p

₂

p

₃

, . . . , x − x

⁰

= m

_n

p

₁

· · · p

_n

36 / 415

(10)

Beispiel

Bestimmung einer L¨ osung x der Kongruenzen x = 6 mod 9 x = 5 mod 10 x = 4 mod 13 Chinesischer Restsatz = ⇒

x = 6 Q

₁

P

₁

+ 5 Q

₂

P

₂

+ 4 Q

₃

P

₃

mod P , P = 9 · 10 · 13 = 1170 mit

P

₁

= 10 · 13 = 130, P

₂

= 9 · 13 = 117, P

₃

= 9 · 10 = 90 und Q

_k

der zu P

_k

inversen nat¨ urlichen Zahl modulo p

_k

, d.h.

Q

_k

P

_k

+ yp

_k

= 1

37 / 415

Bestimmung der Modulo-Inversen Q

₁

:

130 = 14 · 9 + 4 9 = 2 · 4 + 1 R¨ uckw¨ artseinsetzen

1 = 9 − 2 · 4

= 9 − 2 · (130 − 14 · 9) = 29 · 9 + (−2)130

= ⇒ Q

₁

= (−2) mod 9 = 7 Q

₂

:

117 = 11 · 10 + 7 10 = 1 · 7 + 3

7 = 2 · 3 + 1 R¨ uckw¨ artseinsetzen

1 = 7 − 2 · 3

= 7 − 2 · (10 − 1 · 7) = 3 · 7 − 2 · 10

= 3 · (117 − 11 · 10) − 2 · 10 = 3 · 117 − 35 · 10

= ⇒ Q

₂

= 3 mod 10 = 3

38 / 415

Q

₃

:

90 = 6 · 13 + 12 13 = 1 · 12 + 1 R¨ uckw¨ artseinsetzen

1 = 13 − 1 · 12

= 13 − 1 · (90 − 6 · 13) = 7 · 13 + (−1) · 90

= ⇒ Q

₃

= (−1) mod 13 = 12 Einsetzen in die Darstellung der L¨ osung

x = 6Q

₁

P

₂

+ 5Q

₂

P

₂

+ 4Q

₃

P

₃

mod 1170

= 6 · 7 · 130 + 5 · 3 · 117 + 4 · 12 · 90 mod 1170

= 11535 mod 1170 = 1005

Vektorraum

Ein Vektorraum ¨ uber einem K¨ orper K (K -Vektorraum) ist eine

kommutative Gruppe (V , +), auf der zus¨ atzlich zu der Gruppenoperation

” +“ eine Skalarmultiplikation

” · “ definiert ist, K × V 3 (s , v ) 7→ s · v ∈ K , die folgende Eigenschaften besitzt:

(s

₁

+ s

₂

) · v = s

₁

· v + s

₂

· v s · (v

₁

+ v

₂

) = s · v

₁

+ s · v

₂

(s

₁

· s

₂

) · v = s

₁

· (s

₂

· v ) 1 · v = v

f¨ ur alle Skalare s, s

₁

, s

₂

∈ K , Elemente v , v

₁

, v

₂

∈ V und das Einselement

1 ∈ K .

(11)

Der Einfachheit halber wird das Pluszeichen sowohl f¨ ur die Addition in V als auch f¨ ur die Addition in K verwendet. Ebenso wird der Malpunkt f¨ ur die Skalarmultiplikation meist weggelassen.

F¨ ur K = R bzw. K = C spricht man von einem reellen bzw. komplexen Vektorraum.

41 / 415

Beispiel

Reeller (komplexer) Vektorraum der Polynome p vom Grad ≤ n p(x ) = a

₀

+ a

₁

x + · · · + a

_n

x

ⁿ

, a

_k

∈ R (a

_k

∈ C ) Definition der Addition und Skalarmultiplikation in der nahe liegenden Weise:

(p + q)(x ) = p(x ) + q(x ), (sp)(x ) = sp(x )

Polynome mit Grad n (a

_n

6= 0) bilden auf Grund eventueller Gradreduktion bei Addition keinen Vektorraum,

z.B.

(x

²

− 1

| {z }

Grad 2

) + (3 − x

²

| {z }

Grad 2

) = 2

|{z}

Grad 0

42 / 415

Beispiel

Reeller Vektorraum der Folgen (a

_n

), a

_n

∈ R Addition: (a

_n

) + (b

_n

) = (a

_n

+ b

_n

) Skalarmultiplikation: s (a

_n

) = (sa

_n

) Vektorr¨ aume spezieller Folgen:

beschr¨ ankte Folgen, konvergente Folen, konvergente Folen, komplexe Folgen

Monotone Folgen bilden keinen Vektorraum, denn Summen monotoner Folgen sind nicht notwendig monoton; z.B.

(n

²

) + (−2

ⁿ

) : −1, 0, 1, 0, −7, −28, . . . .

43 / 415

Vektorraum der n-Tupel

F¨ ur einen K¨ orper K bilden die n-Tupel oder n-Vektoren

a =





 a

₁

.. . a

_n





 , a

_k

∈ K

den K -Vektorraum K

ⁿ

mit der komponentenweise definierten Addition und Skalarmultiplikation, d.h.





 a

₁

.. . a

_n





 +





 b

₁

.. . b

_n





 =







a

₁

+ b

₁

.. . a

_n

+ b

_n





 , s ·





 a

₁

.. . a

_n





 =





 s · a

₁

.. . s · a

_n





 f¨ ur a

_k

, b

_k

, s ∈ K .

44 / 415

(12)

Oft schreibt man n-Tupel als Zeilenvektor

a

^t

= (a

₁

, . . . , a

_n

) bzw. a = (a

₁

, . . . , a

_n

)

^t

. Durch das Symbol

” t“ der Transposition wird von der Standardkonvention als Spaltenvektor unterschieden.

F¨ ur K = R bzw. K = C erh¨ alt man die Vektorr¨ aume der n-Tupel reeller und komplexer Zahlen R

ⁿ

und C

ⁿ

.

45 / 415

Beispiel

Addition und Skalarmultiplikation in R

³

und C

²

(i) Reelle (Spalten-) Vektoren im Raum:



 1

−2 3



 +





−4 5

−6



 =





1 + (−4)

−2 + 5 3 + (−6)



 =





−3 3

−3





2 

 3

−1 4



 =





2 · (3) 2 · (−1)

2 · 4



 =



 6

−2 8



 (ii) (Zeilen-) Vektoren in der komplexen Ebene:

1, i

+ 2 − i, 1 + 3i

= 3 − i, 1 + 4i (2 − 3i) 1 + i, 1 − i

= 5 − i, −1 − 5i

46 / 415

Unterraum

Ein Unterraum U eines K -Vektorraums V besteht aus Elementen

u ∈ U ⊆ V , die mit der in V definierten Addition und Skalarmultiplikation selbst einen Vektorraum bilden.

Um zu pr¨ ufen, ob U ⊂ V ein Unterraum ist, gen¨ ugt es zu zeigen, dass U bzgl. der Addition und Skalarmultiplikation abgeschlossen ist:

u, v ∈ U = ⇒ u + v ∈ U s ∈ K , u ∈ U = ⇒ s · u ∈ U .

Unterr¨ aume U werden oft durch Bedingungen an die Elemente von V definiert:

U = {u ∈ V : A(u)},

mit einer Aussage A, die f¨ ur Elemente von U erf¨ ullt sein muss.

Beispiel

Unterr¨ aume des Vektorraums der reellen Funktionen f : R → R ,

definiert durch zus¨ atzliche Eigenschaften

Eigenschaft Unterraum (un)gerade ja

beschr¨ ankt ja monoton nein

stetig ja

positiv nein

linear ja

(13)

exemplarische Begr¨ undungen beschr¨ ankt:

|f

_k

| ≤ c

_k

= ⇒ |f

₁

(x ) + f

₂

(x)| ≤ |f

₁

(x )| + |f

₂

(x )| ≤ c

₁

+ c

₂

|f | ≤ c = ⇒ |sf (x )| ≤ sc jeweils ∀x

f

₁

+ f

₂

und sf sind beschr¨ ankt Unterraumkriterium erf¨ ullt monoton:

h(x ) = exp(x ) − x nicht monoton wegen lim

x→±∞

h(x) = +∞

trotz Monotonie von f (x ) = exp(x) und g (x ) = x

49 / 415

Beispiel

Gerade in einem K -Vektorraum V :

U : u = a + tb, t ∈ K mit fest gew¨ ahlten Elementen a, b ∈ V

(i) a = 0 Unterraum:

u

₁

, u

₂

∈ U = ⇒ u

₁

+ u

₂

= t

₁

b + t

₂

b = (t

₁

+ t

₂

| {z }

t

)b ∈ U s ∈ K , u ∈ U = ⇒ su = s(tb) = (st)b ∈ U

(ii) 0 ∈ / U, d.h. a 6= 0 und b 6= sa kein Unterraum:

u ∈ U = ⇒ su = s(a + tb) = 0 6∈ U f¨ ur s = 0

50 / 415

Linearkombination

F¨ ur Elemente v

₁

, v

₂

, . . . , v

_m

eines K -Vektorraums V bezeichnet man s

₁

v

₁

+ s

₂

v

₂

+ · · · + s

_m

v

_m

=

m

X

k=1

s

_k

v

_k

mit Skalaren s

_k

∈ K als Linearkombination der Elemente v

_k

.

Die Menge aller solchen Linearkombinationen nennt man die lineare H¨ ulle der v

_k

:

span(v

₁

, . . . , v

_m

) = (

_m

X

k=0

s

_k

v

_k

: s

_k

∈ K )

.

Allgemeiner definiert man f¨ ur eine Menge U ⊆ V span(U) =

( X

k

s

_k

u

_k

: s

_k

∈ K , u

_k

∈ U )

als die Menge aller Linearkombinationen von Elementen aus der Menge U.

Die so gewonnene lineare H¨ ulle von U ist ein Unterraum von V .

51 / 415

Beispiel

Linearkombinationen in R

ⁿ

(i) Der Vektor v = (1, 2, 3)

^t

ist eine Linearkombination der Vektoren v

₁

= (3, 4, 5)

^t

, v

₂

= (1, 1, 1)

^t

,

denn v = v

₁

− 2v

₂

.

(ii) Der Vektor v = (1, 0)

^t

ist keine Linearkombination der Vektoren v

₁

= (0, 1)

^t

, v

₂

= (0, 2)

^t

,

denn jede Linearkombination von v

₁

und v

₂

hat die Form (0, x )

^t

. (iii) Der Vektor v = (0, 0, 0, 0)

^t

ist auf verschiedene Art als Linearkombination von

v

₁

= (1, 1, 0, 0)

^t

, v

₂

= (0, 2, 2, 0)

^t

, v

₃

= (0, 0, 3, 3)

^t

, v

₄

= (4, 0, 0, 4)

^t

darstellbar:

v = s (12v

₁

− 6v

₂

+ 4v

₃

− 3v

₄

), s ∈ R

52 / 415

(14)

Beispiel

Lineare H¨ ullen in R

³

(i) v

₁

= (1, −1, 0)

^t

, v

₂

= (0, 1, −1)

^t

:

span(v

₁

, v

₂

) = {s

₁

(1, −1, 0)

^t

+ s

₂

(0, 1, −1)

^t

: s

_k

∈ R }

= {(s

₁

, s

₂

− s

₁

, −s

₂

)

^t

: s

_k

∈ R } Ebene, orthogonal zu (1, 1, 1)

^t

(ii) v

₁

= (1, −1, 0)

^t

, v

₂

= (0, 1, −1)

^t

, v

₃

= (−1, 0, 1)

^t

: gleiche lineare H¨ ulle, da

v

₃

= −v

₁

− v

₂

(Darstellung von v

₃

als Linearkombination von v

₁

und v

₂

)

keine eindeutige Darstellung der Vektoren in span(v

₁

, v

₂

, v

₃

), z.B.:

(0, 0, 0)

^t

= s (v

₁

+ v

₂

+ v

₃

), s ∈ R

53 / 415

Konvexkombination

Eine Konvexkombination ist eine Linearkombination s

₁

v

₁

+ s

₂

v

₂

+ · · · + s

_m

v

_m

von Elementen v

_k

eines reellen Vektorraums mit

s

_k

≥ 0, X

k

s

_k

= 1 .

Die Menge aller Konvexkombinationen von Elementen aus einer Teilmenge M ⊆ V wird als konvexe H¨ ulle von M, conv(M), bezeichnet.

Geometrisch ist conv(M) die kleins- te M enthaltende Menge, die f¨ ur je zwei Elemente u, v auch deren Ver- bindungsstrecke

(1 − s)u + sv , 0 ≤ s ≤ 1 , enth¨ alt.

54 / 415

Beispiel

Parametrisierung einer Gerade und eines konvexen Vierecks durch lineare Interpolation

(i) Gerade G:

u , v ∈ G, u 6= v = ⇒

G : x = (1 − t)u + tv , t ∈ R Konvexkombination f¨ ur 0 ≤ t ≤ 1

Geradensegment conv({u, v }) zwischen u und v x teilt conv({u, v }) im Verh¨ altnis t : (1 − t)

(ii) Konvexes Viereck (a, b, c, d ):

z ∈ (a, b, c , d ) ⇐⇒

z = (1 − s )[(1 − t)a + tb

| {z }

x

] + s [(1 − t)c + td

| {z }

y

]

= (1 − s )(1 − t)a + (1 − s )tb + s(1 − t)c + std mit 0 ≤ s, t ≤ 1

Konvexkombination von a, b, c, d: Koeffizienten ≥ 0 mit Summe 1

(15)

Baryzentrische Koordinaten

Die Konvexkombinationen von u, v , w ∈ R

²

,

x = ru + sv + tw , r, s, t ≥ 0, r + s + t = 1

bilden ein Dreieck mit Eckpunkten u , v , w . Die Koeffizienten r, s, t werden als baryzentrische Koordinaten bezeichnet. Sie k¨ onnen durch L¨ osen des definierenden linearen Gleichungssystems bestimmt werden.

r = area(x , v , w ) area(u, v , w ) s = area(u , x , w ) area(u, v , w ) t = area(u, v , x ) area(u, v , w )

57 / 415

Geometrisch entsprechen die baryzentrischen Koordinaten den

Verh¨ altnissen der Fl¨ acheninhalte der durch x definierten Teildreiecke zum Fl¨ acheninhalt des Dreiecks ∆(u, v , w ).

Analog k¨ onnen die baryzentrischen Koordinaten der Punkte in einem Tetraeder im R

³

definiert werden.

58 / 415

Lineare Unabh¨ angigkeit

Elemente v

₁

, . . . , v

_m

eines Vektorraums V sind linear abh¨ angig, wenn ein Element v

_k

als Linearkombination der anderen darstellbar ist, d.h.

s

₁

v

₁

+ · · · + s

_m

v

_m

= 0

_V

(*) mit mindestens einem der Skalare s

_k

6= 0.

Andernfalls bezeichnet man v

₁

, . . . , v

_m

als linear unabh¨ angig. In diesem Fall folgt aus P

k

s

_k

v

_k

= 0

_V

dass s

₁

= · · · = s

_m

= 0.

F¨ ur Vektoren v

_k

∈ R

ⁿ

ist die Bedingung (*) ein homogenes lineares Gleichungssystem, das bei linearer Unabh¨ angigkeit von v

₁

, . . . , v

_m

nur die triviale L¨ osung s

₁

= · · · = s

_m

= 0 besitzt.

59 / 415

Beispiel

Lineare Unabh¨ angigkeit von Vektoren in der Ebene

(i) Zwei Vektoren u, v ∈ R

²

sind genau dann linear unabh¨ angig, wenn keiner der beiden ein Vielfaches des anderen ist.

konkrete Beispiele:

(1, 0)

^t

, (1, 1)

^t

sind linear unabh¨ angig, denn

s (1, 0)

^t

+ t(1, 1)

^t

= (0, 0)

^t

= ⇒ s = t = 0 (2, 3)

^t

, (−4, −6)

^t

sind linear abh¨ angig, denn

(−2)(2, 3)

^t

= (−4, −6)

^t

= ⇒ 2(2, 3)

^t

+ (−4, 6)

^t

= (0, 0)

^t

, d.h. ∃ eine nichttriviale Darstellung des Nullvektors

60 / 415

(16)

(ii) Drei Vektoren u, v , w ∈ R

²

sind immer linear abh¨ angig.

ru + sv + tw = 0

0 unterbestimmtes, homogenes lineares Gleichungssystem ru

₁

+ sv

₁

+ tw

₁

= 0

ru

₂

+ sv

₂

+ tw

₂

= 0 f¨ ur r, s , t, das immer eine nichttriviale L¨ osung besitzt.

konkretes Beispiel:

r 0

1 + s 1

2 + t 2

3 = 0

0 mit der L¨ osung r = λ, s = −2λ und t = λ f¨ ur beliebiges λ ∈ R

61 / 415

Beispiel

Lineare Unabh¨ angigkeit von Vektoren im Raum

(i) Zwei Vektoren u, v ∈ R

³

sind linear abh¨ angig, wenn sie parallel sind, d.h. wenn ein Vektor ein Vielfaches des anderen ist.

(ii) Drei Vektoren u, v , w ∈ R

³

sind linear abh¨ angig, wenn zwei Vektoren parallel sind oder wenn ein Vektor in der von den beiden anderen Vektoren aufgespannten Ebene liegt.

(iii) Vier und mehr Vektoren im R

³

sind immer linear abh¨ angig.

Test f¨ ur lineare Unabh¨ angigkeit:

s

₁

= · · · = s

_n

= 0 ist die einzige L¨ osung des homogenes linearen Gleichungssystems

s

₁



 x

₁

y

₁

z

₁



 + · · · + s

_n



 x

_n

y

_n

z

_n



 =



 0 0 0





62 / 415

Konkrete F¨ alle:

u = (0, 1, 2)

^t

, v = (1, 2, 3)

^t

sind linear unabh¨ angig, da u ∦ v

(ii) u = (1, 0, 0)

^t

, v = (2, 3, 0)

^t

, w = (4, 5, 6)

^t

sind linear unabh¨ angig, da

r



 1 0 0



 + s



 2 3 0



 + t



 4 5 6



 =



 0 0 0



 = ⇒ r = s = t = 0

(iii) (1, 0, 0)

^t

, (0, 2, 0)

^t

, (0, 0, 3)

^t

, (4, 5, 6)

^t

sind linear abh¨ angig, da 5



 1 0 0



 + 2



 0 2 0



 + 2



 0 0 3



 + (−1)



 5 4 6



 =



 0 0 0





Basis

Eine Teilmenge B eines Vektorraumes V ist eine Basis von V , wenn die Vektoren in B linear unabh¨ angig sind und sich jeder Vektor v ∈ V eindeutig als Linearkombination

v = X

k

c

_k

b

_k

, b

_k

∈ B ,

darstellen l¨ asst. Die Koeffizienten c

_k

werden als Koordinaten von v bez¨ glich der Basis B bezeichnet:

v ↔ v

_B

= (c

₁

, c

₂

, . . .)

^t

.

Besitzt ein Vektorraum V eine endliche Basis B = {b

₁

, . . . , b

_n

}, so ist die Anzahl der Basisvektoren eindeutig bestimmt und wird die Dimension von V genannt:

n = dim V .

Man setzt dim V = 0 f¨ ur V = {0} und dim V = ∞ f¨ ur einen Vektorraum

ohne endliche Basis.

(17)

F¨ ur V = R

ⁿ

oder V = C

ⁿ

besteht eine Basis aus n Vektoren b

_k

, und die Matrix B = (b

₁

, . . . , b

_n

) mit den Spalten b

_k

ist invertierbar, d.h.

det B 6= 0.

65 / 415

Beweis

Eindeutigkeit der Dimension im endlichen Fall hinreichend zu zeigen:

Hat ein Vektorraum eine n-elementige Basis b

₁

, . . . , b

_n

,

so sind n + 1 Vektoren v

₁

, . . . , v

_n+1

(und damit auch mehr als n + 1 Vektoren) linear abh¨ angig.

( = ⇒ Widerspruch zur linearen Unabh¨ angigkeit bei Basen mit unterschiedlich vielen Vektoren)

Beweis durch Induktion:

(n − 1) → n: betrachte Basisdarstellung der Vektoren v

_k

: v

_k

=

n

X

`=1

γ

_k,`

b

_`

, k = 1, . . . , n + 1 trivialer Fall:

γ

_n+1,1

= · · · = γ

_n+1,n

= 0

= ⇒ v

_n+1

= 0 = ⇒ lineare Abh¨ angigkeit der Vektoren v

_k

66 / 415

andernfalls, nach geeigneter Nummerierung, γ

_n+1,n

6= 0

definiere Vektoren v

_k⁰

, k = 1, . . . , n, die sich als Linearkombination der n − 1 Vektoren b

₁

, . . . , b

_n−1

darstellen lassen:

v

_k⁰

= v

_k

− γ

_k_,n

γ

_n+1,n

v

_n+1

= (γ

_k,1

b

₁

+ · · · + γ

_k,n

b

_n

) − γ

_k,n

γ

_n+1,n

(γ

_n+1,1

b

₁

+ · · · + γ

_n+1,n

b

_n

) Koeffizient von b

_n

= 0 = ⇒

v

₁⁰

, . . . , v

_n⁰

∈ V

⁰

= span {b

₁

, . . . , b

_n−1

}

Induktionsvoraussetzung, angewandt auf die Basis {b

₁

, . . . , b

_n−1

} von V

⁰

= ⇒ ∃ nichttriviale Linearkombination

λ

₁

v

₁⁰

+ · · · + λ

_n

v

_n⁰

= 0 Einsetzen der Definition von v

_k⁰

Linearkombination der v

_k

, also die behauptete lineare Abh¨ angigkeit

67 / 415

Reelles Skalarprodukt

Ein Skalarprodukt h·, ·i auf einem reellen Vektorraum V ist eine Abbildung V × V 3 (u, v ) 7→ hu, v i ∈ R

mit folgenden Eigenschaften:

Positivit¨ at:

hv , v i > 0 f¨ ur v 6= 0 Symmetrie:

hu, v i = hv , ui Linearit¨ at:

hsu + tv , w i = shu, wi + thv , w i Diese Identit¨ aten gelten f¨ ur alle u , v , w ∈ V und s , t ∈ R .

Aufgrund der Symmetrie ist ein reelles Skalarprodukt auch bez¨ uglich des zweiten Argumentes linear, also eine Bilinearform auf V .

68 / 415

(18)

F¨ ur V = R

ⁿ

ist das kanonische Skalarprodukt

hu, v i = u

^t

v = u

₁

· · · u

_n





 v

₁

.. . v

_n





 = u

₁

v

₁

+ · · · + u

_n

v

_n

, und

|u| = p

hu, ui = q

u

²₁

+ · · · + u

_n²

ist die assoziierte Norm.

69 / 415

Beispiel

Skalarprodukt-Eigenschaften f¨ ur Abbildungen R

²

3 (x , y ) 7→ f (x , y ) ∈ R

f(x,y) Positivit¨ at Symmetrie Linearit¨ at

10x

₁

y

₁

+ x

₂

y

₂

X X X

|x

₁

y

₁

| + |x

₂

y

₂

| X X

x

₁

y

₂

+ x

₂

y

₁

X X

4x

₁

y

₁

+ x

₁

y

₂

+ 2x

₂

y

₁

+ 3x

₂

y

₂

X X x

₁

y

₁³

+ x

₂³

y

₂

X

x

₁

x

₂

+ y

₁

y

₂

X

x

₁

y

₂

+ 2x

₂

y

₁

X

x

₁³

70 / 415

Beispiel

Skalarprodukt auf dem Vektorraum der auf [0, 1] definierten, reellwertigen stetigen Funktionen:

hf , g i = Z

1 0

f (x )g (x ) dx Positivit¨ at, Linearit¨ at, Symmetrie X

Verallgemeinerung mit einer positiven Gewichtsfunktion w : hf , g i

_w

=

1

Z

0

fg w

z.B: gewichtete Skalarprodukte f¨ ur radialsymmetrische Funktionen auf der Kreisscheibe oder Kugel:

Z

1 0

f (r)g (r)r dr, Z

1

0

f (r)g (r )r

²

dr

Komplexes Skalarprodukt

Ein Skalarprodukt h·, ·i auf einem komplexen Vektorraum V ist eine Abbildung

V × V 3 (u, v ) 7→ hu, v i ∈ C mit folgenden Eigenschaften:

Positivit¨ at: hv , v i > 0 f¨ ur v 6= 0 Schiefsymmetrie: hu, v i = hv , ui

Linearit¨ at: hu, sv + tw i = shu, v i + thu, w i

Diese Identit¨ aten gelten f¨ ur alle u , v , w ∈ V und s , t ∈ C .

Aufgrund der Schiefsymmetrie ist ein komplexes Skalarprodukt bez¨ uglich der ersten Variablen nicht linear:

hsu + tv , w i = ¯ shu , v i + ¯ thu, wi .

Lediglich f¨ ur reelle Skalare s , t ist die komplexe Konjugation ohne

Bedeutung.

(19)

F¨ ur V = C

ⁿ

ist das kanonische Skalarprodukt

hu, v i = u

^∗

v = ¯ u

^t

v = u ¯

₁

· · · u ¯

_n





 v

₁

.. . v

_n





 = ¯ u

₁

v

₁

+ · · · + ¯ u

_n

v

_n

, und

|u| = p

hu, ui = q

|u

₁

|

²

+ · · · + |u

_n

|

²

, |u

_k

|

²

= ¯ u

_k

u

_k

, ist die assoziierte Norm.

Gebr¨ auchlich ist auch die komplexe Konjugation des zweiten Arguments des Skalarprodukts,

hu, v i = X

k

u

_k

v ¯

_k

.

Diese andere Definition des Skalarprodukts komplexer Vektoren ist jedoch weniger konsistent mit den Regeln des Matrix/Vektor-Kalk¨ uls - den

” liegenden“ adjungierten Vektor u

^∗

erh¨ alt man durch Transposition und Konjugation des

” stehenden“ Vektors u.

73 / 415

Beispiel

Skalarprodukt von Vektoren in C

²

x =

1 + 2i

−2 − i

, y =

2 2i

komplexes Skalarprodukt hx , y i = ¯ x

₁

y

₁

+ ¯ x

₂

y

₂

(1 + 2i) · 2 + (−2 − i) · 2i = (1 − 2i) · 2 + (−2 + i) · 2i = 2 − 4i − 4i − 2 = −8i Das Konjugieren ist notwendig f¨ ur die Positivit¨ at der assoziierten Norm.

keine Konjugation falsche Definition der L¨ angen q

x

₁²

+ x

₂²

= q

(1 + 2i)

²

+ (−2 − i)

²

= √

1 + 4i − 4 + 4 + 4i − 1 = √ 8i 6∈ R q

y

₁²

+ y

₂²

= q

2

²

+ (2i)

²

= √

4 − 4 = 0 6> 0

74 / 415

richtige Berechnung

|x | = √

¯

x

₁

x

₁

+ ¯ x

₂

x

₂

= p

(1 + 4) + (4 + 1) = √ 10

|y | = p

2 · 2 + (2i) · (−2i) = √ 8

75 / 415

Cauchy-Schwarz-Ungleichung

Ein Skalarprodukt l¨ asst sich mit Hilfe der assoziierten Norm absch¨ atzen:

|hu, v i| ≤ |u||v |, |w| = p

hw , w i . Gleichheit gilt genau dann, wenn u k v .

F¨ ur ein reelles Skalarprodukt kann durch cos ϕ = hu, v i

|u| |v |

ein Winkel ϕ ∈ [0, π] zwischen u und v definiert werden.

76 / 415

(20)

Beweis

v = su Gleichheit

Die Ungleichung bleibt bei Multiplikation von u bzw. v mit einem Skalar unver¨ andert.

o.B.d.A. |u|

²

= |v |

²

= 1, u 6k v

betrachte ein komplexes Skalarprodukt (Argumentation schließt den reellen Fall ein)

hv , ui = r exp(iϕ)

| {z }

=:λ

, r > 0 , u , v nicht parallel, ¯ λλ = 1 = ⇒

0 < hu − λv , u − λv i

= |u|

²

+ ¯ λλ|v |

²

− λ ¯ r exp(iϕ)

| {z }

hv,ui

−λ r exp(iϕ)

| {z }

hu,vi

= 1 + 1 − r − r ,

d.h.

|hu, v i| = r < 1 = |u| |v | X

77 / 415

Beispiel

Illustration der Ungleichung von Cauchy-Schwarz f¨ ur das Skalarprodukt hf , g i =

Z

1 0

f (x )g (x ) dx f

_k

(x ) = x

^k

|f

_k

| = Z

1

0

(x

^k

)

²

dx

1/2

= (2k + 1)

^−1/2

hf

_k

, f

_`

i =

Z

1 0

x

^k

x

^`

dx = (k + ` + 1)

⁻¹

Ungleichung von Cauchy-Schwarz

(k + ` + 1)

⁻¹

= |hf

_k

, f

_`

i| ≤ |f

_k

||f

_`

| = (2k + 1)

^−1/2

(2` + 1)

^−1/2

X , denn Quadrieren und Kehrwertbildung

k

²

+ `

²

+ 1 + 2k` + 2k + 2` ≥ 4k` + 2k + 2` + 1 ⇐⇒ (k − `)

²

≥ 0

78 / 415

Norm

Eine Norm auf einem reellen oder komplexen Vektorraum V ist eine Abbildung

V 3 v 7→ kv k ∈ R mit den folgenden Eigenschaften.

Positivit¨ at:

kv k > 0 f¨ ur v 6= 0 Homogenit¨ at:

ksv k = |s |kv k Dreiecksungleichung:

ku + v k ≤ kuk + kv k

Diese Identit¨ aten gelten f¨ ur alle u, v ∈ V und s ∈ R bzw. s ∈ C .

Mit einem Skalarprodukt ist die Norm

|v | = p

hv , v i, v ∈ V

assoziiert. F¨ ur diese spezielle Norm werden oft einfache Betragsstriche verwendet. Insbesondere ist f¨ ur V = R

ⁿ

und V = C

ⁿ

|x | = q

|x

₁

|

²

+ · · · + |x

_n

|

²

. Mit Hilfe einer Norm kann durch

d (u, v ) = ku − v k

ein Abstand zwischen zwei Vektoren definiert werden.

(21)

Beweis

Uberpr¨ ¨ ufung der Normeigenschaften f¨ ur die einem Skalarprodukt zugeordnete Norm

Positivit¨ at und Homogenit¨ at X Die Dreiecksungleichung folgt aus

|u + v |

²

= hu + v , u + v i

= hu, ui + hu, v i + hu, v i

| {z }

∈R

+hv , v i

≤ |u|

²

+ 2|hu, v i| + |v |

²

≤

Cauchy-Schwarz

|u|

²

+ 2|u||v | + |v |

²

= (|u| + |v |)

²

durch Wurzelziehen.

81 / 415

Beispiel

Normen f¨ ur die Vektorr¨ aume R

ⁿ

und C

ⁿ

2-Norm oder Euklidische Norm

kz k

₂

= q

|z

₁

|

²

+ · · · + |z

_n

|

²

z.B.

k(2, −1, 2)

^t

k

₂

= √

4 + 1 + 4 = 9 Spezielle Notation f¨ ur die, dem kanonischen Skalarprodukt zugeordnete Norm: kz k

₂

= |z|

82 / 415

Maximum-Norm

kzk

_∞

= max

k

|z

_k

| z.B:

k(2 + 3i, 3 − 4i)

^t

k

∞

= max( p

2

²

+ 3

²

, p

3

²

+ 4

²

)

= max( √ 13, √

25) = 5 Verallgemeinerung: kzk

∞,w

= max

k

(w

_k

|z

_k

|) mit Gewichten w

_k

> 0 1-Norm

kz k

₁

=

n

X

k=1

|z

_k

| z.B.

k(1, −2, 3)

^t

k

₁

= |1| + | − 2| + |3| = 1 + 2 + 3 = 6

83 / 415

Orthogonale Basis

Eine Basis B = {u

₁

, . . . , u

_n

} eines Vektorraums V ist orthogonal, wenn hu

_j

, u

_k

i = 0, j 6= k .

Eine normierte orthogonale Basis, d.h. |u

_k

| = 1 ∀ k, wird als Orthonormalsystem oder Orthonormalbasis bezeichnet.

Die Elemente v des Vektorraums besitzen die Darstellung v =

n

X

k=1

c

_k

u

_k

, c

_k

= hu

_k

, v i

|u

_k

|

²

. F¨ ur die Koeffizienten c

_k

gilt

|c

₁

|

²

|u

₁

|

²

+ · · · + |c

_n

|

²

|u

_n

|

²

= |v |

²

.

Ist die Basis normiert, so fallen die Terme |u

_k

|

²

weg, d.h. es gelten die einfacheren Formeln

c

_k

= hu

_k

, v i, |c

₁

|

²

+ · · · + |c

_n

|

²

= |v |

²

.

84 / 415

(22)

F¨ ur einen komplexen Vektorraum ist die Reihenfolge der Argumente im Skalarprodukt von Bedeutung. Bei der Berechnung der Koeffizienten muss h·, ·i bez¨ uglich des Argumentes v linear sein.

85 / 415

Beweis

u

₁

, . . . , u

_n

Basis = ⇒ Existenz von Skalaren c

₁

, . . . , c

_n

mit v =

n

X

j=1

c

_j

u

_j

Skalarprodukt mit u

_k

, Orthogonalit¨ at der Basis (hu

_k

, u

_j

i = 0, j 6= k ) und Linearit¨ at

hu

_k

, v i = hu

_k

, c

_k

u

_k

i = c

_k

hu

_k

, u

_k

i bzw. c

_k

= hv , u

_k

i hu

_k

, u

_k

i Identit¨ at f¨ ur die Koeffizienten = b Verallgemeinerung des Satzes von Pythagoras

Beweis durch Ausmultiplizieren von

|v |

²

= hc

₁

u

₁

+ · · · + c

_n

u

_n

, c

₁

u

₁

+ · · · + c

_n

u

_n

i unter Ber¨ ucksichtigung von

hc

_j

u

_j

, c

_k

u

_k

i = 0, j 6= k

86 / 415

Beispiel

Darstellung des Vektors v = 8 4

t

bez¨ uglich der orthogonalen Basis u

₁

= 1 3

t

, u

₂

= −6 2

t

(i) Koeffizienten und Basisdarstellung:

c

₁

= hu

₁

, v i

hu

₁

, u

₁

i = 1 · 8 + 3 · 4 1

²

+ 3

²

= 20

10 = 2 c

₂

= hu

₂

, v i

hu

₂

, u

₂

i = −6 · 8 + 2 · 4

6

²

+ 2

²

= −40 40 = −1 Linearkombination v = c

₁

u

₁

+ c

₂

u

₂

8 4

= 2 1

3 − −6

2 (iii) Quadratsumme der Koeffizienten:

Uberpr¨ ¨ ufung der Identit¨ at c

₁²

|u

₁

|

²

+ c

₂²

|u

₂

|

²

= |v |

²

2

²

· 10 + (−1)

²

· 40 = 80 = 8

²

+ 4

²

= 80 X

Beispiel

Darstellung des Vektors v = −1 1 3

t

bez¨ uglich der orthonormalen Basis

u

₁

= 1

9 1 4 8

t

, u

₂

= 1

9 4 7 −4

t

, u

₃

= 1

9 8 −4 1

t

|u

₁

| = |u

₂

| = |u

₃

| = 1 Koeffizienten c

_k

= hu

_k

, v i, d.h.

v = hu

₁

, v iu

₁

+ hu

₂

, v iu

₂

+ hu

₁

, v iu

₃

= −1 · 1 + 4 · 1 + 8 · 3

9 u

₁

+ −4 + 7 − 12

9 u

₂

+ −9 9 u

₂

= 3



 1/9 4/9 8/9



 −



 4/9 7/9

−4/9



 −



 8/9

−4/9 1/9



 Kontrolle der Quadratsumme der Koeffizienten:

|3|

²

+ | − 1|

²

+ | − 1|

^{2 !}

= |v |

²

= (−1)

²

+ 1

²

+ 3

²

X

(23)

Beispiel

Darstellung w = su + tv des Vektors w = 2 + 3i 1

t

bez¨ uglich der orthogonalen Basis

u = 1 i

, v = i 1

Uberpr¨ ¨ ufung der Orthogonalit¨ at der Basisvektoren

hu, v i = 1 · i + i · 1 = 1 · i + (−i) · 1 = 0 X Norm der Basisvektoren

|u|

²

= hu, u i = u

₁

u

₁

+ u

₂

u

₂

= 1 · 1 + (−i) · i = 2, |v |

²

= 2 Koeffizienten

s = hu, wi

hu, u i = 1 · (2 + 3i) + i · 1 2

= 1 · (2 + 3i) + (−i) · 1

2 = 2 + 3i − i

2 = 1 + i t = (−i) · (2 + 3i) + 1 · 1

2 = 2 − i

89 / 415

Basisdarstellung 2 + 3i

1 = (1 + i) 1

i

+ (2 − i) i

1

90 / 415

Orthogonale Projektion Die orthogonale Projektion

V 3 v 7→ P

_U

(v ) ∈ U

auf einen Unterraum U eines Vektorraums V ist durch die Orthogonalit¨ atsbedingung

hu, v − P

_U

(v )i = 0, ∀u ∈ U charakterisiert.

Ist {u

₁

, . . . , u

_m

} eine orthogonale Basis von U, so besitzt P

_U

die Darstellung

P

_U

(v ) =

m

X

k=1

hu

_k

, v i hu

_k

, u

_k

i u

_k

.

91 / 415

Insbesondere gilt f¨ ur V = R

ⁿ

P

_U

v =

m

X

k=1

|u

_k

|

⁻²

u

_k

(u

_k^t

v ) mit der Projektionsmatrix P

k

|u

_k

|

⁻²

u

_k

u

_k^t

. F¨ ur v = C

ⁿ

ist der

transponierte Vektor u

^t

durch den adjungierten Vektor u

^∗

(Transposition und komplexe Konjugation) zu ersetzen.

92 / 415