ÄHNLICHE DOKUMENTE
F¨ ur Fermionen gilt das Pauli-Prinzip: zwei Fer- mionen k¨ onnen nicht den gleichen Quantenzustand einnehmen, sondern m¨ ussen sich wenigstens in einer Quantenzahl unterscheiden
Gleichzeitig gehen die Gleichungen ¨ uber diese Ph¨anomene hinaus: wir erwarten, dass sie Allge- meing¨ ultigkeit besitzen und damit auch neue Ph¨anomene enthalten, die noch
Aufgabe 3: Linearer Stark-Effekt (8 Punkte) Der Stark-Effekt ist das Analogon zum Zeeman-Effekt und beschreibt die Aufspaltung der Spektrallinien in einem statischen, elektrischen
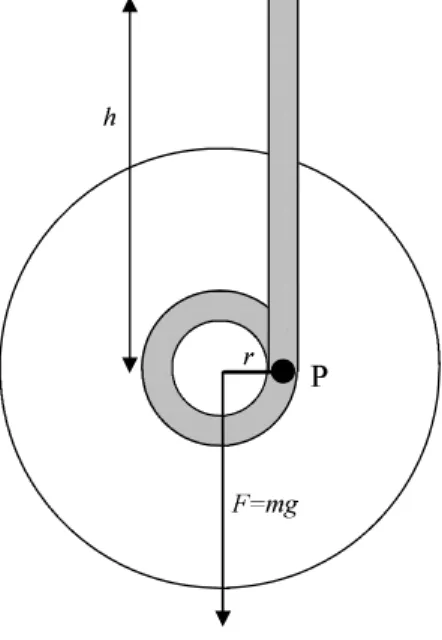
Durch die Impulsübertragung wird die Pendelmasse angehoben, bis sich die kinetische Energie des Pendels vollständig in potentielle Energie umgewandelt
Wenn das Potential eines Feldes nur vom Ort abhängt, so ist die auf einem geschlossenen Weg verrichtete Arbeit Null.. In diesem Fall kann das Kraftfeld auch eindeutig aus
1.)Gase bestehen aus Molekülen, die sich ungeordnet und kontinuierlich bewegen 2.)Die Größe des Moleküls ist vernachlässigbar.. 3.)Moleküle wechselwirken nur über
Schreiben Sie die Maxwell-Gleichungen in Differentialform auf. Leiten Sie für den Fall linearer, isotroper und homogener Medien die Poisson-Gleichung für elektrostatische
F¨ ur eine vorgegebene Ladungsverteilung kann aus der Poissongleichung im Prinzip das Potential und uber dessen Gradienten sogleich das elektrische Feld berechnet werden.. 3 F¨ ur