2.3 Die Maxwell-Gleichungen

18 KAPITEL 2. GRUNDBEGRIFFE UND GRUNDGLEICHUNGEN DER ELEKTRODYNAMIK

2.2.1 Satz von Stokes und Rotation eines Vektorfelds

Wir berachten das Linienintegral eines Vektorfeldes l¨angs einer Kurveγ:

Z

γ

F(r)dr= lim

∆r_i→∞

N→∞

X

i

F(r) ∆ri. (2.24)

Dieses ist also abh¨angig von F undγ. Man bezeichnet das obige Integral auch als vektorielles Kurvenintegral oder Kurvenintegral zweiter Art. Betrachtet man den Spezialfall einergeschlossenen Konturγ, so gilt der

Satz von Stokes:

I

γ(A)

F(r)dr= Z

A

rotF(r)df (2.25)

Man beachte, dass das Resultat ein Skalar ist. Links und rechts liegt also jeweils ein Skalarproduckt zweier Vektoren vor. Man intepretiert die linke Seite als dieWirbelst¨arke (oderZirkulation) des VektorfeldesFin der von γ eingeschlossenen Fl¨acheA. Der Ausdruck auf der rechten Seite enth¨alt die Wirbeldichte, also die lokale Wirbelst¨arke pro Fl¨ache. Sie ist gegeben durch die Rotation des Vektorfeldes, s.u.

Ubungsaufgabe:¨ Man beweise den Satz von Stokes⁸.

Definition der Rotation: Betrachten wir noch einmal den Differentialoperator Rotation genauer. Wir defi- nieren⁹:

rotF(r) : =∇ ×F (2.26)

= ˆex(∂yFz−∂zFy) +... (2.27)

=X

i

ǫijk(∂xjFk−∂xkFj) (2.28) Hierbei istǫijk der antisymmetrische (oder “Levi-Civita”-) Tensor.

ǫijk=







1, i < j < k

0, i=j oderi=koderj=k

−1, i < k < j

2.2.2 Skalares Potential und Gradient

Betrachte den Spezialfall eines wirbelfreien VektorfeldesF(r) mit rotF= 0−→

I

γ

Fdr= 0. (2.29)

W¨ahlen wir auf der Kontur zwei beliebige Punkte, A, B, so l¨asst sich γ aus dem Wegγ1 =A →B und dem restlichen Weg−γ2=B→Azusammensetzen. Daraus folgt sofort

Z

γ1

Fdr= Z

γ2

Fdr= Z B

A

Fdr, (2.30)

das heißt, das Integral ist – bei fixiertem Anfangs- und Endpunkt – wegunabh¨angig. Diese Situation ist die- selbe wie beim Gravitationsfeld. Auch hier ist das Resultat der Integration der Graviationskraft von einem Anfangspunkt (Anfangsh¨ohe) bis Endpunkt (Endh¨ohe) unabh¨angig vom Weg und nicht anderes als die damit

8Die L¨osung findet sich in Abschnitt 6.2.3.

9Hier haben wir einen Unterstrich unter∇gesetzt, um den Vektorcharakter der Operation zu verdeutlichen. Man beachte, dass dies in vielen Texten nicht einheitlich erfolgt. Ob das Resultat von∇ein Skalar ist (wie bei der Divergenz) oder ein Vektor (wie beim Gradienten oder Rotor), ergibt sich aber immer aus dem Zusammenhang.

verbundene potentielle Energie- ¨Anderung (eine skalare Gr¨oße), ∆U =U(B)−U(A). Betrachtet man nun unse- ren allgemeinen Fall und l¨asst einen beliebigen Endpunkt der Integration zu, so folgt die Definition des skalaren PotentialsU(r) und der Zusammenhang mit dem Vektorfeld F zu

− Z r

r0

dr F(r)≡U(r), (2.31)

F(r) =−gradU(r). (2.32)

Dabei wurde die Umkehr-Operation zum unbestimmten Integral mit “Gradient” (grad) bezeichnet. Aus der Gleichung ist evident, dass der Gradient ein Vektor ist, der in kartesischen Koordinaten gegeben ist durch

gradU(r)≡ ∇U(r) = X3

i=1

e_i ∂U

∂xi

= ∂U

∂x,∂U

∂y,∂U

∂z

, (2.33)

wobei der letzte Ausdruck die Darstellung durch kartesische Koordinaten enth¨alt. Analog l¨asst sich der Gradient in beliebige andere Koordinatensysteme transformieren. Wir werden sp¨ater noch die F¨alle von Polar-, Zylinder- und Kugelkoordinaten kennenlernen.

Es gilt folgender Satz:

Satz:Der VektorF(r) steht senkrecht auf der durchrverlaufendenAquipotentialfl¨¨ ache. Hierbei ist die ¨Aquipoten- tialfl¨ache ( ¨AF) definiert als Oberfl¨ache, in derU(r)≡const =U0gilt.

Beweis:

Wir betrachten einen beliebigen infinitesimal kleinen aber endlichen Vektor,δr, der in der ¨AF liegt. Dann gilt U(r) =U(r+δr)≡U0.

Dann muss die Differenz der Potential-Werte verschwinden:

0 =U(r+δr)−U(r)≈ ∂U(r)

∂r ·δr. (2.34)

Der letzte Ausdruck ist das Skalarprodukt zweier Vektoren. Da die Betr¨age sowohl des ersten Faktors (gradU) als auch von δr im allgemeinen ungleich Null sind, ist diese Gleichung nur zu erf¨ullen, wenn beide Vektoren senkrecht aufeinander stehen. Daraus folgt, dass F=−gradU senkrecht auf δr, und damit senkrecht auf der Aquipotentialfl¨ache steht.¨

Aus diesem Satz folgt die wichtige Eigenschaft, dass der Vektor gradU parallel ist zur Richtung der st¨arksten Anderung von¨ U.

2.2.3 Wichtige Eigenschaften der Vektoranalysisoperatoren

Es gelten folgende Relationen, die wir als Behauptungen formulieren¹⁰. Hierbei seien im Folgenden U(r) ein Skalarfeld undF(r) ein Vektorfeld desR³.

1. Behauptung:

div gradU(r) = ∆U(r). (2.35)

Hierbei ist ∆ =∂_x²+∂_y²+∂²_z der sogenannte Laplace-Operator.

2. Behauptung:

grad divF(r)−∆F = rot rotF . (2.36)

3. Behauptung: F¨ur eine beliebiges FeldF(r) gilt

div rotF = 0. (2.37)

10Die Beweise finden sich im Abschnitt 6.2.4.

20 KAPITEL 2. GRUNDBEGRIFFE UND GRUNDGLEICHUNGEN DER ELEKTRODYNAMIK 4. Behauptung: F¨ur ein beliebiges skalares Feldρ(r) existiert eine eindeutige L¨osung derPoissongleichung:

∆U=ρ(r). (2.38)

Die Eindeutigkeit der L¨osung ist f¨ur folgende Randbedingungen gegeben¹¹: das Feld und seine ersten Ableitun- gen verschwinden im Unendlichen¹², d.h. lim

|r|→∞U(r) = 0 und lim

|r|→∞∂riU(r), miti= 1, ...,3. Der Beweis folgt in Kapitel 3.1.2.

Die Poissongleichung (2.38) kann auch auf ein Vektorfeld verallgemeinert werden. Mit der Ersetzung U → F undρ→j, folgt ∆



 F1

F2

F3



=





1

j2

j3



, d.h. der Laplace-Operator wirkt simultan auf jede Komponente des Feldes.

Aufgabe:Man beweise Behauptungen 1.–3.

2.2.4 Fundamentalsatz der Vektoranalysis

Satz: Alle Vektorfelder F(r), mit lim

|r|→∞F(r) = 0 und lim

|r|→∞∂riF(r) = 0, mit i = 1, ...,3, lassen sich eindeutig darstellen alsSumme eines quellenfreien und eines wirbelfreien Beitrages:

F(r) =F_q(r) +F_w(r), (2.39)

mit divF_q = 0 und rotF_w= 0. Dies kann man auch umformulieren zu:

divF(r) = divF_w(r)≡QF(r). QF sind die Quellen vonF (pro Volumen, also die Quelldichte).

rotF(r) = rotF_q(r) =W_F(r). W_F sind die Wirbel vonF (pro Fl¨ache, also die Wirbeldichte).

Beweis des Fundamentalsatzes Der Beweis erfolgt in drei Schritten:

1. Zun¨achst konstruieren wir den quellenfreien AnteilF_q aus einem bekanntenF. Betrachte eine Formulie- rung in obigem Satz und wende auf beide Seiten die Rotation an:

rotF= rotF_q

rot rotF = rot rotF_q= grad(divF_q

| {z }

=0

)−∆F_q,

Also erh¨alt man wegen (2.36) eine Bestimmungsgleichung des quellenfreien Anteils F_q zu:

rot rotF =−∆F_q.

Dies ist die Poissongleichung (2.38), die eine eindeutige L¨osung f¨ur Fq besitzt (siehe Behauptung 4 des vorigen Abschnitts).

2. Jetzt konstruieren wir die Bestimmungsgleichung des wirbelfreien Anteils F_w des gegebenen Feldes F.

Auf die zweite Formulierung des Satzes

divF = divF_w wird der Gradient angewendet:

grad divF = grad divF_w= rot rotF_w

| {z }

=0

+∆F_w,

11Das ist eine hinreichende Bedingung.

12Die Beweisidee ist die Folgende: Die Poisson-Gleichung ist eine Differentialgleichung zweiter Ordnung und erfordert die Angabe von zwei Randbedingungen. Die Asympotenbedingungen f¨ur die L¨osung und ihre erste Ableitung erf¨ullen diese Rolle.

wobei wieder Gleichung (2.36) verwendet wurde, so dass folgende Bestimmungsgleichung gilt:

grad divF = ∆F_w

Auch dies ist wieder eine Poissongleichung f¨ur die Funktion Fw, die also ebenfalls eindeutig bestimmt werden kann.

3. Also ist auch die Summe ∆F = ∆(F_w+F_q) nach vorigem Abschnitt eindeutig l¨osbar. Als Fazit kann man also feststellen, dass ein allgemeines Vektorfeld eindeutig durch seine Quellen und Wirbel bestimmt ist. Das bedeutet: aus gegebenen QF und W_F lassen sich∇ ·F und∇ ×F bestimmen und daraus das GesamtfeldF(r) rekonstruieren.

Obiges Ergebnis gilt f¨ur ein beliebiges VektorfeldF. In der Elektrodynamik gibt es nun zwei relevante Felder (E, B), und es interessieren uns die Bewegungsgleichungen dieser Felder. Die Form der Bewegungsgleichungen ist damit durch den Fundamentalsatz bereits festgelegt. Wir ben¨otigen also lediglich noch die Kenntnis dee Quellen und Wirbel vonE undB:

QE, QB, W_E, W_B.

Dem widmen wir uns im n¨achsten Abschnitt. Das Resultat werden die Maxwell-Gleichungen sein.

2.3 Die Maxwell-Gleichungen

Die Maxwellgleichungen basieren auf der Gesamtheit der experimentellen Beobachtungen zu Ph¨anomenen aus der Elektrizit¨atslehre und Magnetismus. F¨ur jedes Einzelph¨anomen sind sie ableitbar und experimentell

¨uberpr¨ufbar¹³. Gleichzeitig gehen die Gleichungen ¨uber diese Ph¨anomene hinaus: wir erwarten, dass sie Allge- meing¨ultigkeit besitzen und damit auch neue Ph¨anomene enthalten, die noch nicht beobachtet wurden. Ein Bei- spiel f¨ur ein solches Ph¨anomen, das aus den Maxwell-Gleichungen vorhergesagt wurde, sind elektromagnetische Wellen. Sie wurden tats¨achlich erst auf Grund der Vorhersage experimentell gefunden. Die Allgemeing¨ultigkeit der Maxwell-Gleichungen ist ein Postulat, das auch k¨unftig an einzelnen Beobachtungen immer aufs Neue ge- testet werden muss¹⁴.

2.3.1 Allgemeine differentielle und integrale Form der Maxwell-Gleichungen

Um die FelderE und B zu bestimmen, gibt der Fundamentalsatz eine klare Vorschrift: es sind folgende Glei- chungen zu l¨osen, welche die allgemeinste Struktur der Feldgleichungen f¨ur E(r) undB(r) darstellen:

divE=QE divB=QB, (2.40)

rotE=W_E rotB=W_B, (2.41)

wobei die rechten Seiten die Quellen und Wirbel der Felder enthalten, die es zu bestimmen gilt. Dies ist die differentielle Form der Maxwell-Gleichungen: die Gleichungen gelten lokal, an jedem Raumpunktr. Alternativ kann man sie umformulieren, indem diese Relationen auf ein endliches Volumenelement (im Fall der Quell- Terme) oder Fl¨achenelement (im Fall der Wirbel) ausgedehnt werden. Dazu wenden wir den Gaußschen Satz bzw. den Stokesschen Satz an:

I

∆F(∆V)

E(r)df= Z

∆V

QE(r)d³r ,

I

∆F(∆V)

B(r)df =

Z

∆V

QB(r)d³r , (2.42) I

γ(∆A)

E(r)dl= Z

∆A

W_E(r)df,

I

γ(∆A)

B(r)dl = Z

∆A

W_B(r)df. (2.43)

Dies ist die sogenannteIntegralform der Maxwellgleichungen, wobei ∆F(∆V) die geschlossene Oberfl¨ache be- zeichnet, die das Volumen ∆V begrenzt. Analog bezeichnet γ(∆A) die geschlossene Linie, die die Fl¨ache ∆A einschließt. Die linken Seiten enthalten wichtige Eigenschaften der Felder: den Fluss durch eine geschlossene Fl¨ache ∆F (d.h. die Quellst¨arke) bzw. die Zirkulation entlang der geschlossenen Konturγ (Wirbelst¨arke).

Im folgenden Abschnitt bestimmen wir die noch offenen Ausdr¨ucke auf den rechten Seiten dieser Gleichungen, aus der Erfahrung mit elektrischen und magnetischen Prozessen (Experimenten), die wir so weit wie m¨oglich verallgemeinern.

Bevor wir uns mit der Ableitung der Maxwell-Gleichungen besch¨aftigen, besprechen wir noch kurz die Einhei- tensysteme der Elektrodynamik.

13Die Situation ist analog zu den Newtonschen Gleichungen der Mechanik

14Ein einziger Gegenbeweis w¨urde gen¨ugen, um die Maxwell-Gleichungen zu widerlegen. Damit ist die Falsifizierbarkeit der Theorie gew¨ahrleistet.

22 KAPITEL 2. GRUNDBEGRIFFE UND GRUNDGLEICHUNGEN DER ELEKTRODYNAMIK

2.3.2 Kr¨ afte und Einheitensysteme der Elektrodynamik

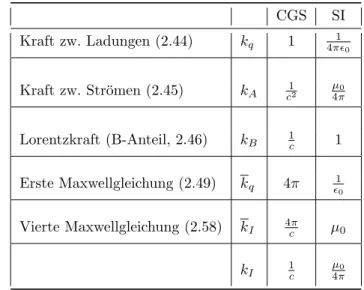
Ausgangspunkt f¨ur die Einf¨uhrung der FelderEundBwaren die Kr¨afte zwischen Ladungen und Str¨omen. Aus der Erfahrung kennen wir drei Kr¨afte:

1. Kraft zwischen Ladungen: das ist die Coulombkraft, deren Betrag von der Form ist FC =kq

Q1Q2

r² . (2.44)

2. Kraft zwischen Str¨omen: das ist das Amperegesetz, das von der Form ist dFA

dl ∼kA

I1I2

d , (2.45)

wobei hier, wegen der Ausdehnung der Dr¨ahte, die Kraft pro L¨angenelementdldes Drahtes angegeben ist unddden Abstand bezeichnet. Die angegebene Formel trifft nur bei geradlinigen und parallelen Dr¨ahten zu (d ist ihr Abstand), im allgemeinen ist die Kraft erheblich komplizierter, wie wir im Kapitel zur Magnetostatik sehen werden. Aus Dimensionsgr¨unden ist klar, dass das Verh¨altnis der beiden Konstanten, kq/kAdie Dimensionm²/s² haben muss, s. Tabelle 2.1.

3. Magnetische Kraft auf eine Ladung: das ist die Lorentz-Kraft (ihr magnetischer Anteil), die von der Form ist

F_LB =kBQ·v×B. (2.46)

Hier haben wir jeweils einen universellen Koeffizienten eingef¨uhrt, der die St¨arke der Kraft bestimmt und der experimentell bestimmt wurde.

Die folgende Tabelle erlaubt uns, zwischen dem CGS- und dem SI-System zu wechseln. F¨ur theoretische Be- trachtungen eignet sich das CGS System besser, weil es der physikalischen ¨Aquivalenz von elektrischem und magnetischem Feld Rechnung tr¨agt und damit eine erh¨ohte Symmetrie vieler Gleichungen liefert. F¨ur die Er- mittlung von Zahlen-Werten ist das SI System intuitiver. Die Einheiten im CGS-System werden in der Literatur nur noch selten verwendet, und wir werden sie nicht benutzen¹⁵. Eine ¨Ubersicht ist in Tabelle 2.2 gegeben.

CGS SI

Kraft zw. Ladungen (2.44) kq 1 _4πǫ¹₀ Kraft zw. Str¨omen (2.45) kA 1

c² µ0

4π

Lorentzkraft (B-Anteil, 2.46) kB 1

c 1

Erste Maxwellgleichung (2.49) kq 4π _ǫ¹₀ Vierte Maxwellgleichung (2.58) kI 4π

c µ0

kI 1 c

µ0

4π

Tabelle 2.1: CGS- und SI-Wert der Konstanten in den verschiedenen Kr¨aften und in den Maxwellgleichungen.

Die hier vorkommenden Konstanten sind die elektrische Feldkonstante (Dielektrizit¨atskonstante des Vakuums) ǫ0= 8.85·10⁻¹² A·s

V ·m die magnetische Feldkonstante (Magnetische Permeabilit¨at des Vakuums)

µ0= 1.26·10⁻⁶ N A²

15Eine Ausnahme stellt die Einheit der Magnetfeldst¨arke dar, f¨ur die beider Varianten verbreitet sind.

und die Lichtgeschwindigkeit

c= 1

√ǫ0µ0

= 299.792.458m s.

Gr¨oße Symbol SI-Einheit Gaußsche Einheit

Ladung q 1 Coulomb (C) 3·10⁹stat Coul

Strom I 1 Ampere (A) 3·10⁹ stat Amp

Spannung U 1 Volt (V) 1/3·10⁻² stat Volt

Elektrische Feldst¨arke E 1^V_m 1/3·10⁻⁴ stat Volt/cm Elektrische Verschiebung D 1^A·s_m² 4π·3·10³stat Volt/cm Magnetische Feldst¨arke H 1^A_m 4π·10⁻³ Oersted (Oe) Magnetische Induktion B 1^V_m^·s2 = 1Tesla (T) 10⁴ Gauß (G) Magnetischer Fluß Φ 1 Weber (W b) 10⁸ Maxwell (M x)

Widerstand R 1 Ohm (Ω) 1/9·10⁻¹¹s/cm

Kapazit¨at C 1 Farad (F) 9·10¹¹ cm

Induktivit¨at L 1 Henry (H) 1/9·10⁻¹¹s²/cm

Tabelle 2.2: Gauß- und SI-Einheiten f¨ur die wichtigsten Gr¨oßen, s. auch Ref. [Gre08]

Befinden sich die Felder in einem Medium, so f¨uhrt das zu einer Modifikation der Felder. In erster N¨aherung kann dies durch eine Ersetzung der Dielektrizit¨ats- und Permeabilit¨atskonstanten ber¨ucksichtigt werden:

ǫ0→ǫ0·ǫr, µ0→µ0·µr,

wobei ǫr undµr die (dimensionslose) relative Dielektrizit¨ats (Permeabilit¨ats)-Konstnate ist, die vom Medium abh¨angt. Tats¨achlich handelt es sich nicht um konstante Gr¨oßen, sondern Eigenschaften die von vielen Para- metern abh¨angen, zum Beispiel von der Frequenz und Wellenl¨ange des Feldes, von der Temperatur und Dichte des Mediums usf. Diese Eigenschaften sind experimentell und theoretisch bestimmbar, was Gegenstand des jeweiligen Teilgebietes der Physik ist.

2.3.3 Die Quellen des E-Feldes (Coulomb-Gesetz)

Die Erfahrung (bzw. das Experiment) legt nahe, als Ursache des Quellenanteils des Feldes elektrische Ladungen zu betrachten. Aus der Coulomb-Kraftwirkung zwischen zwei geladenen Teilchen q und Q hatten wir bereits das elektrische Feld eingef¨uhrt, die Konstante aus dem einf¨uhrenden Abschnitt heißt hierkq:

F =kq

Qq r² r

r =E(r)

| {z }

von Q

q,

wobeirder Verbindungsvektor der Teilchen ist. Die Kraft kann anziehend oder abstoßend sein. Außerdem folgt die radialsymmetrische Feldverteilung einer Punktladung beir= 0:

E(r) =kq

Q r² r r

Q

q r

Abbildung 2.8: Das elektrische Feld einer Punktladung Q beir= 0 erzeugt eine Kraftwirkung auf eine zweite Ladungqentlang der Verbindungslinie. Genauso ist das elektrische Feld orientiert: isotrop, von der Ladung Q ausgehend (beiQ >0).

24 KAPITEL 2. GRUNDBEGRIFFE UND GRUNDGLEICHUNGEN DER ELEKTRODYNAMIK Damit haben wir das elektrische Feld f¨ur den Spezialfall einer einzelnen Punktladung gefunden. Jetzt verallge- meinern wir dieses Ergebnis schrittweise. Entsprechend der Struktur der Maxwell-Gleichungen, besteht unser erstes Ziel in der Berechnung von divE, die wir ¨uber den Gaußschen Satz bestimmen k¨onnen.

1. Wir betrachten den Fluss desE-Feldes, ΦE, durch eine Fl¨achedf. Betrachte hierzu zun¨achst eine Kugel um Q. Es gilt dann:

dV =dr r²sin(θ)dθdϕ

| {z }

dΩ

| {z }

df

Das FeldEist radial gerichtet. Betrachtet man also ein Fl¨achenelementdf, so ist der Fl¨achennormalenvektor ein radialer und es gilt:df =df^r_r. Also gilt f¨ur den FlussdΦE durch ein Fl¨achenelementdf:

dΦE =E df =kq

Q r² r rr²dΩr

r dΦE =kqQdΩ dΦE

dΩ =kqQ

Dieses Ergebnis ist deshalb bemerkenswert, weil es nur von der Ladung abh¨angt und nicht vonroder von einem Winkel. Der Fluss durch die gesamte Kugel ergibt sich folgendermaßen:

ΦE= I

F(V) R=const.

E df =E4πr²=kqQ4π=kqQ (2.47)

Abbildung 2.9: Zur Definition des Raumwinkel- und Fl¨achenelements bei der Berechnung des elektrischen Flusses einer PunktladungQ.

2. Wir verallgemeinern dieses Ergebnis nun auf beliebige Oberfl¨achen. Betrachte hierzu folgendes Volumen V, welches durch die beiden Fl¨achenKundF (eine beliebige Fl¨ache) begrenzt wird.

Abbildung 2.10: VolumenV, das von den Ober߬achenF undKbegrenzt wird.

Hierbei sind die Fl¨achennormalenvektoren f¨ur F definiert zu:

E◦n_F >0

und f¨urKdefiniert zu:

E◦n_K <0

Die Gesamtoberfl¨acheO istO=F∪K. Der Gesamtfluss durchO ergibt sich zu:

ΦE|O = I

O

Edf= I

F

Edf− I

K

Edf= Z

V(O)

divEdV,

wobei die letzte Gleichung aus dem Gaußschen Satz folgt. Wir betrachten nun den Integranden:

divE=kqQ∇r r³

=kqQ 1

r³∇r+r∇ 1 r³

=kqQ 3

r³ − 3 r³

= 0 Hierbei wurde benutzt:

divr= ∂

∂x(x) + ∂

∂y(y) + ∂

∂z(z) = 3 und

grad 1

r³ =−3r r⁴

r

r =−3r² r⁵ Hieraus folgt also insgesamt:

ΦE|O= 0

Da dieses Resultat f¨ur ein beliebiges VolumenV gilt, ziehen wir das Fazit:

Der Fluss vonE durch eine geschlossene Oberfl¨ache h¨angt nur von der eingeschlossenen Ladung ab.

3. Verallgemeinert man dieses Ergebnis auf N Punktladungen, die von einer Ober߬ache F eingeschlossen sind, so gilt:

I

F

Edf=kq

XN

i=1

Qi=kqQ^Ges.

4. Wir gehen jetzt ¨uber zu einer lokalen Betrachtung. Sei wiederum eine LadungQbei r = 0 gegeben. Sei K(R) eine Kugeloberfl¨ache mit Radius Rum die Ladung. Es gilt dann wie oben gezeigt:

kqQ= Z

V(K)

divEdV

Hier wurde mit Gleichung (2.47) und dem Satz von Gauss argumentiert. Dieses Resultat ist unabh¨angig von R. Das heißt bei dV →0 muss divE → ∞ gelten, damit das konstante Ergebnis links reproduziert wird. Also muss divE von der Form einer Deltafunktion sein, da gilt:

Z

δ(r)dV = 1 Die L¨osung ist gegeben durch:

divE=kqQδ(r). Dieses verallgemeinern wir aufN Ladungen an den Ortenr_i:

divE(r) =kq

XN

i=1

Qiδ(r−r_i)

| {z }

ρ(r) ist die Ladungsdichte f¨ur N Punktladungen

5. Der letzte Schritt besteht in der Verallgemeinert auf eine beliebige (auch r¨aumlich ausgedehnte) Ladungs- dichteρ(r), d.h.P

iQiδ(r−ri)→R

d³rρ(r)

Mit all diesen Verallgemeinerungen (jede ist eine Hypothese, die experimentell ¨uberpr¨uft werden muss), erhalten wir die