(a) Die Menge der rationalen Zahlen Q ;

Lineare Algebra Winter Semester 2007-2008 Ubungsblatt 1: Zu l¨ ¨ osen bis 10. Oktober

(1) Bestimmen Sie ob die folgenden Mengen mit der ¨ ublichen Multiplkation und Addition Vektorr¨ aume ¨ uber R sind:

(a) Die Menge der rationalen Zahlen Q ;

(b) Die einpunktige Menge



 



 









 0 0 0 0











 



 



⊆ R

⁴

;

(c) Die Menge aller zweidimensionalen Spaltenvektoren mit ganzzahligen Koordinaten;

(d) Die Menge P

3

der Polynome mit Grad h¨ochstens drei:

P

3

=

a

0

+ a

1

x + a

2

x

²

+ a

3

x

³

| a

0

, a

1

, a

2

, a

3

∈ R .

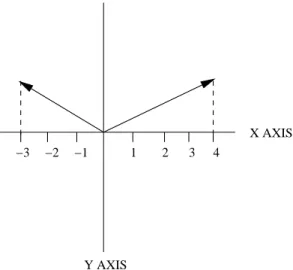
(2) Finden Sie die Summe der zwei Vektoren (Figur 1) mit dem Verfahren:

(a) Spitze zu Schaft;

(b) Parallelogramregel;

(c) Addition der Komponenten;

(3) Gegeben sind zwei Vectoren a, b in R

²

. Finden Sie reelle Skalare λ und µ so dass:

(−3)(0.5a − 0.2b) + (4a + 0.5b) = λa + µb.

(4) Zeigen Sie, dass sich zwei nicht parallele Geraden im R

²

in genau einem Punkt schneiden.

X AXIS

Y AXIS

1 2 3 4

−1

−2

−3

Figure 1. Vektoren for problem II-1

1

1. Bestimmen Sie, ob die Vektoren u =







1

−2 5





 , v =







2 3 1





 und w =







3 8

−3





 linear abh¨angig oder linear unabh¨angig sind. Wie verh¨alt es sich, wenn man nur je zwei Vektoren betrachtet, d.h. u , v oder u , w oder v , w ?

2. Es sind folgende Abbildungen f i : R ³ → R ⁿ

ⁱ

(1 ≤ i ≤ 5) gegeben:

(a) n 1 = 2, f 1 :







x y z





 7→





y 2 z 1+ x

²





(b) n 2 = 1, f 2 :







x y z





 7→ x − y + z + 1

(c) n 3 = 3, f 3 :







x y z





 7→











2x + ^y ₂ + z

−x − ^2z ₃ x − y + z











(d) n 4 = 2, f 4 :







x y z





 7→ y z x

!

(e) n 5 = 3, f 5 :







x y z





 7→







x − y − 1 y − z + 2 z − x − 1







Bestimmen Sie, welche f _i lineare Abbildungen sind.

3. Gegeben sind die folgenden Abbildungen g i (1 ≤ i ≤ 3). Zeigen Sie, dass die g i lin- eare Abbildungen sind und finden Sie zu jedem g _i eine Matrix A _i , die g _i repr¨asentiert.

Ist A i durch g i eindeutig bestimmt?

(a) g 1 : R ² → R ² , ξ 1

ξ 2

!

7→ ξ 2 − ξ 1

2 ξ 1

!

(b) g 2 : R ³ → R ⁴ ,







ξ 1

ξ 2

ξ 3





 7→











ξ 1 − ξ 3 + 3ξ 2

0 ξ 4 + ξ 3

ξ 1 + ξ 2 + ξ 3 − ξ 4











(c) g 3 : R ² → R ² , ξ 1

ξ 2

!

7→ v 1

v 2

!

, wobei v 1

v 2

!

L¨osung des Gleichungssystems v 1 − 2 v 2 = ξ 1

−2v 1 + 3v 2 = ξ 2

ist.

4. (Schriftlich) Zeigen Sie: F¨ ur alle λ ∈ R sind die beiden Vektoren







1 λ λ





 und







λ λ

−1







linear unabh¨angig.

5. Stellen Sie den Vektor







1 1 1





 als Linearkombination der drei Vektoren







−2 7 1





 ,







2

−1 1







und







2 5 3





 dar. Finden Sie ferner einen Vektor im R ³ , der sich nicht als Linearkom- bination dieser drei Vektoren schreiben l¨aßt.

6. Zeigen Sie, dass drei Vektoren im R ² immer linear abh¨angig sind.

1. (a) Berechnen Sie Real- und Imagin¨arteil folgender komplexen Zahlen:

(2 − 8i) + (5 + 4i) ; (2 − 8i) − (5 + 4i) ; (2 − 8i) · (5 + 4i) ; 2 − 8i 5 + 4i (b) Ein Argand Diagramm ist die graphische Darstellung von komplexen Zahlen

als Punkte in der komplexen Ebene, wobei auf der x -Achse (= reelle Achse) der Realteil und auf der y-Achse (= imagin¨are Achse) der Imagin¨arteil einer komplexen Zahl aufgetragen wird.

Zeichnen Sie 1 + 3i, 2 − 2i, − 4 + i, − 2 − 2i in ein Argand Diagramm ein, und berechnen Sie die Betr¨age dieser komplexen Zahlen.

2. Bestimmen Sie alle komplexen Zahlen α = ℜ(α) + iℑ(α) die die Gleichung α ² = −5 − 12i

erf¨ ullen.

Bestimmen Sie weiters die L¨osungen der quadratische Gleichung z ² − (4 + i) z + (5 + 5i) = 0.

3. Bestimmen Sie das Bild des Punktes z = 2 + it , t ∈ R unter den folgenden Trans- formationen:

• z 7→ iz,

• z 7→ z ² ,

• z 7→ e ^z ,

• z 7→ 1 /z .

4. Zeigen Sie:

(a) Wenn eine Menge S = {0} nur den Nullvektor enth¨alt, dann ist S linear abh¨angig.

(b) Jede Menge von Vektoren, die den Nullvektor enth¨alt, ist linear abh¨angig.

(c) Ist A m × n eine Matrix so dass ^{P n} _j=1 a ij = 0 f¨ ur alle i = 1, 2, . . . , m gilt (also jede Zeilesumme 0 ergibt), dann sind die Spalten von A linear abh¨angig.

(d) Jede Teilmenge einer linear unabh¨angigen Menge von Vektoren ist linear un- abh¨angig.

(e) Jede Obermenge einer linear abh¨angigen Menge von Vektoren ist linear abh¨angig.

5. Bestimmen Sie alle L¨osungen der folgenden Systeme linearer Gleichungen:

( x − 2y = −2 x − 2y = 2 ;

( x − 2y = −2

−2x + 4y = 4 ;



 

 

2x + z = 3

x − y − z = 1

3 x − y = 4

.

Geben Sie eine graphische Deutung der Resultate.

6. Es sei P ∈ R ⁿ , und V 2 ⊂ R ⁿ ein zweidimensionaler Untervektorraum. Zeigen Sie:

Es gibt genau eine Ebene E ⊂ R ⁿ mit P ∈ E und ⁿ −→

P Q | P, Q ∈ E ^o = V 2 , n¨amlich E = ⁿ X ∈ R ⁿ | −−→

P X ∈ V 2

o .

1. Sei K ein K¨orper. Gegeben sei die Menge V = {alle Funktionen f : K → K}.

(a) Wir definiern eine Vektorsumme ( f + g )( x ) = f ( x ) + g ( x ) und eine skalare Multiplikation (kf )(x) = kf (x) f¨ ur f, g ∈ V und k ∈ K;

Zeigen Sie dass V mit den obigen Operationen ein Vektorraum ¨ uber K ist.

2. Gegeben ist der Vektorraum V aller Funktionen von dem Zahlenk¨orper R in den Zahlenk¨orper R. Bestimmen Sie in jedem der folgenden F¨alle ob W ein Unterraum von V ist:

(a) W = { f : R → R | f (− x ) = f ( x ) f¨ ur alle x ∈ R. } (b) W = { f : R → R | x ≤ y ⇒ f ( x ) ≤ f ( y )}

3. Gegeben sei V = R ³ .

(a) Zeigen Sie, dass W = {(a, b, 0)|a, b ∈ R} ein Unterraum von V ist.

(b) Ist C ∪ W einen Unterraum von V , wobei C = {(0, 0, c)|c ∈ R}?

4. F¨ ur 2 × 2 Matrizen mit Eintr¨agen in R definieren wir eine Vektorsumme so:

a 11 a 12

a 21 a 22

!

+ b 11 b 12

b 21 b 22

!

= a 11 + b 11 a 12 + b 12

a 21 + b 21 a 22 + b 22

!

und skalare Multiplication

k a 11 a 12

a 21 a 22

!

= ka 11 ka 12

ka 21 ka 22

!

,

mit a _ij , b _ij ∈ R und k ∈ R . Mit diesen obigen Operationen ist die Menge der 2 × 2 Matrizen mit Eintr¨agen in R ein Vektorraum. Finden Sie α und β so, dass

C = −1 −4

−9 −10

!

= αA + βB, wobei

A = 1 1 0 1

!

und B = 1 2

3 4

!

.

5. Gegeben ist die Menge V aller (n × n) Matrizen mit Eintr¨agen in R. Wir definieren eine Vektoraddition und eine skalare Multiplikation analog wie f¨ ur 2 × 2 Matrizen im letzten Beispiel (also komponentenweise). Sei

W := {symetrische Matrizen; das heißt a ij = a ji f¨ ur alle 0 ≤ i, j ≤ n}.

Bestimmen Sie, ob W ein Unterraum von V ist.

1. Bestimmen Sie alle L¨osungen des folgenden linearen Gleichungssystems ¨ uber C : (1 + i) x − 3 y + i z = −1

7 i x − (2 + i )y + z = i (1 − 2i)x − y − i z = 0

2. Sei R[X] der R-Vektorraum aller Polynomfunktionen f : R → R, X 7→ ^{P n} _i=0 a i X ⁱ , wobei a 0 , . . . , a _n ∈ R . Untersuchen Sie, welche der folgenden Abbildungen linear sind:

(a) D : R[X] → R[X], ^{P n} _i=0 a i X ⁱ 7→ ^{P n} _i=1 (i · a i )X ^{i − 1} (Differentiation) (b) gr : R[X] → R, f 7→ gr(f ) (Gradabbildung)

(c) ω a : R[X] → R, f 7→ f(a) (Auswertung an der Stelle a ∈ R) (d) Die Abbildung κ _l : R[X] → R, ^{P n} _i=0 a _i X ⁱ 7→ a _l , mit l ∈ N 0

3. Es seien a, b, c ∈ C. Unter welchen notwendigen und hinreichenden Bedingungen hat das lineare Gleichungssystem

ax + by = c x + y = 1 (a) eine L¨osung ( ^x y ) ∈ C ² ?

(b) eine L¨osung ( ^x y ) ∈ R ² ?

Bestimmen Sie s¨amtliche L¨osungen in C ² bzw. R ² . Deuten Sie die reellen L¨osungen geometrisch.

4. (schriftlich) Sei K ein K¨orper, V ein endlichdimensionaler K-Vektorraum, und seien V 1 und V 2 Untervektorr¨aume von V . Zeigen Sie, dass folgende Aussagen

¨aquivalent sind:

(a) V = V 1 + V 2 und die Summe ist direkt.

(b) Ist [ x 1 , . . . , x _m ] eine Basis von V 1 und [ y 1 , . . . , y _n ] eine Basis von V 2 , dann ist [x 1 , . . . , x m , y 1 , . . . , y n ] eine Basis von V .

5. Es sei K ein K¨orper und φ : V → W ein Isomorphismus von K-Vektorr¨aumen.

Zeigen Sie, dass f¨ ur K -Untervektorr¨aume V 1 , . . . , V _n von V folgende Aussagen ¨aquivalent sind:

1

(a) V = ^{P n} _i=1 V i und die Summe ist direkt.

(b) W = ^{P n} _i=1 φ(V i ) und die Summe ist direkt.

Warum ist diese Aussage im Allgemeinen falsch, wenn φ kein Isomorphismus ist?

2

1. Betrachten Sie die folgende drei Abbildungen R ² → R ² :

(a) f

¹

: Rotation um den Winkel θ gegen den Uhrzeigersinn.

(b) f

²

: Spiegelung an der x- Achse.

(c) f

³

: Projektion auf die Gerade y = x.

(a) Zeigen Sie, dass die Abbildungen f _i sind linear.

(b) Finden Sie zu jedem f _k eine Matrix A _k = [ a _ij ] die f _k repr¨asentiert:

f _k (p) = f _k x 1

x 2

!

= a 11 x 1 + a 12 x 2

a 21 x 1 + a 22 x 2

!

.

2. Eine Dreiecksmatrix ist eine n × n Matrix, f¨ ur die alle Eintr¨age unterhalb (obere

Dreiecksmatrix) bzw. oberhalb (untere Dreiecksmatrix) der Hauptdiagonalen Null

sind. Zeigen Sie: Ist T eine Dreiecksmatrix mit t ii 6= 0 f¨ ur alle i = 1, . . . , n, dann sind die Zeilen von T linear unabh¨angig; weiters sind die Spalten von T linear unabh¨angig.

3. Gegeben sind die folgenden Teilmengen des R ⁴ :

A =



 

 

 

 











1 2 2 3











,











2 4 1 3











,











3 6 1 4













 

 

 

 

, B =



 

 

 

 











0 0 1 1











,











1 2 3 4













 

 

 

 

.

Zeigen Sie, dass gilt: lineare H¨ ulle von A = lineare H¨ ulle von B.

4. Geben Sie eine geometrische Darstellung der linearen H¨ ullen der folgenden Vektoren in R ³ :

(a)



 

 







1 3 2





 ,







2 6 4





 ,







−3

−9

−6









 

 

,

(b)



 

 







−4 0 0





 ,







0 5 0





 ,







1 1 0









 

 

,

(c)



 

 







1 0 0





 ,







1 1 0





 ,







1 1 1









 

 

.

5. A = { a 1 , a 2 , . . . , a _n } sei eine Basis des Vektorraum V ¨ uber K .

(a) Zeigen Sie, dass sich jeder Vektor von V auf h¨ochstens eine Weise als Linearkombination der a _i schreiben l¨asst,

v = β 1 a 1 + β 2 a 2 + · · · + β n a n ,

d.h. , die β _i ∈ K sind durch v eindeutig bestimmt.







1 1

−1





 ,







1 5

−1





 ,







−3 0 0







des R ³ .

UE Lineare Algebra I, Wintersemester 2007/2008 7. ¨ Ubungsblatt, bis 28.11.2007

1. Nehmen Sie an dass x,y, und z linear unabh¨angige Vektoren sind. Zeigen Sie, dass die drei Vektoren x + y, x − y und x − 2y + z auch linear unabh¨angig sind.

2. Finden Sie eine Basis und erkl¨aren warum dies eine Basis ist f¨ ur:

(a) den Vektorraum V aller 3 × 3 Matrizen mit komplexen Eintr¨agen ¨ uber dem K¨orper C .

(b) den Vektorraum V aller Polynome vom Grad h¨ochstens 4 ¨ uber dem K¨orper R.

3. Gegeben sei der Vektorraum V aller Funktionen f : R → R .

(a) Zeigen Sie, dass die Funktionen g = x ² and h(x) = x ² + 1 linear unabh¨angig sind. (Zwei Funktionen sind als Vektoren des Vektorraums genau dann gleich, wenn sie f¨ ur alle x ∈ R desselben Wert annehmen).

(b) Geben Sie ein Beispeil zweier Funktionen, die linear abh¨angig sind.

4. Entscheiden Sie, ob {(3,3,3),(1,2,3),(4,-2,2)} eine Basis des R ³ ist.

5. Gegeben {(1,2,3),(1,1,1)}, finden Sie einen dritten Vektor, um eine Basis des R ³ zu erhalten.

6. Gegeben ist der Unterraum des R ⁴ definiert durch {(a, b, c, d)|a − b = 0, c = 4d}.

Finden Sie eine Basis f¨ ur diesen Unterraum.

7. Sei W eine Unterraum eines endlich dimensionen Vektroraums V der Dimension n.

Beweisen Sie

(a) die Dimension von W ist kleiner gleich n.

(b) wenn die Dimension von W gleich n ist, dann ist W = V .

8. (Wiederholung) Seien U und W Unter¨aume eines endlich dimensionalen Vektor-

raums. Sei {u 1 , .., u n } eine Basis von U und {w 1 , .., w m } eine Basis von W und sei

V = U ⊕ W . Beweisen Sie, dass { u 1 , .., u _n , w 1 , .., w _m } eine Basis von V ist.

1. Gegeben sind die zwei Vektoren

v 1 =











1

−3 0

−1











, v 2 =











2 1

−1 0











des R ⁴ . Erg¨anzen Sie v 1 , v 2 zu einer Basis [ v 1 , v 2 , v 3 , v 4 ] des R ⁴ .

2. Der K¨orper C der komplexen Zahlen ist verm¨oge der Skalarmultiplikation R × C → C, λ(x + iy) = (λx) + i(λy) ein zweidimensionaler R-Vektorraum mit der Basis [1 , i ]. Sei z = a + ib ∈ C mit a, b ∈ R . Durch Multiplikation mit z ist eine R -lineare Abbildung x 7→ zx von C nach C gegeben. Finden Sie die Matrixdarstellung dieser Abbildung bzgl. der Basis [1, i].

3. F¨ ur Funktionen f, g : R → R definieren wir das Produkt f g : R → R (wie ¨ ublich) wertweise: (f g)(x) = f(x)g(x). Bestimmen Sie die Menge aller Abbildungen f : R → R f¨ ur die die Menge {f, f ² , f ³ , . . . } linear abh¨angig im R-Vektorraum aller Funktionen von R nach R ist.

4. (schriftlich) Uberlegen Sie sich, ob die Menge ¨ {sin(x), cos(x)} linear abh¨angig oder linear unabh¨angig im R-Vektorraum aller Funktionen von R nach R ist.

5. Stellen Sie die bzgl. der Standardbasen des R ³ bzw. R ⁴ gegebenen Matrix











0 1 −1

0 2 0

1 1 1

−3 0 0











bzgl. der neuen Basen











1

−1 0 0











,











1 0

−1 0











,











1 0 0

−1











,











1 0 0 0











und







1

−1 0





 ,







1 0

−1





 ,







0 0 1







dar.

6. Sei V der R-Vektorraum aller Polynomfunktionen von R nach R deren Grad ≤ 3

ist. Sei d _i : V → V die Abbildung, die jeder Polynomfunktion ihre i -te Ableitung

zuordnet (1 ≤ i ≤ 3). Finden Sie die Matrixdarstellung von d _i bzgl. der Basis

[1, x, x ² , x ³ ].

UE Lineare Algebra I, Wintersemester 2007/2008 9. ¨ Ubungsblatt, bis 12.12.2007

1. Sei P 3 der R -Vektorraum aller Polynomfunktionen f : R → R , x 7→ a 0 + a 1 x + a ₂ x ² + a ₃ x ³ wobei a ₀ , a ₁ , a ₂ , a ₃ ∈ R . Dann hat das Polynom ˜ f (x) = 1 − x + 3x ² − x ³

die Darstellung











0 1 1 2











bzgl. der Basis B = {1 + x, 1 − x, x ² + x ³ , x ² − x ³ }. Finden

Sie einen neuen Basis D des P ₃ , so dass das Polynom ˜ f (x) die Darstellung











1 0 2 0











bzgl. der neuen Basis D hat.

2. Mit M m×n ( K ) bezeichnen wir die Menge aller m × n-Matrizen ¨ uber K ; mit der

¨

ublichen Addition und skalaren Multiplikation ist M m×n ( K ) ein linearer Raum ¨ uber K . Gegeben seien V ein n-dimensionaler Vektorraum und W ein m-dimensionaler Vektorraum ¨ uber K . Dann ist L(V, W ) = {f : V → W |f ist K − linear } ein K -Vektorraum mit der ¨ ublichen Addition + : L(V, W ) × L(V, W ) → L(V, W ), (f + g)(x) = f(x) + g(x) und Skalarmultiplikation · : K × L(V, W ) → L(V, W ), (λf )(x) = λf(x).

Zeigen Sie, dass M m×n ( K ) zu L(V, W ) isomorph ist.

3. Gegeben sei eine Menge S. Betrachten Sie den R -Vektorraum L aller Funktionen f : S → R mit der ¨ ublichen Addition + : L × L → L, (f + g)(x) = f(x) + g(x) und der ¨ ublichen Skalarmultiplikation · : R × L → L, (λf )(x) = λf (x).

Zeigen Sie:

(a) wenn S = {1, 2, . . . , n}, dim L = n;

(b) wenn S = R , dim L = ∞.

  3x ₁ + 6x ₂ + x ₃ + 4x ₄ = 0

auf reduzierte Echelon-Form, und bestimmen Sie alle seine L¨ osungen ¨ uber R .

5. Gegeben ist die folgende Menge

S =



 

 

 

 











2 3

−1 1











,











1 5 7 3











,











−2 4 16 4











,











0

−2 6 0











,











1

−1 3 2











,











−3

−1 3

−6













 

 

 

 

⊂ R ⁴

(a) Zeigen Sie, dass [S] = R ⁴

(b) Finden Sie eine Teilmenge von S die eine Basis des R ⁴ ist.

UE Lineare Algebra I, Wintersemester 2007/2008 10. ¨ Ubungsblatt, bis 09.01.2008

1. Seien f : R → R und g : R → R Abbildungen. Wir definieren (f ◦ g)(x) :=

f ( g ( x )). Zeigen Sie: Wenn f und g bijektiv sind, dann ist auch ( f ◦ g ) bijektiv.

2. Sei die Menge F = { f 1 , f 2 , ..., f _n } eine Basis f¨ur den Vektorraum V und E = {e 1 , e 2 , ..., e _n } ebenfalls eine Basis f¨ur V . Wir k¨onnen dann jeden Basisvektor von F als Linearkombination von Vektoren von E schreiben, das heißt

f i = a i1 e 1 + a i2 e 2 + a i3 e 3 + · · · + a in e n .

Sei P diejenige Matrix deren i-te Spalte der Koordinatenvektor des Vektors f i

bez¨uglich der Basis E ist. Die invertierbare Matrix P heißt

” Ubergangsmatrix“ ¨ von der Basis E zur Basis F . F¨ur jeden Vektor v ∈ V gilt dann die Gleichung P [v] f = [v] e , wobei zum Beispiel [v] e den Spaltenvektor bezeichnet, dessen Eintr¨age die Koordinaten von v bez¨uglich der Basis E sind.

(a) Verwenden Sie das Konzept

” Inverse Matrix“ und finden die ¨ Ubergangsmatrix von F nach E .

(b) Nehmen Sie an dass T : V → V ein lineare Abbildung ist und [T ] e die Marixdarstellung von T bez¨uglich der Basis E ist, das heißt [T v] e = [T ] e [v] e . Verwenden Sie das Konzept

” Inverse Matrix“ und finden Sie eine Formel f¨ur die Marixdarstellung von T bez¨uglich der Basis F .

3. Gegeben sind die folgenden Mengen ⊂ R ³ :

A =



 

 







1 1 1





 ,







3 4 1





 ,







5 3 9









 

 

, B =



 

 







1

−2 7





 ,







2

−3 12





 ,







3

−4 17









 

 

.

Bestimmen Sie, ob die lineare H¨ulle von A gleich der linearen H¨ulle von B ist.

4. Gegeben ist die 3 × 3 Matrix

A =







1 0 2

2 −1 3

4 1 8





 .

Finden Sie A ^{− 1} .

1

2 0 0 invertierbar? Begr¨unden Sie Ihre Aussage.

(b) Ist

A = 1 0 0

0 1 0

!

invertierbar? Begr¨unden Sie Ihre Aussage.

6. Gegeben sei die lineare Abbildung T (x, y, z) = (x + 2y − z, y + z, x + y + 2z). Finden einen Basis f¨ur Kern( T ).

2

UE Lineare Algebra I, Wintersemester 2007/2008 11. ¨ Ubungsblatt, bis 16.01.2008

1. Bestimmen Sie ob die folgende Matrix invertierbar ist und berechnen Sie gegebenenfalls die Inverse:







1 3 −1

−4 0 2

−5 2 2







2. Bestimmen Sie ob die folgende Matrix invertierbar ist und berechnen Sie gegebenenfalls die Inverse:











1 −1 0 −1

4 2 0 2

6 0 2 2

1 3 5 0











3. Bestimmen Sie eine Basis f¨ur den Kern und das Bild folgender Matrix:











1 −1 −1 0

4 3 8 6

6 0 6 6

1 3 7 4











4. Sei A eine n × n Matrix ¨uber R und k ∈ N 0 . Wir definieren die k-te Potenz A ^k von A rekursiv durch A ⁰ := I, A ^k := A · A ^{k − 1} , wobei I die n × n Einheitsmatrix bezeichnet.

(a) Zeigen Sie, dass Kern(A) ⊂ Kern(A ² ) ⊂ Kern(A ³ ) ⊂ · · · ⊂ Kern(A ^k ) ⊂ . . . gilt, und dass es ein k 0 ≥ 0 mit Kern( A ^k

⁰

) = Kern( A ^k ) f¨ur alle k ≥ k 0 gibt.

Wir definieren dann K(A) := Kern(A ^k

⁰

).

(b) Zeigen Sie, dass Bild( A ) ⊃ Bild( A ² ) ⊃ Bild( A ³ ) ⊃ · · · ⊃ Bild( A ^k ) ⊃ . . . gilt, und dass es ein k 0 ≥ 0 mit Bild(A ^k

⁰

) = Bild(A ^k ) f¨ur alle k ≥ k 0 gibt. Wir definieren dann B (A) := Bild(A ^k

⁰

).

5. Seien die Voraussetzungen und Bezeichnungen wie im vorigen Beispiel.

(a) Zeigen Sie, dass K(A) invariant unter A ist, d.h., dass Ax ∈ K(A ) f¨ur alle x ∈ K ( A ) gilt. Ditto f¨ur B ( A ).

(b) Beweisen Sie, dass R ⁿ = K ( A ) + B ( A ), und dass die Summe K ( A ) + B ( A ) direkt ist.

1

[A] ^b von A bzgl. der Basis b = (v 1 , . . . , v l , w 1 , . . . , w m ) die folgende Gestalt hat:

[ A ] ^b = X 0 l,m

0 m,l Y

!

Hierbei bezeichnen X eine l × l Matrix, Y eine m × m Matrix und 0 α,β die α × β Nullmatrix.

7. Bestimmen Sie den Rang folgender Matrix:











0 −1 1 1 0

−2 2 −2 2 0

−3 1 4 3 1

0 1 0 4 −1











2

UE Lineare Algebra I, Wintersemester 2007/2008 12. ¨ Ubungsblatt, bis 30.01.2008

1. Gegeben ist die 3 × 4 Matrix

A =







1 3 1 −4

−1 −3 1 0

2 6 2 −8





 .

Uberpr¨ ¨ ufen Sie, dass rang A ^T A = rang (A) = rang AA ^T .

2. Ein System linearer Gleichungen Ax = b von m linearen Gleichungen in n Variablen

¨

uber R heißt konsistent, wenn es eine L¨osung hat. Sonst heißt es inkonsistent.

(a) Im Fall b = 0 (homogenes Gleichungssystem), zeigen Sie:

i. das lineare Gleichungssystem Ax = 0 ist immer konsistent.

ii. das lineare Gleichungssystem Ax = 0 hat genau eine L¨osung (d.h. x = 0)

⇔ rang(A) = n.

(b) Im Fall b 6= 0 (inhomogenes Gleichungssystem), zeigen Sie:

i. das lineare Gleichungssystem Ax = b ist konsistent ⇔ rang([A|b]) = rang (A).

ii. das lineare Gleichungssystem Ax = b hat genau eine L¨osung ⇔ rang(A) = n.

3. Finden Sie ein homogenes System von 3 linearen Gleichungen in 4 Variablen ¨ uber R das die folgende allgemeine L¨osung hat

x 2











−2 1 0 0











+ x 4











−3 0 2 1











.

(b) A C 0 s,r B

! −1

= A ⁻¹ − A ⁻¹ CB ⁻¹ 0 s,r B ⁻¹

!

.

5. Eine quadratische Matrix heißt nilpotent vom Index k, wenn N ^k = 0 und N ^{k −1} 6= 0 f¨ ur die positive nat¨ urliche Zahl k gilt.

(a) Sei N ∈ R ^{n × n} nilpotent vom Index n und y ein Vektor, sodass N ^{n −1} y 6= 0.

Zeigen Sie dass, B = {y, N y, N ² y, . . . , N ^{n −1} y} eine Basis von R ⁿ ist.

(b) Zeigen Sie: [ N ] B =



















0 0 · · · 0 0 1 0 · · · 0 0 0 1 · · · 0 0 ... ... ... ... ...

0 0 · · · 1 0



















(c) Seien A und B zwei nilpotente n × n Matrizen vom Index n . Dann existiert eine invertiebare Matrix P , sodass A = P ⁻¹ BP ( das folgt nach (b) ).

6. Gegeben ist die 2 × 2 Matrix

0 1

−2 3

!

.

Finden Sie alle Unterr¨aume V ⊂ R ² die invariant unter A sind, d.h., alle V ⊂ R ² mit Ax ∈ V f¨ ur alle x ∈ V .

7. Gegeben sei die Matrix

A = 1 −1

1 1

!

.

Berechnen Sie alle Eigenwerten und Eigenvektoren von A .

8. F¨ ur quadratische Matrizen A ¨ uber einem K¨orper K

A =













a 11 a 12 · · · a 1n

a 21 a 22 · · · a _2n ... ... ... ...

a _n1 a _n2 · · · a _nn













definiert man die Spur (”trace” auf English), sp(A), als die Summe der Diagonalelemente: sp(A) = a 11 + a 22 + · · · + a _nn =

n

X

i=1

a _ii . Zeigen Sie die folgenden Eigenschaften:

(a) sp A ^T A ≥ 0.

(b) sp A ^T A = 0 ⇔ A = 0.

(c) F¨ ur Matrizen A _m × n und B _n × m gilt sp (AB) = sp(BA).

(d) Invarianz der Spur unter zyklischen Vertauschungen:

f¨ ur n × n Matrizen A, B, C gilt sp (ABC) = sp (BCA) = sp (CAB).

(e) Die Spur ist invariant unter Basistransformationen:

f¨ ur eine Matrix A und eine invertierbare Matrix B gilt sp (B ⁻¹ AB) = sp (A).