Mentorierte Arbeit in Fachdidaktik Mathematik
Der K -Means Algorithmus
David Stotz
Inhalt Im ersten Kapitel wird die Problemstellung anhand einer Anwendung motiviert. Das zweite Kapitel gibt eine kurze Einf¨uhrung in die Datenanalyse und das dritte Kapitel behandelt den Schwerpunkt einer endlichen Punktmenge. Im vierten Kapi- tel wird derK-Means Algorithmus vorgestellt und untersucht.
Die Implementierung und Anwendung des Algorithmus auf das Einf¨uhrungsbeispiel sind Gegenstand des f¨unften Kapitels.
Zielpublikum 3.–4. Klasse Kurzzeitgymnasium (11.–12. Schuljahr)
Voraussetzungen Grundkenntnisse in Vektorgeometrie, Algorithmen und Informatik
Form Lesetext mit Aufgaben
Bearbeitungsdauer 5 Lektionen Betreuung Kristine Barro Datum 28. Juli 2016
Inhaltsverzeichnis
1 Einf ¨uhrung 3
2 Datenanalyse 4
2.1 Cluster und ihre Repr¨asentanten . . . . 5
3 Der Schwerpunkt einer endlichen Punktmenge 6
3.1 Geometrische Eigenschaft des Schwerpunktes . . . . 8
4 Clustering mit demK-Means Algorithmus 10
4.1 Spielzeugbeispiel in Geogebra . . . 11 4.2 Beispiel mit synthetischen Daten . . . 13 5 Implementierung des Algorithmus und Anwendung auf ein Photo 19 5.1 Implementierung des Algorithmus . . . 21 5.2 Ergebnis . . . 25
Didaktische Vorbemerkungen
Gemessen an der derzeitigen wissenschaftlichen, industriellen und wirtschaftlichen Be- deutung der Datenanalyse, ist diese im heutigen Schulcurriculum unterrepr¨asentiert. Das Thema f¨ur die Unterrichtseinheit wurde ausgew¨ahlt, um den Sch¨ulerinnen und Sch¨ulern einen Zugang zur Mathematik der Datenanalyse zu erm¨oglichen und ihnen die Anwen- dung auf praktische Probleme erfahrbar zu machen.
Als zentraler Motivationsanker dient die Anwendung des K-Means Algorithmus auf eine Photo-Datei, um das Photo in einer geringen Anzahl von Farben m¨oglichst gut dar- zustellen. Das Beispiel eignet sich einerseits gut zur Motivation der Sch¨ulerinnen und Sch¨uler, da viele von ihnen einen Bezug zu Photo-Dateien mitbringen und die Ergebnis- se direkt sichtbar gemacht werden k¨onnen. Andererseits spielt das Anwendungsbeispiel in der tats¨achlichen Datenanalyse eine eher marginale Rolle, da in der Bildverarbeitung andere Algorithmen demK-Means Algorithmus ¨uberlegen sind. Die St¨arke desK-Means Algorithmus liegt vor allem in seiner Einfachheit, wodurch er flexibel in andere Algorith- men integriert werden kann. Aus dieser ¨Uberlegung heraus wurde versucht, die Bedeu- tung der Datenanalyse und des Clusterns von Daten auch in einem allgemeineren Kontext zumindest anzudiskutieren.
Lernziele
• Probleme in der Datenkomprimierung und praktische Anwendung eines Algorith- mus kennenlernen.
• DenK-Means Algorithmus mathematisch analysieren.
• Die Bedeutung des Schwerpunktes eines endlichen Systems kennenlernen.
• Ein Grundverst¨andnis der Implementierung entwickeln.
ben¨otigtes Vorwissen
• Grundlagen in der Vektorgeometrie, insbesondere Vektoralgebra und Abstandsbe- griff
• Verst¨andnis dar¨uber, was ein Algorithmus ist
• Grundwissen in der Informatik (if-Bedingung, for-Schleifen)
Quellen
Die Beschreibung des Algorithmus und die Idee f¨ur die Anwendung stammt aus [Bishop, 2006]. Die Beweisidee f¨ur die Konvergenz desK-Means Algorithmus in endlich vielen Schritten stammt aus [jkabrg, 2015].
1 Einf ¨uhrung
Daten enthalten Informationen. Im digitalen Zeitalter werden Unmengen von Daten erzeugt, gespeichert und zwischen Ger¨aten ¨ubertragen, alleine schon durch Mitteilungen, Bilder und Videos auf unseren Smartphones und PCs. Experten sch¨atzen, dass der Internet-Datenverkehr im Jahr 2016 circa 1.1 Zettabyte betragen wird [Cisco, 2016], das sind 1.1 Billionen Gigabyte und entspricht ungef¨ahr der Gr¨osse eines Liedes mit einer Spieldauer von einer Milliarden Jahre. Beim Umgang mit grossen Datenmengen stossen Computer an ihre Kapazit¨atsgrenzen. Ein wichtiger Faktor, um Datenmengen zu verkleinern und dennoch dabei die relevanten Informationen zu erhalten, ist die Komprimierungvon Daten. Zur Veranschaulichung der Komprimierung untersuchen wir ein Beispiel einer Photo-Datei.
Abbildung 1: Beispielphoto
Das Photo besteht aus einer Anzahl von Pixeln, von denen jedes eine bestimmte Farbe annehmen kann. Da f¨ur eine naturgetreue Abbildung sehr viele Farben und Schattierungen zu Verf¨ugung stehen m¨ussen, ist die Datenmenge, die das Photo beschreibt, relativ gross.
Um die Datenmenge zu verkleinern, k¨onnten wir die Anzahl der m¨oglichen Farben und Schattierungen einschr¨anken. Je nachdem auf welche Farben wir uns dabei beschr¨anken, resultiert daraus ein mehr oder weniger grosser Qualit¨atsverlust bei der Abbildung.
Angenommen wir m¨ochten das abgebildete Photo mit nur f¨unf Farben m¨oglichst gut wiedergeben, welche Farben w¨urden wir w¨ahlen? Durch Betrachten des Photos k¨onnten wir darauf kommen, rot zu w¨ahlen, um das Spielzeugauto im Vordergrund darzustel-
len, orange, um den Blumentopf abzubilden, gr¨un f¨ur die Str¨aucher im Hintergrund und schwarz f¨ur das Lenkrad des Spielzeugautos sowie das Auto im Hintergrund. Ist das ei- ne gute Wahl? Welche Farben w¨urden wir w¨ahlen, wenn wir zehn Farben ausw¨ahlen k¨onnten?
In dieser Projektarbeit werden wir einen mathematischen Algorithmus kennenlernen, derautomatischgute Farben ausw¨ahlt. Der Algorithmus teilt zun¨achst die Pixel in Gruppen ein, die sp¨ater jeweils die gleiche Farbe erhalten. Diese Farben werden dann vom Algorith- mus so bestimmt, dass in einem gewissen Sinn, den wir mathematisch pr¨azisieren werden, der Qualit¨atsverlust der Abbildung m¨oglichst gering ist.
2 Datenanalyse
Die Verarbeitung von grossen Datenmengen hat in den letzten Jahrzehnten enorm an Be- deutung gewonnen. Empirische Wissenschaften, wie Physik, Biologie und Chemie sind immer st¨arker mit der Herausforderung konfrontiert, die Vielfalt von Messungen auszu- werten und zu interpretieren.
Einen grossen Schub hat die Entwicklung der Datenanalyse durch die Finanzindustrie und grosse Internetfirmen erfahren. Die statistische Auswertung von Aktienkursen und Preisentwicklungen sind das zentrale Werkzeug f¨ur das Treffen von Handelsentscheidun- gen von Banken an den Aktienm¨arkten. Suchmaschinen wie Google basieren fundamental darauf, auf schnelle Art und Weise relevante Informationen aus dem Datendschungel des Internets herauszufiltern. Schliesslich verwenden auch soziale Netzwerke wie Facebook hochentwickelte Algorithmen um Informationen ¨uber die Nutzer zu sammeln und zum Beispiel f¨ur personalisierte Werbeanzeigen auszuwerten.
Um mathematische Analyseverfahren einsetzen zu k¨onnen, ist es zun¨achst wichtig, den Informationen geeignete Zahlenwerte zuzuordnen. F¨ur die Messwerte in empirischen Wis- senschaften ist dies zumeist schon der Fall, jedoch ist zum Beispiel nicht klar, wie man den Beziehungsstatus eines Facebookprofils durch eine Zahl ausdr¨ucken soll. Ein naiver Ansatz ist, f¨ur jede solche Information eine Regel zu erfinden und diese durch eine Zahl auszudr¨ucken. Zum Beispiel k¨onnten wir vereinbaren, dasssingledurch eine0undin ei- ner Beziehungdurch eine1 ausgedr¨uckt wird. Wenn wir dies in ¨ahnlicher Weise f¨ur alle m¨oglichen Parameter durchf¨uhren, k¨onnen wir schliesslich ein Facebookprofil durch eine Datenpunkt darstellen, dessen Koordinaten durch die Werte all dieser Parameter gege- ben sind. Jede Koordinate entspricht dabei einer Dimension des Raums, in dem der Punkt
liegt; zum Beispiel liegt ein Punkt(−3,5), bestehend aus zwei Koordinaten, im zweidi- mensionalen Raum. Da in der beschriebenen Situation viele Parameter einen Datenpunkt beschreiben, liegen die Datenpunkte in einem hoch-dimensionalen Raum.
F¨ur die Entwicklung von Verfahren zur Datenverarbeitung stellen wir uns von nun al- so eine grosse (aber endliche) Menge von Datenpunkten in einem hoch-dimensionalen Raum vor, sodass wir nicht gen¨ugend Rechenleistung zu Verf¨ugung haben, um jeden Da- tenpunkt individuell zu untersuchen. Die informationelle Gehalt dieser Daten h¨angt von der jeweiligen Anwendung ab und soll hier nicht im Zentrum der Diskussion stehen.
2.1 Cluster und ihre Repr¨asentanten
Ein grundlegendes Konzept bei der Analyse von Daten ist, die Datenpunkte zuclustern, das heisst, in Gruppen einzuteilen, die “¨ahnlich” aussehen. Die ¨Ahnlichkeit kann zum Beispiel gemessen werden durch den Abstand, den die Datenpunkte im umgebenden Raum besit- zen. Wenn wir dann jeden Cluster durch einen geeigneten “repr¨asentantiven” Datenpunkt ersetzen, k¨onnen wir so die Anzahl der zu untersuchenden Datenpunkte erheblich redu- zieren. Bei diesem Prozess verlieren wir offenbar Informationen, denn wir kennen nicht mehr die exakte Positionen aller Datenpunkte, jedoch hoffen wir, dass wir durch gutes Clustering die f¨ur uns wichtigen Informationen erhalten k¨onnen.
Wenn wir zum Beispiel ein Tier durch viele Parameter wie Geschlecht, Gr¨osse, Alter, Le- bensraum, Nahrung usw. beschreiben (jeweils durch Zahlen ausgedr¨uckt), und diese Daten f¨ur sehr viele Tiere sammeln, so k¨onnen wir durch Gruppierung der Daten eine m¨ogliche Einteilung in Tierarten erhalten. Wir k¨onnen auch noch einen Schritt weitergehen und in- nerhalb jeder Tierart die Daten erneut gruppieren und so eine Tierart weiter in bestimmte Gattungen unterteilen. Eine solche Gruppierung erleichtert bekanntlich den Umgang mit den Informationen ¨uber Tiere, da wir uns nicht mehr nur auf spezielle Individuen beziehen m¨ussen.
Nachdem wir die Daten in Cluster eingeteilt haben, m¨ochten wir f¨ur jeden der Cluster einen geeigneten Repr¨asentanten ausw¨ahlen, der die “typischen” Eigenschaften der Da- ten innerhalb eines Clusters m¨oglichst gut wiedergibt. Wir k¨onnen solche Repr¨asentanten auf unterschiedliche Weise w¨ahlen, je nachdem welche spezifischen Eigenschaften erf¨ullt werden sollen. Zum Beispiel k¨onnten wir versuchen, denjenigen Punkt zu finden, der die Summe aller Abst¨ande zu den Punkten im Cluster minimiert. Diese Wahl hat den Nach- teil, dass die Bestimmung dieses Punktes relativ aufwendig ist und er sich nicht durch eine einfache Formel berechnen l¨asst. F¨ur einen Cluster, der aus drei PunktenA, B, Cbe-
steht, ist der Punkt, der die Summe der Abst¨ande zuA, B, C minimiert, bekannt als der Fermat-Punktdes DreiecksABC. Die Koordinaten dieses Punktes sind nicht leicht zu be- stimmen und die Situation wird bei gr¨osseren Clustern noch erheblich komplizierter. Wir werden daher stattdessen den im Folgenden besprochenenSchwerpunkt des Clusters als Repr¨asentanten verwenden, der eine ¨ahnliche Eigenschaft erf¨ullt, sich jedoch mit deutlich weniger Aufwand bestimmen l¨asst.
3 Der Schwerpunkt einer endlichen Punktmenge
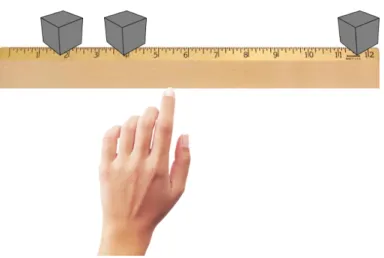
Stell dir vor, du legst einige gleich schwere Baukl¨otze an verschiedenen Stellen auf ein Lineal. An welcher Stelle m¨usstest du das Lineal mit dem Finger balancieren, damit es im Gleichgewicht bleibt?
Abbildung 2: Ein Lineal balancieren
In einer idealisierten Situation stellen wir uns vor, dass jede Einzelmasse jeweils in einem Punkt konzentriert ist. Der gesuchte Punkt, an dem wir das Lineal balancieren k¨onnen, heisst der Schwerpunkt des physikalischen Systems. Liegen in den Punkten P1, . . . , Pn die Massenm1, . . . , mn, so wird im Physikunterricht gezeigt, dass der Schwerpunkt des physikalischen Systems durch das gewichtete Mittel
m1~p1+. . .+m2~pn
m1+. . .+mn
gegeben ist.1 In der Situation, die wir betrachten, sollen alle Einzelmassen gleich gross
1F¨ur zwei Massenm1, m2an den PositionenP1, P2auf dem Lineal folgt diese Formel sofort aus dem He-
sein, das heisstm1 = . . . = mn. Wenn wir diese Masse mit mbezeichnen, so l¨asst sich der Ortsvektor zum Schwerpunkt folglich durch die Formel
~s= m(~p1+. . .+~pn) mn
= 1
n(~p1+. . .+~pn) (1) berechnen. In diesem Fall wird die Lage des Schwerpunktes also nur durch die relative Position der Massenpunkte bestimmt und ist unabh¨angig von der tats¨achlichen Massem in den Punkten.
Die Berechnungsformel kann f¨ur 1-dimensionale Vektoren (also Zahlen), 2- dimensionale Vektoren, 3-dimensionale Vektoren oder auch217-dimensionale Vektoren (das sind Vektoren mit 217 Komponenten) angewendet werden. Wir k¨onnen also Schwerpunkte berechnen von Objekten in beliebig hoch dimensionalen R¨aumen.
Handelt es sich um eine Punktmenge, die nur aus zwei Punkten besteht, so besagt die Formel, dass der Schwerpunkt den Ortsvektor 12(~p1 +~p2) besitzt, also gerade mit dem Mittelpunkt der beiden PunkteP1undP2 ¨ubereinstimmt.
Aufgabe 1 Betrachte die idealisierte Form der Situation in Abbildung 2, bei der die drei Massen jeweils an den (eindimensionalen) Punkten P1 = (1.8),P2 = (3.9)undP3 = (11.7)konzentriert sind. Berechne die Stelle, an der wir das Lineal balancieren m¨ussten, damit es im Gleichgewicht bleibt.
Aufgabe 2 Berechne (im 4-dimensionalen Raum) den Schwerpunkt der Punktmenge {P1, . . . , P5}mit den Ortsvektoren
~ p1 =
3 0 1
−2
, ~p2 =
1 2 0 4
, p~3=
0 3 0 1
, ~p4 =
−2
−1 6 2
, ~p5 =
3 1
−2 0
.
Aufgabe 3
(a) Bestimme den Schwerpunkt der Punktmenge{A, B, C}wobeiA= (1,2,0),B = (0,4,1)undC= (−1,−1,−1).
belgesetz. Im allgemeinen Fall folgt die Formel ebenso leicht aus dem Drehmomentensatz.
(b) Stelle die Geradengleichungen der Seitenhalbierenden im DreieckABC auf und zeige, dass sich diese im Schwerpunkt der Punktmenge{A, B, C}schneiden.
Abbildung 3: Aufgabe 4
Aufgabe 4
(a) Bestimme geometrisch den Schwerpunkt der in Abbildung 3 abgebildeten Punkt- menge.
Tipp: Du kannst den Schwerpunkt als Mittelpunkt zwischen den beiden Diagonalen- mittelpunkten bestimmen. Begr¨unde dies anhand der Berechnungsformel(1).
(b) Wie w¨urdest du das Bild durch einen weiteren Punkt im abgebildeten Bereich erg¨anzen, sodass der Schwerpunkt der neuen Punktmenge ausserhalb des Vierecks ABCDliegt?
3.1 Geometrische Eigenschaft des Schwerpunktes
Wir wollen nun eine weitere Eigenschaft des Schwerpunktes kennenlernen. ¨Offne hierzu die Geogebra-Datei “uebung4.ggb”, welche die Situation aus Abbildung 3 zeigt.
Aufgabe 5
(a) Konstruiere in der Geogebra-Datei den Schwerpunkt der Punktmenge bestehend aus A, B, C, D auf die Weise aus Aufgabe 4(a).
(b) Zeichne einen beliebigen weiteren Punkt “X” ein und gebe d= D i s t a n c e [A, X] ˆ 2 + D i s t a n c e [B , X] ˆ 2 +
D i s t a n c e [C , X] ˆ 2 + D i s t a n c e [D, X] ˆ 2
in die Inputzeile (am unteren Rand des Geogebra-Fensters) ein. (In der deutschen Ausgabe von Geogebra muss “Distance” durch “Abstand” ersetzt werden.) (c) Was f¨allt dir auf, wenn du X in die N¨ahe des Schwerpunktes aus Teilaufgabe (a)
verschiebst? Stelle eine allgemeine Vermutung auf, welche Eigenschaft der Schwer- punkt einer endlichen Punktmenge erf¨ullt.
Die Eigenschaft, die wir in Aufgabe 5 kennengelernt haben, gilt tats¨achlich immer f¨ur den Schwerpunkt. Wir werden nun versuchen, die Eigenschaft zu beweisen f¨ur den Fall, dass die Punkte im eindimensionalen Raum liegen.
Aufgabe 6 Es seienp1, . . . , pn ∈RPunkte im eindimensionalen Raum. Zeige, dass die Funktion
d(x) = (p1−x)2+ (p2−x)2+. . .+ (pn−x)2 ihr (globales) Minimum annimmt an der Stelles= n1(p1+p2+. . .+pn).
Mithilfe der Vektorrechnung ist der Beweis auch im h¨oherdimensionalen Fall leicht zu adaptieren (siehe L¨osungen). Wir halten das Resultat hier nochmals explizit fest:
F¨ur eine endliche Punktmenge{P1, . . . , Pn}nimmt die Funktion d(~x) =k~p1−~xk2+k~p2−~xk2+. . .+k~pn−~xk2
den minimalen Wert f¨ur~x=~san, wobei~sin (1) definiert wurde. In Worten heisst das:
Die Summe der Abstandsquadrate einer endlichen Punktmenge zu einem PunktXist minimal, wennXder Schwerpunkt der Punktmenge ist.
4 Clustering mit demK-Means Algorithmus
Wir m¨ochten nun einen Algorithmus kennenlernen, der eine gegebene Menge von Daten- punkten automatisch clustert. Das Ziel ist, dass jeweils diejenigen Datenpunkte, die sich in einem Gebiet sammeln, dem selben Cluster zugeordnet werden. Schliesslich sollen f¨ur jeden Cluster gute Repr¨asentanten gefunden werden, das heisst der Fehler, der durch das Ersetzen der Cluster durch die Repr¨asentanten entsteht, soll m¨oglichst klein sein.
BeimK-Means Algorithmus handelt es sich um eineniterativenAlgorithmus, das heisst, der Algorithmus besteht aus einem Grundschritt, der dann wiederholt2durchlaufen wird, bis ein gew¨unschtes Ergebnis erreicht ist. Beim Finden von geeigneten Repr¨asentanten spielt der Schwerpunkt, den wir zuvor besprochen haben, eine wichtige Rolle. Daher ent- springt auch der Name des Algorithmus, wobei “Means”3sich auf die Schwerpunktsformel (1) bezieht und als eine Verallgemeinerung des Durchschnitts auf die Vektorgeometrie ver- standen wird.
Beschreibung desK-Means Algorithmus
Ausgangslage (Input):N “Datenpunkte”,K“Clusterpunkte”, wobeiN K
1. Schritt: Clustering Ordne jeden Datenpunkt dem n¨achstgelegenen Clusterpunkt zu.
Anschaulich: F¨ur jeden Clusterpunkt haben wir einen Sack, und ein Datenpunkt kommt in den Sack, der zum n¨achstgelegenen Clusterpunkt geh¨ort.
2. Schritt: Update der Clusterpunkte Berechne f¨ur jeden Sack den Schwerpunkt aller Da- tenpunkte innerhalb eines Sacks. Ersetze die Clusterpunkte durch diese Schwerpunkte.
Gehe zur¨uck an den Anfang mit den neuen Clusterpunkten.
Das Verfahren wird beendet, entweder nach einer zu Beginn festgelegten Anzahl an Ite- rationen (Durchl¨aufen), oder wenn sich in einem Durchgang die Zuordnung in die S¨acke nicht mehr ver¨andert im Vergleich zum vorherigen Durchgang.
Der Input, mit dem der Algorithmus aufgerufen wird, besteht aus der gegebenen Menge von Datenpunkten und zus¨atzlichKClusterpunkten. Die Wahl der Anfangsclusterpunk- te, mit denen die Iteration das erste Mal durchlaufen wird, kann unterschiedlich erfolgen, zum Beispiel k¨onnen gute Repr¨asentanten gesch¨atzt werden oder einfach zuf¨allig aus den
2lat. iterativus = wiederholend
3engl. mean = Durchschnitt
Datenpunkten ausgew¨ahlt werden. Diese Clusterpunkte werden im Laufe jedes Durch- gangs durch modifizierte Clusterpunkte ersetzt, die dann als Input f¨ur die n¨achste Itera- tion dienen. Die am Ende der Durchl¨aufe erhaltenen Clusterpunkte sollen dann gute Re- pr¨asentanten f¨ur die erhaltenen Cluster ergeben. Wichtig ist es zu bemerken, dass wir uns zu Beginn festlegen auf die AnzahlKvon Clustern, in die wir die Datenpunkte einteilen m¨ochten.
4.1 Spielzeugbeispiel in Geogebra
Um ein Verst¨andnis f¨ur die Funktionsweise des Algorithmus zu entwickeln, sollst du ihn nun einmal selbst durchspielen. ¨Offne hierzu die Geogebra-Datei “kmeans.ggb”. Gegeben sind die folgenden 10 Datenpunkte (A-J) und 2 Clusterpunkte (Y und Z) im zweidimensio- nalen Raum.
Abbildung 4: Spielzeugbeispiel
Um den ersten Schritt desK-Means Algorithmus durchzuf¨uhren, m¨ussen wir jeden Da- tenpunkt dem n¨achstgelegenen Datenpunkt zuordnen.
Aufgabe 7
(a) Wie kannst du f¨ur einen Datenpunkt geometrisch bestimmen, welche der n¨ahere Clusterpunkt ist, ohne dazu alle Abst¨ande berechnen zu m¨ussen?
(b) F¨uhre den ersten Schritt desK-Means Algorithmus aus und f¨arbe jeden Datenpunkt entsprechend der Farbe des n¨aheren Clusterpunktes ein.
Nun haben wir jeden der Datenpunkte in einen von zwei S¨acken gesteckt. Im zweiten Schritt m¨ussen wir jeweils den Schwerpunkt aller Punkte innerhalb eines Sackes bestimmen. M¨ochten wir in Geogebra den Schwerpunkt S der Punktmenge {P1, P2, P3, P4, P5}bestimmen, so k¨onnen wir dies erreichen, indem wir
S= B a r y c e n t e r [{P1 , P2 , P3 , P4 , P5},{1 , 1 , 1 , 1 , 1}]
in die Inputzeile (am unteren Rand des Geogebra-Fensters) eingeben. (In der deutschen Version muss “Barycenter” durch “Massenmittelpunkt” ersetzt werden.) Das Bary- zentrumeiner Punktmenge ist eine allgemeinere Form des Schwerpunktes, bei dem jeder Punkt in der Menge unterschiedlich gewichtet werden kann. In obigem Befehl stehen die Zahlen im zweiten Argument f¨ur die Gewichtungsfaktoren. Den Schwerpunkt erhalten wir, wenn wir, wie oben, die Gewichtungsfaktoren alle auf1setzen. Das heisst, im zwei- ten Argument des Befehls muss die Anzahl an1en gerade der Anzahl an Punkten in der untersuchten Menge entsprechen.
Aufgabe 8 F¨uhre f¨ur das Beispiel den zweiten Schritt des K-Means Algorithmus aus.
Die neuen Clusterpunkte sollen “Y2” und “Z2” heissen.
Nun haben wir eine vollst¨andige Iteration des Algorithmus durchgef¨uhrt und k¨onnen wieder von vorne beginnen, wobei die Clusterpunkte nun durch Y2 und Z2 ersetzt werden.
Aufgabe 9
(a) F¨uhre eine weitere Iteration aus. Die neuen Clusterpunkte sollen “Y3” und “Z3” heis- sen.
(b) Was ist bei einer dritten Iteration zu beobachten?
Bei den einzelnen Iterationen k¨onnen wir gut erkennen, wie sich durch die Zuordnung in die beiden S¨acke die Clusterpunkte verschieben und sich dadurch wiederum die Zuord- nung in die S¨acke im n¨achsten Schritt ver¨andert.
4.2 Beispiel mit synthetischen Daten
Wir haben nun die Funktionsweise desK-Means Algorithmus in einem Spielzeugbeispiel kennengelernt. Da wir alle Schritte von Hand ausgef¨uhrt haben, konnten wir in diesem Beispiel nur eine relativ kleine Punktmenge untersuchen. Als n¨achstes betrachten wir eine gr¨ossere, k¨unstlich erzeugte Menge von Datenpunkten, die n¨aher an der Anwendungssi- tuation liegen soll als das Spielzeugbeispiel.
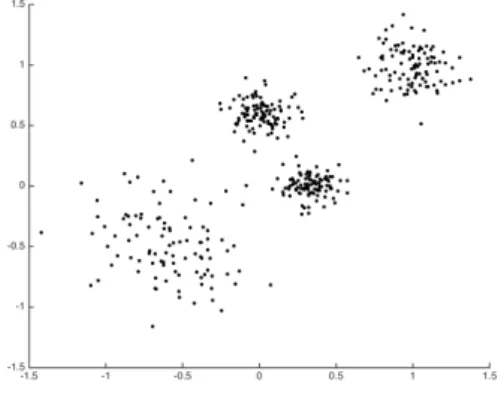
Die folgenden Datenpunkte im zweidimensionalen Raum wurden mit einer Simulati- onssoftware erzeugt.
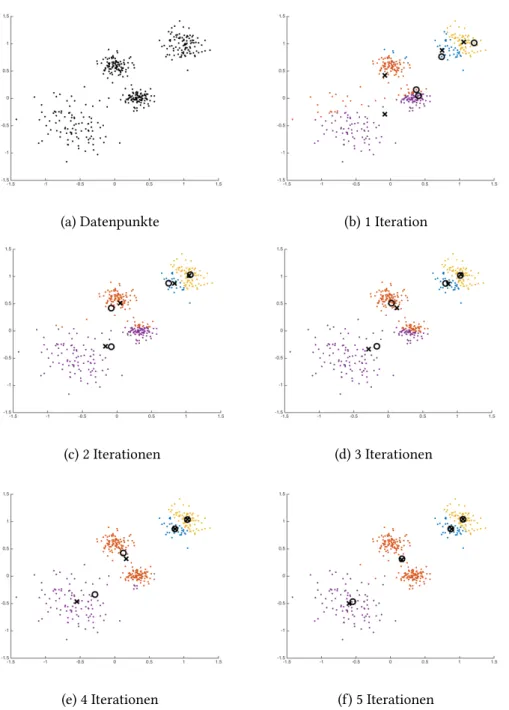
Abbildung 5: Datenpunkte
Aus dem Bild lassen sich vier Cluster von Datenpunkten erkennen. Um eine solche Einteilung zu erreichen, m¨ochten wir denK-Means Algorithmus mitK = 4anwenden.
Hierf¨ur werden zun¨achst zuf¨allig vier Punkte aus den Datenpunkten alsAnfangscluster- punktedeklariert. Dann wird der K-Means Algorithmus mit diesen Datenpunkten und Clusterpunkten gef¨uttert und mit einem Computer ausgef¨uhrt.
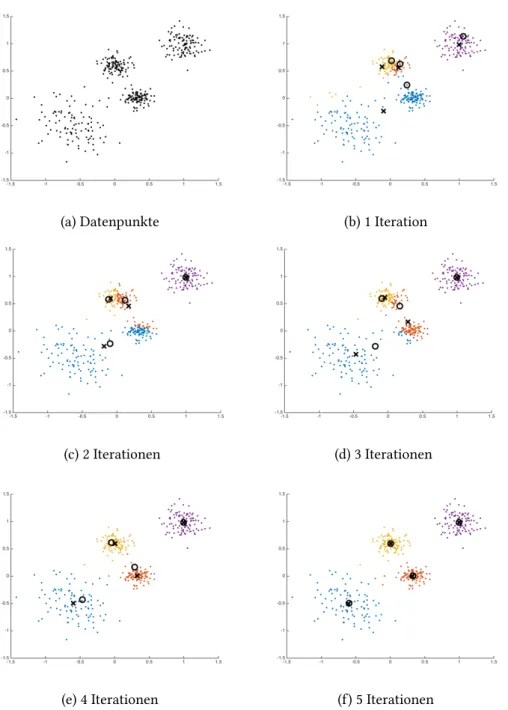
Das Ergebnis der einzelnen Iterationen ist in Abbildung 6 zu sehen. Es l¨asst sich gut erkennen, wie sich die Clusterpunkte gegenseitig in eine Gleichgewichtslage verschieben und am Ende in der Tat die Datenpunkte in die vier Cluster eingeteilt sind, die einem optisch plausibel erscheinen.
Aufgabe 10 Untersuche Abbildung 6 und begr¨unde in jedem Schritt stichwortartig, warum sich die Clusterpunkte wie dargestellt verschieben.
(a) Datenpunkte (b) 1 Iteration
(c) 2 Iterationen (d) 3 Iterationen
(e) 4 Iterationen (f) 5 Iterationen
Abbildung 6: Anwendung desK-Means Algorithmus auf synthetisch erzeugte Daten. Je- de Farbe zeigt einen Cluster an. Die Clusterpunktezu Beginnder Iteration sind mit einem “o” und ihre Updates am Endeder Iteration mit einem “x” markiert.
Abh¨angigkeit von der Wahl der Anfangsclusterpunkte
Eine wichtige Frage, die es zu er¨ortern gilt, ist die Abh¨angigkeit des Ergebnisses von der Wahl an Anfangsclusterpunkten, mit denen wir denK-Means Algorithmus f¨uttern. Wenn der Algorithmus jedes mal die selbe Einteilung liefern w¨urde, unabh¨angig von der Wahl der Anfangsclusterpunkte, dann br¨auchten wir uns keine Gedanken machen, was eine “gu- te” und was eine “schlechte” Wahl von Anfangsclusterpunkten w¨are. In Abbildung 7 wird der Algorithmus auf die gleichen Datenpunkte wie in Abbildung 6 angewendet, jedoch mit einer anderen Wahl von Anfangsclusterpunkten. Es zeichnet sich nach5Iterationen eine andere Einteilung in Cluster ab als in Abbildung 6, woraus wir schliessen k¨onnen, dass die Einteilung in Cluster, dir wir aus der Anwendung desK-Means Algorithmus erhalten, tats¨achlich von der Wahl der Anfangsclusterpunkte abh¨angt.
Aufgabe 11 Untersuche Abbildung 7 und versuche zu beschreiben, wie die Lage der Anfangsclusterpunkte zu der am Ende erhaltenen Einteilung gef¨uhrt hat.
Aufgrund der grossen Menge an Datenpunkten ist es kompliziert, alle m¨oglichen Abl¨aufe, die aus der Wahl von Anfangsclusterpunkten resultieren k¨onnen, mathematisch exakt zu beschreiben. Zwei einfache M¨oglichkeiten, mit der Abh¨angigkeit umzugehen, die in der Praxis h¨aufig gut funktionieren, sind:
• W¨ahle die Anfangsclusterpunkte zuf¨allig aus den Datenpunkten und f¨uhre das Ex- periment mehrmals durch, bis das Ergebnis zufriedenstellend ist.
• Sch¨atze eine “gute” Wahl von Anfangsclusterpunkten aus den Datenpunkten.
(a) Datenpunkte (b) 1 Iteration
(c) 2 Iterationen (d) 3 Iterationen
(e) 4 Iterationen (f) 5 Iterationen
Abbildung 7: Anwendung desK-Means Algorithmus auf synthetisch erzeugte Daten. Je- de Farbe zeigt einen Cluster an. Die Clusterpunktezu Beginnder Iteration sind mit einem “o” und ihre Updates am Endeder Iteration mit einem “x” markiert.
Kostenfunktion
In welchem Sinne verbessert sich die Situation am Ende einer Iteration im Vergleich zum Beginn? Wir haben in den bisherigen Beispielen beobachten k¨onnen, wie sich im Lau- fe der Iterationen eine Dynamik entwickelt, die am Ende zu einer plausiblen Gruppierung der Datenpunkte f¨uhrt. Um zu verstehen, warum das so ist und wie die Bezeichnung “plau- sibel” mathematisch zu verstehen ist, werden wir eine neue Funktion kennenlernen, die ein wesentliches Merkmal desK-Means Algorithmus ist.
Wir bleiben bei dem Beispiel aus Abbildung 6 und bezeichnen in jeder Iteration mitdblau die Summe der Abstandsquadrate zu ihrem Clusterpunkt, das heisst
dblau =k~b1−~sblauk2+k~b2−~sblauk2+. . .+k~bn−~sblauk2
wobei~b1,~b2, . . . ,~bndie Ortsvektoren zu den blauen Punkten sind und~sblauder Ortsvektor zum Clusterpunkt des blauen Clusters ist. In gleicher Weise definieren wirdgelb,dorangeund dviolett. Schliesslich z¨ahlen wir alle diese Gr¨ossen zusammen und bezeichnen die Summe mitdgesamt:
dgesamt=dblau+dgelb+dorange+dviolett
Die Gr¨osse dgesamt heisst Kostenfunktion zumK-Means Algorithmus. Sie h¨angt ab von der Einteilung in die Cluster und von den Lagen der Clusterpunkte. Der Name “Kosten- funktion” bezeichnet allgemein bei der Theorie von Algorithmen eine Gr¨osse, die es zu minimieren gilt. Mit Hilfe der Kostenfunktion k¨onnen wir nun pr¨azise erkl¨aren, in wie fern sich die Situation am Ende einer Iteration verbessert hat, n¨amlich, dass sich die Kos- ten verringert haben.
Aufgabe 12
(a) Argumentiere, warumdgesamtbei der Durchf¨uhrung des 1. Schritts imK-Means Al- gorithmus (siehe S. 10) h¨ochstens kleiner (aber nicht gr¨osser) werden kann.
(b) Argumentiere, warumdgesamtbei der Durchf¨uhrung des 2. Schritts imK-Means Al- gorithmus (siehe S. 10) h¨ochstens kleiner (aber nicht gr¨osser) werden kann.
Tipp: Schaue dir noch einmal Abschnitt 3.1 an.
Ist es m¨oglich, dass unendlich viele Iterationen n¨otig sind?
In der Beschreibung desK-Means Algorithmus wurde vereinbart (siehe S. 10):
“Das Verfahren wird beendet, entweder nach einer zu Beginn festgelegten Anzahl an Durchl¨aufen, oder wenn sich in einem Durchgang die Zuordnung in die S¨acke nicht mehr ver¨andert im Vergleich zum vorherigen Durchgang.”
Wenn wir darauf warten, dass sich die Zuordnung in die S¨acke (Cluster) nicht mehr ver¨andert, sollten wir sicherstellen, dass es in jedem Falle irgendwann einmal dazu kommt, denn andernfalls warten wir wom¨oglich f¨ur immer darauf. Es w¨are n¨amlich denkbar, dass sich in einer bestimmten Situation beijeder Iteration die Zuordnung in die Cluster ver¨andert, und somit unendlich viele Iterationen n¨otig sind.
Der Schl¨ussel zur L¨osung dieses Problems ist wiederum die Kostenfunktion. Wenn wir einen Datenpunkt einem Cluster zuteilen m¨ochten, so haben wirK M¨oglichkeiten dies zu tun. F¨ur die Einteilung von zwei Datenpunkten haben wir f¨ur jeden der beiden K M¨oglichkeiten, also insgesamt K2 m¨ogliche Zuteilungen in Cluster. Indem wir diese
¨Uberlegung weiterf¨uhren finden wir, dass wirKN m¨ogliche Einteilungen derN Daten- punkte in K Cluster haben. Dies ist zwar eine grosse Anzahl, jedoch k¨onnen wir nun argumentieren, dass wir niemals mehr alsKN Iterationen ben¨otigen, bevor der Algorith- mus beendet wird. Insbesondere ist es also unm¨oglich, dass unendlich viele Iterationen ben¨otigt werden. In Aufgabe 12 haben wir uns ¨uberlegt, dass der Wert von dgesamt im Laufe einer Iteration entweder gleich bleibt (wenn sich in der Zuordnung in die Cluster nichts ver¨andert und der Algorithmus somit beendet wird) oder kleiner wird. Sp¨atestens nachKN Iterationen kann es aber keine Zuordnung in Cluster mehr geben, bei derdgesamt noch kleiner wird als den Wert, den wir schon erreicht haben. Somit mussdgesamtgleich bleiben und der Algorithmus findet ein Ende.
Aufgabe 13 Erkl¨are nochmals in eigenen Worten, warum es nicht m¨oglich ist, dass sich in unendlich vielen aufeinanderfolgenden Iterationen die Zuordnung in die Cluster ver¨andert.
Globales oder lokales Minimum
Wir haben nun gelernt, dass derK-Means Algorithmus beendet wird, wenn die Kosten- funktiondgesamtin einer Iteration nicht mehr kleiner wird sondern stattdessen gleich bleibt.
Nun k¨onnte man meinen, dass in diesem Falle der minimal m¨ogliche Wert vondgesamter- reicht wurde. Dem muss aber keineswegs so sein. Alles was man weiss ist, dass man mit den erreichten Clusterpunkten keine bessere Einteilung in Cluster erreichen kann, und
sich somit die Lage stabilisiert wie in Abbildung 6 und 7 jeweils nach 5 Iterationen zu se- hen. M¨oglicherweise existiert aber noch eine ganz andere Wahl von Clusterpunkten, mit denen man noch einen kleineren Wert vondgesamterreichen kann. Dieser Sachverhalt l¨asst sich gut mit dem Verh¨altnis von lokalen und globalen Minima erkl¨aren: Wenn der Algo- rithmus aufgrund einer Stabilisierung der Einteilung beendet wird, wissen wir lediglich, dass wir ein lokales Minimum der Kostenfunktion erreicht haben, jedoch nicht, ob es sich hierbei auch um ein globales Minimum handelt. Die Frage, in welchem lokalen Minimum wir landen, wird entschieden durch die Wahl der Anfangsclusterpunkte.
5 Implementierung des Algorithmus und Anwendung auf ein Photo
Um den Nutzen desK-Means Algorithmus zu demonstrieren, soll er nun auf das Photo aus dem Einf¨uhrungsbeispiel angewendet werden.
Abbildung 8: Beispielphoto
Das Photo hat eine Aufl¨osung von500×667und besteht somit aus500×667 = 333500 Pixeln. Die Farbtiefe des Photos betr¨agt8bit pro Farbkanal im RGB-Farbraum. Was be- deutet das? Jeder Pixel kann eine Farbe annehmen, die aus einem Rot-, Gr¨un- und Blauan- teil zusammengesetzt ist; die Grundfarben rot, gr¨un und blau sind die sogenannten Farb- kan¨ale. Innerhalb eines Farbkanals stehen8bit, das heisst,28 = 256Werte, zur Abstufung der Helligkeit zu Verf¨ugung. Diese Werte werden durch eine ganze Zahl zwischen0und 255ausgedr¨uckt, wobei 0 = dunkel und 255 = hell. Eine m¨ogliche Farbe besteht so- mit aus drei Zahlen, zum Beispiel(34,144,80), die die Helligkeitsstufen des Rot-, Gr¨un-
und Blauanteils (in dieser Reihenfolge) beschreiben. Ausf¨uhrliche Informationen ¨uber den RGB-Farbraum kannst du in [Wikipedia, 2016] finden.
Aufgabe 14
(a) Wieviele Farben lassen sich mit8bit pro Farbkanal audr¨ucken?
(b) Versuche, in Abbildung 9 die folgenden Farben zu finden:(0,255,0),(255,0,255), (0,0,153),(0,204,204)
Abbildung 9: Farben im RGB-Farbraum (Quelle: [rgb, 2016])
Damit wir die Gr¨osse der Datei reduzieren, m¨ochten wir nun das Photo in Abbildung 8 durch eine geringere Anzahl an Farben darstellen. Dabei soll jedoch das dargestellte Motiv m¨oglichst gut erhalten bleiben. Wie k¨onnen wir eine geeignete Auswahl f¨ur die Farben treffen? F¨ur dieses Vorhaben werden wir denK-Means Algorithmus einsetzen.
Da die Farbe jedes Pixels durch ein Tupel aus drei Zahlen festgelegt ist, k¨onnen wir uns diese Information als einen Punkt im3-dimensionalen Raum vorstellen. Das gesamte Photo ist somit dargestellt als eine Menge von333500(Daten-)punkten im Raum. Den Ort jedes Pixels im Bild merken wir uns und legen diese Information dann f¨ur f¨ur den Moment beiseite (zum Beispiel k¨onnen wir alle Pixel durchnummerieren).
Aufgabe 15 Was bedeutet es, die vorliegenden Datenpunkte im Raum zu clustern? Was repr¨asentieren dabei die Cluster und was die Clusterpunkte?
Damit wir eine “gute” Darstellung des Motivs im Photo erhalten, m¨ussen wir also die vorliegenden Datenpunkte geeignet clustern. DerK-Means Algorithmus liefert nicht nur
diese Einteilung, sondern auch die zugeh¨origen Clusterpunkte. Dabei repr¨asentieren die Clusterpunkte jeweils diejenige Farbe, durch die die tats¨achliche Farbe eines Pixels im Originalphoto ersetzt wird.
5.1 Implementierung des Algorithmus
Der folgende Code implementiert denK-Means Algorithmus in der mathematischen Si- mulationssoftware MATLAB. Alternativ kann der identische Code auch in der kostenlosen Software Octave [Eaton, 2016] eingesetzt werden. Du kannst den untenstehenden Code in das Programm kopieren und auf eigene Photos oder andere Daten anwenden, um sie zu clustern. Neben dem elementaren Syntax zur Definition von Konstanten, Vektoren und Matrizen, werden hierbei die MATLAB-Funktionen “norm” und “min” verwendet. Dar¨uber hinaus kommen einigefor-Schleifen zum Einsatz. Wir werden hier nicht jeden Befehl be- sprechen, sondern nur die wichtigsten Schritte f¨ur den Algorithmus erkl¨aren. Falls du die genaue Funktion bestimmter Befehle verstehen m¨ochtest, kannst du [MathWorks, 2016]
konsultieren.
K-Means Zun¨achst wird eine Funktion “kmeans” programmiert, welche unter Angabe der Datenpunkte, Anfangsclusterpunkte und Anzahl an durchzuf¨uhrenden Iterationen den K-Means Algorithmus durchf¨uhrt und am Ende jeden Datenpunkt durch den zugeh¨origen Clusterpunkt (aus der letzten Iteration) ersetzt.
Der Name “MATLAB” ist eine Abk¨urzung f¨urmatrix laboratoryund das Programm ba- siert darauf, m¨oglichst viele mathematische Gr¨ossen als Matrizen zu behandeln. In diesem Geiste stellen wir uns beim Programmieren der Funktion f¨ur denK-Means Algorithmus vor, dass die Datenpunkte nicht als Menge gegeben sind, sondern die Koordinaten jedes Punktes zeilenweise in einer MatrixAgespeichert sind. Ebenso seien die Anfangscluster- punkte in den Zeilen einer MatrixS gespeichert. Mit diesem Model k¨onnen wir also die Anzahl an DatenpunktenN in Zeile 8 direkt aus der Anzahl an Zeilen inAbestimmen.
In den Zeilen 11–42 programmieren wir die Iterationsschleife, die die darauf folgen- de K-Means-Iteration M Mal durchl¨auft. Der Schritt des Clustering wird in Zeile 19–
27 programmiert. Um jeden Datenpunkt dem n¨achstgelegenen Clusterpunkt zuordnen zu k¨onnen, berechnen wir in Zeile 23 die Distanz vomi-ten Datenpunkt zumk-ten Cluster- punkt f¨ur alle m¨oglicheni= 1, . . . , Nundk= 1, . . . , Kund speichern den Wert in einer DistanzmatrixD. In deri-ten Zeile vonDstehen dann die Distanzen vomi-ten Daten- punkt zu allen Clusterpunkten. Mit Hilfe desmin-Befehls k¨onnen wir in Zeile 25 nicht nur
den minimalen Wert in deri-ten Zeile vonDbestimmen, sondern, was f¨ur uns vor allem wichtig ist, den Index dieses minimalen Wertes in deri-ten Zeile finden. Dieser Index wird inL(i)gespeichert und sagt uns also, welcher der zumi-ten Datenpunkt n¨achstgelegene Clusterpunkt ist.
Als n¨achstes berechnen wir im zweiten Schritt der Iteration die neuen Clusterpunkte (ab Zeile 29). In Zeile 33–37 addieren wir alle Datenpunkte, die demselben Clusterpunkt zugeordnet wurden und speichern dies in den Zeilen der Clusterpunktmatrix S. Dabei z¨ahlen wir in Zeile 36 mit, wie viele Datenpunkte wir jeweils addieren, da zur Berechnung des Schwerpunktes in (1) durch diese Anzahl noch dividiert werden muss. Diese Division wird in Zeile 39–41 durchgef¨uhrt.
Nachdem wir alle M Iterationen durchgef¨uhrt haben, konstruieren wir die Output- MatrixX, in desseni-ter Zeile derjenige Clusterpunkt steht, der zum i-ten Datenpunkt am n¨achsten liegt.
1 f u n c t i o n X = kmeans (A, S , M)
2 % I n p u t : − D a t e n p u n k t e a l s Z e i l e n i n M a t r i x A , 3 % − C l u s t e r p u n k t e a l s Z e i l e n i n M a t r i x S , 4 % − A n z a h l d e r D u r c h l a e u f e M d e s A l g o r i t h m u s 5 % O u t p u t : M a t r i x X , i n d e r j e d e r D a t e n p u n k t d u r c h d e n 6 % n a e c h s t g e l e g e n e n C l u s t e r p u n k t e r s e t z t wurde 7
8 N=s i z e(A , 1 ) ; %D e f . A n z a h l d e r D a t e n p u n k t e 9 X=z e r o s(s i z e(A ) ) ; %D e f . O u t p u t m a t r i x
10
11 f o r m= 1 :M % D u r c h l a u f s c h l e i f e d e s A l g o r i t h m u s 12
13 K=s i z e( S , 1 ) ; %D e f . A n z a h l C l u s t e r p u n k t e 14 D=z e r o s(N, K ) ; %D e f . e i n e r ‘ ‘ D i s t a n z m a t r i x ’ ’ 15 L=z e r o s(N , 1 ) ; %D e f . e i n e s ‘ ‘ L a b e l v e k t o r s ’ ’ 16 Z=z e r o s(N , 1 ) ; %D e f . e i n e s H i l f s v e k t o r s 17
18 % C l u s t e r i n g
19 f o r i = 1 :N % B e s t i m m e n a e c h s t g e l e g e n e n
20 % C l u s t e r p u n k t zum i−t e n D a t e n p u n k t
21 f o r k = 1 :K % B e s t i m m e D i s t a n z vom i−t e n D a t e n p u n k t
22 % zum k−t e n C l u s t e r p u n k t
23 D( i , k )=norm(A( i , : )−S ( k , : ) ) ;
24 end
25 [Z ( i ) L ( i ) ] =min(D( i , : ) ) ; % S e t z e L ( i ) a l s d e n I n d e x d e s
26 % A b s t a n d s−m i n i m i e r e n d e n C l u s t e r p u n k t s
27 end
28
29 % B e r e c h n u n g d e r n e u e n C l u s t e r p u n k t e
30 S=z e r o s(s i z e( S ) ) ; % L o e s c h e a l t e C l u s t e r p u n k t e 31 n=z e r o s( K , 1 ) ; % D e f . ‘ ‘ Z a e h l v e k t o r ’ ’
32
33 f o r i = 1 :N % Summiere a l l e D a t e n p u n k t e m i t g l e i c h e m L a b e l 34 l =L ( i ) ; % D e f . L a b e l d e s i−t e n D a t e n p u n k t e s
35 S ( l , : ) = S ( l , : ) + A( i , : ) ;
36 n ( l )= n ( l ) + 1 ; % E r h o e h e Z a e h l e r zum l−t e n L a b e l
37 end
38
39 f o r k = 1 :K % T e i l e d i e Summen d u r c h d i e A n z a h l d e r Summanden 40 S ( k , : ) = 1 / n ( k ) ∗ S ( k , : ) ;
41 end
42 43 end 44
45 f o r i = 1 :N % D e f . i−t e Z e i l e d e r O u t p u t m a t r i x d u r c h d e n zum 46 % i−t e n D a t e n p u n k t n a e c h s t l i e g e n d e n C l u s t e r p u n k t
47 l =L ( i ) ;
48 X( i , : ) = S ( l , : ) ;
49 end
50 51 end
Anwendungsbefehl F¨ur die Anwendung auf die Photo-Datei schreiben wir als n¨achstes einen kurzen Befehl, der die eingelesene Datei geeignet umformt und dann die
kmeans-Funktion mit zuf¨allig ausgew¨ahlten Anfangsclusterpunkten aufruft.
Die eingelesene Photo-Datei A ist eine Matrix, in der jeder Eintrag einen Pixel re- pr¨asentiert, das heisst in jedem Eintrag steht ein3-dimensionaler Vektor aus dem RGB- Farbraum. Damit wir unserenkmeans-Befehl auf diese Daten anwenden k¨onnen, m¨ussen wirAso umformen, dass die Datenpunkte in den Zeilen einer Matrix stehen.
Wir bestimmen zun¨achst in Zeile 9 die Gesamtanzahl m an Pixeln im Photo. Da die Eintr¨age aus der eingelesenen Photo-DateiA RGB-Farbwerte mit8bit Farbtiefe re- pr¨asentieren, k¨onnen diese nur ganze Zahlwerte zwischen0 und255annehmen. Dieser
Typ heisstuint8. Wir m¨ochten jedoch bei der Berechnung von Schwerpunkten auch Wer- te zulassen, die nicht ganzzahlig sind. Daher ¨andern wir in Zeile 10 den Typ insingle, der alle Dezimalzahlen (auf “single-precision”) speichern kann. In Zeile 11 organisieren wir die MatrixAso um, dass wir eine Matrix mitmZeilen und3Spalten erhalten. Diese Spalten enthalten gerade die Koordinaten im RGB-Farbraum.
Nun m¨ussen wir noch die Anfangsclusterpunkte ausw¨ahlen. In Zeile 12 generieren wir hierzu K zuf¨allige Zahlen zwischen1 und m und w¨ahlen in Zeile 13 die entsprechen- den Zeilen vonAals die Anfangsclusterpunkte. Schliesslich wenden wir in Zeile 15 den
kmeans-Befehl an und wandeln das Ergebnis wieder in denuint-Typ zur¨uck (dabei wird jeweils auf einen ganzzahligen Wert gerundet). Das Ergebnis wird in Zeile 19 angezeigt.
1 f u n c t i o n X = anwendung (A, K , M)
2 % I n p u t : − D a t e n p u n k t e A a u s e i n g e l e s e n e r B i l d d a t e i 3 % − A n z a h l d e r zu f o r m e n d e n C l u s t e r K ,
4 % − A n z a h l d e r D u r c h l a e u f e M d e s A l g o r i t h m u s 5 % O u t p u t : − M a t r i x X , i n d e r j e d e r D a t e n p u n k t d u r c h d e n 6 % n a e c h s t g e l e g e n e n C l u s t e r p u n k t e r s e t z t wurde 7
8 n1=s i z e(A , 1 ) ; n2=s i z e(A , 2 ) ; % D e f . G r o e s s e d e s B i l d e s
9 m=n1 ∗ n2 ; % D e f . A n z a h l an P i x e l
10 A= s i n g l e (A ) ; % A n p a s s u n g D a t e n t y p von A
11 A=reshape(A , [ m, 3 , 1 ] ) ; % O r g a n i s a t i o n i n Z e i l e n e i n e r M a t r i x 12 c=randperm(m, K ) ; % K z u f a e l l i g e Z a h l e n z w i s c h e n 1 und m 13 S=A( c , : ) ; % D e f . S a l s K z u f a e l l i g e Z e i l e n von A 14
15 X=kmeans (A, S ,M) ; % Anwendung d e r kmeans−f u n k t i o n 16 X= u i n t 8 (X ) ; % A n p a s s u n g D a t e n t y p von X
17 X=reshape( X , [ n1 , n2 , 3 ] ) ; % R e o r g a n i s a t i o n i n Form d e s B i l d e s 18
19 imshow (X ) ; % A n z e i g e d e s E r g e b n i s s e s 20
21 end
Aufruf M¨ochten wir den Algorithmus3Mal auf die Dateibild.jpganwenden und das Bild in4Farben darstellen lassen, so geben wir folgendes in die Befehlszeile ein:
A= imread ( ’ b i l d . jpg ’ ) ; % E i n l e s e n d e r B i l d d a t e i
anwendung (A, 3 , 4 ) ; % A u f r u f d e s A n w e n d u n g s b e f e h l s
5.2 Ergebnis
In Abbildung 10 sehen wir schliesslich das Ergebnis f¨urK = 2,3,5,10,30jeweils nach 5Iterationen desK-Means Algorithmus. Man beachte, dass die Anfangsclusterpunkte je- weils zuf¨allig aus den Datenpunkten gew¨ahlt wurden und das Ergebnis von dieser Wahl abh¨angt (siehe S. 15). Es l¨asst sich erkennen, dass wir das Motiv durch sorgf¨altige Auswahl an Farben schon mit10bzw.30Farben gut abbilden k¨onnen.
(a) 2 Farben (b) 3 Farben (c) 5 Farben
(d) 10 Farben (e) 30 Farben (f) Original
Abbildung 10: Anwendung desK-Means Algorithmus auf ein Photo
L¨osungen zu den Aufgaben
Aufgabe 1 Das Lineal muss am Schwerpunkt balanciert werden, der sich zus= 13(1.8+
3.9 + 11.7) = 5.8berechnet.
Aufgabe 2
~ s= 1
5(~p1+. . .+~p5) =
1 1 1 1
Aufgabe 3 (a)
~s= 1
3(~a+~b+~c) =
0 5/3
0
(b) Die Mittelpunkte der Seiten a, b und c ergeben sich zu Ma = (−1/2,3/2,0), Mb = (0,1/2,−1/2)und Mc = (1/2,3,1/2). F¨ur die Geradengleichungen der Seitenhalbierenden erhalten wir dann
sa: ~x=
1 2 0
+α
−3/2
−1/2 0
sb: ~x=
0 4 1
+β
0
−7/2
−3/2
sc: ~x=
−1
−1
−1
+γ
3/2
4 3/2
Wir schneiden exemplarisch die beiden Geradensaundsb. Durch Gleichsetzen er- halten wir das Gleichungssystem
1−3 2α= 0 2−1
2α= 4−7 2β 0 = 1−3
2β
Es ergibt sich direktα = β = 23 und somit erhalten wir den Schnittpunkt S = (0,5/3,0)wie in Teilaufgabe (a). Durch das Schneiden der anderen Paare von Ge- raden erhalten wir das gleiche Ergebnis.
Aufgabe 4
(a) Wir k¨onnen den Schwerpunkt bestimmen, indem wir zun¨achst zwei Paar von Punk- ten bilden, zum BeispielAundBsowieC undD. Dann konstruieren wir die Mit- telpunkte der Paarem~1 = 12(~a+~b)undm~2 = 12(~c+d)~. Der Mittelpunkt dieser Mittelpunkte ist dann12(m~1+m~2) = 14(~a+~b+~c+d)~ und stimmt somit mit dem Schwerpunkt der vier Punkte ¨uberein.
(b) Indem wir den zus¨atzlichen Punkt m¨oglichst weit im rechten unteren Bildran w¨ahlen, k¨onnen wir den Schwerpunkt so weit verschieben, dass er nicht mehr in- nerhalb des VierecksABCDliegt.
Aufgabe 5
(c) Der Wert vondwird minimal am Schwerpunkt. Hieraus ergibt sich die allgemeine Vermutung, dass der Schwerpunkt die Summe der Abstandsquadrate zu den Punkten aus der Menge minimiert.
Aufgabe 6 Wir werden zeigen, dass f¨ur beliebigesx∈R d(x)−d(s)>0




![Abbildung 9: Farben im RGB-Farbraum (Quelle: [rgb, 2016])](https://thumb-eu.123doks.com/thumbv2/1library_info/4065376.1546360/22.892.303.588.355.555/abbildung-farben-im-rgb-farbraum-quelle-rgb.webp)