Genauigkeitsuntersuchung der graphischen Triangulation

Research Collection

Doctoral Thesis

Genauigkeitsuntersuchung der graphischen Triangulation

Author(s):

Kobelt, Karl Publication Date:

1917

Permanent Link:

https://doi.org/10.3929/ethz-a-000090528

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Genauigkeitsuntersuchung

der

graphischen Triangulation

Von der

Eidgenössischen Technischen Hochschule

in Zürich

zur Erlangung ^der

Würde eines Doktors der technischen Wissenschaften

genehmigte

Promotionsarbeit

vorgelegt ^von

Karl Kobelt, dipl. Ingenieur

aus Marbach (St. Gallen)

Referent: Herr Prof. Dr. F. BAESCHL1N Korreferent: Herr Prof. Dr. M.OROSSMANN

177

ZÜRICH d 1917.

Diss.-Druckerei Gebr. Leemann & Co.

Stockerstr. 64,

Leer Vide Empty

Meinen Eitern gewidmet.

Leer Vide Empty

Inhaltsverzeichnis

Seite A. Genauigkeitsuntersuchung ^beim graph. RUckwärtseinschneiden.

Einleitung 7

I. Analytische Bestimmung ^der Punktgenauigkeit ^{.... 9}

II. Bestimmung der Konstanten _mt 16

III. Graph. Bestimmung ^der Punktgenauigkeit ²¹

1. Methode (mit gebräuchlichen Zeichnungsinstrumenten) ^{. .} 21

2. Methode (mit Nomogramm) ²²

IV. Punktfehlerkurveaplan ³²

V. Zulässige Genauigkeit und Grenzkurve 38 B. Genauigkeitsuntersuchung ^beim graph. Vorwärtseinschneiden.

I. Analytische Bestimmung ^{des mittleren} Punkt fehlers ... 50

II. Punktfehlerkurvenplan ⁵²

C. Der mittlere Ho'henfehler bei graph, eingeschnittenen Punkten.

I. Analytische Bestimmung ^des mittleren Höhenfehlers .

•

. . 53

II. Tabelle fur den mittleren Höhenfehler ₆₁

III. Nomogramm für den mittl Höhenfehler 63

Leer Vide Empty

A. Genauigkeitsuntersuchung ^beim graph. Rückwärtseinschneiden.

Einleitung.

Die pothenot'sche

Aufgabe

^{wird inder}

topographischen

^Praxis fast durchwegs ^{nach dem} indirekten Lehmann'schen Verfahren mit Hilfe des

fehlerzeigenden

Dreiecks

gelöst.

Die

Genauigkeit

des ^aus drei

gegebenen

^Punkten

A, B,

^C rückwärts bestimmten neuen Punktes P hängt ^{nicht allein von} den Fehlern

ab,

welche durch Instrument und Beobachter ver¬

ursacht

werden,

sondern die

Hauptfehlerquelle liegt

^{im Probleme} selbst. Je nach der Lage des Punktes P zu den

Ausgangspunkten,

und

je

nach der

Lage

dieser

Ausgangspunkte

^unter

sich,

wird die erreichbare

Genauigkeit

eine andere sein.

Sowohl bei der

indirekten,

als bei der direkten

Auflösungs¬

methode machen sich in

jedem

^{Fall 2} Fehlereinflüsse

geltend,

wenn auch in etwas verschiedener Form.

1. Je weiter P von den Punkten A,

B,

C entfernt

liegt,

^umso schleifender werden sich die 3 Visurstrahlen bei der in¬

direkten Methode

schneiden,

und umso

weniger

genau lassen sich beim direkten Verfahren die Zentren der 3 Konstruk¬

tionskreise konstruieren!

2.

Liegt

^P auf dem durch ABC

gehenden Kreise,

^{oder in} seiner unmittelbaren

Nähe,

so ist die

Bestimmung

^{von P} keine

eindeutige,

^{oder eine} ganz ungenaue. Die Ursache

liegt

ⁱⁿ der nicht erkennbaren fehlerhaften

Orientierung

beim indirekten Verfahren und in zu schleifender

Schnittbildung

der 3 Konstruktionskreise bei direkter

Lösung.

Es ist somit in Rücksichtauf diese

systematischen

^Fehler

belanglos,

^{nach welchem von} den vielen in der Literatur ange¬

gebenen

^Verfahren die

Punktbestimmung durchgeführt wird,

^ins¬

besondere ob nach direkter oder indirekter Methode. Die _ge¬

nannten Fehlerursachen haften an den Verhältnissen des Pro¬

blèmes selbst.

In

nachfolgenden Ausführungen

^{werden die}

Genauigkeits¬

verhältnisse eines

beliebigen pothenotischen

^Falles

(also

^für ganz

beliebige Gruppierung

^{der 4 Punkte} A,

B,

^{C und}

P)

^{näher unter¬}

sucht.

1. Vorerst wird ein

analytischer

Wert für den mittleren Fehler des Punktes P

angegeben.

2. Dann stellen wir

graphische

Verfahren

auf,

^damit der

Topograph

^{auf dem}

Felde,

^ohne

jede

Rechenarbeit bei

beliebigen Punktgruppierungen

die erreichbare

Genauigkeit

des poth. bestimmten Punktes

prüfen

^kann.

3. Ferner möchten wir durch Punktfehler-Kurven¬

pläne

die Genauigkeitsverhältnisse ^im Bilde

festlegen.

4. Es soll eine

Genauigkeitsgrenze vorgeschlagen

werden.

Dabei

geben

^{wir dem}

Topographen

ein Mittel an die

Hand,

das ihn

befähigen soll,

^ohne

Rechnung

und ohne Zwischenkonstruktion ausden Lageverhältnissender 4 Punkte A,

B, C,

^{P beurteilen zu}

können,

^{ob die}

zulässige Genauig¬

keit erreicht werden kann oder nicht.

I. Analytische Bestimmung ^der Punktgenauigkeit.

In den Astronomischen Nachrichten Nr. 1117

(Bd. 47)

^ver¬

öffentlicht der dänische Finanzminister Andrä im Jahre 1858 eine

analytische Bestimmung

^der

Genauigkeit

^des

pothenotisch

ermittelten Punktes.

Andrä bestimmt nach dem Gauß'schen

Fehlergesetz

^{die Glei¬}

chung

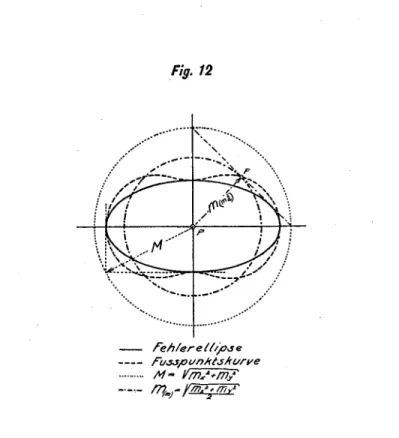
der wahrscheinlichsten

Fehler-Ellipse

und leitet Formeln ab für die große ^{und kleine} Halbachse

derselben,

^woraus sich der mittlere Punktfehler

angeben

läßt.

Unsere

nachfolgende Ableitung

^{führt auf} etwasanderem

Wege

zum selben Resultat

(siehe Fig. 1):

Man bezeichnet mit

A, B,

C die wahren

Projektionen

^der

Objekte

^{auf dem}

Meßtischblatt,

^{mit P den}wahrenOrt der

Station,

mit

Q

die fehlerhafte Bestimmung

derselben,

^mit uu a2) a3 die Winkel der Visuren

PA, PB,

^{PC mit einer}

beliebigen

^{durch P}

gezogenen x-Achse. Unter der

Voraussetzung,

daß die Einstel-

lungsfehler

als verschwindend anzusehen

sind,

^{werden die in den} verschiedenen

Einstellungen

^durch

Q, parallel

mit der Kante des Lineals _gezogenen Linien

QA', QB', QC

^{unter sich dieselben} Winkel

(«3

^—

a,)

^und (a2^—ai) einschließen wie die Strahlen

PA, PB,

^PC.

Wird durch

Q

^ein neues

System

von Linien

QA", QB", QC"

beziehungsweise

zu

PA, PB,

^PC

parallel

gezogen, ^so bilden diese Linien überall

denselben,

^{von der} fehlerhaften

Orientierung

des Meßtisches herrührenden Winkel ^m mit den

Richtungen QA', QB'r QC.

Die

Perpendikel

^{von A auf}

QA',

^{von B auf}

QB'

^{und von C} auf

QC

können als die zusammengesetzten mit derselben

Genauig¬

keit

gegebenen

^wirklichen

Beobachtungsfehler angesehen

^werden.

Bezeichnet man daher diese

Fehler,

die zum Teil aus fehlerhafter

Tischorientierung,

^{zum Teil aus}

Zeichnungsfehlern bestehen,

^mit

Vi, v2, v3, so ergeben ^{sich bei}

Berücksichtigung

^{nur der ersten} Potenzen von ^co und _q nach

Fig.

^{1 die}

Gleichungen:

Vi ^— i-iw

+

q sin

Op + «i)|

v2 ⁼ r2w

+

q sin

[ff + a2) (1)

v3 ⁼ r3w

+

q sin

(ff + «3) 1

Wir setzen nach Fig. 1:

qsin<p

⁼ y; qcos<p ^{= x} und führen als

Abkürzungen

^ein:

cosa ⁼ a; sin^{a =} b.

Obiges Gleichungssystem geht

^{über in:}

Vi =r1w

+

aiy

+ biX|

v2 ⁼r2«

+

a2y

+ ^b2x

^'

⁽²⁾

v2 ⁼r3w

+

a3y

+ b3x I

Diese

Gleichungen (2)

^{können als}

Fehlergleichungen

mit den drei Unbekannten _œ, x, y

angesprochen

^{werden. Wir}

setzen eine

Ausgleichung

nach der Methode der kleinsten

Qua¬

drate _an, trotzdem diese nicht

notwendig

^{wäre zur}

Bestimmung

von 3 Unbekannten aus nur 3

Gleichungen.

^Es steht uns aber nichts im

Wege, gleichwohl

diesen Ansatz zu machen. Er _emp¬

fiehlt sich

geradezu

zur

Bestimmung

^der mittleren Fehler von x und _y, also in 2 zueinander senkrechten Richtungen, ^weil die direkte

Bestimmung

^{mit Hilfe des} Gauß'schen

Fehlerfortpflan¬

zungsgesetzes

algebraisch

^sehr

kompliziert

sein würde.

Die

Verbesserungen

Vi, v2, v3 sind

je

⁼

0,

weil keine Wider¬

sprüche

im

Gleichungssystem (2)

^auftreten.

Die

Absolutglieder

^der

Fehlergleichungen

^{sind =}

0,

weil der

Koordinatenanfangspunkt

als mit P zusammenfallend angenommen worden ist.

Die

Normalgleichungen

^für

Gleichungssystem (2)

lauten:

[rr> + [ar]y + [br]x +

^{0 = 0}

|

[ar> + [aa]y + [ab]x +

^{0 = 0}

(3)

[br> + [ab]y + [bb]x +

^{0 = 01}

— 11 ^—

Wir eliminieren w. Aus der ersten der

Gleichungen (3) folgt:

~

[rr]

^'

[rr]

Diesen Wert für ^œ in

(2) eingesetzt ergibt:

^die umgewan¬

delten

Fehlergleichungen

^{mit nur} 2Unbekannten

xundy.

Vi ⁼ U

[ar]

C "$> ⁺ (*

_Ijrj/ oder in

v3 ⁼

as'y 4- b3'x

^=(»,-,0), ⁺ ^-^):

^Form

(4)

Die mittleren Fehler der Unbekannten x und y

ergeben

^{sich zu:}

m ^_

1/

*

_

|/ [aV]

M*^- mi

F _[b'b'-l]

^{- mi '}

r [aVïïbV] -[a'b']2

M _M

1/TbVT

^_ m

1/ ^[bV]

Das

Quadrat

des mittleren Punktfehler sistdefintions¬

gemäß gleich

der Summe der

Quadrate

^der mittleren Fehler in zwei auf einander senkrecht stehenden

Richtungen:

M? ⁼

Mx2 + My2 oder,

^wenn

obige

Werte

eingesetzt:

[aV3 + [bV]

M2--

mî

[a'a'][b'b']-[aV]2

Hierbei kann der mittlere Fehler der Gewichtseinheit

(5)

m,

nicht

angegeben werden,

^weil

[pvv]

^{=0 und n—u=0. In} Abschnitt II wird

gezeigt,

^wie nu auf anderem

Wege,

^durch

praktische Beobachtungen gefunden

werden kann.

Die Ausdrücke

a',

b' in Gl.

(5)

werden wieder durch die ur¬

sprünglichen

Koeffizienten _a,

b,

^r

ausgedrückt.

[a'a]

⁼

(3l

^—

nfe) ^{+ (as}

^—r,

[bV]

⁼

[bb]

^-

W

[ar]

2[rrJ

Somit

Jf2:

[^^(.-^(^-^^....(a

r3[rr]J

=

[aa]

^-

^*

[rrj

r»[rr]nbs l3[rr]

=

[ab]

^-

[aa]

^—

^ -f [bb]

^—

^

N-^N-fêîVN-W

[arHbr]

[rrj.

mï (6)

a,⁼ cos a,;

b, ⁼ sin _a,

siehe Gl.

(1)

^und

(2)

Lassen wir die x-Achse mit der

Mittel-Richtung

zusammen¬

fallen,

^{so kann nach}

Fig.

² gesetzt werden:

a2=0

«3=^—»?

somit:

[aa]

⁼

cos21 -f~

^cos2'J

~f"

¹

[bb]

^{== sin2}

§ -f- sin21)

[ab]

^{= sin}

|

^cos

|

^—_{sin »/}cos ij

[ar]

^{= a^os}

|

-f-

bx

^cos17

-f-

ct

[br]

⁼a! sin

£

^—

bx

sin r\

[rr]

⁼

a! + b? + c?

} (7)

— 13 ^—

[ar]2

⁼ aj

cos21 -\- bf

^cos2

rt-\- ^c\-\-2

&t

bt

^cosScos_rj

-\-

2 ax ct ^cos

| -f- -(-

²

bi

ct ^cosjj

[br]2

⁼

af sin21 -\- bf sin21;

^{— 2 aj}

^bx

^{sin £}sin ?j

[ar] [br]

⁼

af

^sin

|

^cos

|

^—

bf

_{sin 17}^cosrç

-|-

a!bx ^sin

|

^cos

17"—

— a!

bx

^cos

£

_{sin 17}

-f-

ax cx sin£^— bxCx sin 77

„,_m,

([aa] [rr]

^-

[ar]2 + [bb] [rr]

^-

[br]2) [rr]

-mi"

([aa][rr]_[ar]2)([bb][rr]-[br]2)-([ab][rr]-[ar][br])2

_ m2

([aa]

⁺

[bb])[rr]-[ar]2-[br]2

~

m]

([aa][bb]-[ab]2) [rr]

^-

[ar]^[bb]

^-

[br]2[aa] + 2[ar][br][ab]

I II III IV

Zahler= 3^•

(af + bf -j- cf)

^—

(a? + bf + cf -j-

2 at

bt

^cos

(£+>?) + -(-

2 at Ci ^cos

£ -j-

²

^bx

ct ^cos»7

=

2af + 2bf + 2cf —2aib!

^cos

(£ + r;)

^—2 ax cx cos£^—

— 2

bi

cx ^cosj;

aus der

Figur

^2:

bf -j- ^cf

^—2

bi

Cx cost] ⁼a2J

a? + cf

^— 2 ax Cx ^cos

£

^{= b2 !} -f-

a? + bf

^—2 ax

bi

^cos

(rj + D

⁼

c2)

Zähler ⁼ a2

+

^b2

-f

^c2

I.[rr]

IV.

II.

111.

a?

^{sin2 £}_{cos2 rj}

-f- b2sin2£cos2

_rj

-\-

^c2sin2

(£ -f- rj) +

^{a2 cos2}

£sin2

_rj

-f- b2£0S2£sin2

_rj +

cxsin2£

-f-

²

^a?

^sin

^£

^cos

^£sin

»;^cosjj

-j-

²

b?

^sin

£

^cos

£

_{sin r;}cos»/

-f- c|

^sin2/;

+

^a2

sin21 + afsin2»;

+ b2sin2£

-\- bfsin2r;

> pos.

2a2sin2

£eos2£

^•2

b?

^sin

|

^cos

£ sin»;

cos»;

-f-2ax bx

^sin

2£

^cos

£

^cos_>;

—(—

2 ax cx sin2

£

^cos

£

2a2sin

£

^cos

£sin

_»/cosrj

-j-

^{2b2 sin2}»;cos2 _»y

2ax

bx ^sin

^sin

>; cos2 rj —2 ax cx sin

£

_{sin »;}

-(-2b!

^{cx sina} rjcos»;

2bx

cx sin

£

^cos

£

^sin

2.

—2 axbx^sin

£

^cos2

£

_{sin »;}

+

2 ax

bx

^cos

£ sin21?

^cosrj

COSTJ

a2sin2

£cos2£-f- b,sin2£cos2

»;

-f-c2sin2£ -}~2ax

bx ^sin2

£cos£cos

_rj

-f-2ax

^{cx sin2}

£cos£ -f- 2bx

cx

sin2£cos

_>;

-f-

^{a2 cos2}

£

^sin2_jj

-f-

^{b2 sin2}

»ycos2

»;

+c2sin2»y -[-2ax bx cos£sin2»;

cos»;

+ 2ax

cx

cos£ sin2»; -(-

²

bj

cx sin2 rj^cos17

af

^sin2

£

^cos2

£ -f~ bf

^cos2

£sin2

rj

+

^{a2 sin2}

£

_{cos2 »;}

+

^b2sin2

»ycos2

»;

-f- a2sin2£ -)- b2sin2»;

—2 ax bx ^sin

£

^cos2

£

sin »;

—2 ax

bx

^sin

£

^sin _i?^cos2_»;

—

2ax

bx ^sin

£sin

_rj

I

^neg.

Nenner = a2 sin2_/^

-f- b^

^sin2

£ -J- ^ci

^sin2

(£

⁺

»?) +

2 ax

bx

^sin

£

_{sin »;} ^— 2 ax cx sin r\sin

(£ + rj)

Nenner =

(ax

^sinrj

+ bx

^sin

£

^—cx sin

(£ + *?))2

2bxcx sin

£

^sin

(£ -f- »?)

If2 :m

a2

+

^b2

+

^c2

(ax

sin rj

-f- bx

^sin

£

^- cx sin

(£ -f- »?) )2 (A)

pos.

neg

— 15 ^—

In Gl.

(A)

^treten 8 variable Größen auf. Ihrer 5

genügen jedoch,

^{um die}

Lage

^{der Punkte}

A, B, C,

^P

eindeutig festzulegen.

Die 3

überzähligen

Variabein können auf Grund des

geometrischen Zusammenhanges

^{mit den 5}

notwendigen

Variabein durch diese letztern ausgedrückt werden.

Aus

Fig.

²

folgt:

. , a sin^{ri =} sintf, ^—

Ci

... b

sinS⁼ sina, ^—

Ci

bf

^4-c2—a

.

a24-c?-b2

cos|^——~

2at

C!

Diese Werte in Gl.

(A)

eingesetzt:

at sin »/+

bt

^sin

f

^—ct sin

(| -f- rj)

⁼

a , b _, . , . bf+cf—-a2

= ^—ax ^sin A H bt ^sinat ^{-r- b sin}ax ^———i

Cj Ci .

2

bx

cx

. a

a'f + cf-b2

aSinft

2alCl

a .

a

fa2-c2 + b2\

, b .

fb2-c?4-a2\

=^—sin/ïj^{•b cos}a1

-|

^sin«,^•acospx

=

—sin(«! 4-/?i)

ci somit

3f-a^bXsinTa^^'mi ^(B)

Diese Formel B hatnun 6 Variable. Es ist nicht

zweckmäßig,

die letzte

überzählige

Variable auch noch

auszuschalten,

weil der Ausdruck für AI eine sehr

komplizierte

Form annehmen würde.

Andrä1)

^{hat ebenfalls diese}

Gleichungsform

für die Diskussion verwendet.

Die

Ergebnisse

der einleitend

gemachten Betrachtungen

über die Grenzwerte von M werden durch

obige

Formel

bestätigt.

!) ^{Siehe Andrä} (Astr. Nachr., ^Nr. 1117, Bd. 47).

Es ist:

21=^co für P im Unendlichen

„ P auf demKreisdurch ABC

(oder

^aufder Geraden

ABC)

21⁼unbestimmt für P zusammenfallend mit

A,

^{B oder C.}

21=Minimum für das Centrum des dem Dreieck ABC

einge¬

schriebenen

Kreises,

^{und unter} allen Dreiecken für das Centrum des

gleichseitigen

^Dreiecks.

II. Bestimmung ^{der Konstanten}

^{m^}

Der numerische Wert der Konstanten nu wird ermittelt aus

dem mittleren Punktfehler AI für

irgend

einen bestimmten

Fall,

am besten für das Zentrum des einem

gleichseitigen

^Dreieck

eingeschriebenen

^{Kreises. Bei diesem}

günstigsten

Fall würden sich die Fehlereinflüsse

infolge

schiefer Schnitte und

infolge

der

Orientierungsschwierigkeiten

^{auf ein Minimum} reduzieren.

Die

praktischen

^{Versuche zur}

Bestimmung

^{von nii sind von} der Schweiz.

Landestopographie (Abteilung

^für

Topo¬

graphie)

^{in Bern unter}

Leitung

^{von Herrn}

Ingenieur

^{Le u}pin

wie

folgt durchgeführt

^worden:

Der Punkt

„Landestopographie"

^{auf der Zinne der}

Topo¬

graphischen

^{Anstalt ist}

pothenotisch

^mit dem Meßtisch

aufge¬

nommen worden aus den 3 Punkten:

„A

^Brauerei Gurten"

„

ti

Pauluskirche"

A

Schloßhalde Schulhaus.

Der

Neupunkt

ist durch 5

Topographen (Leupin, Schwarz, Perrin, Nußberger

^und

Tank) je

viermal, voneinander

unbeeinflußt,

konstruiert

worden,

so daß 20vollständig voneinander

unabhängige Beobachtungen

^für die drei Maßstäbe:

1 : 10 000 1 : 25 000 1 : 50 000 vorliegen.

— 17 ^—

Es wurde Meßtisch Nr. 34 von der L. T.

(Hildebrand)

^ver¬

wendet. Die Meßtischblätter wurden auf dünne Aluminiumblätter

aufgezogen,

^so daß der

Papiereinsprung

^{zu Null} angenommen werden konnte. Zum Auftragen der Dreieckspunkte, ^{sowie zum}

Abgreifen

der Koordinaten des neu bestimmten Punktes wurde der

Koordinatograph

^{Coradi der}

Eidg.

Techn. Hochschule Zürich verwendet.

Die Differenzen zwischen den aus den Koordinaten der Aus¬

gangspunkte

berechneten und den auf dem Meßtischblatt ab¬

gegriffenen

Koordinaten des

Neupunktes ergaben

^{die Werte}

Ax

und

Ay,

^{als wahre Fehler in}

Richtung

^{der x-}

beziehungsweise y-Achse.

Diese Werte sind von 2 Herren .voneinander unbeein¬

flußt erhoben worden.

Der wahre Punktfehler in der Form eines Vektors

ergibt

sich zu:

e=

VÄTTÄ!

und der mittlere Punktfehler aus den 20

Bestimmungen

zu:

M= +

1/13,

'

n

mit einem mittleren Fehler der

Bestimmung

von .1/:

Jf„⁼±

0,707^

^•

Vn

a)

^{1 :} 10 000:

Ax Ay

^{£ £6}

Ax Ay

^{£ ££}

mm mm mm mm mm mm

0,04 0,00 0,040 0,00160 0,04 0,03 0,050 0,00250

0,09 0,08 0,120

0,01440

0,13 0,12 0,177 0,03140

0,05 0,10 0,112 0,01255 0,09 0,15

0,175

0,03060

0,01 0,05 0,051 0,00260 0,01 0,01 0,014 0,00019

0,04

0,03

0,050 0,00250 0,01 0,01 0,014 0,00019

0,03 0,07 0,076

0,00577

0,05 0,12 0,130 0,01690

0,02 0,02

0,028 0,00078

0,03 0,02 0,036

0,00130

0,12 0,08 0,144 0,02075 0,12 0,11 0,163 0,02650

0,04

0,05 0,064

0,00410 0,07

0,06 0,092 0,00846

0,01 0,02

0,022 0,00048

0,02

0,00 0,020

0,00040

Ax Ay

^{e ee}

Ax Ay

^{£ ee}

mm mm mm mm mm mm

0,05 0,02 0,054 0,00292 0,01 0,01 0,014

0,00019

0,11 0,02

0,112

0,01256

0,09

0,03 0,095

0,00901

0,00 0,01

0,010

0,00010 0,05 0,04 0,064

0,00410 0,14 0,05

0,149 0,02220

0,13

0,02

0,134 0,01799 0,13 0,02

0,131 0,01720

0,14

0,02 0,141 0,01986 0,00 0,01 0,010 0,00010

0,03

0,01 0,032 0,00102 0,02

0,08

0,082 0,00671

0,05

0,13

^0,139 0,01932

0,04

0,08

0,089 0,00790 0,04 0,11 0,117 0,01368

0,03 0,05 0,058

0,00336

0,01

0,06

0,061 0,00372 0,00 0,03 0,030

0,00090 0,03

0,01 0,032 0,00102

(XI

⁼⁼

^0,13948 [££]

^{== 0,20835}

M=

1/0.13948 ⁺

^0,20835 = ( Q93

1 40

MB ⁼

-^=--0,707

=0,010 ^mm

V ⁴⁰ Somit

M— ± (0.093 ⁺

0,010)

^mm

b,

^{1 : 25000:}

Ax Ay

^{e ££}

Ax Ay

^{£ ££}

mm mm mm mm mm mm

0,04 0,01 0,041 0,00168

0,03

0,01 0,032

'

0,00102

0,01

0,04

0,041 ^•

0,00168

^0,03

0,05 0,058

0,00336 0,08 0,02

0,082 0,00671 0,11 0,00 0,110 0,01212

0,01 0,03 0,032 0,00102

0,03 0,06 0,067 0,00449

0,01 0,03

0,032

0,00102 0,03 0,02 0,036

^'

0,00130

0,01 0,01 0,014 0,00019 0,00 0,06 0,060 0,00360

0,06 0,07 0,092 0,00846

0,05 0,09 0,103

0,01060

0,08 0,03 0,085

0,00721 0,06 0,01

0,061 0,00372

0,06

^0,05

0,078 0,00609

0,05

0,02

0,054

0,00291

0,00 0,03

0,030

0,00090 0,02 0,07 0,073 0,00531

19 ^—

Ax Ay

^{e ££}

Ax Ay

^{£ ee}

mm mm mm mm mm mm

0,06

0,02 0,063 0,00396

0,05 0,03

0,058

0,00336

0,00

^0,02

0,020 0,00040

0,03

0,06

0,067 0,00449

0,01 0,02 0,022

0,00049 0,03

0,07 0,076 0,00578

•

0,00 0,01 0,010 0,00010 0,03 0,06 0,067 0,00449 0,07 0,04

0,081 0,00656

0,02 0,04 0,045 0,00203 0,00 0,08 0,080

0,00640

0,02 0,10 0,102 0,01040 0,14 0,10 0,172 0,02960 0,15 0,11

0,186 0,03460

0,06 0,03 0,067

0,00449

0,04 0,04 0,057 0,00325

0,04 0,11 0,117

[>]

⁼

0,01368

0,05

0,15 0,158

[££]

⁼

0,02500

= 0,10064 ⁼

0,14183

M=

1/0,10064 + 0,14183

^_ _{+ „ogo}

J

^~ ₃₈

MB ⁼

0,707

^•

-i==

⁼ ±

0,009

^mm

V

³⁸

Somit

M= ±

(0,080

⁺

0,009)

^mm c) ^{1 :} 50 000:

Ax Ay

^{e ee •}

Ax Ay

^{£ ££}

mm mm mm mm mm mm

0,06

0,06 0,085

0,00721 0,01

0,03

0,032

0,00102 0,02

0,09

0,092

0,00847

0,00

0,06

0,060

0,00360

0,01 0,05 0,051

0,00260 0,00

0,04 0,040

0,00160 0,13 0,10 0,164 0,02690

0,11 0,08

0,136 0,01850

0,04 ^• 0,04

0,057 0,00325 0,05 0,02 0,054

0.00291

0,01 0,01

0,014

0,00019 0,00 0,06

0,064

0,00360

0,01

0,01 0,014 0,00019 0,04 0,05

0,064

0,00410

0,09

0,03

0,095

0,00901 0,08 0,07 0,106 0,01122 0,00 0,00 0,000

0,00000 0,00

0,04 0,040 0,00160

•0,00

0,01

0,010

0,00010

0,00 0,04 0,040 0,00160

Ax Ay

^{£ £6}

^Ax Ay

^{£ ££}

mm mm mm mm mm mm

0,04 0,05 0,064 0,00410 0,04 0,05 0,064 0,00410 0,05 0,07 0,086

0,00740 0,04

0,06 0,072 0,00519 0,02 0,03

0,036

0,00130 0,01 0,03 0,032 0,00102

0,05

0,02 0,054 0,00292

0,05

0,05 0,071 0,00503

0,01

0,05

0,051

0,00260 0,02

0,04 0,045

0,00203 0,08 0,07 0,106 0,01122

0.05

0,07 0,086 0,00740 0,06 0,01 0,061 0,00372

0,07

0,02 0,073 0,00532

0,00

0,00 0,000 0,00000

0,00

0,01 0,010

^0,00010

0,02

0,00 0,020

0,00040 0,00 0,00 0,000 0,00000 0,00 0,03 0,030

0,00090

0,06

0,02 0,063 0,00396

lee]-.

⁼

^0,09248 M

⁼⁼

^0,08390

1/0,09248+0,08390

V 40

— ± 0,066^mm J/b⁼

0,707-

^{°<066 = +}

0,007

^mm

l/40

Somit M⁼ ±

(0,066

^{± 0}

007)

^mm

Nach Gl.

(B) ^ergibt

^{sich unter}

^Beachtung

^der

vorliegenden

Verhältnisse: ir 1010,

M ^— 1,2134 nii

a) ^Für Maßstab 1:10 000:

1,2134

m1 ⁼ ±

(0,093

^±

0,010)

^mm

nii ⁼ +

(0.077

±

0,008)

^mm

'b)

^{Für Maßstab 1:25000:}

1,2134

nii ⁼ ±

(0,080

^±

0,009)

^mm

mt ^{= +}

(0,066

⁺

0,007)

^mm

c)

^{Für Maßstab 1:50000:}

1,2134

nii ^{= +}

(0,066

⁺

0,007)

^mm

mi ^{= +}

(0,054

⁺

0,006)

^mm

Für die Maßstäbe 1:25 000 und 1:50000

ergibt

^{sich ein}

gerundeter

^{Mittelwert von:}

mt ^{= +}

(0,060

±

0,007)

^mm

— 21 ^—

III. Graphische Bestimmung ^{der Punkt¬}

genauigkeit.

1. Methode.

Die in Abschnitt I

abgeleitete

Formel

(A)

^{kann wie}

folgt graphisch gelöst

werden

(siehe Fig. 3)

^:

,, ,

Va2

₊b2

+

^{c2 Z}

M=+ mj ^{: j-t—.—?—!—} ,t-j—:⁼mi -cr

at ^sin T]-f- bj sin £ ^—ct ^sin(g-)- »;) ^JN Der Wert des Zählers ^Z ergibt ^{sich aus den Dreiecks¬}

abmessungen

als

Hypothenuse

^eines

rechtwinkligen

Dreiecks mit den Katheten c und _p, wobei _p wiederum

Hypothenuse

^eines

rechtwinkligen

Dreiecks mit a und b als Katheten ist.

Z⁼

ÄE

_(nach

Fig. 3).

Zur

Bestimmung

des Nennerwertes N wird die Strecke a! der einen Außenvisur um P gedreht und auf der andern Außen¬

visur

abgetragen. Analog

^wird

bt

auf dieser zweiten Außenvisur

um P

gedreht

^{und auf} der ersteren

abgetragen.

^{Von den neuen}

Endpunkten

^F und G werden die Lote auf die Mittelvisur

gefällt.

Die Strecke Ci auf der Mittelvisur wird um P

gedreht

^und auf einer der beiden Außenvisuren

abgetragen.

^Vom

Endpunkt

K aus fällen wir das Lot k auf die andere Außenvisur.

1. f

-+-

g

+

^{k = N für P innerhalb} des Dreiecks ABC.

2.

f-f-g

^—k== N für P außerhalb des Dreiecks A D C.

wobei

f,

g und k als

positive

Strecken einzusetzen sind.

Erläuterung:

^Winkel £ und Winkel _y

liegen

^immer zwischen 0° und 180°. Sini und

sin»;

^{sind somit immer} po¬

sitiv,

^{also sind} die Strecken

aisin_»;⁼f und bisin £⁼g immer

positiv.

Zur Diskussion von k unterscheiden wir zwei Fälle:

1. P innerhalb des Dreiecks ABC:

dann ist

(f + >?)

^>180» somit k⁼Cisin

(f +

ij)

negativ

;

2. P außerhalb des Dreiecks ABC:

(f + i7)<180°

somit k⁼_Cisin

(£

+

»;) positiv.

Zur Konstruktion von Z und N brauchen die in Fig. ^{3 ein¬}

gezeichneten Hilfslinien

(Kreisbögen

^und

Lote)

gar nicht not¬

wendigerweise gezeichnet

^{zu werden.}

Die Konstruktion kann mit Zirkel und Winkel

genügend

ge¬

nau

durchgeführt werden,

ohne daß ein

einziger

Bleistiftstrich _ge¬

zogen werden muß.

Auf Seite 24 u. ff. wird

gezeigt,

^{wie auch noch nu auf} N

ganz einfache Weise

graphisch gelöst

werden kann.

Will man nicht die

Punktgenauigkeit

^{als solche}

bestimmen,

sondern nur

nachprüfen,

^{ob der}

vorliegende

Fall innerhalb einer bestimmten

Genauigkeitsgrenze liegt,

^{so kann aus} dem Verhältnis

—"p

^ohne

^Rechnung

^sofort entschieden werden, ^ob M

zulässig

ist oder nicht.

Für Mml ⁼

0,3

^mm

und _m1 ⁼ 0,06mm

folgt

_z

— .

0,06

⁼

0,3

N 7

-7TZ-<f⁵ wenn M7M nicht überschritten werden soll.

N

Z 5 7

z.B. In

Figur 3)

^:_-^^{= '} > 5 weit außerhalb der Grenze.

2. Methode.

Nomogramm

oder Rechentafel.

Wir stellen den

analytischen

Ausdruck für die

Punktgenauig¬

keit durch eine Rechentafel dar,

die,

^einmal

konstruiert,

^zur

Anwendung

^nur noch einer kleinen Zwischenkonstruktion

bedarf;

dafür ist

jede

Rechenarbeit ausgeschaltet.

Maurice

d'Ocagne

entwickelt in seinem Werk:

„Traité

de

Nomographic"

^die Methoden zur Konstruktion der Nomo- gramme.

— 23 ^—

Im

Folgenden

soll die Theorie

auszugsartig

^{soweit skizziert}

werden,

^{als dies für das} Verständnis zur

Herstellung

unseres

speziellen Genauigkeitsnomogrammes notwendig

^{erscheint. Wir} halten uns dabei

hauptsächlich

an die

Ausführungen

^{von F.}

Schilling: „Über *die Nomographie

von M.

d'Ocagne.

^Eine

Einführung

ⁱⁿ dieses Gebiet."

Leipzig

^1900.

1.

Begriff

^der Funktionsskala.

Um eine Funktion x⁼f

(a)

^{in Form einer Skala}

darzustellen,

werden auf einer Geraden als

Abszisse,

^{von einem}

Anfangspunkt

aus, für aufeinanderfolgende ^{Werte von} a, die

entsprechenden

Strecken 1. f

(o)

aufgetragen, wobei über den konstanten Modul 1 noch zweckmäßig

verfügt

^{werden kann. Die}

Bedeutung

des Moduls besteht

darin,

^{daß man} die Länge ^{der Skala}

passend

wählen kann. An die durch kleine

Querstriche

bezeichneten End¬

punkte

^{der auf der Geraden}

aufgetragenen

Strecken werden nicht die

Funktionswerte,

sondern die Werte der

unabhängigen

Variabein a angeschrieben.

2. Rechentafeln für Gleichungen zwischen 2 Variabein,

a) Rechentafeln mit vereinigten ^Skalen.

Haben wir die Gleichung fi

(a±)

⁼

f2 (a2),

^{d. h. F}

(a,

a2)⁼⁰ graphisch

darzustellen,

^so tragen wir auf einer Geraden vom ge¬

meinsamen

Anfangspunkt

^{aus in}

gleicher Richtung

^die beiden Skalen _xt⁼1.fi

(«i)

^und x2⁼1.

f2

(a,) auf und erhalten sofort für einen Wert «i den

korrespondierenden

^Wert a2.

Z. B. a2⁼

logb

x⁼1.a2 und x⁼1.

log

^b.

(Siehe Fig. 4.) b)

Cartesische Rechentafel.

In der

Gleichung

^f

(au

a2)^{~0 setzen wir x=}\1a1 und y⁼

12

a2, wobei x und _y

rechtwinklige

Koordinaten seien. Man trägt also auf zwei senkrechten Koordinatenachsen zwei Skalen mit

geeigneten

Modulen auf. Je zwei

zusammengehörende

^Werte

«i, «2 werden dann mit Hilfe der durch

folgende Gleichung

«(«>.«.)

⁼

f(t -t)=-0

dargestellten

Kurve aufeinander

bezogen.

3. Rechentafel für

Gleichungen

zwischen 3 Variabein.

a)

Cartesische Rechentafel.

Es sei die

Gleichung

f

(ax

a2

as)

^{=0 zwischen 3 Variabein}

ai, a2, a3

gegeben.

Setzen wir wieder wie oben x⁼

lx

au y⁼

12

a2, so stellt die

gegebene Gleichung

in der Form f

1-r—,-p~,a3l

⁼⁰

für variable Werte a3 eine ganze Kurvenschar dar. Jede Kurve der Schar wird wiederum mit dem Parameter a3 beschrieben.

Sind dann außer dieser Kurvenschar

(a3)

^{auch durch die kotierten} Punkte der Skalen auf den Koordinatenachsen die

Parallelgeraden

zur Ordinaten-

beziehungsweise

Abszissenachse als Kurvenscharen

(at)

^und

(a2) gezeichnet,

^so

befriedigen

^{3 Werte} au a2, «3 die

gegebene Gleichung,

^{wenn die drei}

zugehörigen

^{Kurven durch} denselben Punkt

gehen.

Werden also zwei bestimmte Werte _«i und a, in die Tafel

eingesetzt,

^{so ist der nach der}

Gleichung

^f

(at

a2

a3)

^{=0 kor¬}

respondierende

^Wert as ohne weiteres als Index der durch den

Schnittpunkt

«ia2

gehenden

Kurve _as herauszulesen.

Für die

Herstellung

^des

Nomogrammes

^bieten

jene

^Fälle besondere

Einfachheit,

bei denen auch die Kurven

(a3) Geraden,

z. B. Strahlenbüschel sind.

Die im

vorigen Paragraphen

^{erwähnte erste}

graphische

^Me¬

thode zur

Bestimmung

des mittleren Punktfehlers

ergab

^einen

•7

Schlußwert M ⁼ _{nu —,} der nach einer cartesischen Rechentafel N

mit den 3 Variabein

M,

Z und N

gelöst

werden soll. Gerade in diesem Fall kann die Kurvenschar

(a3)

^{durch ein vom} Koordinaten-

Nullpunkt ausgehendes

Strahlenbüschel

dargestellt

^werden.

Wir setzen x⁼U.Z und y⁼UN und erhalten die Aus-

gangsgl.

in der Form:

— 25 ^—

m_

.

y

^

=0

mx

12 lj

welche Gleichung ^für jeden ^{bestimmten Wert von M eine ihm}

entsprechende

^Gerade

darstellt,

die durch den Koordinaten-An¬

fangspunkt geht.

Für

l1=l2

⁼10mm und m1⁼

0,06mm

erhalten wir für einen konstanten Abzissenwert x⁼ 100mm die

entsprechenden

^Ordi-

natenwerte _y.

M

(mm)

y

(mm)

0,05

¹²⁰

0,10 ⁶⁰

0,15

⁴⁰

0,20

³⁰

0,25

²⁴

0,30

²⁰

0,35 17,13

0,40 ¹⁵

0,45

13,33

0,50 ¹²

0,55 10,90

0,60

¹⁰

Die Größen Z und N brauchen nicht

zahlenmäßig

^{erhoben zu} werden. Die

Zirkelgrößen

können direkt als Abszissen und Ordi- naten

abgetragen

^werden. Die Gerade des

Strahlenbüschels,

^die durch den so bestimmten Punkt

(Z, N)

^hindurch

geht,

trägt als Index den gesuchten mittleren Punktfehler M.

Will man nicht den mittleren Punktfehler selbst

erheben,

sondern nur

feststellen,

^{ob der}

vorliegende

^{Fall innerhalb der auf¬}

gestellten ^Grenzen

liegt

^oder

nicht,

^{so braucht man sich nur die}

Neigung

^eines

einzigen

^{Strahles zu merken.}

Z. B.i'für

-Mzulassig

⁼

^0,3

^mm

hat der Grenzstrahl die

Neigung

20

=

±

100 5

Man kann sich auf dem Meßtischblatt irgendwo ^nebenaus dieses

rechtwinklige

Dreieck mit dem Kathetenverhältnis ^—- 5

aufzeichnen,

und hat dann nur zu

prüfen,

^{ob der} Punkt mit den

Zirkelgrößen

N und Z als Abszisse und

Ordinate,

innerhalb oder außerhalb des Dreiecks liegt.

b)

^Collineare Nomogramme.

Wir unterwerfen die Cartesische Rechentafel einer duali- listischen oder

reziproken Transformation,

^wie

eine solche im

speziellen

^Falle

beispielsweise

^die Polarenver¬

wandtschaft in Bezug ^{auf einen}

Kegelschnitt

^darbietet

(Prinzip

der Dualität der

projektiven Geometrie).

^Wenn wir noch die Kote

jeder

Geraden dem letzterer

entsprechenden

^Punkte zufügen, so treten also an Stelle der drei Systeme ^{kotierter Geraden drei} Kurven kotierter Punkte.

(Siehe

d'Ocagne, p. 125 oder

Schilling,

S.

24.)

Fig. ^6.

Die

Gerade,

^{welche die den}

gegebenen

^{Werten at und} a2

entsprechenden

^{Punkte der} Punktreihen

(at),

(a2)

verbindet,

schneidet die dritte Skala

(«3)

^{in einem}

Punkte,

dessen Kote «3

die

gesuchte

^Größe

gibt.

Praktisch kann die dualistische Umformung umgangen werden durch

Einführung

^von Parallel-Koordinaten _/n, v, denen 2 Gerade als _/*- und v-Achsen mit den

Anfangspunkten

^{A und B}

zu Grunde liegen. Als Parallelkoordinaten _^ und v einer Ge¬

raden _g sind die mit Vorzeichen zu nehmenden Strecken zu

verstehen,

welche

jene

auf den Achsen abschneidet. Fig ^7.

Die

Gleichung

ersten Grades: _a^

+

^bv+^c=0 stellt dann in unsern Linienkoordinaten einen Punkt dar.

Führen wir

zugleich

noch ein cartesisches

Koordinatensystem ein,

dessen

Anfangspunkt

^{0 der}

Mittelpunkt

von AB und dessen i-und

jy-Achsen

die Gerade OB und die Parallele durch 0 zu den

i»v-Achsen sind,

^{so ist in} demselben der durch die letzte Glei¬

chung

definierte Punkt auch durch die Koordinaten bestimmt:

e ^.b^— a

_

c

^-°b^fa;

^{?; ~ ~}

^H"a

i no AB.,

wo o = OB =^——- ist.

— 27 ^—

In unserem

Genauigkeitsnomogramm

^müssen

folgende

^Glei¬

chungstypen dargestellt

^werden:

1.

Typus

^{: F}

(«t

«2

c3)

⁼

f, (ßl) +

f2

(«2) + f3 (a3)

^{= 0}

2.

Typus

^{: F}

(«x

«2

ß3)

⁼

fx («,)-f3 («,) + f2 (a2)

^{= 0}

Im

Folgenden

^wird fi

(ax)

^der Einfachheit halber mit

fi,

f2

(a2)

^mit

f2,

f3 (as) ^mit f3 bezeichnet.

1.Typus: ft +

fg

+ f»

⁼⁰

Wir setzen

U

fi⁼_^ und

12.

^f2=v, worauf dieGleichung ^über¬

geht ^in:

u v

f"

⁺

-f ^{+ f3}

^{= 0}

Diese neue

Gleichung

bestimmt in dem eben definierten cartesischen

Hilfskoordinatensystem

die Punkte:

Während die _^t- und v-Achsen unmittelbar als Träger der Funktionsskalen

(at)

^und

(a2)

^{mit den. Modulen}

li

^und

12 gewählt

sind, wird der

Träger

^der Funktionsskala

(a3)

^durch die Parallele

zu diesen

geliefert,

welche die Strecke AB in einem Punkte C

so teilt, daß

AC

_lt

CB

_

12

ist,

und zwar ist auf dieser mit

positiver Richtung

^versehenen Parallelen einfach von C aus die Funktionsskala w⁼l3f3 zu kon¬

struieren,

^wobei

1 ^-

^2

13 -"17+17

Die 3 Punktskalen sind also auf 3

Parallelgeraden aufzutragen.

2.

Typus:

f!.f3

+ f2

^=0.

Wir wählen wiederum lt fi^=u; 12

f2

⁼v, als Punktskalen auf 2

parallelen

Geraden. Diese Werte oben

eingesetzt ergibt:

f ^- ₊ ^V

12

== 0, eine

Gleichung

von der

allgemeinen

Form

(a

f.i

-\-

^{b•v + c =}

0)

wobei a=

b ⁼ i

i2

c= 0

somit die cartesischen Koordinaten im

Hilfssystem:

Biese dritte Punktskala

liegt

auf der die

Nullpunkte

der [x- und v-Skalen verbindenden Geraden AB.

4. Rechentafeln für

Gleichungen

^zwischen mehr als 3 Variabeln.

Wir erwähnen hier nur die

vereinigte

^{collineare Re¬}

chentafel,

^{die in} unserem Falle zur Anwendung ^{kommt. Die ver¬}

einigte cartesische Tafel würde

analog

behandelt.

Ist eine Funktion

F(au

u2, a3, aà,

a5)

^{mit 5 Variabein} »i, «2, o-z, «4, a5

darzustellen,

^{so werden}

je

^{zwei der Variabein zusammen¬}

gefaßt

zu einer Hilfsvariabeln.

Z.B.:

(au a2)

⁼z1

(«3, a4)=Z2

wodurch die eine Funktion aus 5 Variabein

übergeht

^{in 3 Funk¬}

tionen zu 3 Variabein:

f

(«1,

Ö2,

Zl)=0

f

(a8,

a4)

z2)

⁼⁰

f

(zi,

Z2,

a5)

⁼⁰

welche,

^{wie oben}

angegeben,

^{z. B.} durch oollineare Rechentafeln

gelöst

^{werden können.}

Wir erhalten 7 Punktskalen für die Variabein:

ai, a2, a3, a4, ab, Zi, Z2,

welche in ihrer Gesamtheit die

Ausgangsfunktion

darstellen.

— 29 ^—

Die Skalen Zi und z2 sind

Hilfsskalen,

^{die nicht}

aufgezeichnet

zu werden

brauchen,

^{da wir uns um ihre besondern} Werte nicht interessieren. Jedoch bilden ihre Träger, ^die

sogenannten Zapfen¬

linien,

^den Zusammenhang ^der einzelnen collinearen Rechentafeln

zu 3 Variabein untereinander.

Die n Variabein der

Ausgangsfunktion

könnten natürlich auch auf andere Arten

gruppiert werden,

^{z. B.:}

F(a1,a2,as,a4, ab)

^—

0.

f

Ol,

«2,

Zi)

⁼⁰

f

(z1(«3, z2)

^{= 0}

f

O2, «4,05)

^{= 0}

Konstruktion des Nomogrammes für den mittleren Punktfehler.

(Fig. 8.)

Im Abschnitt II ist die Zahl der Variabein in Gl.

(B)

^{bis auf}

1

Überzählige

reduziert worden.

Wie schon

erwähnt,

würde der Ausdruck für M

kompliziert

und für die

Darstellung

^{durch ein}

Nomogramm ungeeignet»

wollten wir diese

überzählige

Variable auch noch eliminieren.

Wir

gehen

^{daher aus von Gl.}

(B):

M=mi?d«±V±* _(B)

ab.sin

(ßj 4-A)

Das Nomogramm soll konstruiert werden für die Maßstäbe 1 : 50 000 und 1: 25

000,

also für Maximalabmessungen ^auf dem Meßtischblatt für

abccx

^{von 15} cm, und für eine

Skalenlänge

von 10 cm.

Wir setzen:

1.)

^{a2 + b2=z2}

a2

+

^{b2 - z2=0}

(ft

+

f» + fs

⁼

0)

u=

l!a2; aL*

⁼225 somit 10⁼

lt

^•

225;

^u=0,0445a2

(1)

v⁼

l2b2; bLx

^{=225 somit l0=}

l2-225;

^v=

0,0445b2 (2)

w=

l3(-zO;l3

⁼

-^4^^=-0,0222;w

⁼

^0,0222ZH3)

AC:CB= 1 :1

2.)

^a2

+

^b2

+

^{c2= z2}

i\ 4-

^c2—

z|

⁼⁰

11 ⁼

1! zï;

^u=

0,0222

^z2

(4)

v⁼

l2c2; cl«

⁼225 t⁼

0,0445

^c2

(5)

i / ai

0,0222-0,0445

w=l3(-zj);l3=-0!Q222 + 0)0445=-0,0148;w

⁼

0,0148z2(6)

A C:CB⁼0,0222 ^:

0,0445

^{= 1:2} Skala

(4)

^ist identisch mit

(3).

Skala

(5)

lassen wir mit

(1)

zusammenfallen im Sinne einer

Vereinfachung

des

Nomogrammes.

3.)

^{Va ~T " ~i~c2 =}z3 z3max

(praktisch)

⁼20 angenommen

Z2max ⁼⁼ ^O

Zjj^*ä Z2 ^U

f^.f, —f,

⁼⁰

u=

l1f1;

¹⁰

=+-20

^u=

0,5-z3 (7)

v =

12 f2

; 10 ⁼

la

^{•26 v =}

0,385

z2

(neg) (8)

lx—l2a

^{, ,J,5—}

0,385-a

W==(5lT+l^;

^{<î==5'5 an^nommen; W = 5'50,5}

⁺

^0,385-a

^<9>

i/o ^{i i o • o}

4.)

^{'a ~r} "t"c =z4; z4max

(praktisch)

^=1,4 angenommen, a-b

z4-b

^— z3 ⁼ 0

fi-fs+f.=

^{= 0}

u =

l1z4;

^{10 =}

1,-1,4

^{u= 7•}z4

(10)

v =

12 (— Zj)

; siehe

(7)

^v=

^0,5

^z3

(neg) (11)

w= d-

}-\2l

_; d= 5,5

li +- h

^b

K K 7 ^— 0,5^b

w-5'5

7+0,5

b

Zömax

(praktisch)

⁼²⁰

(12)

c ,

Va2 +

^b2

+

^c2

5.)- ^{• •}

a-b -Ci-Zs,

Z4-Cj z5 ⁼ 0

fl-t»-f.=

⁼⁰

u=

lt

z4; siehe

(10)

^{u =} 7-z4

(13)

v =

l2(-z5);

^{10 =}

¹²

^{20 v = 0,5z5}

(neg) (14)

U—l*Ci

^{. ..7 —}0,5Cj

-; d ^{= 5,5} w= 5,5 /

(15)

li+U-c/ ^{' *} 7

+ 0,5

Cl

Va2 +

^b2

+

^c2

_%i

''

a-b-sin(a1

⁺

ßi)'Gi~

^mi