Sommersemester 2010 Universität Bielefeld
Klausur zur Vorlesung Mathematik f¨ ur BiologInnen, BiotechnologInnen und BiochemikerInnen (240109)
2. Termin: 04. Oktober 2010
Aufgaben und L¨osungen Aufgaben:
1. Berechnen Sie die Determinante und die Inverse der folgenden Matrix:
A=
1 2 1 1 0 2 2 3 2
2. F¨ur einen Radfahrer soll ein Getr¨ank aus drei verschiedenen Fl¨ussigkeiten gebraut werden. Fl¨ussigkeit A enth¨alt pro Liter 1mg von Stoff X und 2mg von Stoff Y, Fl¨ussigkeit B pro Liter 2mg von Stoff X und 2mg von Stoff Y, und Fl¨ussigkeit C pro Liter 2mg von Stoff X und 1mg von Stoff Y. Der Radfahrer soll insgesamt 4 Liter trinken, und dabei 6mg von Stoff X und 7mg von Stoff Y zu sich nehmen.
Wieviel Liter jeder Fl¨ussigkeit werden gebraucht?
3. Die Halbwertszeit von238PU (Plutonium) liegt bei ca. 88 Jahren.
a) Um wieviel Prozent reduziert sich eine Menge an238PU im Verlaufe von einem Jahr?
b) Um wieviel Prozent reduziert sich eine Menge an 238PU im Verlaufe von 10 Jahren?
c) In welchem Zeitraum reduziert sich eine vorgegebene Menge an238PU auf 25 Prozent der Ausgangsmenge ?
4. Die Anzahl von Mikroben in einer Population nach t Tagen werde durch m(t) beschrieben. F¨ur deren Wachstum gelte
m0(t) = 10te2t.
Wir nehmen an, dass die Anzahl an Mikroben zum Zeitpunktt= 0 durchm(0) = 10 gegeben ist. Wie viele Mikroben gibt es nach genau drei Tagen?
5. Berechnen Sie die folgenden Ausdr¨ucke und geben Sie die Zwischenschritte an.
a)
4π
R
0
(sin(x))2dx b) lim
x→∞
(1+2x)2 x2+8x
6. Berechnen Sie die beiden komplexen L¨osungen xder folgenden Gleichung:
x2−2x+ 2 = 0.
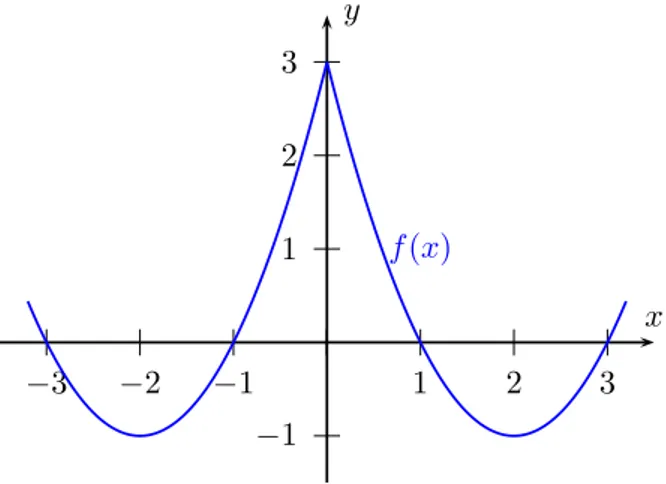
7. Seif :R→Rgegeben durchf(x) =x2−4|x|+ 3.
a) Bestimmen Sie die vier Nullstellen von f.
b) Bestimmen Sie die Extremstellen (Minima und Maxima) von f mit den zu- geh¨origen Funktionswerten und geben Sie an, ob es sich um Maxima oder Minima handelt.
8. Bestimmen Sie alle L¨osungen U(t) = (u1(1), u2(t)) des Differentialgleichungssys- tems
U0(t) = 0 1
6 1
U(t)
L¨osungen 1. Es ist
det(A) = 0 + 8 + 3−0−6−4 = 1.
Wir berechnen nun A−1 mit Hilfe des Gauß-Algorithmus:
1 2 1 1 0 0
1 0 2 0 1 0
2 3 2 0 0 1
| ·(−1)
←−−−−−−+
| ·(−2)
←−−−−−−−−−−−−−−−+
→
1 2 1 1 0 0
0 −2 1 −1 1 0
0 −1 0 −2 0 1
| ·(−2)
←−−−−−−+
→
1 2 1 1 0 0
0 0 1 3 1 −2
0 −1 0 −2 0 1
| ·2
←−−−+
→
1 0 1 −3 0 2
0 0 1 3 1 −2
0 −1 0 −2 0 1
| ·(−1)
←−−−−−−+
| ·(−1)
→
1 0 0 −6 −1 4
0 0 1 3 1 −2
0 1 0 2 0 −1
Also ist
A−1 =
−6 −1 4
2 0 −1
3 1 −2
.
2. Bezeichnen wir mita, bbzw.cdie Mengen der Fl¨ussigkeitenA, Bbzw.C, so ergibt sich aus den im Aufgabentext genannten Bedingungen f¨ur das Getr¨ank ein lineares Gleichungssystem
a +b +c = 4
a +2b +2c = 6 2a +2b +c = 7
,
das wir als erweiterte Koeffizientenmatrix schreiben und mit Hilfe des Gauß- Algorithmus l¨osen k¨onnen:
1 1 1 4
1 2 2 6
2 2 1 7
| ·(−1)
←−−−−−−+
| ·(−2)
←−−−−−−−−−−−−−−−+
→
1 1 1 4
0 1 1 2
0 0 −1 −1
Aus der dritten Zeile ergibt sich nun c= 1 und dies eingesetzt in die zweite Zeile liefert b+ 1 = 2⇔b= 1. Schließlich ergibt sich aus der ersten Zeile
a+ 1 + 1 = 4 ⇔a= 2. Das Getr¨ank ergibt sich also aus 2 Litern von Fl¨ussigkeit A, 1 Liter von Fl¨ussigkeit B und 1 Liter von Fl¨ussigkeit C.
3. h= 88⇒λ=−ln(2)h ≈ −0,0079.
(a) Die Anfangsmenge an Plutonium werde mit c bezeichnet. Der exponentielle Zerfall von238PU nach tJahren wird beschrieben durch die Funktion
f(t) =c·eλt.
Im Verlaufe eines Jahres reduziert sich eine Menge an 238PU um 1−f(1)
f(0) = 1−eλ ≈0,7846%.
(b) Im Verlaufe von zehn Jahren reduziert sich eine Menge an238PU um 1−f(10)
f(0) = 1−e10λ ≈7,57%.
(c) Ganz leicht ergibt sich die gesuchte Zeitdauer durch Verdoppelung der Halb- wertszeit, also 176 Jahre. Dies ergibt sich nat¨urlich auch rechnerisch:
Wir bestimment derart, dass f(t)
f(0) = 0,25⇔eλt= 0,25⇔t= ln(0,25)
λ = 176.
Im Verlaufe von 176 Jahren reduziert sich die vorgegebene Menge an 238PU auf 25 Prozent der Ausgangsmenge.
4. Gesucht ist diejenige Stammfunktion m, f¨ur die m(0) = 10 gilt. Wir verwenden die Technik der partiellen Integration:
m(t) =
t
Z
0
m0(s)ds+ 10 =
t
Z
0
10s e2sds+ 10
=
10s1 2e2s
t 0
−
t
Z
0
5e2sds+ 10
= 5te2t−5
2e2t+5
2 + 10 =e2t
5t− 5 2
+ 12,5
Damit ergibt sich der Mikrobenbestand nach drei Tagen:
m(3) = 12,5·e6+ 12,5≈5055.
5. (a) Mit partieller Integration und der Identit¨at sin2(x) + cos2(x) = 1 folgt
4π
Z
0
(sin(x))2dx=
4π
Z
0
sin(x)·sin(x)dx
=−sin(x)·cos(x)
4π
0
| {z }
=0
+
4π
Z
0
(cos(x))2dx=
4π
Z
0
(1−(sin(x))2)dx
⇔2
4π
Z
0
(sin(x))2dx= 4π⇔
4π
Z
0
(sin(x))2dx= 2π.
(b) Unter Verwendung der binomischen Formel gilt
x→∞lim
(1 + 2x)2
x2+ 8x = lim
x→∞
4x2+ 4x+ 1
x2+ 8x = lim
x→∞
4 +x4 +x12
1 +8x = 4.
6. Unter Verwendung der p, q-Formel erhalten wir x1,2= 1±√
1−2 = 1±√
−1 = 1±i.
Damit lauten die beiden L¨osungenx1= 1−iundx2= 1 +i.
7. Die gegebene Funktionf ist achsensymmetrisch, d.h. es giltf(−x) =f(x) f¨ur jedes x∈R, sodass wir uns bei der Diskussion zun¨achst auf den DefinitionsbereichD= [0,∞) beschr¨anken k¨onnen. In Abbildung finden Sie den Graphen der Funktion f.
(a) F¨ur x ∈ D ist f(x) = x2 −4x+ 3. Die beiden L¨osungen der quadratischen Gleichungx2−4x+ 3 = 0 lauten
x1 = 2 +√
4−3 = 3 und x2= 2−√
4−3 = 1.
Die vier Nullstellen der Funktion f sind also x1 = 3, x2 = 1, x3 = −3 und x4 =−1.
(b) F¨urx∈(0,∞) lauten die Ableitungen vonf
f0(x) = 2x−4 und f00(x) = 2.
Es ist nun 2x−4 = 0⇔x= 2 und f(2) =f(−2) =−1. Außerdem istf00>0 und folglich sind die beiden Punkte (−2,−1) und (2,−1) Minima vonf. Weiterhin istf0(x)<0 f¨urx∈(0,2), woraus sich ergibt, dass der Punkt (0,3) ein Maximum vonf ist.
1 2 3
−1
1 2 3
−1
−2
−3
x y
f(x)
Abbildung 1: Graph der Funktion f(x) in Aufgabe 7
8. Um ein Fundamentalsystem von L¨osungen des angegebenen Differentialgleichungs- systems zu bestimmen, berechnen wir zun¨achst die Eigenwerte und Eigenvektoren der Matrix A=
0 1 6 1
. F¨ur das charakteristische Polynom von Afolgt det(A−λI2) =λ2−λ−6.
Die Nullstellen dieses Polynoms lauten
λ1 =−2, λ2= 3.
Wir bestimmen nun die Eigenvektoren zum Eigenwertλ1. Dazu betrachten wir das Gleichungssystem
2 1 0 6 3
0
→
2 1 0 0 0
0
.
Damit sind der Vektor u= −1
2
und seine Vielfachen die Eigenvektoren von A zum Eigenwertλ1.
Wir bestimmen nun die Eigenvektoren zum Eigenwertλ2. Dazu betrachten wir das Gleichungssystem
−3 1 0 6 −2
0
→
−3 1 0
0 0
0
.
Damit sind der Vektor v = 1
3
und seine Vielfachen die Eigenvektoren von A zum Eigenwertλ2.
L¨osungen des obigen Differentialgleichungssystems sind somit eλ1·t·u und eλ2·t·v.
Das Fundamentalsystem der L¨osungen des Differentialgleichungssystems ist be- stimmt durch die beiden obigen L¨osungen, d.h. die allgemeine L¨osung ist gegeben durch
U(t) =c1·eλ1·t·u+c2·eλ2·t·v, wobeic1, c2 beliebige reelle Zahlen sind.