Fachbereich Informatik und Mathematik
Institut für Informatik
Implementierung von Algorithmen zur erweiterten Alpha-Äquivalenz für Programmiersprachen mit rekursiven
Bindungen
Omar El Goss 21 Sep. 2015
Prof. Dr. Manfred Schmidt-Schauß
Professur für Künstliche Intelligenz/Softwaretechnologie unter Betreuung und Begleitung von
Dr. David Sabel
←- : uml. `−Kanten
−−−−−−−−−−→, L= bestimmtes Label BV(.) : Menge der gebundenen Variablen
CH : chain
DVC : Distinct Variable Convention
Env : Environement
FV(.) : Menge der freien Variablen
gc : garbage collection
gc-free : ohne unbenutzte Bindungen
Lch : chain language
LDG : Labeled Directed Graph
OOLDG : Outgoing-Ordered Labeled Directed Graph
ROOLDG : Rooted Outgoing-Ordered Labeled Directed Graph
SOOLDG : Outgoing-Ordered Labeled Directed Graph mit Startknoten
Inhaltsverzeichnis
Abkürzungenverzeischnis und Schreibweisen 5
1 Einführung 7
2 Grunlagen 9
2.1 Graphen und Graphisomorphismus . . . 9
2.2 Definition wichtige Begriffe und Notationen . . . 9
2.3 Komplexitätsüberblick . . . 12
2.4 Funktionale Kernsprachen . . . 18
3 Alpha-Äquivalenz für Sprachen höherer Ordnung mit Letrec 24 3.1 Komplexität von CH . . . 26
3.2 Graph Konstruktion für CH-Ausdrücke . . . 28
4 Ein effizienter Algorithmus für Ausdrücke ohne Garbage 31 4.1 Garbage Collection . . . 31
4.2 Die Idee Var-Kanten umzukehren . . . 33
5 Algorithmen 36 5.1 Design . . . 36
6 Implementierung 46 6.1 Haskell . . . 46
6.2 Wichtige Funktionen . . . 47
7 Laufzeitmessung (Benchmarking) 53
8 Zusamenfassung und Ausblick 54
1 Einführung
Alpha-Umbenennung in Programmkalkülen, wie z.B. dem reinen Lambda-Kalkül, be- zeichnet die konsistente Umbenennung von gebundenen Variablen. Die Abstraktion λxλy → (x, y, z) kann durch Alpha-Umbenennungen inλyλy0 →(y0, y, z) umbenannt werden. Zwei Ausdrücke werden als alpha-äquivalent bezeichnet, wenn sie bis auf die Alpha-Umbenennung gleich sind.
Für Programmkalküle mit syntaktischen Konstrukten für Mengen von Bindungen, wie z.B. let oder letrec, ist der entsprechende Begriff der Alpha-Äquivalenz-Permutation innerhalb der Bindungsmengen zu erweitern.
Zum Beispiel sind
letrec x= 1, y= 2, z= 2∗x in (x, y, z) und
letrec a= 2, z= 2∗a, b= 1in (b, a, z) alpha−äquivalent.
In [1] wurde gezeigt, dass für solche Programmkalküle das Entscheidungsproblem der Alpha-Äquivalenz vollständig für das Graph-Isomorphismus-Problem ist.
Allerdings kann durch Abänderung der Alpha-Äquivalenz-Definition (als zusätzlicher Schritt werden unbenutzte Bindungen entfernt) ein effizientes Entscheidungsprozedur- Verfahren angegeben werden ([1] Theorem 3.13.). Ziel dieser Arbeit ist dieses effiziente Entscheidungsprozedur-Verfahren zu diskutieren und ihre algorithmische Umsetzung in die funktionale Programmiersprache Haskell zu implementieren.
Überblick
In diesem Abschnitt geben wir eine kurze Anleitung über die Struktur und die Inhalte dieser Arbeit. Sie gliedert sich hauptsächlich in drei Hauptteile, die sich wiederum in Abschnitte unterteilen. Das erste Teil beinhaltet allgemeine Grundlagen über Graphen und wichtige Ergebnisse der Komplexitätstheorie, in der für diese Arbeit relevante Begriffe und Schreibweisen festgehalten werden. Weiterhin wird das Graph-Isomorphie-Problem, kurz geschrieben GI, vorgestellt und die GI-Vollständigkeit einiger Graphklassen einge- führt. Insbesondere haben wir den Fokus auf eine spezielle Graphklasse, den sogenannten OOLDGs (outgoing-ordered labelled directed graphs) gelegt, die im weiteren Verlauf dieser Arbeit eine wichtige Rolle spielen wird. Die OOLDGs sind GI-hart. Allerdings lässt sich durch die Hinzunahme der Root-Eigenschaft das Graph-Isomorphie-Problem unter Graphen innerhalb dieser Klasse effizient lösen. Das wurde in [1] Proposition. 2.9. bewie- sen. Dieses Ergebnis wird unter anderem zur Lösung des ”Alpha Äquivalenz-Problems für Sprachen mit rekursiven Bindungen” benutzt.
Schwerpunkt dieser Arbeit liegt darin, der in [1] Theorem 3.13. vorgestelltem Verfahren in die funktionale Programmiersprache Haskell zu implementieren. Um eine Grundlage
zu schaffen, wird das Lambda-Kalkül vorgestellt.
In Kapitel 3 wird der Begriff der ”Alpha-Äquivalenz für Sprachen mit rekursiven Bin- dungen” eingeführt. Um das Problem in die Komplexitätsklassenhierarchie einzuordnen, wird es von einer komplexitätstheoretischen Perspektive betrachtet und untersucht. Diese Untersuchung hat gezeigt, dass das Problem GI-vollständig ist. In Definition 3.2. wird eine Methode zur Umwandlung eines CH-Ausdrucks in einen Graphen vorgestellt. Die konstruierten Graphen zeigten eine Ähnlichkeit zu ROOLDGs. Die Intuition sagt, dass durch gezielte Handgriffe diese Eigenschaften, die für einen effizienten Isomorphietest für ROOLDGs verantwortlich sind, den konstruierten Graphen verliehen werden könnten.
was automatisch bedeutet einen effizienten Alpha-Äquivalenz-Test für CH-Ausdrücke Ohne Unbenutzten Bindungen wäre möglich. Dieser Intuition wird gefolgt und daraus ein Verfahren zum effizienten Isomorphietest für SOOLDGs (OOLDGs mit Startkno- ten) entwickelt. Dieses basiert auf dem in [1] präsentierten Verfahren mit dem kleinen Unterschied, das Isomorphietest auf andere Graphen durchgeführt wird (siehe Lemma 2.3.
In Kapitel 5 werden die kritischen Stellen, die bei der algorithmischen Behandlung des Alpha-Äquivalenz-Problems Schwierigkeiten auslösen können, geortet und untersucht und Ideen, diese zu unterbinden, diskutiert. Daraus sind Algorithmen entstanden, die dann in die funktionale Programmiersprache Haskell implementiert werden.
Kapitel 6.2 enthält einige ausgewählte Ausschnitte dieser Implementierung.
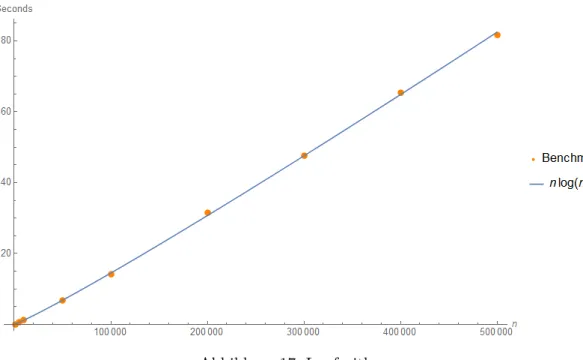
Kapitel 7 enthält die ermittelten Testdaten zur Nachweis der Laufzeit.
2 Grunlagen
2.1 Graphen und Graphisomorphismus
Graphen spielen in der Informatik eine große Rolle. Sie sind für die Informatik, wie etwa die natürlichen Zahlen für die Mathematik oder die Integral- und Differentialrechnung für die Physik, weil viele Probleme, die bei der Behandlung praktischer Fragestellungen auftreten, sich leicht durch Graphen modellieren lassen.
Graphen können verschiedene Eigenschaften haben. Ein Graph kann z.B. zusammenhän- gend, planar, oder bipartit sein.
Es kann nach der Existenz spezieller Teilgraphen gefragt werden, wie z.B. eine Clique im Graphen, Knotenüberdeckung der Größe K oder es können bestimmte Parameter un- tersucht werden. Die verschiedenen Eigenschaften können zueinander in Beziehung stehen.
Definition 2.1.
Die Graphentheorie ist ein Teilgebiet der Mathematik, dass die Eigenschaften von Graphen und ihre Beziehungen zueinander untersucht.
Dadurch, dass zahlreiche Alltagsprobleme mit Hilfe von Graphen sich modellieren lassen und die Lösung graphentheoretischer Probleme oft auf Algorithmen basiert, ist die Gra- phentheorie auch in der Informatik, insbesondere der Komplexitätstheorie, von großer Bedeutung.
2.2 Definition wichtige Begriffe und Notationen
In diesem Abschnitt werden einige grundlegende und für diese Arbeit wichtige Begriffe und Definitionen aus der Graphentheorie wiederholt und entsprechende Notationen fest- gelegt.
Definition 2.2.
Ein Graph G= (V, E) besteht aus einer Menge V von Knotenund aus einer Menge E von Kanten; E ⊆ {{u, v} |u, v∈V, u6=v}. Wir verlangen, dass die Knotenmenge nicht leer ist. Wir beschränken uns in dieser Arbeit auf endlicheKnotenmengen, hierbei darf die Kantenmenge allerdings leer sein.
• Eine Kante wird als (u, v) notiert
• Eine Kante (v, v) heißt Schleifeoder Schlinge
• Eine ungerichtete Kante
– wird durch ein ungeordnetes Paar (u, v) beschrieben, d.h. sie verbindet die Knoten u und v ohne eine Richtungsangabe.
• Eine gerichtete Kante
– wird durch ein geordnetes Paar (u, v) beschrieben, d.h. sie verbindet die beiden Knoten u und v in einer bestimmten Richtung.
Es gilt: (u, v)6= (v, u) ( zwei verschiedene Kanten)
• Wenn die Knoten und Kanten in Graphen gekennzeichnet sind, nennt man den Graph einen beschrifteten Graph.
• Eine Folge von Knotenv1, v2, v3, ... vnheißtWeg(engl. path) vonv1 nachvn, wenn es gilt: ∀ 16i < n : (vi, vi+1)∈E
• Ein Zyklus ist eine Weg bei dem zumindest ein Knoten mehrfach vorkommt
• Der Eingangsgrad(engl. indegree) eines Knotens ist definiert als die Anzahl der in den Knoten eingehenden Kanten
• Der Ausgangsgrad (engl. outdegree) eines Knotens ist definiert als die Anzahl der aus dem Knoten ausgehenden Kanten.
• Ein Knoten v∈V heißt Wurzel (root):
– falls er keine eingehenden Kanten hat, d.h. (Eingangsgrad von v = 0 ) und alle weiteren Knoten im Graphen von diesem Knoten aus erreichbar sind.
Definition 2.3.
Einungerichteter Graph G= (V, E) hat eine endliche Menge V von Knoten und eine Menge Eungerichteter Kanten mit E ⊆ {{u, v} |u, v∈V}.
Definition 2.4.
Ein gerichteter GraphG= (V, E) hat eine endliche Menge V von Knoten und eine Menge Egerichteter Kanten, mit E⊆ {{u, v} |u, v∈V}.
v5 v4
v3 v1
v2
Beispiel-Graph
Ein Graph mit Knotenmarkierungen oderknotenmarkierter Graph liegt vor, wenn zusätzlich zu G= (V, E) auch noch eine Abbildung lV :V−> LV gegeben ist, die für jeden Knoten v seine MarkierunglV(v) festlegt.
Ein Graph mit Kantenmarkierungen oderkantenmarkierter Graph (Labeled Graph) liegt vor, wenn zusätzlich zuG= (V, E) auch noch eine AbbildunglE :E−> LE gegeben ist, die für jede Kante e∈E ihre MarkierunglE(e) festlegt.
Definition 2.5.
Ein beschrifteter gerichteter Graph(LDG = Labeled Digraph) ist ein Tupel G = (V, E, L, lab), wobei V eine endliche Menge von Knoten, E ⊆ (V ×V ×L) eine Menge von Beschriftungen (labels) undlab:V −→Leine Funktion ist, die jedem Knoten eine Beschriftung zuweist. Wenn |L|= 1 ist, dann ist G unbeschriftet (unlabeled) und wenn (v1, v2, l)∈E⇐⇒(v2, v1, l)∈E gilt, so ist G ungerichtet.
Bemerkung. In einem LDG hat nicht nur jeder Knoten durch die lab-Funktion eine Beschriftung, sondern durch die Wahl von E ⊆ (V ×V ×L)) auch jede Kante eine Beschiftung.
Notation. In unbeschrifteten Graphen G= (V, E, L, lab) werden die Komponenten L und lab manchmal weggelassen.
Definition 2.6.
Ein LDG heißt genau dann Outgoing-Ordered (OOLDG), wenn für alle Knoten u∈V gilt. Falls (u, v1, l)∈E und (u, v2, l)∈E , so ist v1=v2.
In Worten: in einem (OOLDG) G= (V, E, L, lab) von einem Knoten u ∈ G sind nur ausgehende Kanten mit unterschiedlichen Beschriftungen erlaubt.
Diese Graphklasse besitzt einige gute Eigenschaften, die für die Lösung mancher algo- rithmischer Probleme zugutekommen, worauf im Laufe dieser Arbeit in mehreren Stellen zurückgegriffen wird.
Können Graphen gleich sein, obwohl sie unterschiedlich aussehen? Um diese Frage zu beantworten muss nur die „Struktur“ von Graphen untersucht werden, aber nicht welcher Knoten bzw. welche Kanten wie benannt sind. Das liegt daran, dass manchmal derselbe Graph unterschiedlich graphisch dargestellt werden kann und die Struktur aber invariant bleibt. Hier kommt der Begriff der „Isomorphie von Graphen“ zu Hilfe.
Definition 2.7.
Ein Graph G1 = (V1, E1) heißt isomorphzu einem Graphen
G2 = (V2, E2), wenn es eine bijektive Abbildungf :V1−→V2 gibt mit der Eigenschaft:
∀x∈V1 :∀y∈V1 : (x, y)∈E1 ⇐⇒(f(x), f(y))∈E2.
Mit anderen Worten, ein Isomorphismusf beschreibt einfach eine „Umbenennung“ der Knoten, ohne dass die „Struktur“ des Graphen verändert wird.
Die Abbildungf heißt dann auch ein (Graph-)Isomorphismus.
Definition 2.8.
Zwei LDGs G1 = (V1, E1, L, lab1), G2 = (V2, E2, L, lab2) heißen genau dann isomorph, wenn es eine bijektive Funktionf :V1 −→V2 gibt, so dass∀(v1, v2, l)∈E1 : (v1, v2, l)∈ E1 ⇔(f(v1), f(v2), l) ∈ E2 und ∀v ∈ V1 :lab1(v) = lab2(f(v)) gilt. In diesem Zusam- menhang istf ein Isomorphismus vonG1 nach G2.
Notation. G1 'f G2 heißt, G1 ist isomorph zu G2 unter der Abbildung f.
v5 v4
v2
v3 v1
G1
w1 w2
w3
w4 w5
G2
Die zwei BeispielgraphenG1 und G2 sind unter der Abbildung f isomorph zueinander.
Es gilt:
f :V17→V2 und f={v1 7→w5 , v57→w1 , v4 7→w2 , v27→w3 , v1 7→w5 , v37→w4 }
2.3 Komplexitätsüberblick
In diesem Abschnitt wird dasGraphisomorphismus-Problem, abgekürzt geschrieben GI, aus komplexitätstheoretischer Perspektive betrachtet. Ziel ist die Klassifizierung des GI-Problems in der Komplexitätsklassenhierarchie. Dadurch wird die Schwierigkeit des Problems geortet. Ergebnisse dieser Untersuchung verhindern, dass sich die Suche nach effizienten Algorithmen auf unerreichbare Ziele konzentrieren.
Die P = N P - Frage ist eines der wichtigsten offenen Probleme der Informatik. Die Intuition sagtP 6=N P. In der Tat glaubt eigentlich niemand, dassP =N P ist, aber ein Beweis konnte seit 50 Jahren nicht geführt werden! Im Laufe dieser Arbeit nehmen wir diese solide begründeten, aber unbewiesenen HypothesenN P 6=P an.
Definition 2.9.
P ist die Klasse der Probleme für die es eine effiziente Lösung gibt, d.h. es gibt einen deterministischen Algorithmus, der in polynomieller Zeit eine Lösung für das Problem liefert.
Die Klasse NP beinhaltet alle Probleme, die anhand einer nicht deterministischen poly- nomiellen Algorithmus entschieden werden können.
• Wir nennen ein Problem NP–hart, wenn es mindestens so schwer ist wie alle NP–vollständigen Probleme.
• Ein Problem, das NP–hart ist, muss nicht notwendigerweise in NP liegen.
• Ein Problem, das NP–hart und in NP liegt, nennt man NP-vollständig.
Das Graph-Isomorphie-Problem ist wie folgt definiert:
Definition 2.10.
Gegeben sind zwei endliche (un-)beschriftete, gerichtete Graphen G1 = (V1, E1) und G2 = (V2, E2). Man soll nun entscheiden, obG1 isomorph zu G2 ist.
Die Graphisomorphie für beliebige endliche (un-)gerichtete Graphen ist eines der wenigen Probleme, für die es bislang weder gelungen ist, die NP -Vollständigkeit zu zeigen, noch zu beweisen, dass es in P liegt.
Erwiesen ist lediglich, dass es in NP liegt, da sich ein Isomorphismus in polynomieller Zeit raten und durch Abbildung der Knoten aufeinander und anschließendem Kantenvergleich in polynomieller Zeit verifizieren lässt.
Je nach den Einschränkungen, die für die beiden Graphen getroffen werden, variiert der Schwierigkeitsgrad dieses Problems.
Komplexität von Graph-Isomorphismus?
• Das Problem liegt in NP, aber
– es liegt keinNP-Vollständigkeits-Beweis vor
– es ist kein P-Time-Algorithmus für das Problem bekannt.
Definition 2.11.
• Ein Entscheidungsproblem L ist in der Klasse GI (oder auch: L∈GI), falls es eine in polynomieller Zeit berechenbare Transformation T gibt, die für jede Eingabe w für L eine Eingabe T(w) für GI erzeugt, so dass (w∈L⇔T(w)∈GI) gilt (L ist also höchstens so schwer wie GI).
NP-hart
NP-vollständig
P
NP-intermediate
Graph-Isomorphie
?
NP
GI-Komplexität
• Ein Entscheidungsproblem K ist GI-hart, falls es eine polynomielle Transformation U gibt, die für jede Eingabe x für GI eine Eingabe U(x) für K erzeugt, so dass (x∈GI ⇔U(x)∈K) gilt.
• Ein Entscheidungsproblem P ist genau dann GI-vollständig (oder auch: P ∈GIV), wennP ∈GI und P GI-hart ist.
Für eine LDGs spielt es keine Rolle, ob ein Graph Beschriftungen an Knoten bzw.
Kanten trägt oder nicht, dadurch wird das Isomorphieproblem nicht einfacher. Also das Isomorphie-Problem zwischen zwei LDGs (beschriftet oder unbeschriftet) ist GI- vollständig (Beweis siehe [1] Prop. 2.4.).
Im folgenden Abschnitt untersuchen wir eine Beobachtung unter LDGs bezüglich des Isomorphie-Problems, dessen Ergebnisse eine wichtige Rolle im Laufe dieser Arbeit spielen werden.
Lemma 2.1.
Für ein LDG, G sei ←G- der Graph, der durch Umkehrung aller Kanten mit Label` aus G entsteht.
Für zwei LDGs,G1 und G2, wobei
←-
Gi=Gi gilt: (G1'G2)⇔(
←-
G1'G←2-).
Beweis.
Seien:Gi= (Vi, Ei, Li) und
←-
Gi= (Vi, Ei0, Li) zwei LDGs wobei:
(v, w, l)∈Ei⇒(v, w, l)∈E0i fallsl6=` (v, w, l)∈Ei⇒(w, v, l)∈E0i fallsl=`.
Seiφ:V1 →V2 ein Isomorphismus vonG1 nach G2. Dann gilt für allev, w∈V1 und alle Labelsl:
Fall 1: l6=`
(v, w, l)∈E10
⇔(v, w, l)∈E1
⇔(φ(v), φ(w), l)∈E2
⇔(φ(v), φ(w), l)∈E20 Fall 2: l=`
(v, w, `)∈E10
⇔(w, v, `)∈E1
⇔(φ(w), φ(v), `)∈E2
⇔(φ(v), φ(w), `)∈E20
Es folgt
←-
G1∼=
←-
G2 ⇒
(1)
←-
←-
G1∼=
←-
←-
G2 ⇒
←-
←-
G=G
G1 ∼=G2
und somit
G1 ∼=G2 ⇔ G←1-∼=
←-
G2
Die Isomorphie inG entspricht also der Isomorphie in←G-. Notation. ←G-:= G mit umgekehrten `−Kanten,
in Worten←G-entsteht durch Umkehrung der Kanten inG= (V, E, L) die mit` beschriftet sind G uml.`−Kanten
−−−−−−−−−→ ←G-.
Die OOLDGs besitzen die Eigenschaft, dass deren ausgehenden Kanten eindeutig geordnet sind. Folglich kann der Test zweier Knoten in Graphen dieser Klasse auf Isomorphie effizient durchgeführt werden. Man kann dies direkt mit „ja“ beantworten, wenn die Beschriftung der Knoten und deren ausgehenden Kanten übereinstimmen. Das heißt, jeder Nachfolgerknoten für den ersten Knoten muss erfolgreich auf einen Nachfolgerknoten vom zweiten Knoten abgebildet werden und die Beschriftung jeder Kante von zwei Knoten, die erfolgreich aufeinander abgebildet werden, muss übereinstimmen. Wird eine Unstimmigkeit in einem Zwischenschritt festgestellt, wird der Test mit „nein“ abgebrochen.
Speichert man die Knoten, anders als in einer Datenstruktur, wo man direkt auf die Nachbarn jedes einzelnen Knoten schnell zugreifen kann, kann diese Überprüfung sehr effizient durchgeführt werden.
In Graphen, die diese Eigenschaft nicht besitzen, muss das Verhalten der Knoten, die
getestet werden sollen, überprüft werden, indem der ausgehender Pfad der Knoten verglichen wird bis eine Unstimmigkeit gefunden wird. Dann sind die Knoten nicht isomorph zueinander oder der Test läuft erfolgreich, dann sind die zwei Knoten isomorph.
Aber reicht diese Eigenschaft für einen effizienten Isomorphietest von zwei OOLDGs?
Wir behaupten „nein“.
Lemma 2.2. Das Isomorphie-Problem zwischen zwei OOLDGs ist GI-vollständig.
Beweis.
Der Beweis hierzu erfolgt anlehnend an ([1], Prop. 2.6.). Dass das Problem in GI liegt, folgt automatisch aus ([1], Prop. 2.4.). Nun zeigen wir, dass es GI-hart ist. Um die GI-Härte des Problems zu zeigen, transformieren wir einen beliebigen unbeschrifteten Graphen G(V, E) in einen OOLDG. Die Transformation beschreiben wir wie folgt:G0(V0, E0).
Zwischen je zwei benachbarten Knoten (verbunden durch eine Kante) im G fügen wir einen neuen Knoten hinzu und splitten die Kante in zwei Kanten
( v1 → v2 ⇒
(τ)v1 ←−1 v −→2 v2 ). Daraus folgt, dass jede Kante (v1, v2) ∈ E aus G durch zwei Kanten (v, v1,1)∈E0 und (v, v2,2)∈E0 in G0 ersetzt wird, wobei v∈V0 ein neuer Knoten ist.
Die folgende Abbildung stellt eine einfache Beispieltransformation dar, wobeiτ :τ(G) = G0 die verwendete Transformationsrelation ist.
−−→τ
2
1
2
1
1 2
2
1
1
2
Abbildung 4: Beispieltransformation
SeienG1undG2zwei unbeschriftete gerichtete Graphen mitτ(G1) =G01und τ(G2) =G02. G1 und G2 sind dann genau isomorph, wenn auch G01 und G02 isomorph sind. Jeder Isomorphismus zwischenG01 und G02 bildet ausschließlich alte Knoten auf alten Knoten und neue Knoten auf neuen Knoten ab, weil nur die alten Knoten eingehende Kanten haben und nur die neuen Knoten ausgehende Kanten haben. Dank der Beschriftung 1 und 2 bleiben die Kantenrichtungen erhalten. Dadurch, dass die Transformationτ die Größe des Graphen G höchstens verdoppelt und das Isomorphieproblem für unbeschriftete gerichtete Graphen GI-hart ist, folgt, dass das Isomorphieproblem für OOLDG mindestens so schwer wie das Isomorphieproblem für unbeschriftete gerichtete Graphen ist. Also das
Problem ist GI-hart und liegt in GI. Somit ist er GI-vollständig.
Definition 2.12.
Sei G= (V, E, L, lab) ein OOLDG.
Für einen Knoten u∈V definieren wir:
f ingerprint(u) = (lab(u), L1u,1, Lu,2)
mit
Lu,1 ={lab(u, v) |(u, v)∈E } als M ultimenge.
Lu,2 ={lab(v, u) |(v, u)∈E } als M ultimenge.
Ein Knoten u heißt „Startknoten“ gdw. für alle Knotenu0 in G gilt:
f ingerprint(u)6=f ingerprint(u0) und alle u0 sind von aus u erreichbar.
Ein Graph G hat genau einen „Startknoten“ gdw.
∃ u : u ist ein Startknoten und∀u0∈V : u6=u0 (u0 ist kein Startknoten).
Bemerkung: In dieser Arbeit betrachten wir nur zusammenhängende OOLDGs.
Lemma 2.3.
Seien G1 und G2 OOLDGs mit genau einem Startknoten. Ein Isomorphismus zwischen G1 und G2 in Zeit O(nlog(n)) kann getestet werden mit n=|G1|+|G2|.
Beweis.
Seien G1 = (V1, E1, L1, lab1) und G2 = (V2, E2, L2, lab2) OOLDGs und seien r1und r2 jeweils die Startknoten von G1 und G2. Jeder Isomorphismus zwischenG1 undG2 muss r1 auf r2 abbilden und es muss f ingerprint(r1) =f ingerprint(r2) gelten.
Bevor wir den Isomorphietest auf die Graphen durchführen, können wir einige Kriterien überprüfen, die für eine Vorentscheidung hilfreich sein können. Wir nehmen an, dass die zwei Graphen dieselbe Menge von Beschriftungen benutzen und dass jede Beschriftung l∈Li benutzt wird. Falls L1 6=L2 ist, können G1 und G2 nicht isomorph sein. Stimmen L1 =L2 überein, dann falls|V1 |6=|V2|oder |E1 |6=|E2 |. In diesem Fall kann es keinen Isomorphismus zwischen G1 undG2 geben, weil ein Isomorphismus zwischen G1 und G2 eine bijektive Abbildung zwischen deren Knoten und Kanten ist.
. Fall 1:Lr,i,2 =∅, dann ist der Startknoten eine Wurzel. Der Beweis in diesem Fall geht analog zu [1] Prop. 2.9.
Lr,i,1 6= ∅ , denn die Erreichbarkeit vom Startknoten muss als notwendige Bedingung gewährt sein.
.Fall 2: Die Startknoten beider Graphen haben nur var-kanten als eingehende Kanten und sind eindeutig über diese Eigenschaft identifizierbar.
Wir setzen voraus, dass die Startknotenr1 undr2 in jedem möglichen Isomorphismus zwischenG1 undG2 dank ihrer eindeutigen Eigenschaften zueinander zugeordnet werden müssen und setzen als Anfangsbedingungφ(r1) =r2. Wir laufen alle Knoten inV1nachein- ander durch und solangeφ(v1) =u1 gilt, überprüfen wir deren ausgehenden Kanten, die uns in einer übereinstimmenden sortierten Reihenfolge vorliegen sollen (wenn nicht dann müssen wir es tun) und solange (v1, v1,i, li1)i= 1, ..., m. (u1, u1,i, li2)für i= 1, ..., m, und setzenφ(v1,i) =u1,ifür j= 1, ..., m.ein. Sollte eine Unstimmigkeit festgestellt werden wie zum Beispiel,li1)6=li2) v1,i oder wurdev1,k in einem früheren Vergleich einem anderen Knoten zugeordnet, dann brechen wir ab mitG1 G2. Wird der Test ohne Unterbre- chung erfolgreich durchgeführt, dann ist gerade ein Isomorphismus zwischenG1 und G2
gefunden worden. Dank der Eigenschaften dieser Graphklasse, wird ein Isomorphismus zwischenG1 und G2 falls er gibt. stets vom Startknoten festgestellt werden müssen und es gibt höchsten ein Isomorphismus. Zur effizienten Durchführung des Isomorphietests gehört eine effiziente Datenstruktur zur Speicherung der bereits erfolgreich getesteten Paare, und zur Bereitstellung der Knoten und Kanten der Graphen, zum Beispiel eine dynamische Wörterbuchdatenstruktur.
2.4 Funktionale Kernsprachen
Das Lambda-Kalkül wurde in den 30er Jahren von Alonso Church [6] eingeführt.
Das ist der Kern aller funktionalen Programmiersprachen, denn es ist selbst eine Pro- grammiersprache. Bei dem Lambda-Kalkül handelt es sich um ein formales System zur Beschreibung von Funktionen. Es besteht aus einer simplen Syntax und einfachen Mechanismen zur Manipulation der Ausdrücke, nämlich den Reduktions- und Konversi- onsregeln, die sich auf rein syntaktische Ersetzungen der (Teil-)Ausdrücke beschränken.
Trotz seines einfachen Aufbaus, ist das reine Lambda-Kalkül Turing-vollständig, d.h. jede berechenbare Funktion lässt sich im Lambda-Kalkül repräsentieren.
Das Lambda-Kalkül ist syntaktisch sehr eingeschränkt. Es ist ungetypt und verfügt nicht über Daten, hat also keine Zahlen, keine arithmetischen Wahrheitswerte und keine rekursive Funktionen. Alle diese Merkmale können zwar im Lambda-Kalkül dargestellt werden, macht aber die Arbeit sehr unübersichtlich und die Kodierung aufwändig. Aus diesem Grund ist es als Kernsprache für funktionale Programmiersprachen eher ungeeig- net. Die meisten Kernsprachen1 könnte man auch einfach als syntaktisch angereichertes
1Kernsprachen stehen für funktionale Kernsprachen
Lambda-Kalkül mit Datentypen betrachten.
Im Folgenden betrachten wir zunächst die Syntax des λ−Kalkuelsund führen einige wichtige Definitionen ein.
Dasλ−Kalkuel hat eine einfache Syntax bestehend aus Variablen, Konstanten, Funkti- onsabstraktionen und Funktionsapplikationen:
• Variablen:x
• Applikationen: (st)
• Lambda-Abstraktion: λx.t
Beispiele: (λx.x) : Die Identitätsfunktion
(λf.(λx.(f x))) : Eine Funktionf wird auf ein Argumentx angewendet.
Klammern werden meistens benutzt um Mehrdeutigkeiten zu vermeiden. In dem Lambda- Kalkül gibt es folgende Regeln, um Klammern zu sparen.
Variablen werden nach λaufgelistet :λx1(λx2, ..(λxn.t)...))≡λx1, x2, .., xn.t Applikation ist linksassoziativ : (t1t2t3...tn)≡(...((t1t2)t3)...)tn) λbindet so weit rechts wie möglich :λx.xx≡λx.(xx)6= (λx.x)x Bindungsbereich von Variablen.
In dem Lambda-Kalkül wird prinzipiell zwischen freien und gebundenen Variablen unterschieden. Das Vorkommen einer Variable x in einem λ-Term gehört immer zu der innersten umschließenden Abstraktionλx.e;λxbindet alle Vorkommen von x innerhalb des Ausdrucks e. Mit anderen Worten: e ist der Geltungsbereichder Variablennamen x. Bei dem Ausdruckλx.y (λy.y)) ist das erste y frei, während das zweite y durch die zweite Abstraktion gebunden wird.
• Das Vorkommen von x∈V an Positionpin Term theißt frei, wenn „darüber kein λx. . . . steht“.
• FV(t) = Menge der int frei vorkommenden Variablen (definiere durch strukturelle Induktion).
• Eine Variablex heißt intgebunden, falls teinen Teilausdruck λx.senthält.
• BV(t) = Menge der int gebundenen Variablen.
Dem entsprechend wird die Menge der freien bzw. gebundenen Variablen eines Terms t, mit FV(t) bzw. BV(t) bezeichnet und ist wie folgt induktiv definiert:
Alpha-Konversion.
Die Idee, dass gebundene Variablen nur Platzhalter sind, führt dazu, dass man einen
• F V(x) ={x}, x := Variable
• F V(a) =∅, a := Konstante
• F V(st) =F V(s)∪F V(t)
• F V(λx.t) =F V(t)\ {x}
Menge der freien Variablen
• BV(x) =∅
• BV(a) =∅, a := Konstante
• BV(st) =BV(s)∪BV(t)
• BV(λx.t) =BV(t)∪ {x}
Menge der gebundenen Variablen
Lambda-Term in einen völlig gleichwertigen Term überführen kann und zwar nur durch Umbenennung seiner gebundener Variablen. Zum Beispiel beschreiben die Terme (λx.xy) und(Λz.zy) die gleiche Funktion modulo Umbenennung gebundener Variablen.
Allerdings muss man darauf achten, dass man bei der Umbenennung keine freien Variablen abfängt.
Definition 2.13.
Ein Lambda-Term erfüllt die DVC- (Distinct Variable Convention)Form, wenn alle seine gebundenen Variablen paarweise unterschiedliche Namen haben und die stets verschieden vom Namen freier Variablen sind.
Definition 2.14 (α−Äquivalenz).
Zweiλ-Termet1 undt2 heißen α−äquivalent, geschrieben : (t1 ≡α t2) gdw. t1 durch konsistente Umbenennung derλ-gebundenen Variablen int2 überführt werden kann.
Beispiel:(λx.x y)≡α (λz.z y)6=α(λy.y y)
Kontext.
Um Terme unabhängig von ihrer Umgebung behandeln zu können, ist das Konzept eines Kontextes hilfreich :C[t] heißt Kontext eines Terms t, falls er t als ein Unterterm enthält.
Redex Einλ-Term der Form (λx.s)t heißt Redex(reducible expressi- on)
β−Reduktion β-Reduktion entspricht der Transformation der Funktionsan- wendung auf einem Redex
Substitution s[t/x] erhält man aus dem Term s, wenn man alle freie Vor- kommen von x durch t ersetzt
Normalform Ein Term, der nicht weiter reduziert werden kann, heißt in Normalform
Divergenz Terme, die nicht zu einer Normalform ausgewertet werden, divergieren, d.h. nicht alle Terme haben eine Normalform
Eindeutigkeit Die Normalform eines λ-Terms t ist, sofern sie existiert, eindeutig.
Reduktionsstrategien Normalordnungsreduktion (call-by-name): der am weitesten links stehende äußerster Redex wird zuerst reduziert,
Anwendungsordnung (call-by-value): der am weitesten links stehende innerster Redex wird zuerst reduziert
Church-Rosser-Eigenschaft und Konfluenz Theorem 2.4 (Church-Rosser theorem).
Für beliebige λ-Terme e1 und e2 mit e1
↔∗β e2 existiert einλ-Term e0 mite1
→∗β e0 und e2 →∗β e0.
∗β ∗β
e1 ∗β e2
e’
Church-Rosser-Eigenschaft
• Alle terminierenden Reduktionsfolgen haben das selbe Ergebnis.
• Keine Reduktionsfolge kann ein falsches Ergebnis liefern, schlimmstenfalls terminiert sie nicht.
• Unter normaler Reduktionsordnung findet man die Normalform, sofern eine existiert.
• Im Lambda-Kalkül gilt, wenn ein Term eine β-Normalform hat, dann ist die eindeutig modulo Alpha-Äquivalenz es gilt, wenn s die β-Normalformen e und t hat, dann ist e≡αt ( Beweis siehe [12]).
Wie bereits erwähnt, handelt es sich bei den meisten funktionalen Programmiersprachen um einen syntaktisch erweiterten Lambda-Kalkül mit Datentypen, wie Konstanten, Operationen, Konstruktoren und rekursive Funktionsdefinitionen. Formal wird damit keine Erweiterung der Ausdruckskraft erreicht. Die Lesbarkeit verbessert sich aber deutlich.
Kernsprachen bestehen im Wesentlichen aus der Syntax, die festlegt, welche Ausdrücke in der Sprache gebildet werden dürfen und aus der Semantik, die angibt, welche Bedeutung die Ausdrücke haben.
Lokale Funktionsdefinitionen.
Mittelslet bzw.letreckönnen Variablen- und Funktionsdeklaration besser gestaltet werden. Sie dienen vor allen dazu lokale Aliase für Ausdrücke zu erstellen, um die Schreibarbeit zu ersparen. Sowohl let als auch letrec weisen einen variablen Namen an einem Wert zu, in eine sogenannte Menge von Bindungen (Reihenfolge der Bindungen ist unwichtig). Die Variablen sind nur innerhalb des Rumpfes des Ausdrucks sichtbar.
Allerdings erlaubt letrec rekursive Definitionen, d.h. die Variablen können sich innerhalb der Menge der Bindungen wechselseitig aufrufen (letrec = rekursives let).
Die Syntax von letrec ist wie folgt definiert:letrec {x1=s1, ..., xn=sn} in twobeixi paarweise verschiedene Variablennamen sind undsi und t Ausdrücke. Es ist z.B. erlaubt, dassx1 in s1, s2 vorkommt, und dass gleichzeitig x2 ins1 unds2 vorkommt. Daraus folgt, dass der Gültigkeitsbereich der definierten Variablenxi der ganze let-Ausdruck ist.
Letrec-Ausdrücke benutzen, ebenfalls wie Lambda-Ausdrücke, geschachtelte Geltungsbe- reiche. Die Menge der freien bzw. gebundenen Variablen eines letrec-Ausdrucks ist wie folgt induktiv definiert:
• F V(letrec{x1 =s1, ..., xn=sn}in t) :=F V(t)∪F V(s1)∪....∪F V(sn)\{x1, ...xn}
• BV(letrec{x1=s1, ..., xn=sn}in t) :=BV(s1)∪....∪BV(sn)∪BV(t)∪{x1, ...xn} In letrec {x1 =s1, ..., xn=sn} in twerden genau die Vorkommen der freien Variablen xi, i= 1, ..., n, die in den Ausdrücken si, i= 1, ..., n und t vorkommen, gebunden. Das ist genau der Gültigkeitsbereich der Variablenxi, i= 1, ..., n.
3 Alpha-Äquivalenz für Sprachen höherer Ordnung mit Letrec
In dem vorherigen Kapitel wurde ja bereits erwähnt, dass es sich bei den meisten funk- tionalen Programmiersprachen um einen syntaktisch angereicherten Lambda-Kalkül mit Datentypen handelt. Im Folgenden wollen wir das Fragment einer Kernsprache mit einem rekursiven oder nicht rekursiven let betrachten, die ebenfalls syntaktisch schlicht gehalten ist, aber alle grundlegenden Aspekte einer funktionalen Programmiersprache enthält. Üb- liche Konstruktoren des erweiterten Lambda-Kalküls werden unterstützt, wie z.B. der seq- Ausdruck. Ebenfalls können case-Ausdrücke der Form case s of (c1(x1,1, ..., x1,ar(c1))→ t1)...(cn(x1,1..., xn,ar(cn))→tn) durch case(s, λx1,1, ..., x1,ar(c1).t1, ..., λxn,1, ..., xn,ar(cn).tn) repräsentiert werden. Eine Signatur Σ ist ein Tripel (v, c, arity), wobei:
• {c}eine endliche Menge von Konstruktoren oder Funktionssymbolen c ist, ci ist ausgestattet mit eine Stelligkeit (ar(c)∈N0),
• {v} eine abzählbare unendliche Menge (von Variablen)x, y, z ist.
Die Sprache CH1(über die Signatur Σ) ist durch die folgende Syntax definiert:
r, s, t∈Lch::=x |c(s1, ..., sarc) |λx.s|letrec x1 =s1, ..., xn=sn in s.
Für denletrec-Ausdruck gilt:
• Die Variablen xi sind paarweise verschieden.
• Die Bindungen sind kommutativ, d.h. die Reihenfolge der Bindungen ist austausch- bar.
• Eine leere Menge von Bindungen in einem letrec-Ausdruck ist nicht erlaubt, d.h.
Ausdrücke der Form (letrec in t) sind unzulässig.
Bemerkung: Die Sprache CHNR ist die gleiche Sprache wie CH, außer dass letrec nicht rekursiv ist. Der Einfachheit halber wird in diesem Fall let statt letrec benutzt.
Wir verwenden manchmal folgende Schreibweisen, um verschiedene Ausdrücke verkürzt darzustellen:
• Stattletrec x1 =s1, ..., xn=snin sschreiben wir auch (letrec Env in s) oder auch letrec Env1, Env2 in t.
• Statt λ x1.λ x2....λ xn.s.schreiben wir auch λ x1...xn.s.
1CH steht für chain
Die Anreicherung einer Kernsprache mit dem let(rec)-Konstruktor gilt als benutzerfreund- liche Erweiterung, um mehr Flexibilität bei der Programmierung zu ermöglichen. Mittels let(rec) können lokale Aliase für Ausdrücke erstellt werden. Aus theoretischer Sicht ist es wichtig solche Aliase als äquivalent zu erfassen. Diese Frage wird uns im Laufe dieser Arbeit begleiten, die sogar der Existenzgrund dieser Arbeit ist. Wir nehmen das zum Anlass, den Begriff der Äquivalenz für CH-Ausdrücke zu erläutern. Dabei beschränken wir uns darauf, die Frage von einer rein syntaktischen Seite zu betrachten, da die Frage, ob zwei Ausdrücke s und t semantisch äquivalent sind, generell als unentscheidbar gilt, weil man damit das Halteproblem lösen würde.
Definition 3.1 (α−Äquivalenz in Lch).
Zwei CH-Ausdrücke t1 undt2 heißenα−äquivalent, geschrieben (t1 ≡α,cht2), wenn t1
int2 durch die zwei Operationen:
(i) konsistente Umbenennung der λ-gebundenen Variablen (ii) Permutation der Bindungen in den letrec Umgebungen überführt werden kann.
Beispiel: Betrachten wir den Ausdruck (letrec x= y, y=z in x). Benennen wir die Variablex mity und tauchen wir deren Bindung in die Umgebung um, bekommen wir (letrec x=z, y=x in y), d.h. (letrec x=y , y=z in x)≡α,ch(letrec x=z , y=x in y), wo die Variablex mit y umbenannt und durch Substitution im Bindungsbereich ersetzt wird.
Die Alpha-Äquivalenz für Ausdrücke in dem Lambda-Kalkül bzw. erweiterten Lambda- Kalkül ohne Permutation der Bindungen ist effizient entscheidbar, sogar in O(nlogn) bezüglich der Größe |n|der Ausdrücke[13].
Der Alpha-Äquivalenz-Test für Ausdrücke wird schwieriger, wenn Permutationen der Bindungen erlaubt werden. Das bedeutet, dass die Positionen der Bindungen(xi :=ei) beliebig untereinander innerhalb der Menge (keine Ordnung) der Bindungen getauscht werden können.
Dies ist einfach zu sehen, da für die Alpha-Äquivalenz im schlimmsten Fall alle möglichen Permutationen der letrec-Bindungen untersucht werden müssen, was eine exponentiel- le Laufzeit erfordert. Es lässt vermuten, dass die Schwierigkeit des Alpha-Äquivalenz- Problems darin liegt, für jede letrec-Bindung im ersten Ausdruck eine äquivalente Bindung in der ungeordneten Menge von letrec-Bindungen im zweiten Ausdruck zu finden.
Den nächsten Abschnitt widmen wir zur Untersuchung der Komplexität des Alpha- Äquivalenz-Problems in der CH-Sprache.
Dass das Problem in NP liegt ist offensichtlich. Es reicht eine Permutation der Mengen von Bindungen für zwei letrec Ausdrücke zu raten und deren Alpha-Äquivalenz in poly- nomieller Zeit zu testen.
3.1 Komplexität von CH
Die Analogie des Alpha-Äquivalenz-Problems für Sprachen mit rekursiven Bindungen zu dem Graphisomorphie-Problem ist offensichtlich:
Alpha-Äquivalenz-Problem Graphisomorphie-Problem
gegeben: zwei Ausdrückes1 und s2 gegeben: zwei GraphenG1 und G2 Menge von Untertermen Menge von Knoten
Menge von Bindungen Menge von Kanten
input: sinds1 unds2 ? gesucht: sindG1 und G2 ?
alpha-äquivalent isomorph
Zuerst zeigen wir, dass Alpha-Äquivalenz in CH GI-hart ist.
Proposition 3.1. Auch wenn die Signatur Σleer ist, ist das Alpha-Äquivalenz- Entscheidungsproblem für CH GI-hart.
Beweis.
Den Beweis führen wir anlehnend zu [1].
Wir kodieren das Graphisomorphie-Problem für unbeschriftete gerichtete Graphen in das CH-α-Äquivalenzproblem, in dem wir zwei beliebige unbeschriftete gerichtete Graphen Gi = (Vi, Ei) für i= 1,2 in zwei CH-Ausdrücke exp(Gi) kodieren.
Wir nehmen anfangs an, dass die Signatur Σ nicht leer ist. Sie enthält einen binären Konstruktorc und eine Konstante a. Den Fall, in dem Σ leer ist, behandeln wir später.
Wir nehmen an V1 =v1,1, ..., v1,n und V2=v2,1, ..., v2,n, so dass V1∩V2 =;∅.
Der Ausdruckexp(Gi) entspricht letrec Envi,A , Envi,B in a.
Die Envs sind folgendermaßen definiert: für jeden Knoten vi,j ∈ Vi bilden wir die Komponente vi,j = a in Envi,A und für jede Kante (vi,j, vi,k) ∈ Ei bilden wir die Komponentexi,j,k =c(vi,j, vi,k) in Envi,B.
Annahme:esp(G1)'α,CH exp(G2).
Dann es existiert eine Abbildungσ zur Umbenennung der VariablenVi und xi,j,k mit σ:V1 ∪
∪
{x1,j,k} →V2 ∪∪
{x2,j,k}, d.h. nach Sortieren ( den letrec Bindungen inexp(G2) entsprechen) der letrec-Bindungen istσ(exp(G1)) syntaktisch gleich zu exp(G2).Seiσ0die Einschränkung vonσ auf V1 offensichtlich, σ0eine Bijektion zwischen V1 und V2; d.h. (σ0(v1,j), σ0(v1,k))∈E2 genau dann, wenn (v1,j, v1,k)∈E1. Somit ist auchσ0ein Isomorphismus zwischen G1 und G2.
Jetzt nehmen wir an, dass G1 und G1 isomorph sind. Dann existiert eine bijektive
Abbildung (∗):σ:V1→V2, so dass (σ(v1,j), σ(v1,k))∈E2 genau dann, wenn (v1,j, v1,k)∈ E1. Daraus ergibt sich, dass exp(G1) und exp(G2) alpha-äquivalent sind und σ als Umbenennung angesehen werden kann, das aber um die Variablen xi,j,k erweitert werden muss, so dass es (?): für∀ (x1,j,k)∈E1 ,σ(x1,j,k) =x2,j,k ∈E2 gilt, was immer möglich ist.
Aus (∗?) folgt,σ:V1 ∪
∪
{x1,j,k} →V2 ∪∪
{x2,j,k}. So jeder Isomorphismus zwischen (G1) und (G2) impliziert, Alpha-Äquivalenz zwischenexp(G1) und exp(G2). Nun falls Σ =∅ derselbe Beweis benutzt werden kann, in dem man für aeine freie Variable xa auswählt und für c(vi, vj), letrec y=vi in vj benutzt.Beispiel: Wir kodieren den folgenden Graphen als CH-Ausdruck:
v1
v3
v2
v4
v5
G1
w3
w2
w1
w4
w5
G2
Die Kodierung sieht der si=exp(Gi) wie folgt aus:
s1=letrec v1 =a, v2 =a, v3=a, v4 =a, v5 =a
x1,3 =c(v1, v3), x1,5=c(v1, v5), x2,4 =c(v2, v4), x2,1 =c(v2, v1), x3,5=c(v3, v5), x4,3 =c(v4, v3), x5,2 =c(v2, v1),
in=x;
s2=letrec w1 =a, w2=a, w3 =a, w4=a, w5 =a
x1,5 =c(w1, w5), x1,4 =c(vw, w4), x2,3=c(w2, w3), x4,5 =c(w4, w4), x3,4 =c(w3, w4), x5,1 =c(w5, w1), x5,3 =c(w5, w3),
in=x;
Die Ausdrückes1 unds2 sind alpha-äquivalent dank der Abbildung.σ ={v17→w5, v5 7→
w1, v2 7→ w4, v4 7→ w2, v3 7→ w3, x1 7→ x7, x2 7→ x6, x5 7→ x3, x3 7→ x4, x4 7→ x5, x6 7→
x2, x7 7→x1}. Nach Sortieren der letrec-Umgebungen ist der Ausdruckσ(s1) syntaktisch gleich zu s2.
Die Einschränkung der Abbildungσ auf die Variablenv1, ..., v5 entspricht einem Isomor- phismus zwischenG1 und G2.
Isomorphismus={ v17→w5 , v5 7→w1 , v27→w4 , v4 7→w2 , v37→w3 }
3.2 Graph Konstruktion für CH-Ausdrücke
Im Folgenden stellen wir eine Methode zur Darstellung eines CH-Ausdrucks als Graphen vor.
Definition 3.2.
Sei s ein CH-Ausdruck, wir beschreiben die Konstruktion von Gs, den beschrifteten gerichteten Graphen entsprechend zu s.
Für jeden Unterausdruck von s konstruieren wir einen Knoten. Die Variablen in s sind in drei Kategorien unterteilt:
{x1, ..., xk} : Menge der freien Variablen {y1, ..., ym} : lambda gebundene Variablen {z1, ..., zn} : letrec gebundene Variablen und seiV(s) die Union der drei Mengen.
Seic1, ..., ck der Konstruktoren und Funktionssymbole vorkommend in s, q sei die maxi- male Stelligkeit von diesen Symbolen. Der LDG G(s)hat die Labelmenge
L={var, lamvar, lvar, body, letvar, bind, letrec, in, λ}∪{c1, ..., ck}∪{1, ..., q}∪{x1, ..., xk}.
Für die Variablew∈V ar(s) gibt es einen KnotenN(w) im Graphen G(s).
Wir setzen ein:node(w) :=N(w).
Für jede freie Variablexisetzen wirlab(N(xi)) :=xi, für jede lambda gebundene Variable yi setzen wir lab(N(yi)) =lamvar und für jede letrec gebundene Variable zi setzen wir lab(N(zi)) =letvar ein.
Für die Konstruktion des Graphen G(s), jeden Unterausdrucks inspiziert entsprechend den folgenden Fällen (Variablen haben wir oben vorgestellt):
I Wenn der Unterausdruck ein λ x.r ist, dann konstruieren wir einen neuen Knoten v mit lab(v) :=λund ziehen die Kanten (v, node(x), lvar),(v, node(r), body). Für den gesamten Unterausdruck setzen wirnode(λ x.r) :=v ein.
IWenn der Unterausdruck ein letrec ist (letrec x1 =s1...., xn=sn in t), dann setzen wir einen neuen Knoten u für den gesamten Unterausdruck mit lab(u) := letrec, d.h.
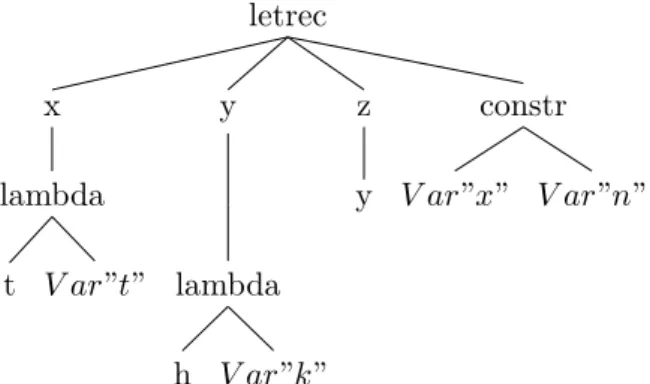
node(letrec x1 =s1...., xn=sn in t) :=u. Für jedenxi einen Knotennode(si) konstruie- ren mit label lab(xi) :=letvar. si und t sind selbst CH-Ausdrücke. Diese werden in dem entsprechenden Fall (var, letrec, lamda, constr) rekursiv behandelt.
Die Kanten werden wie folgt definiert:
(u, node(xi), var) : Kante vom Knoten u zunode(xi) mit dem label var (u, node(t), in) : Kante von Knoten u zunode(t) mit dem label in (node(xi), node(si)) : Kante vonnode(xi) zunode(si) mit dem label bind.
Jetzt schauen wir den letzten Fall eines syntaktisch korrekten CH-Unterausdrucks an.
IWenn der Unterausdruck ein c(s1, ..., sn) ist, dann konstruiere einen neuen Knoten node(c(s1, ..., sn)) :=ufür den gesamten Unterausdruck mit dem label(u):= c. Konstruiere ebenfalls für jedes Argumentsieinen Knoten. Zu jedem Knotennode(si) wird vonnode(c) eine Kante mit den label(si) :=N umi gezogen. Hier gilt, dass auch die si gültige CH- Ausdrücke sind und werden dementsprechend behandelt, um daraus einen Untergraphen zu konstruieren.
Graphisch entsprechen die oben eingeführten Konstruktionen folgenden Fällen:
s∈CH;s:=x |λx.s|letrec x1=s1, ...xn=sn in t |c(s1...sarc). mit (ar'arity), fallss:= Variable wird einfach ein Knoten mit den Variablennamen erstellt.
lambda
lvar
bo dy
lamvar
s
Abbildung 7:lambda
constr
num
1 num ar
c
s1 sarc
Abbildung 8: constr letrec
var
var In
letvar
Bind
letvar Bind
s1 sn
S
Abbildung 9:letrec
Beispiel:Für den CH-Ausdruck letrec x=y, y=z in x, der entsprechender LDG ist G= (V, E, L, lab), wobei L={var, lamvar, lvar, body, letvar, bind, letrec, in, λ, z},V = {v1, v2, v3, v4},E ={(v4, v1, var),(v4, v2, var),(v1, v2, bind),(v2, v3, bind),(v4, v1, in)}, undlab=v17→letvar, v27→letvar, v37→z, v47→letrec ist. Graphisch entspricht diese Beschreibung dem folgenden Graphen:
letvar bind letrec in
var var
letvar bind z
Abbildung 10: CH-Ausdrucks-Beispielgraph
Bis jetzt haben wir gezeigt, dass das CH-alpha-Äquivalenz-Problem GI-hart ist, indem wir das GI-Problem für allgemeine ungerichtete unbeschriftete Graphen effizient in CH-Alpha- Äquivalenz-Problem transformiert (polynomielle Reduktion) haben. Die Modellierung CH-Ausdrücke als Graphen mittels der Definition 3.2. zeigte, dass die konstruierten Gra- phen LDGs sind. Daher die Vermutung (Beweis), dass das CH-alpha-Äquivalenz-Problem in GI liegt.
Proposition 3.2. CH-alpha-Äquivalenz ist in GI.
(Beweis siehe [1] Propostion 3.7.)
4 Ein effizienter Algorithmus für Ausdrücke ohne Garbage
Die bisherigen Ergebnisse zeigten, dass die allgemeinen CH-Ausdrücke ein hartes Alpha- Äquivalenz-Problem haben. Die Frage, ob zwei CH-Ausdrücke bis zum Entfernen von nicht verwendeten Bindungen alpha-äquivalent sind, kann jedoch effizient beantwortet werden, wie wir sehen werden. Konkret definieren wir die folgenden Ersetzungsregeln auf CH-Ausdrücke; garbage collection (gc), dabei werden nicht verwendete Bindungen (garbage) iterativ entfernt.
4.1 Garbage Collection
Garbage collection (gc) ist die Entfernung unbenutzter Bindungen (gc1) letrec x1 = s1, ..., xn=sn, y1=t1, ..., ym=tm in tm+1
−→gc letrec y1 =t1, ..., ym =tm in tm+1 wenn
m+1
S
i=1
F V(ti)∩ {x1, ..., xn}=∅.
Dieser Schritt besteht darin die Variablen xi, die in Term tm+1 body nicht gebraucht werden, zu löschen. Nach diesem Schritt haben wir einen Ausdruck, wo jede definierte Bindung im letrec Umgebung auch im body eingesetzt wird. Die Syntax von CH erlaubt zwar keine leeren letrecs, aber Bindungen zu definieren, die nicht in body eingesetzt werden, ist erlaubt wie wir gesehen haben. Diese werden dann entfernt. Was danach entsteht ist ein Ausdruck, was nur Bindungen hat, die in body benutzt werden, oder auch einen leeren letrec Term. In diesem Fall besteht der letrec Ausdruck nur aus letrec und body, z.B.: letrec in tm+1. Für diesen durchaus möglichen Fall, definieren wir Schritt zwei der „ Garbage collection“ (gc2).
(gc2) letrec x1=s1, ..., xn=sn in t−→gc t wenn F V(t)∩x1, ..., xn=∅.
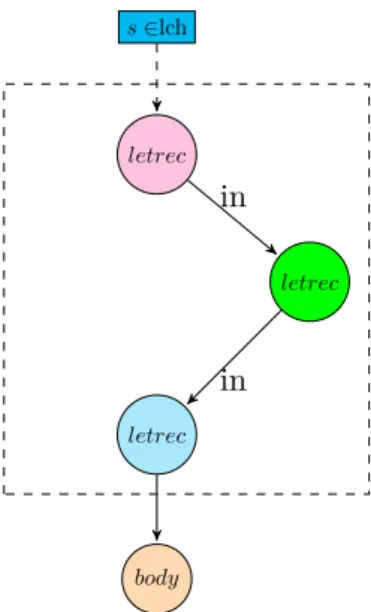
Da Letrecs auch verschachtelt vorkommen können, könnte es sein, dass in body von einem leeren letrec wieder einen leerer letrec vorkommt oder auch eine Kette von leeren Letrecs.
Es ist einfach zu überprüfen, dass durch →gc auf CH induziertes Ersetzungssystem konfluent ist und immer terminiert, d.h. es gibt nur eine gc-Normalform für einen letrec bzw. CH-Ausdrucks. Denn nur letrec (Unter-)Terme können „garbage“ enthalten oder auch nicht. Wenn ein CH-Ausdruck kein „garbage“ enthält, dann liegt er bereits in der Normalform und kein gc-Ersetzungsregel kann auf ihn angewendet werden. Man sagt der CH-Ausdruck ist „garbage free“. Jeder CH-Ausdruck t kann in polynomieller Zeit in die Normalform überführt werden. Die gc-Redexes (letrecs) können effizient ermittelt und die gc-Ersetzungsregeln können mit der „innermost-Strategie“ auf jeden letrec-Ausdruck angewendet werden. Dies kann in O(n log n) durchgeführt werden, wobei n die Größe der Ausdrücke ist.