Zusammenhang- Verschiedene Begrie und einige erklärende Beispiele
Bernhard Stiftner
18. Dezember 2011
Inhaltsverzeichnis
1 Einleitung 3
2 Grundlegende Denitionen und Aussagen 3
2.1 Komponenten . . . 5
2.2 Wegkomponenten und Wegzusammenhang . . . 6
2.3 Bogenkomponenten und Bogenzusammenhang . . . 7
2.4 Hyperzusammenhängend und Ultrazusammenhängend . . . 9
2.5 Lokal zusammenhängend . . . 10
2.6 Zusammenfassung . . . 11
3 Einige Beispiele spezieller Topologischer Räume 11 3.1 The Deleted Integer Topology . . . 11
3.2 The Extended Topologist Sine Curve . . . 12
3.3 Die verkleinerte euklidische Topologie . . . 14
3.4 Divisor Topology . . . 14
1 Einleitung
Die vorliegende Arbeit beschäftigt sich mit dem topologischen Begri Zusammenhang. Schon in der Überschrift ist hierbei von verschiedenen Begrien die Rede. In der Tat ist es möglich etliche ähnliche Begrie zu denieren, die zunächst alle recht ähnlich zum Begri zusammenhängend erscheinen.
Bei genauerer Betrachtung sind jedoch sehr wohl Unterschiede festzustellen, weswegen ein Titel wie Der topologische Begri Zusammenhang unpräzise erscheint. Diese Unterschiede herauszuarbeit- en und durch Angabe von Beispielen zu verdeutlichen wird der zentrale Punkt dieser Arbeit sein.
Grundlegendes Wissen zu topologischen Räumen wird dabei vorausgesetzt.
2 Grundlegende Denitionen und Aussagen
Die folgenden Lemmata und Dentionen sind für den Rest dieser Arbeit wesentlich und werden an dieser Stelle noch einmal zusammengefasst.
Denition 1 (Topologie). Sei X ein beliebige Menge und sei ein Mengensystem T ⊂ P(X) . Man nennt T eine Topologie auf X, wenn
• ∅,X∈ T
• S
i∈I
Oi ∈ T für Oi ∈ T ∀i∈I für eine beliebige Menge I
•
n
T
i=1
Oi ∈ T für Oi ∈ T ∀i∈ {1, . . . , n} und n ∈N
Wird X mit der Topologie T versehen, so schreibt man kurz (X,T). Man nennt dies einen topolo- gischer Raum.
Denition 2 (Disjunktion und zusammenhängender Raum). Sei (X,T) ein topologischer Raum.
Die Mengen U,V ∈ T heiÿen Disjunktion von X wenn U,V 6= ∅, U ∩V = ∅ und U ∪V = X. Ein Raum (X,T)heiÿt zusammenhängender Raum, wenn er keine Disjunktion besitzt.
Denition 3 (Getrennte Mengen). Nicht notwendigerweise oene MengenM1,M2 ⊂XmitM1,M2 6=
∅ heiÿen getrennt, wennM1∩M2 =M1∩M2 =∅.
Denition 4 (Zusammenhängende Menge). Sei E ⊂ X und (X,T) ein topologischer Raum. Man nennt E ⊂ X eine zusammenhängende Menge, wenn E nicht als Vereinigung getrennter Mengen geschrieben werden kann.
Es ist eine wichtige Aussage, das zwischen den Begrien zusammenhängender Raum aus Def- inition 2 und zusammenhängende Menge aus Denition 4 nicht unterschieden werden muss, wie folgendes Lemma zeigt.
Lemma 5. Sei(X,T)ein topologischer Raum undE ⊂X, dann sind die folgenden beiden Aussagen äquivalent.
• E ist eine zusammenhängende Menge.
• E ist zusammenhängend als Raum bezüglich der Spurtopologie T ∩E. Beweis. siehe [KAL] (Lemma 12.6.8; Seite 156)
Über die Vereinigung von zusammenhängenden Mengen kann die folgende Aussage gemacht wer- den.
Lemma 6. Sei(Ei)i∈Ieine Familie von zusammenhängenden Mengen im topologischem Raum(X,T) und gelte weiters T
i∈I
Ei 6=∅, dann ist S
i∈I
Ei eine zusammenhängende Menge.
Beweis. siehe [KAL] (Lemma 11.6.10; Seite 157)
Die Voraussetzung, das der Durchschnitt nichtleer ist kann dabei keineswegs weggelassen werden.
Beispiel 7. Setze (X,T) = (R,E) und E1 = (0,1) bzw. E2 = (2,3), dann gilt E1∩E2 =∅ aber E1 und E2 sind zwei getrennte oene Mengen, womit E1∪E2 sicher nicht zusammenhängend ist.
Die Eigenschaft einer Menge zusammenhängend zu sein bleibt unter stetigen Abbildungen erhalten, wie folgendes Lemma zeigt.
Lemma 8. Seien(X,T) und (Y,O)topologische Räume und sei
f : (X,T)−→(Y,O) (1)
eine stetige Abbildung. Für eine zusammenhängende MengeE ⊂X gilt dann: f(E)⊂Y ist zusam- menhängend.
Beweis. siehe [KAL] (Proposition 12.6.9; Seite 156)
Auch für den Abschluss von zusammenhängenden Mengen in einem topologischen Raum kann eine Aussage gemacht werden, es gilt sogar noch mehr.
Lemma 9. Sei (X,T) ein topologischer Raum und E ⊂ X zusammenhängend. Sei F ⊂X, sodass E ⊂F ⊂E, dann ist F zusammenhängend.
Beweis. AngenommenF wäre nicht zusammenhängend dann existieren nach Lemma 5U, V ∈ T mit U,V 6=∅ mit U ∩F 6=∅ und V ∩F 6=∅ mit:
(F ∩U)∪(F ∩V) = F (2)
(F ∩U)∩(F ∩V) =∅ (3)
weiters gilt dann:
F ∩E =E = (F ∩U∩E)∩(F ∩V ∩E) = (E∩U)∩(E∩V) =∅ (4) Somit muss entweder E ∩U =∅ oder E∩V =∅, dennE ist zusammenhängend (vgl. Lemma 5).
Gelte nun o.E.d.A.E∩V =∅. Laut Annahme muss dann aber:
F ∩V = (F \E∩V)∪(E∩V)
| {z }
=∅
(5) Somit muss∀x∈F∩V schonx∈∂E\E undx∈V gelten. Andererseits ist aberE∩V =∅, was aber ein Widerspruch ist. Damit muss die obige Annahme falsch sein und F ist zusammenhängend.
Bemerkung 10. Aus Lemma 9 folgt auch schon für zusammenhängendes E das E zusammenhän- gend ist.
Bemerkung 11. Für das Innere einer zusammenhängenden MengeE ⊂X gilt eine analoge Aussage nicht, auch wennE 6=∅ ist. Betrachte dazu die Menge
E1 :=
x1 x2
∈R2 |
x2 x2
− −2
0
2
≤1
(6)
E2 :=
x1 x2
∈R2 |
x1 x2
− 1
0
2
≤1
(7)
E3 :=
x1 x2
|x1 ∈[−1,1], x2 = 0
(8) und setze
E :=E1∪E2∪E3 (9)
Dann ist E zusammenhängend und es gilt
E˚=E1∪E2 (10)
Das sind aber zwei getrennte oene Mengen, womit E˚sicher nicht zusammenhängend ist.
2.1 Komponenten
Sei nun wieder (X, T) ein topologischer Raum. Es soll nun der Frage nachgegangen werden, welche Art von zusammenhängenden Mengen man um ein festesx∈X legen kann. Diese Mengen werden dann in einem gewissen Sinn maximal sein.
Denition 12. Bezeichne(X,T) einen topologischen Raum und für x,y∈X sei
x∼1 y:⇐⇒ ∃E ⊂X zusammenhängend und x,y∈E (11)
Satz 13 (Komponenten).
(i) Die in Denition 12 festgelegte Relation ∼1 ist eine Äquivalenzrelation.
(ii) Bezeichne für die zu x ∈ X gehörige Äquivalenzklasse mit A1x, dann ist A1x die gröÿte zusam- menhängende Menge die x enthält, d.h. für eine zusammenhängende Menge E ⊂X mit x∈E folgt E ⊂A1x.
(iii) A1x ist abgeschlossen.
Beweis.
(i) ∼1 ist reexiv denn für x ∈ X ist {x} sicher eine zusammenhängende Menge die x enthält.
Denition 12 ist klarerweise symmetrisch. Weiters ∼1 ist auch transitiv denn für x, y, z ∈ X mit x ∼1 y und y∼1 z folgt die Existenz zweier zusammenhängender Mengen E1, E2 ⊂X mit x, y ∈E1 und y, z ∈E2. Nun ist aber y∈E1∩E2 womit E1∩E2 6=∅. Laut Lemma 6 ist dann E1∪E2 zusammenhängend und x, z∈E1∪E2. Insgesamt ist ∼1 eine Äquivalenzrealtion.
(ii) Sei x ∈ X und x ∈ E ⊂ X eine beliebige zusammenhängende Menge. Für alle y ∈ X gilt klarerweise x∼1 yund somit y∈A1x. Daher giltE ⊂A1x. Angenommen A1x wäre für einx∈X nicht zusammenhängend, dann existieren sicher Mengen U, V ∈ T mit A1x∩U 6=∅, A1x ∩V 6=
∅ und (A1x∩U) ∪ (A1x∩V) = A1x. Für y1, y2 ∈ A1x und eine beliebige zusammenhängende Menge E mit y1, y2 ∈ E gilt einerseits lt. obigen Ausführungen dann E ⊂ A1x und deswegen auch (E∩U) ∪ (E∩V) = E. Weiters gilt sowohl E ∩ U 6= ∅ als auch E ∩ V 6= ∅. Das ist aber ein Widerspruch, denn E ist zusammenhängend. Es muss also auch A1x für x ∈ X zusammenhängend sein.
(iii) Mit Lemma 9 ist A1x abgeschlossen.
Bemerkung 14. Die Äquivalenzklassen der Relation aus Denition 13 werden als Komponenten bezeichnet. Hat (X,T) nur eine Komponente so ist X klarerweise zusammenhängend in Sinn von Denition 4.
2.2 Wegkomponenten und Wegzusammenhang
Denition 15. In einem topologischem Raum (X,T) ist für x, y ∈X:
x∼2 y:⇐⇒ ∃f : [0,1]−→X stetig mit f(0) =x f(1) = y (12)
Satz 16. Die in Denition 15 denierte Relation ist eine Äquivalenzrelation.
Beweis.
• Reexivität: Für x∈X gilt x∼2 x. Setze hierfür:
f : [0,1]−→X :t7−→x (13)
f ist sicher stetig, da konstante Abbildungen zwischen beliebigen topologischen Räumen immer stetig sind. Klarerweise gilt f(0) =xund f(1) = 1.
• Symmetrie: Für x, y ∈ X und x ∼2 y gilt auch y ∼2 x, denn aus x ∼2 y folgt die Existenz eines stetigenf : [0,1]−→X mit f(0) =x und f(1) =y. Setze dann:
h: [0,1]−→X :t7−→f(1−t) (14)
h ist dann als Zusammensetzung stetiger Funktionen sicher stetig und es gilt darüberhinaus h(0) =y und h(1) =x; also insgesamt y∼2 x.
• Transitivität: Seien x, y, z ∈ X und es gelte x ∼2 y sowie y ∼2 z. Es existieren also f : [0,1]−→X mit f(0) =xund f(1) =yund g : [0,1]−→X mitg(0) =y undf(1) =z. Setze nun
h: [0,1]−→X :t7−→
(f(2t), t ∈ 0,12 g(2t−1), t ∈1
2,1 (15)
h ist wohldeniert, denn 2t ∈ [0,1] für t ∈ 0,12
und ebenso 2t −1 ∈ [0,1] für t ∈ 1
2,1 Klarerweise isth auf[0,1]\1
2 als Zusammensetzung stetiger Funktionen stetig. Da f 212
= g 212 −1
folgt auch die Stetigkeit an t = 12 und damit auf [0,1]. Durch Einsetzen erhält man h(0) =x und h(1) =z und somit auchx∼2 z. Die Relation ∼2 ist also auch transitiv.
Insgesamt ist∼3 eine Äquivalenzrelation.
Denition 17. Die Äquivalenzklassen von ∼3 werden als Wegkomponenten bezeichnet. Für x∈X schreibe dafür A2x. Eine Menge E ⊂ X heiÿt wegzusammenhängend wenn für alle x, y ∈ X x ∼2 y gilt. Hat(X,T)nur eine Wegkomponente, so wird er wegzusammenhängend genannt.
2.3 Bogenkomponenten und Bogenzusammenhang
Das folgende Konzept ist ganz ähnlich zu dem des Wegzusammenhangs.
Denition 18. Sei(X,T) ein topologischer Raum und x, y ∈X. Es soll dann
x∼3 y :⇐⇒ ∃f : [0,1]−→X stetig und injektiv mit f(0) =x mit f(1) =y oderx=y (16)
Satz 19. Die in Denition 18 denierte Relation ist eine Äquivalenzrelation.
Beweis. ∼3 ist per denitionem reexiv. Die Symmetrie folgt genauso wie in Satz 16. Es bleibt die Transitivität zu zeigen.
• Betrachte hier nur den Fallx, y, z ∈X mitx6=y 6=z; alle anderen Fälle sind trivial. Seix∼3 y und y ∼3 z. Es existieren nun also f, g : [0,1] 7→X, jeweils stetig und injektiv mit f(0) =x, f(1) = y bzw. g(0) = y, g(1) = z. Es muss nun ein stetiges und injektives h : [0,1] → X gefunden werden. Das ist aber nicht so einfach wie in Satz 16, denn für
f([0,1])∩g([0,1]) 6=∅ (17) wird
h: [0,1]−→X :t7−→
(f(2t) t∈ 0,12 g(2t−1) t∈1
2,1 (18)
im Allgemeinen nicht injektiv sein. Es müssen deswegen einige Fälle unterschieden werden.
• Sei x∈ g([0,1]). Es existiert also ein s ∈ [0,1] mit g(s) = x. Es gilt sogar s ∈ (0,1) denn lt.
Voraussetzung giltx6=y6=z. Setze nun
h: [0,1]→X :t7→g((1−s)t+s), (19) dann gilt h(0) = x und h(1) = z. Die Stetigkeit und die Injektivität folgen aus der Stetigkeit und Injektivität von g und der anen Transformation.
• Sei nunx /∈g([0,1]) und zustätzlich z∈f([0,1]). Wie oben folgt die Existenz eines m∈(0,1]
mit f(m) =z. Setze nun
h: [0,1]→X :t7→f(ts). (20)
Die Stetigkeit und Injektivität folgt analog zum vorherigen Punkt.
• Schlieÿlich muss noch der Fall x /∈ g([0,1]) und z /∈ f([0,1]). Es müssen nun t1, t2 ∈ [0,1]
existieren, mitf(t1) = g(t2). Setze nun
M :={t1 ∈[0,1] :∃t2 ∈[0,1] mit f(t1) =g(t2)} (21) und weiters
m := inf
t1∈MM. (22)
Es ist nun m ∈ M, denn für eine Folge (mn)n∈
N wobei für die Folgenglieder mn ∈ [0,1] gilt und mn → m. Es existiert nun eine Folge (tn)n∈
N, wobei auch hier tn ∈ [0,1] für n ∈ N gilt.
Insbesondere ist (tn)n∈
N auch beschränkt; es gibt also ein s∈ [0,1] und eine Teilfolge (tnk)k∈
mit tnk →s. Zudem gilt nun aber auch mnk →m. Es ist nun: N
f(m) = lim
k→∞f(mnk) = lim
k→∞g(tnk) =g(s) (23)
wobei die beiden äuÿeren Gleichheiten aus der Stetigkeit vonf undgund die mittlere Gleichheit aus der Konstruktion der beiden Folgen (mnk)k∈
N und (tnk)k∈
N folgen. Insgesamt gilt nun m∈ M. Da jax /∈g(0,1]folgt aber auch m >0. Es gilt nun
f([0, m))∩g([0,1]) =∅. (24)
Zusätzlich muss auchs <1, denn fürs = 1wäref(m) = g(1) =z /∈f([0,1])lt. Voraussetzung.
Setze nun:
h: [0,1]−→X :t7−→
(f(2mt) t∈
0,12 g(2 (1−s)t+ 2s−1) t∈1
2,1 (25)
Nun ist f(m) = g(t) und damit ist h auch an t = 12 stetig. Die Wohldeniertheit folgt wie in Satz 16. Lt. Vorausetzung giltz 6=f(m) =g(s). Deswegen, weil die anen Transformationen injektiv sind und mit (24) folgt die Injektivität von h.
• Das waren aber schon alle Fälle und so folgt, dass ∼3 eine Äquivalenzrelation ist.
Denition 20 (Bogenkomponenten und Bogenzusammenhang). In einem topologischen Raum(X,T) heiÿen die Äquivalenzklassen von ∼3 Bogenkomponenten von X. Für ein x ∈ X werden sie mit A3x bezeichnet. Eine Menge E ⊂ X heiÿt bogenzusammenhängend, wenn für alle x, y ∈ X x ∼3 y gilt.
(X,T)heiÿt bogenzusammenhängend, wenn er nur eine Bogenkomponente hat.
Der folgende Satz zeigt, wie die Begrie Komponenten, Wegkomponenten und Bogenkomponenten zusammenhängend.
Satz 21. Sei(X,T)ein topologischer Raum, dann gilt mit den Notationen von vorher für einx∈ T:
A3x ⊂A2x ⊂A1x (26)
oder in Worten: Komponenten ⊂Wegkomponenten ⊂ Bogenkomponenten
Beweis. Zeige für ein festes x∈X gilt: x ∼3 y ⇒x∼2 y ⇒x∼1 y, dann folgt bereits die Aussage.
Für x=y ist das klar, da alle Relationen unter anderem reexiv sind. Nimm also an x6=y.
• x ∼3 y ⇒ x ∼2 y ist klar, da für x ∼3 y die Existenz von speziellen (nämlich injektiven) stetigen Funktionen f : [0,1]−→X mit f(0) =xund f(1) =y gefordet wird.
• Aus x ∼3 y folgt für f : [0,1]−→ X stetig mit f(0) = x und f(1) = y, dass x, y ∈ f([0,1]). Damit ist f stetig und da [0,1] zusammenhängend ist folgt aus Lemma 8 x∼1 y
Bemerkung 22. Laut Denition 17 und 20 und mit den Sätzen 5 und 21 gilt in einem topologis- chen Raum (X,T) für beliebige Teilmengen E ⊂ X,dass aus bogenzusammenhängend wegzusam- menhängend und aus wegzusammenhängend zusammenhängend folgt. Im allgeinen gilt aber nicht mal für E = X eine einzige Umkehrung dieser Aussagen. Deswegen macht es auch wirklich Sinn zwischen zusammenhängend, wegzusammenhängend und bogenzusammenhängend zu unterscheiden.
Erklärende Beispiele hierfür werden später angegeben.
2.4 Hyperzusammenhängend und Ultrazusammenhängend
Sei im folgenden immer X ein Raum versehen mit der Topologie T und schreibe dafür (X,T). Denition 23. (X,T) heiÿt hyperzusammenhängend, wenn fürU, V ∈ T und U, V 6=∅ immer
U ∩V 6=∅ (27)
gilt.
Denition 24. (X,T) heiÿt ultrazusammenhängend, wenn für abgeschlossene Mengen A, B ⊂ X und A, B 6=∅ immer
A∩B 6=∅ (28)
gilt.
Satz 25. Sei(X,T)hyperzusammenhängend, dann folgt auch schon dass(X,T)zusammenhängend ist.
Beweis. WennXnicht zusammenhängend wäre, so müsste zumindest es zwei oene MengenU, V 6=∅ geben mitU ∩V =∅, das widerspricht aber der Denition von hyperzusammenhängend.
Satz 26. Sei (X,T) ultrazusammenhängend, dann folgt, dass (X,T) auch wegzusammenhängend ist. Insbesondere ist(X,T) damit auch zusammenhängend.
Beweis.
• Wähle a, b∈X beliebig und o.E.d.A a6=b, denn ein einpunktiger Raum ist sicher wegzusam- menhängend, da∼2 reexiv ist. Betrachte nun weiters ein beliebigesp∈ {a} ∩ {b}. Ein solches kann sicher gefunden werden, denn (X,T) ist nach Voraussetzung ultrazusammenhängend.
Setze nun
f : [0,1]−→X :t 7−→
a t ∈ 0,12 p t = 12 b t ∈ 12,1
(29)
• Sei nun A⊂X eine abgeschlossene Menge. Dann ist:
f−1(A) =
∅ a, b, p /∈A 0,12
a, p∈A, b /∈A 1
2,1
b, p∈A, a /∈A [0,1] a, b, p∈A
(30)
Das sind aber auch schon alle Fälle denn füra∈Aoderb ∈Afolgt, daAabgeschlossen ist und wegen der der Wahl vonp, dass dann auch p∈A. In jedem Fall istf−1(A)aber abgeschlossen und somit ist, daA⊂Xbeliebig warf stetig. Laut Konstruktion ist nunf(0) = aundf(1) =b und somit gilta∼2 b. Daa undb beliebig waren folgt schon das(X,T)wegzusammenhängend ist.
• (X,T)ist nun wegen Satz 21 auch zusammenhängend.
Bemerkung 27. Die Eigenschaften hyper- und ultrazusammenhängend sind, auch wenn aus beiden zusammenhängend folgt, unabhängig voneinander. Es gibt topolgische Räume die sowohl hyper- als auch ultrazusammenhängend sind, aber auch solche die jeweils nur eine der beiden Eigenschaften haben oder gar keine der beiden Eigenschaften haben.
2.5 Lokal zusammenhängend
Denition 28. Ein topologischer Raum (X,T) heiÿt lokal zusammenhängend, wenn er eine Basis bestehend aus zusammenhängenden Mengen hat.
Beispiel 29. (R,E)mit den oenen Intervallen als Basis ist, da Intervalle zusammenhängend sind, sicher lokal zusammenhängend. (R,E) ist auch zusammenhängend.
Bemerkung 30. Die Eigenschaft eines topologischen Raums (X,T) lokal zusammenhängend zu sein, ist unabhängig von den Eigenschaften zusammenhängend, wegzusammenhängend oder gar bo- genzusammenhängend zu sein. Es gibt topologische Räume die zusammenhängend, wegzusammen- hängend oder bogenzusammenhängend sind, aber nicht lokal zusammenhängend. Zusätzlich ist auch ultrazusammenhängend von lokal zusammenhängend unabhängig. Für einen hyperzusammenhängen- den topologischen Raum kann jedoch eine Aussage gemacht werden.
Satz 31. Sei(X,T)ein hyperzusammenhängender topologischer Raum, dann folgt, dass(X,T)auch lokal zusammenhängend ist.
Beweis. Es kann sogar noch mehr gezeigt werden, nämlich, dass für (X,T) hyperzusammenhän- gend, dann schon jedes O ∈ T zusammenhängend sein muss. Wähle dazu ein beliebiges O ∈ T. Angenommen O wäre nicht zusammenhängend, dann folgt aus Denition 2 die Existenz von zwei Menge U, V ∈ T mit
(U∩O)
| {z }
∈T,6=∅
∩(V ∩O)
| {z }
∈T,6=∅
=∅ (31)
Das widerspricht aber der Eigenschaft von (X,T) hyperzusammenhängend zu sein. Somit muss O ∈ T zusammenhängend sein und da O beliebig war folgt die Gültigkeit des Satzes.
2.6 Zusammenfassung
Die Inklusionen aus den Sätzen 21, 25, 31und 26 lassen sich nun für einen topologischen Raum(X,T) in der folgenden Skizze zusammenfassen:
bogenzusammenhängend =⇒ wegzusammenhängend =⇒ zusammenhängend
⇑ ⇑
ultrazusammenhängend hyperzusammenhängend
⇓
lokal zusammenhängend
3 Einige Beispiele spezieller Topologischer Räume
In der Zusammenfassung in 2.6 sind alle Implikationen verzeichnet, wie sie für die Begrie aus dem theoretischen Teil für einen topologischen Raum (X,T) gelten. Im Allgemeinen gelten keiner- lei Umkehrungen dieser Impliktionen. Für einige spziellen Implikationen soll dies nun anhand von Beispielen verdeutlicht werden. Diese Räume stammen alle aus [STE].
3.1 The Deleted Integer Topology
Mit diesem Beispiel soll gezeigt werden, dass aus lokalzusammenhängend nicht zusammenhängend folgen muss.
• Betrachte dazu den topologischen Raum (X,T), wobei X := R \N versehen mit der Spur- topologie der euklidischen Topologie, also T := E ∩ (R \N). Setze nun U := (−∞,1) und V := (1,∞)\N. Dann gilt U ∩V = ∅ mit U, V 6= ∅ und U ∩V = X; also ist (X,T) nicht zusammenhängend.
• (X,T) ist aber lokal zusammenhängend. Betrachte dazu für eine beliebige Menge O ∈ T, O 6=∅ ein beliebiges x ∈O. Es existiert nun ein ∈R+ mit (x−, x+)⊂O und zusätzlich (x−, x+)∩N=∅. Also gilt auch (x−, x+)∈ T. Betrachte nun:
f : ((x−, x+),E ∩(x−, x+))→((x−, x+)∩ T,(x−, x+)) :t7→t+x (32) Diese Abbildung ist stetig, da T ⊂ E. (x−, x+) ist als stetiges Bild einer Zusammenhän- genden Menge zusammenhängend in (X,T), Es gibt also eine Basis aus zusammenhängenden Mengen und damit ist (X,T) lokal zusammenhängend.
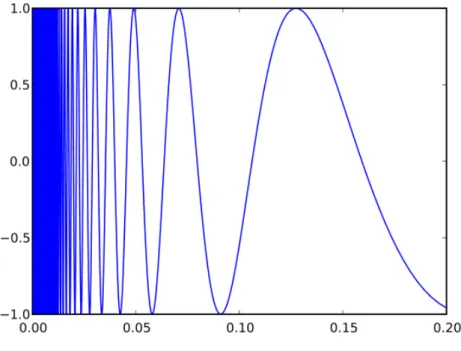
Abbildung 1: The Extended Topologist Sine Curve; Quelle: wikipedia.org
3.2 The Extended Topologist Sine Curve
In der Deleted Integer Topology wurde gezeigt das für einen topologischen Raum(X,T)aus zusam- menhängend nicht lokal zusammenhändend folgen muss. Es gilt aber auch nicht die Umkehrung, d.h aus zusammenhängend muss auch nicht lokal zusammenhängend folgen. Setze dazu:
S :=
n x y
∈R2 :y= sin 1
x
, x∈
0,1 π
o
und S1 :=S∪n 0 0
o
(33) Es giltS ⊂S1 ⊂S. undS ist als stetiges Bild einer zusammenhängenden Menge zusammenhängend.
Mit Lemma 9 ist auchS1 zusammenhängend. Für die weiteren Überlegungen betrachte dann(S1,T) als zusammenhängenden topologischen Raum versehen mit der Spurtopologie, alsoT :=E∩S1 (vgl.
Lemma 5). Betrachte ferner auch noch die Abbildung 1.
• Es soll nun gezeigt werden, dass (S1,T) nicht lokalzusammenhängend ist. Betrachte dazu die Menge
U˜ :=n x1 x2
∈R2 | k x1
x2
k2 < 1 2
o∩S ∈ T. (34) Damit (S1,T) lokal zusammenhängend ist muss es eine Menge O˜ = O ∩S1 ∈ T geben, mit O ∈Eund O˜ ∈U˜ und zusätzlich (0,0)T ∈O˜.
• Setze nun
Vn:=
2
(2n+ 1)π, 2 (2n+ 2)π
×(−1,1)∩S1 mit n ∈N0. (35) Nun gilt
Vn ∈ T ∀n∈N0 und O˜ ⊂ [
n∈N
Vn. (36)
Es existiert nun ein n0 ∈ N0 mit Vn∩O˜ 6= ∅ ∀n ≥ n0, denn sonst müsste es eine Teilfolge (Vnk)k∈
N mit Vnk∩O˜ =∅ ∀nk ∈N geben. Betrachte in diesem Fall die Folge (xnk)k∈
N, wobei xnk = (cnk,0)∈Vnk für ein cnk ∈R geeignet. Somit gilt aber nun
xnk −−→T
k∈N
0 0
(37) und zusätzlich Vnk ∩S1 = ∅, was aber einen Widerspruch darstellt. Es muss also ein solches n0 ∈N0 geben.
• Beobachte nun, dass
O˜∩
n0
[
n=0
Vn6=∅, O˜∩
∞
[
n=n0+1
Vn 6=∅, (38)
O˜ = O˜∩
n0
[
n=0
Vn
!
∩ O˜∩
∞
[
n=n0+1
Vn
!
=∅, (39)
und
O˜ = O˜∩
n0
[
n=0
Vn
!
∪ O˜∩
∞
[
n=n0+1
Vn
!
= ˜O (40)
gilt.
Die Menge O˜ kann also als Vereinigung zweier nichtleerer oener Mengen aus T dargestellt werden und ist somit nicht zusammenhängend. Der Punkt(0,0)T ∈S1 verfügt also über keine Umgebungsbasis bzgl. T zusammenhängender Mengen. Daher ist (S1,T) nicht lokal zusam- menhängend.
Bemerkung 32. Die beiden vorangegangenen Beispiele zeigen in der Tat, dass die beiden Eigen- schaften lokal zusammenhängend und zusammenhängend völlig getrennt voneinander auftreten kön- nen. Insbesondere ist das lokal in lokal zusammenhängend keineswegs als die topologisch lokale Aussage des Begris Zusammenhang zu verstehen.
Das Beispiel der Extended Topologist's Sine Curve eignet sich auch dazu zu zeigen, dass aus aus zusammenhängend nicht wegzusammenhängend folgen muss, doch dazu noch das folgende Lemma.
Lemma 33. Seien(X,T)und (Y,O)topologische Räume und sei(X,T)kompakt und lokal zusam- menhängend und (Y,O) Hausdor. Es existiere weiters eine stetige und surjektive Abbildung f : (X,T)→(Y,O), dann ist (Y,O)lokal zusammenhängend.
Beweis. SeiA⊂Xabgeschlossen. Zeige nun dassf(A)⊂Y abgeschlossen ist. Aus der Abgeschlossen- heit von A, folgt mit der Kompaktheit von (X,T) das A kompakt ist. Als stetiges Bild einer kom- pakten Menge ist auch f(A) kompakt. Da (Y,O) auch Hausdor ist, ist f(A) abgeschlossen. Aus der Surjektivität von f folgt nun aber auch f(A)c = f(Ac). f ist also oen. Für eine beliebige Menge V ∈ (X,T) folgt nun aus der Stetigkeit die Existenz von U ∈ T mit f(U) ⊂ V, aber auch f(U)∈ O, denn f ist oen. Da(X,T)lokal zusammenhändend ist kann man O.e.d.AO zusammen- hängend wählen. Dann ist f(U) auch zusammenhängend. Da V ∈ O beliebig war, ist auch (Y,O) lokal zusammenhängend.
• Mit diesem Lemma soll nun gezeigt werden, dass(S1,T)auch nicht wegzusammenhängend ist.
Angenommen das Gegenteil wäre der Fall. Betrachte nun die beiden Punkte a = (0,0)T und b = π1,0T
. Damit (S1,T) wegzusammenhängend ist, muss es nun ein stetiges f : [0,1] → S1 geben mit f(0) = a und f(1) = b. Es ist klar, dass wegen der Stetigkeit ein solches f surjektiv sein muss. (S1,T) ist Hausdor denn, T ist Spurtopologie einer Hausdorschen Topologie. ([0,1],E ∩[0,1]) ist aber kompakt. Mit Lemma 33 ist nun aber (S1,T) aber lokal zusammenhängend. Das ist aber lt. oben nicht richtig. Somit kann es kein solchesf geben und (S1,T)ist nicht wegzusammenhängend.
Bemerkung 34.
• In der Notation von Denition 15 haben wir hier also die beiden Wegkomponenten {(0,0)T} und S1\ {(0,0)T}, aber nur eine Zusammenhangskomponente im Sinn von Denition 12.
• Der vorliegende Raum ist damit auch nicht hyperzusammenhängend, denn sonst wäre er lt.
Lemma 31 lokal zusammenhängend.
3.3 Die verkleinerte euklidische Topologie
Betrachte die Menge X := [−1,1]und versehe sie mit der Topologie T :={O∈ E ∩X :−1
2 ∈/O,1
2 ∈O} ∪X∪ ∅ (41)
wobei E die euklidische Topolgie bezeichnet. Es ist klar, dass T eine Topologie ist und dass sicher T ⊂ E gilt.
• Seien nun O1, O2 ∈ T und gelte O1, O2 6= ∅, dann gilt 1
2 ⊂ O1 ∩O2 6= ∅. Da diese beiden Mengen beliebig waren, muss (X,T) hyperzusammenhängend sein. Aus Satz 31 folgt auch, dass(X,T)lokal zusammenhängend ist. Satz 25 impliziert, dass(X,T)zusammenhängend ist.
• (X,T)ist auch ultrazusammenhängend, denn für abgeschlossene MengenA, B ⊂X mitA, B 6=
∅folgt schon, dass
−12 ⊂A∩B 6=∅; also ist(X,T)ultrazusammenhängend.
• (X,T)ist auch bogenzusammenhängend. Betrachte dazu für x, y ∈ X eine injektive, stetige Abbildung
f : ([0,1],E ∩[0,1])→(X,E ∩X) (42) mit f(0) = x und f(1) = y (z.B.: ane Abbildung). Wegen T ⊂ E ∩[−1,1] ist aber f auch stetig auf (X,T) und damit ist (X,T) auch bogenzusammenhängend. Sowohl aus Satz 26 als auch aus Satz 21 folgt weiters, dass (X,T)wegzusammenhängend ist.
• Insgesamt vereint (X,T) also alle Eigenschaften des theoretischen Teils in sich.
3.4 Divisor Topology
Betrachte die Menge X :=N\ {1}
Un:={x∈X :x|n} mit n∈N (43)
und
T :=Tini({Un :n∈N}) (44) die initiale Topologie des Mengensystems aller Vielfachen für ein n∈N. Dann ist (X,T)ein topolo- gischer Raum. Dieser Raum ist wegzusammenhängend aber nicht bogenzusammenhängend. Ähnlich wie das vorherige Beispiel, vereint auch dieser Raum viele der Eigenschaften aus dem theoretischen Teil in sich.
• Es gilt nun∀x∈N:
[
n∈N
{nx} ⊂ {x}, (45)
denn für eine abgeschlossene Menge A ⊂ X mit x ∈ A folgt natürlich, dass Ac oen ist, und dass x /∈Ac. Nun ist auch nx /∈Ac ∀ ∈N, denn wenn nicht, dann gäbe es ein n0 ∈N mit
n0x∈Ac=[
i∈I n
\
k=1
Unik (46)
also existiert eini0 ∈I mit
n0x∈Ac=
n
\
k=1
Uni
0k (47)
und somit gilt
n0x∈Ac=Uni
0k ∀k ∈ {1, . . . n} (48) und da ja auch x|n0x gilt ist somit
x∈Ac=Uni0k ∀k ∈ {1, . . . n}. (49) Insgesamt gilt nun x ∈ Ac, was aber ein Widerspruch ist. Also muss obige Annahme richtig sein.
• Für abgeschlossene MengenA, B ⊂X mit A, B 6=∅ und x∈A und y∈B gilt also:
∅ 6= [
n∈N
{nxy} ⊂ {x} ∩ {y} ⊂A∩B ∀n ∈N (50) Also ist(X,T)ultrazusammenhängend und lt. Satz 26 auch wegzusammenhängend wegen Satz 21 auch zusammenhängend.
• (X,T)ist sicher nicht bogenzusammenhängend, da X abzählbar ist. (vgl. Denition 20)
• (X,T)ist auch hyperzusammenhängend. Da für n1, n2 ∈N
Un1 ∩Un2 ⊃ {x∈X :x|n1n2}=Un1n2 (51) gilt, ist das Mengensystem {Un : n ∈ N} eine Basis der initialen Topologie. Seien weiters O1, O2 ∈ T beliebige oene Mengen mit O1, O2 6=∅. Es folgt die Existenz von n1, n2 ∈ N mit O1 ⊃Un1 und O2 ⊃Un2. Nun gilt
O1∩O2 ⊃Un1 ∩Un2 ⊃ {x∈X :x|n1n2}=Un1n2 6=∅ (52) und damit folgt die Richtigkeit der Aussage.
• Mit Satz 31 ist(X,T) auch lokal zusammenhängend.
Literatur
[KAL] M. KALTENBÄCK, Analysis 2. Vorlesungsskritpum, TU Wien; 2010
[STE] L. A. STEEN, J.A SEEBACH, Counterexamples in Topology, Springer, New York, 1970 [WIKI] http://en.wikipedia.org/wiki/Topologist%27s_sine_curve; Zugri 9.Dezember 2011