Statistik f¨ur Ingenieure 3 Zufallsgr¨oßen

Statistik f¨ ur Ingenieure 3 Zufallsgr¨ oßen

Prof. Dr. Hans-J¨ org Starkloff

TU Bergakademie Freiberg Institut f¨ur Stochastik

Wintersemester 2019/2020

letzte ¨ Anderung: 7.10.2019

3 Zufallsgr¨ oßen

3.1 Zufallsgr¨ oßen und ihre Verteilung

I

H¨ aufig sind Zahlenwerte Ergebnisse von Zufallsversuchen.

I

Oft ist es auch in anderen F¨ allen f¨ ur eine mathematische

Behandlung g¨ unstig, den Versuchsergebnissen Zahlen zuzuordnen (etwa 1 f¨ ur

” Erfolg“ und 0 f¨ ur

” Misserfolg“).

⇒ Beschreibung des Ergebnisses eines Zufallsversuches durch eine Zufallsgr¨ oße X (oder mehrere Zufallsgr¨ oßen X

, X

, . . . , X

) .

I

Beispiele

I

Zuf¨ allige Zeit X (Lebensdauer, Ausfallzeit,. . . ) mit m¨ oglichen Werten { x ∈ R : x ≥ 0 } .

I

Messergebnis X (L¨ ange, Kraft, Temperatur, . . . ) mit entsprechenden Zahlenwerten (ohne Maßeinheit) als m¨ oglichen Werten.

I

Augenzahl X beim W¨ urfeln mit m¨ oglichen Werten { 1, 2, 3, 4, 5, 6 } .

Mathematische Definition einer Zufallsgr¨ oße

I

Mathematische Definition einer Zufallsgr¨ oße:

Eine Abbildung (Funktion) X : Ω → R heißt Zufallsgr¨ oße (reelle Zufallsvariable), falls f¨ ur jedes Intervall (a, b) ⊂ R , a < b, die Menge { ω ∈ Ω : a < X (ω) < b } ein zuf¨ alliges Ereignis ist

( ” Messbarkeitsbedingung“ im Sinne der mathematischen Maß- und Integrationstheorie; dabei wird ein System von zuf¨ alligen Ereignissen mit bestimmten nat¨ urlichen Eigenschaften als gegeben

vorausgesetzt).

I

Es gilt:

Sind X , Y Zufallsgr¨ oßen zu einem Zufallsversuch, dann sind auch X + Y , X − Y , X · Y , X /Y , falls Y 6 = 0 , a · X mit a ∈ R und

¨

ahnliche durch mathematische Operationen gebildete Gr¨ oßen

Zufallsgr¨ oßen (d.h. die Messbarkeitsbedingung bleibt erhalten).

Grundtypen von Zufallsgr¨ oßen

I

F¨ ur Zufallsgr¨ oßen interessieren vor allem Wahrscheinlichkeiten der Art P(X ≤ b), P(a < X < b), P(a ≤ X ≤ b) (mit reellen Zahlen a < b) oder ¨ ahnliche.

I

Diese bilden die Verteilung oder Wahrscheinlichkeitsverteilung der Zufallsgr¨ oße.

I

Abgeleitete Kenngr¨ oßen, wie zum Beispiel Erwartungswert oder Varianz liefern ebenfalls wichtige Informationen.

I

Zwei wichtige Grundtypen von Zufallsgr¨ oßen (mit zum Teil unterschiedlichen mathematischen Hilfsmitteln bei Berechnungen oder Untersuchungen) sind:

I

Zufallsgr¨ oßen mit diskreter Verteilung (diskrete Zufallsgr¨ oßen) und

I

Zufallsgr¨ oßen mit (absolut) stetiger Verteilung

(stetige Zufallsgr¨ oßen) .

Zufallsgr¨ oßen mit diskreter Verteilung

I

Definition Eine Zufallsgr¨ oße X heißt diskret, wenn sie nur endlich viele oder abz¨ ahlbar unendlich viele m¨ ogliche Werte x

, x

, . . . annehmen kann.

I

Die Wahrscheinlichkeitsfunktion der diskreten Zufallsgr¨ oße X ist die Zuordnung p

:= P(X = x

) , i = 1, 2, . . . , die Werte p

sind die zu den m¨ oglichen Werten zugeh¨ origen Wahrscheinlichkeiten.

I

Oft wird eine Verteilungstabelle gegeben:

m¨ ogliche Werte x

x

x

x

. . . zugeh¨ orige Wahrscheinlichkeiten p

p

p

p

. . .

I

Die Bestimmung der Wahrscheinlichkeiten p

erfolgt durch

Berechnung aus Grundannahmen (typische Verteilungen, spezielle

Modelle) oder experimentell mittels statistischer Methoden.

Wahrscheinlichkeiten bei diskreten Verteilungen

I

Beispiel Gerechtes W¨ urfeln, Zufallsgr¨ oße X . . . Augenzahl.

x

1 2 3 4 5 6 p

I

F¨ ur die Wahrscheinlichkeiten p

gelten allgemein :

I

0 ≤ p

≤ 1 ;

I

X

i

p

= 1 .

I

F¨ ur beliebige Mengen I ⊆ R gilt P(X ∈ I ) = X

xi∈I

p

, z.B. f¨ ur reelle Zahlen a < b P(a < X < b) = X

a<xi<b

p

.

I

Beispiel Zweimaliges W¨ urfeln (fairer W¨ urfel), Zufallsgr¨ oße X . . . Augensumme.

Ges. P(X ≤ 4) .

Zufallsgr¨ oßen mit stetiger Verteilung

I

Definition Eine Zufallsgr¨ oße X heißt (absolut) stetig, wenn es eine integrierbare reelle Funktion f

: R → R gibt, so dass

P(a ≤ X ≤ b) = Z

a

f

(x) dx f¨ ur beliebige reelle Zahlen a ≤ b gilt.

I

Die Funktion f

heißt Dichtefunktion (oder Verteilungsdichte) der Zufallsgr¨ oße X und besitzt die Eigenschaften:

1. f

(x) ≥ 0 f¨ ur alle x ∈ R ; 2.

Z

−∞

f

(x ) dx = 1 .

I

Bemerkungen

I

Eine stetige Zufallsgr¨ oße kann beliebige Werte aus einem Intervall (oder einer ¨ ahnlichen Menge) annehmen.

I

Eine Dichtefunktion muss nicht stetig oder beschr¨ ankt sein !

I

Eine Dichtefunktion gibt die Verteilung der

” Wahrscheinlichkeitsmasse“ auf der reellen Achse an.

Beispiel Zufallsgr¨ oße mit stetiger Verteilung

I

Beispiel Rein zuf¨ allige Auswahl eines Punktes (Wertes) X aus dem Intervall [0, 1] (auf dem Intervall [0, 1] gleichverteilte oder gleichm¨ aßig verteilte Zufallsgr¨ oße).

I

F¨ ur 0 ≤ a < b ≤ 1 gilt P(a ≤ X ≤ b) = b − a .

I

Die Dichtefunktion ist f

(x) =

1 , 0 ≤ x ≤ 1 ;

0 , sonst.

Verteilungsfunktion einer Zufallsgr¨ oße

I

Die Verteilung einer beliebigen Zufallsgr¨ oße kann eindeutig durch die Verteilungsfunktion der jeweiligen Zufallsgr¨ oße beschrieben werden.

I

Definition Die Funktion F

einer reellen Variablen mit reellen Funktionswerten, die durch

F

(x) = P(X < x) = P( −∞ < X < x) , x ∈ R , definiert wird, heißt Verteilungsfunktion der Zufallsgr¨ oße X .

I

Der Funktionswert ist f¨ ur jede reelle Zahl x die Wahrscheinlichkeit daf¨ ur, dass die Zufallsgr¨ oße X einen Wert annimmt, der kleiner als x ist.

I

Bemerkung: Mitunter wird die Verteilungsfunktion einer

Zufallsgr¨ oße X auch durch F e

(x) = P(X ≤ x) , x ∈ R , definiert,

insbesondere in der Zuverl¨ assigkeitstheorie.

Verteilungsfunktion einer diskreten Zufallsgr¨ oße

I

F¨ ur ¨ ubliche diskrete Zufallsgr¨ oßen ist die Verteilungsfunktion eine Treppenfunktion mit Spr¨ ungen der H¨ ohe p

an den Werten x

.

I

Beispiel Verteilungsfunktion F

der Zufallsgr¨ oße

X . . . Augenzahl beim W¨ urfeln mit einem gerechten W¨ urfel .

Verteilungsfunktion einer stetigen Zufallsgr¨ oße

I

F¨ ur stetige Zufallsgr¨ oßen ist die Verteilungsfunktion eine in allen Punkten stetige Funktion.

I

Beispiel Verteilungsfunktion F

einer Zufallsgr¨ oße X , die auf

[0, 1] gleichverteilt ist (hier: unterschiedliche Achsenskalierung !)

Allgemeine Eigenschaften von Verteilungsfunktionen

I

Eine Verteilungsfunktion F

ist monoton nicht fallend.

I

Es gelten lim

x→−∞

F

(x) = 0 , lim

x→+∞

F

(x) = 1 .

I

Eine Verteilungsfunktion F

ist linksseitig stetig.

I

Es gilt f¨ ur beliebige reelle Zahlen a < b :

P(a ≤ X < b) = F

(b) − F

(a) .

I

F¨ ur stetige Zufallsgr¨ oßen gelten

P(a ≤ X < b) = P(a < X < b) = P(a < X ≤ b) = P(a ≤ X ≤ b).

I

Außerdem gelten f¨ ur stetige Verteilungen F

(x) =

Z

−∞

f

(t) dt , x ∈ R und f

(x) = F

(x)

an den Stellen x ∈ R , in denen die Ableitung existiert.

3.2 Kenngr¨ oßen der Verteilung einer Zufallsgr¨ oße

I

Die Gesamtinformation, die mit einer Wahrscheinlichkeitsverteilung gegeben wird (oder gegeben werden muss) ist h¨ aufig zu

umfangreich.

I

Deshalb nutzt man Kenngr¨ oßen, die in praktischen Situationen gut zu nutzen sind.

I

Die beiden wichtigsten Gruppen von Kenngr¨ oßen sind die der Lageparameter und der Streuungsparameter.

I

Die am h¨ aufigsten genutzte Kenngr¨ oße ist der Erwartungswert EX einer Zufallsgr¨ oße X (auch Mittelwert der Zufallsgr¨ oße genannt).

I

Der Erwartungswert ist ein Lageparameter, eine (nichtzuf¨ allige)

reelle Zahl und beschreibt die Lage des Schwerpunkts der

Wahrscheinlichkeitsmasse.

Definition Erwartungswert einer Zufallsgr¨ oße

I

Definition F¨ ur eine diskrete Zufallsgr¨ oße X mit m¨ oglichen Werten x

, x

, . . . und zugeh¨ origen Wahrscheinlichkeiten p

= P(X = x

), p

= P(X = x

), . . . wird der Erwartungswert definiert durch

EX = X

i

x

p

.

F¨ ur eine stetige Zufallsgr¨ oße X mit der Dichtefunktion f

wird der Erwartungswert definiert durch

EX = Z

−∞

x · f

(x) dx .

I

Beispiele Zufallsgr¨ oßen

I

X

. . . Augenzahl beim W¨ urfeln mit einem gerechten W¨ urfel.

I

X

gleichm¨ aßig verteilt auf dem Intervall [0, 1].

Beispiele Erwartungswerte von Zufallsgr¨ oßen

X

. . . Augenzahl beim W¨ urfeln X

gleichverteilt auf [0, 1]

Einzelwahrscheinlichkeiten Dichtefunktion

und Erwartungswert und Erwartungswert

Eigenschaften von Erwartungswerten

I

Nicht jede Zufallsgr¨ oße besitzt einen Erwartungswert.

I

Linearit¨ atseigenschaft von Erwartungswerten:

f¨ ur Zufallsgr¨ oßen X , Y und reelle Zahlen a, b gelten E(a + bX ) = a + bEX ;

E(X + Y ) = EX + EY .

I

Ist g : R → R eine (z.B. stetige) Funktion und X eine

Zufallsgr¨ oße, dann kann man den Erwartungswert der Zufallsgr¨ oße Y = g(X ) wie folgt berechnen, ohne erst die Verteilung von Y zu bestimmen:

EY = Eg (X ) = X

i

g (x

)p

f¨ ur diskrete ZG X ; EY = Eg (X ) =

Z

−∞

g (x)f

(x) dx f¨ ur stetige ZG X .

Varianz und Standardabweichung einer Zufallsgr¨ oße (ZG)

I

Die wichtigste Kenngr¨ oße f¨ ur die Variabilit¨ at von Zufallsgr¨ oßen ist die Varianz (auch Streuung oder Dispersion) der Zufallsgr¨ oße.

I

Definition Die Varianz VarX der Zufallsgr¨ oße X ist die nichtnegative reelle Zahl

VarX = E (X − EX )

= ( P

i

(x

− EX )

p

, diskrete ZG ; R

−∞

(x − EX )

f

(x) dx , stetige ZG .

I

Die Varianz, falls sie existiert, gibt die erwartete quadratische Abweichung der Zufallsgr¨ oße von ihrem Erwartungswert an.

I

Definition Die Standardabweichung σ

der Zufallsgr¨ oße X ist die positive Quadratwurzel aus der Varianz der Zufallsgr¨ oße:

sd (X ) = σ

= √

VarX .

Eigenschaften von Varianzen und Standardabweichungen

I

Varianz und Standardabweichung sind Streuungsparameter.

I

Die Varianz l¨ asst sich meistens bequemer berechnen mit Hilfe der Formel

VarX = E X

− (EX )

.

I

Ist a eine reelle Zahl und X eine Zufallsgr¨ oße mit endlicher Varianz, dann gelten

I

Var(aX ) = a

VarX ,

I

Var(a + X ) = VarX ,

I

σ

= | a | σ

,

I

σ

= σ

.

I

Es gilt genau dann VarX = σ

= 0 , wenn es eine reelle Zahl x

gibt, so dass P(X = x

) = 1 gilt.

Die Zufallsgr¨ oße X heißt dann einpunktverteilt.

Beispielberechnungen Varianzen

I

ZG X

: Augenzahl beim W¨ urfeln mit einem gerechten W¨ urfel.

EX

= 1

6 + 2

6 + 3

6 + 4

6 + 5

6 + 6

6 = 91 6 VarX

= 91

6 − 7

2

= 35

12 = 2.917 .

I

ZG X

: gleichm¨ aßig verteilt auf dem Intervall [0, 1] . EX

=

Z

x

· 1 dx = 1 3 VarX

= 1

3 − 1

2

= 1

12 = 0.0833 .

Variationskoeffizient

I

Definition F¨ ur eine Zufallsgr¨ oße X mit endlicher Varianz und EX > 0 wird der Variationskoeffizient V

(auch relative

Standardabweichung) definiert durch V

= σ

EX .

I

Mit dem Variationskoeffizienten wird die Streuung der m¨ oglichen Werte zum mittleren Wert (Erwartungswert) in Beziehung gesetzt.

I

Der Variationskoeffizient ist unabh¨ angig von den Einheiten und er hilft beim Vergleich der St¨ arke der zuf¨ alligen Schwankungen der Werte von unterschiedlichen Zufallsvariablen, insbesondere wenn diese in unterschiedlichen Einheiten gemessen wurden.

I

Der Variationskoeffizient kann f¨ ur solche Zufallsgr¨ oßen verwendet

werden, bei denen die Quotientenbildung der m¨ oglichen Werte auch

inhaltlich sinnvoll ist.

Quantile einer stetigen Zufallsgr¨ oße

I

F¨ ur 0 < q < 1 heißt die reelle Zahl x

ein q − Quantil der stetigen Zufallsgr¨ oße X , wenn X Werte links von x

mit einer

Wahrscheinlichkeit q annimmt, d.h. x

ist eine L¨ osung der Gleichung

Z

−∞

f

(x) dx = q bzw. F

(x

) = q .

I

q − Quantile k¨ onnen auch f¨ ur diskrete und andere Zufallsgr¨ oßen betrachtet werden.

I

Wichtige Quantile sind:

I

das 0.5–Quantil, es heißt Median von X ;

I

das 0.25– bzw. 0.75–Quantil, dies sind die sogenannten

Viertelquantile oder Quartile von X (das untere bzw. das obere) ;

I

die α − bzw. (1 − α ) − Quantile f¨ ur kleine Werte α , sie spielen bei

statistischen Fragen eine große Rolle.

Beispiel Exponentialverteilung

Eine Zufallsgr¨ oße X heißt exponentialverteilt mit Parameter λ > 0 , falls f¨ ur die Verteilungsfunktion F

bzw. die Verteilungsdichte f

gilt:

F

(x) =

0 , x ≤ 0 ,

1 − exp( − λx) , x > 0 , f

(x ) =

0 , x ≤ 0 ,

λ exp( − λx) , x > 0 .

Verteilungsfunktion (λ = 2) Dichtefunktion (λ = 2)

Quantile f¨ ur die Exponentialverteilung

I

Es sei X exponentialverteilt mit Parameter λ = 2 , d.h.

F

(x) = P(X < x) =

0 , x ≤ 0 , 1 − exp( − 2x) , x > 0 .

I

Dann gilt f¨ ur das q − Quantil x

(mit 0 < q < 1) F

(x

) = 1 − exp( − 2x

) = q , also x

= − 1

2 ln (1 − q) .

I

q x

0.25 0.144

0.5 0.347 0.75 0.693 0.95 1.498

Verteilungsfunktion Dichtefunktion

3.3 Wichtige diskrete Wahrscheinlichkeitsverteilungen 3.3.1 Diskrete Gleichverteilung

I

Zufallsgr¨ oße X mit endlich vielen m¨ oglichen Werten x

, x

, . . . , x

(x

6 = x

falls i 6 = j ) .

I

Wahrscheinlichkeitsfunktion:

p

= P(X = x

) = 1

n , i = 1, 2, . . . , n .

I

Im Spezialfall x

= 1 , x

= 2 , . . . , x

= n gelten EX = n + 1

2 und VarX = n

− 1 12 .

I

Anwendung: Laplace-Experiment.

I

Bezeichnung: X ∼ U( { x

, x

, . . . , x

} ) .

3.3.2 Bernoulli-Verteilung

I

Parameter: p ∈ [0, 1] .

I

Zufallsgr¨ oße X mit zwei m¨ oglichen Werten x

= 1 , x

= 0 .

I

Wahrscheinlichkeitsfunktion:

P(X = 1) = p , P(X = 0) = 1 − p .

I

Kenngr¨ oßen: EX = p und VarX = p(1 − p) .

I

Bezeichnung: X ∼ B(p) .

I

Anwendung: Bernoulli-Experiment:

I

Experiment mit zwei m¨ oglichen Versuchsausg¨ angen, die durch die zuf¨ alligen Ereignisse A bzw. A

beschrieben werden.

I

Das Ereignis A tritt mit einer Wahrscheinlichkeit p = P(A) ein.

I

Die Zufallsgr¨ oße X wird dann wie folgt definiert X (ω) = 1

(ω) =

( 1 , wenn ω ∈ A ;

0 , wenn ω 6∈ A .

3.3.3 Binomialverteilung

I

Parameter: n ∈ N , 0 ≤ p ≤ 1 .

I

Zufallsgr¨ oße X mit m¨ oglichen Werten x

= 0, x

= 1, . . . , x

= n .

I

Wahrscheinlichkeitsfunktion:

p

= P(X = i) = n

i

p

(1 − p)

, i = 0, 1, . . . , n .

I

Kenngr¨ oßen: EX = np und VarX = np(1 − p) .

I

Bezeichnung: X ∼ Bin(n, p) .

I

Eigenschaften:

I

Bin(1, p) = B(p) ;

I

X

∼ Bin(n

, p) , X

∼ Bin(n

, p) , unabh¨ angig

⇒ X

+ X

∼ Bin(n

+ n

, p) ;

I

Insbesondere X

∼ B(p) , . . . , X

∼ B(p) , unabh¨ angig

⇒ X

+ . . . + X

∼ Bin(n, p) .

Wahrscheinlichkeitsfunktionen von Binomialverteilungen

Typische Situation f¨ ur Binomialverteilung

I

Typische Situation:

I

Der Zufallsversuch besteht aus n unabh¨ angigen und gleichartigen Teilversuchen.

I

Bei jedem Teilversuch kann ein bestimmtes Ereignis mit einer Wahrscheinlichkeit p eintreten oder (mit Wahrscheinlichkeit 1 − p) nicht.

I

Mit der Zufallsgr¨ oße X z¨ ahlt man die Anzahl der Teilversuche, bei denen das interessierende Ereignis eingetreten ist.

I

X ist also die zuf¨ allige Anzahl der eingetretenen Ereignisse unter obigen Bedingungen.

I

Typische Anwendung:

Stichprobenentnahme mit Zur¨ ucklegen in der Qualit¨ atskontrolle

(X . . . Anzahl von Ausschussteilen in einer Stichprobe).

Beispielaufgabe Binomialverteilung

I

Ein idealer W¨ urfel wird 20 mal geworfen. Wie groß ist die Wahrscheinlichkeit daf¨ ur, dass mindestens zwei mal eine Sechs geworfen wird ?

I

Zufallsgr¨ oße X . . .

” Anzahl der geworfenen Sechsen bei 20 W¨ urfen dieses W¨ urfels“.

I

Die Zufallsgr¨ oße X ist binomialverteilt.

I

Die Wahrscheinlichkeit f¨ ur das Werfen einer Sechs bei einem W¨ urfelwurf betr¨ agt 1/6 , dies ist der Parameter p .

I

Der Parameter n beschreibt die Anzahl der Wiederholungen des Einzelversuchs, hier also n = 20 .

I

Gesucht ist P(X ≥ 2) .

3.3.4 Hypergeometrische Verteilung

I

Parameter: N, M , n ∈ N , M ≤ N , n ≤ N .

I

Zufallsgr¨ oße X mit m¨ oglichen Werten x

= k ∈ N

, mit max { 0, n − (N − M ) } ≤ k ≤ min { M, n } .

I

Wahrscheinlichkeitsfunktion:

p

= P(X = k ) =

M k

·

N n

,

max { 0, n − (N − M) } ≤ k ≤ min { M , n } .

I

Kenngr¨ oßen:

EX = n · M

N ; VarX = n · M

N · N − M

N · N − n N − 1 .

I

Bezeichnung: X ∼ Hyp(N, M, n) .

Wahrscheinlichkeitsfunktionen hypergeom. Verteilungen

Typische Situation f¨ ur die hypergeometrische Verteilung

I

Typische Situation:

I

Unter N Dingen befinden sich M ausgezeichnete;

I

von den N Dingen werden n zuf¨ allig ausgew¨ ahlt (ohne Zur¨ ucklegen);

I

die Zufallsgr¨ oße X repr¨ asentiert die zuf¨ allige Anzahl der ausgezeichneten Dinge unter den n ausgew¨ ahlten.

I

Anwendungsbeispiele:

I

Stichprobennahme ohne Zur¨ ucklegen, z.B. bei der Qualit¨ atskontrolle;

I

Anzahl der richtigen Zahlen bei einem Tipp im Lottospiel;

I

Ist das Verh¨ altnis n

N sehr klein (< 0.05) , so gilt Hyp(N, M , n) ≈ Bin

n, M

N

.

Beispielaufgabe hypergeometrische Verteilung

I

Ein Kunde ¨ ubernimmt alle 50 gelieferten Schaltkreise, wenn in einer Stichprobe von 10 Schaltkreisen h¨ ochstens ein nicht voll

funktionsf¨ ahiger Schaltkreis enthalten ist. Ansonsten wird die gesamte Lieferung verworfen.

I

Man berechne die Wahrscheinlichkeit daf¨ ur, dass die 50 Schaltkreise a) abgenommen werden, obwohl diese 12 nicht voll funktionsf¨ ahige

Schaltkreise enthalten,

b) zur¨ uckgewiesen werden, obwohl nur 3 nicht voll funktionsf¨ ahige Schaltkreise enthalten sind !

I

Zufallsgr¨ oße X . . .

” Anzahl der nicht voll funktionsf¨ ahigen Schaltkreise in der Stichprobe“.

I

Die Zufallsgr¨ oße X ist hypergeometrisch verteilt.

I

N = 50 , n = 10 , M = 12 bzw. M = 3 .

I

Ges. P(X ≤ 1) bzw. P(X > 1) .

3.3.5 Geometrische Verteilung

I

Parameter: 0 < p < 1 .

I

Zufallsgr¨ oße X mit m¨ oglichen Werten k = 1, 2, 3, . . . .

I

Wahrscheinlichkeitsfunktion:

p

= P(X = k ) = p(1 − p)

, k = 1, 2, 3, . . . .

I

Kenngr¨ oßen: EX =

und VarX =

.

I

Bezeichnung: X ∼ Geo(p) .

I

Anwendung:

I

Gleichartige unabh¨ angige Teilversuche, bei denen jeweils

” Erfolg“ mit Wahrscheinlichkeit p oder

” Misserfolg“ mit Wahrscheinlichkeit 1 − p eintreten k¨ onnen, werden so lange durchgef¨ uhrt, bis zum ersten Mal

” Erfolg“ eingetreten ist.

I

Der Wert von X ist gleich der Anzahl der durchgef¨ uhrten

Teilversuche.

Geometrische Verteilungen, Beispielaufgabe

Beispielaufgabe:

I

Ein Relais falle mit einer Wahrscheinlichkeit von 0.0001 bei einem Schaltvorgang zuf¨ allig aus, wobei diese Ausf¨ alle unabh¨ angig voneiander eintreten sollen.

I

Wie groß ist die Wahrscheinlichkeit daf¨ ur, dass der erste Ausfall

nicht vor dem tausendsten Schaltvorgang passiert ?

Verallgemeinerung: negative Binomialverteilung

I

Werden in derselben Situation die Teilversuche solange wiederholt, bis der r − te

” Erfolg“ eingetreten ist (r ∈ N ), besitzt die zuf¨ allige Anzahl X der durchgef¨ uhrten Teilversuche eine negative

Binomialverteilung mit den Parametern r und p. Dann gelten P(X = k ) =

k − 1 r − 1

p

(1 − p)

, k = r , r + 1, . . . , EX = r

p und VarX = r (1 − p) p

.

I

Bemerkung: Bei anderen Varianten der geometrischen und der

negativen Binomialverteilung wird die Anzahl der Misserfolge

(Fehlversuche) und nicht die Anzahl der Teilversuche als Zufallgr¨ oße

betrachtet. Darauf sollte man bei Formeln aus der Literatur bzw. bei

Nutzung von Statistikprogrammen achten.

3.3.6 Poissonverteilung

I

Parameter: λ > 0 (die

” Intensit¨ at“ der Poissonverteilung).

I

Zufallsgr¨ oße X mit m¨ oglichen Werten k = 0, 1, 2, . . . .

I

Wahrscheinlichkeitsfunktion:

p

= P(X = k) = λ

k ! e

, k = 0, 1, 2, . . . .

I

Kenngr¨ oßen: EX = λ und VarX = λ .

I

Bezeichnung: X ∼ Poi(λ) .

I

Eigenschaft: X

∼ Poi(λ

) , X

∼ Poi(λ

) , unabh¨ angig

⇒ X

+ X

∼ Poi(λ

+ λ

) .

Wahrscheinlichkeitsfunktionen von Poissonverteilungen

Anwendungen der Poissonverteilung

I

Typische Anwendung: Poissonverteilte Zufallsgr¨ oßen beschreiben h¨ aufig die Anzahl von bestimmten Ereignissen (

” Poissonereignisse“, z.B. Schadensf¨ alle) in festen Zeitintervallen, wenn die Ereignisse zu zuf¨ alligen Zeitpunkten eintreten (auch analog an zuf¨ alligen Orten oder ¨ ahnliches) und folgendes gilt:

I

Die Wahrscheinlichkeit f¨ ur das Eintreten einer bestimmten Anzahl dieser Poissonereignisse h¨ angt nur von der L¨ ange des betrachteten Zeitintervalls ab, nicht wann dieses beginnt oder endet (Stationarit¨ at).

I

Die zuf¨ alligen Anzahlen der eintretenden Poissonereignisse sind f¨ ur sich nicht ¨ uberschneidende Zeitintervalle stochastisch unabh¨ angig (Nachwirkungsfreiheit).

I

Die betrachteten Poissonereignisse treten einzeln ein, nicht

gleichzeitig, die zuf¨ alligen Anzahlen ¨ andern sich somit von Moment zu Moment h¨ ochstens um den Wert 1 (Ordinarit¨ at).

I

Beispiele: Anzahl von Telefonanrufen, Anzahl von emittierten

Teilchen in Physik (radioaktiver Zerfall), Anzahl von Unf¨ allen,

Anzahl von Schadensf¨ allen, Anzahl von Niveau¨ uberschreitungen.

Poissonverteilung und Binomialverteilung

I

Ist eine zuf¨ allige Z¨ ahlgr¨ oße X binomialverteilt, der Parameter n aber groß und der Parameter p klein (Faustregel: n ≥ 30, p ≤ 0.05 und gleichzeitig np ≤ 10 , sogenannte

” seltene Ereignisse“), dann kann man die Wahrscheinlichkeiten n¨ aherungsweise mit Hilfe einer Poissonverteilung mit Parameter λ = np berechnen, d.h.

P(X = k) = n

k

p

(1 − p)

≈ λ

k! e

(dies folgt aus dem Grenzwertsatz von Poisson).

Ubungsaufgaben Poissonverteilung ¨

I

An einer Tankstelle kommen werktags zwischen 16:00 und 18:00 Uhr durchschnittlich 4 Fahrzeuge pro Minute an.

Wie groß ist die Wahrscheinlichkeit daf¨ ur, dass w¨ ahrend einer Minute im betrachteten Zeitbereich mindestens 3 Fahrzeuge ankommen, wenn man davon ausgeht, dass die zuf¨ allige Anzahl der ankommenden Fahrzeuge poissonverteilt ist ?

I

Es werden 50 Erzeugnisse aus einer Lieferung mit einer Ausschusswahrscheinlichkeit von 0.01 untersucht.

Wie groß ist die Wahrscheinlichkeit daf¨ ur, dass sich h¨ ochstens ein

fehlerhaftes Erzeugnis unter den 50 Erzeugnissen befindet ?

Zusatz zur Poissonverteilung

Ergebnisse der ber¨ uhmten Rutherfordschen und Geigerschen Versuche:

Anzahlen der α − Teilchen, die von radioaktiven Substanzen in n = 2608 Zeitabschnitten von 7.5 Sekunden emittiert wurden

i n

n p ˆ

0 57 54.399

1 203 210.523 2 383 407.361 3 525 525.496 4 532 508.418 5 408 393.515 6 273 253.817 7 139 140.325

8 45 67.882

9 27 29.189

10 16 11.296

Durchschnittliche Anzahl:

λ ˆ = X n

· i

n = 3.87 ; ˆ

p

= λ ˆ

i ! e

.

( Quelle: Fisz, Wahrscheinlichkeitsrechnung und

mathematische Statistik, Berlin 1973 )

3.4 Wichtige stetige Verteilungen 3.4.1 Exponentialverteilung

I

Parameter: λ > 0 .

I

Zufallsgr¨ oße X mit Dichtefunktion f

bzw. Verteilungsfunktion F

f

(x) =

0 , x < 0 ,

λe

, x ≥ 0 ; F

(x) =

0 , x < 0 , 1 − e

, x ≥ 0 .

I

Beispiele: λ = 0.5 (blau), λ = 1 (rot), λ = 5 (gr¨ un) .

Exponentialverteilung

I

Kenngr¨ oßen:

EX = 1

λ , VarX = 1

λ

und x

= ln 2

λ ≈ 0.693

λ .

I

Bezeichnung: X ∼ Exp(λ) .

I

Exponentialverteilte Zufallsgr¨ oßen nehmen nur nichtnegative Werte an, daher sind sie prinzipiell zur Modellierung von zuf¨ alligen Lebensdauern oder Wartezeiten geeignet.

I

Beispielaufgabe:

Die zuf¨ allige Lebensdauer eines Bauteils sei exponentialverteilt, dabei betrage die erwartete Lebensdauer 3 Jahre.

Wie groß ist die Wahrscheinlichkeit, dass das Bauteil l¨ anger als 6

Jahre funktioniert ?

Exponentialverteilung als Lebensdauerverteilung

I

Wird die zuf¨ allige Lebensdauer eines Bauteils durch eine Exponentialverteilung modelliert, dann werden Alterungseffekte nicht mit ber¨ ucksichtigt (sogenannte Ged¨ achtnislosigkeit der Exponentialverteilung).

I

Angenommen, das Bauteil hat schon das Alter x

> 0 erreicht.

Dann gilt f¨ ur die Restlebensdauer X

und x > 0

P(X

≥ x) = P (X ≥ x

+ x | X ≥ x

) = P(X ≥ x

+ x) P(X ≥ x

)

= e

e

= e

= P(X ≥ x).

I

Damit kann die Exponentialverteilung als Lebensdauerverteilung nur

dann ein gutes Modell sein, wenn ¨ außere Ereignisse das Leben

beenden und keine Alterung vorliegt.

Zusammenhang von Exponential- und Poissonverteilung

I

Es werden bestimmte Ereignisse betrachtet, die zu zuf¨ alligen Zeitpunkten T

, T

, . . . mit einer Intensit¨ at λ > 0 (mittlere Anzahl der Ereignisse pro Zeiteinheit) eintreten.

I

Bezeichnet man mit N

die zuf¨ allige Anzahl der eingetretenen Ereignisse im Zeitintervall [0, t], dann sind die Zufallsgr¨ oßen N

f¨ ur verschiedene Zeitpunkte t genau dann poissonverteilt mit Parameter µ = λt, falls die zuf¨ alligen Zeitabst¨ ande zwischen zwei aufeinanderfolgenden Ereignissen stochastisch unabh¨ angig und exponentialverteilt mit dem Parameter λ sind.

I

Die zuf¨ alligen Zeitmomente T

, T

, T

, . . . bilden dann einen sogenannten Poissonschen Ereignisstrom.

I

Die Zufallsgr¨ oßen (N

, t ≥ 0) definieren dann einen sogenannten

Poissonprozess.

3.4.2 Normalverteilung (Gauß-Verteilung)

I

Parameter: µ ∈ R , σ

> 0 .

I

Zufallsgr¨ oße X mit Dichtefunktion f

bzw. Verteilungsfunktion F

f

(x) = 1

√ 2πσ e

, F

(x) = 1

√ 2πσ Z

−∞

e

dt, x ∈ R .

I

Kenngr¨ oßen: EX = µ und VarX = σ

.

I

Bezeichnung: X ∼ N(µ, σ

) .

I

Die Dichtefunktion ist symmetrisch bez¨ uglich der Geraden x = µ ,

deshalb gilt f¨ ur den Median auch x

= µ .

Dichtefunktion Normalverteilung

Quelle: http://images0.dhd.de/61107000 xl.jpg

Dichte- und Verteilungsfunktionen Normalverteilung

links: µ = 0, σ = 0.5 (blau), σ = 1 (rot), σ = 2 (gr¨ un) ;

rechts: µ = − 2, σ = 0.5 (blau), µ = 0, σ = 1 (rot), µ = 1, σ = 2 (gr¨ un) .

Standardnormalverteilung

I

Die Zufallsgr¨ oße X ist standardnormalverteilt, falls X normalverteilt ist und µ = EX = 0 sowie σ

= VarX = 1 gelten, d.h.

X ∼ N(0, 1) .

I

Die Dichte- bzw. Verteilungsfunktion sind dann

φ(x ) = 1

√ 2π e

2

2

bzw.

Φ(x ) = 1

√ 2π Z

−∞

e

2

2

dt, x ∈ R .

I

Ist die Zufallsgr¨ oße X normalverteilt mit Erwartungswert µ und Varianz σ

, dann ist die standardisierte Zufallsgr¨ oße

Z := X − µ σ

standardnormalverteilt, d.h. normalverteilt mit Erwartungswert 0

und Varianz 1.

Berechnung von Wahrscheinlichkeiten

I

Geg.: X ∼ N(µ, σ

) , a < b .

I

Ges.: P(a ≤ X ≤ b) .

I

Wegen Z = X − µ

σ ∼ N(0, 1) gilt P(a ≤ X ≤ b) = P

a − µ

σ ≤ X − µ

σ ≤ b − µ

σ

= P

a − µ

σ ≤ Z ≤ b − µ

σ

= Φ

b − µ σ

− Φ

a − µ σ

.

I

Die Funktionswerte von Φ k¨ onnen aus einer Tabelle abgelesen werden oder mit einem Taschenrechner o.¨ a. berechnet werden.

I

Es gilt Φ( − x) = 1 − Φ(x) f¨ ur beliebige reelle Zahlen x .

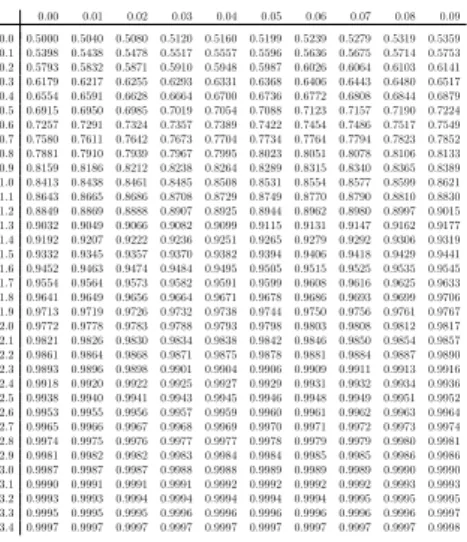
Tabelle zur Verteilungsfunktion der Standardnormalverteilung Die folgende Tabelle enthält Werte der Verteilungsfunktion

Φ(x) = 1

√2π Zx

−∞

e^−z22dz

der Standardnormalverteilung für Argumentex= 0.00,0.01, . . . ,3.49. Werte vonΦfür entsprechende negative Argumente erhält man über die BeziehungΦ(−x) = 1−Φ(x). Zum Beispiel gilt (näherungs- weise)Φ(1.96) = 0.9750und entsprechendΦ(−1.96) = 1−0.9750 = 0.0250.

Zur Bestimmung eines QuantilsΦ⁻¹(p)suche man den gegebenen Wertpder Verteilungsfunktion Φ(bzw. einen möglichst naheliegenden) im Tabellenkörper und bestimme das zugehörige Argumentx.

Zum Beispiel ist das 99%-QuantilΦ⁻¹(0.99)ungefährΦ⁻¹(0.9901) = 2.33.

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981 2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 3.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998

Quelle Formelsammlung

Rechenbeispiel Normalverteilung

I

Geg.: X ∼ N(30, 25) .

I

Ges.: P(28 ≤ X ≤ 35) .

k · σ − Regeln f¨ ur Normalverteilung

I

Frage: Wie groß ist die Wahrscheinlichkeit daf¨ ur, dass der Wert einer Zufallsgr¨ oße X ∼ N(µ, σ

) um mehr als 3 · σ vom Erwartungswert (

” Sollwert“) µ abweicht ?

I

Antwort:

P( | X − µ | > 3σ) = P

| X − µ | σ > 3

= P( | Z | > 3)

= 2 P(Z > 3) = 2 (1 − Φ(3)) = 2 (1 − 0.9987) = 0.0026 .

I

Folglich und analog gilt:

3 σ − Regel: Innerhalb von µ ± 3σ liegen ≈ 99.74% der Messwerte.

2 σ − Regel: Innerhalb von µ ± 2σ liegen ≈ 95.5% der Messwerte.

1 σ − Regel: Innerhalb von µ ± σ liegen ≈ 68.3% der Messwerte.

Umgekehrte Fragestellung

I

Frage In welchem Intervall I = [µ − c ; µ + c ] liegen im Mittel (z.B.) 90% der Messwerte f¨ ur X ∼ N(µ, σ

) ?

I

Ges. c , so dass P( | X − µ | ≤ c ) = 0.9 .

I

Lsg.

0.9 = P( | X − µ | ≤ c ) = P

| X − µ |

σ ≤ c

σ

= P

| Z | ≤ c σ

= P

− c

σ ≤ Z ≤ c

σ

= 2Φ c σ

− 1

⇒ Φ c

σ

= 0.9 + 1

2 = 0.95 c

σ = z

= 1.645 (0.95-Quantil) c = 1.645 · σ .

⇒ Zwischen µ − 1.645σ und µ + 1.645σ liegen im Mittel 90% der

Messwerte.

Quantilezpder StandardnormalverteilungN(0,1)

Hier giltzp=−z1−p, so ist z.B.z0.05=−z0.95=−1.6449.

p zp p zp p zp p zp

0.50 0.0000 0.780 0.7722 0.9760 1.9774 0.9960 2.6521 0.51 0.0251 0.785 0.7892 0.9765 1.9863 0.9961 2.6606 0.52 0.0502 0.790 0.8064 0.9770 1.9954 0.9962 2.6693 0.53 0.0753 0.795 0.8239 0.9775 2.0047 0.9963 2.6783 0.54 0.1004 0.800 0.8416 0.9780 2.0141 0.9964 2.6874 0.55 0.1257 0.805 0.8596 0.9785 2.0237 0.9965 2.6968 0.56 0.1510 0.810 0.8779 0.9790 2.0335 0.9966 2.7065 0.57 0.1764 0.815 0.8965 0.9795 2.0435 0.9967 2.7164 0.58 0.2019 0.820 0.9154 0.9800 2.0537 0.9968 2.7266 0.59 0.2275 0.825 0.9346 0.9805 2.0642 0.9969 2.7370 0.60 0.2533 0.830 0.9542 0.9810 2.0749 0.9970 2.7478 0.61 0.2793 0.835 0.9741 0.9815 2.0858 0.9971 2.7589 0.62 0.3055 0.840 0.9945 0.9820 2.0969 0.9972 2.7703 0.63 0.3319 0.845 1.0152 0.9825 2.1084 0.9973 2.7822 0.64 0.3585 0.850 1.0364 0.9830 2.1201 0.9974 2.7944 0.65 0.3853 0.855 1.0581 0.9835 2.1321 0.9975 2.8070 0.66 0.4125 0.860 1.0803 0.9840 2.1444 0.9976 2.8202 0.67 0.4399 0.865 1.1031 0.9845 2.1571 0.9977 2.8338 0.68 0.4677 0.870 1.1264 0.9850 2.1701 0.9978 2.8480 0.69 0.4959 0.875 1.1503 0.9855 2.1835 0.9979 2.8627 0.70 0.5244 0.880 1.1750 0.9860 2.1973 0.9980 2.8782 0.71 0.5534 0.885 1.2004 0.9865 2.2115 0.9981 2.8943 0.72 0.5828 0.890 1.2265 0.9870 2.2262 0.9982 2.9112 0.73 0.6128 0.895 1.2536 0.9875 2.2414 0.9983 2.9290 0.74 0.6433 0.900 1.2816 0.9880 2.2571 0.9984 2.9478 0.75 0.6745 0.905 1.3106 0.9885 2.2734 0.9985 2.9677 0.76 0.7063 0.910 1.3408 0.9890 2.2904 0.9986 2.9889 0.77 0.7388 0.915 1.3722 0.9895 2.3080 0.9987 3.0115 0.920 1.4051 0.9900 2.3263 0.9988 3.0357 0.925 1.4395 0.9905 2.3455 0.9989 3.0618 0.930 1.4758 0.9910 2.3656 0.9990 3.0902 0.935 1.5141 0.9915 2.3867 0.9991 3.1214 0.940 1.5548 0.9920 2.4089 0.9992 3.1559 0.945 1.5982 0.9925 2.4324 0.9993 3.1947 0.950 1.6449 0.9930 2.4573 0.9994 3.2389 0.955 1.6954 0.9935 2.4838 0.9995 3.2905 0.960 1.7507 0.9940 2.5121 0.9996 3.3528 0.965 1.8119 0.9945 2.5427 0.9997 3.4316 0.970 1.8808 0.9950 2.5758 0.9998 3.5401 0.975 1.9600 0.9955 2.6121 0.9999 3.7190

Quelle: Formelsammlung

Unabh¨ angigkeit von Zufallsgr¨ oßen

I

Die Zufallsgr¨ oßen X

, . . . , X

heißen (stochastisch) unabh¨ angig, wenn f¨ ur beliebige reelle Zahlen a

< b

, . . . , a

< b

gilt

P(a

≤ X

< b

, . . . , a

≤ X

< b

)

= P(a

≤ X

< b

) · . . . · P(a

≤ X

< b

) .

I

Zufallsgr¨ oßen, die z.B. zu unterschiedlichen, sich nicht

beeinflussenden Teilversuchen geh¨ oren, k¨ onnen als unabh¨ angig angesehen werden. Oft wird die Unabh¨ angigkeit von Zufallsgr¨ oßen aber auch angenommen, um ¨ uberhaupt etwas berechnen zu k¨ onnen.

I

Sind zwei Zufallsgr¨ oßen X und Y mit endlichen Erwartungswerten stochastisch unabh¨ angig, dann gilt immer E(X · Y ) = EX · EY .

I

Satz Sind zwei Zufallsgr¨ oßen X und Y mit endlichen Varianzen unabh¨ angig, dann gilt f¨ ur deren Summe

Var(X + Y ) = VarX + VarY .

I

Letztere Eigenschaft gilt aber im Allgemeinen nicht f¨ ur abh¨ angige

Zufallsgr¨ oßen!

Summen von unabh¨ angigen normalverteilten Zufallsgr¨ oßen

I

Eigenschaft

X

∼ N(µ

, σ

) , X

∼ N(µ

, σ

) , unabh¨ angig, a

, a

∈ R ⇒ a

X

+ a

X

∼ N(a

µ

+ a

µ

, a

σ

+ a

σ

) (Additionssatz).

I

Die Summe S

= P

X

von n unabh¨ angigen N(µ, σ

)-verteilten Zufallsgr¨ oßen X

, . . . , X

ist normalverteilt mit Erwartungswert nµ und Varianz nσ

.

I

N¨ aherungsweise gilt eine ¨ ahnliche Aussage auch f¨ ur Zufallsgr¨ oßen

mit anderen Verteilungen.

Zentraler Grenzwertsatz

I

H¨ aufig ergeben sich Zufallsgr¨ oßen (z.B. Messfehler) durch (additive) Uberlagerung vieler kleiner stochastischer Einfl¨ ¨ usse. Der zentrale Grenzwertsatz zeigt dann, dass man diese Gr¨ oßen (n¨ aherungsweise) als normalverteilt ansehen kann.

I

Satz

F¨ ur unabh¨ angige, identisch verteilte Zufallsgr¨ oßen X

, X

, . . . mit EX

= µ , VarX

= σ

> 0 konvergiert die Verteilung der

standardisierten Summe gegen die Standardnormalverteilung, d.h. es gilt f¨ ur beliebige z ∈ R

P

S

− ES

√ VarS

< z

= P

S

− nµ

√ nσ

< z

−−−→

→∞

Φ(z) ; bzw. f¨ ur große n gilt: P (S

< x) ≈ Φ

x − nµ

√ nσ

.

Spezialfall: Satz von Moivre-Laplace

Satz von Moivre-Laplace

Sind die unabh¨ angigen Zufallsgr¨ oßen X

, ... , X

identisch

Bernoulli-verteilt, d.h. X

∼ Bin(1, p) = B(p ) , so gilt f¨ ur die Summe S

∼ Bin(n, p) und nach dem zentralen Grenzwertsatz gilt f¨ ur z ∈ R :

P S

− np p np(1 − p) < z

!

−−−→

→∞

Φ(z) , bzw. f¨ ur große n

n >

gilt

P (S

< x) ≈ Φ x − np p np(1 − p)

!

.

Beispiel Zentraler Grenzwertsatz

I

Eine Weinkellerei l¨ adt 200 Kunden zur Weinverkostung ein. Es kaufen erfahrungsgem¨ aß 60% der Kunden. Wie groß sind die Wahrscheinlichkeiten, dass genau 130 bzw. mehr als 130 Kunden einen Kaufvertrag abschliessen ?

I

Zufallsgr¨ oße X . . . Anzahl der Abschl¨ usse ∼ Bin(200, 0.6) , E(X ) = 120 , Var(X ) = 48 .

I

P(X = 130) =

· 0.6

· 0.4

= 0.0205 , P(X > 130) = 0.0639 .

I

Approximation mittels Normalverteilung P(X = 130) = P(129.5 < X < 130.5)

≈ Φ

130.5 − 120

√ 48

− Φ

129.5 − 120

√ 48

≈ 0.0204 P(X > 130) = 1 − P(X < 130.5) ≈ 1 − Φ

130.5 − 120

√ 48

≈ 0.0649 .

3.4.3 Stetige Gleichverteilung

I

Parameter: Intervall [a, b] ⊂ R .

I

Zufallsgr¨ oße X mit Dichtefunktion f

bzw. Verteilungsfunktion F

f

(x) = (

b−a

, a ≤ x ≤ b ;

0 , sonst , F

(x) =

 



0 , x < a ;

x−a

b−a

, a ≤ x ≤ b ; 1 , x > b .

I

Beispiel: a = 0 , b = 1 .

Charakteristiken der stetigen Gleichverteilung

I

Kenngr¨ oßen:

EX = a + b

2 = x

und VarX = (b − a)

12 .

I

Bezeichnung: X ∼ U[a, b] .

I

F¨ ur Teilintervalle [c , d ] ⊆ [a, b] gilt P(c ≤ X ≤ d ) = d − c

b − a = L¨ ange von [c , d ] L¨ ange von [a, b]

(wird genutzt bei der geometrischen Wahrscheinlichkeitsdefinition).

I

Diese Verteilung ist eine stetige Verteilung ¨ uber dem Intervall

[a, b] , wobei kein Teilintervall einer bestimmten L¨ ange vor anderen

Teilintervallen derselben L¨ ange bevorzugt wird.

Pseudozufallszahlen

I

Um zuf¨ allige Modelle am Computer zu realisieren, erzeugen Rechnerprogramme Pseudozufallszahlen (auch kurz Zufallszahlen genannt), die sich wie Realisierungen von unabh¨ angigen, auf dem Intervall [0, 1] gleichverteilten Zufallsgr¨ oßen verhalten, diese werden bei Monte-Carlo-Simulationen verwendet.

I

Daraus lassen sich mit Hilfe der folgenden Eigenschaft

Realisierungen von Zufallsgr¨ oßen mit anderen Verteilungen erzeugen.

Satz: Sind u

, u

, . . . gleichverteilte Zufallszahlen auf [0, 1] und ist F

die Verteilungsfunktion einer reellen Zufallsgr¨ oße X mit der Umkehrfunktion F

, dann sind x

= F

(u

) , i = 1, 2, . . . nach F

verteilte Zufallszahlen (Inversionsmethode).

I

Es existieren noch weitere Transformationsmethoden, um f¨ ur h¨ aufig gebrauchte Verteilungen, wie z.B. die Normalverteilung,

entsprechende Zufallszahlen zu generieren.

3.4.4 Gammaverteilung

I

Parameter: λ > 0 (Skalenparameter), p > 0 (Formparameter).

I

Dichtefunktion: f

(x) =

( 0 , x < 0 ;

λ^p

Γ(p)

x

e

, x ≥ 0 .

I

Gammafunktion:

Γ(1) = 1 , Γ(p) = (p − 1)Γ(p − 1) ⇒ Γ(n) = (n − 1)! f¨ ur n ∈ N . Allgemeine Definition: Γ(p) =

Z

0

e

t

dt (p > 0).

I

Kenngr¨ oßen: EX = p

λ und VarX = p

λ

.

I

Bezeichnug: X ∼ Gam(p, λ) .

I

Anwendung: Lebensdauerverteilung, flexibler als Exponentialvert.

(die Exponentialverteilung ergibt sich als Spezialfall f¨ ur p = 1) .

Spezielle Gammaverteilungen

I

Beispiel: links p = 2 , λ = 1 (rot), λ = 0.5 (blau), λ = 5 (gr¨ un);

rechts λ = 1 , p = 2 (rot), p = 0.9 (blau), p = 5 (gr¨ un).

I

X

∼ Gam(p

, λ) , i = 1, 2 , unabh. ⇒ X

+ X

∼ Gam(p

+ p

, λ) .

I

X

∼ Exp(λ), i = 1, ..., n, unabh¨ angig ⇒ P

i=1

X

∼ Gam(n, λ).

I

Spezialfall p = n ∈ N ⇒ Erlangverteilung

Die Wartezeit bis zum Eintreten des n − ten Poissonereignisses kann

z.B. durch eine erlangverteilte Zufallsgr¨ oße beschrieben werden

(Parameter: n , λ).

3.4.5 Weibullverteilung

I

Parameter: β > 0 (Skalenparam.), m > 0 (Formparam.), α ∈ R .

I

Dichtefunktion: f

(x) =

 



0 , x ≤ α ;

m β

e

x−α β

m

, x > α .

I

Verteilungsfunktion: F

(x) =

( 0 , x < α ;

1 − e

x−α β

m

, x ≥ α .

I

Erwartungswert: EX = α + β · Γ

1 + 1 m

.

I

Varianz: VarX = β

Γ

1 + 2 m

− Γ

1 + 1 m

.

I

Median: x

= α + β (ln 2)

.

I

Spezialf¨ alle:

α = 0 sogenannte zweiparametrische Weibullverteilung

α = 0 , m = 1 , β =

Exponentialverteilung Exp(λ) .

Weibullverteilungen

I

Beispiele: α = 0,

links: m = 1.5, β = 1 (rot), β = 0.5 (blau), β = 5 (gr¨ un);

rechts: β = 1, m = 1 (rot), m = 0.9 (blau), m = 5 (gr¨ un).

I

Die Weibullverteilung ist durch die 3 Parameter anpassungsf¨ ahig.

I

Eine Weibullverteilung kann als Grenzverteilung f¨ ur das Minimum einer großen Zahl von unabh¨ angigen Zufallsgr¨ oßen auftreten (Verteilung des schw¨ achsten Kettengliedes), deshalb sind

Lebensdauern von Systemen oft weibullverteilt. F¨ ur m < 1 bzw.

m > 1 werden Fr¨ uh- bzw. Verschleißausf¨ alle besonders gewichtet.

Historische Bemerkung

I

In der mechanischen Verfahrenstechnik findet die Weibullverteilung Anwendung als eine spezielle Partikelgr¨ oßenverteilung. Hier wird sie RRSB-Verteilung (nach Rosin, Rammler, Sperling und Bennet) bezeichnet.

I

Siehe dazu z.B.:

Paul Otto Rosin-Gedenkschrift anl¨ asslich des Jubil¨ aums 80 Jahre

RRSB-Verteilung 2013, Schriften des IEC, Heft 6, September 2015,

TU Bergakademie Freiberg, Insitut f¨ ur Energieverfahrenstechnik und

Chemieingenieurwesen.

3.4.6 Logarithmische Normalverteilung

I

Die Zufallsgr¨ oße X mit positiven Werten unterliegt einer logarithmischen Normalverteilung (ist lognormal-verteilt) falls ln X ∼ N(µ, σ

) gilt.

I

Dichtefunktion: f

(x) =

( 0 , x ≤ 0 ;

√1

2πσx

e

, x > 0 .

I

Erwartungswert: EX = e

2 2

.

I

Varianz: VarX = e

e

− 1 .

I

Median: x

= e

.

I

Bezeichnung: X ∼ LogN(µ, σ

) .

Logarithmische Normalverteilungen

I

Beispiele: µ = 0, σ = 1 (rot), µ = − 2, σ = 0.5 (blau), µ = 1, σ = 2 (gr¨ un).

I

Typische Anwendungen:

I

bei Zeitstudien und Lebensdaueranalysen in ¨ okonomischen, technischen und biologischen Vorg¨ angen;

I

bei Untersuchungen in der analytischen Chemie, wie Konzentrations- und Reinheitspr¨ ufungen;

I

f¨ ur zuf¨ allige nichtnegative Materialparameter, z.B. Permeabilit¨ aten;

I

als Grenzverteilung f¨ ur Produkte unabh¨ angiger positiver Zufallsgr¨ oßen

(unter bestimmten Bedingungen).

3.4.7 Weitere stetige Verteilungen

I

Statistische Pr¨ ufverteilungen, u.a.

I

χ

-Verteilung (Chi-Quadrat-Verteilung);

I

t-Verteilung (Student-Verteilung);

I

F-Verteilung (Fisher-Verteilung).

I

Logistische Verteilung (dient u.a. zur Beschreibung von Wachstumsprozessen mit einer S¨ attigungstendenz).

I

Betaverteilungen 1. und 2. Art.

I

Extremwertverteilungen.

I

. . .

3.5 Transformation von Zufallsgr¨ oßen

I

H¨ aufig m¨ ussen bei der Untersuchung stochastischer Modelle Zufallsgr¨ oßen transformiert werden.

I

Wichtige Transformationen sind die Bildung von Summe, Minimum oder Maximum von mehreren Zufallsgr¨ oßen.

I

Ist X eine Zufallsgr¨ oße mit Verteilungsfunktion F

und g : R → R eine stetige, streng monoton wachsende Funktion (z.B. g (x ) = e

), dann ist Y := g (X ) eine Zufallsgr¨ oße mit Verteilungsfunktion

F

(y ) = P(Y < y) = P(g(X ) < y) = P(X < g

(y))

= F

(g

(y))

(g

ist die Umkehrfunktion (inverse Funktion) von g ).

I

Die Dichtefunktion (falls sie existiert) kann z.B. durch

Differentiation bestimmt werden.

Summe unabh¨ angiger Zufallsgr¨ oßen, Faltung

I

Oft m¨ ussen unabh¨ angige Zufallsgr¨ oßen addiert werden und folglich muss die Verteilung einer Summe von unabh¨ angigen Zufallsgr¨ oßen bestimmt werden.

I

Die zugeh¨ orige Operation f¨ ur die Verteilungen (Verteilungsdichten, Verteilungsfunktionen) nennt man Faltung.

I

Sind X und Y unabh¨ angige stetige Zufallsgr¨ oßen mit

Verteilungsdichten f

bzw. f

, dann gilt f¨ ur die Verteilungsdichte f

der Summe S = X + Y :

f

(z ) = Z

−∞

f

(z − y)f

(y) dy = Z

−∞

f

(z − x)f

(x) dx .

I

In wichtigen F¨ allen ergeben sich wieder spezielle Verteilungen.

Maximum unabh¨ angiger Zufallsgr¨ oßen

I

Auch bei der Bildung des Minimums oder Maximums von Zufallsgr¨ oßen kann f¨ ur die Berechnung der entsprechenden Verteilungsfunktion die Unabh¨ angigkeit ausgenutzt werden.

I

Sind X

unabh¨ angige Zufallsgr¨ oßen mit Verteilungsfunktionen F

, i = 1, . . . n , dann gilt f¨ ur das Maximum X

F

(x) = P(X

< x) = P

\

i=1

{ X

< x }

!

= Y

i=1

P(X

< x) = Y

i=1

F

(x) , x ∈ R .

I

Sind die Zufallsgr¨ oßen X

, i = 1, . . . , n , unabh¨ angig und identisch verteilt (i.i.d.) mit Verteilungsfunktion F

, dann gilt

F

(x) = F

(x) , x ∈ R .

Minimum unabh¨ angiger Zufallsgr¨ oßen

I

Analog gilt f¨ ur das Minimum X

unter obigen Bedingungen 1 − F

(x) = P(X

≥ x) = P

\

i=1

{ X

≥ x }

!

= Y

i=1

P(X

≥ x) = Y

i=1

(1 − F

(x)) , x ∈ R .

I

Sind die Zufallsgr¨ oßen X

, i = 1, . . . , n , unabh¨ angig und identisch verteilt (i.i.d.) mit Verteilungsfunktion F

, dann gilt

F

(x) = 1 − (1 − F

(x))

, x ∈ R .

I

Beispiele f¨ ur solche zuf¨ alligen Extremwerte sind

I

H¨ ochstwasserst¨ ande (wichtig f¨ ur D¨ amme);

I

minimale Festigkeiten (der einzelnen Kettenglieder einer Kette).