10 Das Riemannsche Integral

10 Das Riemannsche Integral 50

10 Das Riemannsche Integral

Ziel dieses Paragraphen ist es, den Inhalt einer Fl¨ache, die vom Graphen einer Funktion berandet wird, exakt zu definieren.

a = t₀ t₁ t₂ t₃ t₄ t₅ t = b₆

f(a) f(b)

Abbildung 11: Graph einer Funktion mit Untersumme

Wir approximieren diesen Fl¨acheninhalt, indem wir zun¨achst das Intervall [a, b] unterteilen:

a=t0< t1<· · ·< tn−1< tn =b.

In diesem Fall spricht man von einerZerlegung derL¨angenin dieTeilintervalle Ii= [ti−1, ti] ; i= 1, . . . , n.

F¨ur jedes dieser Teilintervalle definieren wir

mⁱ:= inf{f(x)|tⁱ₋1≤x≤tⁱ}, Mⁱ:= sup{f(x)|tⁱ₋1≤x≤tⁱ}.

Falls die Funktion f beschr¨ankt ist, dann existieren diese Zahlen f¨ur jede Un- terteilung des IntervallsI = [a, b].

Definition Es sei f : I = [a, b] → R eine beschr¨ankte Funktion und P = {t0, t1, . . . , tn}eine Zerlegung vonI, d.h. t0=a < t1< ... < tn =b. Die Zahlen mi, Mi;i= 1, . . . , nseien wie oben definiert.

(i) DieUntersumme vonf bez¨uglich der ZerlegungP ist definiert durch U(f, P) :=

n

X

i=1

mi(tⁱ−ti−1).

(ii) DieObersumme von f bez¨uglich der ZerlegungP ist definiert durch O(f, P) :=

n

X

i=1

Mi(tⁱ−ti−1).

Unmittelbar aus der Definition folgt, dass stets gilt U(f, P)≤O(f, P).

Wir vergleichen nun, was passiert, wenn wir verschiedene Zerlegungen be- trachten.

Definition Wir sagen, dass eine ZerlegungQ={t⁰0, . . . , t⁰m}eineVerfeinerung der ZerlegungP ={t0, . . . , tn}ist, falls P⊂Qgilt.

Satz 10.1 Es sei Qeine Verfeinerung vonP. Dann gilt U(f, P)≤U(f, Q)≤O(f, Q)≤O(f, P).

Beweis. Wir haben bereits bewiesen, dass die zweite Ungleichung gilt. Wir werden hier die erste Ungleichung zeigen, die dritte geht analog. Ferner gen¨ugt es, die Situation zu betrachten, wo

P ={t0, . . . , tⁿ}, Q={t0, . . . , t^k₋1, u, t^k, . . . , tⁿ} mit

a=t0< t1<· · ·< t^k₋1< u < t^k <· · ·< tⁿ =b.

Es sei

m⁰ := inf{f(x)|t^k₋1≤x≤u}

m⁰⁰:= inf{f(x)|u≤x≤t^k}. Es gilt dann

U(f, P) =

n

X

i=1

mⁱ(tⁱ−tⁱ₋1).

U(f, Q) =

k−1

X

i=1

mi(tⁱ−ti−1) +m⁰(u−tk−1) +m⁰⁰(t^k−u) +

n

X

i=k+1

mi(tⁱ−ti−1).

Vergleichen wir die beiden Summen, so sehen wir, dass wir die folgende Un- gleichung beweisen m¨ussen:

m^k(t^k−t^k₋1)≤m⁰(u−t^k₋1) +m⁰⁰(t^k−u).

Nun gilt nach Definition der Gr¨oßenm^k, m⁰ undm⁰⁰: mk ≤m⁰, mk≤m⁰⁰. Damit gilt

m^k(t^k−t^k₋1) =m^k(u−t^k₋1) +m^k(t^k−u)≤m⁰(u−t^k₋1) +m⁰⁰(t^k−u).

2

10 Das Riemannsche Integral 52

Satz 10.2 Es sei f :I = [a, b] →Reine beschr¨ankte Funktion. Dann gilt f¨ur zwei beliebige Zerlegungen P1 undP2 vonI, dass

U(f, P1)≤O(f, P2).

Beweis. Es seiP =P1∪P2diegemeinsame Verfeinerung vonP1undP2. Dann gilt nach Satz 10.1

U(f, P1)≤U(f, P)≤O(f, P)≤O(f, P2).

2 Wir betrachten nun die Mengen

U :={U(f, P)|P ist Zerlegung von [a, b]}, O:={O(f, P)|P ist Zerlegung von [a, b]}.

Nach Satz 10.2 ist die Menge U nach oben und die Menge O nach unten beschr¨ankt. Daher besitztU ein Supremum undO ein Infimum.

Definition Es seif :I = [a, b]→Reine beschr¨ankte Funktion.

(i) DasUnterintegral vonf auf dem IntervallI ist definiert durch

U

b

Z

a

f(x)dx= sup{U(f, P)|P ist Zerlegung vonf}.

(ii) DasOberintegral vonf auf dem IntervallI ist definiert durch

O

b

Z

a

f(x)dx= inf{O(f, P)|P ist Zerlegung vonf}.

Aus Satz 10.2 folgt sofort, dass U

Z ^b

a

f(x)dx≤O Z ^b

a

f(x)dx.

Definition Eine beschr¨ankte Funktion f : I = [a, b] → R heißt auf dem Intervall I (Riemann) integrierbar, falls gilt:

U Z ^b

a

f(x)dx=O Z ^b

a

f(x)dx.

Schreibweise: Man schreibt:

Z ^b

a

f(x)dx:=

Z

I

f(x)dx:=U Z ^b

a

f(x)dx=O Z ^b

a

f(x)dx.

1 2

1 2

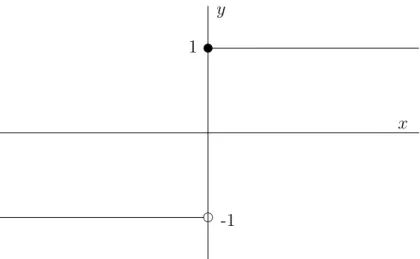
Abbildung 12: Die Funktionf aus Beispiel 10.1 Beispiel 10.1 Es seiI = [0,2] und

f(x) :=

1 f¨ur 0≤x <1 2 f¨ur 1≤x≤2.

F¨ur jede ZerlegungP, die den Punkt 1 enth¨alt, gilt U(f, P) = 1 + 2 = 3 =O(f, P).

Also ist f integrierbar und es gilt Z ²

0

f(x)dx= 3.

Beispiel 10.2 Es seiI = [0,1] und f(x) =

0 f¨ur x∈Q 1 f¨ur x∈R\Q.

Dann gilt f¨ur jede ZerlegungP von [0,1]:

U(f, P) =

n

X

i=0

0·(tⁱ−ti−1) = 0,

O(f, P) =

n

X

i=0

1·(tⁱ−tⁱ₋1) = 1.

Also gilt

0 =U

1

Z

0

f(x)dx < O Z ¹

0

f(x)dx= 1 und die Funktionf ist nicht integrierbar.

Satz 10.3 Es seia < c < b. Dann ist eine beschr¨ankte Funktion f genau dann auf dem Intervall[a, b]integrierbar, wenn sie auf[a, c]und[c, b]integrierbar ist.

In diesem Fall gilt

b

Z

a

f(x)dx=

c

Z

a

f(x)dx+

b

Z

c

f(x)dx.

10 Das Riemannsche Integral 54

Beweis. Man betrachte die Partitionen von [a, b], die den Punktc enthalten. 2 Satz 10.4 Falls f und g auf I = [a, b] integrierbar sind, dann ist auch f +g auf I = [a, b]integrierbar, und es gilt

b

Z

a

(f +g)(x)dx=

b

Z

a

f(x)dx+

b

Z

a

g(x).

Beweis. Es seiP ={t0, . . . , tⁿ}eine Zerlegung von [a, b]. Wir definieren m⁰i:= inf{f(x)|tⁱ₋1≤x≤tⁱ},

m⁰⁰i := inf{g(x)|ti−1≤x≤ti}, mⁱ:= inf{f(x) +g(x)|tⁱ₋1≤x≤tⁱ} und analogMi⁰, Mi⁰⁰undMⁱ. Dann gilt

mⁱ≥m⁰i+m⁰⁰i, Mⁱ≤Mi⁰+Mi⁰⁰. Damit gilt f¨ur jede ZerlegungP:

U(f, P) +U(g, P)≤U(f+g, P)≤O(f +g, P)≤O(f, P) +O(g, P).

Hieraus folgt die Behauptung sofort. 2

Satz 10.5 Die Funktionf sei aufI = [a, b] integrierbar,c∈R. Dann ist auch die Funktioncf auf I = [a, b]integrierbar, und es gilt

Z ^b

a

(cf)(x)dx=c Z ^b

a

f(x)dx.

Beweis. Klar. 2

Satz 10.6 Die Funktionf sei auf I = [a, b]integrierbar. Es gelte m≤f(x)≤M, x∈[a, b].

Dann gilt

m(b−a)≤ Z ^b

a

f(x)dx≤M(b−a).

Beweis. F¨ur jede ZerlegungP des IntervallsI = [a, b] gilt m(b−a)≤U(f, P)≤O(f, P)≤M(b−a).

2 Bemerkung 10.1 (1) Ista > b, so definiert man

Z ^b

a

f(x)dx:=− Z ^a

b

f(x)dx.

(2) Istf ≥0, so versteht man das IntegralR^b

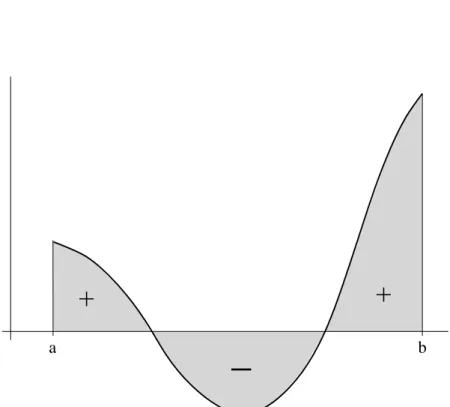
af(x)dxals denFl¨acheninhalt, der vom Graphen der Funktion und derx-Achse eingeschlossen wird. Istf ≤0, so wird dieser Fl¨acheninhalt negativ gez¨ahlt.

b a

+ +

_

Abbildung 13: Das Integral als Fl¨acheninhalt

11 Der Hauptsatz der Differential- und Integralrechnung 56

11 Der Hauptsatz der Differential- und Integral- rechnung

In diesem Kapitel wird der Zusammenhang zwischen Differentiation und Inte- gration hergestellt.

Theorem 11.1 (1. Hauptsatz) : Es sei f auf I = [a, b] integrierbar und im Punkt c∈(a, b) stetig. Dann ist die Funktion

F(x) :=

Z x

a

f(t)dt im Punktc differenzierbar, und es gilt

F⁰(c) =f(c).

Beweis. Wir m¨ussen den Grenzwert

h→0lim

F(c+h)−F(c) h untersuchen. Es sei zun¨achsth >0. Dann gilt

F(c+h)−F(c) = Z c+h

c

f(t)dt.

Wir definieren

mh:= inf{f(t)|c≤t≤c+h}, Mh:= sup{f(t)|c≤t≤c+h}. Dann gilt nach Satz 10.5:

mh·h≤ Z c+h

c

f(t)dt≤Mh·h,

und damit

mh≤ F(c+h)−F(c)

h ≤Mh.

Diese Beziehung gilt auch f¨urh <0 mit

mh:= inf{f(t)|c+h≤t≤c}, Mh:= sup{f(t)|c+h≤t≤c}. Es gilt dann n¨amlich

m_h·(−h)≤ Z c

c+h

f(t)dt≤M_h·(−h).

Wegen

F(c+h)−F(c) = Z c+h

c

f(t)dt=− Z c

c+h

f(t)dt

folgt

mh·(−h)≤F(c)−F(c+h)≤Mh·(−h).

Division durch −h >0 zeigt dann, dass (1) auch in diesem Fall gilt.

Jetzt ben¨utzen wir, dassf im Punktcstetig ist. Daraus folgt dann n¨amlich, dass

lim

h→0m_h=f(c) = lim

h→0M_h. Damit gilt

lim

h→0

F(c+h)−F(c)

h =f(c).

2 Korollar 11.1 Die Funktionf sei stetig und integrierbar auf I= [a, b]und es gelte f =g⁰ f¨ur eine Funktiong. Dann gilt

Z b

a

f(x)dx=g(b)−g(a).

Beweis. Nach Theorem 11.1 ist die Funktion F(x) =

Z x

a

f(t)dt differenzierbar, und es gilt

F⁰(x) =f(x) =g⁰(x).

Also gibt es eine reelle Zahlcmit

F =g+c.

Man kann die Konstantecwie folgt bestimmen:

c=F(a)−g(a) =−g(a).

Damit gilt

Z b

a

f(x)dx=F(b) =g(b) +c=g(b)−g(a).

2 Dieses Korollar ist die Grundlage f¨ur viele Integralberechnungen in der Praxis.

Bemerkung 11.1 Wir werden sp¨ater sehen, dass die Voraussetzung, dass f integrierbar ist, bereits aus der Voraussetzung, dassf stetig ist, folgt.

Beispiel 11.1 Wir berechnenRb

a x²dx. In diesem Fall ist also f(x) = x² und f¨ur g(x) k¨onnen wir g(x) = x³/3 w¨ahlen (oder auch g(x) = x³/3 +c f¨ur ein beliebigesc). Dann gilt

Z b

a

x²dx=g(b)−g(a) =1

3(b³−a³).

11 Der Hauptsatz der Differential- und Integralrechnung 58

Definition Eine Funktiong mitg⁰=f heißt eineStammfunktion vonf. Wir versch¨arfen jetzt Korollar 11.1 indem wir zeigen, dass die Voraussetzung, dassf stetig ist, unn¨otig ist.

Theorem 11.2 (2. Hauptsatz:) Die Funktion f sei integrierbar auf dem In- tervall I= [a, b] und es geltef =g⁰. Dann gilt

Z b

a

f(x)dx=g(b)−g(a).

Beweis. Es sei P = {t0, . . . , t_n} eine Zerlegung von I = [a, b]. Nach dem Zwischenwertsatz der Differentialrechnung gibt es dann Punkte x_i ∈ [t_i−1, t_i], f¨ur die gilt

g(t_i)−g(t_i−1) =g⁰(x_i)(t_i−t_i−1) =f(x_i)(t_i−t_i−1).

Es sei

m_i:= inf{f(x)|t_i−1≤x≤t_i}, M_i:= sup{f(x)|t_i−1≤x≤t_i}. Dann gilt offensichtlich

mi(ti−t_i−1)≤f(xi)(ti−t_i−1)≤Mi(ti−t_i−1), bzw.

mi(ti−ti−1)≤g(ti)−g(ti−1)≤Mi(ti−ti−1).

Summation ¨uberi= 1, . . . , nergibt

n

X

i=1

mi(ti−t_i−1)≤g(b)−g(a)≤

n

X

i=1

Mi(ti−t_i−1).

Damit gilt f¨ur jede ZerlegungP, dass

U(f, P)≤g(b)−g(a)≤O(f, P) und daraus folgt sofort, dass

Z b

a

f(x)dx=g(b)−g(a).

2 Schließlich zeigen wir noch, dass jede stetige Funktion integrierbar ist.

Theorem 11.3 Falls f auf dem Intervall I= [a, b] stetig ist, dann istf auch integrierbar.

Beweis. Wir definieren FunktionU =U(x) undO=O(x) aufI durch

U(x) =U

x

Z

a

f(t)dt, O(x) =O Z x

a

f(t)dt.

Es seix∈(a, b) undh >0. Wir definieren f¨urh >0 mh:= inf{f(t)|x≤t≤x+h}, Mh:= sup{f(t)|x≤t≤x+h}. Dann gilt

mh·h≤U Z x+h

x

f(t)dt≤O Z x+h

x

f(t)dt≤Mh·h.

Hieraus folgt

mh·h≤U(x+h)−U(x)≤O(x+h)−O(h)≤Mh·h, bzw.

mh≤U(x+h)−U(x)

h ≤ O(x+h)−O(x)

h ≤Mh.

Wie im Beweis von Theorem 11.1 zeigt man, dass diese Ungleichung auch f¨ur h <0 gilt, wenn man setzt

mh:= inf{f(t)|x+h≤t≤x}, Mh:= sup{f(t)|x+h≤t≤x}. Daf stetig ist, gilt

lim

h→0m_h= lim

h→0M_h=f(x).

Dies zeigt, dass

U⁰(x) =O⁰(x) =f(x).

Also gibt es einc∈Rmit

U(x) =O(x) +c, x∈I.

DaU(a) = 0 =O(a) mussc= 0 sein. D.h.

U(x) =O(x), x∈[a, b]

und damit gilt U

Z b

a

f(x)dx=U(b) =O(b) =O Z b

a

f(x)dx

und daher istf integrierbar. 2

Bemerkung 11.2 Es gibt viele integrierbare Funktionen, die nicht stetig sind, wie das Beispiel derTreppenfunktion zeigt.

12 Raumkurven 60

12 Raumkurven

Wir beginnen in diesem Kapitel mit den Anf¨angen dermehr-dimensionalen Ana- lysis. Dern-dimensionale reelle Raum ist das kartesische Produkt

Rⁿ=R× · · · ×R (n Kopien).

D.h. die Elemente desRⁿ sindn-Tupel

Rⁿ3x= (x¹, . . . , xⁿ); xⁱ∈R.

Wir f¨uhren aufRⁿ eineMetrik ein, indem wir den L¨angenbegriff der EbeneR², bzw. des RaumsR³verallgemeinern:

||x||:=

q

x²1+· · ·+x²n. Diese L¨angenfunktion hat die folgenden Eigenschaften:

(L1) ||x|| ≥0 und||x||= 0 genau dann, wennx= 0 (L2) ||λx||=|λ|||x||, λ∈R

(L3) ||x+y|| ≤ ||x||+||y||(Dreiecksungleichung).

DerAbstand zwischen zwei Punktenx, y∈Rⁿ wird dann durch d(x, y) :=||x−y||

definiert.

Definition Es seiI⊂Rein Intervall. EineKurve imRⁿ ist eine Abbildung f = (f1, . . . , fⁿ) : I→Rⁿ

t7→(f1(t), . . . , fⁿ(t)).

Das Bildf(I) heißt dieSpur der Kurvef.

Man beachte, dass verschiedene Kurven dieselbe Spur haben k¨onnen, die Kurven unterscheiden sich dann durch ihre Parametrisierung.

Definition Wir nennen f stetig (differenzierbar, stetig differenzierbar), falls die Funktionenfⁱ;i= 1, . . . , nstetig (differenzierbar, stetig differenzierbar) sind.

Beispiel 12.1 (a) Es seiυ∈Rⁿ, 06=w∈Rⁿ. Die Kurve f :R−→Rⁿ

f(t) =υ+tw

parametisiert eineGerade durch den Punktυ mit Richtungsvektorw. Istυ = (υ1, . . . , υⁿ) undw= (w1, . . . , wⁿ), dann ist

fⁱ(t) =υⁱ+twⁱ.

(b) Die Kurve

f : [0,2π]→R²

f(t) = (rcost, rsint), r >0 parametisiert einen Kreismit Radius r.

(c) Es seienr, c >0. Dann stellt die Kurve f :R→R³ f(t) = (rcost, rsint, ct) eineSchraubenlinie dar.

Definition Es seif :I →Rⁿ eine differenzierbare Kurve,t∈I. Der Vektor f⁰(t) := (f1⁰(t), . . . , fn⁰(t))

heißt derTangentenvektor der Kurvef im Punktt.

Bemerkung 12.1 Man kann den Tangentenvektor als den Limes

f⁰(t) = lim

h→0

f(t+h)−f(t) h

verstehen, wobei dieser Limes komponentenweise zu interpretieren ist.

Man verbindet hiermit oft die Vorstellung, dassf(t) die Kurvef in Abh¨angigkeit der Zeit t durchl¨auft. Dann kann man f⁰(t) als den Geschwindigkeitsvektor interpretieren. Die L¨ange des Vektors f⁰(t), d.h.

||f⁰(t)||=q

(f1⁰(t))²+· · ·+ (fn⁰(t))² ist dann der Betrag der Geschwindigkeit.

Definition Es sei f : I → Rⁿ eine differenzierbare Kurve. Ein Punkt t ∈ I mit f⁰(t)6= 0 heißt ein regul¨arer Punkt der Kurvef. Gilt f⁰(t) = 0, so nennt mant einensingul¨aren (oderstation¨aren) Punkt der Kurve.

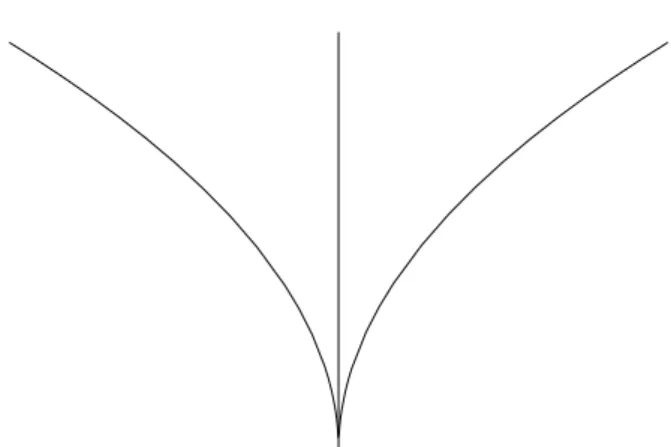
Beispiel 12.2 Die Kurve

f :R→R² f(t) = (t², t³) heißt Neilsche Parabel. Wegen

f⁰(t) = (2t,3t²)

besitztf genau einen singul¨aren Punkt, n¨amlich den Nullpunktt= 0.

Definition Es seif : [a, b]→Rⁿ eine stetig differenzierbare Kurve. DieL¨ange dieser Kurve ist dann definiert durch

L:=

Z ^b

a

||f⁰(t)||dt.

Man beachte, dass es sich hier um ein gew¨ohnliches Integral ¨uber eine stetige Funktion in einer Variablen handelt.

12 Raumkurven 62

–0.4 –0.2 0 0.2 0.4

0.2 0.4

Abbildung 14: Neilsche Parabel

Beispiel 12.3 (a) Wir betrachten wieder den Kreis f(t) = (rcost, rsint), t∈[0,2π]. Dann gilt

f⁰(t) = (−rsint, rcost) und damit

||f⁰(t)||=p

r²sin²t+r²cos²t=r.

D.h.

L= Z ^2π

0

rdt= 2πr.

Dies ist die bekannte Formel f¨ur den Kreisumfang.

(b) Wir betrachten die L¨ange derZykloide f :R→R² f(t) = (t−sint,1−cost).

Dies ist die Bahn eines Punktes auf dem Umfang eines Kreises vom Radius 1, der in der (x, y)- Ebene auf derx-Achse abgewickelt wird.

Wir wollen nun die Bogenl¨ange der Zykloide berechnen. Es gilt f⁰(t) = (1−cost,sint).

Man beachte, dass die Punktexⁿ= 2πn, n∈Zstation¨are Punkte der Kurvef sind. Es gilt

||f⁰(t)||² = (1−cost)²+ sin²t

= 1−2 cost+ cos²t+ sin²t

= 2−2 cost

= 2−2(cos²2^t −sin^2t2)

= 2−2(1−2 sin²₂^t)

= 4 sin^{2 t}2.

t =

t = 0 t =2π

π

1 2

1 2 3 4 5 6

Abbildung 15: Zykloide

Also gilt

L= Z ^2π

0

||f⁰(t)||dt= Z ^2π

0

2|sint 2|dt.

Durch die Substitution u=t/2 ergibt sich hieraus

L= 4 Z ^π

0

sinu= 4 [−cosu]^π0 = 8.

Definition Man sagt, dass eine Kurvef :I →Rⁿ nach der Bogenl¨ange para- metisiert ist, falls ||f⁰(t)||= 1 f¨ur allet∈I gilt.

Bemerkung 12.2 Ist f[a, b] →Rⁿ nach der Bogenl¨ange parametisiert, dann gilt

L= Z ^b

a

||f⁰(t)||dt= Z ^b

a

1dt=b−a.

Dies erkl¨art die Bezeichnung dieses Begriffs.

Analysis A

Sommersemester 2004 Dozent: Prof. Dr. K. Hulek

Diese Vorlesung beruht auf der Ausarbeitung von Prof. Dr. W. Ebeling

aus dem Sommersemester 2000.

1

Literatur

[1] S. L. Salas, E. Hille: Calculus. Spektrum Akademischer Verlag, Heidel- berg, Berlin, Oxford, 1994. ISBN 3-86025-130-9

[2] M. Spivak: Calculus. Third Edition. Publish or Perish, Houston, 1994.

ISBN 0-914098-89-6 (amerikanisch)

[3] O. Forster: Analysis 1. 5., ¨uberarb. Auflage. Vieweg, Wiesbaden, 1999.

ISBN 3-528-47224-3

1 Grenzwerte

Notation Im folgenden istf : D→R immer eine Funktion mit Definitions- bereichD ⊂R. Wenn wir D im folgenden nicht angeben, so sollD immer der maximale Definitionsbereich sein, auf demf definiert ist. Ferner sinda, l usw.

reelle Zahlen.

Der Grenzwertbegriff wird in dieser Vorlesung eine zentrale Rolle spielen.

Wir wollen zun¨achst erkl¨aren was

x→alimf(x) =l bedeuten soll.

Provisorische Definition:Es gilt lim_x→af(x) =l gdw. man erreichen kann, dassf(x) beliebig nahe beil liegt, wenn man verlangt, dassxhinreichend nahe beia, aber verschieden vona, ist.

Man beachte, dassf(a) nicht definiert zu sein braucht.

Wir untersuchen nun diese Definition an einem Beispiel. Wir betrachten die Funktionf(x) =xsin¹_x an der Stellea= 0. Wir wollen zeigen

x→0limxsin1 x = 0.

Wie erreichen wir, dassxsin¹_x in einem Abstand von ₁₀¹ von 0 liegt? Wir wollen also

−1

10 < xsin1 x< 1

10 oder

xsin1 x

< 1 10. Das ist aber leicht zu erreichen. Wir wissen

sin1 x

≤1 f¨ur allex6= 0,

also

xsin1 x

≤ |x| f¨ur allex6= 0.

Das bedeutet also

|x|< 1

10, x6= 0 ⇒

xsin1 x

< 1 10.

1 Grenzwerte 2

Abbildung 1:f(x) =xsin¹_x

Statt ₁₀¹ h¨atten wir ein beliebiges ε > 0 nehmen k¨onnen, und dann gilt f¨ur f(x) =xsin¹_x:

|x−0|< ε ⇒ |f(x)−0|< ε.

Betrachten wir ein anderes Beispiel: die Funktionf(x) =p

|x|an der Stelle a= 0. Um|p

|x||< εzu erreichen, m¨ussen wir

|x|< ε² verlangen.

Sehen wir uns ein drittes Beispiel an. F¨ur die Funktion f(x) = sin¹_x ist es falsch, dass sie gegen 0 geht, wennxgegena= 0 geht. Es ist nicht wahr, dass wir f¨ur jedesε >0 erreichen k¨onnen, dass|f(x)−0|< εgilt, sofern|x|hinreichend klein und ungleich 0 ist. Dazu brauchen wir nureinε >0 zu finden, f¨ur das die Bedingung|f(x)−0| < ε nicht mehr garantiert ist, auch wenn wir verlangen, dass|x|noch so klein ist. Zum Beispiel tut esε=¹₂: es gilt nicht|f(x)|< ¹₂ f¨ur alle hinreichend kleinen |x|. Denn f¨ur jedes δ > 0 finden wir ein x= _π/2+2nπ¹ mit |x|< δ, f¨ur dasf(x) = 1 gilt.

Wir wollen nun unsere provisorische Definition zu einer mathematisch pr¨a- zisen machen. Wir pr¨azisieren die Teile der provisorischen Definition wie folgt:

Man kann erreichen, dass f(x) be- liebig nahe beilliegt,

F¨ur ein beliebig gew¨ahltesε >0 gilt

|f(x)−l|< ε, wenn man verlangt, wenn man verlangt, dassxhinreichend nahe beia, aber

verschieden vona, ist.

dass x eine Ungleichung der Form 0 <|x−a|< δ f¨ur ein hinreichend kleinesδ >0 erf¨ullt.

Damit kommen wir zu der folgenden Definition.

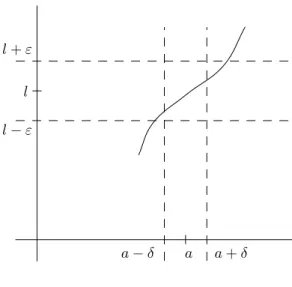
Definition Es gilt lim_x→af(x) =l gdw. es f¨ur jedesε >0 einδ >0 gibt, so dass f¨ur jedesxaus 0<|x−a|< δ folgt, dass|f(x)−l|< εgilt.

Abbildung 2:f(x) =p

|x|

Abbildung 3:f(x) = sin¹_x

1 Grenzwerte 4

a

a−δ a+δ

l l−ε l+ε

Abbildung 4: lim_x→af(x) =l

In unserem Beispielf(x) =xsin_x¹konnten wirδ=εw¨ahlen. In dem Beispiel f(x) =p

|x|tat esδ=ε².

Es ist wichtig, sich die logische Struktur dieser Definition noch einmal klarzu- machen. Deswegen schreiben wir diese Definition auch noch einmal formal hin:

x→alimf(x) =l⇐⇒ ∀ε >0 ∃δ >0∀x(0<|x−a|< δ⇒ |f(x)−l|< ε).

Was haben wir zu tun, wenn wir lim_x→af(x) = l beweisen wollen? Wir m¨ussen uns zun¨achst ein beliebiges ε > 0 vorgeben. Dann m¨ussen wir dazu ein geeignetes δ > 0 finden, so dass f¨ur alle xmit 0< |x−a|< δ folgt, dass

|f(x)−l|< εgilt.

Wie kann man zeigen, dass lim_x→af(x) =l nicht gilt? Wenn esnicht wahr ist, dass gilt

es gibt zu jedemε >0 einδ >0, so dass f¨ur allex, f¨ur die 0<|x−a|< δ gilt, auch|f(x)−l|< εgilt,

dann gilt:

es gibteinε >0, so dass f¨urjedes δ >0 es einxgibt, f¨ur das 0<|x−a|< δ aber nicht|f(x)−l|< εgilt.

Um also zu zeigen, dass f(x) = sin¹_x nicht den Grenzwert 0 bei 0 hat, betrachten wirε=¹₂ und stellen fest, dass es f¨ur jedesδ >0 einxmit 0<|x− 0|< δaber nicht|sin¹_x−0|<¹₂ gibt, n¨amlich einxvon der Formx= _π/2+2nπ¹ , wobei nso groß ist, dass _π/2+2nπ¹ < δ gilt.

Beispiel 1.1 (a) F¨ur die konstante Funktionf(x) =cgilt lim_x→af(x) =cf¨ur jeden Punkta: Da|f(x)−c|= 0 f¨ur allexgilt, tut es jedes beliebigeδ.

(b) F¨ur die Funktionf(x) = xgilt limx→af(x) =a f¨ur jeden Punkt a: Zu einem gegebenenε >0 k¨onnen wirδ:=εw¨ahlen, denn aus 0<|x−a|< εfolgt

|f(x)−a|< ε.

(c) Nun betrachten wir ein weniger einfaches Beispiel, an dem wir auch das allgemeine Vorgehen klarmachen k¨onnen. Wir betrachten die Funktionf(x) = x²und einen beliebigen Punkta∈R. Es ist zu zeigen:

x→alimx²=a².

Es seiε >0 gegeben. Wir untersuchen zun¨achst, wie wir

|x²−a²|< ε erreichen k¨onnen. Es gilt

|x²−a²|< ε ⇔ |x−a| · |x+a|< ε.

Der Faktor |x−a| wird beliebig klein, wenn wirxgegena gehen lassen, nicht so aber der Faktor |x+a|. Es ist aber auch gar nicht n¨otig, auch diesen Faktor besonders klein werden zu lassen, er darf nur nicht unbeschr¨ankt wachsen. Wir suchen also eine obere Schranke f¨ur diesen Faktor. Denn wenn wir zum Beispiel

|x+a|<1000000 haben, so brauchen wir nur |x−a| < _1000000^ε zu verlangen.

Da wir nurxzu untersuchen brauchen, die nahe bei aliegen, k¨onnen wir vor- aussetzen, dass |x−a|<1 gilt (man k¨onnte statt 1 auch jede beliebige andere positive Zahl nehmen). F¨ur solchexgilt dann

|x+a| ≤ |x−a+ 2a|

≤ |x−a|+ 2|a|

<1 + 2|a|.

Das f¨uhrt dazu, dass wir

δ:= min

1, ε 2|a|+ 1

setzen. Denn dann gilt f¨ur allex

|x−a|< δ ⇒ |x²−a²|< ε.

Beispiel 1.2 Wir betrachten die Funktion

f(x) =

0, xirrational, 1, xrational.

Diese Funktion hat f¨ur keinen Punkt a einen Grenzwert. Denn f¨ur jede Zahl l k¨onnen wirε = ¹₄ w¨ahlen. Wie klein wir auch δ >0 w¨ahlen, so k¨onnen wir immer sowohl ein rationales als auch ein irrationales xmit |x−a|< δ finden.

F¨ur eines dieser beidenxkann dannnicht|f(x)−l|<¹₄ gelten.

Wir formulieren und beweisen nun zwei grundlegende S¨atze.

Satz 1.1 (Die Eindeutigkeit des Grenzwertes) Wennlim_x→af(x) =lund lim_x→af(x) =m ist, so giltl=m.

1 Grenzwerte 6

Beweis. Da dies unser erster Beweis ist, soll er ausf¨uhrlich dargestellt werden.

Wenn man einen Beweis beginnt, macht man sich zuerst die Voraussetzungen klar. Dazu schreiben wir einfach die Definitionen aus:

x→alimf(x) =l

bedeutet, dass es f¨ur jedesε >0 einδ1>0 gibt, so dass f¨ur allexgilt:

wenn 0<|x−a|< δ₁ ist, so folgt|f(x)−l|< ε.

Andererseits bedeutet

x→alimf(x) =m,

dass es f¨ur jedesε >0 einδ2>0 gibt, so dass f¨ur allexgilt:

wenn 0<|x−a|< δ2 ist, so folgt|f(x)−m|< ε.

Wir mußten dabei zwei verschiedene Zahlen δ1 und δ2 benutzen, da es keinen Grund gibt, warum dasδ, das es in dem einen Fall tut, auch f¨ur den anderen Fall geeignet ist. Wir k¨onnen nun aber leicht schließen, dass es f¨ur alleε >0 ein δ >0 gibt, so gilt f¨ur allexgilt

wenn 0<|x−a|< δ ist, so folgt|f(x)−l|< εund|f(x)−m|< ε, denn wir k¨onnen einfachδ:= min(δ₁, δ₂) w¨ahlen.

Wir wollen nun einen Widerspruchsbeweis f¨uhren. Das bedeutet, dass wir die Annahme l 6= m auf einen Widerspruch f¨uhren wollen. Wir nehmen also l6=man. Wir wollen nunεso w¨ahlen, dass die beiden Bedingungen

|f(x)−l|< εund|f(x)−m|< ε

nicht beide gelten k¨onnen. Man mache sich an einer Skizze klar, wie wirεw¨ahlen k¨onnen. Wir w¨ahlen

ε:= |l−m|

2 .

Dann folgt, dass es einδ >0 gibt, so dass f¨ur allexmit 0<|x−a|< δ gilt:

|f(x)−l|< |l−m|

2 und|f(x)−m|< |l−m|

2 . Daraus folgt aber f¨ur allexmit 0<|x−a|< δ

|l−m|=|l−f(x) +f(x)−m| ≤ |l−f(x)|+|f(x)−m|

< |l−m|

2 +|l−m|

2

= |l−m|,

ein Widerspruch. 2

Satz 1.2 (Rechenregeln f¨ur Grenzwerte) Wennlim_x→af(x) =lundlim_x→ag(x) = m ist, so gilt

(1) limx→a(f+g)(x) =l+m,

(2) lim_x→a(f·g)(x) =l·m, und, wennm6= 0,

(3) limx→a

1 g

(x) = _m¹.

Beweis.Wir beweisen nur (1). Die Beweise von (2) und (3) sind schwieriger und sollen nicht ausgef¨uhrt werden.

Es seiε >0 gegeben. F¨ur den Beweis von (1) m¨ussen wir zeigen, dass es ein δ >0 gibt, so dass,

wenn 0<|x−a|< δ ist,|(f+g)(x)−(l+m)|< εfolgt.

Dabei ben¨otigen wir die Ungleichung

|(f+g)(x)−(l+m)| = |f(x) +g(x)−l−m|

= |(f(x)−l) + (g(x)−m)|

≤ |f(x)−l|+|g(x)−m|

Um also |(f +g)(x)−(l+m)| kleiner als ε zu machen, gen¨ugt es, wenn wir sowohl |f(x)−l| als auch |g(x)−m| kleiner als ^ε₂ machen. Aus ε > 0 folgt

ε

2 >0. Wegen

x→alimf(x) =l und lim

x→ag(x) =m gibt es ein δ1>0, so dass f¨ur allexgilt:

wenn 0<|x−a|< δ1 ist, so folgt|f(x)−l|< ε 2, und einδ2>0, so dass f¨ur allexgilt:

wenn 0<|x−a|< δ₂ist, so folgt|g(x)−m|< ε 2. Setzen wir jetztδ:= min(δ1, δ2), so folgt f¨ur allex

0<|x−a|< δ

⇒ 0<|x−a|< δ₁ und 0<|x−a|< δ₂

⇒ |f(x)−l|< ε

2 und|g(x)−m|< ε 2

⇒ |(f +g)(x)−(l+m)| ≤ |f(x)−l|+|g(x)−m|< ε,

was zu zeigen war. 2

Wir wollen nun auch noch einseitige Grenzwerte und Grenzwerte f¨urxgegen

∞definieren.

Definition Es gilt lim_x→a+f(x) =l (l ist rechtsseitiger Grenzwert von f(x) f¨ur x gegen a) gdw. es f¨ur jedes ε > 0 ein δ > 0 gibt, so dass f¨ur jedes xaus 0< x−a < δ folgt, dass |f(x)−l|< εgilt.

Definition Es gilt lim_x→a−f(x) = l (l ist linksseitiger Grenzwert von f(x) f¨ur x gegen a) gdw. es f¨ur jedes ε > 0 ein δ > 0 gibt, so dass f¨ur jedes xaus 0< a−x < δfolgt, dass |f(x)−l|< εgilt.

1 Grenzwerte 8

e u

x y

-1 1

Abbildung 5: Die Funktion aus Beispiel 1.3

Beispiel 1.3 Wir betrachten die Funktion

f(x) =

−1, x <0, 1, x≥0.

Es gilt

lim

x→0⁻f(x) =−1, lim

x→0⁺f(x) = 1, aber lim

x→0f(x)6=l f¨ur jede Zahll.

Definition Es gilt lim_x→+∞f(x) = l gdw. es f¨ur jedes ε > 0 eine Zahl N gibt, so dass f¨ur alle xaus x > N folgt, dass |f(x)−l| < ε gilt. Ebenso gilt lim_x→−∞f(x) = l gdw. es f¨ur jedesε >0 eine Zahl N gibt, so dass f¨ur allex mit x < N folgt, dass|f(x)−l|< εgilt.

2 Stetigkeit

Es soll nun der Begriff der Stetigkeit in einem Punkt definiert werden.

Definition Die Funktionf heißtim Punktastetig gdw.

x→alimf(x) =f(a).

Beispiel 2.1 (a) Die konstante Funktion f(x) =c ist in jedem Punkt a∈ R stetig.

(b) Die identische Funktionf(x) =xist in jedem Punkta∈Rstetig.

(c) Die Funktionf(x) =x² ist in jedem Punkta∈Rstetig.

(d) Die Funktion

f(x) =

−1, x <0, 1, x≥0, ist in 0 nicht stetig.

(e) Die Funktion

f(x) =xsin1 x

ist in 0 nicht definiert. Sie kann aber in 0stetig erg¨anzt werden. Denn die neue Funktion

F(x) =

xsin¹_x, x6= 0,

0, x= 0,

ist in 0 stetig.

(f) Die Funktion

f(x) = sin1 x kann nicht stetig in 0 erg¨anzt werden.

(g) Die Funktion

f(x) =

0, xirrational, 1, xrational, ist nach Beispiel 1.2 in keinem Punktastetig.

Satz 2.1 (Rechenregeln f¨ur stetige Funktionen) Wennf undgim Punkt astetig sind, dann ist

(1) f+g stetig ina, (2) f·g stetig ina.

Gilt dar¨uberhinausg(a)6= 0, so ist (3) 1/g stetig ina.

Beweis. Zu (1): Daf undg im Punktastetig sind, gilt

x→alimf(x) =f(a) und lim

x→ag(x) =g(a).

Nach Satz 1.2 folgt daraus

x→alim(f+g)(x) =f(a) +g(a) = (f+g)(a).

Das bedeutet aber gerade, dass f+gim Punktastetig ist.

Die Beweise zu (2) und (3) gehen analog. 2

2 Stetigkeit 11

Beispiel 2.2 Aus Satz 2.1 folgt, dass die Funktion f(x) = x³−x

x²−5x+ 6 = x³−x (x−2)(x−3)

in jedem Punktamit Ausnahme der Stellena= 2 unda= 3, an denen sie nicht definiert ist, stetig ist. Die Funktion kann in diesem Punkte stetig fortgesetzt werden.

Wir wollen nun den Begriff der Stetigkeit in einem Punkt in dieε-δ-Sprache

¨

ubersetzen. Eine direkte ¨Ubersetzung von

x→alimf(x) =f(a) w¨are:

F¨ur jedes ε >0 gibt es einδ >0, so dass f¨ur allexgilt:

wenn 0<|x−a|< δ ist, so folgt|f(x)−f(a)|< ε.

Die Forderung 0<|x−a|ist hierbei ¨uberfl¨ussig, denn f¨urx=agiltf(x) =f(a) und damit|f(x)−f(a)|= 0< ε. Damit erhalten wir

Satz 2.2 (ε-δ-Charakterisierung der Stetigkeit) Die Funktionf ist stetig in a gdw. es f¨ur jedes ε >0 ein δ >0 gibt, so dass f¨ur alle x aus |x−a| < δ

folgt: |f(x)−f(a)|< ε. 2

Wir betrachten nun die Hintereinanderschaltungf◦g von zwei Funktionen f undg. Wir erinnern an die Definition: (f◦g)(x) =f(g(x)).

Satz 2.3 (Verkettung stetiger Funktionen) Ist g stetig in a und f stetig in g(a), so ist f ◦g stetig in a. (Man beachte, dass wir verlangen, dass f in g(a)stetig ist, nicht ina.)

Beweis. Es seiε >0 gegeben. Gesucht ist einδ >0, so dass f¨ur allexgilt:

|x−a|< δ ⇒ |(f◦g)(x)−(f ◦g)(a)|< ε

⇔ |f(g(x))−f(g(a))|< ε.

Wir nutzen zun¨achst die Stetigkeit vonf im Punktg(a) aus, um abzusch¨atzen, wie dichtg(x) beig(a) liegen muß, damit diese Ungleichung erf¨ullt ist. Daf in g(a) stetig ist, gibt es einδ⁰>0, so dass f¨ur alley gilt

|y−g(a)|< δ⁰⇒ |f(y)−f(g(a))|< ε.

Insbesondere k¨onnen wir hiery=g(x) einsetzen:

|g(x)−g(a)|< δ⁰⇒ |f(g(x))−f(g(a))|< ε. (1) Nun nutzen wir die Stetigkeit von g im Punkt a aus. Wir k¨onnen das δ⁰ als unserεin der Definition der Stetigkeit vonginanehmen. Wir schließen daraus, dass es einδ >0 gibt, so dass f¨ur allexgilt:

|x−a|< δ⇒ |g(x)−g(a)|< δ⁰. (2) Aus (1) und (2) erhalten wir das gew¨unschte Resultat: F¨ur allexgilt

|x−a|< δ⇒ |f(g(x))−f(g(a))|< ε.

2

Beispiel 2.3 Wir betrachten erneut die Funktion

f(x) =

xsin_x¹, x6= 0,

0, x= 0.

Wir haben bereits gesehen (Beispiel 2.1), dass f stetig in 0 ist. Aus Satz 2.1 und 2.3 folgt, dassf auch in allen Punktena6= 0 stetig ist.

Nun betrachten wir Funktionen, die in allen Punkten eines Intervalls stetig sind.

Notation Wir erinnern daran, dass

(a, b) ={x∈R|a < x < b}

dasoffene Intervallund

[a, b] ={x∈R|a≤x≤b}

dasabgeschlossene Intervallmit Anfangspunkt aund Endpunkt bbezeichnet.

Definition Eine Funktion f heißt auf (a, b) stetig gdw. f in allen Punkten x0∈(a, b) stetig ist.

Eine Funktionf heißtauf [a, b] stetiggdw. gilt:

(1) f ist stetig in allen Punkten x0∈(a, b), (2) lim_x→a+f(x) =f(a) und lim_x→b−f(x) =f(b).

Die folgende wichtige Eigenschaft der Stetigkeit werden wir noch oft anwen- den.

Satz 2.4 Es seif inastetig undf(a)>0. Dann gibt es einδ >0, so dass f¨ur allexmit|x−a|< δ gilt: f(x)>0. Wennf(a)<0ist, so gibt es entsprechend einδ >0, so dass f¨ur allexmit|x−a|< δ gilt: f(x)<0.

Beweis. Wir betrachten den Fallf(a)>0. Da f inastetig ist, gibt es f¨ur alle ε >0 einδ >0, so dass f¨ur allexgilt:

|x−a|< δ⇒ |f(x)−f(a)|< ε.

Daf(a)>0 ist, k¨onnen wir f¨ur unserεdie Zahlf(a) nehmen. Also gibt es ein δ >0, so dass f¨ur allexgilt:

|x−a|< δ⇒ |f(x)−f(a)|< f(a).

Die letzte Ungleichung bedeutet aber, dassf(x)>0.

Den Fallf(a) <0 behandelt man analog oder wendet den ersten Teil auf

die Funktion−f an. 2

3 Drei grundlegende S¨atze 13

3 Drei grundlegende S¨ atze

Wir formulieren in diesem Kapitel drei grundlegende S¨atze. Die Beweise dieser S¨atze stellen wir zun¨achst zur¨uck.

Satz 3.1 (Zwischenwertsatz) Wenn f auf [a, b] stetig ist und c eine Zahl zwischen f(a) und f(b) ist, dann gibt es mindestens ein x ∈ [a, b], f¨ur das f(x) =c ist.

Satz 3.2 (Beschr¨ankheitssatz) Wenn f auf [a, b] stetig ist, dann ist f auf [a, b] beschr¨ankt, d.h. es gibt ZahlenK und N, so dass f¨ur alle x∈ [a, b] gilt:

K≤f(x)≤N.

Satz 3.3 (Maximum-Minimum-Satz) Wennf auf[a, b]stetig ist, dann nimmt f auf [a, b] sowohl ein Maximum M als auch ein Minimum m an, d.h. es gibt x∈[a, b] undy ∈[a, b]mit f(x) =M und f(y) =m und f¨ur alle z∈[a, b] gilt m≤f(z)≤M.

Offensichtlich folgt Satz 3.2 aus Satz 3.3.

Wir wollen uns zun¨achst klarmachen, dass die Aussagen dieser S¨atze nicht zu gelten brauchen, wennf in einem Punkt des Intervalls [a, b] nicht stetig ist.

Beispiel 3.1 Es sei

f(x) =

−1 f¨ur −3≤x <0, 1 f¨ur 0≤x≤3.

Dann istf in jedem Punkt von [−3,3] mit Ausnahme von 0 stetig. Die Funktion f nimmt keinen Wertcmit −1< c <1 an.

Beispiel 3.2 Es sei

f(x) =

1

x f¨ur 0< x≤1, 0 f¨urx= 0.

Dann istf in allen Punkten von [0,1] mit Ausnahme von 0 stetig. Die Funktion f ist nicht nach oben beschr¨ankt.

Beispiel 3.3 Es sei

f(x) =

x² f¨ur 0≤x <1, 0 f¨ur 1≤x≤2.

Dann ist f in allen Punkten von [0,2] außer in 1 stetig. Die Funktion f ist beschr¨ankt, nimmt aber kein Maximum an.

Wir betrachten nun eine Anwendung des Zwischenwertsatzes.

Satz 3.4 Jede positive Zahl besitzt eine Quadratwurzel, d.h. f¨ur jede Zahlα >0 gibt es eine Zahl x >0 mitx²=α.

Beweis. Es seiα >0 gegeben. Wir betrachten die Funktionf(x) =x². Diese Funktion ist nach Beispiel 2.1 (c) ¨uberall stetig. Dann kann die Behauptung des Satzes so formuliert werden: Die Funktion f nimmt den Wert α an. Um den Zwischenwertsatz anwenden zu k¨onnen, m¨ussen wiraundbfinden, so dass f(a) < α < f(b) ist. Wegen f(0) = 0 und α > 0 k¨onnen wir a = 0 w¨ahlen.

Da f f¨ur x gegen ∞ unbeschr¨ankt w¨achst, k¨onnen wir auch ein b finden mit α < f(b). Genauer gilt folgendes. Wenn α > 1 ist, w¨ahlen wir b = α(denn dann gilt f(b) = α² > α), und wenn α <1 ist, w¨ahlen wir b= 1. (F¨ur α= 1 gilt 1²= 1.) Wenden wir nun den Zwischenwertsatz auf die Funktionf und das Intervall [a, b] an, so folgt, dass es einx∈[a, b] mitf(x) =αgibt. 2 Wie findet man nun in der Situation des Zwischenwertsatzes so ein xmit f(x) =c? Der Zwischenwertsatz selber sagt dar¨uber nichts aus. Die einfachste Methode, so einxn¨aherungsweise zu bestimmen, ist die sogenannteBisektion- smethode. Um sie darzustellen, betrachten wir die folgende Situation.

Es seif auf [a, b] stetig und

f(a)<0< f(b) oder f(b)<0< f(a).

Gesucht ist eine L¨osung x der Gleichung f(x) = 0 im Intervall [a, b]. Der Zwischenwertsatz besagt, dass die Gleichung f(x) = 0 mindestens eine L¨osung in [a, b] hat. Der Einfachheit halber nehmen wir an, dass nur eine solche L¨osung existiert. Wir nennen sie ξ. Die Bisektionsmethode ist ein iterativer Prozeß, um einen N¨aherungswert f¨urξzu bestimmen.

Zu Beginn setzen wira1 :=a undb1 :=b. Nun halbieren wir das Intervall [a1, b1]. Es seim1:=a1+^b1−a₂ ¹ der Mittelpunkt von [a1, b1]. Giltf(m1) = 0, so istξ:=m1 die gesuchte L¨osung und wir sind fertig. Andernfalls ist f(m1)>0 oderf(m1)<0. Habenf(a1) undf(m1) verschiedene Vorzeichen, so muß nach dem Zwischenwertsatz das gesuchteξim Intervall [a1, m1] liegen und wir setzen a2 := a1 und b2 := m1. Andernfalls muß ξ in [m1, b1] liegen und wir setzen a2:=m1 undb2:=b1.

Nun halbieren wir das Intervall [a2, b2]. Es sei m2 :=a2+^b2−a₂ ² der Mit- telpunkt von [a₂, b₂]. Gilt f(m₂) = 0, so sind wir fertig. Andernfalls setzen wir [a₃, b₃] := [a₂, m₂] oder [a₃, b₃] := [m₂, b₂], je nachdem obf(a₂) undf(m₂) oderf(m₂) undf(b₂) verschiedene Vorzeichen haben. Nun halbieren wir wieder [a₃, b₃] usw.

Nach n Halbierungen untersuchen wir den Mittelpunkt m_n des Intervalls [an, bn]. Wir k¨onnen dann sicher sein, dass

|ξ−m_n| ≤ 1

2(b_n−a_n) = 1 2

b_n−1−a_n−1 2

=· · ·= b−a 2ⁿ

ist. Wenn wir also ξdurch mn bis auf einen Fehlerε >0 ann¨ahern wollen, so m¨ussen wirnIterationsschritte ausf¨uhren, wobei

b−a 2ⁿ < ε ist.

Beispiel 3.4 Wir betrachten die Funktionf(x) =x²−2. Nach Satz 3.4 besitzt die Gleichungf(x) = 0 eine L¨osung, n¨amlichx=√

2. Daf(1)<0 undf(2)>0

3 Drei grundlegende S¨atze 15

a1 m1 b1 a2m2 b2 b3

m3

a3

Figure 6: Die Bisektionsmethode

ist, k¨onnen wir √

2 durch Anwenden der Bisektionsmethode auf das Intervall [1,2] absch¨atzen. Angenommen, wir wollen √

2 bis auf einen Fehler von 0,15 absch¨atzen. Dazu brauchen wir mindestensnIterationsschritte, wobei

2−1

2ⁿ <0,15 ist. Das ist aber der Fall, wennn≥3 ist.

a1= 1, b1= 2, m1= 1,5 : f(m1) = 0,25>0 a₂= 1, b₂= 1,5, m₂= 1,25 : f(m₂) =−0,4375<0 a3= 1,25, b3= 1,5, m3= 1,375

Wir schließen daraus, dass√

2 vonm3= 1,375 mit einer Genauigkeit von 0,15 approximiert wird.

4 Supremum, Infimum

Es sollen nun wichtige neue Begriffe eingef¨uhrt und die wichtigste Eigenschaft der reellen Zahlen betrachtet werden.

Definition Eine MengeAvon reellen Zahlen heißtnach oben beschr¨anktgdw.

es eine Zahlxgibt, so dass

a≤xf¨ur allea∈A gilt. Eine solche Zahl xheißt eineobere Schrankef¨urA.

Definition Eine Zahlx heißt kleinste obere SchrankeoderSupremum von A (in Zeichenx= supA) gdw. gilt:

(i) xist eine obere Schranke vonA, und

(ii) wenny eine obere Schranke vonAist, so giltx≤y.

Satz 4.1 (Eindeutigkeit des Supremums) Sindxundykleinste obere Schranken vonA, so giltx=y.

Beweis. Es gilt

x≤y,

day eine obere Schranke undxeine kleinste obere Schranke vonAist, und y≤x,

daxeine obere Schranke undyeine kleinste obere Schranke vonAist. Deshalb

folgt x=y. 2

Wegen Satz 4.1 k¨onnen wir vondemSupremum vonAsprechen.

Definition Eine ZahlxheisstMaximum vonA(in Zeichenx= maxA), falls (i) xist Supremum vonA,

(ii) x∈A.

Entsprechend k¨onnen wir definieren:

Definition Eine MengeAvon reellen Zahlen heißtnach unten beschr¨anktgdw.

es eine Zahlxgibt, so dass

x≤af¨ur allea∈A

gilt. Eine solche Zahl xheißt eineuntere Schrankef¨urA.

Definition Eine Zahlxheißtgr¨oßte untere SchrankeoderInfimumvonA(in Zeichen x= infA) gdw. gilt:

(i) xist eine untere Schranke von A, und

(ii) wenny eine untere Schranke vonAist, so gilty≤x.

4 Supremum, Infimum 17

Wie im Fall des Supremums kann man auch im Fall des Infimums zeigen, dass das Infimum, wenn es existiert, eindeutig bestimmt ist.

Definition Eine ZahlxheisstMinimum von A(in Zeichenx= minA), falls (i) xist Infinum vonA,

(ii) x∈A.

Definition Eine MengeAheißtbeschr¨anktgdw.Anach oben und nach unten beschr¨ankt ist.

Beispiel 4.1 Es seif eine Funktion, die auf [a, b] definiert ist. Wir betrachten die Menge

A:={f(x)|x∈[a, b]}.

Dann istf genau dann auf [a, b] beschr¨ankt, wennAbeschr¨ankt ist. Die Funk- tionf nimmt auf [a, b] genau dann ein Maximum und ein Minimum an, wenn Aein Maximum und ein Minimum besitzt.

Beispiel 4.2 (a) Die leere Menge ist nach oben beschr¨ankt. Denn jede Zahlx ist eine obere Schranke f¨ur∅: Die Bedingung

a≤x f¨ur jedesa∈ ∅

ist einfach deswegen erf¨ullt, weil es kein a ∈ ∅ gibt. Da jede Zahl eine obere Schranke f¨ur∅ ist, gibt es offensichtlich keine kleinste obere Schranke.

(b) Es sei

A:={x∈R|x²<2}.

Dann istA nach oben beschr¨ankt,√

2 ist eine obere Schranke vonAund dies ist auch das Supremum vonA.

Beweis. Die Zahl √

2 ist eine obere Schranke vonA, denn f¨ur allexgilt x²<2⇔ |x|<√

2.

Diese Zahl ist auch die kleinste obere Schranke: Angenommen, α < √ 2 w¨are auch eine obere Schranke vonA. Diese Annahme f¨uhren wir zum Widerspruch, indem wir einhmit 0< h <1 so bestimmen, dassα+h∈Agilt. Es gilt

α+h∈A⇔(α+h)²<2⇔2hα+h²<2−α². Wegenh <1 gilt

2hα+h²<2hα+h.

Setze

2hα+h= 2−α²d.h. h:= 2−α² 2α+ 1. Wegen 1< α <√

2 gilt 0< h <1 und nach Konstruktion vonhgiltα+h∈A.

(c) Es sei

A:={x∈Q|x²<2}.

Dann istAnach oben beschr¨ankt, z.B. ist 2 eine obere Schranke vonA, aberA hat kein Supremum inQ.

Wir sehen an diesem Beispiel, dass im allgemeinen eine nicht leere, nach oben beschr¨ankte Menge kein Supremum zu haben braucht. Es ist eine besondere Eigenschaft der reellen Zahlen, dass jede nicht leere, nach oben beschr¨ankte Menge ein Supremum besitzt. Diese Eigenschaft ist so grundlegend, dass wir sie nicht ableiten k¨onnen, sondern als Axiom betrachten m¨ussen.

Axiom (Das Supremumsaxiom) Jede nicht leere, nach oben beschr¨ankte Menge von reellen Zahlen besitzt ein Supremum.

Wie wir in Beispiel 4.2 (c) gesehen haben, besitzen die rationalen Zahlen diese Eigenschaft nicht.

Wir sind nun in der Lage, den Zwischenwertsatz zu beweisen. Es reicht, den folgenden Satz zu beweisen.

Satz 4.2 Ist f auf [a, b] stetig und f(a) < 0 < f(b), dann gibt es eine Zahl x∈[a, b] mitf(x) = 0.

Ableitung von Satz 3.1 aus Satz 4.2.. Es sei f(a) < c < f(b). Dann setze g(x) :=f(x)−c. Dann istg auf [a, b] stetig und es giltg(a)<0< g(b). Nach Satz 4.2 gibt es einx∈[a, b] mitg(x) = 0. Das bedeutet aber f(x) =c.

Giltf(b)< c < f(a), so betrachte mang(x) :=c−f(x). 2 Beweis von Satz 4.2.. Definiere

A:={x∈[a, b]|f negativ auf dem Intervall [a, x]}.

Dann istA6=∅, daa∈A. Tats¨achlich folgt aus Satz 2.4 und der Vorausset- zungf(a)<0, dass es einδ >0 gibt, so dassAalle Punktexmita≤x < a+δ enth¨alt.

Die MengeAist nach oben beschr¨ankt, dabeine obere Schranke f¨urA ist.

Tats¨achlich folgt wieder aus Satz 2.4 und der Voraussetzungf(b)>0, dass es einδ >0 gibt, so dass alle Punktexmitb−δ < x≤b obere Schranken vonA sind.

Aus dem Supremumsaxiom folgt daher, dassAein Supremumαbesitzt. Aus den obigen Bemerkungen folgt a < α < b. Wir wollenf(α) = 0 zeigen. Dazu f¨uhren wir die Annahmenf(α)>0 undf(α)<0 zum Widerspruch.

Angenommen,f(α)<0. Nach Satz 2.4 gibt es einδ >0, so dassf(x)<0 f¨ur alle x mit α−δ < x < α+δ gilt. Nun gibt es eine Zahl x₀ in A mit α−δ < x₀ < α, denn sonst w¨are α nicht die kleinste obere Schranke. Das bedeutet, dass f auf dem ganzen Intervall [a, x₀] negativ ist. Ist andererseits x₁ eine Zahl mitα < x₁ < α+δ, so ist f auch negativ auf [x₀, x₁]. Daher ist f negativ auf dem Intervall [a, x₁]. Das bedeutet aber, dassx₁in Aliegt. Das steht aber im Widerspruch zu der Tatsache, dassαeine obere Schranke von A ist. Also war die Annahmef(α)<0 falsch.

Angenommen, f(α) > 0. Nach Satz 2.4 gibt es dann ein δ > 0, so dass f(x)>0 f¨ur allexmitα−δ < x < α+δgilt. Wie oben schließen wir, dass es dann einx0 inAmitα−δ < x0< αgibt. Das bedeutet aber, dassf auf [a, x0] negativ ist. Das ergibt aber einen Widerspruch zu f(x0)> 0. Also war auch die Annahme f(α) >0 falsch, und es bleibt als einzige M¨oglichkeit f(α) = 0

¨

ubrig. 2

4 Supremum, Infimum 19

Die Beweise der S¨atze 3.2 und 3.3 verlaufen nach einem ¨ahnlichen Muster und sollen hier nicht gegeben werden.

Wir wollen nun noch andere Folgerungen aus dem Supremumsaxiom darstellen.

Satz 4.3 Die MengeN der nat¨urlichen Zahlen ist nicht nach oben beschr¨ankt.

Beweis. Angenommen,Nist nach oben beschr¨ankt. DaN6=∅, gibt es dann ein Supremumαf¨urN. Es gilt also

n≤α f¨ur allen∈N. Andererseits gibt es einn₀∈Nmit

n0> α−1,

denn sonst w¨areα−1 obere Schranke vonNim Widerspruch dazu, dassαdie kleinste obere Schranke vonNist. F¨urn0 gilt also

n0+ 1> α,

ein Widerspruch. 2

Satz 4.4 (Satz von Archimedes) Zu jedem a ∈ R mit a > 0 und jedem b∈Rgibt es einn∈N, so dassna > b gilt.

Beweis. Andernfalls w¨urde f¨ur allen∈N

na≤b d.h. n≤ b a

gelten, _a^b w¨are also eine obere Schranke f¨urN. 2

Satz 4.5 Zu jedemε >0 gibt es eine nat¨urliche Zahln6= 0mit _n¹ < ε.

Beweis. Da

1

n < ε⇔nε >1,

folgt die Behauptung aus dem Satz von Archimedes mita=εundb= 1. 2

a h

a+h f(a)

f(a+h)−f(a) f(a+h)

Figure 7: Steigung der Sekante von (a, f(a)) nach (a+h, f(a+h))

5 Differenzierbarkeit

Wir kommen nun zur Definition der Differenzierbarkeit.

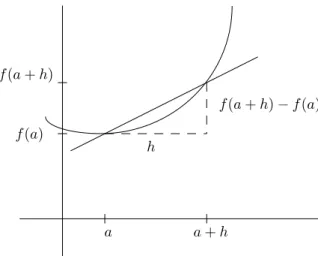
Anschaulich gibt die Ableitung von f im Punkt a die Steigung der Tan- gente an den Graphen vonf im Punkt (a, f(a)) an. Man erh¨alt diese Steigung als Grenzwert der Steigungen der Sekanten durch (a, f(a)). Die Sekante von (a, f(a)) nach (a+h, f(a+h)) hat die Steigung

f(a+h)−f(a)

h .

Definition Die Funktionf heißtdifferenzierbar in agdw.

h→0lim

f(a+h)−f(a)

h existiert.

In diesem Fall wird dieser Grenzwert mitf⁰(a) bezeichnet und heißt dieAbleitung vonf ina.

Wir nennenf differenzierbargdw.f in jedem Punktaaus dem Definitions- bereich vonf differenzierbar ist.

Beispiel 5.1 Die Funktion f(x) =

x²sin¹_x f¨urx6= 0, 0 f¨urx= 0, ist in 0 differenzierbar, denn es gilt

h→0lim

f(h)−f(0)

h = lim

h→0

h²sin_h¹ h

= lim

h→0hsin 1 h

= 0.

5 Differenzierbarkeit 21

Figure 8: f(x) =x²sin_x¹ Also giltf⁰(0) = 0.

Eine inastetige Funktion braucht nicht inadifferenzierbar zu sein.

Beispiel 5.2 Die Funktion f(x) =

xsin_x¹ f¨ur x6= 0, 0 f¨ur x= 0,

ist in 0 stetig. Sie ist aber in anicht differenzierbar, denn es gilt f¨urh6= 0 f(h)−f(0)

h = hsin_h¹

h = sin1 h.

Wir haben aber bereits gezeigt, dass die Funktion sin¹_h in 0 keinen Grenzwert hat.

Obwohl nicht jede stetige Funktion differenzierbar ist, ist jede differenzier- bare Funktion stetig.

Satz 5.1 Wennf inadifferenzierbar ist, so istf auch in astetig.

Beweis.

h→0limf(a+h)−f(a) = lim

h→0

f(a+h)−f(a)

h ·h

= lim

h→0

f(a+h)−f(a)

h ·lim

h→0h

= f⁰(a)·0

= 0.

Man sieht aber sofort, dass

h→0limf(a+h)−f(a) = 0⇔ lim

x→af(x) =f(a).

Also istf inastetig. 2 Wir stellen nun die wichtigsten Ableitungsregeln zusammen, die Sie inCal- culus A gelernt haben.

Satz 5.2 (Ableitungsregeln) (a) (Ableitung von Summen) Sind f und g inadifferenzierbar, so ist auch f+g inadifferenzierbar und es gilt

(f+g)⁰(a) =f⁰(a) +g⁰(a).

(b) (Produktregel) Sind f und g in a differenzierbar, so ist auch f ·g in a differenzierbar und es gilt

(f ·g)⁰(a) =f⁰(a)·g(a) +f(a)·g⁰(a).

(c) (Quotientenregel)Sind f und g in adifferenzierbar und ist g(a)6= 0, so ist auch ^f_g ina differenzierbar und es gilt

f

g 0

(a) =f⁰(a)·g(a)−f(a)·g⁰(a) [g(a)]² .

(d) (Kettenregel)Istg inadifferenzierbar undf in g(a), so ist auchf◦g in adifferenzierbar und es gilt

(f ◦g)⁰(a) =f⁰(g(a))·g⁰(a).

(e) (Ableitung der Umkehrfunktion)Es seif eine auf einem Intervall definierte stetige injektive Funktion. Dann besitztf eine Umkehrfunktion f⁻¹. Wir nehmen an, dass f in f⁻¹(b) differenzierbar ist und dort die Ableitung f⁰(f⁻¹(b))6= 0 besitzt. Dann istf⁻¹ inb differenzierbar und es gilt

(f⁻¹)⁰(b) = 1 f⁰(f⁻¹(b)).

Istf differenzierbar, so k¨onnen wir eine neue Funktionf⁰ bilden.

Definition Es sei f eine differenzierbare Funktion, die auf einem Intervall (a, b) definiert ist. Dann heißt f stetig differenzierbar gdw. die Funktion f⁰ stetig ist. Istf⁰sogar differenzierbar, so sagt man,f istzweimal differenzierbar.

Die Ableitung von f⁰ wird dann die zweite Ableitung von f genannt und mit f⁰⁰ bezeichnet. Solange Differenzierbarkeit vorliegt, k¨onnen wir auch f⁰⁰⁰ usw.

bilden. Dien-te Ableitung schreibt manf⁽ⁿ⁾.

In Tabelle 1 sind die wichtigsten inCalculus Abetrachteten Funktionen und ihre Ableitungen zusammengestellt.

Bezeichnung Anstelle der Bezeichnungf⁰verwendet man auch die auf G. W. Leib- niz (1646–1716) zur¨uckgehende Schreibweise

dy

dx oder d dxf(x).

5 Differenzierbarkeit 23

Table 1: Funktionen ausCalculus Aund ihre Ableitungen

f D f⁰

e^x R e^x

lnx x >0 ¹_x

sinx R cosx

cosx R −sinx

tanx x6= ^π₂ +πk, k∈Z cos¹²x

cotx x6=πk, k∈Z _sin⁻¹²_x

arcsinx [−1,1] ^{√ 1}

1−x², x6=−1,1

arccosx [−1,1] ^√−1

1−x², x6=−1,1

arctanx R _1+x¹2

arccotx R _1+x⁻¹2

Die Ableitungf⁰(a) an einer Stelleadr¨uckt sich in dieser Schreibweise wie folgt

aus: dy(a)

dx . Die h¨oheren Ableitungen schreiben sich

d²y dx² = d

dx

dy

dx

, d³y dx³ = d

dx d²y

dx²

, usw.

oder d²

dx²[f(x)] = d dx

d

dx[f(x)]

, d³

dx³[f(x)] = d dx

d² dx²[f(x)]

, usw..

6 Die Bedeutung der Ableitung

Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung R¨uckschl¨usse ¨uber die Funktion f ziehen kann.

Zun¨achst besch¨aftigen wir uns mit Extremwerten.

Definition Es sei f eine Funktion und A eine Menge von Zahlen, die im Definitionsbereich vonf enthalten ist.

Ein Punktx∈A heißt eineMaximumstellevonf aufA gdw.

f(y)≤f(x) f¨ur alley∈A.

Die Zahlf(x) wird dann einMaximumvon f aufA genannt. Man sagt auch, f nimmt aufAsein Maximum inxan.

Ein Punktx∈A heißt eineMinimumstellevon f aufAgdw.

f(x)≤f(y) f¨ur alley∈A.

Die Zahlf(x) wird dann einMinimumvonf aufAgenannt. Man sagt auch,f nimmt aufAsein Minimum inxan.

Definition Es sei f eine Funktion und A eine Menge von Zahlen, die im Definitionsbereich von f enthalten ist. Ein Punkt x ∈ A heißt eine lokale Maximumstelle (Minimumstelle) f¨ur f auf A gdw. es ein δ >0 gibt, so dassx eine Maximumstelle (Minimumstelle) f¨urf auf

A∩(x−δ, x+δ) ist.

Satz 6.1 (Lokales Extremwertkriterium) Es sei f eine Funktion, die auf (a, b) definiert ist. Hat f in xeine lokale Maximum- oder Minimumstelle und istf in xdifferenzierbar, dann istf⁰(x) = 0.

Beweis. Wie betrachten den Fall, dass f eine lokale Maximumstelle in xhat.

Es seiδ >0 so gew¨ahlt, dassxeine Maximumstelle f¨urf auf (x−δ, x+δ) ist.

Dann gilt f¨ur allehmit |h|< δ

f(x+h)≤f(x), also

f(x+h)−f(x)≤0.

Wennh >0 ist, gilt daher

f(x+h)−f(x)

h ≤0,

also

lim

h→0⁺

f(x+h)−f(x)

h ≤0.

Andererseits gilt, wennh <0 ist,

f(x+h)−f(x)

h ≥0,