Mathematik f¨ur Ingenieure II Sommersemester 2014 W. Ebeling

Sommersemester 2014

W. Ebeling

Wolfgang Ebeling c

Institut f¨ ur Algebraische Geometrie Leibniz Universit¨ at Hannover Postfach 6009

30060 Hannover

E-mail: ebeling@math.uni-hannover.de

Kurven im R ⁿ

7.1 Ebene Kurven

Wir wollen nun Kurven in der Ebene betrachten.

Definition Eine ebene Kurve ist die L¨ osungsmenge einer Gleichung:

C = {(x, y) ∈ R

| F (x, y) = 0}.

Eine andere M¨ oglichkeit, Kurven zu beschreiben, ist eine Parameterdarstel- lung. Wir betrachten eine vektorwertige Funktion

~ r(t) =

x(t) y(t)

, (a ≤ t ≤ b).

L¨ asst man t variieren, so durchl¨ auft der Punkt ~ r(t) eine Kurve. Die Funktion

~ r(t) heißt Parameterdarstellung dieser Kurve, t der Parameter und [a, b] das Parameterintervall.

Kinematische Deutung

Man fasst t ∈ [a, b] als Zeit und ~ r(t) ∈ R

als Ort auf. Die Parameterdarstel- lung beschreibt dann die Bewegung eines Massenpunktes auf der Kurve.

Zu einer Kurve gibt es unendlich viele verschiedene Parameterdarstellun- gen, denn es k¨ onnen auf ihr ganz verschiedene Bewegungen stattfinden.

Beispiel 7.1.1 (1) Die Gerade durch die Punkte P

= (x

, y

) und P

= (x

, y

) (P

6= P

) hat die Gleichung

y − y

y

− y

= x − x

x

− x

⇔ (y

− y

)(x − x

) − (x

− x

)(y − y

) = 0.

3

Sie besitzt die Parameterdarstellung

~ r(t) =

x

+ t(x

− x

) y

+ t(y

− y

)

, (t ∈ R ).

(2) Der Kreis um P

= (x

, y

) vom Radius R hat die Gleichung (x − x

)

+ (y − y

)

= R

und die Parameterdarstellung

~ r(t) =

x

+ R cos t y

+ R sin t

, (0 ≤ t ≤ 2π).

(3) Kegelschnitte (in Hauptachsenlage):

x

a

+ y

b

= 1

a

b Ellipse

x

a

− y

b

= 1

a

b Hyperbel

Hier ist a, b > 0.

x

− y = 0 Parabel

Die Ellipse hat die Parameterdarstellung

~ r(t) =

a cos t b sin t

, (0 ≤ t ≤ 2π).

Abbildung 7.1: Die Ellipse als Kegelschnitt

Abbildung 7.2: Die Hyperbel als Kegelschnitt

(4) Ein Graph y = f (x) (a ≤ x ≤ b) besitzt die Parameterdarstellung

~ r(t) =

t f (t)

, (a ≤ t ≤ b).

Von einer Parameterdarstellung x = x(t), y = y(t), kann man im Allgemei- nen nur st¨ uckweise zu einer expliziten Darstellung y = f(x) oder x = g(y)

¨ ubergehen: Zum Beispiel beim Kreis gilt f¨ ur 0 ≤ t ≤ π, π ≤ t ≤ 2π:

y = y

+ p

R

− (x − x

)

(0 ≤ t ≤ π), y = y

− p

R

− (x − x

)

(π ≤ t ≤ 2π).

(5) Zykloiden: L¨ asst man einen Kreis K vom Radius R auf der x-Achse

abrollen, so beschreibt ein Punkt P auf K, der vom Kreismittelpunkt M den

Abbildung 7.3: Die Parabel als Kegelschnitt Abstand a hat, eine Zykloide (oder Radkurve). Bild f¨ ur a = R:

0 Rt 2πR

M R t P

Sie besitzt eine Parameterdarstellung

~ r(t) =

Rt − a sin t R − a cos t

, (0 ≤ t ≤ ∞).

Denn nach dem Abrollen um den Winkel t liegt M in (x

, y

) = (Rt, R) und P in (x(t), y(t)) mit

x(t) = x

− a sin t = Rt − a sin t, y(t) = y

− a cos t = R − a cos t.

Eine Epizykloide entsteht, wenn der Kreis nicht auf der x-Achse, sondern auf dem Kreis x

+ y

= ρ

abrollt. Sie hat die Parameterdarstellung

~ r(t) =

(ρ + R) cos t − a cos

t (ρ + R) sin t − a sin

t

a = R =

Spezialfall: ρ = R = a: Herzlinie (Kardiode)

a = R = ρ

Eine Hypozykloide entsteht beim Abrollen in Innern des Kreises. Sie hat die Parameterdarstellung

~ r(t) =

(ρ − R) cos t + a cos

t (ρ − R) sin t − a sin

t

a = R =

Spezialfall: a = R =

: Astroide

a = R =

Es sei

~ r(t) =

x(t) y(t)

die Parameterdarstellung einer Kurve K. Wir setzen nun voraus, dass x(t), y(t) differenzierbare Funktionen sind.

Definition Der Vektor

~ ˙

r(t) := lim

h→0

~ r(t + h) − ~ r(t)

h =

x(t) ˙

˙ y(t)

heißt der Tangentialvektor an K zum Parameterwert t.

Geometrische Deutung

~ r(t) l¨ ˙ asst sich als Limes von Sekantenvektoren auffassen.

Kinematische Deutung

Beschreibt ~ r(t) die Bewegung eines Massenpunktes, dann ist ˙ ~ r(t) der mo- mentane Geschwindigkeitsvektor zum Zeitpunkt t.

Ist der Vektor

~ r(t) = ˙

x(t) ˙

˙ y(t)

vom Nullvektor verschieden, so gibt der Vektor

~ n(t) :=

− y(t) ˙

˙ x(t)

die positive Normalenrichtung in diesem Punkt an.

Definition Die Parameterdarstellung ~ r(t) =

x(t) y(t)

, (a ≤ t ≤ b) einer Kurve heißt regul¨ ar, wenn die Funktionen x(t), y(t) ¨ uber [a, b] stetig diffe- renzierbar sind und ˙ x(t)

+ ˙ y(t)

6= 0 f¨ ur t ∈ [a, b] gilt ( ˙ x(a), ˙ x(b) einseitige Ableitungen).

Satz 7.1.1 (Bogenl¨ ange) (a) Die L¨ ange eines Kurvenbogens mit regul¨ arer Parameterdarstellung ~ r(t) =

x(t) y(t)

, a ≤ t ≤ b, betr¨ agt

L = Z

a

| ~ r(t)|dt ˙ = Z

a

p x(t) ˙

+ ˙ y(t)

dt

(b) Die Bogenl¨ ange des Graphen y = f(x) einer stetig differenzierbaren Funktion f : [a, b] → R betr¨ agt

L = Z

a

p 1 + f

(x)

dx

Beispiel 7.1.2 (1) Der Kreisumfang: Ein Kreis vom Radius R hat die L¨ ange L =

Z

p R

sin

t + R

cos

tdt = Z

0

Rdt = 2πR.

(2) Die Bogenl¨ ange der Ellipse x

a

+ y

b

= 1 : Sie hat die Parameterdarstellung

~ r(t) =

a cos t b sin t

, (0 ≤ t ≤ 2π).

F¨ ur die L¨ ange ergibt sich

L =

Z

p a

sin

t + b

cos

tdt

= a Z

0

s 1 −

1 − b

a

cos

tdt

= 4a Z

0

√ 1 − k

cos

tdt mit k :=

√ a

− b

a

Die Zahl k nennt man auch die numerische Exzentrizit¨ at der Ellipse. Durch die Substitution τ =

−t (beachte sin

τ = cos

τ) erh¨ alt man die Bogenl¨ ange der Ellipse in der Form (τ wieder durch t ersetzt)

L = 4aE(k) mit E(k) :=

Z

0

p 1 − k

sin

tdt.

E(k) ist ein elliptisches Integral zweiter Gattung und nicht elementar inte- grierbar.

(3) Der Zykloidenbogen x = R(t − sin t), y = R(1 − cos t) (0 ≤ t ≤ 2π) (a = R) hat die L¨ ange

L = R Z

0

q

(1 − cos t)

+ sin

tdt = 2R Z

0

sin t

2 dt = 8R.

Es sei

~ r(t) =

x(t) y(t)

eine regul¨ are Parameterdarstellung, a ≤ t ≤ b, mit zweimal differenzierbaren Funktionen x(t), y(t). Es sei

ϕ(t) := Winkel zwischen x-Achse und Tangentialvektor ˙ ~ r(t) =

x(t) ˙

˙ y(t)

s(t) :=

Z

p x(τ ˙ )

+ ˙ y(τ )

dτ

(L¨ ange des Kurvenbogens ¨ uber dem Intervall [a, t])

Die ¨ Anderung ∆ϕ der Tangentenrichtung bezogen auf die ¨ Anderung ∆s der Bogenl¨ ange ¨ uber dem Intervall [t, t + ∆t], also

, ist ein Maß f¨ ur die durch- schnittliche Kr¨ ummung des Kurvenbogens ¨ uber diesem Teilintervall.

Definition Die Zahl

κ(t) := lim

∆t→0

∆ϕ

∆s = ϕ(t) ˙

˙ s(t)

heißt die Kr¨ ummung der Kurve im Punkt P (t) = (x(t), y(t)).

Satz 7.1.2 (a) Die Kr¨ ummung einer Kurve mit zweimal stetig differen- zierbarer regul¨ arer Parameterdarstellung ~ r(t) =

x(t) y(t)

, a ≤ t ≤ b, in P (t) = (x(t), y(t)) betr¨ agt

κ(t) = x(t)¨ ˙ y(t) − y(t)¨ ˙ x(t) p ( ˙ x(t)

+ ˙ y(t)

)

(b) Die Kr¨ ummung des Graphen y = f (x) einer zweimal differenzierbaren Funktion f : [a, b] → R im Punkt (x, f(x)) betr¨ agt

κ(x) = f

(x)

p (1 + f

(x)

)

Wegen ˙ s = p

˙

x

+ ˙ y

> 0 haben κ und ˙ ϕ dasselbe Vorzeichen. Aus I, Satz 4.4.6, folgt

κ > 0 ⇒ ϕ w¨ achst ⇒ Linkskr¨ ummung κ < 0 ⇒ ϕ f¨ allt ⇒ Rechtskr¨ ummung Beispiel 7.1.3 Kr¨ ummung der Ellipse:

x y

=

a cos t b sin t

,

x ˙

˙ y

=

−a sin t b cos t

,

x ¨

¨ y

=

−a cos t

−b sin t

,

κ = x¨ ˙ y − y¨ ˙ x

p ( ˙ x

+ ˙ y

)

= ab(sin

t + cos

t)

p (a

sin

t + b

cos

t)

= ab

p (a

sin

t + b

cos

t)

. Spezialfall: a = b = R: κ =

.

Beispiel 7.1.4 Kr¨ ummung der Parabel y = x

: κ = y

p (1 + y

)

= 2 p (1 + 4x

)

.

Definition Es sei P = (x(t), y(t)) ein Kurvenpunkt. Der zu P geh¨ orige Kr¨ ummungskreis ist der durch P gehende Kreis mit derselben Kr¨ ummung und Tangentenrichtung in P wie die Kurve. Der Radius r des Kr¨ ummungskrei- ses in P heißt der Kr¨ ummungsradius der Kurve in P .

Falls κ 6= 0 ist, gilt nach Beispiel 7.1.3 r = 1

|κ|

Der Mittelpunkt (x

, y

) des Kr¨ ummungskreises liegt auf der Normalen im Abstand

von P und hat die Koordinaten

x

= x(t) − 1 κ

˙ y(t)

p x(t) ˙

+ ˙ y(t)

= x − y ˙ x ˙

+ ˙ y

˙

x¨ y − y ˙ x ¨ y

= y(t) + 1

κ

˙ x(t)

p x(t) ˙

+ ˙ y(t)

= y + ˙ x x ˙

+ ˙ y

˙

x¨ y − y¨ ˙ x

Durchl¨ auft t das Parameterintervall, dann durchl¨ auft (x

, y

) eine Kurve,

die Evolute der gegebenen Kurve genannt wird.

Beispiel 7.1.5 Evolute der Parabel x = t, y = t

: x

= t − 2t 1 + 4t

2 = −4t

y

= t

+ 1 + 4t

2 = 3t

+ 1 2 Diese Kurve heißt Neilsche Parabel.

Statt in kartesischen Koordinaten kann man eine Kurve auch in Polarko- ordinaten darstellen und den Winkel als Parameter nehmen.

Die Umrechnungsformeln kartesische Koordinaten ↔ Polarkoordinaten lauten

(a) x = r cos ϕ, y = r sin ϕ (b) r = p

x

+ y

, ϕ =







arccos

, falls y ≥ 0, 2π − arccos

, falls y < 0

unbestimmt, falls r = 0.

Lassen wir einen Zeiger, der sich um den Nullpunkt dreht und seine L¨ ange ver¨ andern kann, auf einer Kurve laufen, so hat er beim Winkel ϕ die L¨ ange r(ϕ). Die Polarkoordinaten des entsprechenden Kurvenpunktes sind (r(ϕ), ϕ), (α ≤ ϕ ≤ β).

Definition Die Darstellung

r = r(ϕ), α ≤ ϕ ≤ β,

heißt Polardarstellung der Kurve. Die x-Achse heißt Polarachse.

Die Parameterdarstellung der Kurve r = r(ϕ), α ≤ ϕ ≤ β, mit dem Winkel ϕ als Parameter lautet:

ϕ 7→

r(ϕ) cos ϕ r(ϕ) sin ϕ

(α ≤ ϕ ≤ β)

Mit dieser Parameterdarstellung kann man Tangentialvektoren, Bogenl¨ ange, Kr¨ ummung usw. berechnen. Insbesondere folgt aus Satz 7.1.1(a) f¨ ur die Bo- genl¨ ange der Kurve r = r(ϕ), α ≤ ϕ ≤ β

L = Z

α

s

r(ϕ)

+

dr(ϕ) dϕ

dϕ

Beispiel 7.1.6 (1) Polardarstellung eines Kreises vom Radius c um 0: r = c.

(2) Die Archimedische Spirale hat die Polardarstellung r = aϕ (a > 0, 0 ≤ ϕ < ∞).

Die Bogenl¨ ange nach einem Umlauf betr¨ agt:

L =

Z

p (aϕ)

+ a

dϕ

= a Z

0

p ϕ

+ 1dϕ Substitution: ϕ = sinh t, dϕ = cosh t

= a

Z

cosh

tdt

= a 2

2π p

1 + (2π)

+ ln(2π + p

1 + (2π)

)

.

(3) Die Herzlinie hat die Polardarstellung

r = a(1 + cos ϕ) (a > 0, 0 ≤ ϕ ≤ 2π).

(Zugeh¨ orige Parameterdarstellung:

ϕ 7→

2

+

(2 cos ϕ + cos 2ϕ)

a

2

(2 sin ϕ + sin 2ϕ)

(0 ≤ ϕ ≤ 2π)

Bogenl¨ ange:

L = a Z

0

q

(1 + cos ϕ)

+ sin

ϕdϕ = 8a.

Wir wollen nun Sektorfl¨ achen ¨ uber Kurvenst¨ ucken betrachten. Es sei t 7→

x(t) y(t)

, a ≤ t ≤ b,

eine st¨ uckweise stetig differenzierbare Parameterdarstellung eines ebenen Kur- venst¨ ucks K , das von jedem Ursprungsstrahl h¨ ochstens einmal getroffen wird.

Dann besitzt K eine Polardarstellung r = r(ϕ), α ≤ ϕ ≤ β, so dass jedem Winkel ϕ h¨ ochstens ein Parameterwert t entspricht. Wir betrachten dann die von K begrenzte Sektorfl¨ ache.

Satz 7.1.3 (Leibnizsche Sektorformel) Der Inhalt der durch K begrenz- ten Sektorfl¨ ache betr¨ agt

F = 1 2

Z

[x(t) ˙ y(t) − y(t) ˙ x(t)]dt

Satz 7.1.4 (Sektorformel in Polarkoordinaten) Der Inhalt der durch K begrenzten Sektorfl¨ ache betr¨ agt in Polarkoordinaten

F = 1 2

Z

r(ϕ)

dϕ

Beispiel 7.1.7 (1) Der Fl¨ acheninhalt des Ellipsensektors t 7→

a cos t b sin t

0 ≤ t ≤ π 2

betr¨ agt nach der Leibnizschen Sektorformel:

F

= 1 2

Z

0

[ab cos

t + ab sin

t]dt = ab π

4 .

Also ist der Fl¨ acheninhalt der Ellipse gleich F = abπ.

(2) F¨ ur 0 ≤ ϕ ≤ 2π begrenzt die Archimedische Spirale r = aϕ eine Sektor- fl¨ ache mit dem Inhalt

F = 1 2

Z

a

ϕ

dϕ = 4 3 a

π

.

7.2 Kurven im R ⁿ

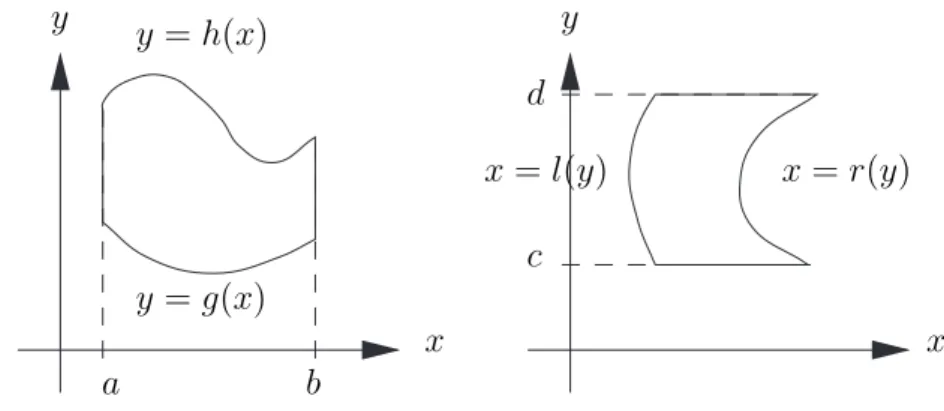
F¨ ur ebene Kurven haben wir verschiedene Darstellungsarten kennengelernt:

• abschnittsweise explizite Darstellung als Graph y = f(x) einer Funkti- on

• implizite Darstellung F (x, y) = 0

• Parameterdarstellung t 7→

x(t) y(t)

• Polardarstellung r = r(ϕ)

F¨ ur die allgemeine Behandlung von Kurven, insbesondere auch von Raum- kurven, eignet sich am besten die Parameterdarstellung.

Wir betrachten nun eine auf einem Intervall I ⊆ R erkl¨ arte vektorwertige Funktion

~ x : I −→ R

t 7−→ ~ x(t) =









 x

(t) x

(t)

.. . x

(t)











Die Funktionen x

: I → R , t 7→ x

(t), heißen die Komponentenfunktionen von ~ x(t).

Die grundlegenden Begriffe der Analysis lassen sich nun auf solche Funk- tionen verallgemeinern, indem man sie komponentenweise erkl¨ art:

Definition

t→t

lim









 x

(t) x

(t)

.. . x

(t)











=









 c

c

.. . c











:⇔ lim

t→t₀

x

(t) = c

(1 ≤ i ≤ n)

Definition Eine Funktion ~ x : I → R

heißt

stetig

differenzierbar

in t

∈ I auf I

:⇔ alle Komponentenfunktionen sind

stetig

differenzierbar

in t

∈ I auf I

.

~ ˙

x(t) = d

dt ~ x(t) := lim

h→0

1

h [~ x(t + h) − ~ x(t)] =











˙ x

(t)

˙ x

(t)

.. .

˙ x

(t)











Wie im ebenen Fall heißt ˙ ~ x(t) der Tangentialvektor von ~ x an der Stelle t ∈ I.

Die geometrische und kinematische Interpretation ist die gleiche wie im Fall von ebenen Kurven.

Man hat folgende

Ableitungsregeln (~ x, ~ y : I → R

, α, β ∈ R ) (a) d

dt (α~ x(t) + β~ y(t)) = α ~ x(t) + ˙ β ~ y(t) (Linearit¨ ˙ at).

(b) d

dt [~ x(t) · ~ y(t)] = ˙ ~ x(t) · ~ y(t) + ~ x(t) · ~ y(t) (Produktregel f¨ ˙ ur das Skalarpro- dukt)

(c) n = 3: d

dt [~ x(t) × ~ y(t)] = ˙ ~ x(t) × ~ y(t) + ~ x(t) × ~ y(t) (Produktregel f¨ ˙ ur das Vektorprodukt)

(d) d

dt [α(t)~ y(t)] = ˙ α(t)~ y(t) + α(t) ˙ ~ y(t) (Produktregel f¨ ur die Multiplikation mit einer skalaren Funktion).

Ubungsaufgabe 7.2.1 ¨ Man zeige

|~ x(t)| = const. f¨ ur t ∈ I ⇒ ~ x(t) ⊥ ~ x(t) f¨ ˙ ur t ∈ I.

Beweis.

|~ x(t)| = const. ⇒ ~ x(t) · ~ x(t) = |~ x(t)|

= const.

⇒ d

dt ~ x(t) · ~ x(t) = 2 ˙ ~ x(t) · ~ x(t) = 0

⇒ ~ x(t) ˙ ⊥ ~ x(t)

2

Definition Ein Kurvenst¨ uck im R

ist eine stetig differenzierbare Funktion

~ x : [a, b] → R

oder auch das Bild {~ x(t) | a ≤ t ≤ b} einer solchen Funktion.

Der Punkt ~ x(a) heißt Anfangspunkt, ~ x(b) Endpunkt des Kurvenst¨ ucks. Ein Kurvenst¨ uck ~ x heißt regul¨ ar, wenn ˙ ~ x(t) 6= ~ 0 f¨ ur alle t ∈ [a, b] gilt. Ein Punkt

~ x(t) mit ˙ ~ x(t) = ~ 0 heißt singul¨ arer Punkt des Kurvenst¨ ucks.

Es sei nun ~ x : [a, b] → R

ein regul¨ ares Kurvenst¨ uck im R

, t ∈ [a, b]. F¨ ur die Bogenl¨ ange des Kurvenst¨ ucks ¨ uber [a, b] gilt:

s(t) = Z

a

~ ˙ x(t)

dt.

Nach dem Hauptsatz der Differential- und Integralrechnung gilt ds

dt = ˙ s(t) =

~ ˙ x(t)

.

Definition Es sei nun ~ x hinreichend oft differenzierbar. Wir definieren nun T ~ (t) := 1

~ x(t) ˙

~ ˙

x(t) Tangenten(einheits)vektor

F¨ ur T ~ ˙ (t) 6= ~ 0 setzen wir N ~ (t) := 1

~ ˙ T (t)

~ ˙

T (t) Hauptnormalen(einheits)vektor

B ~ (t) := T ~ (t) × N ~ (t) Binormalen(einheits)vektor

Nach der obigen ¨ Ubungsaufgabe stehen die Vektoren N ~ (t) und T ~ (t) zu jeder Parameterstelle t senkrecht aufeinander. Deswegen bildet

( T ~ (t), ~ N (t), ~ B(t))

eine Orthonormalbasis des R

. Man nennt dieses Tripel von Vektoren das begleitende Dreibein der Kurve an der Parameterstelle t. Die von T ~ (t) und N ~ (t) aufgespannte Ebene durch ~ x(t),

~ r = ~ x(t) + λ ~ T (t) + µ ~ N (t), λ, µ ∈ R ,

heißt die Schmiegebene der Kurve zum Parameterwert t. Sie ist der Grenzwert der Ebenen durch ~ x(t) und zwei weitere Kurvenpunkte.

Die Kr¨ ummung einer ebenen Kurve hatten wir eingef¨ uhrt als die ¨ Anderung der Tangentenrichtung bezogen auf die ¨ Anderung ∆s der Bogenl¨ ange. Die Anderung der Tangentenrichtung wurde in diesem Fall durch die ¨ ¨ Anderung des Winkels der Tangente ∆ϕ gegeben. Im allgemeinen Fall m¨ ussen wir die Anderung des Tangentenvektors ¨

∆ T ~ = T ~ (t + ∆t) − T ~ (t) auf dem Intervall [t, t + ∆t] betrachten. Wir definieren Definition

∆t→0

lim 1

∆s ∆ T ~ = 1

˙ s(t)

~ ˙

T (t) Kr¨ ummungsvektor

κ(t) := 1

˙ s(t)

~ ˙ T (t)

=

~ ˙ T (t)

~ x(t) ˙

Kr¨ ummung

F¨ ur die Darstellung von ˙ ~ x und ¨ ~ x im begleitenden Dreibein ( T , ~ ~ N , ~ B) erh¨ alt man

~ ˙ x(t) =

~ x(t) ˙

T ~ (t) = ˙ s(t) T ~ (t)

~ ¨

x(t) = d

dt ( ˙ s(t) T ~ (t))

= ¨ s(t) T ~ (t) + ˙ s(t) T ~ ˙ (t) = ¨ s(t) T ~ (t) + ˙ s(t)

~ ˙ T (t)

N(t) ~

= ¨ s(t) T ~ (t) + ˙ s(t)

κ(t) N ~ (t),

also

~ ˙

x(t) = s(t) ˙ T ~ (t)

~ ¨

x(t) = ¨ s(t) T ~ (t) + ˙ s(t)

κ(t) N ~ (t) Kinematische Deutung

~ x : [a, b] → R

beschreibt die Bewegung eines Massenpunktes

• ~ x(t) = ˙ ˙ s(t) T ~ (t) Geschwindigkeitsvektor, tangential zur Bahn

•

~ x(t) ˙

= ˙ s(t) Momentangeschwindigkeit

Die Vektoren ˙ ~ x(t) und ¨ ~ x(t) haben bez¨ uglich der Basis ( T , ~ ~ N ) der Schmieg- ebene die Koordinaten

~ ˙ x(t) =

s(t) ˙ 0

, ~ x(t) = ¨

s(t) ¨

˙

s(t)

κ(t)

. Satz 7.1.2 ergibt f¨ ur die Kr¨ ummung in der Schmiegebene

κ

(t) = s(t) ˙ · s(t) ˙

κ(t) − 0 · s(t) ¨

p ( ˙ s(t)

)

= κ(t).

Es folgt 1

κ(t) = Radius eines Kr¨ ummungskreises in der Schmiegebene Weiter berechnen wir

~ x(t) ˙ × ~ x(t) = ¨

˙

s(t) T ~ (t)

×

¨

s(t) T ~ (t) + ˙ s(t)

κ(t) N ~ (t)

= s(t)¨ ˙ s(t) T ~ (t) × T ~ (t) + ˙ s(t)

κ(t) T ~ (t) × N ~ (t)

= s(t) ˙

κ(t) B ~ (t)

~ x(t) ˙ × ~ x(t) ¨

= s(t) ˙

κ(t) (da

B(t) ~ = 1) Also folgt

κ(t) =

~ ˙

x(t) × ~ x(t) ¨

~ ˙ x(t)

3

B(t) = ~ 1

~ x(t) ˙ × ~ x(t) ¨

~ ˙

x(t) × ~ x(t) ¨ (falls

~ ˙

x(t) × ~ x(t) ¨

6= 0)

F¨ ur eine ebene Kurve

~ x(t) =



 x(t) y(t) 0



 ergibt die Formel f¨ ur κ

κ =





˙ x

˙ y 0



 ×





¨ x

¨ y 0





p ( ˙ x

+ ˙ y

)

= | x¨ ˙ y − y¨ ˙ x|

p ( ˙ x

+ ˙ y

)

Dies ist bis auf das Vorzeichen die Formel von Satz 7.1.2(a). (Nur falls ˙ x¨ y −

˙

y¨ x > 0 haben ~ n und N ~ die gleiche Richtung!)

Aufgrund der Formel f¨ ur B ~ (t) bestimmt man das begleitende Dreibein ( T , ~ ~ N , ~ B) in der Reihenfolge

T ~ = 1

~ ˙ x

~ ˙ x,

B ~ = 1

~ ˙ x × ~ x ¨

~ ˙ x × ~ x, ¨ N ~ = B ~ × T . ~

Bei Raumkurven kommt zus¨ atzlich zu der Kr¨ ummung eine weitere Gr¨ oße ins Spiel, die Torsion. Sie beschreibt das Herauswinden der Kurve aus der Schmiegebene. Dies wird durch die ¨ Anderungsrate des Binormalenvektors, bezogen auf die Bogenl¨ ange, gemessen:

Definition Der Vektor

∆t→0

lim 1

∆s [ B(t ~ + ∆t) − B(t)] = ~ 1

˙ s(t)

~ ˙ B(t) heißt der Torsionsvektor.

Nach der ¨ Ubungsaufgabe ist wegen | B(t)| ~ = 1 der Vektor B ~ ˙ orthogonal zu B. Aus ~

~ ˙ B = d

dt ( T ~ × N ~ ) = T ~ ˙ × N ~ + T ~ × N ~ ˙ = T ~ × N ~ ˙ folgt auch B ~ ˙ ⊥ T ~ , also B ~ ˙ k N ~ . Deshalb gibt es ein τ(t) mit

1

˙ s(t)

~ ˙

B(t) = −τ (t) N ~ (t).

Definition Die Zahl τ(t) heißt die Torsion der Kurve zum Parameterwert t.

Es gilt

τ = − 1

˙ s

~ ˙ B · N ~

= 1

˙ s

B ~ · N ~ ˙ ( B ~ · N ~ = 0 ⇒ B ~ ˙ · N ~ + B ~ · N ~ ˙ = 0)

= 1

˙ s

B ~ · 1

˙ s

κ

...

~ x

aus d dt

~ ¨ x = d

dt (¨ s ~ T + ˙ s

κ ~ N )

=



 1

˙ s

1

~ x ˙ × ~ x ¨

~ ˙ x × ~ x ¨



 · 1

˙ s

κ

...

~ x

=

h ~ x, ˙ ~ x, ¨ ...

~ x i

~ x ˙ × ~ x ¨

2

Also erhalten wir

τ (t) =

h ~ x(t), ˙ ~ x(t), ¨ ...

~ x (t) i

~ ˙

x(t) × ~ x(t) ¨

2

Wir fassen die Resultate in einem Satz zusammen

Satz 7.2.1 Eine dreimal stetig differenzierbare Kurve ~ x : [a, b] → R

besitzt f¨ ur jeden Parameterwert t mit ~ x ˙ × ~ x(t) ¨ 6= 0

Tangentenvektor T ~ (t) = 1

~ ˙ x(t)

~ ˙ x(t) Binormalenvektor B ~ (t) = 1

~ ˙

x(t) × ~ x(t) ¨

~ x(t) ˙ × ~ x(t) ¨ Hauptnormalenvektor N ~ (t) = B(t) ~ × T ~ (t)

Kr¨ ummung κ(t) =

~ ˙

x(t) × ~ x(t) ¨

~ ˙ x

3

Torsion τ (t) =

h ~ x(t), ˙ ~ x(t), ¨ ...

~ x (t) i

~ ˙

x(t) × ~ x(t) ¨

2

Beispiel 7.2.1 (Schraubenlinie) Die neutrale Faser einer Schraubenfeder ist eine Schraubenlinie und besitzt die Parameterdarstellung

~ x(t) =





r cos t r sin t

ht



 (0 ≤ t ≤ 2πn)

(r Radius, 2πh Gangh¨ ohe, n Windungszahl).

x y

2πh r

z

Es gilt

~ x(t) = ˙





−r sin t r cos t

h



 , ~ x(t) = ¨





−r cos t

−r sin t 0



 , ...

~ x =





r sin t

−r cos t 0



 .

Wir setzen zur Abk¨ urzung

R :=

~ ˙ x(t)

= √

r

+ h

Damit errechnet man T ~ (t) = 1

R





−r sin t r cos t

h





~ ˙

x(t) × ~ x(t) = ¨





−r sin t r cos t

h



 ×





−r cos t

−r sin t 0



 =





rh sin t

−rh cos t r





B(t) = ~ 1 R





h sin t

−h cos t r





N ~ (t) = 1 R





h sin t

−h cos t r



 ×





−r sin t r cos t

h



 =





− cos t

− sin t 0



 κ(t) = r

r

+ h

τ (t) = 1

r

(r

+ h

)

−r sin t −r cos t r sin t r cos t −r sin t −r cos t

h 0 0

= h

r

+ h

Man beachte, dass κ(t) und τ (t) konstant sind.

Funktionen mehrerer Ver¨ anderlicher

8.1 Differentiation

Wir wollen nun Funktionen mehrerer Ver¨ anderlicher betrachten.

Es sei D ⊆ R

. Eine reellwertige Funktion ist eine Funktion

f : D −→ R

~ x =









 x

x

.. . x











7−→ f (~ x) = f (x

, . . . , x

) =: z

Eine reellwertige Funktion f : D → R wird auch als Skalarenfeld bezeichnet (einem ~ x ∈ D wird eine skalare physikalische Gr¨ oße, z.B. H¨ ohe, Temperatur, zugeordnet).

Die Funktion f kann gegeben sein

• durch eine explizite Vorschrift, z.B. f (x, y) = 3 − x

.

• durch eine implizite Gleichung, z.B. f (x, y) ist die positive L¨ osung von x

+ y

+ z

= 1 (D = {(x, y) ∈ R

| x

+ y

< 1})

Der Graph von f : D → R ist die Menge

Γ

:= {(~ x, z) ∈ D × R | z = f(~ x)} ⊆ R

.

Um eine Funktion f : D → R zu beschreiben, betrachtet man auch

25

• die Niveaumengen (Niveaukurven, Niveaufl¨ achen) von f zum Niveau c ∈ R :

N

:= {~ x ∈ D | f (~ x) = c}.

• die ”partiellen” Funktionen

x

7→ f (a

, . . . , a

, x

, a

, . . . , a

)

mit ~a = (a

, . . . , a

)

∈ D (definiert auf einer zu der i-ten Koordina- tenachse parallelen Geraden).

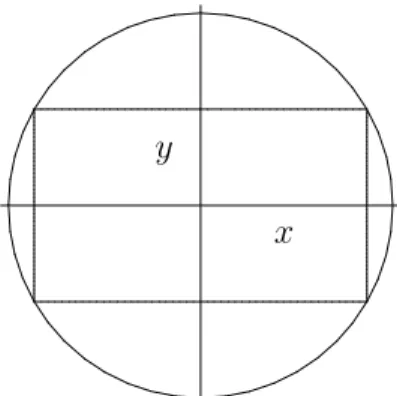
Anschauliche Darstellung im Fall n = 2

Im Fall n = 2 schreiben wir auch f(x, y). Der Graph Γ

= {(x, y, z) ∈ R

| z = f (x, y)} ⊆ R

ist eine Fl¨ ache im R

. Sie wird beschrieben durch

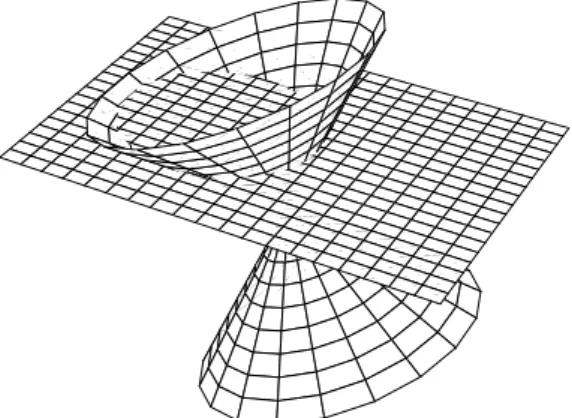
(a) Blockbild (b) H¨ ohenkarte (a) Blockbild

Beispiel: f(x, y) = 3 − x

auf D = {(x, y) ∈ R

| |x| ≤ 1, |y| ≤ 1}

y

x

Zur Erstellung eines Blockbildes muss man die Graphen der partiellen Funk-

tionen z = f (a

, y) bzw. z = f (x, a

) bestimmen.

(b) H¨ ohenkarte

Beispiel: f (x, y) = 1 − x

− y

x y

Die Funktion kann auch durch ihre Niveaukurven N

= {(x, y) ∈ D | f (x, y) = c} (H¨ ohenlinien einer Landkarte) veranschaulicht werden.

Wir wollen nun Grenzwerte solcher Funktionen betrachten. Dazu brau- chen wir ein Maß f¨ ur den Abstand zweier Punkte des R

.

Der Abstand zweier Punkte ~ x, ~ y ∈ R

ist definiert durch

|~ x − ~ y| = v u u t

n

X

i=1

(x

− y

)

.

Die Definitionsmengen von Funktionen einer Ver¨ anderlichen waren meistens Intervalle. Dabei machte es f¨ ur viele Betrachtungen einen Unterschied, ob wir uns im Innern des Intervalls oder in einem Randpunkt befanden. Zur Beschreibung der Definitionsmengen im R

brauchen wir einige topologische Begriffe.

Definition Es sei ~a ∈ R

, ε > 0. Die Menge

U

(~a) := { ~ x ∈ R

| |~ x − ~a| < ε}

heißt ε-Umgebung von ~a.

Beispiel 8.1.1 n = 1: U

(a) := (a − ε, a + ε)

n = 2: U

(~a) ist eine Kreisscheibe vom Radius ε um ~a ohne Rand.

n = 3: U

( ~a) ist eine Kugel um ~a vom Radius ε ohne Punkte auf der Ober-

fl¨ ache.

Definition Es sei D ⊆ R

.

(a) Ein Punkt ~a ∈ D heißt innerer Punkt von D, wenn es eine ε-Umgebung von ~a gibt, die ganz in D enthalten ist.

(b) D heißt offen, wenn jeder Punkt von D ein innerer Punkt ist.

(c) Ein ~b ∈ R

heißt Randpunkt von D, wenn jede ε-Umgebung U

( ~b) von ~b mindestens einen Punkt aus D und mindestens einen Punkt nicht aus D enth¨ alt.

(d) Die Menge aller Randpunkte von D heißt Rand von D, in Zeichen ∂D.

(e) D heißt abgeschlossen, wenn sie alle ihre Randpunkte enth¨ alt.

(f) D heißt beschr¨ ankt, wenn es eine Konstante K > 0 gibt mit

|~ x| < K f¨ ur alle ~ x ∈ D.

(g) D heißt kompakt, wenn D beschr¨ ankt und abgeschlossen ist.

Beispiel 8.1.2 Die Kreisscheibe (ohne Rand)

K

= {(x, y) ∈ R

| (x − x

)

+ (y − y

)

< r

} ist eine offene Menge. Rand:

∂K

= {(x, y) ∈ R

| (x − x

)

+ (y − y

)

= r

}.

Die Menge

K = K

∪ ∂K

= {(x, y) ∈ R

| (x − x

)

+ (y − y

)

≤ r

} ist abgeschlossen und beschr¨ ankt, also kompakt.

Warnung Es gibt Mengen, die weder offen noch abgeschlossen sind, z.B.

halboffene Intervalle, R = {(x, y) ∈ R

| 0 ≤ x < 1, 0 ≤ y ≤ 1}.

Definition Eine Folge (~ x

)

, ~ x

∈ R

, heißt konvergent gegen ~a ∈ R

, in Zeichen

k→∞

lim ~ x

= ~a oder ~ x

→ ~a f¨ ur k → ∞, wenn gilt:

k→∞

lim |~ x

− ~a| = 0.

Beispiel 8.1.3 Die Folge

~ x

=

k

cos

2π k

sin

liegt auf der Archimedischen Spirale und konvergiert gegen 0.

Definition Es sei D ⊆ R

, f : D → R , ~a ∈ D ∪ ∂D.

(a) f hat in ~a den Grenzwert c ∈ R , in Zeichen lim

~x→~a

f (~ x) = c oder f(~ x) → c f¨ ur ~ x → ~a,

wenn f¨ ur jede Folge (~ x

)

aus D mit ~ x

→ ~a und ~ x

6= ~a f¨ ur alle k die Folge (f (~ x

))

gegen c strebt.

(b) f heißt stetig in ~a ∈ D :⇔ lim

~x→~a

f(~ x) = f(~a).

(c) f heißt stetig auf D, wenn f in jedem ~a ∈ D stetig ist.

Da die Definitionen v¨ ollig analog zu den Definitionen im Fall einer Va- riablen sind, ¨ ubertragen sich die Rechenregeln f¨ ur Grenzwerte und stetige Funktionen aus Kapitel 3. Insbesondere sind Summe, Produkt, Quotient ste- tiger Funktionen stetig.

Beispiel 8.1.4 Die Projektionen

p

: R

−→ R

~ x =













 x

.. . x

.. . x















7−→ x

sind stetig und damit auch jedes Polynom in n Variablen p(~ x) = X

0≤ki≤m .. . 0≤kn≤m

α

x

x

· · · x

(z.B. p(x, y) = α

x + α

y + α

x

+ α

xy + α

y

).

Warnung Die Stetigkeit von f (x, y ) ergibt sich nicht aus der Stetigkeit der partiellen Funktionen x 7→ f (x, y

), y 7→ f(x

, y). Gegenbeispiel:

f : R

−→ R

x y

7−→ f(x, y) :=







2xy

x

+ y

, (x, y) 6= (0, 0) 0, (x, y) = (0, 0) Es gilt

f (x, 0) = f(0, y) = 0, f(x, x) = 1, f(x, −x) = −1.

Bei Ann¨ aherung von ~ 0 auf der x- oder y-Achse ergibt sich als Grenzwert 0, bei Ann¨ aherung auf den Geraden y = x und y = −x der Grenzwert 1 bzw.

−1. Also ist f nicht stetig in 0.

Wir kommen nun zur Frage der Differenzierbarkeit von Funktionen meh- rerer Ver¨ anderlicher.

Definition Es sei D ⊆ R

offen, f : D → R , ~a =





 a

.. . a





 ∈ D. Wir betrachten die partielle Funktion

x

7→ f(a

, . . . , a

, x

, a

, . . . , a

).

Existiert die Ableitung dieser Funktion an der Stelle x

= a

, so nennt man diese die partielle Ableitung von f nach x

in ~a, in Zeichen

∂f

∂x

(~a) oder ∂f (~ x)

∂x

, f

, also

∂f

∂x

(~ x) := lim

t→0

f (x

, . . . , x

+ t, . . . , x

) − f (x

, . . . , x

, . . . , x

) t

= lim

t→0

f (~ x + t~ e

) − f (~ x) t

(Ableiten nach x

(variabel), andere Variablen als konstant ansehen.) Beispiel 8.1.5 f (x, y) = x

sin y + e

y

.

∂f

∂x (x, y ) = 3x

sin y + e

y

, ∂f

∂y (x, y) = x

cos y + 2e

y.

Definition f heißt partiell differenzierbar, wenn alle partiellen Ableitungen f

existieren.

Ist f partiell differenzierbar, so fasst man die partiellen Ableitungen zu einem Vektor zusammen. Diesen Vektor schreibt man zweckm¨ aßig als Zeilen- vektor.

Definition Der Vektor grad f (~ x) :=

∂f

∂x

(~ x), ∂f

∂x

(~ x), . . . , ∂f

∂x

(~ x)

heißt der Gradient von f in ~ x.

Die Funktion ~ x 7→ grad f(~ x) ist eine vektorwertige Funktion (ein Vektor- feld): jedem ~ x ∈ D wird der Vektor grad f(~ x) ∈ R

zugeordnet.

Beispiel 8.1.6 f(x, y) = x

sin y + e

y

.

grad f (x, y) = (3x

sin y + e

y

, x

cos y + 2e

y).

Man kann nun auch h¨ ohere partielle Ableitungen betrachten.

Notation (f(x, y)) f

= ∂

f

∂x

, f

= ∂

∂y ∂f

∂x

= ∂

f

∂y∂x , f

= ∂

f

∂y

. Beispiel 8.1.7 f(x, y) = x

sin y + e

y

.

∂

f

∂x

(x, y) = 6x sin y + e

y

, ∂

f

∂y∂x (x, y) = 3x

cos y + 2e

y,

∂

f

∂x∂y (x, y) = 3x

cos y + 2e

y, ∂

f

∂y

(x, y) = −x

sin y + 2e

. Warnung In diesem Beispiel gilt ∂

f

∂y∂x = ∂

f

∂x∂y . Das braucht aber nicht der Fall zu sein. Gegenbeispiel:

f : R

−→ R

x y

7−→ f (x, y) :=







xy x

− y

x

+ y

, (x, y) 6= (0, 0) 0, (x, y) = (0, 0) Es gilt

f (x, 0) = f(0, y) = 0 ⇒ f

(0, 0) = f

(0, 0) = 0.

f

= y x

− y

x

+ y

+ xy 2x(x

+ y

) − 2x(x

− y

) (x

+ y

)

= y

x

− y

x

+ y

+ 4x

y

(x

+ y

)

, (x, y) 6= (0, 0) f

= x

x

− y

x

+ y

− 4x

y

(x

+ y

)

, (x, y) 6= (0, 0).

Daraus folgt

f

(0, 0) = lim

y→0

f

(0, y) − f

(0, 0)

y = lim

y→0

−y

y

= −1, f

(0, 0) = lim

x→0

f

(x, 0) − f

(0, 0)

x = lim

x→0

x

x

= 1.

Es gilt aber der folgende Satz:

Satz 8.1.1 (Schwarz; Vertauschbarkeit der partiellen Ableitungen) F¨ ur jede Funktion f : D → R , D ⊆ R

offen, deren zweite partielle Ablei- tungen existieren und stetig sind, gilt

∂

∂x

∂f

∂x

= ∂

∂x

∂f

∂x

(1 ≤ i, j ≤ n).

Neben dem Begriff der partiellen Differenzierbarkeit gibt es f¨ ur Funktio- nen mehrerer Ver¨ anderlicher auch den Begriff der totalen Differenzierbarkeit.

Dabei geht man von der Deutung der Ableitung als lineare Approximation aus. Zur Beschreibung der G¨ ute der Approximation f¨ uhren wir folgendes Symbol ein.

Definition (Definition des o-Symbols) F¨ ur f, g : D → R , D ⊆ R

,

~ x

∈ D, k ∈ N , schreibt man

f (~ x) = g(~ x) + o(|~ x − ~ x

|

) (f¨ ur ~ x → ~ x

), falls

lim

~x→~x0

f (~ x) − g(~ x)

|~ x − ~ x

|

= 0.

also

f(~ x) = g(~ x) + o(|~ x − ~ x

|

) ⇔ lim

~x→~x0

f(~ x) − g(~ x)

|~ x − ~ x

|

= 0.

Die Gleichung f (~ x) = g(~ x) + o(|~ x − ~ x

|

) besagt: Der bei der Approxima-

tion von f durch g in der N¨ ahe von ~ x

gemachte Fehler f (~ x) − g (~ x) ist klein

im Vergleich zu |~ x − ~ x

|

.

Beispiel 8.1.8 Es sei I ⊆ R ein offenes Intervall, f : I → R eine differen- zierbare Funktion, x

∈ I. Dann gilt

f (x) = f (x

) + f

(x

)(x − x

) + o(|x − x

|).

Definition Es sei D ⊆ R

offen. Eine Funktion f : D → R heißt in ~ x

∈ D total differenzierbar, wenn es einen Vektor ~a ∈ R

gibt mit

f(~ x) = f (~ x

) + ~a · (~ x − ~ x

) + o(|~ x − ~ x

|) f¨ ur ~ x → ~ x

.

Warnung Aus der partiellen Differenzierbarkeit folgt nicht die totale Dif- ferenzierbarkeit!

Satz 8.1.2 Es sei f in ~ x

∈ D total differenzierbar, f(~ x) = f(~ x

) + ~a · (~ x − ~ x

) + o(|~ x − ~ x

|).

Dann ist f partiell differenzierbar und es gilt

~a = grad f (~ x

).

Nach Satz 8.1.2 gilt also: Ist f in ~ x

∈ D total differenzierbar, so gilt f (~ x) = f(~ x

) + grad f(~ x

) · (~ x − ~ x

) + o(|~ x − ~ x

|) f¨ ur ~ x → ~ x

.

Dies ist der Grund, weshalb man grad f(~ x

) ¨ ublicherweise als Zeilenvektor schreibt.

Anschauliche Deutung f¨ ur n = 2

Die Fl¨ ache (Graph) z = f (x, y) wird in der N¨ ahe von (x

, y

, f(x

, y

)) durch die Ebene

z = f (x

, y

) + f

(x

, y

)(x − x

) + f

(x

, y

)(y − y

)

mit einem Fehler o( p

(x − x

)

+ (y − y

)

) approximiert. Diese Ebene heißt Tangentialebene der Fl¨ ache z = f ((x, y) in (x

, y

, f(x

, y

)).

Die Tangentialebene enth¨ alt alle Fl¨ achentangenten in dem Punkt.

Satz 8.1.3 (stetig partiell diffbar ⇒ total diffbar) Es sei D ⊆ R

of- fen. Ist f : D → R auf D partiell differenzierbar und sind alle partiellen Ableitungen stetig, so ist f auf D total differenzierbar.

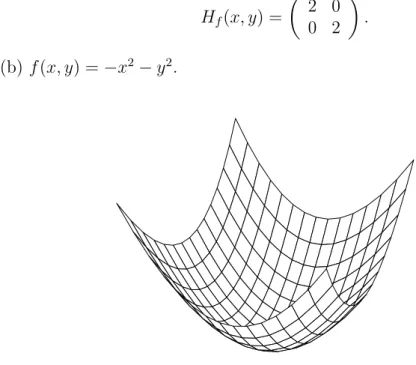
Beispiel 8.1.9 f (x, y) = 3 − x

− y

. (a) (x

, y

) = (0, 0):

f (x, y) = 3 + (0, 0) · x

y

+ o( p

x

+ y

).

Gleichung der Tangentialebene in (0, 0, 3): z = 3 (b) (x

, y

) = (1, 1):

f (x, y) = 1 + (−2, −2) ·

x − 1 y − 1

+ o( p

(x − 1)

+ (y − 1)

).

Gleichung der Tangentialebene in (1, 1, 1):

z = 1 − 2(x − 1) − 2(y − 1).

Bemerkung 8.1.1 F¨ ur eine erste N¨ aherung wird der o-Anteil vernachl¨ assigt und f(~ x) in der N¨ ahe von ~ x

durch f (~ x

) + grad f (~ x

) · (~ x − ~ x

) ersetzt:

f (~ x) ≈ f (~ x

) + grad f (~ x

) · (~ x − ~ x

).

8.2 Richtungsableitung

Die partiellen Ableitungen ∂f

∂x

(~ x) geben die ¨ Anderung der Funktionswer- te in Richtung der Kordinatenachsen (d.h. in ~ e

-Richtung) an. Allgemeiner definiert man:

Definition Es sei ~ v ∈ R

, |~ v| = 1. Dann heißt der Grenzwert

∂

f (~ x) := lim

t→0

f (~ x + t~ v) − f (~ x) t

(falls er existiert) die Richtungsableitung (oder der Anstieg) von f an der Stelle ~ x in Richtung ~ v .

Notation Andere Bezeichnungen: D

f (~ x), ∂f

∂~ v (~ x).

Anschauliche Deutung f¨ ur n = 2

Betrachte die Schnittkurve des Graphen z = f(x, y) mit der zur z-Achse parallelen Ebene durch die Gerade

~

x

+ t~ v = x

y

+ t v

v

, |~ v | = 1.

Diese Kurve besitzt die Parameterdarstellung

~ x(t) =





x

+ tv

y

+ tv

f (x

+ tv

, y

+ tv

)



 .

Der Tangentialvektor im Punkte (x

, y

, f(x

, y

)) lautet:

~ ˙ x(t) =





v

v

∂

f(x

, y

)



 . Die Tangente hat die Steigung ∂

f (x

, y

).

Physikalische Deutung

Wir betrachten eine ebene Platte mit einer Druckverteilung p = f (x, y) und einen Querschnitt durch die Platte durch den Punkt (x

, y

). Die momentane Druck¨ anderung l¨ angs dieses Querschnitts in (x

, y

) wird durch ∂

f(x

, y

) gegeben.

Satz 8.2.1 Es sei D ⊆ R

offen, f : D → R total differenzierbar, ~ v ∈ R

,

|~ v| = 1. Dann gilt

∂

f(~ x) = grad f (~ x) · ~ v =

n

X

i=1

∂f

∂x

(~ x)v

Beispiel 8.2.1 f (x, y) = 3 − x

− y

.

Richtungsableitung im Punkt (1, 1) in Richtung ~ v =

cos α sin α

:

∂

f (~ x) = grad f (1, 1) ·

cos α sin α

= (−2, −2)

cos α sin α

= −2(cos α + sin α).

Bemerkung 8.2.1 Es gilt:

∂

f (~ x) > 0 ⇒ f steigt in Richtung ~ v an.

∂

f (~ x) < 0 ⇒ f f¨ allt in Richtung ~ v ab.

Satz 8.2.2 (Kettenregel) Es sei D ⊆ R

offen, f : D → R total differen- zierbar, [a, b] ⊆ R , ~ x : [a, b] → D ein Kurvenst¨ uck. Dann gilt

d

dt f(~ x(t)) = d

dt f(x

(t), x

(t), . . . , x

(t))

= ∂f

∂x

(~ x(t)) ˙ x

(t) + . . . + ∂f

∂x

(~ x(t)) ˙ x

(t)

= grad f(~ x(t)) · ~ x(t) ˙