s ∈ { 0, ǫ, . . . , nǫ = τ }

Hohdimensionale Integrale

Das Pfadintegral kann nur für sehr einfahe Systeme wie den harmonishen Oszillator

oder dasfreieTeilhen explizitberehnetwerden. FürkompliziertereSystememahtman

Gebrauh von Störungstheorien(z.B. semiklassishe Entwiklung, Störungstheorie inder

Wehselwirkung, Hohtemperaturentwiklung) oder numerishen Methoden. Wir haben

gesehen,dassdiePfadintegralefürthermodynamisheGröÿenundKorrelationsfunktionen

durh endlihdimensionale Integrale approximiert werden. Dabei wird die Zeit diskreti-

siert,

s ∈ { 0, ǫ, . . . , nǫ = τ }

^{, und die Wirkung durh eine Riemannshe Summegenähert.}

Diese hängtvon den Werten

q

= { q 0 , q 1 , . . . , q n } = { q(0), q(ǫ), . . . , q(nǫ) }

des Weges

q(s)

^anden Gitterpunkten

s k = kǫ

^{ab. In dieser} Gitterapproximationist jeder Erwartungswert durhein endlih-dimensionalesIntegral gegeben,

h O i =

R D

^q

O(

^q

) e ^{− S(}

^q

⁾

R D

^q

e ^−S(

^q

⁾ ,

^mit

Z

D

^q

= Z ∞

−∞

Y n

1

dq _j ,

^(3.1)

mitder in (2.53) eingeführten euklidishen Gitterwirkung

S(

^q

) = S(q ₁ , . . . , q _n )

^(statt

S _E

shreiben wir in diesem Abshnitt

S

^).

3.1 Hohdimensionale Integrale

Niht nur in Quantenstatistik, Festkörperphysik, euklidshen Quanenfeldtheorie, Hoh-

energiephysikoderanderen Teilgebieten derPhysik und Chemiegilteshohdimensionale

Integrale möglihst ezient zu berehnen und dabei den Fluh der Dimenion zu vermei-

den.Zum Beispiellästsih derErwartungswert von Zinsderivatienalshohdimensionales

Integral shreiben. Bei einer Laufzeit von 30 Jahren zu je 12 Monaten und Verwendung

eines eigenen Zinssatzes für jeden Monat handelt es sih hier um 360-dimensionale Inte-

grale. Integrale von noh vielhöherer Dimension sind in Physik und Chemieniht unge-

wöhnlih. Hier sind eziente Algorithmen gefragt, die derartige Integrale bis auf einen

abshätzbaren Fehler berehnen.

3.1.1 Numerishe Algorithmen

Numerishe Integrationsmethoden werden seit Jahrhunderten benutzt. Es gibt zwei be-

kannte Kategorien:Formeln,welhe den Integrand anäquidistanten Stützstellen auswer-

ten(Newton-CotesIntegrationsregeln)undFormeln,welhedenIntegrandenansorgfältig

ausgewählten,aberniht äquidistanten Stützstellenauswerten (Gauÿshe Integrationsre-

geln). FürspezielleIntegranden führtdiezweite Klasse meistenszu besseren Resultaten.

Die numerishen Algorithmen beruhen auf der Riemannshen Denition von Integra-

len. Um nahzuprüfen, ob ein Funktion

f : [a, b] →

^R Riemann-integrierbar ist, wähle man eine Einteilung des Intervalls,

γ : a = x 0 < x 1 < x 2 < . . . < x n−2 < x n−1 < x n = b

^(3.2)

und deniert die zu dieser Einteilung gehörendeRiemannshe Unter- und Obersumme

U (f, γ) = X n−1

i=0

(x i+1 − x i ) · inf { f(x) | x i ≤ x ≤ x i+1 } O(f, γ) =

X n−1

i=0

(x _i+1 − x _i ) · sup { f (x) | x _i ≤ x ≤ x _i+1 } ,

mit

O(f, γ) ≥ U (f, γ)

^{. Ist}

sup

γ

U (f, γ) = inf

γ O(f, γ),

dann heiÿt

f

^im Riemannshen Sinneintegrierbar und

Z b a

f (x)dx ≡ sup

γ

U (f, γ)

^(3.3)

das Riemannshe Integral von

f

^{.DieseDenition kann leihtauf}mehrdimensionaleInte- grale ausgedehnt werden und wird beinumerishen Rehnungen gebrauht.

Die meistenAlgorithmen beruhen darauf,dass jedeglatteFunktiondurhInterpolati-

onspolynome approximiert werden kann. Wirerinnern daran,dass es genauein Polynom

P m

^vomGrade

≤ m

^{gibt,welhesan}

(m+1)

vorgegebenenStützstellen

x 0 , x 1 , . . . , x m−1 , x m

vorgegebeneWerte

f 0 , . . . , f m

^{annimmt,wobei}

f i = f (x i )

^{ist.Zurexpliziten}Konstruktion deniert man die

m + 1

Lagrangeshen Polynome vom Grade

m

^:

L ^(m) _p (x) = Y m

i=0 i6=p

x − x i

x p − x i

, p = 0, . . . , m,

^mit

L ^(m) _p (x q ) = δ pq .

^(3.4)

Das interpolierende Polynom vomGrade

m

^{ist dann}

P _m (x) =

X m

p=0

f (x _p )L ^(m) _p (x).

^(3.5)

Es giltnun der folgende

Satz: Es sei

f

^{eine auf dem Intervall}

∆ (m + 1)

^{-mal stetig dierenzierbare Funktion,}

und sei

P m

^{das zu den} Stützstellen

x 0 , . . . , x m ∈ ∆

^gehörige Interpolationspolynom vom Grade

≤ m

^{. Dannexistiertzujedem}

x ∈ ∆

^einPunkt

ξ(x)

^{(gelegenimkleinstenIntervall,}

welhes die Punkte

(x 0 , . . . , x m , x)

^{enthält) derart, dass}

f (x) − P m (x) = f ^(m+1) (ξ(x))

(m + 1)! L ^(m) (x), L ^(m) (x) = Y m

i=0

(x − x i ).

^(3.6)

AufgrunddesSatzesergibtsihfürdasIntegral

R dxf (x)

^{vonderkleinstenbiszurgröÿten}

Stützstelle dieFormel

Z x

m

x

0

dx f(x) = X m

p=0

f (x _p ) Z

dx L ^(m) _p (x)

| {z }

γ

p^(m)

+ Z

dx f ^(m+1) (ξ(x))

(m + 1)! L ^(m) (x).

^(3.7)

Die

γ p ^(m)

^{heiÿen Gewihte und die}

x p

^{Knoten der} Integrationsformel. Für äquidistante Knotenan den Stellen

x 0 , x 1 = x 0 + ǫ, x 2 = x 0 + 2ǫ, . . . , x m = x 0 + mǫ

^(3.8)

erhalten wir mit der Substitution

x = x 0 + ǫt, t ∈ [0, m]

^dieGewihte

γ _p ^(m) = ǫ

Z m 0

Y m

i=0 i6=p

t − i

p − i dt := ǫw ^(m) _p = ǫw _m−p ^(m) , p = 0, 1, . . . , p.

^(3.9)

Wendenwir das allgemeineResultat (3.7)auf diekonstanteFunktion

f = 1

^{an, soergibt}

sih dieSummenformel

p γ p = mǫ

^{oder auh}

w ^(m) ₀ + w ₁ ^(m) + . . . + w _m ^(m) = m.

^(3.10)

Die Newton-Cotes-Formelnlauten nun

Z x

m

x

0

dxf(x) ∼ X m

p=0

ǫ w ^(m) _p f(x 0 + ǫp), x m = x 0 + mǫ.

^(3.11)

Man ndetfolgende Gewihte

m

^Name

w ^(m) p (p = 0, 1, . . . , m) 0

Rehtekregel

1

1

^Trapezregel

¹ ₂ ¹ ₂ 2

Simpson-Regel

1 3

4 3

1 3

3 3/8 −

^Regel

³ ₈ ⁹ ₈ ⁹ ₈ ³ ₈ 4

Milne-Regel

14 45

64 45

24 45

64 45

14 45

5 ₂₈₈ ^{95 375} ₂₈₈ ²⁵⁰ ₂₈₈ ²⁵⁰ ₂₈₈ ³⁷⁵ _{288 288} ⁹⁵ 6

^Weddle-Regel

41 140

216 140

27 140

272 140

27 140

216 140

41 140

(3.12)

x f (x)

− ǫ 0 ǫ

Wir illustrieren die Fehleranalyse für

die Simpson-Regel. Dazu betrahten

wirdieDierenzzwishendemIntegral

der Funktion

f(x)

^von

− ǫ

^bis

ǫ

^(sie-

heAbbildung)undderNäherung(3.11)

für

m = 2

^{, alsoden Fehler}

E ₂ (ǫ) =

Z ǫ

−ǫ

dx f (x) − ǫ

3 (f ( − ǫ) + 4f (0) + f (ǫ)) .

Wir leiten

E 2 (ǫ)

^dreimalnah

ǫ

^{abund erhalten}

E ₂ ^′′′ (ǫ) = − ǫ

3 ( − f ^′′′ ( − ǫ) + f ^′′′ (ǫ)) .

Dies kann betragsmäÿigwie folgt abgeshätzt werden:

| E ₂ ^′′′ (ǫ) | = ǫ

3 | f ^′′′ (ǫ) − f ^′′′ ( − ǫ) | ≤ 2ǫ

3 M 3

^mit

M 3 = sup

t∈[−ǫ,ǫ] | f ^′′′ (t) | .

Die Integration ergibtdie Fehlerabshätzung

| E ₂ (ǫ) | ≤ M ₃ · ǫ ⁴

36 .

^(3.13)

Falls dieFunktion

f

^{mindestens viermal stetig} dierenzierbar ist, kann man auf

E ₂ ^′′′

^den

Mittelwertsatzanwenden,

E ₂ ^′′′ (ǫ) = 2ǫ

3 ǫ · f ⁽⁴⁾ (ξ),

und es folgtdieverbesserte Abshätzung

| E 2 (ǫ) | ≤ M 4 · ǫ ⁵

90

^mit

M 4 = sup

t∈[−ǫ,ǫ] | f ⁽⁴⁾ (t) | .

^(3.14)

Hieraus ergibt sih die bemerkenswerte Tatsahe, dass durh die Keplershe Fassregel

sogar kubishe Polynomeexakt integriert werden. Fürdie anderen Verfahren erhältman

analoge Fehlershranken für das Integral von der kleinsten bis zur gröÿten Stützstelle

(

M m = sup _[x

₀

_,x

_m

_] | f ^(m) |

^):

m

^Name

E m (ǫ) m

^Name

E m (ǫ)

0

Rehtekregel

1

2 ǫ ² M 1 4

Milne-Regel

8 945 ǫ ⁷ M 6

1

^Trapezregel

₁₂ ¹ ǫ ³ M 2 5 ₁₂₀₉₆ ²⁷⁵ ǫ ⁷ M 6

2

Simpson-Regel

1

90 ǫ ⁵ M 4 6

^Weddle-Regel

9

1400 ǫ ⁹ M 8

3 3/8 −

^Regel

₈₀ ³ ǫ ⁵ M 4

(3.15)

Allgemeingilt,dassfürgerade

m

^{sogarPolynomevomGrad}

m+1

^{exaktintegriertwerden.}

Für groÿe

m

^{werden dieKoezienten inden} Newton-CotesFormelnallerdingsgross und haben wehselndeVorzeihen. Dies führtzu Dierenzengrosser Zahlenund auh deshalb

werdendieNewton-Cotes Verfahrenhöherer Ordnunginder Praxiskaum eingesetzt.Für

niht genügend oft dierenzierbare Funktionen können die auf Interpolationspolynomen

beruhenden Methoden völligfalshe Resultateliefern!

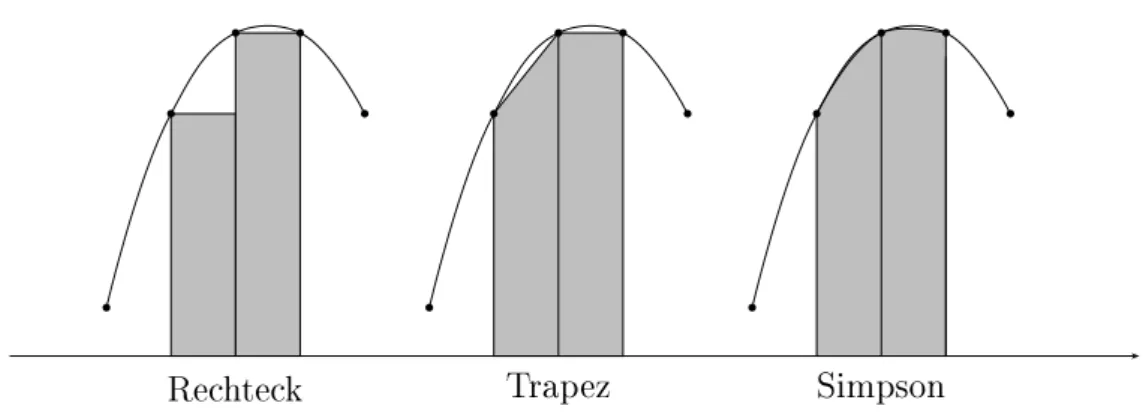
Zusammengesetzte Integrationsformeln: Indem das Integrationsintervall, über

das die Funktion

f

^{integriert werden soll, in kleinere, gleih groÿe Teilintervalle zerlegt}

wird, gelangt man zum Rehtek-, Trapez-, Simpson-oder den höheren Integrationsver-

fahren. Die Anzahl Intervalle sollte ein Vielfahes von

m

^{sein. Zum Beispiel wird beim}

Simpsonverfahrendie Keplershe Fassregel auf Doppelintervalleangewandt.

Milne Simpson

WirbetrahtendiezusammengesetzteSimpsonregeletwasnäher.DasIntegrationsintervall

[a, b] = [x 0 , x 2n ]

^enthalte

2n

^TeilintervallederLänge

ǫ

^,

b − a = 2nǫ

^.Die

2n + 1

Stützstellen sind

x _j = a + ǫj, j = 0, 1, . . . , 2n

^{. Das Integral wird} approximiert durh

S 2 (f ) ≈ ǫ 3

{ f (x 0 ) + 4f (x 1 ) + f (x 2 ) } + { f(x 2 ) + 4f(x 3 ) + f(x 4 ) } + . . . . . . + { f (x 2n−2 + 4f (x 2n−1 ) + f(x 2n }

= ǫ

3 f(x 0 ) + 4

n − 1

X

j=0

f (x 2j+1 ) + 2

n − 1

X

j=1

f (x 2j ) + f(x 2n )

! .

Der Fehler kann wie folgt abgeshätzt werden

Z b a

f(x)dx − S 2 (f) ≤ 1

90 ǫ ⁵ · n sup

t ∈ [a,b]

f ⁽⁴⁾ (t)

| {z }

M

4

= b − a

180 ǫ ⁴ M 4 .

^(3.16)

Allgemeiner giltfür eine äquidistante Einteilung des Integrationsintervalls in

m · n

^Teil-

intervalle,sodass

b − a = (mn)ǫ

^{ist, dieAbshätzung}

Z b

a

f (x)dx − S m (f )

≤ b − a

mǫ E m (ǫ)

^(3.17)

mit

E m (ǫ)

^{aus (3.15). Dabei istnatürlih}

M m = sup _[a,b] f ^(m)

^.

Mit Hilfe eines C-Programms berehnen wir das Integral einer Funktion über das In-

tervall

[a, b]

^{und zwar aufvier Arten: mitdem Rehtek-, Trapez- und} Simpsonverfahren sowie mitHilfederMonte-CarloMethode.DasletzteVerfahrenwirdweiteruntenbespro-

hen. Nohmals zur Erinnerung:

Rehtekregel

:

n − 1

X

i=0,1,2

ǫf(x i )

Trapezregel

:

X n−1

i=0,1,2

ǫ

2 (f (x _i ) + f (x _i+1 ))

^(3.18)

Simpson-Methode

:

X n−2

i=0,2,4

ǫ

3 (f (x _i ) + 4f(x _i+1 ) + f(x _i+2 )) .

In der letzten Formel soll

n

^{eine gerade Zahl sein. Die Näherungen sind inder folgenden}

Figur skizziert.

Rehtek

Trapez Simpson

b b

b b

b

b b

b b

b

b b

b b

b

Das Programm1dintegral. auf Seite 47 berehnet das Integral

R 1

0 dx e ^x

^für

ǫ ∈

10 ⁻ⁿ | n = 1, 2, . . . , 6 .

Die Werte für die stükweise konstante, lineare oder quadratishe Näherung sind in der

folgenden Tabelle enthalten. Für das Simpsonverfahren konvergiert wie erwartet dieNä-

herung sehr shnell gegen den exakten Wert

1.7182818

^.

n, log M

^{einfah Trapez Simpson MC}

1 1.633799 1.719713 1.718283 1.853195 2 1.709705 1.718296 1.718282 1.793378 3 1.717423 1.718282 1.718282 1.720990 4 1.718196 1.718282 1.718282 1.711849 5 1.718273 1.718282 1.718282 1.719329 6 1.718281 1.718282 1.718282 1.718257

3.1.2 Monte-Carlo Integration

Die Monte-Carlo Methode stammt wahrsheinlih von Stanislaw Ulam. Er fand die

Methode 1946, als ersih Gedanken über dieGewinnwahrsheinlihkeiten beim Solitair-

Spiel mahte. In seinen Worten:

The rst thoughts and attempts I made to pratie [the Monte Carlo Method℄

were suggested by a question whih ourred to me in 1946 as I was onva-

lesing from an illness and playing solitaires. The question was what are the

hanesthataCaneldsolitairelaidoutwith52ardswillomeoutsuessful-

ly? Afterspending a lot of time trying toestimate them bypure ombinatorial

alulations, I wonderedwhether a more pratialmethod thanabstrat thin-

king mightnotbeto lay it out sayone hundredtimes andsimply observe and

ount the number of suessful plays....

Einige Jahre später wurdedie Methode auf das Neutronendiusionsproblem angewandt,

das mit anderen Methoden niht lösbar shien [25℄. Eine wihtige Anwendung ist die

Berehnung hohdimensionalerIntegrale. Einsehr einfaher Algorithmuswäre:

•

^erzeuge

M

gleihverteiltePunkte

{ x 1 , . . . , x M }

^imIntegrationsgebiet

G

^,

•

^{berehne für jeden Punkt den F}unktionswert

f (x i ), i = 1, . . . , M

^,

•

^{berehne den Mittelwert}

I(M ) =

^Vol

( G ) M

X M

i=1

f(x i ).

^(3.19)

FüreineRiemann-integrierbareFunktionkonvergiert

I (M )

^fürgroÿe

M

^{gegendasIntegral}

R

G f

^{.Die Werte inder letztenSpalteder obigenTabelleenthalten}

I (M = 10, 100, . . .)

^für

das Integral der Exponentialfunktion.

Die folgende Abbildung illustriert das Konvergenzverhalten der drei Integrationsme-

thoden mit äquidistanten Stützstellen und der einfahen Monte-Carlo Integration. Für

die Exponentialfunktion liefert die Methode von Simpson shon für zehn Intervalle das

rihtige Resultat

e

^{bisauf die}

6.

^{Stelle hinter dem Komma.}

1.62 1.70 1.78

log ₁₀ n

b

b

b b b b

einfah

b b b b b b

Trapez

b b b b b b

Simpson

b

b

b

b b

MC

1 2 3 4 5 6

Unpraktikabelwerden Standardverfahren wenn dieDimension

n

^{des Integrals}

I =

Z

dq ₁ . . . dq _n f(q ₁ , . . . , q _n ) ≡ Z

d ⁿ qf (

^q

)

^(3.20)

gross wird. Sind zum Beispiel die Integrationsgrenzen in jeder Dimension gleih

0

^und

1

^{, und wählt man in jeder Dimension den gleihen Abstand}

ǫ

^{zwishen den} Stützstellen, dann istderen Anzahl

ǫ ⁻ⁿ

^.Der Rehenaufwand istproportionalzur Anzahl Stützstellen.

Nehmen wir alsBeispiel

ǫ = 0.1

^{, was siherlih eine grobe Einteilungdes Intervalls}

[0, 1]

ist, dann ist die Anzahl Stützstellen

∼ 10 ⁿ

^{. Die Auswertung einer} Stützstelle auf einem PC dauert etwa

10 ^{− 7} s

^{und dieBerehnung eines}

12

^{-fahen Integral etwa einen Tag.}

Hit-or-miss Monte Carlo Methode und Binomialverteilung

Gesuht seiwiederder Wert des Integrals

I = R

dx f (x)

^,

x 1 1 y

wobei wir ohne Beshränkung der Allgemeinheit

annehmendürfen,dass wirvon

0

^bis

1

integrieren.

Mit einem Zufallszahlengenerator, der zwishen

0

und

1

gleihverteilte Zahlen liefert, werden zwei Zufallszahlen

0 ≤ r 1 , r 2 ≤ 1

^erzeugt,

x = r ₁ , y = r ₂ .

Wir haben getroen, wenn

y ≤ f(x)

^{ist. Die}

Wahrsheinlihkeitfür einen Treer ist

p =

^{Anzahl Treer}

Anzahl Versuhe

=

^{dunkle Flähe}

Gesamtähe

= I

1 = I.

^(3.21)

Bei

M

^statistishunabhängigenVersuhenkönnenwir

k ∈ { 0, . . . , M }

^{Treerlandenund}

dieWahrsheinlihkeit dafür istdurh dieBinomialverteilung

P (M, k) = M

k

p ^k (1 − p) ^M−k

^mit

X M

k=0

P (M, k) = 1

^(3.22)

gegeben.HieristzumBeispiel

p ^k (1 − p) ^M−k

^dieWahrsheinlihkeitdafür,dassdieersten

k

Versuhe Treer und dieletzten

M − k

^{Versuhe Nieten ergeben. Der}Binomialkoezient zählt dieAnzahl Möglihkeiten, aus der Menge von

M

^Versuhen

k

^Treer auszuwählen.

Die Binomialverteilung beshreibt eine bei

pM

lokalisierte Glokenkurve und ist in der folgendenFigur für

M = 10

^und

p = 0.3

^geplotted.

b b

b b

b

b

b

b b b b

2 4 6 8 10

1 2 3

P (M, k)

k M = 10

p = 0.3

rehnet werden,

Z(t) = e ^tk

= X M

k=0

e ^kt P (M, k)

= e ^t p + (1 − p) M

.

^(3.23)

Als Summe von Wahrsheinlihkeiten ist

Z(0) = 1

^. Erwartungswerte von beliebigen Potenzen von

k

^{können durh ableiten der}

erzeugenden Funktion gewonnenwerden.

Nihtunerwartet istder mittlere Anteil Treer gleih

k M

= 1 M

X M

k=0

k P (M, k) = 1 M

dZ dt

t=0 = p.

^(3.24)

Das Quadrat der Streuung um den Ursprung ist

k ² M ²

= 1 M ²

X M

k=0

k ² P (M, k) = 1 M ²

d ² Z dt ²

t=0 = p M +

1 − 1

M

p ²

^(3.25)

und für das Quadrat der Streuung um diemittlere AnzahlTreer ndet man

σ ² = 1 M ²

D k − h k i 2 E

= 1 M ²

d ² log Z dt ²

t=0 = p(1 − p)

M .

^(3.26)

DieStreuungumdenMittelwertvermindertsihrelativlangsammitderAnzahlVersuhe,

σ ∼ M ^−1/2

^{. Eine Shätzung von}

p

^ist

h/M

^,wobei

h

^{die AnzahlTreer bei}

M

^Versuhen

ist.Die folgende Tabelle enthält die Shätzwerte

p

^und

σ

^{fürdas Integral}

I =

Z 1 0

f(x), f (x) = x ² e ^x

1 − x + xe ^x .

^(3.27)

für vershiedene Anzahl

M

^{von Versuhen. Die Streuung um den wahren Wert des Inte-}

grals,

I = 0.376370

^{,nimmt mit}

M

^{ab. Die Werte in den ersten drei Spaltenwurden mit}

dem Programmhitmissflaehe. auf Seite 48 generiert.

Die grobe Hit-or-Miss Methode kann mit wenig Aufwand verbessert werden. Wenn

nämlih

p

^gegen

1

^oder

0

^{strebt so wird}

σ

^{sehr klein} (allerdings wird für

p → 0

^der

relative Fehler gross). Wir nehmen nun eine Hilfsfunktion

g(x)

^{, die}

f(x)

^{möglihst gut}

approximiert aber analytish noh integriertwerden kann. Ist das erste Integral in

I = Z

(f (x) − g(x)) dx

| {z }

p wird klein

+ Z

g(x)dx

| {z }

bekannt

(3.28)

kleinund der Integrand zwishen

0

^und

1

^{, dannkönnen wir dieses Integralmit dem Hit-}

or-miss Verfahren mitverminderter Varianz berehnen. Für

f(x)

^{in(3.27) wählen wir}

g(x) = x ²

^mit

Z

g(x) dx = 1/3.

Dannergeben sihfürdas Integraldieverbesserten Shätzwerte inder drittletztenSpalte

und die Varianz in der letzten Spalte der Tabelle. Diese Werte wurden ebenfalls mit

hitmissflaehe. berehnet.

log ₁₀ M p I − p σ p verb I − p verb σ verb

1 0.500000 − 0.123630 0.158114 0.333333 0.043037 0.000000 2 0.330000 0.046370 0.047021 0.363333 0.013037 0.017059 3 0.399000 − 0.022630 0.015485 0.377333 − 0.000963 0.006486 4 0.378900 − 0.002530 0.004851 0.376833 − 0.000463 0.002040 5 0.376570 − 0.000200 0.001532 0.377693 − 0.001323 0.000651 6 0.374857 0.001513 0.000484 0.376305 0.000065 0.000203 7 0.376273 0.000097 0.000153 0.376303 0.000067 0.000064

Summen von Zufallszahlen, Gauÿverteilung und Grenzwertsatz

Das Programmgaussdistr. auf Seite 49erzeugt dieSumme

s

^von

n

^{auf demIntervall}

[0, 1]

gleihverteiltenunabhängigen Zufallszahlen

x 1 , . . . , x n

^{.Die erzeugendeFunktionfür}

dieSumme ist

Z(t) = e ^ts

= Z

I

ⁿ

d ⁿ x e ^t(x

¹

^+...+x

ⁿ

⁾ = Z 1

0

dx e ^{tx n}

= t ^{− n} e ^t − 1 n

,

^(3.29)

und für den Mittelwert von

s

^{nden wir}

m = h s i = dZ

dt

t=0 = Z

I

ⁿ

d ⁿ x (x 1 + . . . + x n ) = n

2 .

^(3.30)

und für dessen Streuungsquadrat

d ² log Z dt ²

t=0 = σ ² = h s ² i − m ² = n

12 .

^(3.31)

Nah dem Gesetz der grossenZahlen erwarten wir dieGauÿverteilung

P s = 1

√ 2π σ e ^−(s−m)

²

^/2σ

²

.

^(3.32)

DasProgrammgaussdistr. aufSeite49berehnet dieVerteilungvon

s

^fürdieSumme

von

10, 50

^und

100

Zufallszahlen. Zur Bestimmung der Verteilung werden jeweils eine MillionVersuhe gemaht.Mit den zufälligenWerten für

s

^{wird einHistogrammerstellt}

und im array mean[100℄ gespeihert. Wir haben die Zufallsvariable

s

^mit

n

^reskaliert,

so dass das Maximum der Verteilung bei

1/2

^{liegt. In der folgenden Abbildung werden}

die Resultate der MC-Simulation (Punkte, Dreieke, Viereke) mit den entsprehenden

Gauÿverteilungen verglihen.

u

t ut ut

u t

u t

u t

u t

u t

u

t ut ut ut

u t

u t

u t

u t

u t

u t

u t

u t q

p qp qp qp qp

q p

q p

q p

q p

q p

q p

q p

q p

q p

q p

q

p qp qp qp qp

b b b b

b b

b b

b b b

b

b

b

b

b

b b

b b

˜ 1/2 s

P (n, ˜ s)

n = 10 n = 50

n = 100 α = σ/n

˜ s = s/n

Fit:

P (n, s) ˜ ∝ e ^{− (˜ s − 0.5)}

²

^/2α

²

ImAnhang CndetsiheinBeweisfürdas Gesetz der groÿen Zahlen.Für gleihverteilte

Zahlen in

[0, 1]

^{ist der Mittelwert}

1/2

^{und die Varianz}

1/12

^{. Die Ungleihung (3.56) für}

die Wahrsheinlihkeit dafür, dass

s/n

^{mehr als}

δ

^{vom Mittelwert}

1/2

^{abweiht, nimmt}

folgende Form an

Pr s n − 1

2 ≥ δ

≤ 1

12nδ ² .

^(3.33)

3.2 Important Sampling

Numerishe Integrationsverfahren nähern Integrale durh endlihe Summen,

Z

d ⁿ q f (

^q

) ∼ X M

µ=1

f(

^q

µ )∆

^q

µ .

Für groÿe

n

^{und shwah} veränderlihe Funktionen

f

^{kann es}vorteilhaft sein, dieStütz- punkte q

µ

^{zufällig zu wählen. In vielen} Anwendungen variiert der Integrand allerdings um Gröÿenordnungen fürvershiedene Punkte undman vergeudet Rehenzeitwenn man

Stützpunkte mitsehr kleinemIntegrandenauswählt.Beimimportant sampling,zumBei-

spiel dem Metropolis-Algorithmus, werdenbevorzugtPunkte q

µ

^mitgroÿem Integranden berüksihtigt. Die Stützstellen liegen überwiegend da, wo der Integrand gross ist und

dies verringert dieVarianz der einzelnen Shätzung für das Integral.

Dazu nimmtman eine Funktion

g(

^q

)

^{, derenIntegralberehenbar istund welhe}

f (

^q

)

möglihst gut annähert, und shreibt

Z 1 0

f(

^q

) d ⁿ q = Z 1

0

f(

^q

)

g(

^q

) g(

^q

) d ⁿ q.

^(3.34)

Durh dieErzeugung von Zufallspunkten q

µ

^diemit

g (

^q

)d ⁿ q

^{verteiltsind, ergibt sihbei}

M

^{Messungen die Shätzung}

Z

f(

^q

)d ⁿ q ≈ f ¯ = 1 M

X M

µ=1

f (

^q

_µ )

g(

^q

µ ) ,

^(3.35)

unddabeivariierendieSummandenjetztnihtmehrsostark.AllerdingsmuÿdasIntegral

von

g

^{bekannt sein, um aus} gleihverteilten Zufallszahlen solhe zu erhalten, die mit

g

verteiltsind.

Bei der Berehnung vonErwartungswerten inGitterfeldtheorien,

h O i ≈ 1 Z

Z

D

^q

O(

^q

)e ^−S(

^q

⁾ , D

^q

= d ⁿ q, Z = Z

e ^−S(

^q

⁾ D

^q

,

^(3.36)

wäre es wünshenswert dieBoltzmannverteilung

P (

^q

) = 1

Z e ^−S(

^q

⁾ ,

^(3.37)

alsVergleihsfunktion

g

^{zu wählen, weildannnurnohüberdieimVergleihzu}

P

^inden

meistenFällen glattenObservablen

O(

^q

)

^{gemitteltwerden müsste,}

h O i ≈ O ¯ = 1

M X M

µ=1

O(

^q

_µ ).

^(3.38)

Hier ist

M

^{die Anzahl der erzeugten Punkte q}

µ

^{. Damit wird dieMonte} Carlo-Shätzung

O ¯

^{fürdenMittelwertvon}

O

^zueinemarithmetishenMittel.Passendverteilte

{

^q

1 ,

^q

2 , . . . }

sind aber niht ohne Weiteres zu erzeugen.

Wir haben folgendes Problem:Die

n −

dimensionalen Integrale

h O i = Z

dq ₁ . . . Z

dq _n O(

^q

)P (

^q

), Z

D

^q

P (

^q

) = 1,

^(3.39)

sollen für vershiedene Funktionen (Observablen)

O (

^q

)

^{, aber diegleihe} Wahrsheinlih- keitsdihte

P (

^q

)

^{berehnet werden. Dazu sollen} Algorithmen gefunden werden, die nah

P

^{verteilte Punkte} generieren. Der folgende Metropolis-Algorithmus[25℄ (er wird später begründet werden) erzeugt

{

^q

^µ }

^{, diegemäÿ}

P (

^q

)

^{verteilt sind:}

1. Beginne mit

µ = 0

^{und einem beliebigenStartpunkt q}

µ

^imIntegrationsbereih.

2. Wähle einen zweiten zufälligenPunkt q

′

und einZufallszahl

r ∈ [0, 1]

^.

3. Ist

P (

^q

^′ )/P (

^q

µ ) > r

^{dann setze man q}

µ+1 =

^q

^′

^, andernfallsq

µ+1 =

^q

µ

^.

4. Erhöhe

µ

^{um eins und wiederholedie Shritte}

2, 3

^und

4

^.

Die soerzeugten Punkte q

µ

^im Integrationsgebiet sind gemäÿ

P (

^q

)

^{verteilt, sodass}

O ¯ = 1

M X M

µ=1

O (

^q

µ )

^(3.40)

ein Shätzwert für

h O i

^{ist, der für groÿe}

M

^gegen

h O i

konvergiert. Jeder Punkt q

µ

^der

Markovkette heisst Konguration.

Das Programmsamplingflaehe. auf Seite 50 berehnet mitHilfe des Metropolis-

Algorithmus Shätzwerte für das eigentlihe Integral

I = 128 · R 1

0 dxdydz x ³ y ² z exp ( − x ² − y ² − z ² ) R 1

0 dxdydz exp ( − x ² − y ² − z ² ) = 128 · h x ³ y ² z i ≈ 2.4313142,

wobeifür

P

^dieExponentialfunktiongewähltwurde. DieKonvergenzzum exaktenResul- tat ist langsam, der Fehler ist vonder Ordnung

1/ √

M

^{. Die folgende Tabelle enthält die}

berehnetenShätzwerte.DerletzteEintragistdasResultatvon

M = 10 ⁶

MC-Iterationen