Definition 7.9 Ist σ : sig 0 → sig Signaturmorphismus, A , B sig-Algebren und h : A → B sig-Homomorphismus, dann ist h| σ := {h σ(s ) | s ∈ S 0 }, wobei sig 0 = (S 0 , F 0 , τ 0 ), ein

Signaturmorphismen - Parameterübergabe

Vergißbilder für Homomorphismen

Definition 7.9 Ist σ : sig ⁰ → sig Signaturmorphismus, A , B sig-Algebren und h : A → B sig-Homomorphismus, dann ist h| _σ := {h _{σ(s )} | s ∈ S ⁰ }, wobei sig ⁰ = (S ⁰ , F ⁰ , τ ⁰ ), ein

sig ⁰ -Homomorphismus:

(h| _σ ) s = h _{σ(s )} : A _{σ(s )} → B _{σ(s )}

q q

(A| _σ ) s → (B | _σ ) s

h| _σ heißt Vergißbild von h entlang σ

Signaturmorphismen - Parameterübergabe

Vergißbilder

Eigenschaften von h| _σ ( Vergißbild von h entlang σ) sig ⁰ σ - sig σ ⁰ - sig ⁰⁰

ALG(sig ⁰ ) | _σ

ALG(sig) | _σ

ALG(sig ⁰⁰ )

∈ ∈ ∈ ∈

A | _σ ^h| →

B | _σ A → ^h B

Verträglichkeit mit Identität, Komposition und Homomorphismen.

Signaturmorphismen - Parameterübergabe

Parameterspezifikation

ALG(Formal) | _incl

ALG(Body) Formal

incl - Body

Actual σ

?

⊂

incl’ - Value σ ⁰

? ALG(Actual)

| _σ 6

| _incl’ ALG(Value)

| _σ

6

Signaturmorphismen - Parameterübergabe

Parameterspezifikation

σ : sig ⁰ → sig, A , B , sig-Algebren.

h : A → B , sig-Homomorphismus.

hσ _σ = {h _{σ(s )} | s ∈ S ⁰ }, sig ⁰ = (S ⁰ , F ⁰ , τ ⁰ ) = mit hσ _σ : A| _σ → B | _σ Vergißbild von h entlang σ.

σ ⁰ ◦ σ

-

sig ⁰ σ - sig σ ⁰ - sig ⁰⁰

Alg(sig ⁰ ) ←− ^|

Alg(sig) ←−Alg(sig ^|

⁰⁰ )

| _(σ

_◦σ)

Signaturmorphismen - Parameterübergabe

Parameterspezifikation

A | _σ | _σ

A

B | _σ h| _σ

? | _σ

B h

?

Semantik der Parameterübergabe (nur Signatur)

Semantik der Parameterübergabe (nur Signatur)

Definition 7.10 Sei Body[Formal] Parameterspezifikation.

σ : Formal → Actual Signaturmorphismus.

Semantik der Parameterübergabe [Actual, σ].

Zuordnung: σ : Formal → Actual

↓

initiale Semantik von Value. D. h.

T Body[Actual,σ]

Betrachte: S ::(T _Actual , σ) 7→ T Body[Actual,σ]

Abbildung zwischen init Algebren. Kann aufgefasst werden als Zuordnung

zwischen Formal Algebren → Body-Algebren.

Semantik der Parameterübergabe (nur Signatur)

Semantik Parameterübergabe

(T Actual | _σ 7→ (T Body[Actual,σ] )| _σ

Actual

- Body[Actual, σ ]

T Body[Actual,σ]

init-Sem.

?

(T Body[Actual,σ] ) _|

Vergissbild

?

h _init : T _Actual init-Sem.

? - (T Body[Actual,σ] ) _|

Semantik der Parameterübergabe (nur Signatur)

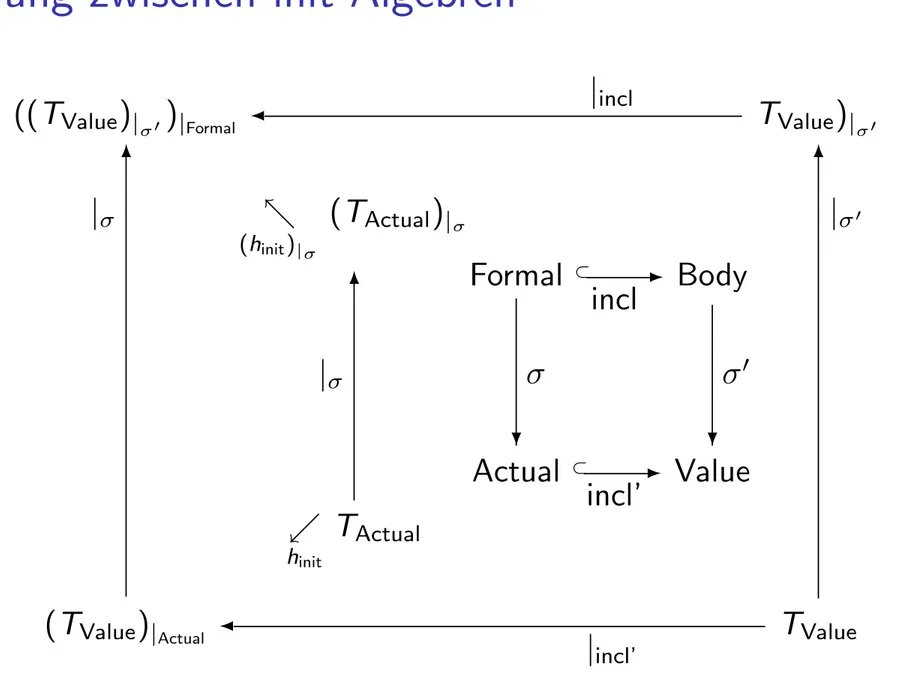
Abbildung zwischen init Algebren

((T _Value ) _|

σ0

) _|

| _incl

T _Value ) _|

σ0

-

( h

)

(T _Actual ) _|

Formal

incl - Body

Actual σ

?

⊂

incl’ - Value σ ⁰

?

.

h

T Actual

| _σ 6

(T Value ) _|

| _σ 6

| _incl’ T Value

| _σ

6

Semantik der Parameterübergabe (nur Signatur)

Abbildung zwischen init Algebren

Formal

sorts elem

ops a, b :→ elem eqns a = b

elem → nat

−→ σ

a → 0 b → 1

Actual

sorts nat

ops 0, 1 :→ nat

A = T _Actual A _nat = {0, 1}

A | _σ ∈ Alg(sig Formal) (A| _σ ) _elem = {0, 1}

a| ^A

σ

= 0 6= 1 = b| ^A

Gleichung von Formal nicht erfüllt! D. h.

A | _σ 6∈ Alg(Formal).

Semantik der Parameterübergabe (nur Signatur)

Parameterübergabe (Actual , σ )

Body[Formal]

σ : sig(Formal) → sig(Actual) Signatur Morphismus

Formal

incl - Body

Actual σ

?

⊂

incl’ - Value = Body[Formal, σ ]

σ ⁰ (mit Umbenennung)

?

Vor: sig(Actual) und sig(Value) strikt.

Semantik der Parameterübergabe (nur Signatur)

Parameterübergabe (Actual , σ )

Vergißbilder: | _σ : Alg(sig) → Alg(sig ⁰ )

A | _σ für σ : sig ⁰ → sig h : A → L sig-Homomorphismus

h| _σ : A | _σ → L | _σ

sig ⁰ -Homomorphismus

Semantik der Parameterübergabe (nur Signatur)

Parameterübergabe (Actual , σ )

((T _Value ) _|

σ0

) _|

| _incl

T _Value ) _|

σ0

-

(h

)

(T _Actual ) _|

∈ Alg(Formal)

.

h

T _Actual

| _σ 6

(T _Value ) _|

| _σ 6

| _incl’ T _Value

| _σ

6

Probleme: 1) (T _Actual )| _σ 6∈ Alg(Formal), 2) h _init keine Bijektion.

Spezifikationsmorphismus

Spezifikationsmorphismus

Definition

Seien spec ⁰ = (sig ⁰ , E ⁰ ), spec = (sig, E ) (allg.) Spezifikationen. Ein

Signaturmorphismus σ : sig ⁰ → sig heißt Spezifikationsmorphismus, falls für alle s = t ∈ E ⁰ gilt σ(s ) = σ(t ) ∈ Th(E ).

Schreibe: σ : spec ⁰ → spec

Fakt: Für A ∈ Alg(spec) gilt A | _σ ∈ Alg(spec ⁰ ) D. h. | _σ : Alg(spec) → Alg(spec ⁰ )!

Oft verlangt man „nur“ σ(s ) = σ(t ) ∈ ITh(E ).!

Spezifikationsmorphismus

Spezifikationsmorphismus

Eine Parameterübergabe für Body[Formal] ist ein Paar (Actual, σ):

Actual Spezifikation und σ : Formal → Actual Spezifikationsmorphismus.

(T _Actual )| _σ ∈ Alg(Formal)

- verlange auch h _init Bijektion, syntaktische Einschränkungen.

Spezifikationssprachen

CLEAR, Act-one, -Cip-C, Affirm, ASL, Aspik, OBJ, ASF,

+ neuere

Sprachen: - Spectrum, - Troll.

Spezifikationsmorphismus

Beispiel

Beispiel 7.7

Formal ::

 

 

 

 

 

 

 

 

 



spec ELEMENT use BOOL

sorts elem

ops . ≤ . : elem, elem → bool eqns x ≤ x = true

imp(x ≤ x and y ≤ z , x ≤ z ) = true

x ≤ y or y ≤ x = true

Spezifikationsmorphismus

Beispiel (Forts.)

spec LIST[ELEMENT]

use ELEMENT

sorts list

ops nil :→ list

· : elem, list → list

insert : elem, list → list

case : bool, list, list → list

sorted : list → bool

Spezifikationsmorphismus

Beispiel (Forts.)

eqns insert(x , nil) = x .nil

insert(x , y .l ) = case(x ≤ y , x . insert(y , l ), y . insert(x , l )) case(true, l ₁ , l ₂ ) = l ₁

case(false, l ₁ , l ₂ ) = l ₂ sorted(nil) = true sorted(x , nil) = true

sorted(x , y , l ) = if x ≤ y then sorted(y , l ) else false

Eigenschaft: sorted(insert(x , l )) = true

Spezifikationsmorphismus

Beispiel (Forts)

ACTUAL ≡ BOOL

σ : elem → bool, bool → bool . ≤ . → impl

Die Gleichungen von ELEMENT sind in Th(BOOL)

Spezifikationsmorphismus

Spezifikationsmorphismus

Beispiel (Forts.)

ACTUAL ≡ NAT

σ : bool → nat elem → nat true → suc(0) nicht erlaubt false → 0

not → suc or → plus and → times .. .

. ≤ . → · · ·

kein Spezifikationsmorphismus not(false) = true

not(true) = false gilt nicht!.