Verbesserung des Versuchs Spektroskopie am J

am J ₂ - Molek¨ ul des Fortgeschrittenen Praktikums

Wissenschaftliche Arbeit f¨ur das Staatsexamen im Fach Physik

Martine Meyer Physikalisches Institut

Albert-Ludwig-Universit¨at Freiburg

07.Oktober 2014

Inhaltsverzeichnis

1 Vorwort 1

2 Theoretische Grundlagen 1

2.1 Energieniveaus und Wellenfunktionen zweiatomiger Molek¨ule . . 1

2.1.1 Die Born-Oppenheimer-N¨aherung. . . 1

2.1.2 Berechnung und Klassifikation von Elektronenwellenfunk- tionen ΨE . . . 3

2.1.3 Beschreibung der Kernbewegung . . . 7

2.1.4 Wechselwirkung zwischen Elektronenbewegung und Kern- bewegung . . . 14

2.2 Zur Interpretation der beobachteten Absorptions¨uberg¨ange bei Jod 17 2.2.1 Zu welchem angeregten elektronischen Zust¨anden sind Ab- sorptions¨uberg¨ange m¨oglich (Auswahlregeln)? . . . 17

2.2.2 Welche Schwingungs- und Rotationsstruktur besitzt das Absorptionsspektrum? . . . 19

2.3 Zur Interpretation der beobachteten Intensit¨aten der Absorpti- onsbanden . . . 23

2.3.1 Wie sind die Jod- Molek¨ule auf die Schwingungs- und Ro- tationsniveaus des Grundzustands verteilt? . . . 24

2.3.2 Betrachtung der ¨Ubergangsmomente f¨ur Schwingungs¨uberg¨ange 27 2.3.3 Franck-Condon-Faktor . . . 28

3 Aufgabenstellung 29 4 Die alte Versuchsanordnung 29 4.1 Ziel der Arbeit . . . 29

4.2 Versuchsaufbau und Durchf¨uhrung . . . 30

4.3 Fazit . . . 32

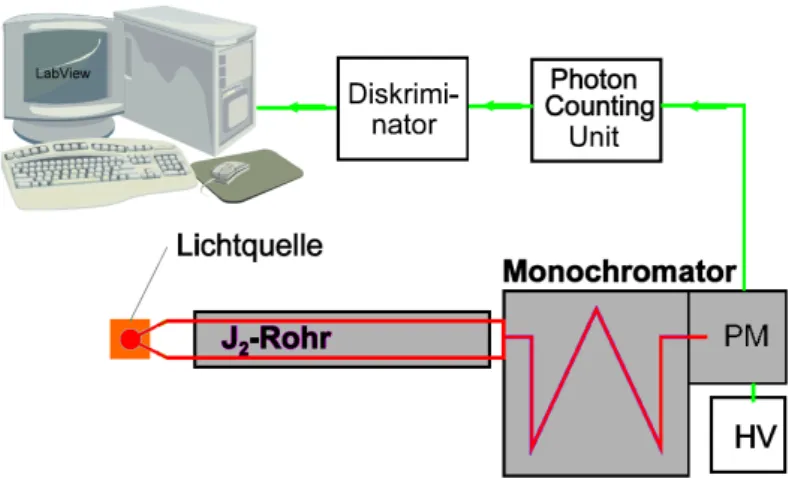
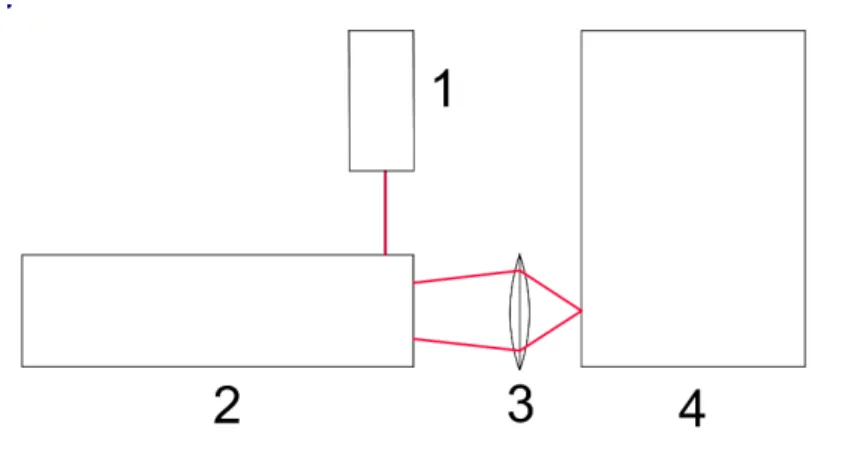
5 Verbesserungsprozess 32 6 Versuchsaufbau 35 6.1 Absorptionsmessung . . . 35

6.2 Emissionsmessung . . . 35

6.3 Ger¨atebeschreibung. . . 37

6.3.1 Lampen . . . 37

6.3.2 Laser . . . 37

6.3.3 Jod-Rohr . . . 38

6.3.4 Spektrometer . . . 39

6.3.5 Monochromator. . . 39

6.3.6 Photomultiplier. . . 41

6.3.7 Photon Counting Unit . . . 42

6.3.8 Diskriminator . . . 42

6.4 Software . . . 43

6.4.1 SpectraSuite . . . 43

6.4.2 JodAnalog . . . 43

7 Aufgabenstellung 44 7.1 Absorption . . . 44

7.2 Emission. . . 45

8 Musterversuch 46 8.1 Durchf¨uhrung . . . 46

8.1.1 Absorption . . . 46

8.1.2 Emission . . . 47

8.2 Auswertung . . . 49

8.2.1 Absorption . . . 49

8.2.2 Emission . . . 56

8.3 Ergebnisse . . . 61

8.3.1 Absorption . . . 61

8.3.2 Emission . . . 62

9 Zusammenfassung 62 10 Literatur 63 11 Anlagen 64 Versuchsanleitung f¨ur den vorl¨aufigen Versuch im Sommersemester 2014 64 Poster . . . 78

Identifizierte Schwingungsbanden, Wellenzahlen und Termdifferenzen mit Fehlern . . . 79

Beispielhafte Aufstellung der berechneten Wellenzahlen . . . 80

Versuchsanleitung . . . 81

1 Vorwort

Die Spektroskopie ist ein wichtiges Hilfsmittel in der Physik und der Chemie, um mehr ¨uber die Struktur von Molek¨ulen und Atomen zu erfahren. Durch die Spek- troskopie lassen sich vor allem Energieniveaus, ¨Ubergangswahrscheinlichkeiten, Symmetrie und Kopplung der Zust¨ande und deren Lebensdauern bestimmen.

Schon 1868 gelang es Angstr¨om die Emissionslinien des Sonnenspektrums auf- zulisten, die erste quantitative Spektralanalyse fand allerdings erst 1925 statt.

Wurde Spektroskopie anfangs mit Gitterspektralapparaten und Photoplatten durchgef¨uhrt so werden aufgrund der hohen Aufl¨osung heute meistens laser- spektroskopische Verfahren verwendet [2], [14].

Dieser Versuch soll eine Einf¨uhrung in die Molek¨ulspektroskopie sein, bei dem wichtige Molek¨ulkonstanten, wie die Schwingungskonstanten und Dissoziations- energien eines Molek¨ulzustands bestimmt werden. Eine Emissions- und eine Absorptionsmessung, jeweils durchgef¨uhrt mit verschiedenen Messanordnungen, sollen die Vielfalt spektroskopischer M¨oglichkeiten andeuten.

Als zu untersuchendes Molek¨ul wird in diesem Versuch das Jod-Molek¨ul verwen- det. Jod steht im Periodensystem der Elemente an 53. Stelle und z¨ahlt zu den Halogenen. Es hat eine relative Atommasse von 126,9u und eine Dichte von 4,93 gcm⁻³. Die Siedetemperatur von Jod liegt bei 184,4 ˆA°C. Diese Molek¨ul eignet sich sehr gut f¨ur spektroskopische Untersuchungen, da es eine sehr ausgepr¨agte Bandenstruktur besitzt.

2 Theoretische Grundlagen

In diesem Abschnitt werden einige Elemente zur Theorie zweiatomiger Molek¨ule, die f¨ur diesen Versuch relevant sind, eingef¨uhrt. Die theoretischen Grundlagen sind zum Großteil aus [1] entnommen worden. An einigen Stellen wurden sie pas- send zum neuen Versuchsaufbau gek¨urzt oder erweitert und es wurden teilweise neue Quellen und Literaturverweise verwendet.

2.1 Energieniveaus und Wellenfunktionen zweiatomiger Mo- lek¨ ule

2.1.1 Die Born-Oppenheimer-N¨aherung

Exakte Eigenfunktionen und Energieeigenwerte f¨ur ein zweiatomiges Molek¨ul ergeben sich aus der Eigenwertgleichung:

HΨ =EΨ (1)

Der Hamilton-Operator f¨ur zwei durch Coulomb-Wechselwirkung wechsel- wirkende Teilchen A und B ist folgendermaßen definiert (vgl. [4], Kap. 11.1.1):

H =−~²

2m∆ +Epot(qA, qB, r) Epot(qA, qB, r) = qA·qB

r

(2)

ˆ m: Masse

ˆ Epot: potentielle Energie der Wechselwirkung zweier Objekte (hier: Elek- tron oder Kern)

ˆ qA: Ladung eines beteiligten Objekts

ˆ qB: Ladung des anderen beteiligten Objekts

ˆ r: Abstand der beiden Teilchen

So ergibt sich durch Einsetzen f¨ur die Eigenwertgleichung eines zweiatomigen- Molek¨uls:

H =− ~² 2me

X

i

∆i

| {z }

TE

− ~² 2MA

∆A− ~² 2MB

∆B

| {z }

TN

+X

i>j

e² rij

| {z }

VEE

−X

i

Z1·e² rAi −X

i

ZB·e² rBi

| {z }

VEN

+ZAZB·e² rAB

| {z }

VN N

(3)

ˆ TE ist der Operator der kinetischen Energie aller Elektroneni(xi, yi, zi).

ˆ TN ist der Operator der kinetischen Energie der beiden Kerne A und B (xA, yA, zA;xB, yB, zB)

ˆ VEE, VEN, VN N sind die potentiellen Energien der wechselseitigen elektro- statischen Abstoßung bzw. Anziehung der Elektronen und Kerne.

Der L¨osungsansatz

Ψ = ΨE(..., xi, yi, zi, ...)·ΨN(xA, yA, zA, xB, yB, zB), (4) wobei ΨE und ΨN L¨osungen der abseparierten Gleichungen

HEΨE= (TE+VEE+VEN)ΨE =EE·ΨE (5) HNΨN = (TN +VN N+EE)ΨN =EN·ΨN (6) sind, bildet dann eine befriedigende N¨aherungsl¨osung von (1), wenn die Dif- ferentiale nach den Kernkoordinaten ^∂Ψ_∂x^E

A, . . . ,^∂_∂x^2Ψ2^E

A , . . . klein bleiben, d.h. wenn sich die Elektroneneigenfunktion ΨE nur wenig mit dem Kernabstand ¨andert.

Dies ist gew¨ohnlich erf¨ullt, da sich die Elektronen sehr viel schneller bewegen, als die durch ihre sehr viel gr¨oßere Masse tr¨ageren Kerne. Gezeigt wurde dieser Sachverhalt 1927 von M. Born und R. Oppenheimer.

(5) stellt die Schr¨odinger-Gleichung der Elektronenbewegung f¨ur festgehaltenen Kernabstand rAB =r dar. F¨ur verschiedene Kernabst¨ande ist auchVEN ver- schieden, deshalb h¨angen ΨE undEE vonrals Parameter ab.

(6) ist die Schr¨odinger-Gleichung der Bewegung der Kerne im Potential VN N+ EE.

Die wesentliche Aussage der Born-Oppenheimer-N¨aherung besteht also darin, dass die Bewegung der Elektronen und die der Kerne unabh¨angig voneinander behandelt werden k¨onnen. Die Wechselwirkung zwischen den Elektronen und dem Kern wird dadurch ber¨ucksichtigt, dass einerseits ΨE undEE vom Kern- abstand r abh¨angen, andererseits die elektronischen Eigenwerte EE(r) einen Teil des Potentials bilden, in dem sich die Kerne bewegen. (vgl. [2], Kap. 9.5.1;

[4, Kap. 11.2)

2.1.2 Berechnung und Klassifikation von Elektronenwellenfunktio- nenΨE

Da Gleichung (5) f¨ur das Jod-Molek¨ul nicht exakt l¨osbar ist, muss die L¨osung angen¨ahert werden. Ein N¨aherungsweg besteht darin, N¨aherungsl¨osungen Φ von ΨE aus Einelektronen- Molek¨ulorbitalen (MO’s) zu konstruieren, die ihrerseits als Linearkombinationen von Einelektronen- Atomorbitalen (AO’s) angesetzt werden (vgl. [4], S.42-43). In einer so erhaltenen

”LCAO/MO- Wellenfunktion

“(LCAO: linear combination of atomic orbitals) Φ sind Parametercienthalten, die es erlauben, Φ so zu variieren, dass Φ eine m¨oglichst niedrige Energieliefert:

= P

i

P

kc^∗_ickR

Φ^∗_iHEΦkd³~r P

i

P

kc^∗_ickR

Φ^∗_iΦkd³~r (7)

Durch Berechnung des Minimums vonbekommt man einen Wert, der dem tats¨achlichen (gemessenen) EigenwertEE am n¨achsten kommt.

Aufbau von Elektronenwellenfunktionen durch Einelektronen- Mo- lek¨ulorbitale am Beispiel des Jod- Molek¨uls

Ein Molek¨ulorbital eines Elektrons wird durch eine Wellenfunktion beschrieben, die nur von den Koordinaten dieses Elektrons abh¨angt. Dieses”Modell der un- abh¨angigen Teilchen“ impliziert, dass die Wechselwirkung eines Elektrons mit den anderen Elektronen nur pauschal dadurch ber¨ucksichtigt wird, dass jene das Axialfeld der beiden Kerne teilweise abschirmen und zu einem resultieren- den Axialfeld beitragen (vgl. [2], Kap. 6.1.1)

In einem axialen Kraftfeld ist nur noch die Komponente lz (Molek¨ulachse z) des Bahndrehimpulses~leines Elektrons Konstante der Bewegung (vgl. [4], Kap.

11.6.1).

Es gilt:

lz=ml·~ (8) mit m¨oglichen Wertenml=l, l−1, . . . ,−l. Hierbei stelltl die Bahndrehim- pulsquantenzahl gem¨aß|~l|=p

l(l+ 1)~dar.

Das Vorzeichen von ml beschreibt den Drehsinn der Bewegung des Elektrons um die z- Achse. Da die Energie des Elektrons aber unabh¨angig von diesem Drehsinn ist, gen¨ugt es, die Quantenzahlλ=|ml|= 0, . . . , lzu verwenden, um den Zustand des Elektrons zu spezifizieren. Der Bahndrehimpulszustand eines Elektrons wird f¨urλ= 0,1,2,3, . . . alsσ, π, δ, φ, . . .- Zustand bezeichnet.

Um anzuzeigen, welche Atomorbitale nl-linear zu einem Molek¨ulorbital kom- biniert werden, notiert man das betreffende Molek¨ulorbital meist in der Form λnl (vgl. [6], S. 121 ff). (Diese Bezeichnung ist bei homonuklearen zweiatomi- gen Molk¨ulen deshalb m¨oglich, weil hier die Bindung auf der ¨Uberlappung von gleichnamigen Atomorbitalen beruht, z.B. zwei 1s- Orbitalen.) In jedem Orbital sind zwei verschiedene Spinzust¨ande m¨oglich, außerdem ist jedes Orbital mit λ≥1 zweifach entartet (die beiden Zust¨ande haben gleich großes, aber entge- gengesetzt gerichtetesml). Deshalb haben in einemσ- Orbital zwei Elektronen Platz, inπ, δ, φ- Orbitalen jeweils vier.

Bei homonuklearen Molek¨ulen kann die Symmetrieoperation i

”Punktspiegelung am Symmetriezentrum“ auf die Orbitalwellenfunktion angewendet werden. Je nach seinem Verhalten kann dann das Orbital als eines mit gerader oder unge- rader Parit¨at identifiziert werden:

iλg= (+1)·λg (9)

iλu= (−1)·λu (10)

Die Parit¨atseigenschaft gibt Auskunft ¨uber die Bindef¨ahigkeit eines Orbitals:

Ist das Symmetrieverhalten der Orbitale so, dass zwischen den beiden Kernen eine große Aufenthaltswahrscheinlichkeit f¨ur das Elektron besteht, so ist das Orbital bindend. (vgl. [4] S.46)

Dazu geh¨oren z.B. die Orbitaleσgns, σgnp, πunp.

Ist das Symmetrieverhalten aber so, dass zwischen den beiden Kernen eine Kno- tenstelle der Aufenthaltswahrscheinlichkeit liegt, so ¨uberwiegt die Abstoßung der Kerne, das Orbital ist antibindend und wird dazu oft mit einem * verse- hen, z.B.σ^∗_uns, σ_u^∗np, π^∗_gnp. Die Energieniveaus der Molek¨ulorbitale, die von den Atomorbitalen ns und np ausgehen, liegen i.A. (bei schweren Molek¨ulen) in der in Abb. 1dargestellten Anordnung.

Wie beim Atom kann man die Elektronenkonfiguration eines Molek¨uls mit vielen Elektronen feststellen, indem man

”von unten her“ die Orbitale gem¨aß dem Pauli- Prinzip auff¨ullt (d.h. maximal zwei Elektronen inσ- Orbitalen, ma- ximal vier Elektronen inπ, δ, . . . - Orbitalen)(vgl. [2, Kap. 9.3.1).

Im Falle des Jod- Molek¨uls, das durch die Bindung zweier Jodatome (Elektro- nenkonfiguration des Grundzustands KLM 4d¹⁰5s²5p⁵) entsteht, erh¨alt man als

Abbildung 1: Veranschaulichung der Energieniveaus der Molek¨ulorbi- tale

Elektronenkonfiguration des Grundzustand:

. . .(σg5s)²(σ_u^∗5s)²(σg5p)²(πu5p)⁴(π^∗_g5p)⁴ (11) Da im Wesentlichen nur die Elektronen der ¨außeren Schale der Atome zur Molek¨ulbindung beitragen, sind nur die Orbitale angeschrieben, die von den Elektronen der Atomschalen= 5 gebildet werden.

Die Elektronenkonfiguration des ersten angeregten Zustands betr¨agt:

. . .(σg5s)²(σ^∗_u5s)²(σg5p)²(πu5p)⁴(π_g^∗5p)³(σ^∗_u5p) (12) Kennzeichnung der Elektronenzust¨ande durch Drehimpulsquan- tenzahlen und Angabe des Symmetrieverhaltens am Beispiel des Jod- Molek¨uls

Es ist ¨ublich, einen elektronischen Zustand durch Angabe der vorliegenden Ge- samtdrehimpulsquantenzahlen (wie beim Atom) und durch Angabe des Sym- metrieverhaltens der ihm zugeordneten Wellenfunktion zu kennzeichnen.

Wie bei Atomen vom LS- Kopplungstyp bilden in den meisten Molek¨ulen die ein- zelnen Elektronenbahndrehimpulse einen Gesamt- Elektronenbahndrehimpuls L~ = P

i~li und die einzelnen Elektronenspins einen Gesamt- Elektronenspin S~=P

i~si.

Die Komponente des Gesamt- Bahndrehimpulses der Elektronen entlang der Molek¨ulachse betr¨agt:

Lz=ML·~ (13)

mitML=P

imli undML=L, L−1, . . . ,−L(L aus|~L|=p

L(L+ 1)~).

Wieder h¨angt die Energie eines Zustands nur vom Wert Λ =|ML|ab.

Der Bahndrehimpulszustand eines Molek¨uls wird f¨ur Λ = 0,1,2,3, . . . als Σ,Π,∆,Φ, . . .- Zustand bezeichnet. Jeder Zustand mit Λ ≥ 1 ist wiederum zweifach entartet. (Feinere Wechselwirkungen heben diese Entartung auf, vgl.

Abschnitt

”Zur Interpretation der beobachteten Absorptions¨uberg¨ange“) Die Bahnbewegung der Elektronen in Zust¨anden mit Λ≥1 erzeugt ein Magnet- feld entlang der Molek¨ulachse und zwingt den GesamtspinS~ zur Pr¨azession um diese Achse.

Erhalten bleibt wieder nur die Komponente:

Sz= Σ~, (14)

wobei Σ die (2S+ 1) m¨oglichen WerteS, S−1, . . . ,−Sbesitzt (Saus|S~|= pS(S+ 1)~).

Der Betrag der Komponente des Gesamtdrehimpulses entlang der Achse betr¨agt:

|Λ~+ Σ~|=|Λ + Σ|~=: Ω~ (15) Die Spin-Bahn-Wechselwirkung ergibt einen Beitrag in der Elektronenener- gie, der verschieden groß ausf¨allt f¨ur jede Stellung von S~ zur Molek¨ulachse, d.h. f¨ur jeden Wert von Λ + Σ. Dies f¨uhrt zu einer Multiplettaufspaltung der Molek¨ulterme in (2S+ 1) verschiedene Niveaus.

Deshalb benennt man jeden Λ - Zustand mit seiner Multiplizit¨at 2S+1 (links oben) und dem gerade vorliegenden Wert von Λ + Σ (rechts unten).

Elektronenwellenfunktionen werden mit Φ⁺_Eoder Ψ⁻_Ebezeichnet, je nachdem ob die Symmetrieoperation σ

” Spiegelung an einer Ebene durch die beiden Kerne“ das Vorzeichen der Wellenfunktion ¨andert oder nicht; z.B.:

σΣ⁺= (+1)·Σ⁺ (16)

σΣ⁻= (−1)·Σ⁻ (17)

Elektronenwellenfunktionen homonuklearer Molek¨ule k¨onnen außerdem mit ΨEg oder ΨEu (gerade oder ungerade Parit¨at)

bezeichnet werden, je nachdem ob die Operation i

”Punktspiegelung am Symmetriezentrum“ das Vorzeichen der Wellenfunktion ¨andert oder nicht, z.B.:

iΠg= (+1)·Πg (18)

iΠu= (−1)·Πu (19)

(vgl. [2], S.290) Zust¨ande mit gleichen Drehimpulsquantenzahlen Λ,2S+ 1 und Λ+Σ, aber unterschiedlichem Symmetrieverhalten, k¨onnen sich in der Elek- tronenenergie unterscheiden. Beispielsweise kann jedem der beiden - bei Λ≥1 auftretenden - in Λ entarteten Zust¨ande eine Wellenfunktion mit unterschiedli- chem Symmetrieverhalten Ψ⁺_E bzw. Ψ⁻_E zugeordnet werden.

Aufgrund der Wechselwirkung zwischen Elektronenbewegung und Molek¨ulro- tation wird diese Entartung aufgehoben, es bilden sich zwei nur im Symmetrie- verhalten der zugeordneten Wellenfunktionen unterschiedene Energiezust¨ande.

Ein und derselben Elektronenkonfiguration kann entweder genau ein Molek¨ulterm

oder auch mehrere - in den Drehimpulsen und dem Symmetrieverhalten verschie- dene - zugeordnet werden. (vgl. [6], 130 ff.)

So ergibt sich aus der Konfiguration (11) der Term

X¹Σ⁺_g (20)

als resultierender elektronischer Grundzustand des Jod- Molek¨uls, w¨ahrend f¨ur die Konfiguration (12) die Terme

1Πu,³Π2u, A³Π1u, B³Π⁺_0u,³Π⁻_0u (21) m¨oglich sind (vgl. [9], S. 755).

2.1.3 Beschreibung der Kernbewegung

Im Rahmen der Born-Oppenheimer-N¨aherung bildet die ElektronenenergieEE(r) einen Teil der potentiellen Energie der Kernbewegung:

V(r) =VN N(r) +EE(r) = Z_I²·e²

r +EE(r) (22)

(Die KernladungszahlZI des Jodatoms betr¨agt 53.)

Das Jodmolek¨ul ist ein so schweres (d.h. kompliziert aufgebautes) Molek¨ul, dass eine approximative L¨osung der elektronischen Schr¨odinger- Gleichung (5) (z.B.

durch das LCAO/MO- Verfahren) keine guten EE(r)- Werte ergibt (vgl. [6], S.147).

Deshalb bestimmt man in der PraxisV(r) auf einem anderen Weg:

Die Form der potentiellen Energie bestimmt die Kernbewegung. Deshalb kann man auch umgekehrt aus der Kernbewegung (d.h. aus den Schwingungs- und Rotationskonstanten, siehe unten) den Verlauf der potentiellen Energie bestim- men. N¨aheres dazu im AbschnittDie Morse-Funktion.

Die potentielle Energie V innerhalb eines elektronischen Zustands h¨angt nur vom Kernabstand r ab. Deshalb kann die Schr¨odinger-Gleichung (6) in Schwerpunktsystemen in der Form

∇²ΨN +2µ

~²(E−V(r)) = 0 (23)

geschrieben werden, mit der reduzierten Masseµ=_M^MA·MB

A+MB.

Schreibt man ∇² in Kugelkoordinaten und separiert die Wellenfunktion gem¨aß:

ΨN(r, θ, φ) = 1

rS(r)Y(θ, φ) (24)

so gelten f¨ur den RadialanteilS und WinkelanteilY die Gleichungen:

1 sinθ

∂

∂θ

sinθ∂Y

∂θ

+ 1

sin²θ

∂²Y

∂φ² +J(J+ 1)Y = 0 (25) (J = 0,1, . . . Quantenzahl des Gesamtdrehimpulses) und

d²S dr² +2µ

~²

E−V(r)−J(J+ 1)~² 2µr²

S= 0 (26)

(vgl. [2], S.302 links). (26) beschreibt die Schwingung der Kerne, genauer des Teilchensµ, im PotentialV(r) +^J(J+1)_2µr2^~2, wobei der zweite Summand die Rota- tion des Molek¨uls im (variierenden) Abstandrber¨ucksichtigt. Die L¨osung ergibt f¨ur jeden Wert vonJ einen Satz von Schwingungseigenfunktionen und Energie- eigenwertenE=EvJ, die durch eine Quantenzahlvunterschieden werden. Um diese Energieeigenwerte des”schwingenden Rotators“ approximativ anzugeben, ist es sinnvoll, zuerst die Quantisierung der Rotations- und Schwingungsenergie anhand zweier Grenzmodelle zu untersuchen:

Der starre Rotator(r=const.)

MitV(r) =: 0 und ^S(r)_r =: 1 wird Gleichung (23) zu Gleichung (25) unter der Bedingung, dass

E=J(J+ 1)~²

2µr² =B^∗J(J+ 1) mit B^∗= ~²

2µr_E²

(27)

Da in der Molek¨ulphysik die Energien spektroskopischer ¨Uberg¨ange gew¨ohn- lich in cm⁻¹- Einheiten gemessen werden, ist es ¨ublich, alle Energiewerte in cm⁻¹ (Wellenzahlen) auszudr¨ucken. Z.B. lauten dann die Rotationsterme:

F(J) :=E(J)

hc = J(J + 1~²)

4πµcr²_E =:BJ(J+ 1) mitB= ~²

4πµcr²_E

(28)

Der rotationslose Oszillator (J = 0)

Die Schwingungsbewegung, die nur eine Funktion des Kernabstands rist, wird durch Gleichung (26) beschrieben. F¨urJ = 0 wird sie zu

d²S dr² +2µ

~²(E−V(r)) = 0 (29)

Ihre Eigenfunktionen und Eigenwerte h¨angen von der potentiellen Energie V(r) ab. Wenn V(r) ein stabiles Molek¨ul beschreiben soll, muss es folgende Eigenschaften besitzen:

r→0 :V(r)→ ∞ (30a)

r→ ∞:V(∞)→const. (30b)

f¨ur ein remit 0< re<∞nimmtV(r)ein Minimum an. (30c)

Ganz allgemein kannV(r) als Taylor- Reihe umreentwickelt werden:

V(r) =V(re) +V⁰(re)(r−re) +V⁰⁰(re)

2! (r−re)²+V⁰⁰⁰(re)

3! (r−re)³+. . . (31) DaV(re) gleich Null gesetzt und außerdem das Minimum der potentiellen Ener- gie ist, fallen die beiden ersten Summanden weg.

Befindet man sich nun im Bereich kleiner Auslenkungen um die Gleichge- wichtslage re (d.h. unten im Potentialtopf), so sind die h¨oheren Potenzen klein gegen (r−re)², und die potentielle Energie des harmonischen Oszillators (vgl.

[4], Kap. 11.2.4)

Vharm(r) = V⁰⁰(re)

2 (r−re)²=: ke

2 (r−re)² (32) n¨ahert dort das reale Potential an (siehe Abb.37).keist die Kraftkonstante f¨ur kleine Schwingungen im realen PotentialV(r).

Setzt manVharm(r) in (29) ein, so erh¨alt man als Schwingungsenergieterme die

¨aquidistante Termleiter des harmonischen Oszillators Gharm(v) := E

hc =ωe(v+1

2) mit v= 0,1,2, . . . , (33) ωe=νe

c = 1 2πc

ske

µ (34)

(νeist die klassische Schwingungsfrequenz)

Mit zunehmender Schwingungsauslenkung n¨ahertVharm V(r) immer schlechter an, insbesondere wird Bedingung (30)b verletzt (vgl. Abb.37).

Setzt man nun die anharmonische potentielle Energie (31) in (29) ein und ste- hen die Vorfaktoren der Anharmonizit¨atsterme im Verh¨altnis ^V00₂^{(re V000}3!^(re) . . . zueinander, was bei den meisten Molek¨ulen richtig ist, so erh¨alt man nach einer St¨orungsrechnung (vgl. [5], S. 93) die Energieterme des anharmonischen Oszillators

G(v) =ωe(v+1

2)−ωexe(v+1

2)²+ωeye(v+1

2)³+. . . (35) wobei die Schwingungskonstanten im Verh¨altnisωeωexeωeye>> . . . zueinander stehen.

Der Oszillator besitzt eine Nullpunktsenergie, deren Termwert G(0) = 1

2ωe−1

4ωexe+1

8ωeye+. . . (36) lautet.

Der Abstand benachbarter Schwingungsterme betr¨agt:

∆G(v+1

2) :=G(v+1)−G(v) =ωe−ωexe(2v+2)+ωeye(3v²+6v+13

4 )+. . . (37) Bei den meisten molekularen Zust¨anden (so auch bei den beiden betrachte- ten des Jod- Molek¨uls) istωexe positiv undωexeωeye, so dass der Abstand der Schwingungsterme mit zunehmendemv abnimmt.

Da das Potential f¨ur große r mit −r¹⁶ geht (van- der- Waals- Wechselwirkung zwischen den beiden molek¨ulbildenden Atomen), ist die Zahl der Schwingungs- terme im Potentialtopf endlich. (Dies gilt f¨ur alle potentiellen Energien mit

−r^1s, s > 2.) F¨ur ein endliches vdiss wird ∆G(v+ ¹₂) zu Null. Oberhalb von G(vdiss) befindet sich ein Energiekontinuum, in dem das Molek¨ul dissoziiert vorliegt.

Die Dissoziationsenergie D0, gemessen vom tiefsten Niveau v = 0 aus, be- tr¨agt:

D0=

vXdiss

v=0

∆G(v+1

2) (38)

Die DissoziationsenergieDe, gemessen vom Potentialminimum aus, betr¨agt dann:

De=G(0) +D0 (39)

Abbildung 2: Veranschaulichung der Energieniveaus mit Kontinuum und Dissoziationsenergien

Diese Art der Berechnung der Dissoziationsenergie wurde von Raymond Bir- ge und Hertha Sponer entwickelt und nach ihnenBirge- Sponer- Plot genannt.

Zur Bestimmung vonvdiss, tr¨agt man ∆G(v+¹₂) gegenv+¹₂ auf und bestimmt vdissaus dem Schnittpunkt der mithilfe von (37) angelegten Funktion mit der x- Achse. Die Schwingungskonstantenωe,ωexeundωeyekann man dann ebenfalls

aus dieser Funktion ablesen. (vgl. [8]) Die Morse- Funktion

Um mit Hilfe gemessener Molek¨ulkonstanten den Verlauf der potentiellen Ener- gie zu bestimmen, lassen sich zwei Methoden unterscheiden:

Erstens gibt es eine Reihe von analytischen Funktionen, die die Eigenschaf- ten (30) besitzen und zur Approximation der potentiellen Energien realer Mo- lek¨ulzust¨ande verwendet werden. Sie enthalten zun¨achst einige freie Parameter, die dann mittels der gemessenen Molek¨ulkonstanten festgelegt werden.

Die bekannteste ist die Morse- Funktion (vgl. [8]):

V(r) =De(1−e^−a(r−re))²

mit re= 2,979 ˚A (40)

Setzt man sie in (31) ein, so erh¨alt man als Schwingungsenergieterme G(v) =a

s~De

πcµ(v+1

2)− ~a² 4πcµ(v+1

2)² (41)

Aus dem Vergleich mit (35) erh¨alt man ωe=a

s~De

πcµ (42)

ωexe= ~a²

4πcµ (43)

µ= 1,053·10⁻²⁵ kg entspricht der reduzierten Masse von Jod.

Durch Eliminieren vonaergibt sich De= ω_e²

4ωexe

(44) Je besser die berechneten und gemessenen Werte von ωexe und De uber-¨ einstimmen, umso besser approximiert die Morse-Funktion die reale potentielle Energie des betrachteten Zustands.

Zweitenskann man mit der Rydberg-Klein-Rees-Methode (RKR- Methode) die tats¨achliche Potentialfunktion eines Zustands graphisch aus den gemessenen Molek¨ulkonstanten konstruieren (vgl. [12]).

Der schwingende Rotator

Ein reales Molek¨ul vollf¨uhrt gleichzeitig Schwingungen und Rotationen.

Zur Bestimmung der Energieterme des schwingenden Rotators muss man als ers- tes das Modell des starren Rotators aufgeben: Die Tatsache der Molek¨ulschwin- gungen legt nahe, die Rotation besser durch ein Modell des

”nichtstarren Rota-

Abbildung 3:Veranschaulichung der Approximation des realen Poten- tials durch das des harmonischen Oszillator und der Morse-Funktion [2]

tors“ zu beschreiben.

Die elastische Dehnung des Kernabstands w¨ahrend der Rotation wird dabei durch Zuf¨ugung eines ”Dehnungsterms“ im RotationstermF(J) ber¨ucksichtigt (vgl. [5], S. 103 ff).

F(J) =B·J(J+ 1)−D·J²(J+ 1)²+. . . , DB (45) L¨asst man Schwingung und Rotation gleichzeitig zu, so muss man die Ro- tationskonstanteB = _4πcµr^~ 2 eines Molek¨uls mit konstantem Kernabstandrso korrigieren, dass sie dessen ¨Anderung w¨ahrend der Schwingung ber¨ucksichtigt.

Da die Schwingungsfrequenz allgemein ca. zwei Zehnerpotenzen gr¨oßer ist als die Rotationsfrequenz, kann man ¨uber den Kernabstandrmitteln (vgl. [5], S.106 ff):

Bv:= ~ 4πcµh1

r²i^v (46)

und erh¨alt so f¨ur jedes Schwingungsniveauv einen mittleren WertBv. Rechnungen ergeben (vgl. [5], S. 106 ff), dassBvals Potenzreihe von (v+¹₂) darstellbar ist:

Bv =Be−αe(v+1

2) +γe(v+1 2)²+. . . mitBe= ~

4πcµ 1

r²_e, Beaere. . .

(47)

Auf ¨ahnliche Weise erh¨ahlt man einen mittleren Wert der Dehnungskonstan- ten D zu:

Dv :=De+βe(v+1 2) +. . . mitDe= 4B²_e

ω²_e , Deβe. . .

(48)

Die Termwerte des schwingenden Rotators lauten somit:

T(v, J) =G(v)+Fv(J) =ωe(v+1

2)−ωexe(v+1

2)²+ωeye(v+1

2)³+· · ·+BvJ(J+1)−DvJ²(J+1)²+. . . (49)

Weil die Rotationskonstanten viel kleiner als die Schwingungskonstanten sind, liegen ¨uber jedem SchwingungsniveauG(v) die RotationsniveausG(v) + Fv(J) angeordnet als

”Rotationsleitern “.

Abbildung 4: Veranschaulichung der Struktur der verschiedenen Uberg¨ange [15]¨

Eine sorgf¨altige Studie der feineren Wechselwirkungen zwischen Schwingung und Rotation durch Dunham (vgl. [5], S. 109; [4], Kap. 11.3.6) ergab die Term- werte des schwingenden Rotators, ausgedr¨uckt als Doppelreihe:

T(v, J) =X

lj

Ylj(v+1

2)^l·J^j(J+ 1)^j (50) Mit großer Genauigkeit gelten z.B. die Entsprechungen:

Y10=ωe, Y20=ωexe, Y30=ωeye, . . . , Y01=Be, . . . (51) so dass man in der Literatur weitgehend dieωe, ωexe, . . . , Be, . . . statt der Ylj weiter verwendet, um die Terme und Spektrallinien zu beschreiben.

Die Schwingungs-RotationstermeT(v, J) eines gegebenen elektronischen Zu- stands haben das Minimum seiner Potentialkurve als Bezugspunkt (Nullpunkt).

Betrachtet man die Gesamtheit aller elektronischen Zust¨ande eines Molek¨uls, so werden die Energieterme ¨ublicherweise auf das Minimum des tiefsten Zustands bezogen. Die Termformel eines angeregten Zustands lautet dann:

T(v, J) =Te+G(v) +Fv(J) (52) wobei Te die Termwertdifferenz zwischen dem Minimum des betrachteten angeregten Zustands und des Grundzustands angibt.

2.1.4 Wechselwirkung zwischen Elektronenbewegung und Kernbe- wegung

Bei der Herleitung der Termformel (?? wurde zwar die Wechselwirkung zwi- schen der Schwingungs- und der Rotationsbewegung der Kerne ber¨ucksichtigt, noch nicht aber die Wechselwirkung zwischen der Kernrotation und der Elek- tronenbewegung. Wechselwirkungen zwischen verschiedenen Bewegungsformen eines atomaren Teilchens k¨onnen qualitativ durch Drehimpuls-Vektormodelle beschrieben werden (vgl. [6], S. 116 ff).

Man geht zun¨achst davon aus, dass gewisse Drehimpulse, von denen jeder mit einer bestimmten Bewegungsform (z.B. der Bahnbewegung der Elektronen, dem Elektronenspin oder der Kernrotation) verkn¨upft ist, unabh¨angig voneinander erhalten bleiben.

Will man dann die Wechselwirkung zwischen bestimmten Bewegungsformen ber¨ucksichtigen, so wird dies im Rahmen des Vektormodells dadurch beschrie- ben, dass die betreffenden Drehimpulsvektoren nicht mehr streng erhalten wer- den, sondern um gemeinsame Feldachsen pr¨azedieren, so dass nur noch ihre quantisierten Komponenten entlang dieser Achsen erhalten bleiben.

Durch die Angabe der Quantenzahlen solcher quantisierter Drehimpulskom- ponenten entlang der Molek¨ulachse wurden z.B. die Elektronenzust¨ande eines zweiatomigen Molek¨uls gekennzeichnet.

Die Schreibweise¹Σ0oder etwa³Π0 setzte dabei aber voraus, dass die Kompo- nenten Λ,Σ,Ω einzeln definiert sind, dass also das elektrostatische Kernfeld so groß ist, dassL~ undS~ unabh¨angig voneinander r¨aumlich quantisiert werden.

Wird aber die Wechselwirkung zwischenL~ und S~ relativ st¨arker als deren Wechselwirkung mit dem Kernfeld, koppeln~LundS~ zu einem Elektronen- Ge- samtdrehimpulsJ~e, und nur noch dessen Achsenkomponente Ω ist definiert.

Entsprechend werden die elektronischen Zust¨ande nur noch mit dem Wert von Ω bezeichnet, die beiden Zust¨ande¹Σ0und³Π0z.B. gehen also in Zust¨ande Ω = 0 ¨uber

(eventuell noch charakterisiert durch die Bezeichnung des Symmetrieverhal- tens).

Will man nun auch die Wechselwirkung zwischen der Elektronenbewegung und der Kernbewegung ber¨ucksichtigen, so koppelt zu den genannten Elektronen- drehimpulsen der Drehimpuls der Kernrotation, und alle zusammen bilden den GesamtdrehimpulsF~.

Je nach den dominierenden Wechselwirkungen sind verschiedene Kopplungsf¨alle als Grenzf¨alle formulierbar: die Hundschen Kopplungsf¨alle (vgl. [4], Kap. 11.6.4):

Die meisten Molek¨ule zeigen aber ein ¨Ubergangsverhalten zwischen zwei- en (oder mehreren) Kopplungsf¨allen. So liegen die Zust¨ande des Jod- Molek¨uls

”zwischen“ den beiden Kopplungsf¨allen (a) und (c):

Kopplungsfall (a):

Abbildung 5: Hundscher Kopplungsfall (a) Quelle: [4], S.62

Die Kopplung zwischen der Rotation der AtomkerneN und den elektroni- schen Drehimpulsen L und S ist sehr schwach. Dagegen ist die Kopplung des Bahndrehimpulses an die internukleare Achse stark und der Spin koppelt mit dem parallel zur Molek¨ulachse ausgerichteten Magnetfeld.

Daraus folgt:

Ω =|Λ + Σ| J~=Ω +~ N~ mitJ <Ω

(53)

Kopplungsfall (c):

Abbildung 6:Hundscher Kopplungsfall (c) Quelle: [4], S.63

Die Kopplung des BahndrehimpulsesLan die internukleare Achse ist schwach.

Es bildet sich ein elektronischer GesamtdrehimpulsJ~e=~L+S~, der seinerseits an die internukleare Achse koppelt. Die Projektion des Gesamtdrehimpulses Ω koppelt wieder mit der KernrotationN zum GesamtdrehimpulsJ:

J~=Ω +~ N~

mitJ <Ω (54)

Man sieht, dass sich die beiden Kopplungsf¨alle nur gering unterscheiden.

Den Bezeichnungen¹Σ0,³Π0, . . . entspricht der Kopplungsfall (a), wo Λ,Σ,Ω und J =|J~| =p

J(J+ 1)~ definiert sind, den Bezeichnungen Ω = 0, . . . ent- spricht der Kopplungsfall (c), wobei Ω und J unabh¨angig quantisiert sind.

Eine St¨orungsrechnung, die die Wechselwirkung zwischen der Elektronen- und der Kernbewegung ber¨ucksichtigt, ergibt kleine additive Beitr¨age zum Schwingungs- und Rotationsterm:

Als Beitrag zum Schwingungsterm erg¨abe sichBv(−Ω²+L²_p), wobeiL²_p den

zeitlichen Mittelwert der Komponente des elektronischen Drehimpulses senk- recht zur Molek¨ulachse angibt (vgl. [6], S. 201 ff).

Dieser Term soll hier unber¨ucksichtigt bleiben, da Bv ωe. Außerdem ist f¨ur die beiden beteiligten Zust¨ande (siehe unten) Ω = 0 undL²_pauch f¨ur den Π- Zustand sehr klein.

F¨ur die Rotationsterme erh¨alt man einen Beitrag Φi(J), der sehr klein ist und auch deshalb hier nicht weiter ber¨ucksichtigt wird, weil die Rotationsstruktur im Detail sowieso nicht aufgel¨ost werden kann (siehe unten).

F¨ur Λ>0 hat Φi f¨ur jedesJ zwei verschiedene Werte, d.h. die Λ-Entartung wird durch die Wechselwirkung zwischen der Elektronen- und der Kernbewegung aufgehoben.

2.2 Zur Interpretation der beobachteten Absorptions¨ uberg¨ ange bei Jod

2.2.1 Zu welchem angeregten elektronischen Zust¨anden sind Ab- sorptions¨uberg¨ange m¨oglich (Auswahlregeln)?

Ein atomares System befinde sich im ZustandEm, es besitze noch weitere (dis- krete) Energieeigenwerte, z. B.En. Ber¨ucksichtigt man nun in der Schr¨odinger- Gleichung dieses Systems die Wechselwirkung mit einem elektromagnetischen Feld, das Strahlung der Wellenzahl ^En−E_hc ^m =:σmnenth¨alt, so findet man, dass das System mit einer gewissen Wahrscheinlichkeit in den ZustandEn ubergeht¨ (vgl. [5], S. 18 ff). Dies wird als Absorption oder Emission von Lichtquanten der Wellenzahlσmn interpretiert.

Die Zahl der bei einem Absorptions¨ubergang absorbierten LichtquantenN_abs^mn der Wellenzahl σmn ist proportional zu (vgl. [5], S. 19 ff)

1. der Zahl der auf das Fl¨achenelement einfallenden Lichtquanten der Wel- lenzahlσmn. (Dabei wird vorausgesetzt, dass die einfallende Strahlung in einem Wellenzahlintervall umσmn, das die ganze Linienbreite ¨uberdeckt, konstante Intensit¨at besitzt. Dies ist bei einer kontinuierlichen Lichtquelle erf¨ullt.)

2. der Zahl der sich im unteren Zustand befindlichen Teilchen in einem der Strahlung ausgesetzten Volumenelement.

3. einer quantenmechanischen Gr¨oße |R~^mn|², die die ¨Ubergangswahrschein- lichkeit misst. R~^mn heißt ¨Ubergangsmoment und hat f¨ur elektrische Di- pol¨uberg¨ange (das sind die bei weitem h¨aufigsten ¨Uberg¨ange) die Form

R~^mn= Z

Ψ^∗_nP~Ψmdτ (55)

wobei P~ das elektrische ¨Ubergangs-Dipolmoment des atomaren Systems und Ψmund Ψn die Wellenfunktionen der beteiligten Zust¨ande sind.

Bei homonuklearen Molek¨ulen ist das elektrische Dipolmoment in jedem Au- genblick einer Schwingung oder Rotation aus Symmetriegr¨unden gleich Null.

Deshalb sind alle ¨UbergangsmomenteR~mnf¨ur Schwingungs-Rotations- ¨Uberg¨ange innerhalb eines bestimmten elektronischen Zustands gleich Null. Das Jod-Molek¨ul macht also keine reinen Schwinguns-Rotations- ¨Uberg¨ange.

Andererseits sind bei homonuklearen Molek¨ulen elektronische ¨Uberg¨ange (mit Schwingungs- und Rotationsstruktur) sehr wohl m¨oglich, da sich das momen- tane Dipolmoment w¨ahrend der Neuverteilung der elektronischen Ladung, die der elektronische ¨Ubergang mit sich bringt, ¨andert (vgl. [6], S. 220).

Welche elektronischen ¨Uberg¨ange sind beim Jod-Molek¨ul m¨oglich?

Auskunft dar¨uber geben die Auswahlregeln f¨ur elektronische ¨Uberg¨ange. Man erh¨alt durch Berechnung der ¨Ubergangsmomente R~mn, die nur dann ungleich Null sind, wenn die Quantenzahlen und Symmetrieeigenschaften der beiden je- weils betrachteten Zust¨ande bestimmten Beziehungen gen¨ugen, d.h. wenn sie

”Auswahlregeln“ erf¨ullen.

Man unterscheidet Auswahlregeln, die allgemein gelten, und solche, die nur f¨ur einen bestimmten Drehimpuls-Kopplungsfall gelten (beide betrachteten Zust¨ande m¨ussen zum gleichen Kopplungsfall geh¨oren).

Folgende Auswahlregeln kommen beim Jod-Molek¨ul in Betracht (vgl. [5], S.

240):

g↔u, g=g, u=u(allgemeing¨ultig)

∆Ω = 0,±1

∆Λ = 0,±1 (Kopplungsfall a)

0⁺↔0⁺,0⁻↔0⁻,0⁺=0⁻ (Kopplungsfall c)

(56)

Der Grundzustand des Jod- Molek¨uls heißt¹Σ⁺_0g.

Als angeregte Zust¨ande (der ersten angeregten Elektronenkonfiguration) kom- men die Zust¨ande¹Πu,³Π2u,A³Π1u,B³Π⁺_0u,³Π⁻_0u in Betracht.

Nach den obigen Auswahlregeln sind nun davon die ¨Uberg¨ange¹Σ⁺_0g↔³Π⁻_0u und¹Σ⁺_0g↔³Π2unicht erlaubt.

Nach [9] wurde der Absorptions¨ubergang zum Zustand ¹Πu nicht beob- achtet und ist deshalb vermutlich sehr schwach. Beobachtbar sind Absorpti- ons¨uberg¨ange zu den Zust¨andenA³Π1u undB³Π⁺_0u. Dabei findet der ¨Ubergang X → B ¨uber den ganzen sichtbaren Spektralbereich verteilt (von ca. 500 nm an) recht kr¨aftig statt, w¨ahrend auf dem ¨UbergangX →Anur zu etwa 3−4%

des ¨UbergangsX →B - und zwar vorwiegend im Roten - absorbiert wird (vgl.

[9]).

Das Auftreten und die Auspr¨agung weiterer Bandensysteme im Ultravio- letten (z.B. zwischen 180−200 nm) h¨angen teilweise stark von Temperatur und Druck ab, so dass die experimentelle Realisierung mit großem Aufwand

verbunden ist. Außerdem liegen in diesem Bereich mehrere angeregte Zust¨ande energetisch eng beieinander, so dass die theoretische Analyse und Zuordnung der Banden schwierig wird (vgl. [9]). Es bietet sich also zur spektroskopischen Analyse der ¨UbergangX¹Σ⁺_g →B³Π⁺_0u an.

2.2.2 Welche Schwingungs- und Rotationsstruktur besitzt das Ab- sorptionsspektrum?

Durch Lichtabsorption geht das Jodmolek¨ul von einem bestimmten Schwingungs- Rotations- Zustand des GrundzustandsT⁰⁰=G⁰⁰(v) +F_v⁰⁰00(J⁰⁰) in einen anderen des angeregten ZustandsT⁰=T_e⁰+G⁰(v⁰) +F_v⁰0(J⁰) ¨uber.

Dementsprechend besitzt das absorbierte Licht die Wellenzahl

σ:=T⁰−T⁰⁰=T_e⁰+G⁰(v⁰)−G⁰⁰(v⁰⁰) +F_v⁰0(J⁰)−F_v⁰⁰00(J⁰⁰) (57) Rotationsstruktur

Zun¨achst soll nur die Rotationsstruktur F_v⁰0(J⁰)−F_v⁰⁰00(J⁰⁰) betrachtet werden.

Mit Formel (49) erh¨alt man (Te⁰+G⁰(v⁰)−G⁰⁰(v⁰⁰) =:σ0):

σ=σ0+B⁰_vJ⁰(J⁰+1)−D_v⁰J⁰²(J⁰+1)²+· · ·−(B_v⁰⁰J⁰⁰(J⁰⁰+1)−D⁰⁰_vJ⁰⁰²(J⁰⁰+1)²+. . .) (58) Dabei sind f¨ur die Betrachtung der Rotationsstruktur folgende Auswahlre- geln wichtig (vgl. [6], S. 220 ff):

∆J = 0,±1 (J = 0=J = 0) (59)

∆J = 0 verboten bei ¨Uberg¨angen mit Ω = 0↔Ω = 0 (60)

+↔ −,+=+,−=− (61)

s↔s, a↔a, s=a(f¨ur homonukleare Molek¨ule) (62) Bemerkung:

Die beiden letzten Auswahlregeln beziehen sich auf das Symmetrieverhalten der Gesamtwellenfunktion Ψ = ΨE ·ΨN des Molek¨uls (nicht ber¨ucksichtigt:

Kernspin- Anteil). Wie die Elektronenwellenfunktion ΨEkann Ψ durch ihr Sym- metrieverhalten gekennzeichnet werden (vgl. [2], S.290):

Molek¨ulwellenfunktionen werden mit Ψ⁻ bzw. Ψ⁺ gekennzeichnet, je nach- dem ob die Symmetrieoperation

”Inversion aller Koordinaten“ das Vorzeichen der Wellenfunktion ¨andert oder nicht.

Wellenfunktionen homonuklearer Molek¨ule besitzen eine weitere Symmetrieei- genschaft: Sie werden mit Ψ^a(antisymmetrisch) bzw. Ψ^s(symmetrisch) gekenn- zeichnet, je nachdem ob die Symmetrieooperation

”Austausch der Kernkoordi- naten“ das Vorzeichen der Wellenfunktion ¨andert oder nicht.

Betrachtet man die Rotationsniveaus beim ¨Ubergang X → B so sieht man,

dass die Auswahlregeln (61) und (62) nichts Neues gegen¨uber (59) bringen.

Wohl aber schr¨ankt (60) (59) dahingehend ein, dass nur Rotations¨uberg¨ange mit ∆J =±1 m¨oglich sind.

Bezeichnet man die Rotationsquantenzahlen J⁰⁰ des Grundzustands mitJ, erh¨alt man mit dieser Auswahlregel folgende zwei Linienserien (Zweige):

∆J = +1 :σ=σ0+Fv⁰(J+ 1)−Fv⁰⁰(J) =:R(J)R-Zweig (63)

∆J=−1 :σ=σ0+Fv⁰(J−1)−Fv⁰⁰(J) =:P(J)P-Zweig (64) (vgl. Abb.7). Mit Gleichung (58) erh¨alt man daraus unter Vernachl¨assigung der Dehnungsterme Dv:

R(J) =σ0+B_v⁰(J+ 1)(J+ 2)−B_v⁰⁰J(J+ 1)

=σ0+ 2B_v⁰ + (3B_v⁰ −B⁰⁰_v)J+ (B_v⁰ −B⁰⁰_v)J² (65)

P(J) =σ0+B_v⁰(J−1)J −B_v⁰⁰J(J−1)

=σ0−(B_v⁰ +B_v⁰⁰)J+ (B_v⁰ −B_v⁰⁰)J² (66) Mitm :=J + 1 f¨ur den R- Zweig und m:= −J f¨ur den P- Zweig k¨onnen beide Formeln durch eine einzige dargestellt werden:

σ=σ0+ (B⁰_v+B_v⁰⁰)m+ (B_v⁰ −B_v⁰⁰)m² (67) F¨urB_v⁰ 6=B_v⁰⁰liegen die Wellenzahlenσ=σ(m) auf einer Parabel.

Abbildung 7:Fortrat-Parabel der Rotationslinien des Schwingungs¨uber- gangsv⁰⁰= 0→v⁰= 36

Quelle: [1], S. 28a

P(J) =−0,058J−0,016J²

R(J) = 0,042 + 0,026J−0,016J² (68) Formeln und Bild folgen aus (66),(65),(47),(48), sowie den Rotationskon- stanten aus [10] und [11].

Dies hat zur Folge, dass die Wellenzahlenσentweder zu großen oder zu klei- nen Wellenzahlen hin f¨ur ein gewissesm=mseinen Maximalwert (Scheitelwert) annehmen.

Man erh¨altms aus _dm^dσ = 0 zu:

ms=− B⁰_v+B_v⁰⁰

2(B_v⁰ −B_v⁰⁰) (69)

Setzt manmsin Gleichung (67) ein, so erh¨alt man f¨ur den Abstand zwischen der ”Nulllinie“ σ0 (sie entspricht dem - verbotenen, vgl. (59) - rotationslosen Ubergang zwischen den beiden betrachteten Schwingungsniveaus, d.h.¨ J⁰⁰ = J⁰= 0 und dem Scheitel

σs−σ0=−(B⁰_v+B_v⁰⁰)²

4(B_v⁰ −B⁰⁰_v) (70)

Man kann unterscheiden:

ˆ σs> σ0, d.h. der Scheitel liegt auf der kurzwelligen (blauen) Seite vonσ0, wennB⁰_v< B_v⁰⁰

ˆ σs< σ0, d.h. der Scheitel liegt auf der langwelligen (roten) Seite vonσ0, wennB⁰_v> B_v⁰⁰

Inwieweit kann die vorliegende spektroskopische Apparatur die Rotationsstruktur aufl¨osen?

Die Aufl¨osung des verwendeten Spektrometers liegt bei ca. 0,4 nm. Kann man damit zwei benachbarte (∆m = 1) Rotationslinien aufl¨osen? Ihr Abstand be- tr¨agt:

∆σ:=σ(m)−σ(m−1) = 2B_v⁰⁰+ 2m(B⁰_v−B_v⁰⁰) (71) Setzt man hier die aus der Literatur bekannten (vgl. [10],[11]) Werte der Rotati- onskonstanten der beiden Jodzust¨ande ein (B⁰⁰e = 0,037 cm⁻¹,B⁰_e= 0,029 cm⁻¹, α⁰_e= 0,00016 cm⁻¹), so erh¨alt man etwa f¨urm≈30: ∆σ≤0,6 cm⁻¹. Dies ent- spricht bei einer mittleren Wellenl¨ange von 570 nm einer Wellenl¨angendifferenz von ∆λ≈0,015 nm. Die Aufl¨osung des Spektrometers reicht also bei Weitem nicht aus, um einzelne Rotationslinien aufzul¨osen.

Dies hat zur Folge, dass die Vielzahl an Rotations¨uberg¨angen eines bestimmten Schwingungs¨ubergangs im Spektrum nur als breite Absorptions

”banden“ sicht- bar wird, die auf einer Seite durchσs, den

”Bandenkopf“, scharf begrenzt wird.

Da f¨ur die beiden betrachteten Jodzust¨ande B_v⁰ < B_v⁰⁰ ist, istσs > σ0, d.h. es

ist zu erwarten, dass die Absorptionsbanden des Jod- Molek¨uls nach der blauen Seite hin scharf begrenzt und

”rotschattiert “sind.

Der Abstand zwischen dem Bandenkopf und der Nulllinie betr¨agt mit der Formel (70)σs−σ0≤0,13 cm⁻¹, d.h.σsundσ0liegen innerhalb der Meßungenauigkeit der Apparatur.

Tr¨agt man die Fortrat-Parabel auf und betrachtet die Verteilung der Pro- jektionen auf die σ-Achse, so sieht man, dass unter der Voraussetzung, dass die Intensit¨aten der Rotations¨uberg¨ange einer Schwingungsbande von gleicher Gr¨oßenordnung sind, in der Gegend des Bandenkopfes und der Nulllinie beson- ders viel Licht absorbiert wird. N¨aheres dazu im AbschnittBesetzungsverteilung auf die Rotationsniveaus.

Die Schwingungsstruktur des ¨Ubergangs

Zur Untersuchung der Schwingungsstruktur h¨alt man beide betrachteten Zust¨ande rotationslos, d.h.J⁰ =J⁰⁰= 0 , alsoF_v⁰⁰(J⁰⁰)−F_v⁰(J⁰) = 0. Mit Gleichungen (57) und (35) erh¨alt man dann:

σ=T_e⁰+G⁰(v⁰)−G⁰⁰(v⁰⁰)

=T_e⁰+ω_e⁰(v⁰+1

2)−ω_e⁰x⁰_e(v⁰+1

2)²+ω⁰_ey⁰_e(v⁰+1 2)³+. . .

−(ω_e⁰⁰(v⁰⁰+1

2)−ω_e⁰⁰x⁰⁰_e(v⁰⁰+1

2)²+ω_e⁰⁰y⁰⁰_e(v⁰⁰+1

2)³+. . .)

(72)

Es gibt keine strengen Auswahlregeln f¨ur die Schwingungsquantenzahlv, es kann im Prinzip jedes Schwingungsniveau des unteren mit jedem Schwingungs- niveau des oberen Zustands kombinieren.

Wenn die Schwingungsniveaus relativ zumv= 0-Niveau jedes Zustands gemes- sen werden, erh¨alt man aus den Gleichungen (35) und (36):

σ=σ0+ω₀⁰v⁰−ω⁰₀x⁰₀v⁰²+ω⁰₀y⁰₀v⁰³+· · ·−(ω₀⁰⁰v⁰⁰−ω⁰⁰₀x⁰⁰₀v⁰⁰²+ω⁰⁰₀y₀⁰⁰v⁰⁰³+. . .) (73) Dabei gibt:

σ00=T_e⁰+G⁰(0)−G⁰⁰(0)

=T_e⁰+1 2ω_e⁰ −1

4ω_e⁰x⁰_e+1

8ω_e⁰y⁰_e+. . .

−(1 2ω⁰⁰_e−1

4ω⁰⁰_ex⁰⁰_e+1

8ω_e⁰⁰y_e⁰⁰+. . .)

(74)

die Wellenzahl des ¨Ubergangsv⁰= 0→v⁰⁰= 0 an.

Zur Analyse der Schwingungsstruktur ist es n¨utzlich, Banden in

”Progressionen“

zusammen zu fassen: Zu einer Progression geh¨oren ¨Uberg¨ange, die von einem bestimmten Schwingungsniveau eines Zustands (z.B. v⁰⁰ = 0) zu aufeinander-

folgenden Niveaus des anderen Zustands (z.B.v⁰ =. . . ,6,7,8, . . .) f¨uhren. Eine

”v⁰⁰-Progression“ besteht aus Banden, deren Wellenzahlen mit wachsendem v⁰ zunehmen. Sie endet in einem Kontinuum, wo der obere elektronische Zustand dissoziiert.

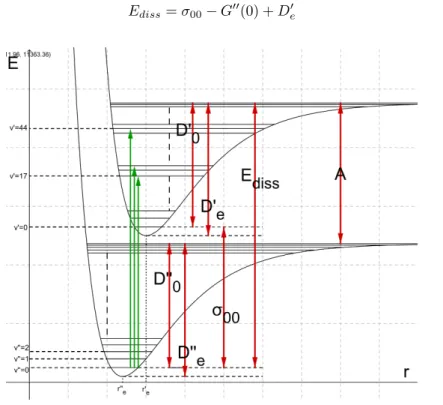
Um die Energie zu berechnen, bei der das Jod-Molek¨ul dissoziiert, findet man durch Betrachtung von Abb.8:

Ediss=σ00−G⁰⁰(0) +D⁰_e (75)

Abbildung 8:Veranschaulichung aller Energien f¨ur den Grundzustand und den ersten angeregten Zustand

2.3 Zur Interpretation der beobachteten Intensit¨ aten der Absorptionsbanden

Nachdem die Zahl der m¨oglichen ¨Uberg¨ange durch die Auswahlregeln einge- schr¨ankt wurde, bleibt nun noch zu untersuchen, wovon die St¨arke der Absorp- tion einer bestimmten (festen) einfallenden Lichtintensit¨at der Wellenzahlσmn

auf einem erlaubten ¨UbergangEm→En abh¨angt.

Man muss dazu laut Abschnitt 2.1 die zahlenm¨aßige Verteilung der Jod- Mo- lek¨ule auf die m¨oglichen unteren Niveaus und die Gr¨oße der ¨Ubergangsmomente wissen.

2.3.1 Wie sind die Jod- Molek¨ule auf die Schwingungs- und Rotati- onsniveaus des Grundzustands verteilt?

Jeder Energiezustand eines zweiatomigen Molek¨uls sei identifiziert durch die QuantenzahlenJ undv, sowie eine Zahl , die den elektronischen Zustand an- gibt. Dann befinden sich nach dem Maxwell- Boltzmann- Verteilungsgesetz von N vorliegenden Molek¨ulen, die sich bei einer Temperatur T in thermischem Gleichgewicht befinden, ein Anteil von:

NvJ =N gvJ

exp(−^E(,v,J)kT ) Qi

(76) Molek¨ulen in einem bestimmten Energiezustand E(, v, J). Dabei ist

Qi= X

,v,J

gvJexp(−E(, v, J)

kT ) (77)

die”innere Verteilungsfunktion“. Die statistischen GewichtegvJ geben die Entartung der Niveaus (, v, J) an.

Man nimmt nun an, dass die gesamte innere Energie eines Molek¨uls separat aufgespalten werden kann in

E(, v, J) =Ee() +Ev(v) +Er(J) (78) Dies impliziert, dass das Molek¨ul separate elektronische, Schwingungs- und Ro- tationsfreiheitsgrade besitzt, die unabh¨angig angeregt werden k¨onnen.

(Dass diese Annahme nur N¨aherungscharakter hat, sieht man z.B. daran, dass die Rotationskonstanten Bv = Be−αe(v+ ¹₂) + . . . sehr wohl von v abh¨angen und weiter die Konstanten Be, αe, . . . vom elektronischen Zustand abh¨angen). Unter dieser Annahme kann man zeigen (vgl. [6], S. 216 ff), dass sichNvJ schreiben l¨asst als

NvJ =N(g

exp(−^EekT⁽⁾⁾

Qe

)

| {z }

f

(gv

exp(−^EkT^v(v)) Qv

)

| {z }

fv

(gJ

exp(−^EkT^r(J)) Qr

)

| {z }

fJ

(79)

Dabei gebenQe, Qv undQJ die Verteilungsfunktionen f¨ur verschiedene Ar- ten von Freiheitsgraden an:

Qe=X

gexp(−Ee() kT ), Qv =X

v

gvexp(−Ev(v) kT ), Qr=X

J

gJexp(−Er(J) kT )

(80)

g, gv, gJ geben die Entartungen des betrachteten elektronischen, Schwingungs-

und Rotationszustands an.

Die Faktorenf, fv undfJ sind die Bruchteile von Molek¨ulen im elektroni- schen Zustand, im Schwingungszustandv und im RotationszustandJ bei der TempearaturT.

Diese Faktoren und deshalb auch die relative Verteilung der Molek¨ule in jedem Freiheitsgrad sind (in der betrachteten N¨aherung) unabh¨angig voneinan- der.

Wie sieht nun die Verteilung beim Jod- Molek¨ul aus?

1. Bei 300 K betr¨agt kT = 0,2585 eV (208,5 cm⁻¹).

Der erste angeregte elektronische Zustand des Jodmolek¨uls A³Π1u liegt ca. 12000 cm⁻¹uber dem Grundzustand, so dass sich¨ fE≈10⁻²⁶bei 300 K ergibt. Es befinden sich also so gut wie alle Molek¨ule im elektronischen Grundzustand.

2. Interessant ist beim Jod- Molek¨ul die Besetzungsverteilung auf die Schwin- gungsniveaus des Grundzustands:

F¨ur die Schwingungen eines zweiatomigen Molek¨uls istgv= 1.

Da die (unteren) Schwingungsniveaus durch die FormelG⁰⁰(v) =ω⁰⁰_e(v+

1

2)−ω⁰⁰_ex⁰⁰_e(v+¹₂)²gut beschrieben werden und nach [10]ω⁰⁰_e = 214,5 cm⁻¹ undω⁰⁰_ex⁰⁰_e = 0,61cm⁻¹ betragen, ergibt sich:

Qv=X

v

exp(−Ev(v) kT ) =X

v

exp(−G⁰⁰(v)hc

kT )≈0,9357 (81) und f¨ur die Besetzungsverteilung auf die Schwingungsniveaus des Grund- zustands das Bild.

Infolge der großen Masse des Jod- Molek¨uls ist das Schwingungsquantω⁰⁰_e so klein, dass bei Zimmertemperatur auch die Schwingungsniveausv⁰⁰ = 1,2, . . . merklich besetzt sind.

3. Besetzungsverteilung auf die Rotationsniveaus:

Der GewichtsfaktorgJl¨asst sich als Produkt schreiben:gJ=gn·(2J+ 1).

2J+ 1 gibt die Entartung des J-ten Rotationsniveaus an, denn der Dre- himpulsvektorJ~ mit |J~|=p

J(J+ 1)~ kann (2J+ 1) verschiedene Ori- entierungen im Raum annehmen (vgl. [6], S.179). Um den Gewichtsfaktor gn zu ber¨ucksichtigen, muss man bei der Gesamtmolek¨ulwellenfunktion noch einen Kernanteil Ψn als Faktor ber¨ucksichtigen. Ψn wird aus den jeweils (2I + 1)- fach entarteten Wellenfunktionen der einzelnen Kerne konstruiert (I: Kernspin). Mit wachsendem J ist Ψn abwechselnd sym- metrisch und antisymmetrisch bzgl. Kernaustausch. Man kann nun zei- gen, dass bei homonuklearen Molek¨ulen symmetrische Wellenfunktionen Ψ^s_n auf g^s_n = (2I + 1)(I + 1) verschiedene Weisen aus den Einzelkern- wellenfunktionen konstruiert werden k¨onnen, w¨ahrend antisymmetrische Wellenfunktionen Ψ^a_n aufg_n^a = (2I+ 1)I verschiedene Weisen.

Abbildung 9: Thermische Besetzungsverteilung der Schwingungsnive- aus des Jodgrundzustands beiT = 300K.

Diese Variation ingn ¨andert die Besetzung aufeinander folgender Rotati- onsniveaus im Verh¨altnis

g^s_n

g^a_n =I+ 1

I (82)

Da der KernspinI beim Jod- AtomI= ⁵₂ bet¨agt, lautet diese Verh¨altnis beim Jod- Molek¨ul 7:5.

gnbleibt aber im Weiteren unber¨ucksichtigt, da der Einfluss dieser Varia- tion l¨angst nicht aufgel¨ost werden kann und andererseits die Grobstruktur einer Schwingungsbande nicht beeinflusst wird.

fJ lautet dann:

fJ = (2J+ 1)exp(−^F(J)hckT ) Qr

mitQr= X∞ J=0

(2J+ 1) exp(−F(J)hc kT )

(83)

Qrkann man f¨urT = 300 K f¨ur das Jod- Molek¨ul (Be= 0,037 cm⁻¹, vgl.

[10]) zu 2,82·10³ approximieren (vgl. [6], S.187).

F¨ur die unteren Schwingungszust¨ande des Grundzustands ergibt sich mit diesemQr, F(J) = BeJ(J + 1)(v klein!) und T = 300 K als Besetzungs- verteilung der Rotationsniveaus.