x , bc ℜ∈ a )( +−= bcxxf

***LÖSUNGSVORSCHLAG***

Themen:

Grundlagen der Integralrechnung

Umfang: 4 Aufgaben

Hilfsmittel: Sind keine notwendig. Eine Formelsammlung und ein nicht programmierbarer Taschenrechner können aber verwendet werden.

Aufgabe A1 (Integralrechnung mit Parameter):

Gegeben sei eine Parabel mit der Gleichung

b cx x

f( )=− ² + ,

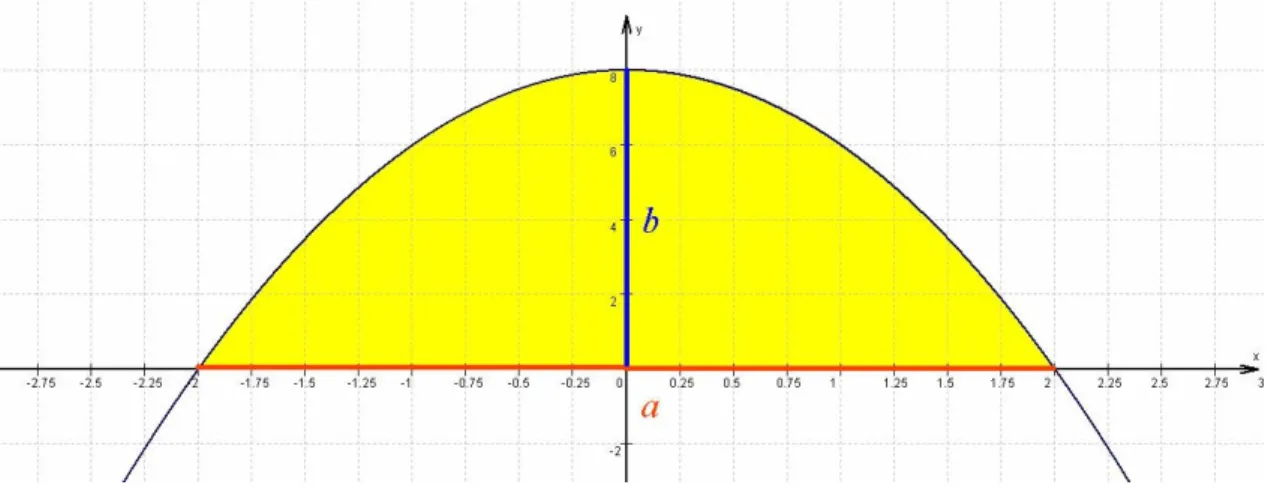
wobei c,b∈ℜ⁺. Es sei a der Abstand ihrer Nullstellen und A der Flächeninhalt, den die Parabel mit der x-Achse einschließt. Zeigen Sie, dass

ab A 3

= 2 .

Lösung:

Figur 1: Beispielskizze für die Berechnung des gesuchten Flächeninhaltes.

•

••• Allgemeine Form dieses Parabeltyps:

b cx x

f( )=− ²+ , wobei c>0 und b>0.

•

••• Berechnung der Nullstellen:

c x b

c x b

c x b b

cx x

f( )=0⇒− ²+ =0⇒ ² = ⇒ ₁ =− ₂ =+ Der Zusammenhang mit a gestaltet sich folgender Maßen:

c a b c

b c

b = ⋅ =









−

− 2

•

••• Aufstellen und ausrechnen des Integrals:

( )

=























−

⋅

 +











−

−

−























⋅

 +











− 

 =

 

− +

= +

−

=

− +

−

∫

^{cx b dx cx bx c} _c^{b b b}_c ^{c b}_c ^{b b}_c

A

c b

c b c

b

c b

3 3

3

³ 3

² 3

= +

⋅

⋅

−

=

⋅

⋅ +

⋅

⋅

−

=

⋅

 +











⋅

−

⋅

 +











⋅

−

=

=

⋅ ⋅

 =











 a ba

c b c c

b b c b c b c c

b b c b c c b b c b c

c a b c

b c b c

b 2 3

3 2 3

3 ₂

3 3

3

ab ab

ab 3

2 3 =

−

=

Anmerkung: Die Konstante k, die beim Integrieren hinzukommt, verschwindet durch die Subtraktion.



Aufgabe A2 (Extremwertaufgabe mit Produktintegration):

Die Wachstumsgeschwindigkeit einer speziellen Gummibaumart im Gewächshaus wird beschrieben durch die Funktion

t

sG t a t e

w ( )= ⋅ ⋅ ²⁻ , mit a∈ℜ⁺ und t∈ℜ⁺ in Monaten. (1)

Die Höhe des ausgewachsenen Bäumchens werde mit H bezeichnet und wird in Metern gemessen.

a) Wann ist die Wachstumsgeschwindigkeit extremal? Wann ändert sich die Wachstumsgeschwindigkeit am schnellsten?

b) Stellen Sie eine Formel für den Zusammenhang zwischen a und der maximalen Höhe H auf. Wir groß ist a, wenn der Baum ausgewachsen 3,70 Meter misst?

Runden Sie sinnvoll!

Wir verwenden nun a=0,50 in obiger Formel.

c) Der Baum gilt als ausgewachsen, wenn sich seine Größe im Verlauf eines Monats um weniger als 0,1 cm ändert. Wann ist dieser Zeitpunkt erreicht und wie groß ist der Baum dann?

Eine genauere Untersuchung zeigt, dass bei Bäumen dieser (fiktiven) Art, welche im Januar eines Jahres im Gewächshaus gepflanzt werden, die Formel



 



⋅ 

−

⋅

⋅

= t e ⁻ t

t

w_sG ^t

cos 6 05 , 0 5

, 0 )

( ²

2

π , mit a∈ℜ⁺ und t∈ℜ⁺ in Monaten, (2)

bessere Ergebnisse liefert.

d) Ein Baum ist nun nach genau drei Jahren ausgewachsen. Wie groß ist er dann? Wie groß ist ein Baum, der durch Formel (1) mit a=0,50 beschrieben wird? Wie erklären Sie sich das Vergleichsergebnis und wie lässt sich der Zusatzterm in Formel (2) interpretieren? Wie könnte Formel (2) aussehen, wenn ein Baum Anfang Juli gepflanzt wird und sonst gleichen Voraussetzungen unterliegt?

Lösung:

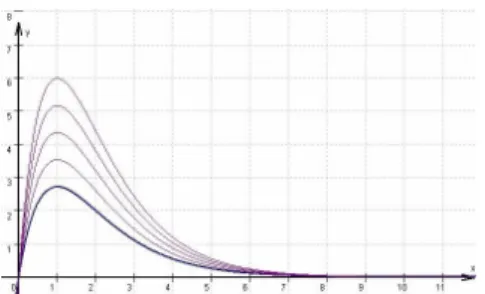
a) Das Schaubild der Wachstumsfunktion des Gummibaumes sieht wie folgt aus (Zeichnung für mehrere Werte von a):

Figur 1: Graph der Funktion der Wachstumsgeschwindigkeit.

Die Wachstumsgeschwindigkeit ist extremal, wenn

0 ) (

' t =

w_sG und w''_sG(t)≠0

gilt. Wir bilden also die Ableitungen:

( )

^t

t t

sG t a e a t e a t e

w' ( )= ⋅ ²⁻ − ⋅ ⋅ ²⁻ = ⋅ 1− ⋅ ²⁻ ,

wobei wir die Produktregel verwendet haben und es ist

( )

^t

( )

^t

t

sG t a e a t e a t e

w'' ( )=− ⋅ ²⁻ − ⋅ 1− ⋅ ²⁻ = ⋅ −2 ⋅ ²⁻ ,

ebenfalls mit der Produktregel berechnet. Hiermit erhalten wir nun

(

1

)

0

) (

'_sG t =a⋅ −t ⋅e^2−t =

w .

Da a als Konstante nicht 0 werden kann und der e-Teil ebenso wenig, ergibt sich t=1 als Nullstelle. Da

(

1 2

)

0

) 1 ( '

' = ⋅ − ⋅ ²⁻¹ =− <

e e a

a w _sG

ist, liegt sogar immer ein Maximum vor. Dies ist so, da a laut Voraussetzung nur positive Werte annehmen soll.

In diesem Fall beträgt die Wachstumsgeschwindigkeit

e a e a

w_sG(1)= ⋅1⋅ ²⁻¹ = ⋅ ,

wobei die Einheit Meter pro Monat beträgt.

Für die schnellste Änderung der Wachstumsgeschwindigkeit arbeiten wir mit der zweiten Ableitung.

( )

^t

sG t a t e

w'' ( )= ⋅ −2 ⋅ ²⁻ ,

die gleiche Argumentation wie bei der ersten Ableitung liefert t =2. Die Überprüfung mit der dritten Ableitung (welche wir hier nicht zeigen) ergibt, dass wirklich ein Wendepunkt vorliegt.

Einsetzen in die Ableitung der ursprüngliche Funktion ergibt

a e

a

w'_sG(2)= ⋅(1−2)⋅ ²⁻² =− .

Betrachtet man die Randwerte, so erhält man

( )

e a e

a

w'_sG(0)= ⋅ 1−0 ²⁻¹ = ⋅ und

( )

1 0 lim

) ( ' lim

2

− =

= ⋅

∞

→

∞

→ sG t t

t e

t t ae

w .

Bei der Grenzwertbildung wurde die Funktion einfach mit Hilfe der Potenzgesetze umgestellt und unter Berücksichtigung, dass eine e-Funktion schneller als alles andere wächst, berechnet.

Da a⋅e > a nach den Voraussetzungen in der Aufgabe, ändert sich die Geschwindigkeit zum Zeitpunkt t =0 am schnellsten.

b) Die maximale Höhe ergibt sich, wenn der Baum ausgewachsen ist, d.h. bei unserer Modellfunktion nach unendlicher Zeit. Des Weiteren liegt uns nur die Funktion für die Wachstumsgeschwindigkeit vor. Wir müssen also integrieren. Nach dem Gesagten ist

∫

∞

=

0

) (t dt H

w_sG .

Wir rechnen

( )

∫

^{xwsG t dt =}

∫

^{x a⋅t⋅e −t dt}

0 0

) 2

( ,

wobei wir die Produktintegration verwenden. Zur Erinnerung:

PRODUKTINTEGATION:

Die Funktion lautet: f(x)=u(x)⋅v'(x)

Für die Integration gilt dann:

∫ (

^⋅

)

⁼

[

^⋅

]

⁻

∫

^b

(

^⋅

)

a b a b

a

dx x v x u x

v x u dx x v x

u( ) '( ) ( ) ( ) '( ) ( )

In unserem Fall erhalten wir mit u(t)=a⋅t und v'(t)=e^2−t

[ ] [ ] [ ]

( )

[

¹

] ⁽

¹

^{) (}

^{0 1}

^{) (}

¹

⁾

^{( ).}

) (

2 2

0 2 2

0 2

0 2 0

2 0

2 0

2

0 0 '()

2 ) (

x W e e a

x e e a

a e x a e

t a

e a e

t a dt e a e

t a dt e t a dt t w

x sG x x

t

t x t x

x x t t

x x

t v

t t u sG

=

⋅ + +

⋅

− ⋅

=

⋅ +

⋅ +

⋅ +

⋅

−

=

⋅ +

⋅

−

=

⋅

− +

⋅

⋅

−

=

⋅ +

⋅

⋅

−

 =











 ⋅ ⋅

=

−

−

−

−

−

−

−

−

∫

∫ ∫

Durch Grenzwertbildung erhalten wir

H e a e e a

x e a

x x = ⋅ =







 ⋅ ⋅ + + ⋅

−

∞

→

2 2

2 ( 1)

lim .

Damit haben wir die gesuchte Formel gefunden, sie lautet

a e H = ²⋅ .

Der Zusammenhang ist also linear, da e² eine Zahl ist, keine Variable. Damit ergibt sich bei einer Höhe von 3,70 Metern der Wert

50 ,

=0

a .

Figur 2: Baumgröße.

c) Wir wollen wissen, wann der Baum ausgewachsen ist. Dazu verwenden wir nun die Integration aus Teilaufgabe b). Dort erhielten wir

( )

2

2 1

)

( a e

e x e x a

W_sG ⋅ ⋅_x + + ⋅

−

= .

als Funktion für die Baumgröße in Metern. Die Größe soll sich im Verlauf eines Monats um weniger als 0,1 cm (also 0,001 Meter) ändern. In Formeln

001 , 0 ) ( )

1

(x+ −W x ≤

W_{sG sG} .

Wir rechnen

( ) ( )

( ) ( )

. 001 , 2 0

2

1 2

2 2

2 2

2 2

2 1

2

− ≤ +

−

= ⋅

⋅ +

⋅

⋅ +

⋅

−

⋅

⋅

= −

⋅ + −

⋅ + ⋅

⋅ + +

⋅

− ⋅ ₊

x x

x x

e

ae ae

ae ae x e

e a x e a e a x e a

e e a

x e e a

e a x e a

Für den vorgegebenen Wert a=0,50 erhalten wir (numerisch) x≈10,11 Monate. Nach dieser Zeit ist der Baum

(

10,11

)

≈3,693

WsG Meter

hoch.

d) Wir berechnen wieder das entsprechende Integral, wobei ein Jahr ja zwölf Monate hat.

(36) 0 3,6945 . sin 6

05 6 , 0 ) 12 (

cos 6 05 , 0 ) 6 (

cos 05 , 0 5

, 0

) 6 sin(

0 ) 0 sin(

36

0 36

0

36

0 12

3

0

2

m W

t W

dt t dt

t w dt t e

t

sG sG

sG t

≈ +

 =



 



 



 



⋅ 

⋅ +

=



 



⋅  +

 =



 



 



 



⋅ 

−

⋅

⋅

=

=

⋅

−

∫ ∫

∫

π

π π

π π

Wir sehen aus dieser Rechnung, dass der oszillierende Term sich weg hebt und beide Funktionen ((1) und (2)) den gleichen Funktionswert liefern. Integriert man bei den vorliegenden Arten der Sinus- oder Kosinusfunktionen über eine volle Periode oder deren Vielfache (hier: Periode p=2π/^π₆ =12), so ist der orientierte Flächeninhalt gleich

0.

Der Zusatzterm lässt sich als durch die Jahreszeiten bedingte Schwankung der Größe interpretieren, da seine Periode genau ein Jahr umfasst. Im Falle eines um sechs Monate später gepflanzten Bäumchens, könnte z.B. der oszillierende Term addiert statt subtrahiert werden, so dass



 



⋅  +

⋅

⋅

= t e ⁻ t

t

w_sG ^t

cos 6 05 , 0 5

, 0 )

( ²

3

π , mit a∈ℜ⁺ und t∈ℜ⁺ in Monaten verwendet werden kann.

 Aufgabe A3 (Integralrechnung – Basistechniken):

Geben Sie die Stammfunktionen für die Funktionen mit den folgenden Funktionsgleichungen an:

a) a(x)=mxⁿ +nx^m −c mit n=

{

1,2,3,...

}

.

b) b(x)=a⋅sin

(

mx+c

)

−cos

( )

2x c)

x k x

c = 1 − ) (

d)

7 1 ) 2

( ₂

+

−

= −

x x x x

d ^e)

2 3

) 2

(x ae x

e = ^x+ − ^{f )} f(x)=

(

mx+3

)

⁵

g) g(x)=x⋅e^{x h)} h(x)=sin(x)⋅x^{2 i )} i(x)=e^x⋅sin(x)

j ) j(x)=ln(x) Tipp:

( )

x 1x ' ) ln( = .

k) k(x)=sin²(x)+cos²(x) ^{l )}

x x x

l = 1 + )

(

Lösung:

Wir verwenden die folgenden Regeln:

Potenzfunktionen:

1

1 .

1

−

+

⋅

⋅

+ + ⋅

⋅

k

k k

x k c

const k x

x c

c _Aufleiten

Ableiten

Lineare Substitution:

1

1

) (

. )

) ( 1 ( 1 )

(

−

+

+

⋅

⋅

⋅

+ +

⋅ + ⋅

+ ⋅

⋅

k

k k

b x m k m

const b

x k m

b m x m

Nützlich bei Bruch-Funktionen:

Ist ( )

) ( ) '

( f x

x x f

u = , so ist

∫

^u(x)dx=

∫

^f_f^'₍⁽_x^x₎^{)dx=ln f(x) +const.}

e-Funktionen:

c bx

c bx c

bx

e b a

const b e

e a a

+

+ +

⋅

⋅

+

⋅

⋅ .

Trigonometrische Funktionen:

) cos(

. )

cos(

) sin(

b x m m

a

const b

x m m

b a x m a

+

⋅

⋅

⋅

+ +

⋅

− +

⋅

⋅

) sin(

. )

sin(

) cos(

b x m m a

const b

x m m

b a x m a

+

⋅

⋅

⋅

−

+ +

⋅ +

⋅

⋅

Aufleiten

Ableiten

Aufleiten

Ableiten

Aufleiten

Ableiten

Aufleiten

Ableiten

Produktintegration:

Die Funktion lautet: f(x)=u(x)⋅v'(x)

Für die Integration gilt dann:

∫ (

^⋅

)

⁼

[

^⋅

]

⁻

∫

^b

(

^⋅

)

a b a b

a

dx x v x u x

v x u dx x v x

u( ) '( ) ( ) ( ) '( ) ( )

Damit sind wir für die Aufgaben gerüstet. Durch Anwenden der Regeln finden wir die folgenden Stammfunktionen.

a) .

1 ) 1

( )

( ¹ x ¹ cx const

m x n

n x m A c nx mx x

a ^{n m n m} − +

+ +

= +

→

− +

= ^{+ +}

b)

( ) ( ) ( )

sin

( )

2 .

2 cos 1

) ( 2 cos sin

)

( mx c x const

m x a

x c

mx a

x

b = ⋅ + − → =− + − +

c) 1 ( ) ln .

)

( k C x x kx const

x x

c = − → = − +

d) ( ) ln 7 .

7 1 ) 2

( ₂ D x x² x const

x x x x

d → = − + +

+

−

= −

e) .

3 1 ) 2

( )

( ^{2 3 2} ae^{2 3} x³ const

x E x ae

x

e = ^x+ − → = ^x+ − +

f)

( )

⁵

(

3

)

⁶

6 ) 1 ( 3

)

( = + → = ⋅ mx+

x m F mx

x f

g) g(x)=x⋅e^x.

Die Produktintegration liefert

( ) [ ] ∫ ( ) ( )

∫

^{xex dx= xex − 1⋅ex dx= x−1ex +const.}

h) h(x)=sin(x)⋅x².

Die doppelte Produktintegration liefert

( ) [ ] ^{( )} [ ] [ ]

. )

cos(

2 ) sin(

2 ) cos(

) sin(

2 ) sin(

2 ) cos(

) cos(

2 ) cos(

) sin(

2

2 2

2

const x

x x x x

dx x x

x x x

dx x x x

x dx x x

+ +

+

−

=

⋅

− +

−

= +

−

=

⋅

∫ ∫

∫

i) i(x)=e^x⋅sin(x).

Mit Hilfe der doppelten Produktintegration erhalten wir

( ) [ ] ( ) [ ] [ ] ( )

( ) [ ] [ ]

( ) ⁽

^{sin( ) cos( )}

⁾

^.

) 2 sin(

. )

cos(

) sin(

) sin(

2

) sin(

) cos(

) sin(

) cos(

) sin(

) sin(

const x

e x dx x e

const x

e x e dx x e

dx x e x

e x e dx x e

x e dx x e

x x

x x

x

x x

x x

x x

+

−

⋅

⇒ =

+

−

=

⇒ ⋅

−

−

=

−

=

∫

∫

∫

∫

∫

j) j(x)=ln(x). Tipp:

( )

x 1x ' ) ln( = .

Wir wollen diese Funktion integrieren. Dazu schreiben wir sie zuerst als ein Produkt hin:

x x

x

f( )=ln =1⋅ln

Nun interpretieren wir die Faktoren als unsere Funktionen in der Produktintegrations- formel:

1 ) ( '

ln ) (

=

= x v

x x

u

Dann bilden wir die benötigten Auf- und Ableitungen:

x x

u( )=ln und x x

u 1

) (

' =

x x

v( )= und v'(x)=1

Setzen wir nun alles ein, so erhalten wir

[ ]

1

[

ln

]

1 ln .

ln

ln dx x x dx x x x const

x x x x

xdx= ⋅ −

∫

⋅ = ⋅ −

∫

= ⋅ − +

∫

k) k(x)=sin²(x)+cos²(x)

Da sin²(x)+cos²(x)=1 (Additionstheorem) ist K(x)=

∫

1dx=x+const.

l) x

x x

l = 1 + )

( .

Wir schreiben .

2 2 1

) 1 (

)

( ^{2 2}

1 2

1

const x

x x

L x x x x x

l = + = ⁻ + → = ⋅ + + und das ist

2 . 2 1

)

(x x x² const

L = + +

 Aufgabe A4 (Integralrechnung für Fortgeschrittene):

Bestimmen Sie die Stammfunktionen der Funktionen mit den folgenden Funktionsgleichung- en.

a) f(x)=arcsinx

b) g(x)=ln² x Tipp: Verwenden Sie

∫

^{lnxdx= x⋅lnx−x.}

Berechnen Sie die folgenden Integrale.

c) dx

x

x x x

∫

x

− −

+

− +

1 −

1

2 2 3 4

4

1 3

d)

∫

x^⋅

( (

⁻x

)

^⋅

)

dx

3

0

9 2

sin π

π

e)

∫

e ^xdx

1

0

Lösung:

a) Wir arbeiten hier mit der partiellen Integration. Es ist

∫

∫

∫

−

⋅

−



 



 ⋅

=

⋅

= dx

x x

x x

dx x dx

x

u u v

u v v

'

' 1 2

arcsin 1 arcsin

1

arcsin .

Wir sind nun an

∫

− dx x x 1 2

interessiert. Wir setzen u=1−x², womit

xdx du

dx x

du =−2 ⇔ =−2

folgt. Alles einsetzen liefert uns

( )

∫ ∫ ∫

∫

^{= ⋅ =− ⋅ − =−}

−

du u dx

x u xdx

u dx

x

x 1

2 2 1

1 2 1 1

1 ²

.

Wir finden nun relativ leicht, indem wir ²

1

1 −

=u

u verwenden, das Folgende:

c x c

u c

u du

u =− ⋅ ⋅ + =− + =− − +

−

∫

^{− 2 2}

1 2

1

1 1 2 2 1 2

1 .

Schmeißen wir alles in einen Topf, so erhalten wir die gesuchte Stammfunktion:

c x x

x

xdx= ⋅ + − +

∫

^{arcsin arcsin 1 2 .}

 b) Wieder stürzen wir uns auf die partielle Integration und nutzen dabei den gegebenen

Tipp aus. Es ist

( )

[ ] ( )

( ) [ ]

[ ]

( )

[

^{ln 1 1}

] ⁽

^{ln 1}

⁾

^.

1 1 ln 2 ln 2

ln 2 ln

ln ln

ln 1

ln ln

ln

ln 1 ln

ln ln

ln ln

2 2

2 2

2 2

2

c x x

x c x

x

c x

x x c x x x x x

c x x x x x x x x dx x x

x x x

xdx x x x x x x x dx x x xdx

+ +

−

⋅

= + +

−

⋅

=

+ + +

−

⋅

= + +

⋅

−

⋅

=

+

−

−

⋅

−

⋅

−

⋅

=

−

−

⋅

−

⋅

=

⋅

−

⋅

−

⋅

−

⋅

=

⋅

=

∫

∫

∫ ∫



c) Hier müssen wir mit der Polynomdivision beginnen, um einen echt gebrochenratio- nalen Funktionsteil zu erhalten. Es ist

21 13

20 5

13 5

12 3

5 3

4

5 3 )

4 (

: ) 1 3

(

2 2 3

2 3

2 4

4 21 2 13

2 2

3 4

2

+

−

−

− +

−

+

−

−

+ +

−

=

− +

− +

− −

+

−

x x

x x

x x

x x

x x

x x x

x x

x

x x

x

Den ganzrationalen Teil können wir leicht integrieren. Für den gebrochenrationalen wenden wir die Partialbruchzerlegung an. Unser Ansatz lautet:

( ) ( ) ( ) ( )

4 2 4

2 2

2 2

4 21 13

2 2

2 −

−

⋅ +

⋅

= +

−

−

⋅ + +

= ⋅ + +

= −

− +

−

x

B A x

B A x

x B x

A x

B x

A x

x .

Durch Koeffizientenvergleich finden wir hier A=−₄⁵ und B=−11₄³. Nun können wir die Integration durchführen. Es ist

( )

( )

[ ] [ ( ) ]

( ) ( ) ( ) ( ) ( )

( ) ( )

( )

( )

ln

( )

3.

2 21 3 3 32 4 ln 10 42 1

4 ln 3 47 4 ln 47

3 4 ln 1 5 4 ln 1 5 5 2 1

1 3 3 1 1 5 2 1

1 3 3 1

2 4 ln

2 47 4 ln

5 5 2 3 3 1

2 1 4

47 2

1 4 5 5 4 3

1 3

3 2 0 1 ln

2 2 3

3

1 1 1

1 1

1 2

3

1

1 1

1

1

1 2

1

1

2 2 3 4

⋅

−

=

⋅

−

=

⋅ +

⋅

−

⋅ +

⋅

−



 



 ⋅ − − ⋅ − + ⋅ −

−

⋅ +

⋅

−

⋅

=

+

⋅

−

−

⋅

 −

 

 − +

=

⋅ +

− −

⋅

− +

−

− =

+

− +

−

=

−

−

−

−

− −

−

∫

∫ ∫

∫

x x

x x x

x dx x dx

dx x x x dx

x x x x

Damit wären wir „schon“ fertig.

 abziehen

abziehen

abziehen

x2

⋅ ) 3 (− x

⋅

⋅5

Multiplikationen

d) Hier setzen wir u ⁼

(

⁹⁻x²

)

^⋅π. Dann erhalten wir

x dx du

dx x du

π π 2 2

= −

⇔

−

= .

Wir setzen ein und bekommen

( )

( ) ( ) ( ) ( )

[ ( ) ] ( ( ) ( ) ) ( )

1.

2 1 2 2 1 9 1

cos 0 2 cos cos 1

2 1

2 sin 1 sin 2

sin 9

sin

0 9

) 3 (

) 0 ( )

3 (

) 0 ( )

3 (

) 0 ( 3

0

2

=

= +

⋅

=

−

⋅

=

⋅

=

⋅

−

− =

⋅

=

⋅

=

⋅

−

⋅

∫ ∫ ∫

∫

π

π π π

π π

u π

du x u

u du x

dx u x dx

x x

u

u u

u u

u

 e) Hier substituieren wir u = x, womit

du x dx dx x

du = ⇔ =2 ⋅

2 1

ist. Setzen wir das ein, so ergibt sich

du e u du x e dx

e ^u

u

u u

x

∫ ∫

∫

^{= ⋅ = ⋅}

=

=

1

0 1

) 1 (

0 ) 0 ( 1

0

2

2 .

Von nun an geht es mit partieller Integration weiter, da wir einen Funktionsteil haben, der beim Ableiten irgendwann verschwindet und einen, der das eben nicht tut. Wir erhalten

[ ] [ ] [ ] [ ^{( )} ]

( )

[

^{2 1 1}

] [

²

⁽

^{0 1}

⁾ ]

^2.

1 2 2

2 2

2 2

2 0 0

1

1 0 1

0

1 0 1

0

1 0 1

0

=

⋅

−

⋅

−

⋅

−

⋅

=

⋅

−

⋅

=

⋅

−

⋅

=

⋅

−

⋅

=

⋅

−

=

∫ ∫

e e

e u e

ue du

e ue

du

ue^{u u u u u u}

Über so ein Ergebnis kann man wirklich nicht meckern, oder?

