Messungen der elektrischen und thermodynamischen Eigenschaften von EuC

luftinstabiler Materialien und

Messungen der elektrischen und thermodynamischen Eigenschaften von EuC

und LiFeAs

Inaugural Dissertation

zur

Erlangung des Doktorgrades

der mathematisch-naturwissenschaftlichen Fakultät der Universität zu Köln

vorgelegt von

Oliver Heyer

Köln, im Dezember 2012

Vorsitzender

der Prüfungskommission: Prof. Dr. U. Ruschewitz Tag der mündlichen Prüfung: 27.01.2012

1 Einleitung 1

2 Theoretische Grundlagen 5

2.1 Magnetismus . . . 5

2.1.1 Magnetisierung . . . 7

Diamagnetismus . . . 7

Paramagnetismus . . . 7

2.1.2 Wechselwirkungen . . . 8

Ferromagnetismus . . . 11

Antiferromagnetismus . . . 11

2.1.3 Theoretische Beschreibung ferromagnetischer Ordnung . . 12

Molekularfeld-Näherung für das Heisenberg-Modell . . . . 12

Landau-Theorie des Ferromagnetismus . . . 15

Spinwellen Theorie des Heisenberg-Modells . . . 16

2.2 Wärmekapazität . . . 18

2.2.1 Gesetz von Dulong und Petit . . . 19

2.2.2 Quantenmechanische Behandlung der Wärmekapazität . . 20

Gitteranteil . . . 20

Elektronischer Beitrag . . . 21

Magnetischer Beitrag . . . 22

2.3 Thermische Ausdehnung . . . 23

2.3.1 Thermodynamik der thermischen Ausdehnung . . . 24

2.3.2 Thermische Ausdehnung bei Ferromagneten . . . 24

2.3.3 Grüneisenskalierung . . . 25

2.4 Transport von Ladung . . . 26

2.4.1 Elektrische Leitfähigkeit . . . 26

Drude-Sommerfeld-Modell . . . 26

Bloch-Wellen und Bänder . . . 27

Näherung fast freier Elektronen . . . 28

Näherung stark gebundener Elektronen (Tight-Binding- Model) . . . 28

Bänder . . . 29

Streuprozesse . . . 31

Semiklassische Beschreibung . . . 34

2.5 Supraleitung . . . 38

2.5.1 London Theorie . . . 38

2.5.2 Ginzburg-Landau-Theorie . . . 39

3 Experimentelles 43

3.1 Handschuhboxen . . . 43

3.1.1 Bemerkungen zur Handhabung der Handschuhboxen . . . 44

Inbetriebnahme . . . 44

Regeneration der Boxen . . . 45

Undichtigkeiten . . . 45

3.2 Messung thermodynamischer Größen . . . 46

3.2.1 Magnetisierungsmessungen an luftempfindlichen Proben . 47 Pulverproben . . . 48

Probleme bei Pulverproben . . . 49

Einkristalline Proben . . . 51

3.2.2 Messung der Wärmekapazität . . . 52

Probleme . . . 54

3.2.3 Messung der thermischen Ausdehnung . . . 54

3.3 Messung von Transportgrößen . . . 56

3.3.1 Die blaue Box . . . 56

3.3.2 Präparation der elektrischen Kontakte . . . 60

Widerstand . . . 61

Hall-Effekt . . . 62

3.3.3 Details zu Messung und Auswertung von Widerstand und Hall-Effekt . . . 63

Hall-Effekt . . . 64

Widerstand . . . 66

3.4 Messungen mit dem³He-Verdampfereinsatz . . . 67

3.4.1 Einsatz zur Messung der Wärmekapazität . . . 69

3.4.2 Einsatz zur Messung der thermischen Ausdehnung . . . . 69

3.4.3 Probleme . . . 70

3.5 Abschließende Bemerkungen . . . 71

4 Thermodynamische und elektrische Eigenschaften von EuC2 73 4.1 Einführung und Motivation . . . 73

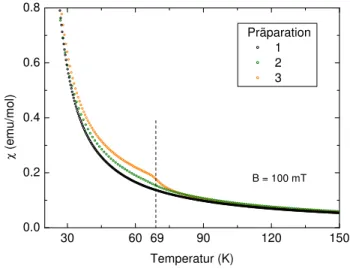
4.2 Präparation der verwendeten Proben . . . 76

4.3 Messergebnisse und Diskussion . . . 78

4.3.1 Magnetisierung . . . 78

4.3.2 Spezifische Wärmekapazität . . . 82

4.3.3 Thermische Ausdehnung und Magnetostriktion . . . 86

4.3.4 Elektrischer Widerstand . . . 90

4.4 Zusammenfassung . . . 94

5 LiFeAs 97 5.1 Einführung . . . 97

5.2 Experimentelle Details . . . 104

5.5 Hall-Effekt . . . 113 5.6 Zusammenfassung . . . 116

6 Zusammenfassung 117

Literaturverzeichnis 133

Abbildungsverzeichnis 136

Publikationsliste 137

Danksagung 139

Kurzzusammenfassung 141

Abstract 143

Offizielle Erklärung 145

Neue Materialien spielen in der modernen Festkörperphysik eine wichtige Rol- le, denn bei ihrer Erforschung treten regelmäßig spannende Ergebnisse auf, die große Aufmerksamkeit auf sich ziehen. Ein bekanntes Beispiel ist die 1986 von J.G. Bednorz und K.A. Müller beobachtete Hochtemperatur Supraleitung in Lanthan-Barium-Kupferoxid (La1.85Ba0.15CuO4) [1]. Die Entdeckung basiert auf einer systematischen Suche nach Supraleitung bei verschiedenen keramischen Oxiden, wozu auch neue Kupferoxid-Verbindungen, wie das La1.85Ba0.15CuO4, synthetisiert wurden. Bereits ein Jahr nach ihrer Beobachtung erhielten Bednorz und Müller den Nobelpreis für Physik. Ein weiteres Beispiel ist der 1984 von D.Shechtman aus einer Aluminium-Mangan-Legierung hergestellte erste Quasi- kristall [2]. In ihrem Experiment kühlten Shechtman und seine Kollegen eine Schmelze aus Aluminium und Mangan enorm schnell ab. Heraus kam eine noch unbekannte quasi-kristalline Form, bei der eine fünfzählige Symmetrie vorfand.

Strukturen mit fünfzähligen Symmetrien treten in Kristallen eigentlich nicht auf da sie sich nicht lückenlos aneinanderreihen lassen. Erst 2011 gab es für diese Arbeit den Nobelpreis in Chemie. Sowohl die Hochtemperatursupraleitung als auch die Quasikristalle waren vor ihrer Entdeckung kaum vorstellbar und haben die Forschungslandschaft bis heute geprägt.

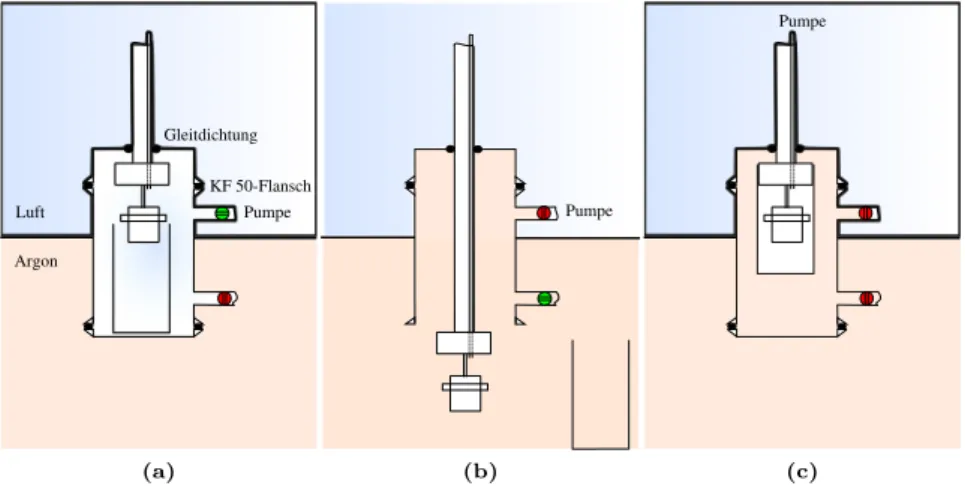
Aber wie findet man heute neue Materialien mit ungewöhnlichen, neuartigen Eigenschaften? An den beiden Beispielen wird sichtbar, dass die Physik, Che- mie und Kristallographie bei der Suche nach neuen Materialien gleichermaßen beteiligt sind. Gerade bei Chemikern gibt es eine große Motivation neue Mate- rialien mit noch unbekannten Strukturen zu suchen. Das Arbeiten unter einer Schutzgasatmosphäre wie Stickstoff oder Argon erweitert die Möglichkeiten bei der Suche enorm, da man sich nicht mehr auf luftstabile Stoffe beschränken muss. In diesen bestimmt der Sauerstoff durch seine hohe Elektronegativität die Oxidationsstufe der anderen Atome und dadurch beispielsweise die elektrischen und magnetischen Eigenschaften. Beispiele hierzu sind die zahlreichen Metall- und Übergangsmetalloxide, bei denen der Sauerstoff in der Regel als O²⁻-Ion vorliegt, und die Oxidationsstufe der Metalle bestimmt. Ersetzt man in neuen Materialien den Sauerstoff durch andere Liganden können die Metalle und Über- gangsmetalle in ungewöhnlichen Oxidationsstufen oder Koordinationen auftre- ten. Hier liegt prinzipiell ein großes Potential, Verbindungen mit neuen oder für Anwendungen besser geeignete Materialien zu finden.

Ein Problem ist, dass diese Materialien nicht nur in einer Inertgas-Atmosphäre synthetisiert werden müssen. Viele dieser Proben zerfallen generell mehr oder weniger schnell in Oxide, wenn sie Luft und/oder Feuchtigkeit ausgesetzt werden.

Daher sind physikalische Messungen schwierig, bzw. oft gar nicht möglich, da bestehende Messaufbauten nicht für luftinstabile Proben ausgelegt sind.

Aus diesem Grund war ein Ziel dieser Arbeit, Methoden zu entwickeln, um thermodynamische Eigenschaften und Transportgrößen an luftinstabilen Mate- rialien messen zu können. Hierzu wurden zwei Handschuhboxen aufgebaut, die zur Vorbereitung der Messungen eingesetzt werden können. Als Konzept wur- de zugrunde gelegt, die Messungen nicht innerhalb der Boxen durchzuführen, sondern vorhandene Messaufbauten auch für die luftinstabilen Proben einsetzen zu können. Die Umsetzung dieses Konzepts ist ein wesentlicher Bestandteil die- ser Arbeit. Parallel wurden regelmäßig Testmessungen an EuC2 durchgeführt, um die neu entwickelten Methoden zu testen. Ein besonderer Vorteil war, dass EuC2bei Kontakt mit Luft in die bekannten Oxide EuO und Eu2O3zerfällt und aufgrund ihrer hohen Empfindlichkeit während der Messungen gleichzeitig als

„Sauerstoffsensor“ eingesetzt werden konnte.

Über EuC2 war zu dem Zeitpunkt nur wenig bekannt. Es gab einige weni- ge Veröffentlichungen über die Synthese und die Struktur, die kontrovers dis- kutiert wurde [3–5]. Nur in einer Veröffentlichung wurden physikalische Mes- sungen der Magnetisierung und des elektrischen Widerstands gezeigt [5]. Die Magnetisierungs-Daten aus dieser Veröffentlichung lassen eindeutig auf einen Eu²⁺-Zustand mit einem magnetischen Moment von 7µBohr schließen. Die Mo- mente ordnen unterhalb vonTC≈20 K ferromagnetisch. Aus den Widerstands- daten konnte EuC2 nicht eindeutig den Isolatoren oder Metallen zugeordnet werden. Auffällig war ein Peak im Widerstand am ferromagnetischen Phasen- übergang, der in einem Magnetfeld deutlich unterdrückt wird. Während die Magnetisierungs-Daten in dieser Arbeit bestätigt werden konnten, weichen die Widerstandsdaten deutlich von denen in Referenz 5 ab und zeigen bei Tempera- turen oberhalbTC ein klares aktiviertes Verhalten, womit EuC2zu den seltenen ferromagnetischen Halbleitern gehört. Mit einsetzender Ordnung fällt der Wider- stand um mehr als 4 Größenordnungen. Solche extremen Widerstandänderungen wurden auch schon bei anderen Eu-Chalkogeniden wie EuO und EuS beobachtet und dort als Metall-Isolator-Übergang (MIT) diskutiert. Insbesondere EuO wird in diesem Zusammenhang seit Anfang der 1970’er Jahre untersucht. Hier konnte nachgewiesen werden, dass das Leitungsband in der magnetisch geordneten Pha- se, aufgrund der energetischen Differenz zwischen Elektronen mit parallelem und antiparallelem Spin zur Magnetisierung, in zwei Unterbänder aufspaltet [6]. Der MIT kann aber nur bei nicht stöchiometrischen EuO1+δbeobachtet werden. Der geringe Überschuss an Europium-Atomen liefert bei diesen Verbindungen zusätz- liche Elektronen auf Donator-Niveaus, die innerhalb der magnetischen Phase im energetisch niederigeren Teil des aufgespaltenen Leitungsbands liegen. Für An- wendungen besonders interessant ist, dass die Elektronen im Leitungsband fast vollständig spinpolarisiert sind. Unter diesem Aspekt ist eine detaillierte Unter- suchung von EuC2 ebenfalls interessant.

Weiterhin werden Widerstands- und Hall-Effekt-Messungen an LiFeAs vor- gestellt. LiFeAs gehört zu den seit 2006 heftig diskutierten Eisen-Arsenid-

leitung eine zentrale Rolle spielen. Anders als die Kuprate sind die Eisenpniktide keine Mottisolatoren, sondern Metalle mit komplexen Bandstrukturen aus bis zu fünf relevanten Bändern im Bereich der Fermikante [7–9]. Der Magnetis- mus beruht auf der Ausbildung von Spin-Dichte-Wellen (SDW) [10, 11], die auf eine starke Schachtelung (Nesting) der Fermi-Flächen von Elektron- und Loch-Bahnen zurückzuführen sind [12]. Es gibt aber nicht nur eine Konkurenz, sondern teilweise auch Koexistenz von Antiferromagnetismus und Supraleitung [13, 14]. Diskutiert wird auch die Symmetrie der Cooper-Paar-Wellenfunktion, bei der vieles für ein erweitertes s-Wellen-Szenario spricht [15–17], bei dem die Wellen-Funktionen für die Loch- und Elektron-Bänder beide eine s-Symmetrie aufweisen, aber unterschiedliche Vorzeichen haben. Im Unterschied zu den Kuprat-Supraleitern mit dx²−y²-Symmetrie kann, bei einer solchen „s^±-Welle“, das Vorzeichen der Wellenfunktion wechseln, ohne dass die Energielücke ver- schwindet.

Im Gegensatz zu den meisten anderen stöchiometrischen Eisen-Pniktid-Ver- bindungen ist LiFeAs ein intrinsischer Supraleiter, ohne Notwendigkeit von La- dungsträgerdotierung oder äußerem Druck, mit einer relativ hohen Sprungtem- peratur vonTc≈18K [18–21]. Weiterhin zeigt LiFeAs keine Schachtelung der Fermiflächen und keine Spin-Dichte-Wellen-Ordnung in der Nähe oder innerhalb der supraleitenden Phase [18, 21–23], was auf eine unterschiedliche elektronische Struktur hinweist [24]. Diese These wird von einer aktuellen theoretischen Ar- beit gestützt, welche überraschenderweise Spin-Triplett-p-Wellen-Supraleitung in LiFeAs favorisiert [25]. Die Paarbildung soll dabei auf ferromagnetische Fluk- tuationen zurückzuführen sein, was aber nicht unumstritten ist [26]. Somit sind noch viele Fragen bei den Eisen-Arsenid-Supraleitern ungeklärt.

Die Arbeit ist wie folgt gegliedert: In Kapitel 2 werden allgemeine theoreti- sche Grundlagen, die für die späteren Kapitel relevant sind, aufgeführt. Nach einer kurze Einführung zur Handhabung der Handschuhboxen, wird in Kapi- tel 3 detailliert beschrieben, wie die Messungen der einzelnen Messgrößen an den luftinstabilen Substanzen durchgeführt werden können. Dies beinhaltet eine Beschreibungen der nötigen Umbauten an den Handschuhboxen, die Vorberei- tung der Proben für die Messungen und den Einbau der Proben in die Mess- apparaturen. Weiterhin wird auch auf Probleme bei den einzelnen Messungen eingegangen. Anschließend werden in den Kapiteln 4 und 5 jeweils die Messun- gen an den Substanzen EuC2und LiFeAs gezeigt und diskutiert. Zum Abschluss wird in Kapitel 6 eine Zusammenfassung der Ergebnisse gegeben.

2.1 Magnetismus

Der Magnetismus begleitet die Menschheit schon seit tausenden von Jahren.

Magnetit, eines der komplexesten magnetischen Materialien, faszinierte schon griechische Schüler und Philosophen und der Kompass war eine der ersten tech- nischen Errungenschaften. Dabei ist die fundamentale Ursache für den Magne- tismus die längste Zeit verborgen geblieben. Um einen theoretische Zugang zum Magnetismus zu bekommen, betrachtet man allgemein die Bewegung von gela- denen Teilchen in einem elektromagnetischem Feld und greift auf die Hamilton- funktion¹

H= 1 2m(p−e

cA)²+eφ(x, t) (2.1) zurück. Hier sind die Felder mit dem VektorpotentialAund dem skalaren Po- tentialφüber

E=−1 c

∂A

∂t − ∇φ; B=∇ ×A (2.2) verknüpft. Unter Anwendung des Korrespondenzprinzipsp→^~_i∇und der Cou- lombeichung∇A= 0lässt sich die Schrödinger-Gleichung schreiben als:

i~∂

∂tψ= (−~²

2m∇²+i~e

mcA·∇+ e²

2mc²A²+eφ)ψ. (2.3) Nimmt man das Magnetfeld als konstant an, lässt sich das Vektorpotential schrei- ben als−¹₂[x×B]. Setzt man dies ein und betrachtet die Teile der Schrödinger Gleichung, welche vom VektorpotentialAabhängen ergibt sich:

i~∂

∂tψ= (−~²

2m∇²+ −e 2mcL·B

| {z }

P aramagnetismus

+ e²

8mc²(x²B²−(x·B)²)

| {z }

Diamagnetismus

+eφ)ψ, (2.4)

wobeiLder Bahndrehimpulsoperator ist. Betrachtet man Atome mit mehreren Elektronen, istLder Gesamtdrehimpuls und entsprechend istLdie dazugehörige Quantenzahl. Für weitere Betrachtungen kannBkez gesetzt werden. Die vom Vektorpotential A abhängigen Teile in Gleichung 2.4 liefern zwei elementare Formen des Magnetismus.

1Es wird nicht konsequent in cgs- oder SI-Einheiten gerechnet.

• Paramagnetismus: Betrachtet man den paramagnetischen Term in Glei- chung 2.4, so lässt sich interpretieren, dass geladene Teilchen mit einem DrehimpulsLein magnetisches Moment erzeugen. Ohne äußeres Feld kann das magnetische Moment in eine beliebige Richtung zeigen. In einem Ma- gnetfeld kommt es zu einer Aufspaltung der Energie bezüglich der Orien- tierung des magnetischen Momentes zum Magnetfeld. Berechnet man die Energieeigenwerte des paramagnetischen Anteils erhält man:

− e

2mcBLzψm_l=−e~B

2mc·mlψm_l⇒∆Em_l= e

2mc·~ml·B=µB (2.5) wobeiµ= _2mc^e ·~mldas magnetische Moment ist. Man nennt die durch das Magnetfeld äquidistante Aufspaltung den normalen Zeeman-Effekt. Ganz allgemein lässt sich das magnetische Moment definieren alsµ≡ −∂H/∂B was für den paramagnetischen Fall

µ_Bahn= e

2mcL (2.6)

bedeutet.

Angeregt durch das 1922 durchgeführte Stern-Gerlach-Experiment wurde klar, dass der paramagnetische Anteil noch um einen Beitrag des Spins erweitert werden muss. Aus dem Experiment geht hervor, dass Elektronen einen inneren Drehimpuls (Spin) besitzen, welcher verbunden ist mit einem magnetischen Moment von

µ_Spin=g e

2mcS. (2.7)

Der Faktor g hat hier den Wert 2, kann aber in der Theorie der Quante- nelektrodynamik genauer zu g ≈ 2.0023bestimmt werden. Das gesamte magnetische Moment eines Elektrons wird damit

µ=µ_Bahn+µ_Spin= e

2mc(L+ 2S). (2.8) Betrachtet man ein freies Atom mit mehreren Elektronen, sind mitLundS die Summen der Bahndrehimpulse bzw. Spins gemeint und mitJ=L+S der Gesamtdrehimpuls des Systems. Für freie Atome kann das gesamte magnetische Moment auch umgeschrieben werden zu

µ_Gesamt= e~

2mc(1 +J(J+ 1) +S(S+ 1)−L(L+ 1)

2J(J+ 1) )

| {z }

Land´e−F aktor g_J

J (2.9)

bzw.

µ_Gesamt=gJµBohrJ. (2.10)

• Diamagnetismus: Während der paramagnetische Anteil vom Drehimpuls abhängt und dementsprechend null sein kann, ist der diamagnetische Anteil in Gleichung 2.4 immer existent, und lässt sich mit der Einschränkung Bkez vereinfachen zu:

e²B²

8mc²(x²+y²)ψ, (2.11)

woraus sich ein diamagnetisches Moment von hµ_diamagneti=−e²B

4mc²hx²+y²i (2.12) ergibt. Betrachtet man an dieser Stelle beispielsweise ein kugelsymmetri- sches Atom (und dies ist insbesondere fürJ= 0eine gute Annahme), dann isthx²i =hy²i= 1/3hr²i und das diamagnetische Moment ist in diesem Fall

hµ_diamagneti=−e²B

6mc²hr²i (2.13)

2.1.1 Magnetisierung

Ein Festkörper enthält eine große Anzahl an magnetischen Momenten wie sie im vorherigen Abschnitt eingeführt wurden. Zur Beschreibung des gesamten Kör- pers wird die Magnetisierung M eingeführt, welche auf einer Längenskala be- trachtet wird bei der die einzelnen magnetischen Momente zu einem mittleren kontinuierlichen Vektorfeld gemittelt werden:

M~ = 1 V

X

V

~

µmag. (2.14)

Diamagnetismus

Aus der diamagnetischen Suszeptibilität einer Elementarladung in Gleichung 2.13 kann die Charakterisierung des makroskopischen Diamagnetismus abgele- sen werden. Er ist linear abhängig vom äußeren Magnetfeld und wirkt diesem entgegen, dementsprechend ist die diamagnetische Suszeptibilität negativ. Da in Festkörpern Ladungsträger wie Elektronen vorkommen, die sich durch ein äuße- res Magnetfeld beeinflussen lassen, ist jeder Festkörper ein Diamagnet. Die dia- magnetischen Beiträge von vollbesetzten Elektronenschalen sind in Referenz 27 tabellarisch zusammengefasst. In Metallen gibt es einen zusätzlichen Beitrag der Leitungselektronen an der Fermi-Kante vonχdia= 1/3∗DOS(EF)·µ²_Bohr. Paramagnetismus

Paramagnetische Substanzen verfügen über magnetische Momente, die aufgrund eines Drehimpulses auftreten (siehe 2.10). Beispiele sind Atome oder Ionen mit einem GesamtdrehimpulsJ bzw. Elektronen mit einem Spin S. Ohne äußeres

Magnetfeld sind die Momente statistisch in alle Richtungen gleichmäßig ver- teilt und es gibt keine makroskopische Magnetisierung. Dagegen gibt es mit einem äußeren Magnetfeld eine Vorzugsrichtung, entlang der sich die Momen- te ausrichten können, wobei es energetisch vorteilhaft ist, wenn sich die Mo- mente möglichst parallel zum äußeren Feld ausrichten. Daher gibt es eine re- sultierende Magnetisierung in Richtung des äußeren Feldes und die Suszepti- bilität ist positiv. Betrachtet man allgemein ein System (Atom, Ion, Elektron, etc.) mit einem Drehimpuls J hat dieses in einem Magnetfeld 2J + 1 äqui- distante Zeeman-Energieniveaus, welche abhängig von der Temperatur über die Boltzmann-Verteilung besetzt werden. Aus der Boltzmann-Verteilung folgt, dass die Niveaus niederigerer Energie höher besetzt sind, woraus eine makroskopische Magnetisierung folgt. Die Herleitung der Magnetisierung ist in Standardlehrbü- chern beschrieben [28] und führt für ein System mitNmagnetischen Momenten zu:

M(T, B) =N gJJ µBohr·BJ

gJµBohrJ B kBT

. (2.15)

BJ ist die Brillouin-Funktion, die definiert ist als BJ(x) =2J+ 1

2J coth

(2J+ 1)x 2J

− 1

2Jcoth x 2J

. (2.16)

Für den Grenzfall, dassx <<1kann die Brillouin-Funktion durch eine Taylor- Entwicklung der coth-Funktionen bis zur ersten Ordnung angenähert werden durch

BJ(x) =J+ 1

3J x+O(x³). (2.17)

Damit ist für kleine Magnetfelder die Suszeptibilität gegeben durch χ= M

H ≈N µ0g_J²µ²_BohrJ(J+ 1)

3kBT =N µ0µ²_{ef f}

3kBT , (2.18) was auch als Curie-Gesetz bekannt ist.µef fwird effektives magnetisches Moment genannt und wird häufig als charakteristische Größe angegeben. Es hängt über die Beziehung

µS=µef f

J

pJ(J+ 1) (2.19)

mit dem SättigungsmomentµSzusammen.

2.1.2 Wechselwirkungen

In den bisherigen Kapiteln wurde gezeigt, dass in Festkörpern unter dem Einfluss eines äußeren Magnetfeldes eine makroskopische Magnetisierung auftritt, welche ursächlich auf die einzelnen Momente zurückzuführen ist. Warum aber Zustände auftauchen, bei denen die einzelnen Momente ohne äußeres Magnetfeld kollekti- ve Ausrichtung haben ist nicht mit einer Wechselwirkung zwischen den Dipolfel- dern der Momente zu verstehen. Diese existiert zwar prinzipiell, ist aber erstens

viel zu schwach, um bei höheren thermischen Energien relevant zu sein, und kann zweitens nicht die vielen verschiedenen beobachteten Ordnungsstrukturen erklären. Magnetische Wechselwirkungen treten letztendlich als Folge der elek- trostatischen Coulomb-Wechselwirkung auf [29, 30], durch die Tatsache, dass es Energie kostet zwei Ladungen gleichen Vorzeichens nahe zusammen zu bringen, bzw. es Energie spart, wenn sie soweit wie möglich voneinander getrennt werden.

Betrachtet man zunächst zwei Elektronen und deren gemeinsame Wellenfunkti- on, lässt sich zeigen [28], dass der spinabhängige Teil des Hamilton-Operators durch

H^Spin=−2JS1·S2 mit J=ES−ET

2 (2.20)

dargestellt werden kann, wobei ES und ET die Energien für Singulett- und Triplett-Zustand der Elektronen sind. J ist die Austauschkonstante, hat die Di- mension einer Energie und gibt damit ein Gefühl für die Größe einer Wechselwir- kung. Aus dem Vorzeichen lässt sich entsprechend ablesen, ob der Singulett- (J

<0,ES< ET,S= 0) oder Triplett-Zustand (J>0,ES> ET,S= 1) Grundzu- stand des Systems ist. Heisenberg erweiterte diesen einfachen Hamilton-Operator für zwei Spins auf ein Vielteilchensystem, in dem er Wechselwirkungen zwischen allen magnetischen Momenten im Festkörper annahm, auf

H^Spin=−X

ij

JijSiSj=−2X

i>j

JijSiSj. (2.21) Jijist die jeweilige Austauschkonstante zwischen demi^tenundj^tenSpin und der Faktor 2 verschwindet, wenn jede Elektronen-Kombination doppelt gezählt wird.

Oft werden aber nur die Wechselwirkungen mit den nächsten Nachbaratomen berücksichtigt. Je nach Vorzeichen und Größe von J können sich langreichweitige Ordnungsstrukturen über den gesamten Festkörper ausbilden, die im nächsten Abschnitt genauer vorgestellt werden.

Damit die Spins zweier Elektronen benachbarter Atome Singulett- oder Triplett-Zustände bilden können, müssen die Wellenfunktionen der Elektronen überlappen. Diesen Fall nennt man direkten Austausch und es bilden sich sogenannte bindende Orbitale für den Singulett-Zustand und antibindende für den Triplett-Zustand. Der Singulett-Zustand ist energetisch günstiger und dementsprechend bei direktem Austausch verwirklicht. Bindungen in dieser Form einzugehen erlaubt den Elektronen sich nicht nur bei den eigenen, sondern auch bei den Nachbaratomen aufzuhalten. Durch diesen Raumgewinn wird die kinetische Energie der Elektronen abgesenkt und für den energetisch güns- tigsten Grundzustand sind nicht mehr ausschließlich Atom-Orbitale sondern Molekül-Orbitale zu betrachten.

Es gibt aber noch andere indirekte Wege auf denen magnetische Momente miteinander wechselwirken, ohne dass die Wellenfunktionen überlappen. Gerade bei Verbindungen der Seltenerd Metalle, die große magnetische Momente auf den räumlich nicht weit ausgedehnten 4f-Orbitalen haben, oder bei ionischen Verindungen, kann magnetische Ordnung nur durch indirekte Austauschwege

auftreten. Im folgenden werden einige Möglichkeiten indirekter Austauschwech- selwirkung vorgestellt:

• In vielen ionischen Verbindungen wie Oxiden und Fluoriden gibt es ma- gnetische Grundzustände, obwohl die Abstände der magnetischen Ionen für einen direkten Austausch viel zu groß sind. In diesen Verbindungen kommt es oft zu einem sogenannten Superaustausch, bei dem die von- einander separierten magnetischen Ionen einen indirekten Austausch über die Orbitale dazwischenliegender, nicht magnetischer Ionen haben. In der Regel ist der Grundzustand antiferromagnetisch, es gibt aber auch Bei- spiele für ferromagnetische Grundzustände. Welche Wechselwirkung grö- ßer ist und sich letztendlich ausbildet, hängt oft von dem Winkel ab, den die Orbitalfunktionen der magnetischen Ionen miteinander einschließen.

In Verbindungen, bei denen der Superaustausch über die p-Orbitale von Sauerstoff-Ionen stattfindet, führt ein Winkel von90^◦beispielsweise zu ei- ner ferromagnetischen, ein Winkel von180^◦zu einer antiferromagnetischen Wechselwirkung. Dieser Zusammenhang ist in den Goodenough-Kanamori- Anderson-Regeln zusammengefasst [31–37].

• Bei Metallen gibt es eine weitere Möglichkeit der indirekten Wech- selwirkung: Die Ruderman-Kittel-Kasuya-Yoshida oder kurz RKKY- Wechselwirkung. Der Effekt beruht auf der Polarisation der Leitungs- elektronen durch lokale magnetische Momente. Die polarisierten Lei- tungselektronen koppeln an benachbarte lokale Momente, wodurch die Wechselwirkung zwischen diesen indirekt vermittelt wird. Die Kopplungs- konstante ist gegeben durch [38]

JRKKY ∝cos(2kFr) r³ ,

wobei eine sphärische Fermi-Fläche mit einem Radius kF angenommen wird, was nur selten realisiert ist. Das Vorzeichen von J kann positiv oder negativ sein, wodurch sowohl ferromagnetische als auch antiferromagneti- sche Ordnung durch RKKY-Wechselwirkung realisiert werden kann.

• In einigen Oxiden gibt es eine weitere Möglichkeit für eine ferromagneti- sche Wechselwirkung, den Doppelaustausch. Er findet statt, wenn die magnetischen Ionen verschieden valente Zustände annehmen können, so dass es bei ferromagnetischer Ordnung zu einer Absenkung kinetischer Energie durch tatsächlichen Elektronentransport kommt [39–42]. Damit sind die Elektronen frei beweglich und es kommt zu metallischer Leitfähig- keit innerhalb einer durch Doppelaustausch geordneten, ferromagnetischen Phase. Ein Beispiel hierfür ist die Verbindung La1−xSrxMnO3, bei der für bestimmtexdas Mn in den Valenzen 3+ und 4+ vorkommt und den Dop- pelaustausch ermöglicht.

Die vorgestellten Wechselwirkungen können die Momente nur langreichweitig ordnen, solange sie stärker sind als die thermische Energie, die bestrebt ist, sich auf alle zur Verfügung stehenden Freiheitsgrade zu verteilen. Daher treten ma- gnetische Ordnungen erst unterhalb einer kritischen Temperatur, der sogenann- ten Phasenübergangstemperatur, auf. Im folgenden werden kurz die wichtigsten magnetischen Ordnungen beschrieben.

Ferromagnetismus

Beim Ferromagnet ist die Austauschkonstante zwischen den magnetischen Mo- menten positiv. Bei einer kritischen TemperaturTC durchläuft er einen Phasen- übergang zweiter Ordnung und es tritt unterhalbTCohne ein äußeres Magnetfeld eine spontane Magnetisierung auf. BeiT = 0K sind theoretisch alle Momente im Grundzustand vollständig parallel ausgerichtet, so dass die Sättigungsmagne- tisierungMSerreicht ist. Oberhalb vonTC verhält sich ein Ferromagnet ähnlich wie ein Paramagnet, was durch das Curie-Weiss-Gesetz

χ= C

(T−θ) (2.22)

beschrieben wird.θwird als paramagnetische Curie-Temperatur bezeichnet und stimmt nicht zwingend mit TC überein. Für Temperaturen unterhalb von TC

ist die qualitative Beschreibung der Magnetisierung schwieriger. Einige theore- tische Modelle sind in Kapitel 2.1.3 erläutert. Tatsächlich sind innerhalb eines Ferromagneten nicht alle Momente parallel ausgerichtet, sondern es bilden sich Domänen (Weisssche Bezirke) mit Momenten gleicher Ausrichtung. Die Magne- tisierungen der Domänen zeigen in unterschiedliche Richtungen und sind durch sogenannte Bloch-Wände voneinander getrennt. Durch die Bildung von Domän- mustern mit vielen überlagerten kleinen Dipolfeldern kann im Vergleich zu einem großen Dipolfeld mehr Energie eingespart werden als durch die Überwindung der Austauschkopplung an den Domänwänden aufgebracht werden muss.

Antiferromagnetismus

Ist die Austauschwechselwirkung negativ, stellen sich die nächsten magnetischen Momente antiparallel zueinander und die zugehörige langreichweitige Ordnung heißt Antiferromagnetismus. Darstellen lässt sich eine solche Ordnung oft durch zwei ferromagnetische Untergitter, deren Magnetisierungen entgegengesetzt und vom Betrag gleich groß sind. Daraus ergibt sich, dass ohne äußeres Magnetfeld in der geordneten Phase keine Magnetisierung auftritt. Oberhalb der kritischen OrdnungstemperaturTN, der Néel-Temperatur, lässt sich in einem äußeren Ma- gnetfeld die Suszeptibilität wieder durch ein Curie-Weiss-Gesetz beschreiben:

χ(T) = C

T+θN (2.23)

Typ A Typ C Typ E Typ G

(a)

T χ

T_N χ

χ

⊥ χ



(b)

Abbildung 2.1:(a) Mögliche antiferromagnetische Ordnungsstrukturen im ein- fachen kubischenGitter: TypA: lagenartig TypC: kettenartig Typ E Typ G. (b) Unterhalb der Néel-Temperatur zeigen die transversale Suszeptibilität χ⊥(T) und die longitudinale Suszeptibilitätχk(T) deutlich verschiedene Temperatur- verhalten.

UnterhalbTN gibt es verschiedene Szenarien für die Suszeptibilität, je nachdem wie das Magnetfeld zur Achse der magnetischen Momente orientiert ist. Der temperaturabhängige Verlauf der Suszeptibilität ist für den Fall paralleler und orthogonaler Orientierung zum äußeren Magnetfeld in Abbildung 2.1 schema- tisch dargestellt.

Es gibt aber noch viele andere antiferromagnetische Gittertypen, bei denen nicht alle benachbarten magnetischen Momente alternierend ausgerichtet sind, die Gesamtmagnetisierung aber Null ist. Abbildung 2.1 zeigt einige Ordnungs- strukturen für ein einfaches kubisches Gitter. Eine umfassende Übersicht ist beispielsweise in [43] gegeben.

2.1.3 Theoretische Beschreibung ferromagnetischer Ordnung

In diesem Abschnitt sollen einige Modelle zur Berechnung der Magnetisierung eines Ferromagneten vorgestellt werden.

Molekularfeld-Näherung für das Heisenberg-Modell

Ursache für ferromagnetische Ordnung sind die im vorherigen Abschnitt vorge- stellten möglichen Wechselwirkungen magnetischer Momente. Der spinabhängi- ge Teil des Hamilton-Operators kann durch 2.21 dargestellt werden. Für einen Ferromagneten in einem von außen angelegten Magnetfeld kann Gleichung 2.21 erweitert werden auf:

H^Spin=−X

ij

JijSiSj+gµBohr

X

j

SjB. (2.24)

Der erste Term repräsentiert die Austausch-Energie, wobei die Kopplungskon- stante im ferromagnetischen Fall positiv ist, der zweite Term ist die Zeeman- Energie, also die Energie aller magnetischen Dipolmomente im äußeren Magnet-

feldB. Eine einfache Methode die Schrödinger-Gleichung zu lösen ist, die Kopp- lung der Spins durch ein, innerhalb des Festkörpers, imaginäres Molekularfeld

Bmf =− 2 gµBohr

X

j

JijSj (2.25)

auszudrücken, welches jeder der Spins spürt. Der Hamilton-Operator kann dann umgeschrieben werden in

H^Spin=gµBohr

X

i

Si(B+Bmf), (2.26) welcher im wesentlichen dem Hamilton-Operators eines Paramagneten in einem MagnetfeldB+Bmf entspricht. Die Ordnung der Spins und damit die Magne- tisierung ist somit abhängig vom Molekularfeld Bmf, was im einfachsten Fall durch einen linearen Zusammenhang

Bmf =λM (2.27)

dargestellt werden kann. Die Molekularfeldkonstanteλsteht mit der Austausch- konstanten Jij in direkter Beziehung. Nimmt man an, dass es nur zwischen den z nächsten Nachbarmomenten eine gleichgroße Austauschwechselwirkung gibt (was bereits eine gute Näherung darstellt), liefern die Gleichungen 2.25 und 2.27 bei vollständiger Sättigung der Magnetisierung die Beziehung

λ= 2zJ

N g²_Jµ²_Bohr (2.28)

zwischenλund J. Wie bereits erwähnt ist die Lösung von H^Spin=gµBohr

X

i

Si(B+λM) (2.29)

identisch mit der Lösung 2.15 eines Paramagneten in einem äußeren Magnetfeld B+λM. Damit ergibt sich

M(T, B) =N gJJ µBohr·BJ

gJµBohrJ(B+λM) kBT

, (2.30)

wobeiN gJJ µBohr =MS die Sättigungsmagnetisierung ist. Hier wird der Un- terschied zum reinen Paramagneten deutlich, da im Argument der Brillouin- Funktion in Gleichung 2.30

y=gJµBohrJ(B+λM)

kBT (2.31)

die Magnetisierung selbst vorkommt und nach dieser somit nicht analytisch auf- gelöst werden kann. In Lehrbüchern wird hier meist eine graphische Lösungsme- thode erläutert: Das Argumentyaus 2.31 wird ebenfalls nach der Magnetisierung

M(y)

0

y 0

T>TC T=TC T<TC

T<TC

(a)

y 0 gJ μBohr J B / kB T

(b)

Abbildung 2.2: Grafische Lösung der Sättigungsmagnetisierung eines Ferro- magneten ohne äußeres Magnetfeld (a). Nur unterhalb vonTC gibt es eine von 0 verschiedene Lösung und es tritt eine spontane Magnetisierung auf. (b) Im Unterschied zu (a) gibt es mit einem angelegten Magnetfeld immer eine endliche Magnetisierung für alle Temperaturen.

M(y)aufgelöst, wodurch sich zusammen mit Gleichung 2.30 zwei Funktionsglei- chungen für die Magnetisierung ergeben:

M(y) = MSBJ(y) (2.32)

M(y) = kBT

gJµBohrJ λy−B

λ (2.33)

In Abbildung 2.2 ist die Auftragung ohne (a) und mit äußerem Magnetfeld (b) schematisch für verschiedene Temperaturen gezeigt. Die Schnittpunkte der bei- den Funktionen 2.32 und 2.33 sind die möglichen Lösungen für die Magnetisie- rung. Betrachtet man zunächst die Magnetisierung ohne äußeres Magnetfeld in Abbildung 2.2(a) gibt es für Temperaturen mitT > TC nur die LösungM = 0, während es fürT < TC immer eine Lösung |M| > 0 gibt. Dabei gibtTC die Übergangstemperatur, unterhalb der eine langreichweitige Ordnung der magne- tischen Momente auftritt, welche ein makroskopisches Moment erzeugt. Bestim- men lässt sich TC über die Bedingung, dass bei T = TC die Funktionen 2.32 und 2.33 im Ursprung gleiche Steigungen haben. Aus der Bedingung folgt für die ferromagnetische Übergangstemperatur

TC=gJµBohr(J+ 1)λMS

3kB

= 2zJJ(J+ 1) 3kB

. (2.34)

Mit einem äußeren Magnetfeld wird die Geradengleichung 2.33 in positive y- Richtung verschoben und es gibt für jede Temperatur eine Lösung mitM6= 0.

Zur Bestimmung der Schnittpunkte wird ein numerisches Verfahren benutzt, das in Abbildung 2.2(b) schematisch durch die eingezeichneten Pfeile dargestellt

M/MS

0 0.5 1

T/TC

0 0.5 1

J = 3.5 1.5 0.5 (a)

T/TC

0 0.5 1 1.5 2

steigendes Magnetfeld (b)

Abbildung 2.3:Magnetisierung eines Ferromagneten für verschiedene Magnet- felder.

ist. Es wird mit einem beliebigen y-Wert gestartet und in Gleichung 2.32 ein- gesetzt. Mit dem errechneten M(y) wird mit Gleichung 2.31 ein neuer Wert für y errechnet, welcher wieder in Gleichung 2.32 eingesetzt wird. Mit jeder Iteration konvergieren yund M näher an die Koordinaten des Schnittpunktes heran, so dass dieser beliebig genau bestimmt werden kann. Mit diesem Ver- fahren kann bei Vorgabe vongJ,J,TC (oderλ) die Magnetisierung nach dem Molekularfeld-Modell in Abhängigkeit von Temperatur und Magnetfeld berech- net werden. Abbildung 2.3(a) zeigt die numerisch berechnete spontane Magneti- sierung von Ferromagneten aufgetragen gegen die Temperatur für verschiedene Drehimpulse J. Um die Kurven vergleichen zu können, sind Magnetisierungs- und Temperatur-Achse jeweils aufMS bzw.TCnormiert. Die Kurven zeigen al- le einen qualitativ ähnlichen Verlauf: Für T > TC ist die Magnetisierung null und für T ≤ TC steigt die Magnetisierung kontinuierlich an, bis bei T = 0 die SättigungmagnetisierungMS erreicht ist. Dies ist ein typischer Verlauf eines Phasenübergangs zweiter Ordnung, bei dem erst in der zweiten Ableitung der freien Energie eine Diskontinuität auftritt, was im vorliegenden Fall die Ablei- tung der Magnetisierung∂M/∂Tist. Die Ergebnisse fürB >0sind in Abbildung 2.3 anhand eines Systems mitJ= 3.5zu sehen.

Landau-Theorie des Ferromagnetismus

Es gibt noch andere Ansätze zur Beschreibung des ferromagnetischen Phasen- übergangs, die ebenfalls auf einem Molekularfeld beruhen. Lev Landau setzte für die freie Energie eines Ferromagneten

F(M) =F0+a(T)M²+bM⁴ (2.35) und bestimmte den Grundzustand des Systems über die Minimierung der freien Energie. Unter der Bedingung, dass die temperaturabhängige Funktiona(T)das

Vorzeichen bei einer bestimmten Temperatur TC wechselt (z.B. durcha(T) = a0(T−TC), folgt für die Magnetisierung

M = 0 (2.36)

M = ±

a0(TC−T) 2b

0.5

, (2.37)

wobei die zweite Lösung nur fürT < TC zutrifft. Durch die Linearisierung von a(T) gilt dies allerdings nur im näheren Bereich des Phasenübergangs bei TC. Molekularfeld-Theorien sind die einfachsten Modelle zur Beschreibung von Pha- senübergängen, allerdings können sie den kritischen Bereich des Phasenüber- gangs nicht gut beschreiben. Gerade im Bereich des Phasenübergangs treten starke Fluktuationen auf, so dass die Voraussetzung eines glatten, gleichmäßi- gen Molekularfeldes an allen Orten innerhalb des Festkörpers nicht erfüllt ist.

Somit ignorieren Molekularfeld-Theorien Korrelationen und Fluktuationen, die im Bereich des Phasenübergangs besonders groß sind und sich gerade im Ord- nungsparameter, wie beispielsweise der Magnetisierung, widerspiegeln. So folgt die Magnetisierung M(T) für T < TC im Bereich des Phasenübergangs, dem Potenzgesetz

M(T) =a·(TC−T)^β (2.38) mit dem kritischen Exponentenβ. Gleichung 2.37 liefert für die Molekularfeld- Theorie ein β = 0.5. Aus Messungen bestimmte kritische Exponenten liegen dagegen im Bereich vonβ= 0.33(für EuS) und0.42(für Ni) und weichen damit deutlich von der Vorhersage der Molekularfeld-Theorie ab.

Spinwellen Theorie des Heisenberg-Modells

Ebenfalls für T →0 sind Molekularfeld-Theorien nicht exakt. Betrachtet man die Situation ohne äußeres Magnetfeld, kommt es rechnerisch zu einer Zeeman- Aufspaltung der magnetischen Energie-Niveaus im Molekularfeld. Bei tiefen Temperaturen wären damit die niedrigsten möglichen magnetischen Anregun- gen die Besetzung der höher liegenden Zeeman-Niveaus. Die Anregung über eine Energielücke führt zu einer exponentiellen Änderung der Magnetisierung, was aber nicht beobachtet wird. Eine bessere Beschreibung liefert die Anregung von Spinwellen bei tiefen Temperaturen. Betrachtet man eine Kette von Spins die nur mit ihren nächsten Nachbarn koppeln, reduziert sich für B = 0 der Heisenberg-Hamilton-Operator zu

H=−J X

i,δN N

Si·Si+δ, (2.39)

wobeiN N bedeutet, dass hier nur die nächsten Nachbarn betrachtet werden.

Ein N-Spin-Zustand ist eindeutig charakterisiert durch

|ψi=|S1, . . . , Si, . . . , SNi (2.40)

mit den SpinquantenzahlenSi=−S,−S+ 1, . . . ,+S ami-ten Gitterplatz. Der ferromagnetische Grundzustand ist dann definiert durch

|ψ0i=|S, . . . , S, . . . , Si (2.41) mit der zugehörigen Grundzustandsenergie

E0=−ZNJS². (2.42)

Z ist hier die Anzahl der nächsten Nachbarn. Es ist naheliegend, für den ersten angeregten Zustand

|ψji=|S, . . . , S−1, . . . , Si (2.43) zu wählen, welcher offenbar aus dem Grundzustand hervorgeht, indem an dem Gitterplatz j der Spin nicht mehr seinen optimalen (maximalen) Wert S an- nimmt, sondern den nächst niedrigeren WertS−1. Tatsächlich aber ist|ψjigar kein Eigenzustand des Heisenberg-Hamilton-Operators:

H|ψji=−J[(ZN S²−2ZS)|ψji+ 2SX

δ

|ψj+δi. (2.44) Es wäre ein Eigenzustand, wenn nur die z-Komponenten der Spins koppeln wür- den, d. h. die |ψji sind Eigenzustände für das Ising-Modell. Betrachtet man 2.44 wird deutlich, dass durch die Anwendung des Hamilton-Operators auf|ψji die Anregung auf demj-ten Platz nicht lokalisiert bleibt, sondern sich auf die Nachbarplätze ausweitet. Aus den angeregten Zuständen|ψjikönnen durch den Ansatz

|ψqi= 1

√ N

X

j

e^iqRj|ψji (2.45)

Eigenzustände konstruiert werden, mit denen sich H|ψqi= E0+ 2ZSJ−2SJX

δ

e^−iqδ

| {z }

E_q

|ψqi (2.46)

ergibt. Die Dispersionsrelation der Spinwellenanregung ist damit Eq= 2JS(Z−X

δ

cosq·δ). (2.47)

Die Summation läuft dabei über die mitδ bezeichneten Vektoren, die das Zen- tralatom mit seinen nächsten Nachbarn verbinden. Damit kann 2.47 für ein ein- faches kubisches Gitter umgeschrieben werden zu

Eq= 4SJ(3−cosqxa−cosqya−cosqza). (2.48) Insbesondere gibt es keine Energielücke zwischen Grundzustand und den an- geregten Zuständen, so dass beliebig kleine Energien für eine Spin-Wellen- Anregung ausreichen, woraus sich ein kontinuierliches Anregungsspektrum

ergibt. Solche Anregungen werden auch Goldstone-Moden genannt. Für tiefe Temperaturen kann die Dispersionsrelation wegen cos(q·δ) ≈ 1−(q·δ)²/2 genähert werden durch

Eq≈2JSa²q². (2.49)

Um die Magnetisierung zu errechnen, benötigt man die Anzahl der angeregten Magnonen, denn jedes Magnon verringert die Magnetisierung um gµBohr. Die Anzahl der Magnonen ergibt sich aus

nmagnon= Z ∞

0

D(ω)d ω exp(~ω/kBT)−1=

kBT 2JSa²

3/2

·0.0587 (2.50) wobei

D(ω)d ω= 1

2π

4πk²d k

d ωd ω= 1 4π²

~ 2JSa²

3/2

·√

ω d ω (2.51) die dreidimensionale Zustandsdichte der Magnonen ist. Die Zahl 0.0587 enthält unter anderem den endlichen Wert des bestimmten IntegralsR∞

0 dx√

x/(exp(x)−

1) = 0.0587·4π. Für die Magnetisierung bei tiefen Temperaturen gilt dann M(T) = N gJµBohrS−gJµBohrnmagnon (2.52)

= M(0)

"

1− 1 N S

kBT 2JSa²

3/2

·0.0587

#

(2.53) was auch als BlochschesT^3/2-Gesetz bekannt ist. Dieses Ergebnis für die Tempe- raturabhängigkeit der Magnetisierung bei tiefen Temperaturen stimmt recht gut mit den experimentellen Beobachtungen überein und liefert dort ein wesentlich besseres Ergebnis als die Molekularfeld-Näherung des vorigen Abschnitts.

2.2 Wärmekapazität

Die Wärmekapazität gibt an, wieviel Energie∆Qeiner Substanz zugeführt wer- den muss, um die Temperatur um∆T zu erhöhen. Vereinfacht ausgedrückt be- schreibt diese Messgröße, wie viele Freiheitsgrade eine Substanz hat, um Energie zu speichern. In der statistischen Physik ergibt sich damit die isochore Wärme- kapazitätCV zu [44]

CV = ∂E

∂T V,N

=T· ∂S

∂T V,N

. (2.54)

Es ist E(S, V, N) = T S−pV +µN die innere Energie einer Substanz und S die Entropie. Hier ist aber gefordert, dass das Volumen konstant ist, was ex- perimentell nicht einfach zu verwirklichen ist. Einfacher ist eine Konstanz des Drucks im Experiment zu erreichen. Dann ist allerdings zu beachten, dass nach dem 1. Hauptsatz die zugeführte Energie∆Q nicht nur in innere Energie der

Substanz umgewandelt wird, sondern eventuell zum Teil für Ausdehnungsarbeit verbraucht wird. Im Falle konstanten Drucks wird die Wärmekapazität mitCp

bezeichnet und ergibt sich aus Cp= ∂H

∂T p,N

=T· ∂S

∂T p,N

, (2.55)

wobeiH(S, p, N) die Enthalpie ist. Mit dem Volumenausdehnungskoeffizientβ und der isothermen Kompressibilität κT = −V⁻¹(∂V /∂p)|T ,N lässt sich Cp

dementsprechend als Summe von CV und der geleisteten Ausdehnungsarbeit schreiben:

Cp=CV+T V β² κT

. (2.56)

Wie bereits erwähnt, ist die isobare Wärmekapazität für Festkörper die experi- mentell besser zugängliche Größe. Dagegen lässt sichCV oft leichter berechnen und ist in Lehrbüchern somit häufiger vertreten. Oft ist die Differenz zwischen CpundCV aber vernachlässigbar, da sie bei den meisten Festkörpern unter 5%

liegt. Üblicherweise wird die spezifische Wärmekapazität oder auch kurz spezifi- sche Wärme angegeben, die sich auf ein Gramm oder ein Mol Substanz bezieht.

In dieser Arbeit wird die spezifische Wärme generell auf ein Mol Substanz bezo- gen und in der Einheit J/mol K angegeben.

2.2.1 Gesetz von Dulong und Petit

Erste Beobachtungen zur Wärmekapazität von Festkörpern veröffentlichten Du- long und Petit 1819. Die spezifische Wärme zahlreicher von ihnen untersuchter Substanzen war praktisch gleich, was später auch durch einfache Überlegungen von Boltzmann erklärt werden konnte. Nach dem Äquipartitionstheorem ver- teilt sich die innere Energie eines Festkörpers gleichmäßig auf die zur Verfügung stehenden Freiheitsgrade. Dabei entfällt auf jeden Freiheitsgrad eine Energie von 1/2kBT. Stellt man sich eine einfache Kristallstruktur vor, die aus einer einatomigen Basis besteht, lassen sich die einzelnen Atome als harmonische Os- zillatoren auffassen, die in drei Dimensionen jeweils sechs Freiheitsgrade haben.

Damit ergibt sich für die Energie jedes Atoms 3kbT, woraus sich eine molare Wärmekapazität von

cp= 3NAkB = 24.94J/mol K (2.57) ergibt.

Tatsächlich erreichen viele Substanzen mit einfachen Kristallstrukturen bei hohen Temperaturen diesen Wert. Zu tiefen Temperaturen hin weicht die tat- sächliche spezifische Wärme aber immer mehr vom Dulong-Petit’schen Wert ab.

Dies resultiert aus der Quantisierung der Gitterschwingungen, die bei tiefen Tem- peraturen nicht mehr angeregt werden können, wennkBT < hνist.

2.2.2 Quantenmechanische Behandlung der Wärmekapazität Gitteranteil

Prinzipiell lässt sich ein Kristallgitter, bestehend aus Atomen bzw. Ionen, als Punktmassen, die über Federkonstanten elastisch miteinander verbunden sind, beschreiben. Für ein solches schwingungsfähiges System lassen sich Bewegungs- gleichungen aufstellen, deren Lösungen laufende Wellen mit zugehörigen Disper- sionsrelationenω(~k)sind. Befinden sichpAtome in der primitiven Einheitszelle eines Kristalls, gibt es3p mögliche Schwingungen für jeden Wellenvektor~k: 3 akustische Moden, bei denen die Gitterteilchen alle in Phase auf einer Wel- le liegen und 3p−3 optische Moden, bei denen die Teilchen in verschiedenen Kombinationen auch gegenläufig ausgelenkt werden. Der Faktor 3 ergibt sich aus den möglichen Polarisationen, wobei es sowohl bei den akustischen als auch bei den optischen Moden zwei transversale und eine longitudinale Welle gibt.

Da die unterschiedlichen Schwingungsmoden verschiedene Energie haben, gibt es dementsprechend auch 3p Äste der Dispersionsrelation. Die Charakteristik von akustischen und optischen Dispersionsrelationen unterscheiden sich deutlich.

Während die akustischen Äste zunächst wie bei Schallwellen linear verlaufen und ω(~k)für~k→0gegen null strebt, haben die optischen Äste dort einen endlichen Wert und sind im gesamten Verlauf flach. Diese charakteristischen Merkmale werden später bei Näherungen zur Berechnung der spezifischen Wärme benutzt.

Die Energie eines Schwingungszustands ist über

= (n+ 1/2)~ω (2.58)

gequantelt, wobei ein Energiequant als Phonon bezeichnet wird, welches eine Energie~ω besitzt. Ist ein Zustand mit der Quantenzahl n angeregt, ist dies nun gleichwertig mit der Aussage, dass der Zustand vonnPhononen besetzt ist.

Phononen sind Bosonen und können damit jeden Zustand unter Berücksichtigung der Bose-Einstein-Verteilung(exp(β~ω(~k))−1)⁻¹beliebig oft besetzen.

Die gesamte Energie aller angeregter Phononen mit Wellenvektor~k und und Polarisationpergibt sich dann zu [29, 45]

Uph=X

p

Z

d ωDp(ω) ~ωp(~k)

exp(~ωp(~k)/kBT)−1. (2.59) Dp(ω)dωist die Anzahl an Schwingungszuständen im Frequenzintervall[ω, ω+ dω]für eine Polarisation und wird Zustandsdichte genannt. Die spezifische Wär- me bei konstantem Volumen ist dann die Ableitung vonUphnach der Temperatur

CV =kB

X

p

Z

dωDp(ω) x²exp(x)

(exp(x)−1)², mit x= ~ω

kBT. (2.60) Rechnerisch gibt es zwei gängige Näherungen:

• Das Debye Modell: Es berücksichtigt nur die drei akustischen Phononen- zweige und ordnet ihnen eine lineare Dispersionsrelationω=vk zu. Die Schallgeschwindigkeitvwird, wie bei einem kontinuierlichen Medium, als konstant angenommen. Die spezifische Wärme ergibt sich dann zu

CV = 3V~² 2π²v³kBT²

Z ω_D

0

dω ω⁴exp(~ω/kBT)

(exp(~ω/kBT)−1)². (2.61) Die Integration wird nur noch bis zu einer festen GrenzfrequenzωD aus- geführt, damit nur die akustischen Äste erfasst werden. Wenn ein Kristall Nprimitive Elementarzellen enthält, gibt es auchNakustische Phononen- zustände und die Grenzfrequenz ergibt sich zuωD= (6π²v³N/V)^1/3. Für tiefe Temperaturen kann das Integral näherungsweise gelöst werden, in- dem man die obere Integrationsgrenze gegen unendlich laufen lässt. Diese Näherung ist als das DebyescheT³-Gesetz bekannt:

CV = 234N kB

T ΘD

3

. (2.62)

ΘD=~ωD/kBist die sogenannte Debye-Temperatur und wird oft als cha- rakteristische Größe eines Systems angegeben. In der Regel liegen Debye- Temperaturen im Bereich von einigen 100 K und das T³-Gesetz ist nur unterhalb von'ΘD/50beobachtbar [44, 45].

• Das Einstein Modell: In diesem Modell wird allen Oszillatoren die gleiche Frequenzω=ω0 zugeordnet, woraus sich eine Wärmekapazität von

CV =N kB

~ω kBT

2

e^~ω/kBT

(e^~ω/kBT−1)² (2.63) ergibt. Oft werden die Beiträge der optischen Phononen, wegen ihrer meist sehr flachen Dispersion, gut durch das Einstein-Modell beschrieben.

Elektronischer Beitrag

Durch das Pauli-Verbot bzw. die Fermi-Dirac-Verteilungf(E)können nicht alle Elektronen, wie man es klassisch erwarten würde, zur Wärmekapazität beitra- gen. Quantenmechanisch tragen nur die Elektronen, die in Zuständen in einem Energie-BereichkBT um die Fermi-EnergieEF sitzen und in freie Energienive- aus oberhalbEF angeregt werden können, zur Wärmekapazität bei. Damit ergibt sich für Energiedifferenz ∆U =U(T)−U(0)eines Systems aus Elektronen im Festkörper

∆U= Z ∞

0

dE D(E)·E·f(E, T)− ZE_F

0

dE D(E)·E. (2.64)

Eine gute Näherung der elektronischen Wärmekapazität für TemperaturenT <

0.01EF/kB, bei denen die Fermi-Kante nur wenig „aufgeweicht“ ist, liefert Cel= 1

2π²N k²_B T EF

=1 2π²N kB

T TF

. (2.65)

TF ist durchkBTF =EF definiert, stellt aber, genau wieΘD, keine tatsächliche Temperatur dar, sondern dient als nützliche Referenzgröße.

Magnetischer Beitrag

Um den magnetischen Anteil der Wärmekapazitätcmag zu berechnen, wurden verschiedene Ansätze in der Arbeit gemacht. Die eine Möglichkeit istcmag, ana- log zu den Gitterschwingungen, über die Energie der Magnonen

Emagnon= Z

~ωD(ω)hn(ω)id ω=

Z ~ωD(ω)d ω

exp(~ω/kBT)−1 (2.66) zu bestimmen. Bei bekannter Dispersionsrelation kann die ZustandsdichteD(ω) bestimmt und das Integral gelöst werden. In der Regel wird hier die für tiefe Tem- peraturen genäherte Dispersion aus Gleichung 2.49 benutzt, umEmagnonzu be- rechnen. Aus der Tieftemperaturnäherung ergibt sich weiterhin der Vorteil, dass das Integral nicht nur über den relevanten Bereich in der ersten Brillouin-Zone laufen muss, sondern bis∞ausgeführt werden kann, weil durch die Charakte- ristik der Planck-Verteilunghn(ω)inur Zustände innerhalb der ersten Brillouin- Zone besetzt sind. Damit wird das Integral analytisch lösbar und es ergibt sich für die spezifische Wärme bei tiefen Temperaturen

dE

dT =cmag= 0.628· NAk^5/2_B

(2πJJ)^3/2T^3/2. (2.67) Würde man die vollständige Dispersionsrelation aus Gleichung 2.47 benutzen, könnte man prinzipiell die spezifische Wärme auch für höhere Temperaturen berechnen. Hier muss allerdings beachtet werden, dass bei einer zu großen Anzahl angeregter Magnonen Wechselwirkungen zwischen diesen auftreten, die nicht berücksichtigt sind.

Eine weitere Möglichkeit besteht darin, die Wärmekapazität in einer Mo- lekularfeld-Näherung zu berechnen. Ausgehend vom spinabhängigen Teil des Hamilton-Operators mit dem eingesetzten Molekularfeld aus Gleichung 2.29 kann der Erwartungswert

H^Spin

n =−3NAkBTcJ

2(J+ 1)M₀²M²(T)−NAµBohrBM (2.68) des Systems berechnet werden.nist die Anzahl magnetischer Ionen im Material undM(T) die Magnetisierung der einzelnen magnetischen Ionen. Gibt mann

in der Einheit Mol undM(T)inµBohr an erhält man den Erwartungswert der Energie in J/mol. Für die spezifische Wärme ergibt sich damit

cmag(T) =−3NAkBTcS

(S+ 1)M₀²M(T)dM(T)

dT −NABdM(T)

dT . (2.69)

Eine ausführliche Behandlung der Wärmekapazität eines Ferromagneten ohne äußeres Magnetfeld ist z.B. in Referenz 46 zu finden.

2.3 Thermische Ausdehnung

Der Volumenausdehnungskoeffizient β gibt an, wie sich das Volumen V eines Festkörpers bei einer Temperaturveränderung∆T ändert:

β= lim

∆T→0

1 V

∆V

∆T p,N

= 1 V

∂V

∂T p,N

. (2.70)

Messtechnisch ist es schwierig die Volumenausdehnung zu bestimmen, deshalb wird in üblicherweise verwendeten Dilatometern die lineare thermische Ausdeh- nung entlang einer Kristallrichtung i

αi= lim

∆T→0

1 L

∆Li

∆T p,N

= 1 L

∂Li

∂T p,N

(2.71) gemessen. Für anisotrope Einkristalle ergeben sich unterschiedliche Ausdeh- nungskoeffizienten αi für verschiedene Kristallrichtungen, wobei aus drei zu- einander orthogonalen Richtungen der Volumenausdehnungskoeffizient über β =P3

i=1αi berechnet werden kann. Für Polykristalle wird dementsprechend bei einer Messung über die verschiedenen Kristallachsen gemittelt, und α ist proportional zum Volumenausdehnungskoeffizienten. Im allgemeinen Fall ist der thermische Ausdehnungskoeffizient ein Tensor zweiter Stufe. In der Theorie der elastischen Konstanten sind Spannungs- σij und Deformationstensor ij über die Elastizitätsmodule cijkl bzw. deren Reziprokes sijkl = c⁻¹_ijkl miteinander verknüpft:

dσij=cijkldkl bzw. dij=sijkldσkl (2.72) Der Spannungstensor oder auch Drucktensor beschreibt die Wirkung von Zug- und Scherkräften auf einen Festkörper. Der Deformationstensor ist durch

ij= 1/2(∂li/∂xj+∂lj/∂xi) (2.73) definiert, wobeixidie Richtungen bezeichnen, in welche die jeweilige Kraft wirkt.

Die thermische Ausdehnungαijstellt nun die Verbindung zwischen kleinen Än- derungen der Verzerrungenijund der Temperatur her [47]:

dij=αijdT. (2.74)

Füri=jergibt sich gerade die uniaxiale Längenänderung. Analog gibt es mit

dij=mijadHa (2.75)

auch eine Beziehung zwischen Verzerrungen eines Festkörpers und einem von außen angelegten Magnetfeld. Zu beachten ist hier, daß eine feldinduzierte Län- genänderung in einer Richtung keine Aussage über eine gleichzeitig mögliche Querkontraktion zulässt. Statt dessen muß man Längs- und Querlängenände- rung abhängig von der jeweiligen Magnetfeldrichtung berücksichtigen.

2.3.1 Thermodynamik der thermischen Ausdehnung

In der statistischen Physik [48] ergibt sich die isobare Wärmeausdehnungβ(T, p) als zweite Ableitung aus der freien Enthalpie:

∂²G

∂T ∂p =−∂S

∂p T ,N

=∂V

∂T p,N

=V·β(T, p). (2.76) Das Volumen im thermodynamischen Gleichgewicht eines isotropen Festkörpers bei einem Druck p0 und einer Temperatur T ist gegeben durch das Minimum der freien Enthalpie

G(T, p, N) =E−T S+pV =F(T, V, N) +pV, (2.77) wobeiF die freie Energie ist.

2.3.2 Thermische Ausdehnung bei Ferromagneten

Betrachtet man die gekoppelten magnetischen Momente in einem Ferromagne- ten ist die freie Enthalpie pro Einheitsvolumen in der Molekularfeld-Näherung gegeben durch [49]

G= − 3 2

J J+ 1

N kBTC

M MS

2

+ 1 2K

v−v0

v0

2

− 1 µ0

BM(2.78) + pv−v0

v0

− T·S(M/MS),

wobeiK die Kompressibilität und pder Druck ist. Der erste Term ist, wie in Kapitel 2.2 zur Berechnung des magnetischen Anteils der spezifischen Wärmeka- pazität, die Energie der Magnetisierung. Der zweite Term beschreibt die Span- nungsenergie durch eine Volumen-Verzerrung, welche bei einem angenommenen Hook’schen Kraftgesetz quadratisch zu(v−v0)/v0 ist, der dritte die Energie im äußeren Magnetfeld, der vierte die Druckarbeit und der fünfte die Entropie in Abhängigkeit von der Magnetisierung.

Ein zentraler Punkt in dem Modell ist die Volumenabhängigkeit der Kopp- lungskonstanten J, welche sich in der Annahme

TC=T0(1 +β(v−v0)/v0) (2.79) widerspiegelt. TC ist die tatsächliche Curie-Temperatur,T0 eine hypothetische Curie-Temperatur für ein inkompressibles Gitter,vist das Volumen,v0das Vo- lumen ohne Austausch-Wechselwirkung undβbeschreibt die Abhängigkeit von TC vom Volumen.

Nimmt man nunp= 0an und setzt Gleichung 2.79 in 2.78 ein, ergibt sich für das Volumen, welches die freie EnergieF minimiert:

v−v0

v0

= 3 2

J

(J+ 1)N kBT0Kβ M

MS

2

. (2.80)

Hieraus ergibt sich eine quadratische Abhängigkeit der Volumenausdehnung von der Magnetisierung

v−v0

v0

= M

MS

2

, (2.81)

wobeiβdie magnetoelastische Kopplung ist.

2.3.3 Grüneisenskalierung

Ist die Gibb’sche freie Enthalpie eines Systems, bei konstanter Teilchenzahl, eine Funktion einer einzigen charakteristischen Energieskala E, gibt es eine direk- te Skalierungsrelation zwischen dem Volumenausdehnungskoeffizient βund der spezifischen Wärmecp. In diesem Fall gilt

G(T, p) = E·g(T /E) (2.82)

S = −G

T =g⁰(T /E) (2.83)

cp = T·∂S

∂T =−T

E·g⁰⁰(T /E), (2.84) woraus sich mit der Maxwell-Relation∂V /∂T|p=−∂S/∂p|T für den Volumen- ausdehnungskoeffizienten

β=−1 V

T

E·g⁰⁰(T /E)· 1 E

∂E

∂p = 1

V ·∂ln(E)

∂p ·cp (2.85) ergibt [50]. FürV ist hier das Volumen der Einheitszelle des betrachteten Materi- als einzusetzen. Dies gilt allerdings nur, wenn die betrachtete EnergieskalaEvon der Temperatur unabhängig ist. Charakteristische Energieskalen sind beispiels- weise die Debye-TemperaturΘDbei der Betrachtung akustischer Phononen, oder die Austausch-Wechselwirkung J bei magnetisch ordnenden Systemen.

2.4 Transport von Ladung

Generell bezieht sich die Transport-Theorie auf die Bewegung von Quasi-Teil- chen im Festkörper unter dem Einfluss äußerer Kräfte. Eine allgemeine Beschrei- bung von Transportphänomenen liefert die Boltzmann-Transportgleichung, wel- che die Änderung der Besetzungswahrscheinlichkeit der Elektronenzustände auf- grund äußerer Kräfte und relaxierender Streuprozesse beschreibt. Äußere Kräfte wirken auf geladene Teilchen durch elektrische und magnetische Felder, kön- nen aber auch auf beliebige Teilchen durch Temperaturgradienten hervorgerufen werden. Neben den Kräften, die auf die Teilchen wirken, spielen die Streupro- zesse eine wesentliche Rolle bei der Bewegung der Teilchen. Aus der Boltzmann- Transportgleichung lassen sich die Gleichungen für die Ladungs- und Wärme- stromdichten und den entsprechenden Koeffizienten ableiten [29, 51–56]. Die Koeffizienten sind die entsprechenden Tensoren für elektrische Leitfähigkeitρ, Seebeck-EffektS, Peltier-EffektΠund Wärmeleitfähigkeitκ. Im folgenden soll aber nur auf den Transport von Ladungen bei isothermen Bedingungen (∇T≈0) eingegangen werden

2.4.1 Elektrische Leitfähigkeit

Die elektrische Leitfähigkeit ist seit der Entdeckung des Elektrons eine sehr in- teressante Eigenschaft von Verbindungen und in der aktuellen Forschung der Festkörperphysik präsent. Die theoretische Beschreibung der Leitfähigkeit ist auf verschiedenen Ebenen der Komplexität möglich. Welche man verwendet ist ab- hängig von dem Problem. In den folgenden Unterkapiteln werden die Grundzüge und Ergebnisse verschiedener Modelle vorgestellt.

Drude-Sommerfeld-Modell

Das Drude-Model war der erste Versuch die elektrische Leitfähigkeit in Fest- körpern zu beschreiben. Es basiert auf der Annahme, dass die Elektronen im Festkörper als ein Gas freier nicht wechselwirkender Teilchen vorliegen. Eine weitere wichtige Annahme des Modells ist, dass die Teilchen mit ihrer Umge- bung wechselwirken, beispielsweise an Phononen oder Gitter-Defekten streuen und ihren Impuls ändern. Wirkt ein elektrisches FeldE, stellt sich ein Gleich- gewicht ein, bei dem die Elektronen permanent beschleunigt werden und nach einer mittleren Streuzeitτ durch einen Streuprozess wieder abgebremst werden.

Damit bewegen sich die Elektronen mit einer Driftgeschwindigkeit durch den Festkörper, aus welcher sich die Stromdichte zu

j=σE=1

ρE=ne²τ me

E (2.86)

errechnen lässt. Mit dieser einfachen klassischen Betrachtung lässt sich zumindest das Ohmsche Gesetz ableiten, es kann aber nicht die spezifische Wärme, Ther- mokraft oder magnetische Suszeptibilität von Metallen erklären. Erst nach der