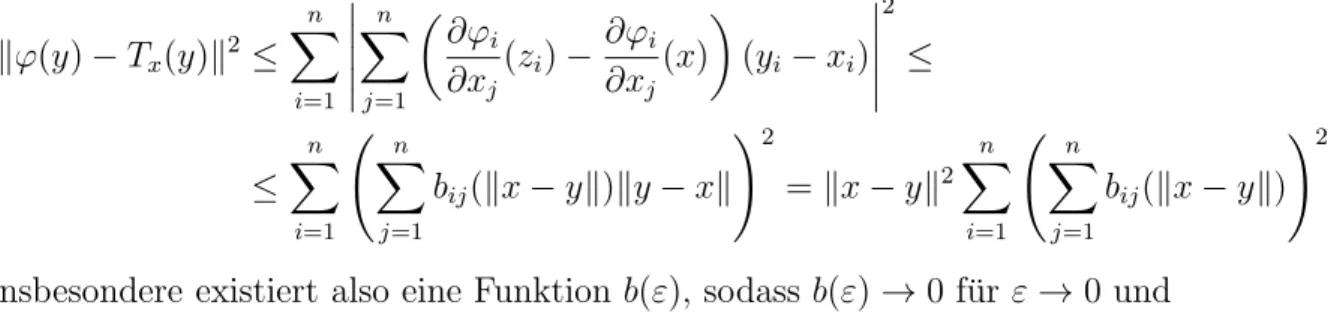Der Satz von Sard

(1)

Der Satz von Sard

Jonathan Gantner

0725250

5. Oktober 2010

(2)

Inhaltsverzeichnis

1 Definitionen 2

1.1 Differenzierbare Mannigfaltigkeiten . . . 2 1.2 Mengen vom Maß null . . . 6

2 Der Satz von Sard 9

3 Verallgemeinerte Transformationsformel 19

(3)

Kapitel 1

Definitionen

1.1 Differenzierbare Mannigfaltigkeiten

Gegenstand dieser Arbeit ist der Satz von Sard - um ihn zu verstehen ben¨otigen wir einige Definitionen und Ergebnisse aus der Differentialgeometrie.

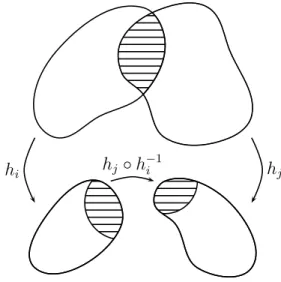
Definition 1.1 (Mannigfaltigkeit). Eine n-dimensionale Mannigfaltigkeit M ist ein to- pologischer Hausdorff-Raum mit abzählbarer Basis der Topologie, der lokal homöomorph zum ^Rⁿ ist — das heißt zu jedem Punkt p ∈ M gibt es eine offene Umgebung U von p und einen Homöomorphismus h:U →U^′, sodass U^′ ⊂^Rⁿ und offen ist.

So ein Hom¨oomorphismus von einer offenen Menge U ⊂ M auf eine offene Menge U^′ ⊂^Rⁿ heißt Karte von M, U das zugeh¨orige Kartengebiet.

Eine Menge von Karten {hi |i∈I} mit S

i∈IUi =M heißt Atlas von M.

Zu zwei verschiedenen Karten (Ui, hi) und (Uj, hj) lässt sich auf dem Durchschnitt Ui∩Uj der Kartengebiete ein Kartenwechsel hij =hj ◦h⁻_i ¹ vonhi(Ui∩Uj)→hj(Ui∩Uj) definieren. Dieser ist als Zusammensetzung von zwei Homöomorphismen selbst wieder ein Homöomorphismus zwischen zwei offenen Teilmengen des ^Rⁿ.

Definition 1.2(differenzierbare Mannigfaltigkeit). Ein Atlas einer Mannigfaltigkeit heißt differenzierbar, wenn alle seine Kartenwechsel differenzierbar sind.

Eine differenzierbare Struktur ist ein bez¨uglich der Hinzunahme weiterer Karten maxi- maler differenzierbarer Atlas.

Ein Paar (M,F) bestehend aus einer Mannigfaltigkeit M und einer differenzierbaren Struktur F heißt differenzierbare Mannigfaltigkeit.

Eine differenzierbare Struktur auf einer Mannigfaltigkeit ist also ein Atlas, dem keine weiteren Karten mehr hinzugefügt werden können, ohne dass Kartenwechsel entstehen, die nicht mehr differenzierbar sind. Es reicht deshalb einen weitaus kleineren Atlas an- zugeben, um eine differenzierbare Struktur vollständig zu definieren. Offensichtlich gilt nämlich:

hii= Id, hjk◦hij =hik und damit auch h⁻_ij¹ =hji. (1.1) Hat man nun einen differenzierbaren AtlasAgegeben, so seiD(A) die Menge aller Karten, f¨ur die jeder Kartenwechsel mit einer Karte ausAdifferenzierbar ist. Dann istD(A) wieder

(4)

differenzierbar, denn jeder Kartenwechselhik kann zumindest lokal dargestellt werden als Zusammensetzunghik =hjk◦hij mit hj ∈A— und offensichtlich istD(A) auch maximal und kann nicht durch zus¨atzliche Karten erweitert werden. Die differenzierbare Struktur D(A) wird also durch Aeindeutig festgelegt.

hi hj ◦h⁻_i ¹ hj

Abb. 1.1: Karten einer Mannigfaltigkeit

Außerdem sind wegen (1.1) die Inversen von Kartenwechseln eines differenzierbaren Atlas wieder Kartenwechsel und somit differenzierbar — Kartenwechsel eines differenzierbaren Atlas sind also Diffeomorphismen. Umgekehrt kann auch jeder Diffeomorphismus zwischen entsprechenden Teilmengen des ^Rⁿ als Kartenwechsel interpretiert werden. Ist n¨amlich (U, h) eine Karte undf ein Diffeomorphismush(U)→Ue ⊂^Rⁿ, dann ist ˜h=f◦h ein Hom¨oomorphismusU →Ue — also eine Karte — undf bzw.f⁻¹ sind genau die Kar- tenwechsel zwischen h und ˜h.

Beispiele 1.3. 1. Jede offene Teilmenge des ^Rⁿ ist offensichtlich eine n-dimensionale differenzierbare Mannigfaltigkeit. Die differenzierbare Struktur darauf wird durch den Atlas {IdU} definiert, der nur eine einzige Karte enth¨alt.

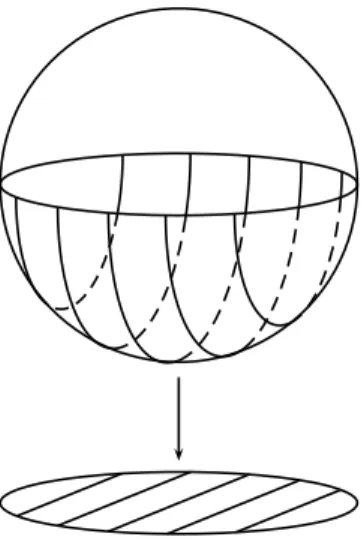
2. Die n-dimensionale Sph¨are Sⁿ ={x∈^Rⁿ⁺¹|p

x²₁+x²₂+. . .+x²_n+1 = 1} ist eine n- dimensionale Mannigfaltigkeit. Auch auf ihr l¨asst sich durch folgende Karten eine differenzierbare Struktur definieren:

h^j_i

(Uij ={x∈Sⁿ|(−1)^jxi >0} → U₁ⁿ(0) ={x∈^Rⁿ| kxk2 <1} (x1, x2, . . . , xn+1) 7→ (x1, . . . , xi−1, xi+1, . . . , xn+1)

wobei i∈ {1, . . . , n+ 1}und j ∈ {1,2}.

Die Abbildungen h^j_i streichen also einfach die i-te Koordinate. Umgekehrt f¨ugt die Inverse (h^j_i)⁻¹ einfach an deri-ten Stelle eine zus¨atzliche Koordinate mit dem Wert

(5)

Abb. 1.2: Koordinatisierung dern-dimensionalen Sph¨are

(−1)^j(1−Pn

k=1x²_k)¹² ein. Die Kartenwechselh^l_k◦(h^j_i)⁻¹ haben dann folgende Form:

h^l_k◦(h^j_i)⁻¹ :





 x1

... xi−1

xi

xi+1

... xk−1

xk

... xn





 7→







x₁ ... xi−1

(−1)^j(1−Pn l=1x²_l)¹² xi

... xk−2

xk−1

...

xn−1

xn





 7→







x₁ ... xi−1

(−1)^j(1−Pn l=1x²_l)¹² xi

... xk−2

xk

...

xn





 .

Sie sind damit auf ihren Definitionsbereichen offensichtlich differenzierbar.

Differenzierbare Strukturen erm¨oglichen es uns nun die Differentialrechnung auf Man- nigfaltigkeiten einzuf¨uhren:

Definition 1.4 (Differenzierbare Abbildung). Seien M und N differenzierbare Mannig- faltigkeiten und ϕ : M → N eine stetige Abbildung. Dann heißt ϕ differenzierbar im Punkt p∈ M, wenn es zwei Karten (U, g) und (V, h) von M bzw. N gibt, sodass p∈ U und ϕ(p)∈V ist, und sodass h◦ϕ◦g⁻¹ differenzierbar im Punkt g(p) ist.

Die Abbildung ϕ heißt differenzierbar, wenn sie in jedem Punkt p∈M differenzierbar ist.

Diese Definition macht Sinn, da ja die Kartenwechsel differenzierbarer Mannigfal- tigkeiten ebenfalls differenzierbar sind, und die Differenzierbarkeit einer Abbildung im

(6)

Punkt p deshalb unabh¨angig von der Wahl der Karten erhalten bleibt.

Analog definiert man Strukturen und Mannigfaltigkeiten der Klasse C^k, indem man for- dert, dass alle Kartenwechsel k-mal stetig differenzierbar sind. Eine Funktionϕ zwischen C^k-Mannigfaltigkeiten heißt k-mal stetig differenzierbar, wenn f¨ur alle Karten g und h die Darstellung h◦ϕ◦g⁻¹ k-mal stetig differenzierbar ist. Man beachte allerdings, dass eine Funktion zwischen C^k-Mannigfaltigkeiten h¨ochstensk-mal stetig differenzierbar sein kann.

Definition 1.5. Seien M und N differenzierbare Mannigfaltigkeiten und ϕ : M → N differenzierbar und seien(U, g)und(V, h)Karten vonM bzw.N mitp∈U undϕ(p)∈V. Weiters sei f =h◦ϕ◦g⁻¹ die Darstellung von ϕ bez¨uglich g und h. Dann ist der Rang von ϕ im Punkt p definiert als der Rang der Jacobimatrix df im Punkt g(p).

Auch der Rang von ϕ ist unabh¨angig von der Wahl der Karteng und h, wie man mit Hilfe der Kettenregel leicht sieht.

Lemma 1.6. Seien M undN zwei m−bzw. n−dimensionaleC¹–Mannigfaltigkeiten und ϕeine stetig differenzierbare AbbildungM →N. Hatϕbeip∈M Rangk, dann existieren Karten (U,e eg) und (V ,e eh) mit p ∈ Ue und ϕ(p) ∈ Ve, auf die bezogen ϕ die Darstellung ψ =eh◦ϕ◦eg⁻¹ hat mit

ψi(x1, . . . , xm) =xi für i= 1. . . k (1.2) Gilt rang ϕ =k auf einer Umgebung von p, kann man eg und eh sogar so wählen, dass ψi(x1, . . . , xm) = 0 für i > k (1.3) Beweis. Seien (U, g) und (V, h) zwei Karten mitp∈U undϕ(p)∈V und seif =h◦ϕ◦g⁻¹ die Darstellung vonϕbezüglich dieser Karten. Dann hat die Jacobimatrix von f beig(p) rang k und o.B.d.A. können wir annehmen, dass

det ∂fi

∂xj

6

= 0 i, j = 1. . . k (1.4)

— andernfalls l¨asst sich die Reihenfolge der Koordinaten mit Hilfe eines Kartenwechsels

¨andern. Betrachtet man nun die Abbildung u:

ui(x1, . . . , xm) = fi(x1, . . . , xm) i= 1. . . , k ui(x₁. . . , xm) = xi i=k+ 1. . . m

dann ist die Jacobi-Matrix du im Punkt g(p) invertierbar - also existiert nach dem Satz uber die inverse Funktion eine Umgebung von¨ g(p), auf der u ein Diffeomorphismus ist und deshalb als Kartenwechsel interpretiert werden kann. Bezüglich der Karten h und eg =u◦g hat ϕ nun die gewünschte Darstellung ψ die (1.2) erfüllt.

Ist zus¨atzlich rang ϕ =k auf einer Umgebung W von p, dann gilt dort auch ^∂ψ_∂xⁱ

j = 0

f¨ur i, j > k. Die Jacobi-Matrix von ψ hat n¨amlich die Form Ik×k 0

∂ψi

∂xji≤k<j

∂ψi

∂xji,j>k

!

(7)

Wäre also ^∂ψ_∂x_jⁱ 6= 0 mit i, j > k, so wäre rangψ > k — deshalb hängt ψ auf W nur von x₁, . . . , xk ab und wir können hier schreiben ψ =ψ(x₁, . . . , xk). Betrachtet man nun die Abbildung z:

zi(y1, . . . , yn2) =yi i= 1, . . . , k zi(y1, . . . , yn2) =yi−ψi(y1, . . . , yk) i=k+ 1, . . . , n2

so sieht man leicht, dass dz im Punkt h◦ϕ(p) invertierbar ist — und mit dem Satz über die inverse Funktion folgt wieder die Existenz einer Umgebung von h◦ϕ(p), sodass z auf dieser Umgebung ein Diffeomorphismus ist. Die Darstellung ψe von ϕ bezüglich der Karten eg und eh =z◦eh — also ψe=eh◦ϕ◦eg⁻¹ =z◦ψ — erfüllt nun zusätzlich (1.3).

1.2 Mengen vom Maß null

Um den Satz von Sard formulieren zu können müssen wir noch erklären, was es bedeutet, dass eine Teilmenge einer differenzierbaren Mannigfaltigkeit Maß null hat. Dazu überlegen wir zuerst, wann das Lebesgue-Maß λd einer Teilmenge des ^R^d null ist. Betrachtet man das Lebesgue-Maß als Vervollständigung der Einschränkung des nach der Borel-Lebesgue- Carathéodory-Methode konstruierten äußeren Maßes auf die Borel-Mengen¹, so ergibt sich die folgende

Definition 1.7. Eine Teilmenge M ⊂ ^R^d hat Lebesgue-Maß null, wenn f¨ur alle ε > 0 eine Folge von W¨urfeln W_n^ε existiert, sodass gilt

M ⊂ [∞ n=1

W_n^ε und

X∞ n=1

vol(W_n^ε)< ε (1.5) wobei vol(W)den elementaren Inhalt a^d (bzw. das Lebesgue-Maß) eines d-dimensionalen W¨urfels mit Seitenl¨ange a bezeichnet.

Eine Menge hat also Maß null, wenn sie sich von höchstens abzählbar vielen ”beliebig kleinen“ Mengen überdecken lässt.

Insbesondere lässt sich mit dieser Definition auch die bekannten Tatsache zeigen, dass jede Teilmenge einer Nullmenge und jede Vereinigung von abzählbar vielen Nullmengen wieder Maß null hat. Ist nämlich A = S

n∈^NAn mit λd(An) = 0, dann gibt es zu ε > 0 f¨ur jedes n ∈ ^N eine ¨Uberdeckung Anm, m ∈ ^N von An mit P

m∈^Nvol(Anm)< 2⁻ⁿε. Es istAnm, n, m∈^Ndann eine abz¨ahlbare ¨Uberdeckung von A mit P

n,m∈^Nvol(Anm)< ε.

Lemma 1.8. Eine Teilmenge M ⊂^R^d hat genau dann Lebesgue-Maß null, wenn f¨ur alle ε >0 eine Folge von Kugeln B_n^ε existiert, sodass gilt

M ⊂ [∞ n=1

B_n^ε und

X∞ n=1

vol(B_n^ε)< ε (1.6)

1Vgl. [Wer07, Kapitel 5 - 8]

(8)

wobei vol(B) den elementaren Inhalt r^dω1 einer d–dimensionalen Kugel mit Radius r bezeichnet, wenn ω1 das Volumen der d-dimensionalen Einheitskugel ist.

Beweis. Sei ε > 0 und M ⊂ ^R^d habe Lebesgue-Maß null. Sei weiters Wn eine Folge von W¨urfeln, sodass gilt P

n∈^Nvol(Wn)<(^√²_d)^dω⁻₁¹ε. Ist mn der Mittelpunkt undan die Seitenl¨ange von Wn, so definiere man Bn als die abgeschlossene Kugel mit Mittelpunkt mn und Radius ^√₂^dan. Dann giltM ⊂S

n∈^NBn und X

n∈^N

vol(Bn) =X

n∈^N

√d 2 an

!d

ω1=

√d 2

!d

ω1

X

n∈^N

a^d_n=

√d 2

!d

ω1

X

n∈^N

vol(Wn)< ε.

Existiert umgekehrt zu jedem ε > 0 eine Folge von Kugeln, die (1.5) erfüllt, so betrachte man zu einer Folge von Kugeln Bn die Folge von Würfeln Wn, sodass Wn den gleichen Mittelpunkt wieBn hat und die Seitenlänge von Wn dem doppelten Radius von Bn entspricht. Dann gilt M ⊂S

n∈^NWn und X

n∈^N

vol(Wn) =X

n∈^N

(2rn)^d= 2^dω⁻₁¹X

n∈^N

r_n^dω₁= 2^dω₁⁻¹X

n∈^N

vol(Bn) Zu beliebigemε >0 w¨ahle man eine ¨UberdeckungB_n^εvonM mitP

n∈^Nvol(Bn)<2⁻^dω1ε.

Die entsprechende Folge von W¨urfeln W_n^ε erf¨ullt dann (1.5). Also hat M Maß null.

Mit ¨ahnlichen Argumenten kann man zeigen, dass es egal ist, ob in Definition 1.7 W¨urfel, Quader oder Kugeln verwendet werden und ob diese offen oder abgeschlossen sind.

Lemma 1.9. Sei O ⊂ ^R^d offen, f : O → ^R^d stetig differenzierbar und A ⊂ O mit λd(A) = 0. Dann hat auch f(A) Maß null.

Beweis. Nehmen wir zuerst an, dass A ganz in einer kompakten Menge enthalten ist. In diesem Fall gen¨ugt f auf A einer Lipschitzbedingung

kf(x)−f(y)k ≤Lkx−yk f¨ur x, y ∈A.

F¨ur beliebiges ε > 0 sei dann An, n ∈ ^N eine ¨Uberdeckung von A aus Kugeln mit P

n∈^Nvol(An) < L⁻^dε und rn sei der Radius von An. Wegen der Lipschitzbedingung ist f(An) ganz in einer Kugel Cn mit Radius L·rn enthalten. Somit gilt f(A) ⊂ S

n∈^NCn

und P

n∈^Nvol(Cn)< ε. Also hat f(A) Lebesgue-Maß null.

Ist A nun nicht ganz in einer kompakten Menge enthalten, dann existieren kompakte Mengen Kn, n ∈ ^N mit Kn ↑ O, sodass f(A) sich als die abz¨ahlbare Vereinigung der Nullmengen f(Bn) mit Bn =Kn∩A darstellen l¨asst und somit selbst Maß null hat.

Dieses Lemma macht es nun sinnvoll von Nullmengen einer differenzierbaren Mannig- faltigkeit zu sprechen.

Definition 1.10. Eine Teilmenge A einer n-dimensionalen differenzierbaren Mannigfal- tigkeit M heißt vom Maß null, wenn sie darstellbar ist als A = S

i∈^NAi, sodass Karten (Ui, hi) existieren mit Ai ⊂Ui und hi(Ai) hat Maß null in ^Rⁿ.

(9)

Wegen Lemma 1.9 ist diese Definition unabhängig von der Wahl der Mengen Ai und der Karten Ui. Tatsächlich hat A genau dann Maß null, wenn für jede beliebige Karte (V, g) die Menge g(V ∩A)⊂^Rⁿ Maß null hat. Es gilt nämlich

g(V ∩A) =[

i∈^N

g(V ∩Ai) = [

i∈^N

g◦h⁻_i ¹ ◦hi(V ∩Ai).

Da aberhi(V ∩Ai)⊂^RⁿMaß null hat und der Kartenwechselg◦h⁻_i ¹ stetig differenzierbar ist, hat mit Lemma 1.9 auch g(V ∩A) Maß null.

Offensichtlich gilt auch, dass jede Teilmenge einer abz¨ahlbaren Vereinigung von Null- mengen wieder Maß null hat. Da die Topologie einer Mannigfaltigkeit eine abz¨ahlbare Basis besitzt, folgt unmittelbar

Korollar 1.11. Sei A Teilmenge einer n-dimensionalen Mannigfaltigkeit M. Hat jeder Punkt p∈M eine Umgebung Up, sodass Up∩A Maß null hat, so hat auch A Maß null.

Beweis. Da die Topologie von M eine abzählbare Basis hat, können wir abzählbar viele Ui auswählen, sodass giltA=S

i∈^N(Ui∩A). Als abz¨ahlbare Vereinigung von Nullmengen hat dann auch A Maß null.

Zu beachten ist allerdings, dass wir auf einer Mannigfaltigkeit kein Maß im eigent- lichen Sinn definiert haben, sondern nur eine Klasse von

”kleinen“ Mengen, die wir als Nullmengen oder

”Mengen mit Maß null“ bezeichnen.

(10)

Kapitel 2

Der Satz von Sard

Definition 2.1. Seien M1 und M2 n1- bzw. n2-dimensionale differenzierbare Mannig- faltigkeiten und ϕ eine differenzierbare Abbildung M1 → M2. Jeder Punkt p ∈ M1 mit rang ϕ < n2 heißt kritischer Punkt von ϕ.

Ein Punkt q∈M₂ heißt kritischer Wert vonϕ, wennϕ⁻¹(q)mindestens einen kritischen Punkt enth¨alt.

Insbesondere ist also f¨ur n1 < n2 jeder Punkt aus M1 kritisch. Der Satz von Sard lautet nun wie folgt:

Satz 2.2 (von Sard). Seien M1 und M2 C^k-Mannigfaltigkeiten der Dimension n1 bzw.

n2 und ϕ eine C^k-Abbildung M1 →M2. Gilt

k−1≥max{n1−n2,0}, (2.1) so hat die Menge der kritischen Werte von ϕ Maß null.

Beweis. Ist n1 < n2 so ist der Beweis einfach — in diesem Fall ist jeder Punkt aus M1 kritisch. Zu zeigen ist also, dass ϕ(M1) eine Nullmenge ist. Um das einzusehen, betrachte man einen abz¨ahlbaren Atlas (Ui, gi)i∈^N von M1 und Karten (Vi, hi) von M2

mit ϕ(Ui) ⊂ Vi. Sei U_i^′ = gi(Ui) ⊂ ^Rⁿ¹ und sei fi = hi ◦ϕ ◦g_i⁻¹ die Darstellung von ϕ bez¨uglich der Karten (Ui, gi) und (Vi, hi). Betrachtet man nun f¨ur jedes i ∈ ^N die Abbildung

f˜i :

U_i^′×^Rⁿ²⁻ⁿ¹ ⊂^Rⁿ² → ^Rⁿ² (x, y) 7→ fi(x)

dann ist ˜fistetig differenzierbar und es giltfi(U_i^′) = ˜fi(U_i^′×{0}). Da aber bekanntermaßen

R

n1

×{0}und somit sicher auchU_i^′×{0}in^Rⁿ² Lebesgue-Maß null haben, ist mit Lemma 1.9 auchfi(U_i^′) eine Nullmenge. Also hat f¨ur jedesi∈^Ndie Mengeϕ(Ui)⊂M₂ Maß null und deshalb auch ϕ(M1) =S

i∈^Nϕ(Ui).

Sei nunn1 ≥n2. Wegen Definition 1.10 lässt sich das Problem auf den Fall reduzieren, dass M₂ = ^Rⁿ², M₁ Teilmenge des n₁-dimensionalen abgeschlossenen Einheitswürfels Eⁿ¹ und f eine C^k-Abbildung von einer Umgebung von Eⁿ¹ in den ^Rⁿ² ist. Ist nämlich (Ui, gi)i∈^N ein abzählbarer Atlas von M1 und (Vi, hi)i∈^N ein Atlas von M2 mit ϕ(Ui)⊂Vi

und ist für alle Ui das Bild U_i^′ =gi(Ui)⊂^Rⁿ¹ beschränkt, dann existiert zu jedem i∈^N eine affine Abbildung ti, sodass ti(Ui)⊂Eⁿ¹ ist. Die Darstellung fi von ϕ bezüglich der Karten gei =ti◦gi und hi bildet (wie verlangt) eine Teilmenge des Eⁿ¹ in den^Rⁿ² ab.

(11)

Ist nunCdie Menge der kritischen Punkte vonϕundCi =Ui∩C, so istCei =gei(Ci) die Menge der kritischen Punkte vonfi. Gilt dann f¨urfider Satz von Sard, sodassfi(Cei) Maß null hat, so ist ϕ(Ci) = h⁻_i ¹(fi(Cei)) eine Nullmenge. Also hat auch ϕ(C) = S

i∈^Nϕ(Ci) als abz¨ahlbare Vereinigung von Nullmengen Maß null.

Falls der Atlas (Ui, gi)i∈^N aber Karten enthält, für dieU_i^′ nicht beschränkt ist, so lässt sich aus ihm ein Atlas konstruieren, der diese Bedingung erfüllt. Jede unbeschränkte Menge U_i^′ lässt sich nämlich von abzählbar vielen beschränkten offenen Mengen U_ij^′ , j ∈

N uberdecken. Ersetzt man jede solche Karte (U¨ i, gi) durch die Karten (Uij, g|^Uij) mit Uij =g⁻¹(U_ij^′ ), so erh¨alt man den gesuchten Atlas.

Betrachten wir nun den Fall n1 =n2. Zu zeigen ist

Lemma 2.3. Sei ϕ = (ϕ1, . . . , ϕn)^T eine Abbildung von Eⁿ nach ^Rⁿ, wobei jede der Abbildungen ϕi auf einer Umgebung von Eⁿ definiert und stetig differenzierbar ist. Dann hat die Menge der kritischen Werte von ϕ Maß null.

Beweis. Zu zwei Punkten x= (x1, . . . , xn)^T und y = (y1, . . . , yn)^T aus Eⁿ existiert nach dem Mittelwertsatz der Differentialrechnung f¨ur jedes i ∈ {1, . . . , n} ein Punkt zi = (zi1, . . . , zi n)^T aus der Verbindungsstrecke von x und y, sodass gilt

ϕi(y)−ϕi(x) = Xn

j=1

∂ϕi

∂xj

(zi)(yj−xj). (2.2)

Also gilt

|ϕi(y)−ϕi(x)| ≤ Xn

j=1

∂ϕi

∂xj

(zi)

|yj−xj| ≤ ky−xk Xn

j=1

∂ϕi

∂xj

(zi)

Und weiter

kϕ(y)−ϕ(x)k² = Xn

i=1

|ϕi(y)−ϕi(x)|² ≤

≤ Xn

i=1

ky−xk Xn

j=1

∂ϕi

∂xj

(zi)

!2

=ky−xk² Xn

i=1

Xn j=1

∂ϕi

∂xj

(zi)

!2

Da die partiellen Ableitungen ^∂ϕ_∂xⁱ

j stetig und somit auf Eⁿ beschr¨ankt sind, l¨asst sich eine Lipschitzkonstante L finden, sodass gilt

kϕ(y)−ϕ(x)k< L ky−xk. (2.3) Sei weitersTx = (Tx1, . . . , Tx n)^T die bei xzu ϕtangentiale AbbildungTx(y) = ϕ(x) + dϕ(x)(y−x). Die einzelnen Komponentenfunktionen haben dann die Form

Tx i(y) =ϕi(x) + Xn

j=1

∂ϕi

∂xj

(x)(yj −xj) Mit (2.2) folgt

(12)

ϕi(y)−Tx i(y) = Xn

j=1

∂ϕi

∂xj

(zi)−∂ϕi

∂xj

(x)

(yj −xj) DaϕeineC¹-Funktion ist, sind die partiellen Ableitungen^∂ϕ_∂xⁱ

j stetig und damit gleichmäßig stetig auf der kompakten Menge Eⁿ. Also existieren für alle i, j ∈ {1, . . . , n} Funktionen bij(ε), sodass gilt: bij(ε) →0 für ε → 0 und |^∂ϕ_∂x_jⁱ(y)− ^∂ϕ_∂x_jⁱ(x)| ≤ bij(kx−yk). Außerdem ist sicher kzi−xk ≤ ky−xk und damit folgt

kϕ(y)−Tx(y)k²≤ Xn

i=1

Xn j=1

∂ϕi

∂xj

(zi)−∂ϕi

∂xj

(x)

(yi−xi)

2

≤

≤ Xn

i=1

Xn j=1

bij(kx−yk)ky−xk

!2

=kx−yk² Xn

i=1

Xn j=1

bij(kx−yk)

!2

Insbesondere existiert also eine Funktion b(ε), sodass b(ε)→0 f¨ur ε→0 und

kϕ(y)−Tx(y)k ≤b(kx−yk)kx−yk (2.4) Ist xein kritischer Punkt von ϕ, dann hat die Jacobi-Matrix dϕ(x) nicht vollen Rang und das Bild von ^Rⁿ unter Tx ist in einer n−1 – dimensionalen EbenePx enthalten.

Sei nun ε so klein, dass b(ε)≤L ist, und es gelte kx−yk ≤ε. Wegen (2.4) gilt dann kϕ(y)−Tx(y)k ≤b(ε)ε. Es ist also ϕ(y) in jener Region Q enthalten, die durch zwei im Abstand von b(ε)ε zu Px parallel liegende n−1–dimensionale Ebenen begrenzt wird.

ϕ

b

ϕ(x)

b

ϕ(y)

Px

εb(ε) εb(ε) Lε

Abb. 2.1: Zwei zu Px parallele Hyperebenen und Würfel um ϕ(x) mit Seitenlänge 2Lε schränken die Position von ϕ(y) ein

Wegen (2.3) ist ϕ(y) außerdem in jedem W¨urfel, dem die Kugel mit Mittelpunkt in ϕ(x) und RadiusLε einbeschrieben werden kann, — also jedem W¨urfel mit Mittelpunkt

(13)

inϕ(x) und Seitenl¨ange 2Lε — enthalten (vgl. Abb. 2.1). SeiW nun ein solcher W¨urfel, der 2 zuPxparallele Seiten hat. Dann istW∩Qeinn–dimensionaler Quader mit Volumen 2ⁿLⁿ⁻¹εⁿb(ε) und es gilt offensichtlich auch ϕ(y)∈W ∩Q.

Teilt man nun Eⁿ in pⁿ Würfel mit Seitenlänge 1/p auf und betrachtet alle jene Würfel, die einen kritischen Punkt x enthalten, dann ist jeder solcher Würfel in einer Kugel um xmit Radius√

n/penthalten. Wählt man pgroß genug, so ist nach der obigen Ausführung also das Bild eines solchen Würfels in einem n–dimensionalen Quader mit Maß 2ⁿLⁿ⁻¹(^√_pⁿ)ⁿb(^√_pⁿ) enthalten.

Die Menge der kritischen Werte von ϕ ist nun aber sicher Teilmenge des Bilds aller Würfel, die zumindest einen kritischen Punkt enthalten. Da es höchstenspⁿsolche Würfel gibt, ist das Maß der Menge der kritischen Werte sicher kleiner gleich

pⁿ2ⁿLⁿ⁻¹ √

n p

n

b √

n p

= 2ⁿLⁿ⁻¹ √ nn

b √

n p

. (2.5)

F¨ur p→ ∞ geht dieser Ausdruck gegen null — also hat die Menge der kritischen Werte Maß null.

Sei nun n1 > n2 — dann muss (2.5) ersetzt werden durch:

pⁿ¹2ⁿ²Lⁿ²

√n1

p n2

b √n1

p

= 2ⁿ²Lⁿ²(√

n1)ⁿ²pⁿ¹⁻ⁿ²b √n1

p

(2.6) Dieser Ausdruck konvergiert f¨urp→ ∞im Allgemeinen allerdings nicht — der Beweis f¨ur den Fall n1 > n2 ist komplexer und erfordert eine genauere Untersuchung des Verhaltens vonϕbei kritischen Punkten. Was wir zeigen wollen ist, dass kϕ(x)−ϕ(y)kbei kritischen Punkten

”schnell genug“ gegen 0 konvergiert, sodass auch (2.6) f¨ur p→ ∞verschwindet.

Lemma 2.6 liefert die benötigte Abschätzung — zunächst benötigen wir jedoch noch die beiden folgenden Resultate:

Lemma 2.4. Sei ϕ : B_ε^m = {x ∈ ^R^m | kxk < ε} → ^Rⁿ eine stetig differenzierbare Abbildung, sodass alle partiellen Ableitungen von ϕ beschr¨ankt sind. Sei weiters f :O ⊂

R

n → ^R mit ϕ(B_ε^m)⊂ O stetig differenzierbar und seien y ∈ B_ε^m, k ∈ ^N⁰ und b(ǫ) eine monotone Funktion mit limǫ→0b(ǫ) = 0, sodass f¨ur alle x∈B_ε^m gilt:

∂f

∂xj

(ϕ(x))

≤b(kx−yk)kx−yk^k j = 1, . . . , n.

Dann existiert eine Konstante K, die nur von ϕ abh¨angt, sodass

|f(ϕ(x))−f(ϕ(y))| ≤Kb(kx−yk)kx−yk^k+1 f¨ur alle x∈B_ε^m gilt.

Beweis. Sei x ∈ B^m_ε und sei F(t) = f(ϕ(y+ (x−y)t)). Dann ist F(t) stetig differenzierbar und es gilt f(ϕ(x)) = F(1) und f(ϕ(y)) = F(0). Mit dem Mittelwertsatz der

(14)

Differentialrechnung folgt f(ϕ(x))−f(ϕ(y)) = F^′(t) f¨ur ein t ∈(0,1). Es gilt aber nach der Kettenregel

F^′(t) =df(ϕ(y+ (x−y)t))·dϕ(y+ (x−y)t)·(x−y) =

= Xn

j=1

Xm i=1

∂f

∂xj

(ϕ(y+ (x−y)t))· ∂ϕj

∂xi

(y+ (x−y)t)·(xi−yi)

und mit K1 =msup ^∂ϕ∂xjⁱ

folgt weiter

|F^′(t)| ≤ Xn

j=1

∂f

∂xj

(ϕ(y+ (x−y)t)) Xm

i=1

∂ϕj

∂xi

(y+ (x−y)t)·(xi−yi) ≤

≤K₁kx−yk Xn

j=1

∂f

∂xj

(ϕ(y+ (x−y)t)) <

< nK1b(kx−yk)kx−yk^k

Setzt man nunK =nK₁, so ist das Lemma bewiesen.

Lemma 2.5. Sei A eine Teilmenge des ^Rⁿ, k ∈ ^N und O ⊂ ^Rⁿ offen mit A ⊂ O.

Dann existieren eine Folge von Mengen Ai, i ∈ ^N⁰ und Abbildungen ϕi, i ∈ ^N, sodass A⊂S_∞

i=0Ai ist, A0 abz¨ahlbar ist und f¨ur i≥1 gilt:

1. ϕi ist eine Einbettung¹ B^m_ε_iⁱ = {x ∈ ^R^mⁱ| kxk < εi} → ^Rⁿ, mit beschr¨ankten partiellen Ableitungen, sodass Ai ⊂ϕi(B_ε^m_iⁱ) ist und f¨ur x, y ∈B_ε^m_iⁱ gilt

kϕi(x)−ϕi(y)k ≥ kx−yk (2.7) 2. F¨ur jede k-mal stetig differenzierbare Funktion f :O →^R, die auf A verschwindet,

existieren monotone Funktionen bi(ǫ) mit limǫ→0bi(ǫ) = 0, sodass

|f(ϕi(x))| ≤bi(kx−yk)kx−yk^k (2.8) f¨ur alle x, y ∈B_ε^m_iⁱ mit ϕi(y)∈Ai gilt.

Beweis. Im Fall n = 1 ist der Beweis einfach. A0 sei die Menge der isolierten Punkte von A. F¨ur jeden Punkt x ∈ A\A₀ existiert dann eine Folge von Punkten xi ∈ A mit x = limi→∞xi. Verschwindet f ∈ C^k(O) auf A, so gilt f(xi) = 0 und es folgt f^′(x) = f⁽²⁾(x) = . . . = f^k(x) = 0. Klarerweise ist n¨amlich f^′(x) = limn→∞

f(xn)−f(x) xn−x = 0.

Induktiv kann man nun f¨ur m≤k zeigen, dass auch f^(m)(x) = 0 ist. Giltf^(j)(x) = 0 f¨ur

1Eine Einbettung ist ein stetig differenzierbarer Hom¨oomorphismusf :O ⊂ ^Rⁿ →f(O) ⊂^R^m mit n≤m, wobeiO6=∅und in^Rⁿ offen undf(O) mit der Spurtopologie versehen ist, sodass df(x) f¨ur alle x∈O maximalen Rangnhat.

(15)

1≤ j < k, so existiert n¨amlich nach dem Satz von Taylor f¨ur alle i ∈^N ein ξi zwischen xi und x, sodass gilt:

0 = f(xi) =

mX−1 j=0

f^(j)(x)

j! (xi−x)^j+ f^(m)(ξi)

m! (xi−x)^m = f^(m)(ξi)

m! (xi−x)^m

Also gilt f^(m)(ξi) = 0 — und da mit (xi)i∈^N auch (ξi)i∈^N gegen x konvergiert, folgt f^(m)(x) = limi→∞f^(m)(ξi) = 0.

A\A0lässt sich sicher durch abzählbar viele Intervalle (ai, bi) mit [ai, bi]⊂Ouberdecken.¨ Wählt man nun ϕi als Translation von (−^bⁱ⁻₂âⁱ,^bⁱ⁻₂âⁱ) nach (ai, bi) und Ai = (A\A₀)∩ (ai, bi), so ist das Lemma erfüllt. Für z1 =ϕi(x) undz2 =ϕi(y)∈Ai gilt nämlich wegen dem gerade Besprochenen nach dem Satz von Taylor:

f(z1) =

k−1

X

j=0

f^(j)(z2)

j! (z1 −z2)^j+ f^(k)(ξ)

k! (z1−z2)^k = f^(k)(ξ)

k! (z1−z2)^k

für ein ξ zwischen z₁ und z₂. Da aber f^(k) stetig und deshalb auf [ai, bi] gleichmäßig stetig ist, existiert eine Funktion bi(ǫ) mit limǫ→0bi(ǫ) = 0, sodass fürx1, x2 ∈[ai, bi] gilt

|f^(k)(x1)−f^(k)(x2)| ≤b(|x1−x2|). Wegen f(z2) = 0 folgt:

|f(ϕ(x))|=|f(z1)|= |f^(k)(ξ)|

k! |z1−z2|^k≤bi(|z1−z2|)|z1−z2|^k =bi(|x−y|)|x−y|^k Auch der Fall k = 0 ist leicht — wobei die Dimension n beliebig sein kann. Da O offen ist, findet man dann zu jedem Punkt p ∈ A eine Umgebung Up von p für deren Abschluss gilt:Up ⊂O — wir könnenUp sogar aus der abzählbaren Basis ausε - Kugeln der Topologie vonOwählen. In Summe erhält man dadurch eine abzählbare Überdeckung Ui, i∈^Nvon A aus ε–Kugeln. Wählt man nun Ai = (A∩Ui) und ϕi als die Translation von Ui zum Ursprung, dann ist f als stetige Funktion auf der kompakten Menge Ui — und damit auch aufUi selbst — gleichmäßig stetig. Also existieren Funktionenbi die (2.8) erfüllen.

Der Beweis funktioniert nun durch vollständige Induktion nach p = n +k — die Induktionsannahme ist, dass Lemma 2.5 fürn+k < pwahr ist. Sei alson+k =p,n >1, k >0 und A⊂^Rⁿ.A¹ sei dann definiert als die Menge aller Punkte x∈A, bei denen für alle f ∈C^k(O), die auf A verschwinden, auch deren partielle Ableitungen verschwinden, wo also gilt:

∂f

∂xj

(x) = 0 f¨ur alle j = 1, . . . , n und sei A² =A\A¹.

Laut Induktionsvoraussetzung existieren nun eine abzählbare MengeA¹₀sowie Mengen A¹_i und Abbildungen ϕ¹_i von B_ε^m_iⁱ →^Rⁿ, i∈^N, sodass gilt:A¹_i ⊂ϕ¹_i(B_ε^m_iⁱ), die ϕ¹_i erfüllen (2.7) und für jede Funktion g ∈ C^k⁻¹, die auf A¹ verschwindet, existieren Funktionen b¹_i(ǫ), mit

|g(ϕ¹_i(x))| ≤b¹_i(kx−yk)kx−yk^k⁻¹ (2.9) wenn x∈A¹_i ist.

(16)

Wegen der Definition von A¹ gilt (2.9) insbesondere f¨ur g = _∂x^∂f

j, wenn f ∈ C^k auf A verschwindet. Wir wollen nun zeigen, dass die Mengen A¹_r und ϕ¹_r (2.8) erf¨ullen. Das folgt aber unmittelbar aus Lemma 2.4, wenn wir entsprechende Funktionen ¯bi(ǫ) finden k¨onnen, die

|∂f

∂xj

(ϕ¹_i(x))| ≤¯bi(kx−yk)kx−yk^k⁻¹ f¨ur allej ∈ {1, . . . , n}erf¨ullen. Die Summen ¯bi(ǫ) =Pn

j=1b¹_ij(ǫ) aller Schrankenfunktionen b¹_ij(ǫ) aus (2.9) für die jeweiligen partiellen Ableitungen _∂x^∂f_j erfüllen dieses Kriterium. Also haben wir Mengen A¹_r und Abbildungen ϕ¹_r gefunden, die ganz A¹ uberdecken und den¨ geforderten Bedingungen genügen. Das Gleiche wollen wir nun für A² tun.

Sei p∈A² — dann gibt es also eine Funktion g ∈C^k, die aufA verschwindet, sodass gilt _∂x^∂g

i(p) 6= 0 für zumindest ein i ∈ {1, . . . , n}. O.b.d.A. können wir annehmen, dass i=n. Nach dem Satz über die implizite Funktion existieren eine UmgebungN vonpund eine k–mal stetig differenzierbare Funktion τn(x1, . . . , xn−1), die auf einer Umgebung M von (p1, . . . , pn−1)^T definiert ist, sodass die vollständige Lösung der Gleichung

g(x1, . . . , xn) = 0

aufN durch die Punkte (x₁, . . . , xn−1, τn(x₁, . . . , xn−1))^T gegeben ist. Betrachtet man nun die Abbildung τ von M →^Rⁿ, die definiert ist durch:

τ((x1, . . . , xn−1)^T) = (x1, . . . , xn−1, τn(x1, . . . , xn−1))^T dann gilt: τ ∈C^k, kτ(x)−τ(y)k ≥ kx−yk und N ∩A⊂τ(M).

Wendet man nun die Induktionsvoraussetzung auf D = τ⁻¹(N ∩A) an, so erh¨alt man Mengen Di, i ∈ ^N0, sodass D ⊂ S

i∈^N⁰Di und D0 abzählbar ist, und Abbildungen ψi, die (2.7) und (2.8) erfüllen, sodass für jede C^k-Funktion h, die auf D verschwindet, Funktionen bi(ǫ) existieren, die

|h(ψi(x))|< bi(kx−yk)kx−yk^k

erfüllen, wenn ψi(y) ∈ Di ist. Verschwindet aber f ∈ C^k auf A, dann verschwindet h = f ◦τ ∈ C^k auf D. Setzt man also ϕi =τ ◦ψi und Ni = τ(Di), so erhält man eine Uberdeckung von¨ N ∩A, die allen geforderten Kriterien genügt.

Da zu jedem Punkt p ∈ A² eine solche Umgebung Np existiert, lässt sich ganz A² durch solche überdecken — und da eine abzählbare Basis der Topologie des ^Rⁿ existiert können wir sogar eine abzählbare Teilüberdeckung Nq, q ∈ ^N auswählen. Verfährt man nun mit jeder dieser Mengen Nq wie oben dargelegt so erhält man in Summe wieder eine abzählbare Überdeckung von A², die die geforderten Kriterien erfüllt. Vereinigt man diese Überdeckung mit der von A¹ und benennt die Vereinigung aller darin enthaltenen abzählbaren Mengen mit A0, so erhält man die gesuchte Überdeckung von A.

Mit Lemma 2.4 und Lemma 2.5 erh¨alt man nun leicht das folgende Lemma 2.6, auf dem der Beweis des Satz von Sard im Falln1 > n2 beruht:

(17)

Lemma 2.6. Sei A⊂ ^Rⁿ, sei O ⊂ ^Rⁿ offen mit A ⊂O und sei q ∈^N. Dann existieren Mengen Ai, i∈^N⁰ mit A⊂S_∞

i=0Ai, sodass A0 abz¨ahlbar ist und f¨ur die Ai, i≥1 gilt:

Für jede q mal stetig differenzierbare Abbildung f :O → ^R, deren kritische Punkte eine Obermenge von A sind, existieren Funktionen bi, i ∈ ^N für die gilt: bi(ǫ) ist monoton fallend, bi(ǫ)→0 für ǫ→ 0und

|f(x)−f(y)|< bi(kx−yk)kx−yk^q (2.10) f¨ur alle x, y ∈Ai.

Beweis. Da jeder Punkt x ∈ A kritischer Punkt von f ist, gilt rang df(x) = 0 — also verschwinden alle partiellen Ableitungen von f auf A. Wenden wir Lemma 2.5 an, so erhalten wir Mengen Ai, i∈^N⁰, und Abbildungen ϕi, i∈^N, sodass A0 abzählbar ist und alle ϕi (2.7) erfüllen. Außerdem existieren für jede partielle Ableitung _∂x^∂f_j, j = 1, . . . , n monotone Funktionen bji(ǫ), i∈^N, mit limǫ→0bji(ǫ) = 0, sodass gilt

∂f

∂xj

(ϕ(x))

< bji(kx−yk)kx−yk^q⁻¹

falls ϕi(y) ∈ Ai ist. Insbesondere gibt es deshalb auch f¨ur jedes i ∈ ^N eine monotone Funktion bi(ǫ) mit limǫ→0bi(ǫ) = 0, sodass dann f¨ur allej ∈ {1, . . . , n} gilt:

∂f

∂xj

(ϕ(x))

< bi(kx−yk)kx−yk^q⁻¹

Aus Lemma 2.4 folgt nun weiter die Existenz von Funktionen ˆbi(ε) mit limε→0ˆbi(ε) = 0, sodass gilt

|f(ϕ(x))−f(ϕ(y))|<ˆbi(kx−yk)kx−yk^q

falls ϕ(y)∈Ai — wegen Ai ⊂ϕ(B_ǫ^m_iⁱ) und (2.7) gilt damit insbesondere f¨ur x, y ∈Ai

|f(x)−f(y)|<ˆbi(kx−yk)kx−yk^q

Der Beweis des Satz von Sard ist nun nicht mehr schwer — zuerst beweisen wir:

Lemma 2.7. Sei ϕ= (ϕ1, . . . , ϕn2) eine Abbildung des n1-dimensionalen Einheitsw¨urfel Eⁿ¹ → ^Rⁿ², wobei jede Funktion ϕi eine auf einer Umgebung von Eⁿ¹ definierte C^q- Funktion ist, und sei A die Menge der Punkte von Eⁿ¹, wo gilt rang ϕ = 0. Gilt q ≥ ⁿ_n¹2, dann hat ϕ(A) Maß null.

Beweis. Wir wenden Lemma 2.6 an und erhalten MengenAr,r ∈^N0, sodassA ⊂S

r∈^NAr

ist. Zu zeigen ist nun, dass ϕ(Ar) für alle r ∈ ^N⁰ Maß null hat. Im Fall r = 0 ist das trivial, da A0 abzählbar ist — betrachten wir also Ar mit r ≥1. Bei einem Punkt x gilt rang ϕ = 0 genau dann, wennxein kritischer Punkt von allenϕi ist. Mit (2.10) existieren nun Funktionen bir(ǫ), sodass für x, y ∈Ar mit kx−yk< ε gilt

|ϕi(x)−ϕi(y)|< bir(ε)ε^q

(18)

und damit existiert auch eine Funktion br(ǫ) mit limε→0br(ε) = 0, sodass gilt

kϕ(x)−ϕ(y)k< br(ε)ε^q. (2.11) Teilt man nun, wie im Beweis von Lemma 2.3, Eⁿ¹ in pⁿ¹ Würfel Wα mit Seitenlänge¹_p, dann ist für jeden dieser Würfel ϕ(Ar ∩Wα) wegen (2.11) in einer Kugel mit Radius b√n1

p

√n1

p

q

enthalten. Da es h¨ochstens pⁿ¹ solcher Kugeln gibt, und ϕ(Ar) sicher ganz in diesen enthalten ist, ist das Maß von ϕ(Ar) ist auf jeden Fall kleiner gleich

pⁿ¹

b √n1

p

√n1

p

qn2

ωn2 =√ n1qn2

ωn2b √n1

p n2

pⁿ¹⁻^qn²

wobei ωn2 das Volumen der n₂-dimensionalen Einheitskugel bezeichnet. Da q ≥ ⁿn¹2 ist, konvergiert dieser Ausdruck f¨urp→ ∞ gegen null — also istϕ(Ar) eine Nullmenge.

Lemma 2.8. Sei ϕ wie in Lemma 2.7 und sei A die Menge der Punkte mit rang ϕ= r (0≤r < n2). Dann hat ϕ(A) Maß null, wenn gilt q ≥ ⁿn¹2⁻−^rr.

Beweis. Den Fallr= 0 haben wir schon in Lemma 2.7 betrachtet — sei alsor≥1. Wegen Lemma 1.11 reicht es zu zeigen, dass f¨ur jeden Punkt aus A eine Umgebung U existiert, sodassϕ(U∩A) eine Nullmenge ist. Sei alsox0 ∈A. Wegen Lemma 1.2 existieren Karten (U, g) um x0 und (V, h) um ϕ(x), auf die bezogen ϕ die Darstellung ψ =h◦ϕ◦g⁻¹ hat mit

ψi(x1, . . . , xn1) =xi i= 1, . . . , r ψi(x1, . . . , xn1) =Fi(x1, . . . , xn) i=r+ 1, . . . , n2

H¨alt man nun x1, . . . , xr fest, dann hat die Abbildung² η:

U(x¹,...,xr) → ^Rⁿ²⁻^r

(xr+1, . . . , xn1) 7→ F(x1, . . . , xr, xr+1, . . . , xn1)

genau dann Rang null, wenn (x1, . . . , xn1) ∈ U ∩A ist — nach Lemma 2.7 hat also die Menge η( (U ∩A)_(x1,...,xr)) = (ϕ(U ∩A))_(x1,...,xr) Maß null in^Rⁿ²⁻^r.

Da nach dem Satz von Fubini f¨ur jede messbare Menge M ⊂^R^d gilt:

λd(M) = Z

R

d1

λd2(Mx)dλd1(x)

falls d=d1+d2 ist, folgt damit unmittelbar, dass ganz ϕ(U ∩A) eine Nullmenge ist.

Der Beweis des Satz von Sard f¨ur den Fall, dass n1 > n2 ist nun einfach:

Sei A die Menge der kritischen Punkte von ϕ, dann gilt A=Sn2−1

r=0 Ar, wobei Ar die Menge der Punkte ist, wo ϕ Rang r hat. Die Menge der kritischen Werte ist dann sicher enthalten in Sn2−1

r=0 f(Ar).

2U(x₁,...,xn)bezeichnet den (x1, . . . , xn)–Schnitt vonU:{(xr+1, . . . , xn₁)∈^Rⁿ¹⁻^r|(x1, . . . , xn₁)∈U}.

(19)

Wegen Voraussetzung (2.1) istk ≥n1−n2+1. Also istk ≥ ⁿ_n¹2⁻−^rr f¨urr ∈ {0, . . . , n2−1} und nach Lemma 2.8 hat deshalb dann jede der Mengen f(Ar) Maß null — und somit auch f(A) selbst.

Aus dem Satz von Sard erh¨alt man insbesondere folgendes

Korollar 2.9. Sei O⊂^Rⁿ offen, f :O →^Rⁿ stetig differenzierbar undC die Menge der kritischen Punkte von f. Dann hat f(C) Lebesgue-Maß null.

(20)

Kapitel 3

Verallgemeinerte

Transformationsformel

SeienX, Y ⊂^R^poffen undt :X →Y einC¹–Diffeomorphismus. Dann lautet die bekannte Transformationsformel f¨ur Integrale

Z

Y

f dλp = Z

X

f◦T · |detdt| dλp (3.1) Mit dem Satz von Sard ist es nun m¨oglich, die Transformationsformel f¨ur Integrale zu verallgemeinern:

Satz 3.1 (Verallgemeinerte Transformationsformel). Seien X ⊂ ^R^p offen, t : X → ^R^p stetig differenzierbar,Y =t(X)undC die Menge der kritischen Punkte vont. F¨ur y∈Y sei N(y)∈[0,+∞] die Anzahl der x∈X\C mit t(x) =y. Dann ist N(y)∈ M⁺(Y,L^p_Y) und f¨ur alle f ∈ M⁺(Y,L^p_Y) gilt:¹

Z

Y

Nf dλp = Z

X

f◦t· |detdt| dλp (3.2) Für Lebesuge-meßbare Funktionen f : Y → ^R oder f : Y → ^C ist Nf genau dann λp- integrierbar über Y, wenn f ◦t· |detdt| über X λ^p-integrierbar ist. In diesem Fall gilt (3.2).

Beweis. Sei zunächst detdt 6= 0 und K ⊂ X kompakt. Zu jedem x ∈ K existieren dann offene Umgebungen Ux von x und Vx von t(x), sodass t|Ûx : Ux → Vx ein C¹- Diffeomorphismus ist. {Ux | x ∈ K} bildet eine offene Überdeckung von K und da K kompakt ist, existieren endlich viele x1, . . . , xm ∈K, sodass giltK ⊂Sm

j=1Uxj. Die MengenA1 =Ux1∩K,A2 = (Ux2∩K)\A1,. . .,Am= (Uxm∩K)\Sm−1

j=1 Aj sind dann disjunkte Lebesgue-Mengen mit Sm

j=1Aj =K. F¨ur jede dieser Mengen Aj gilt nach der Transformationsformel außerdem:

Z

t(Aj)

f dλp = Z

Aj

f◦t· |detdt| dλp

1Anmerkung: M⁺(Y,L^p_Y) bezeichnet die Menge der Lebesgue-messbaren Funktionen von Y nach [0,+∞].