¨Okologie und Epidemiologie

(1)

Okologie und Epidemiologie ¨

Joachim Hermisson 2020

(unter Verwendung von Vorlagen von JH, Ellen Baake und Reinhard B¨urger) 14. November 2020

Literatur

• Sarah P. Otto, Troy Day: A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution, Princeton University Press (∼72 Euro)

• Mark Kot: Elements of Mathematical Ecology, Cambridge University Press (∼62 Euro)

• Nicholas F. Britton: Essential Mathematical Biology, Springer

• Josef Hofbauer, Karl Sigmund: Evolutionary Games and Population Dynamics, Cam- bridge University Press (∼49 Euro)

• Peter Yodzis: Introduction to Theoretical Ecology (1989), Harper & Row.

PDF: www.rug.nl/research/institute-evolutionary-life-sciences/tres/ downloads/bookyodzis.pdf

1

(2)

Vorbemerkungen zur Vorlesung WS 2020/2021 2

Biologie und Mathematik

Es ist wohl keine ¨Ubertreibung zu sagen, dass nicht alle großen Biologen talentierte Ma- thematiker waren. Charles Darwin schreibt zu diesem Thema in seiner Autobiographie von 1876:

During the three years which I spent at Cambridge my time was wasted, as far as the academical studies were concerned, as completely as during the three years which I spent at Edinburgh and at school. I attended mathematics, and even went during the summer of 1828 with a private tutor (a very dull man) to Barmouth, but I got on very slowly. The work was repugnant to me, chiefly from my unbeing able to see any meaning in the early steps in algebra. This impatience was very foolish, and in the after-years I have deeply regretted that I did not proceed far enough at least to understand something of the great leading principles of mathematics for men thus endowed seem to have an extra sense. But I do not believe that I should ever have succeeded beyond a very low grade.

Dennoch verdankt Darwin den entscheidenden Durchbruch zu seiner Theorie der nat¨urlichen Selektion einer Kombination von Naturbeobachtung und mathematischer Modellierung, wie er selbst ausdr¨ucklich betont:

In October 1838, that is, fifteen months after I had begun my systematic enqui- ry, I happened to read for amusements ‘Malthus on Population’, and being well prepared to appreciate the struggle for existence which everywhere goes on from long-continued observation of the habits of animals and plants, it at once struck me that under these circumstances favourable variations would tend to be preserved, and unfavourable ones to be destroyed. The result of this would be the formation of new species. Here then I had at last got a theory by which to work.

Die mathematischen Einsichten von Thomas Malthus (1766-1834), dessenEssay on the Prin- ciple of Population (1798) Darwin mehr zufällig in die Hände bekam, werden wir im ersten Teil der Vorlesung ausführlich besprechen.

Natürlich hat sich seit den Zeiten Darwins in der Biologie viel getan. Generell wird mathematische Modellierung überall dort wichtig, wo die Wissenschaft über das Sammeln von Daten und Fakten (klassisch: neue Spezies beschreiben, heute: Funktion eines Gens beschreiben) hinausgeht und das Gewinnen von neuen Einsichten aus diesen Fakten das Ziel ist. Nach dem Physiker Sir William Bragg ist letzteres die eigentliche Bestimmung jeder Wissenschaft:

The important thing in science is not so much to obtain new facts, but to discover new ways to think about them.

Da die Biologie so komplex und vielfältig ist wie keine andere Naturwissenschaft, steht häufig noch das Sammeln von Daten und Fakten an erster Stelle. Zunehmend können heute aber immer größere Mengen an Daten in kurzer Zeit gewonnen werden (Sequenzdaten, Genexpres- sionen), sodass nicht das Sammeln selbst, sondern die Gewinnung neuer Erkenntnisse aus diesen Daten zum vorrangigen Ziel wird. Dies erfordert oft komplexe Modelle – eine zuneh- mende Mathematisierung der Wissenschaft ist die Folge.

Es wird in dieser Vorlesung nicht möglich sein, einen umfassenden Überblick über Model- le und Methoden der mathematischeen Biologie zu geben. Das Ziel ist es vielmehr, eine Idee

(3)

Vorbemerkungen zur Vorlesung WS 2020/2021 3 davon zu vermitteln, was es heißt “mathematisch zu modellieren” und mit welchen Methoden man in Modellen zu biologischem Verständnis kommen kann. Dies wird im ersten Teil der Vorlesung beispielhaft anhand einiger Modelle aus der Ökologie und der Epidemiologie ge- schehen. Im zweiten Teil werden Modelle aus der Populationsgenetik und der (evolutionären) Spieltheorie behandelt.

Mathematische Modelle in der Biologie

Jedes biologische Modell ist eine Abbildung eines Teils der Natur auf einen mathematischen Formalismus. Modelle sind immer Abstraktionen, d.h. vereinfachende Darstellungen der Wirk- lichkeit. Modellierung beginnt deshalb mit einer Reihe von Modellannahmen: Einige Aspekte eines in der Natur beobachteten Systems werden in das Modell integriert, weil wir davon ausgehen, dass sie für das vorliegende Problem wesentlich sind. Viele andere Aspekte werden ignoriert (bzw. es wird von ihnen abstrahiert), entweder weil sie wahrscheinlich unwichtig sind oder weil wir bewußt eine reduktionistische Perspektive einnehmen wollen. Im letzteren Fall hoffen wir, dass wir ein komplexes System verstehen können, indem wir (Gruppen von einzelnen) Faktoren nacheinander untersuchen. Wenn wir z.B. die zukünftige Bevölkerungsgröße in Osterreich modellieren, sind die derzeitige Gr¨¨ oße und die Altersstruktur sicherlich wesentlich.

Andere Faktoren wie Fortschritte in der medizinischen Behandlung könnten ebenfalls einen gewissen Einfluss auf die Sterblichkeitsraten haben, können aber in einem einfachen Modell ignoriert werden. Noch andere Faktoren, wie Immigration, sind wahrscheinlich wichtig, aber eine Behandlung ohne Einwanderung könnte uns bereits wertvolle Informationen liefern bevor wir die Auswirkungen von Immigration in einem separaten Schritt untersuchen.

Je mehr Faktoren in ein Modell einbezogen werden, desto präziser und spezifischer wird es. Dies ist insbesondere für zuverlässige quantitative Vorhersagen erforderlich (Wettervor- hersage, demographische Modelle). Größere Komplexität bedeutet aber immer auch weniger Handhabbarkeit und meist auch weniger Allgemeingültigkeit. Aus einem Modell, das genauso komplex ist wie das System, das es repräsentiert, können wir keine neuen Erkenntnisse gewinnen. Komplexe quantitative Modelle, die für Vorhersagen verwendet werden, können in der Regel nur durch Computersimulationen behandelt werden. Im Gegensatz dazu sind viele Fra- gen qualitativer Natur, ob zwei Arten koexistieren können oder wann es zu einem Ausbruch einer Infektionskrankheit kommen kann. In diesen Fällen ist es das Ziel der Modellierung, einen minimalen Satz von Faktoren zur Erklärung eines Phänomens zu finden. Ein Modell ist dann umso besser, je einfacher es ist.

Die Kunst der Modellierung besteht also darin, die wesentlichen Faktoren auszuwählen, die in ein Modell einfließen sollen. Dies erfordert einerseits eine gewisse Erfahrung mit dem zugrundeliegenden (z.B. biologischen) System. Andererseits erfordert es Verständnis des mathematischen Mechanismus, um zu erkennen, welche Faktoren entscheidende Konsequenzen haben können, auch wenn ihre Effekte zunächst klein aussehen. Zu diesem Zweck stützt sich die Modellierung auf einen breiten mathematischen Werkzeugkasten, der Elemente aus der Theorie stochastischer Prozesse, dynamischer Systeme, Differentialgleichungen und der Sta- tistik enthält.

Auch wenn die Motivation für eine ernsthafte Modellbildung in ihrer Anwendung liegt, trägt sie auch in der Mathematik als eigenständiger Wissenschaft Früchte. Oft zeigen sich in der Anwendung neue Strukturen, die mit den verfügbaren mathematischen Methoden nur unzureichend beschrieben werden können. Historisch betrachtet gehen deshalb viele der be- deutendsten Entwicklungen in der Mathematik, wie die Differential- und Integralrechnung

(4)

Vorbemerkungen zur Vorlesung WS 2020/2021 4 oder die Wahrscheinlichkeitstheorie, auf ganz konkrete Probleme in der Anwendung zur¨uck.

Neben der Physik hat auch die Biologie immer wieder hierzu beigetragen, etwa bei der Ent- wicklung der mathematischen Statistik durch R.A. Fisher und durch wesentliche Impulse f¨ur die Theorie dynamischer Systeme und stochastischer Prozesse.

Okologie und Epidemiologie¨

Oikos= Haus, Wohnung.Logos = Wort, Studium von. Ökologie bezieht sich auf die wissenschaftliche Untersuchung lebender Organismen in ihrer natürlichen Umgebung. Sie ist eine vielfältige wissenschaftliche Disziplin und deckt verschiedene Ebenen der biologischen Orga- nisation ab.

• Auf der individuellen Ebene diskutiert diephysiologische ¨Okologieden Einfluss von Nah- rung, Licht, Feuchtigkeit, Pestizidkonzentrationen usw. auf das Leben von Individuen.

• Die Populationsökologie untersucht die Wechselwirkungen von Populationen mit ihrer Umwelt und ihre Auswirkungen auf die Bevölkerungsstruktur und Demographie. Auf der gleichen Ebene diskutiert dieVerhaltensökologiedie Konsequenzen unterschiedlicher Verhaltensstrategien.

• Schließlich behandeln dieGemeinschafts¨okologieund dieOkosystemforschung¨ das Schick- sal komplexer ¨Okosysteme mit zwei bis zehntausenden interagierender Arten und Ar- tengruppen.

Die Wechselwirkungen von Populationsdynamik und evolutionärer Dynamik sind Gegenstand derevolutionären Ökologie. Viele Zweige der ökologischen Forschung verwenden mathematische Modelle. So bedient sich die Verhaltensökologie beispielsweise spieltheoretischer Metho- den, um die Auswirkungen von Verhaltensstrategien zu untersuchen. Die Evolutionsökologie stützt sich stark auf die mathematischen Modelle der Evolutionsgenetik. Das Thema dieser Vorlesung muss enger gefasst werden und wird sich hauptsächlich auf die Populationsökologie konzentrieren, wo wir die Dynamik von Populationsgrößen und ihre Gleichgewichte untersuchen. Als wesentliche Anwendung werden wir in einem zweiten Teil dann Modelle der Epi- demiologie besprechen, die die Dynamik von infektiösen Krankheiten in einer Population beschreiben.

(5)

Arbeitsblatt 1 zur Vorlesung WS 2020/2021 5

1 Elementare Populationsdynamik in einer Dimension

Populationsgrößen biologischer Arten und ihre zeitliche Entwicklung gehören zu den funda- mentalsten Bestimmungsgrößen der Ökologie. Mathematisch ist der dynamische Prozess des Populationswachstums und -rückgangs ganz allgemein eine Funktion von Faktoren, die einer Population immanent sind (z.B. ihr Reproduktionspotenzial, ihr Lebenszyklus oder ihre Dich- te) und von Umweltbedingungen. Die Umwelt umfasst alle Ressourcen, die für das Gedeihen einer Population unerlässlich sind, wie Nahrung und Raum, sowie Faktoren, die ihre Größe verringern können, wie Raubtiere und Krankheiten. In der Natur sind viele dieser Faktoren in der Tat selbst dynamische Populationen, die als Nahrungsquelle, Konkurrent, Raubtier oder Parasit eine direkte Auswirkung auf die Dynamik der fokalen Population haben. Da die dynamischen Prozesse von (z.B.) Raubtieren und Beutetieren interagieren, erhalten wir schnell ein komplexes mehrdimensionales Problem. Mit diesen Komplexitäten werden wir uns zweiten und dritten Kapitel der Vorlesung ausführlich beschäftigen. In einem ersten Schritt gehen wir jedoch vereinfachend davon aus, dass wir alle Wechselwirkungen mit anderen dynamischen Aspekten der Umwelt ignorieren können und modellieren die Dynamik einer einzelnen isolierten Population. Biologisch ist solch eine vereinfachte Betrachtung manchmal gerechtfertigt, zum Beispiel wenn sich die Dynamik der interagierenden Populationen auf verschiedenen Zeitskalen abspielt: entweder viel schneller, so dass wir davon ausgehen können, dass sich die interagierende Population in einem dynamischen Gleichgewicht befindet, oder viel langsamer, so dass sich die Größe einer interagierenden Population über die interessierenden Zeitspannen nicht wesentlich ändert. Als weitere wesentliche Annahme gehen wir davon aus, dass die Po- pulation unstrukturiert ist. Dies bedeutet, dass alle Individuen der Population als gleichwertig behandelt werden. Insbesondere gibt es keine Altersklassen, keine phänotypischen Unterschie- de (die für die Dynamik von Bedeutung sind), und wir können die Verteilung der Population

¨

uber den physischen Raum ignorieren.

1.1 Deterministische Prozesse in diskreter Zeit

Viele Prozesse in der Natur werden als in der Zeit kontinuierlich ablaufend betrachtet. Für andere, wie beispielsweise das Wachstum einer Insektenpopulation mit getrennten Genera- tionen oder für Kreuzungsexperimente, ist eine diskrete Zeitskala sinnvoller, auf der nur bestimmte Zeitpunkte, z.B. Vielfache der Generationsdauer ∆t, angegeben werden. Eine diskrete Betrachtungsweise entspricht oft auch der experimentellen Situation, wo meist nicht kontinuierlich, sondern in regelmäßigen Abständen gemessen wird. Messen wir beispielsweise die Populationsgrößex zu den Zeitpunkten 0,∆t,2∆t,3∆t, . . ., so bilden die Werte x₀, x₁, x₂. . . eine Folge, die die zeitliche Veränderung des Systems beschreibt. Eine Folge ist iterativ (oder rekursiv) definiert, wenn eine Vorschrift f gegeben ist, wie man ein Folgenglied aus dem jeweils vorhergehenden gewinnt:

x_n+1=f(x_n). (1)

Die Iterationsfunktion f wird im populationsbiologischen Zusammenhang auch als Repro- duktionsfunktion bezeichnet. Sie stellt eine dynamische Regel dar, die angibt, wie sich die Populationsgröße von einem Zeitschritt (Generation, Jahr) zum nächsten verändert. Die zu- gehörige Folge heißt auch Zeitverlauf oder Populationsentwicklung.

Der entscheidende Schritt zur mathematische Modellierung eines biologischen Prozesses ist die Konstruktion der Reproduktionsfunktion aus biologisch motivierten Überlegungen über das System, das man beschreiben möchte. Im folgenden werden wir einige Beispiele hierfür

(6)

Arbeitsblatt 1 zur Vorlesung WS 2020/2021 6 kennenlernen. In einem zweiten Schritt m¨ochte man dann wissen, wie die Reproduktionsfunk- tion den Zeitverlauf des biologischen Prozesses bestimmt.

Modellbildung I: Geometrisches Wachstum

Betrachten wir, um konkret zu werden, die Vogelpopulation auf einer Insel. Jedes Jahr wird die Populationsgröße bestimmt. Wie kann man die Entwicklung dieser Größe in einem Modell beschreiben? Für das einfachste Modell machen wir die folgenden Annahmen:

Als erstes nehmen wir an, dass die Populationsgröße im Folgejahr,xn+1, nur von der aktuellen Populationsgrößexn abhängt, und nicht von anderen in der Zeit veränderlichen Größen (wir vernachlässigen also z.B. Klimaschwankungen oder den Einfluß von Populationsgrößen anderer Vogelarten). Außerdem nehmen wir an, dass sich die Populationsgröße zwischen den Jahern nur durch Geburten und Todesfälle ändert. Wir setzen also anxn+1 =xn+Bn−Dn, wobei B_n und D_n die Anzahl der Geburten und Todesfälle in einer Population der Größe xn angibt. In der einfachsten Näherung sollten diese Zahlen einfach proportional zur ur- sprünglichen Zahl der Individuen sein, alsoBn=bxnundDn=dxn.bunddsind Konstanten und geben die mittlere Zahl der Geburten und Todesfälle in der Population pro Individuum und pro Jahr an. Mit der Definitionr:= 1 +b−dfinden wir damit die Reproduktionsfunktion x_n+1=f(x_n) =x_n+bx_n−dx_n=rx_n. (2) Die Reproduktionsfunktionf(x) =rxist einfach eine Gerade durch den Ursprung (s. Abb. 3).

Für jeden Anfangswert x0 können wir durch wiederholtes Anwenden der Iterationsvorschrift (2) die Entwicklung der Populationsgröße in aufeinanderfolgenden Jahren voraussagen, d.h:

x1 =rx0, x2 =rx1 =r²x0, ...

Offensichtlich l¨aßt sich der Zeitverlaufexplizitangeben als geometrische Folge

xn=rⁿx0. (3)

0 2 4 6 8

Zeit 0

250 500 750 1000 1250 1500

Population

0 2 4 6 8

Zeit 2.3

3.3 4.3 5.3 6.3 7.3

Lnxn

0 200 400 600 800

Population jetzt 0

250 500 750 1000 1250 1500

Population1Jahrspaeter

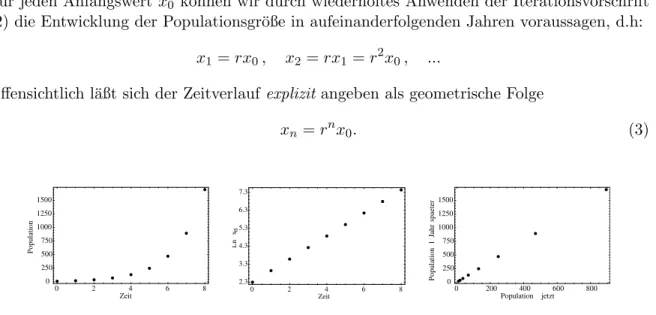
Abbildung 1: Geometrisches Wachstum einer Vogelpopulation. Links: Populationsgr¨oße xn

als Funktion der Zeit n in Jahren; Mitte: Logarithmus der Populationsgröße (sog. halb- logarithmische Auftragung); rechts: Populationsgröße in der nächsten Generation als Funktion der aktuellen Größe (die Punkte liegen auf dem Graphen der Reproduktionsfunktion).

Beispiel In einer Vogelpopulation, die eine Insel neu besiedelt hat, werden pro Jahr und Individuum im Mittel 1.1 neue V¨ogel geboren und 0.2 sterben. Das f¨uhrt zu geometrischem Wachstum mit r= 1.9, alsox_n=rⁿx₀, mitx₀ = 10 in Zahlen:

(7)

Zeit n(in Jahren) 0 1 2 3 4 5 6 7 8

Populationsgröße xn 10 19 36 69 130 248 470 894 1698 Betrachtet man anstelle der Populationsgröße den (natürlichen) Logarithmus,

y_n= ln(x_n) = ln(rⁿx₀) =nln(r) + ln(x₀),

so erhält man einen linearen Anstieg mit Steigung ln(r) und Achsenabschnitt ist ln(x₀). An dieser Darstellung läßt sich das geometrische Wachstum besonders leicht erkennen. Allgemein erhalten wir für eine Reproduktionsfunktion der Form f(x) =rx ein qualitativ unterschied- liches Verhalten abhängig vom Wert vonr≥0:

r= 0 sofortiges Aussterben, 0< r <1 geometrisches “Schrumpfen”,

r= 1 xn=x0 f¨ur alle n, r >1 geometrisches Wachstum . Modellbildung II: Ein komplexeres Modell

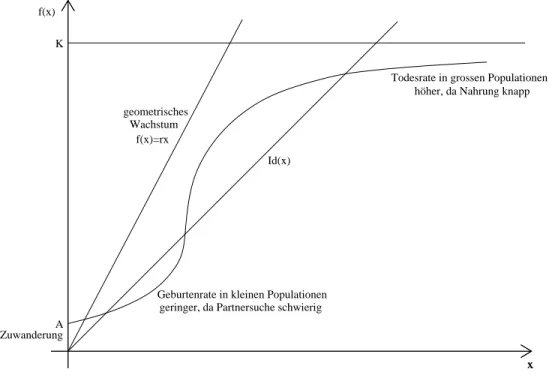
Wir betrachten wieder das Beispiel der Vogelpopulation auf einer Insel. Im letzten Abschnitt hatten wir mit der Iterationsfunktionf(x) = (1 +b−d)x=rx ein sehr einfaches Modell für die zeitliche Dynamik der Populationsgröße konstruiert. Dieses Modell entält zwei Parameter, die Geburtenratebund die Todesrated, die wir aus Beobachtungen im Feld schätzen können (die Dynamik hängt allerdings nur von der Differenzb−d ab). Um das Modell des geometrischen Wachstums realistischer zu machen, wollen wir nun einige Aspekte, die wir bisher vernachlässigt hatten, ergänzen:

• Jedes Jahr wandern einige Vögel vom Festland auf die Insel zu. Wir modellieren dies durch einen Beitrag A zu f(x), wobei Aeinfach eine positive Zahl unabhängig von der Populationsgröße xist.

• Bisher haben wir eine konstante Geburtenrate b angenommen. Die Zahl der Neugebo- renen ist dann einfach proportional zur Populationsgröße B(x) = bx. Für sehr kleine Populationen ist das nicht realistisch. Der Grund ist, dass zur Produktion von Nachkom- men erst einmal ein Partner gefunden werden muss. Dies gelingt bei kleiner Populati- onsgrößexnicht immer. Die effektive Anzahl der Geburten ist deshalb zunächst kleiner und erreicht erst für ein hinreichend großes x (wenn die Partnersuche kein Problem mehr ist) die RelationB(x) =bx. Biologisch nennt man dies einenAlle-Effekt.

• Eine weitere unrealistische Eigenschaft des geometrischen Wachtums-Modells ist es, dass Populationen unendlich groß werden können. In Wirklichkeit ist die Populationsgröße durch den beschränkten Vorrat an Nahrung und Platz immer begrenzt. Wir koennen dies in unserem Modell durch eine maximale PopulationsgrößeK (die sogenanntecarrying capacity) berücksichtigen. Die Iterationsfunktion f(x) kann den Wert K nicht ubersteigen, sondern n¨¨ ahert sich ihm für große xasymptotisch an.

Die Änderungen, die sich aus diesen Überlegungen für die Reproduktionsfunktionf(x) ergeben sind in der Abbildung 2 dargestellt.

(8)

x A

K

x f(x)

geometrisches

Zuwanderung

Todesrate in grossen Populationen

Wachstum f(x)=rx

höher, da Nahrung knapp

geringer, da Partnersuche schwierig Geburtenrate in kleinen Populationen

Id(x)

Abbildung 2: Reproduktionsfunktionen f¨ur das geometrische und das komplexere Modell.

Modellanalyse I: Cobwebbing

Eine graphische Methode, die es erlaubt, auch für kompliziertere Reproduktionsfunktionen qualitative Aussagen über die Entwicklung der Populationsgröße zu treffen ist das sogenannte Cobwebbing:

1. Zun¨achst zeichnen wir den Graphen der Reproduktionsfunktionf und den Graphen der Winkelhalbierenden Id(x) =x und w¨ahlen den Anfangswertx₀.

2. Umx1 ausx0 zu bestimmen, wenden wirf aufx0 an, d.h.x1 ist der Funktionswert von f an der Stellex0. Wir zeichnen einen Pfeil von Punkt (x0, x0) zum Punkt (x0, x1) auf dem Graphen von f.

3. Um x₂ ausx₁ zu bestimmen, müssen wir zunächst den Wert x₁ von der vertikalen auf die horizontale Achse übertragen. Dies erreichen wir dadurch, dass wir einen waage- rechten Pfeil vom Punkt (x₀, x₁) auf dem Graphen von f zum Punkt (x₁, x₁) auf der Winkelhalbierenden zeichnen. Nun erhält man x₂ = f(x₁) analog zu Schritt 2 durch einen senkrechten Pfeil von (x1, x1) zum Punkt (x1, x2) auf dem Graphen vonf. Wenn man Schritt 3 von verschiedenen Anfangspunkten x₀ aus wiederholt ausführt, erhält man das in Abb. 3 dargestellte Bild.

Gleichgewichtspunkte

Von besonderem Interesse in einem dynamischen Prozess sind die Werte x^∗, auf die sich die dynamische Variable (z.B. die Populationsgr¨oße) einstellt wenn man lang genug wartet, also limn→∞x_n=x^∗. Wir definieren:

(9)

x Id(x)

f(x)

Abbildung 3: Iterationsfunktion und Cobwebbing f¨ur das Modell einer Vogelpopulation. Die Reproduktionsfunktion selbst gibt nicht die Populationsgr¨oße als Funktion der Zeit an. Die Zeitentwicklung gewinnen wir erst durch das Cobwebbing.

Definition: Gleichgewichts- oder Fixpunkt Sei f eine Reproduktionsfunktion. Dann heißt eine L¨osung x^∗ der Gleichung

f(x) =x (4)

Fixpunkt oder Gleichgewichtspunkt. Istx^∗ ein Fixpunkt undxn=x^∗, dann istxn+1 =xn= x^∗. Graphisch lassen sich die Fixpunkte bestimmen als Schnittpunkte der Reproduktionsfunk- tion mit der Winkelhalbierenden. Wichtig f¨ur die Analyse des dynamischen Prozesses ist nun die Unterscheidung von stabilen und instabilen Fixpunkten:

• Ein Fixpunkt x^∗ heißt global stabil, wenn die Folge der xn unabh¨angig vom Startwert x₀ gegen x^∗ konvergiert.

• Ein Fixpunkt x^∗ heißt lokal stabil, wenn die Folge der xn f¨ur solche x0, die nah genug an x^∗ liegen, gegenx^∗ konvergiert.

• Ein Fixpunkt x^∗ heißt instabil, wenn er nicht lokal stabil ist.

Kriterium für (lokale) Stabilität bzw. Instabilität: Ob ein Fixpunkt stabil oder instabil ist, können wir am konkreten Beispiel meist leicht mit dem Cobwebbing herausfinden. Für die Vogel-Population erhalten wir zum Beispiel zwei stabile und einen instabilen Fixpunkt (siehe Abb. 3). Mit Hilfe des graphischen Verfahrens können wir aber auch ein allgemeines Kriterium für die lokale Stabilität eines Fixpunktes ermitteln. Wir betrachten dazu wie sich das Cobweb in Abhängigkeit der Steigung der Reproduktionsfunktion am Schnittpunkt mit der Winkelhalbierenden ändert. Wir sehen (vgl. Abb. 3):

(10)

• Ist die Steigung der Reproduktionsfunktion am Fixpunkt gr¨oßer als 1, f⁰(x^∗)>1 (f(x) schneidet die Winkelhalbierende von unten nach oben), so kommt man auf dem Cobweb immer weiter vom Fixpunkt weg: der Fixpunkt ist instabil.

• Ist die Steigung 0≤f⁰(x^∗)<1, so n¨ahert man sich auf dem Cobweb dem Fixpunkt von beiden Seiten aus an: der Fixpunkt ist (lokal) stabil. Dabei ¨uberspringt die Folgex_ndas Gleichgewicht nicht, sondern bleibt jeweils auf einer Seite: monotone Konvergenz.

• Für−1< f⁰(x^∗)<0 ist der Fixpunkt ebenfalls lokal stabil, aber die Folgex_nüberspringt das Gleichgewicht mit jedem Schritt. Wir habenoszillierende Konvergenz (oder gedämpfte Schwingungen).

• Ist die schließlich f⁰(x^∗) < −1, so ist der Fixpunkt wiederum instabil (oszillierende Divergenz).

• Ist die Steigung genau gleich eins oder gleich−1, so l¨aßt dieses Kriterium keine Aussage zu. Das Kriterium liefert auch keine Information ¨uber das globaleVerhalten.

Ubungsaufgaben 1¨

Aufgabe 1.1: Ein Baum w¨achst jedes Jahr um α cm.

(a) Geben Sie die Iterationsfunktion an und stellen Sie sie graphisch dar und führen Sie das Cobwebbing für ein beliebig gewähltes x0 durch.

(b) Geben Sie die Baumh¨ohe im n-ten Jahr explizit an. Um welche Folge handelt es sich?

Aufgabe 1.2: Radioaktive Isotope, wie C¹⁴, zerfallen im Laufe der Zeit. Je nach Isotop zerfällt jedes Jahr ein fester Anteil des noch vorhandenen Materials. Man charakterisiert Iso- tope durch ihreHalbwertszeit, das ist der Zeitraum, innerhalb dessen die Hälfte des Materials zerfällt. Die Halbwertszeit von C¹⁴ ist 5730 Jahre.

(a) Geben Sie die Iterationsfunktion an und ermitteln Sie, wieviel Prozent des noch vorhandenen Materials pro Jahr zerf¨allt.

(b) Das Mischungsverhältnis des radioaktiven C¹⁴und des nichtradioaktiven C¹²im CO2der Atmosphäre ist über geologische Zeitskalen konstant geblieben, und Pflanzen bauen es in demselben atmosphärischen Mischungsverhältnis in ihre organischen Moleküle (z.B.

Cellulose, Lignin) ein. Wenn die Pflanze stirbt, nimmt sie kein neues CO2 mehr auf.

Das radioaktive C¹⁴ in dem toten Pflanzenmaterial zerfällt (gemäß der uns bekannten Iterationsfunktion), das C¹²bleibt unverändert. Somit sinkt das Verhältnis C¹⁴/C¹² im Laufe der Zeit ab. Geben Sie die Iterationsfunktion für dieses Verhältnis an.

(c) Bei einer Ausgrabung wird ein alter Holzrest gefunden, dessen C¹⁴/C¹² Verh¨altnis nur noch 23 % desjenigen Wertes betr¨agt, den man in lebendem Pflanzenmaterial findet.

Finden Sie heraus, wann das Holz geschlagen wurde. Benutzen Sie dazu die vorher ermittelte Zerfallsrate.

(11)

Arbeitsblatt 1 zur Vorlesung WS 2020/2021 11 Aufgabe 1.3: In zwei Behältern I und II befinden sich insgesamt γ Mol einer gelösten Substanz. Die Behälter sind durch eine Membran getrennt, die eine gewisse Durchlässigkeit für die Partikel besitzt. Die Beweglichkeit der Teilchen, die Durchlässigkeit der Membran und die Größe bzw. Form der Behälter sollen so sein, daß jeweils nach 1 min. ein Anteilαder zuvor in I befindlichen Teilchen nach II gewandert ist und ein Anteilβ der zuvor in II befindlichen nach I. Wenn x_n die Stoffmenge (in Mol) in I und y_n die Stoffmenge in II nach n Minuten ist, dann gilt

xn+1 =xn−αxn+βyn, xn+yn=γ wobei 0< α+β <1 sein soll.

(a) Berechnen Sie die resultierende Iterationsfunktion f¨ur die Stoffmenge in I, bestimmen Sie den Fixpunkt und die Stabilit¨at.

(b) Setzen Sie nunγ = 0.2,α = 0.2 undβ = 0.1. Ermitteln Sie (graphisch oder rechnerisch) für die ersten 5 Minuten die Zeitentwicklung für die Stoffmenge in I, und zwar für die Startwerte x₀ = 0 und x₀ = 0.15. Zeichnen Sie beide Zeitverläufe in ein Bild. Auf welchen Wert werden sich die Stoffmengen in I und II einstellen?

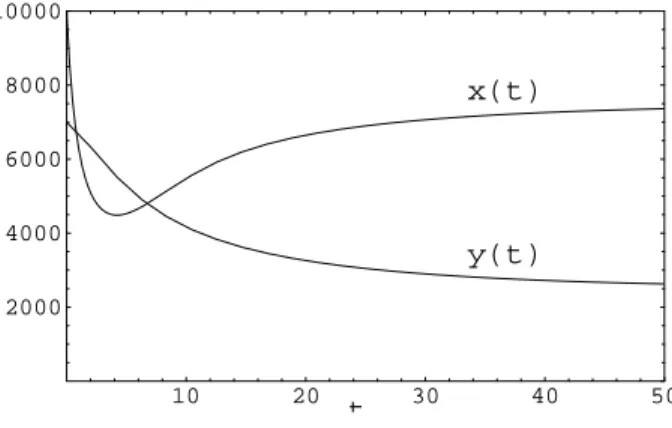
Aufgabe 1.4: Ein Bienenvolk verliert während der Sommermonate in jeder Woche 20% der zu Beginn dieser Woche vorhandenen Arbeiterinnen (weil diese sterben oder nicht zum Stock zurückfinden). Es schlüpfen aber jede Woche 7000 neue Arbeiterinnen.

(a) Wie lautet die Iterationsfunktion? Zeichnen Sie diese Iterationsfunktion. Gibt es Fix- punkte? Sind diese global oder lokal stabil?

(b) Können Sie eine analoge Iterationsfunktion für die Zahl der Arbeiterinnen nach zwei Wochen angeben, also für xn+2 als Funktion von xn? Vergleichen Sie mit der Iterati- onsfunktion für eine Woche.

Aufgabe 1.5: Schauen Sie sich das Cobwebbing für unterschiedliche Iterationsfunktionen an und versuchen Sie hieraus Kriterien für die globale Stabilität von Fixpunkten zu formulieren.

Hinweis: Das geht im allgemeinen Fall nicht so eindeutig wie für die lokale Stabilität. Man kann aber Kriterien für große Klassen von Iterationsfunktionen finden (f hat einen global stabilen Fixpunkt wenn . . . ).

(12)

Arbeitsblatt 2 zur Vorlesung WS 2020/2021 12 1.2 Kontinuierliche Entwicklungsprozesse

Bislang haben wir Prozesse in diskreter Zeit untersucht, d.h. wir haben angenommen, daß nur zu festen Zeitpunkten etwas passiert, z.B. daß sich Bakterien alle gleichzeitig einmal pro Stun- de teilen. Eine solche Annahme ist jedoch nicht immer gerechtfertigt; oft ist es realistischer, anzunehmen, daß der Zuwachs kontinuierlich in der Zeit stattfindet. Wir werden jetzt also eine kontinuierliche Zeitvariablet ≥0 betrachten, die wir auf einer beliebigen Skala messen (Sekunden, Jahre, ...).N(t) bezeichnet die (mittlere) Populationsgröße oder auch die Dichte einer einer Population, z.B. die Zahl der Individuen pro Quadratmeter und kann ebenfalls kontinuierliche Werte inR+ annehmen. Sei ∆tein kurzes Zeitintervall. Wir nehmen an, dass mit einer konstanten Geburtenrate b (pro Individuum) Nachkommen geboren werden und dass Individuen mit einer Todesrate dsterben. Im einfachsten Modell sind diese Raten zeitlich konstant und für alle Individuen in der Population gleich. Insbesondere hängen sie nicht vom Alter ab. Dann ergibt sich die Änderung der Populationsgröße im Zeitintervall ∆t zu

∆N(t) =N(t+ ∆t)−N(t) = (b−d)∆tN(t) (5) Im Grenzfall ∆t→0 ergibt sich

N˙(t) = lim

∆t→0

∆N(t)

∆t = (b−d)N(t) =λN(t) (6)

wobei λ = b−d die sogenannte (intrinsische) Wachstumsrate ist (oder: der Malthus’sche Parameter nach Thomas Malthus, 1766-1834, der das Modell als erster auf die menschliche Population angewendet hat). Die eindeutige L¨osung dieser gew¨ohnlichen Differentialgleichung mit AnfangsbedingungN(0) =N0 ist

N(t) = exp[λt]N₀. (7)

Exponentielles Wachstum in kontinuierlicher Zeit ist das Gegenst¨uck zum geometrischen Wachstum in diskreter Zeit. Die enge Beziehung sieht man auch aus Gleichung (7) wenn man die Konstante exp[λ] als Wachstumsparameter r w¨ahlt. Dann ist

N(t) = exp[λ]t

N₀ =r^tN₀.

Wenn man nun den in kontinuierlicher Zeit ablaufenden Prozess in diskreten Zeitschritten beschreibt (weil man etwa einmal in der Stunde misst), erhält man wieder ein geometrisches Wachstum. In diesem Sinne sind exponentielles und geometrisches Wachstum “ein und dasselbe”. Während beim geometrischen Wachstum die Grenze zwischen Schrumpfen und Wachsen bei r = 1 verläuft, liegt sie beim exponentiellen Wachstum bei λ = 0. Mit λ > 0 folgt Bevölkerungsexplosion und ibei λ <0 stirbt die Population aus.

Das allgemeine deterministische Modell f¨ur die Dynamik einer einzelnen, unstrukturierten Population lautet:

N˙(t) =f(N, t) =c(t) +λ N(t), t

N(t). (8)

Dabei beschreibtc(t) die Immigration von Individuen undλ N(t), t

eine allgemeine Wachs- tumsrate pro Kopf. Abgesehen vom exponentiellen Wachstum gibt es nur wenige Modelle mit einer expliziten L¨osung.

(13)

• Das einfachste Modell mit einer stabilen Gleichgewichtspopulation N(t)>0 ergibt sich aus einer Dynamik mit Einwanderung und Tod (negative Wachstumsrate),

N˙(t) =f(N) =c−dN(t) (9)

mitc, d >0 und L¨osung

N(t) = c d+

N0−c

d

exp[−dt]. (10)

In der Populationsdynamik beschreibt das Modell eine Populationssenke mit Immigra- tion und Tod. Alternativ beschreibt es in einem Kontinent-Insel Modell die ¨Anderung einer lokalen Populationsdichte auf der “Insel” (oder einem anderen lokalen Habitat) durch konstante Einwanderung von einem “Kontinent” (einem Reservoir mit konstan- ter Populationsdichte) und Auswanderung mit einer konstanten Rate pro Kopf. In der Biochemie entspricht dies dem Konzentrationsausgleich durch Diffusion eines Stoffes durch eine Zellmembran, wobei N(t) in dieser Interpretation die variable Konzentrati- on des Stoffes in der Zelle ist und die Konzentration außerhalb der Zelle als konstant angenommen wird.

• Das einfachste Modell mit Populationsregulierung in einer Population, die sich selbst erhalten kann, ist das logistische Wachstum mit

N˙(t) =λN(t)

1− N(t) K

. (11)

Das Modell ist durch eine lineare Dichteabhängigkeit mit einer Pro-Kopf-Wachstumsrate von λ(1−N/K) gekennzeichnet. Der Parameter λ ist die intrinsische Wachstumsrate in Abwesenheit von innerartlicher Konkurrenz. K ist die sogenanntecarrying capacity (Tragfähigkeit). Für N(t) > K ist die Konkurrenz so groß (die Ressourcen werden so knapp), dass die Population schrumpft. Die explizite Lösung für das logistische Wachs- tumsmodell folgt (z.B. durch Trennung der Variablen) als

N(t) = K

1−(1−K/N0) exp[−λt]. (12)

Das logistische Wachstum kann auch für zeitabhängige Pro-Kopf-Wachstumsrate λ(t) noch explizit gelöst werden, wobei man einfach den ExponentλtdurchRt

0λ(t)dtersetzt.

Die allerwenigsten Modelle in der theoretischen Ökologie haben explizite Lösungen. Glück- licherweise sind wir in der Regel nicht so sehr an der expliziten Dynamik interessiert, sondern eher an den qualitativen Eigenschaften wie der Gleichgewichtsstruktur.

Modellanalyse II: Phasenliniendiagramm

Analog zum Cobwebbing im diskreten Fall kann man die Zeitentwicklung auch f¨ur komplizierte Differentialgleichungen graphisch analysieren. Wir betrachten dazu eine beliebige autonome Differentialgleichung in einer Dimension,

N˙(t) =f(N), (13)

bei der die sogenannte Geschwindigkeitsfunktionf(N) nur indirekt über N =N(t) von der Zeit abhängt. All diese Systems kann man mit der Methode desPhasenliniendiagrammsquali- tativ untersuchen, das in Abbildung 4) für das Beispiel des Migrations- oder Diffusionsmodells dargestellt ist.

(14)

N f(N)

c/d c

0 5 10 15 20

tHin JahrenL 2

4 6 8 10 12 14 16

NHtL

Abbildung 4: Migrationsmodell gem¨aß Gleichung (9). Links: Phasenliniendiagramm. Rechts:

Die zugeh¨orige Zeitentwicklung N(t) f¨ur c = 1, d = 0.1 (pro Jahr) und zwei verschiedene Anfangsdichten N₀ = 3 undN₀= 15.

1. Zeichne den Graphen der Funktionf(N) und denkeN(t) als Bewegung auf derx-Achse, deren Geschwindigkeit ˙N an jedem Punkt N durch den Wert f(N) gegeben ist.

2. Deute die Entwicklung der dynamischen Größe in jedem Punkt N durch Pfeile auf der x-Achse an: Wenn ˙N = f(N) positiv (negativ) ist, wirdN größer (kleiner), also zeigt der Pfeil nach rechts (links). Die Geschwindigkeit ist umso größer, je größer der Betrag von f(N) ist. Dies kann man durch verschieden große Pfeile andeuten. Die Bewegung von N(t) folgt dann diesen Pfeilen. Daraus läßt sich qualitativ der Zeitverlauf ablesen, auch wenn man die Differentialgleichung nicht explizit lösen kann.

Fixpunkte und Stabilit¨at

Wie im diskreten Fall interessieren wir uns für Werte, auf die sich die GrößeN(t) nach langer Zeit einstellt. Offensichtlich ändert sich N(t) gerade an den Punkten nicht mehr, an denen die Geschwindigkeitsfunktion f(N) = 0 ist. Geometrisch sind dies die Schnittpunkte von f(N) mit derx-Achse. Die Stabilität der Gleichgewichtspunkte (bzw. Fixpunkte) und andere elementare Eigenschaften lassen sich direkt aus dem Phasenliniendiagramm erschließen:

• Ein GleichgewichtspunktN^∗ istlokal stabil(anziehend), wenn die Pfeile in beiden Rich- tungen auf ihn zulaufen. Eine mathematisch hinreichnde Bedingung daf¨ur ist, ist dass die Ableitung f⁰(N) = _dN^d f(N) < 0 ist. Ist dagegen f⁰(N^∗) > 0, so laufen die Pfeile nach links und rechts vom Fixpunkt weg und das Gleichgewicht istinstabil (abstoßend).

Fürf⁰⁰(N^∗) = 0 hängt die Stabilität von höheren Ableitungen ab (z.B. ist ein internes Gleichgewicht in diesem Fall instabil, wenn f⁰⁰(N^∗)6= 0, usw.). Generell ist ein Gleich- gewichtN^∗ offensichtlich genau dann lokal stabil wenn für einδ >0 und alle 0< < δ gilt: f(N^∗+)<0 undf(N^∗−)>0.

• Sei f(N) kontinuierlich differenzierbar. Wir nennen ein instabiles Gleichgewicht einen Bruchpunkt wenn f¨ur kleine f(N^∗+) >0 und f(N^∗−) < 0 ist. Wenn f(N) nur eine endliche Anzahl von Gleichgewichten hat (genauer: wenn es keine Intervalle mit f(N) = 0 gibt), dann sind asymptotisch stabile Gleichgewichte und Bruchpunkte immer

(15)

Arbeitsblatt 2 zur Vorlesung WS 2020/2021 15 alternierend (d.h. es gibt genau einen stabilen Fixpunkt zwischen zwei Bruchpunkten und umgekehrt).

• Wenn alle Fixpunkte entweder asymptotisch stabile Gleichgewichte oder Bruchpunkte sind (der generische Fall), dann erstreckt sich der Anziehungsbereich jedes stabilen Gleichgewichts bis zu den benachbarten Bruchpunkten oder bis zu den Grenzen des Parameterraums.

Man beachte: ˙N(t) ist stets die Ableitung vonN nach der Zeitt, w¨ahrendf⁰(N) die Ableitung von f nach der dynamischen Gr¨oßeN ist.

Modellbildung III: Erntemodelle

Betrachte eine Fischpopulation mit einer Dynamik gemäß logistischem Wachstum. Wir möch- ten diese Population möglichst optimal als natürliche Ressource nutzen und sind deshalb an einer Fischfang-Strategie (oder Erntestrategie) interessiert, die uns langfristig einen großen und stabilen Ertrag verspricht. Zwei verschiedene Strategien stehen zu Auswahl:

1. ¨Uber Fischereiquoten wird eine maximale Anzahl H an Fischen festgelegt, die in jedem Jahr gefangen werden d¨urfen (sog.constant rate harvesting). Wenn bis zu dieser Grenze gefischt wird, kann die Dynamik der Population durch folgende Differentialgleichung beschrieben werden:

N˙ =rN 1−N

K

−H (fürN >0), N˙ = 0 (fürN = 0). (14) 2. Alternativ kann man die Fangmenge von der Größe des Bestands abhängig machen (relative rate harvesting). In der Praxis geschieht das zum Beispiel über eine Begrenzung der Anzahl und Größe von Fischerbooten.

N˙ =rN

1−N K

−EN, (15)

wobei E den zul¨assigen Aufwand f¨ur Fischerei beschreibt und EN die resultierende Fangmenge.

Wir definieren den größten nachhaltigen Ertrag (maximum sustainable yield, MSY) als den größten Ertrag, der dem Bestand dauerhaft entnommen werden kann. Dabei ist einnachhalti- ger Ertragallgemein die Fangmenge an einem stabilen Gleichgewichtspunkt des dynamischen Systems. Der MSY ist dann das Maximum dieser Fangmenge in Abhängigkeit der Modellpa- rameterH oder E, die die Erntestrategie bestimmen.

Aufgabe 2.1:

(a) Berechne für beide Differentialgleichungen die Gleichgewichtspunkte und ihre Stabilität (mit Hilfe eines Phasenliniendiagramms). Welche qualitativ unterschiedlichen dynamischen Szenarien kann man für verschiedene Werte von H und E bekommen?

(b) Fertige f¨ur beide Strategien eine Abbildung an, die die Lage aller (stabilen und nicht stabilen) Gleichgewichtspunkte als Funktion vonHbzw.E(= x-Achsen Variable) zeigt.

(c) Was ist der MSY und f¨ur welche Werte vonH und E bekommen wir ihn?

(16)

Arbeitsblatt 2 zur Vorlesung WS 2020/2021 16 Modellanalyse III: Bifurkationen

Für eine qualitative Modellanalyse ist es von zentralem Interesse, wie sich die Gleichge- wichtsstruktur verändert, wenn wir bestimmte Modellparameter ändern. Wie wir für die Erntemodelle gesehen haben, können Gleichgewichte verschwinden oder neue Gleichgewich- te entstehen, oder Gleichgewichte können kollidieren und dabei ihre Stabilität austauschen.

Diese qualitativen ¨Anderungen in der Gleichgewichtsstruktur dynamischer Systeme werden Bifurkationen genannt. Man kann diese “Dynamik der Gleichgewichte” in einem sogenannten Bifurkationsdiagramm darstellen und allgemein verschiedene Typen von Bifurkationen unterscheiden. F¨ur eindimensionale dynamische Systeme in kontinuierlicher Zeit sind drei Typen von Bifurkationen besonders wichtig:

1. Transkritische Bifurkation (transcritical bifurcation): zwei Gleichgewichte kollidieren (¨uberkreuzen sich) und tauschen ihre Stabilit¨at aus. DieNormalform der transkritischen Bifurkation mit Bifurkationsparameter α im Punktx=α= 0 lautet

˙

x=αx−x². (16)

Dieses System hat zwei Gleichgewichte bei x^∗₁ = 0 und x^∗₂ =α, die fürα= 0 im Punkt x= 0 kollidieren. Fürα <0 ist das Gleichgewichtx^∗₂ =α stabil und das Gleichgewicht x^∗₁= 0 instabil; fürα >0 ist x^∗₁ = 0 lokal stabil und x^∗₂ =α instabil.

2. Sattel-Knoten Bifurkation (saddle-node bifurcation): zwei Gleichgewichte mit unterschiedlicher Stabilit¨at kollidieren und l¨oschen sich gegenseitig aus – bzw. es entstehen zwei Gleichgewichte aus dem “Nichts”. Die Normalform lautet

˙

x=α−x². (17)

F¨ur α < 0 gibt es kein Gleichgewicht. Bei α = 0 entstehen im Punkt x = 0 zwei Gleichgewichte, f¨ur α > 0 liegen sie bei x^∗₁ = −√

α (instabil) und bei x^∗₂ = √

α (lokal stabil).

3. Heugabelbifurkation (pitchfork bifurcation): drei Gleichgewichte kollidieren. Daf¨ur gibt es zwei M¨oglichkeiten. Bei einer superkritischen Heugabelbifurkation sind die dei Gleich- gewichte stabil – instabil – stabil und werden zu einem einzigen stabilen Gleichgewicht.

Die Normalform lautet

˙

x=αx−x³. (18)

F¨ur die subkritischen Fall sind die drei Gleichgewichte instabil – stabil – instabil und werden zu einem instabilen Gleichgewicht,

˙

x=αx+x³. (19)

4. Im Prinzip sind auch Bifurkationen noch h¨oherer Ordnung m¨oglich, bei denen vier oder mehr Gleichgewichte kollidieren. Sie spielen aber in der Praxis keine Rolle.

5. Außer durch Bifurkationen kann sich die Gleichgewichtsstruktur des dynamischen Sy- stems auch ändern, wenn Gleichgewichte in den relevanten biologischen Zustandsraum hineinlaufen oder ihn verlassen. Für die Populationsdichte N ist die relevante unte- re Grenze des Zustandsraums normalerweise N = 0. Auf der anderen Seite können Gleichgewichte auch im Unendlichen entstehen oder dorthin verschwinden. Allerdings gilt für realistische biologische Modelle gewöhnlich limN→∞f(N) << 0, sodass dies nicht möglich ist.

(17)

Arbeitsblatt 2 zur Vorlesung WS 2020/2021 17 Aufgabe 2.2:

(a) Welche Bifurkationen treten für absolute und relative rate harvesting auf? Diskutiere auch die Konsequenzen beider Bifurkationstypen, wenn man die Ernterate variiert - ggf. auch über den Bifurkationspunkt hinaus. Welche Strategie ist zu befürworten?

(b) Fürrelative rate harvesting bekommt man die maximale Gesamt-Fangmenge für einen mittleren Wert des gesamten zulässigen Fischereiaufwands. Man kann sich aber auch uberlegen, was passiert, wenn mehrere Fischereiunternehmen oder mehrere L¨¨ ander um den selben Bestand konkurrieren. Wie ändert sich dann der individuelle Ertrag mit dem individuellen Aufwand eines einzigen Unternehmens (oder Landes)? Was bedeutet das für die Entwicklung des Gesamtertrags?

Bedeutung der Bifurkationstheorie: Kleine Ursachen können große Effekte haben.Dies ist eine typische Eigenschaft von Ökosystemen, wo man diese plötzlichen Übergänge häufig beobachtet. Die Tatsache, dass kleine stetige Änderungen große sprunghafte Auswirkungen haben können ist für die meisten Menschen kontraintuitiv. Dies kann gefährliche Konsequen- zen haben wenn ein Ökosystem “umkippt” und beispielsweise Arten aussterben. Einblicke in die Bifurkationsstruktur natürlicher Systeme zu geben, ist deshalb eine der wichtigsten Auf- gaben der theoretischen Ökologie. In vielen Fällen ergibt sich die Existenz eines bestimmten Bifurkationspunkts aus der Struktur der Wechselwirkungen und mak kann robuste qualitative Voraussagen erhalten. Natürlich wird es oft schwierig sein, quantitative Schätzungen für die genaue Positionen der Bifurkationspunkte zu erhalten. Zudem weisen natürliche Syste- me immer auch ökologische und demographische Stochastizität auf. Deshalb ist es ratsam, stets einen genügend großen Sicherheitsabstand zu einem katastrophalen Bifurkationspunkt einzuhalten.

Ubungsaufgaben 2¨

Aufgabe 2.3: Die rechte Seite einer Differentialgleichung sei durch die Funktion g(x) = sin(πx/2)

gegeben.

(a) Zeichnen Sie ein Phasenliniendiagramm fürx zwischen 0 und 4. Für welche Werte von x ändert sichx am schnellsten?

(b) Welche Gleichgewichtspunkte gibt es und was können Sie über ihre Stabilität aussagen?

(c) Machen Sie anhand der qualitativen Informationen eine grobe Skizze des Zeitverlaufs f¨ur Startwerte x₀ = 0.5 and x₀ = 3.5. Gibt es Wendepunkte im Zeitverlauf x(t) und wenn ja, wo liegen sie?

Aufgabe 2.4: Chemostat

Ein Chemostat ist ein Apparat, um Bakterien unter Durchflußbedingungen zu kultivieren.

Dabei wird kontinuierlich frische Nährlösung zugeführt; mit derselben Rate wird Kulturme- dium – mitsamt den darin enthaltenen Bakterien – abgeführt, so daß das Volumen insgesamt konstant bleibt.

(18)

Wir nehmen an, daß die Bakterien logistisch wachsen mit Parametern λundK, und das Kulturmedium gut gerührt wird, so daß die Zellen überall gleichmäßig verteilt sind. Seixdie Dichte der Bakterienkultur undα die Auswaschrate (Abflussrate).

(a) Stellen Sie die ODE des Modells auf. Welche Modellannahmen f¨uhren zu dieser Glei- chung?

(b) Zeichnen Sie das Phasenliniendiagramm. Für welchen Wert vonx ist die Änderung von x maximal? Für welche Werte vonxändert sichxnicht? Ermitteln Sie – graphisch und rechnerisch – die Stabilität der Gleichgewichtspunkte.

(c) F¨ur welche Wahl des Anfangswertes x₀ wird der Zeitverlauf x(t) einen Wendepunkt haben?

(19)

Arbeitsblatt zur 3. Vorlesung, WS 2020/2021 19

2 Effekte diskreter Dynamik in einer Dimension

Systeme in kontinuierlicher und diskreter Zeit

Zwischen diskreten dynamischen Systemen und Differentialgleichungen gibt es zahlreiche Ent- sprechungen, die in der folgenden Tabelle zusammengefasst sind.

diskrete Zeit (n) kontinuierliche Zeit (t) dynamisches System diskrete Iteration Differentialgleichung

x_n+1 =f(x_n) N˙(t) =f(N)

charakterisiert durch Iterationsfunktionf(x) Geschwindigkeitsfunktion f(N) gibt an Populationsgr¨oße in der Zuwachsrate der Population

n¨achsten Generation

graphischer Ansatz Cobwebbing Phasenliniendiagramm

Gleichgewicht f(x) =x f(N) = 0

Schnittpunkt mit Winkelhalbierender x-Achse lokal stabil wenn |f⁰(x^∗)|<1 f⁰(N^∗)<0

Neben diesen Entsprechungen gibt es aber auch wichtige Unterschiede. Insbesondere sehen wir aus dem Phasenliniendiagramm, dass die Konvergenz zu einem Gleichgewicht im kontinuierlichen Fall immer monoton ist: ein Gleichgewichtspunkt kann im Zeitverlauf nie übersprungen werden (mathematisch folgt dies aus der Eindeutigkeit der Lösungen für Differentialgleichun- gen). Allgemeiner gilt:

• Zu jedem kontinuierlichen Prozess gibt es eine Menge an analogen diskreten Prozessen.

Wie beim Übergang vom exponentiellen zum geometrischen Wachstum ergeben sich die entsprechenden diskreten Prozesse einfach dadurch, dass man die Populationsgröße nur in (beliebig gewählten) diskreten Zeitschritten aufzeichnet. Insbesondere die Gleichge- wichtspunkte sind dann identisch.

• Umgekehrt gibt es nicht zu jedem diskreten Prozess einen analogen kontinuierlichen Prozess, der sich wie oben beschrieben durch eine gewöhnliche Differentialgleichung darstellen lässt. Dafür werden wir im nächsten Abschnitt einige konkrete Beispiele kennenlernen.

2.1 Nicht-lineare Prozesse in diskreter Zeit

Analog zum logistischen Wachstum in kontinuierlicher Zeit muss das Populationswachstum auch in biologisch realistischen Modellen in diskreter Zeit bei hohen Dichten verlangsamt und schließlich gestoppt werden (wie schon am Beispiel der Vogelpopulation argumentiert). Dafür müssen die mittlere Anzahl der Geburtenbund der Todedpro Individuum und Zeiteinheit von der Populationsgröße abhängen. Die Reproduktionsfunktion nimmt dann die allgemeineren Form

f(x) =x(1 +b(x)−d(x)) =xr(x) (20) an, in derb, d und r selbst Funktionen von x sind. Beim geometrischen Wachstum war die Reproduktionsfunktion eine Gerade. Man nennt den zugeh¨origen Prozess deshalb auch einen

(20)

Arbeitsblatt zur 3. Vorlesung, WS 2020/2021 20 linearen Prozess. Prozesse mit Iterationsfunktionen, die keine Geraden sind, nennt man ent- sprechendnicht-lineare Prozesse. In diesem Abschnitt werden wir Modelle von nicht-linearen Prozessen vorstellen. Wir wollen aber nicht einfach mit den fertigen Formeln beginnen, sondern diese aus einem biologischen Szenario ableiten.

Modellbildung IV: Fischpopulation

Betrachte eine Fischpopulation mit GrößeNtfür den erwachsenen (adulten) Bestand. Während der Brutsaison produzieren die Adulten L_t = bN_t Larven. Wir nehmen an, dass diese Lar- ven während eines Jahres bis zur Fortpflanzungsreife heranwachsen und dass adulte Fische nur eine Saison überleben. Dann bilden die überlebenden Larven die adulte Population der nächsten Generation. Wir brauchen also ein Modell für das Überleben der Larven über ein Jahr.

1. Angenommen, die Larven entwickeln sich während dieses Jahres gemäß gemäß eines (zeitlich kontinuierlichen) logistischen Modells ohne Geburten, d.h,

∂Lt(τ)

∂τ =−m₁Lt(τ)−m2L²_t(τ), (21) wobeim1 die Sterblichkeit aufgrund von extrinsischen (z.B. abiotischen) Faktoren misst and m₂ die dichteabh¨angige Komponente (z.B. aufgrund von Ressourcenkonkurrenz zwischen den Larven oder Jungfischen). Mit L_t(0) =bN_tund der Dauer ∆ einer Saison wird

Lt(∆) = bNtm1

(bNtm2+m1) exp[m1∆]−bNtm2

. (22)

Damit erhalten wir das sogenannte Beverton-Holt Modell, Nt+1=Lt(∆) = c1Nt

1 +c2Nt

(23) mit positiven Konstanten

c1=bexp[−m₁∆] , c2 =bm2

m₁ (1−exp[−m₁∆]).

2. Ein alternativer Ansatz geht davon aus, dass die Larven nicht primär untereinander, sondern mit ihren erwachsenen Artgenossen konkurrieren. Dies trifft insbesondere dann zu, wenn adulte Fische Eier und Larven ihrer eigenen Art fressen (was in der Tat für viele Arten zutrifft, bei denen die Prädation rein größenabhängig ist). Wir erhalten dann

∂L_t(τ)

∂τ =−m₁Lt(τ)−m2NtLt(τ), (24) und

Lt(∆) =bNtexp[−(m₁+m2Nt)∆]. (25) Dies f¨uhrt auf das sogenannteRicker Modell,

Nt+1 =Ntexp[r(1−Nt/K)] (26)

mit Konstanten

r= log[b]−m1∆ , K= log[b]−m1∆ m₂∆ .

(21)

Arbeitsblatt zur 3. Vorlesung, WS 2020/2021 21 3. Schließlich können wir auch annehmen, dass Jungfische (unabhängig voneinander) mit Wahrscheinlichkeitsüberleben und der dichteabhängige Wettbewerb ausschließlich unter den Erwachsenen stattfindet (z.B. um Brutplätze). Dann erhalten wir eine diskrete Version des logistischen Wachstums

Nt+1 =rNt

1−Nt

K

, (27)

wobei r = sb die Zahl der bis zur n¨achsten Saison ¨uberlegenden Larven pro adulten Fisch angibt.

Die Rekrutierung der neuen Generation mittels einer (strikt) monoton steigende Reprodukti- onsfunktion wie beim Beverton-Holt Modell wird als normal-kompensierend (normal compen- sation) bezeichnet: je mehr Eltern es gibt, desto mehr Nachkommen. Sie erreicht eine Asym- ptote vonN_t → ∞ bei L_max(∆) = c₁/c₂. Im Gegensatz dazu ist die Reproduktionsfunktion des Ricker-Modells nicht monoton. Dasselbe gilt f¨ur das diskrete logistische Wachstumsmodell.

In beiden Modellen ist die Rekrutierung überkompensierend (over-compensating). Lmax(∆) durchläuft ein lokales Maximum und nähert sich fürN_t→ ∞dem Wert Null. Die biologische Herleitung der Modelle über die jährliche Erneuerung eines Fischbestands ist nur ein Bei- spiel. Alle drei Modelle können auf viele verschiedene Arten für unterschiedliche biologische Szenarien abgeleitet werden. Sie sind Standardmodelle der theoretischen Ökologie.

Analyse des Beverton-Holt Modells

Betrachte die Reproduktionsfunktion des Beverton-Holt (oder auch Verhulst) Modells, Nt+1=F(Nt) = c1Nt

1 +c2Nt

. (28)

Reproduktionsfunktion und Populationsentwicklung sind in Abb. 5 gezeigt, im Vergleich zum geometrischen Wachstum (c2= 0).

• Im Gleichgewicht gilt

N(1 +c₂N) =c₁N und damit

N₁^∗ = 0, N₂^∗ = c₁−1 c₂ . F¨urc1 >1 istN₂^∗ >0 und biologisch relevant.

• Mit

F⁰(N) = ∂F(N)

∂N = c₁

(1 +c₂N)² ≤c₁ =F⁰(0)

und F⁰(N₂^∗) = 1/c₁<1 f¨urc₁>1, wennN₂^∗ >0 ist. Wir bekommen deshalb monotone Konvergenz gegen N₂^∗ f¨urc1 >1 und ansonsten monotone Konvergenz nach N₁^∗= 0.

(22)

Arbeitsblatt zur 3. Vorlesung, WS 2020/2021 22

0 10000 20000 30000 40000 50000 x

2000 4000 6000 8000 10000 12000

fHxL

0 50 100 150 200

Zeit t 0

2000 4000 6000 8000 10000 12000

Population

Abbildung 5: Reproduktionsfunktionen (links) und Populationsentwicklung (rechts) f¨ur das Beverton-Holt Modell mit N0 = 1, c1 = 1.1, c2 = 1/10000 und geometrisches Wachstum mitr =c₁ = 1,1. Zeit in Generationen gemessen; jede 5. Generation ist gezeigt (Rauten = Beverton-Holt, Sterne = geometrisch).

Analyse des Ricker Modells

Wir betrachten die Reproduktionsfunktion

Nt+1 =F(Nt) =Ntexp[r(1−Nt/K)]. (29)

• Wir erhalten die Gleichgewichte

N₁^∗ = 0, N₂^∗=K .

• Die Ableitung ist

F⁰(N) =

1−N r K

exp[r(1−N/K)]. und damit

Λ₁=F⁰(0) = exp[r]>1, (30)

Λ2=F⁰(K) = 1−r. (31)

• Wir haben ein eindeutiges Maximum von F(N) bei Nmax = K/r (und ein Minimum bei N_min = 0).

Damit k¨onnen wir drei dynamische Regimes f¨ur das Ricker Modell unterscheiden.

1. Fürr <1 enthält das IntervallI = [0, Nmax] beide Gleichgewichtspunkte. DaF(N) inI monoton steigt erhalten wir monotone Konvergenz zum stabilen GleichgewichtN₂^∗ =K für jeden Startwert N₀ ∈I. Für StartwerteN₀ ∈/ I haben wirF(N₀)∈I und dasselbe gilt nach dem ersten Schritt.

2. F¨ur 1< r <2 haben wir keine monotone Konvergenz mehr, aber immer noch |Λ₂|<1.

Daher ist N₂^∗ = K immer noch lokal stabil. Die Populationsgröße nähert sich dem Gleichgewicht in gedämpften Schwingungen.

3. Für r > 2 ist |Λ₂| > 1 und wir haben kein stabiles Gleichgewicht mehr. Insbesondere erhalten wir für das Gleichgewicht beiN₂^∗ =K oszillierende Divergenz. Da das Ricker- Modell eine endliche maximale Populationsgröße hat, stellt sich die Frage, wohin sich der Zeitverlauf entwickelt.

(23)

Arbeitsblatt zur 3. Vorlesung, WS 2020/2021 23 Ubungsaufgaben 3¨

Aufgabe 3.1: Denken Sie sich eine Bakterienkultur, die mit r = 1.5 geometrisch w¨achst.

In dieser Kultur tritt eine Mutante auf, die mit r = 2.0 geometrisch wächst; die Mutante wächst also schneller als der Wildtyp. Wie sieht die Reproduktionsfunktion für den Anteil der Mutanten an der Gesamtpopulation aus? (Hinweise: Man bezeichne mitw_ndie Größe der Wildtyppopulation (in Generation n), mit mn die Größe der Mutantenpopulation und mit Nn:=wn+mn die Größe der Gesamtpopulation. Betrachten Sie nun den Anteilpn der Mu- tanten an der Gesamtpopulation. Versuchen Sie nun,p_n+1 als Funktion vonp_nauszudrücken.

Verwenden Sie dazu das geometrische Wachstumsgesetz f¨urwn und mn sowie die Tatsache, daß der Anteil der Wildtypen gleich 1−pn ist.) Kommt Ihnen die Gleichung bekannt vor?

Aufgabe 3.2: (Biologische Schädlingsbekämpfung) Die Generationen eines schädlichen Insektes sind streng getrennt. Jede Generation besteht aus gleich vielen Männchen und Weib- chen. Weibchen und Männchen paaren sich rein zufällig und nur ein einziges Mal. Seimndie Zahl der fruchtbaren Männchen in der n−ten Generation, 2r (r > 1) sei die mittlere Zahl an Nachkommen pro (fruchtbarer) Paarung. Pro Generation werden s >0 sterile Männchen freigelassen, die sich ansonsten wie die anderen Männchen verhalten. Ziel der Aktion ist es, die Insektenpopulation aussterben zu lassen.

(a) Stellen Sie die Reproduktionsfunktion für mn auf. (Hinweise: Da sich jedes Weibchen zufällig mit irgendeinem Männchen der Population paart, ist die Zahl der fruchtbaren Paarungen gleich der Zahl der Weibchen mal dem Anteil der fruchtbaren Männchen an den Männchen insgesamt; die Gesamtzahl der Männchen istmn+s.)

(b) Berechnen Sie die Fixpunkte der Reproduktionsfunktion und ihre Stabilität. Zeichnen Sie die Reproduktionsfunktion für das Beispiel r = 3/2, s = 1/2 und lesen Sie die Stabilität der Fixpunkte aus der Zeichnung ab.

(c) Wie groß mußs– f¨ur ein gegebenesm0– gew¨ahlt werden, damit die Insektenpopulation ausstirbt?

(24)

Arbeitsblatt zur 4. Vorlesung, WS 2020/2021 24 2.2 Grenzzyklen und Chaos

Modellanalyse IV: Grenzzyklen

Die Grundidee, um weitere Erkenntnisse ¨uber die Langzeitdynamik des Ricker-Modells und

¨ahnlicher Systeme zu gewinnen, ist die Betrachtung der iterierten Abbildung ¨uber k Zeit- schritte,

F⁽²⁾(N) =F(F(N)) resp. F^(k)(N) =F(. . . F(F(N))) k-fach. (32) Offensichtlich handelt es sich wieder um ein diskretes dynamisches System, das auf die gleiche Weise untersucht werden kann wie das urspr¨ungliche. Hinsichtlich seines Langzeitverhaltens beobachten wir die folgenden elementaren Eigenschaften:

1. Gleichgewichte von F sind auch Gleichgewichte von F⁽²⁾ und jeder h¨oheren Iteration F^(k).

2. F¨ur die Ableitung vonF⁽²⁾ an den Fixpunkten folgt mit der Kettenregel,

∂F⁽²⁾(N)

∂N = ∂F(Z)

∂Z

Z=F(N)·∂F(N)

∂N . (33)

und genauso f¨ur die iterierte Abbildung F^(k). Das bedeutet f¨ur die Gleichgewichte N^∗

∂F^(k)(N)

∂N

N=N^∗ =

∂F(N)

∂N N=N^∗

k

. (34)

Stabile Gleichgewichte von F bleiben also auch f¨ur h¨ohere Iterationen stabil und instabile Gleichgewichte bleiben instabil.

3. Weitere (stabile oder instabile) Gleichgewichte von iterierten AbbildungenF^(k) k¨onnen auftreten, wenn die urspr¨ungliche AbbildungF Zyklen hat.

Definition und grundlegende Eigenschaften: Grenzzyklen

1. Ein Punkt N₀ wird Punkt mit Periode k oder k-Zyklus Punkt genannt wenn er ein Gleichgewichtspunkt der k-fach iterierten Abbildung F^(k)(N) ist, aber kein Fixpunkt einer Abbildung F^(k⁰⁾ mit 1≤k⁰ < k. Sein sogenannterOrbit

{N₀, F(N0), . . . , F^(k−1)(N0)}=:{N₀, N1, . . . , Nk−1}

wird der entsprechende k-Zyklus genannt. Alle Punkte Ni in diesem Zyklus sind Fix- punkte von F^(k).

2. Ein Grenzzyklus ist lokal stabil genau dann, wenn die zugeh¨origen Zyklus-Punkte lokal stabile Gleichgewichte derk-fach iterierten Abbildung sind. Mit der Kettenregel erhalten wir f¨ur die AbleitungF^(k) an allen Zyklus-Punkten

Λ^(k) = ∂F^(k)

∂N =

k−1

Y

i=0

∂F(N)

∂N N=Ni

. (35)

Der Zyklus ist mithin lokal stabil wenn |Λ^(k)|<1 ist und instabil f¨ur|Λ^(k)|>1.

(25)

Arbeitsblatt zur 4. Vorlesung, WS 2020/2021 25 Beispiel: diskretes logistisches Wachstum

Wir betrachten die Iterationsfunktion f¨ur das diskrete logistische Wachstum Nt+1 =F(Nt) =rNt

1−Nt

K

, (36)

die sich ¨ahnlich zur Ricker Gleichung verh¨alt, aber leichter zu analysieren ist. F(N) hat ein Maximum bei N = K/2 mit F(K/2) = rK/4. Es gibt zwei Gleichgewichte N₁^∗ = 0 und N₂^∗ =K(r−1)/r. Mit F⁰(N) =r(1−2N/K) erhalten wir F⁰(0) =r und F⁰(N₂^∗) = 2−r.

1. F¨ur 0 < r <1 ist N₁^∗ = 0 das einzige stabile Gleichgewicht und die Population stirbt aus.

2. Für 1 < r <3 entsteht ein zweites, stabiles Gleichgewicht N₂^∗ während N₁^∗ instabil ist (transkritische Bifurkation im Punkt r = 1). Die Konvergenz nach N₂^∗ ist für r < 2 monoton und fürr >2 oszillierend.

3. F¨urr >3 sind beide GleichgewichteN₁^∗ undN₂^∗ instabil und wir erwarten Grenzzyklen oder noch komplexeres Langzeit-Verhalten.

Für ein wohldefiniertes biologisches Modell muss r ≤ 4 sein, da sonst F(N) > K werden kann, was negative Populationsgrößen in der nächsten Generation zur Folge hätte. Um die Dynamik im Detail zu studieren, betrachten wir den Fall K= 1. Damit wird:

F(N) =rN(1−N) (37)

F⁽²⁾(N) =r(rN(1−N))(1−rN(1−N)) =r²N(1−N)(1−rN +rN²) (38)

∂F⁽²⁾(N)

∂N =r 1−2rN(1−N)

r(1−2N) (39)

(Wir haben allgemein die SymmetrieF^(k)(1−N) =F^(k)(N).) Wir bekommen Gleichgewichte F⁽²⁾(N) =N f¨ur

N₁^∗= 0 , N₂^∗ = r−1

r , N_3,4^∗ = 1 +r±p

(r−1)²−4

2r . (40)

Offensichtlich existierenN_3,4^∗ f¨urr≥3. Weiter giltF(N₃^∗) =N₄^∗ und umgekehrtF(N₄^∗) =N₃^∗. Die Ableitung ist

Λ⁽²⁾₁ =r² Λ⁽²⁾₂ = (2−r)² , Λ⁽²⁾_3,4 = 4 + 2r−r² (41)

• Bei r= 3 istN₂^∗ =N₃^∗ =N₄^∗. Wenn wir rweiter erhöhen, ändert das GleichgewichtN₂^∗ seine Stabilität (stabil → instabil). Gleichzeitig entstehen für die iterierte Abbildung F⁽²⁾(N) zwei neue Gleichgewichte, N₃^∗ und N₄^∗. Beide sind stabil: |Λ⁽²⁾_3,4| < 1 für 3 <

r < 1 +√

6 ≈3.45. Das ist die typische Signatur einer Heugabel-Bifurkation. Für die ursprüngliche AbbildungF(N) ändert sich die Zahl der Gleichgewichte nicht. Die neuen Gleichgewichte von F⁽²⁾ bilden fürF(N) einen stabilen Grenzzyklus mit Periode 2.

• F¨ur r > 1 +√

6 ≈ 3.45 wird Λ⁽²⁾_3,4 <−1 und die Gleichgewichte N₃^∗ und N₄^∗ von F⁽²⁾ werden instabil. F¨ur die iterierte Abbildung F⁽⁴⁾ bedeutet das, dass die Ableitung an