Ubungen zu Theoretische Physik IV ¨

Physikalisches Institut Ubungsblatt 9¨

Universit¨at Bonn 18.12.2015

Theoretische Physik WS 15/16

Ubungen zu Theoretische Physik IV ¨

Prof. Dr. Hans Kroha, Christoph Liyanage, Jonas Reuter Abgabe: 08.01.2016, Besprechung: 12.01.-13.01.2016

http://www.kroha.uni-bonn.de/teaching/

Dieses ¨Ubungsblatt enth¨alt 50 m¨ogliche Punkte. Davon sind 25 Punkte Bonuspunkte, die euch erm¨oglichen (falls euch Punkte fehlen), euer Punktekonto zu verbessern.

–Hausaufgaben–

H 9.1 Das ideale Fermi-Gas (3+2+2+1+4=12) Punkte

F¨ur ein ideales Fermigas (freie Teilchen mit Spins= ¹₂ und Massem) sind dir die großkanonische ZustandssummeZG, das großkanonische Potential Ω in Abh¨angigkeit vom chemischen Potential und von der Temperatur sowie die Zustandsdichte aus der Vorlesung bekannt.

(a) Bestimme zun¨achst allgemein die Ausdr¨ucke f¨ur (i) die mittlere Teilchenzahl hNi,

(ii) die EntropieS,

(iii) die innere Energie U und (iv) die freie EnergieF.

(b) Da die TeilchenzahlN vom chemischen Potentialµabh¨angt, ist die Bestimmungsgleichung f¨urN eine implizite Gleichung f¨ur das chemische Potential:

N =N(µ, T).

Bestimme durch implizite Ableitung die Ableitung

∂µ

∂T

N des chemischen Potentialsµnach der TemperaturT bei konstanter Teilchenzahl,N =const.

(c) Berechne den Druck des Gases

(i) bei festem chemischen Potential bzw.

(ii) bei fester Teilchenzahl.

Welches thermodynamische Potential musst du in den jeweilgen F¨allen verwenden? Disku- tiere, warum die Ergebnisse unterschiedlich sind.

(d) Berechne die spezifischen W¨armen bei konstantem chemischen Potential bzw. bei konstenter Terilchenzahl, C_V,µ bzw.C_V,N.

(e) Berechne mit Hilfe der Sommerfeld-Entwicklung die Tieftemperatur Entwicklung der Gr¨oßen aus (a)-(c).

1

H 9.2 Modell f¨ur Neutronensterne (3+1+4+2+2=12) Punkte In einem Neutronenstern sind alle Atome aufgrund der hohen Temperatur in die Kernbausteine und die Elektronen dissoziiert und alle Elektronen mit Protonen zu Neutronen rekombiniert, so dass der Stern einzig aus einem dichten Gas von Neutronen (Masse m und Spin s = ±¹₂) besteht. Die Gravitation sorgt f¨ur den Zusammenhalt des Sterns. Die Neutronendichte betr¨agt typischerweisen= 10³⁵/cm³und die MasseM = 10³⁰kg. Die hohe Dichte bewirkt, dass sich ein großer Anteil der Neutronen relativistisch bewegen, d.h. es gilt die Energie-Impuls-Beziehung (p) =p

(mc²)²+p²c².

(a) Berechne den Fermi-Impulsp_F des Neutronengases in Abh¨angigkeit von der Neutronen- dichten. Berechne f¨ur den oben angegebene Wert der Dichte nden Anteil der Neutronen an der Gesamtneutronenzahl, die sich relativistisch bewegen, d.h. f¨ur die gilt pmc.

(b) Die Temperatur eines Neutronensterns betr¨agt etwa 10⁹ Kelvin. Berechne die Fermi- EnergieF des Neutronensystems f¨ur den oben angegebenen Wert der Dichte des Neutro- nengases und zeige, dass _F k_BT. Es kann deshalb im Folgenden beiT = 0 gerechnet werden.

(c) Berechne die innere EnergieU in Abh¨angigkeit vom RadiusRdes Neutronensterns, zuerst f¨ur den nichtrelativistischen (pF mc) und dann f¨ur den ultrarelativistischen Fall (pF mc). Verwende dabei die folgenden Energie-Impuls-Beziehungen:

nichtrelativistisch: (p) =mc²+ p² 2m ultrarelativistisch: (p) =cp

(d) Gib den DruckP =− ^∂U_∂V

N des Neutronensystems f¨ur die beiden F¨alle an. Dieser Druck wird auch Pauli-Druck genannt. Wieso wird p aus der inneren Energie und nicht aus der freien Energie oder dem großkanonischen Potential berechnet?

(e) Betrachte nun die Gesamtenergie E(R) =U +EGravitation des Sterns, mit EGravitation=

−GM²/R. Skizziere in einem DiagrammE(R) f¨ur kleine (ultrarelativistisch) und f¨ur große (nichtrelativistisch) Sternradien.

Was ist (qualitativ) die Bedingung anE(R), dass ein Radius existiert, bei dem der Stern stabil ist? Zeige, dass der Neutronenstern f¨ur Massen gr¨oßer als eine kritische Masse M_c nicht stabil sein kann. Der Stern st¨urzt dann in sich zusammen und kann ein schwarzes Loch bilden. BestimmeM_c.

Hinweis:

Plancksches Wirkungsquantum: ~= 1.05·10⁻³⁴kg m²/s Boltzmann-Konstante: k_B = 1.38·10⁻²³J/K

Neutronenmasse: m= 1.674·10⁻²⁷kg

Lichtgeschwindigkeit: c= 3·10⁸m/s

2

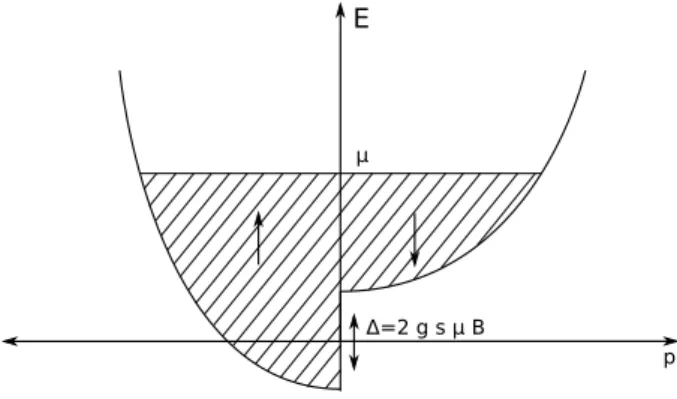
H 9.3 Pauli-Spin-Paramagnetismus (2+3+2+2+1+1+1=12) Punkte Wir betrachten ein freies Elektronengas mit der Energie-Impuls-BeziehungEp = _2m^p2 und dem

E

p Δ=2 g s μ B

μ

Abbildung 1: Energie-Impuls Beziehung mit angelegtem Magnetfeld.

chemischen Potential µ≈F bei der Temperatur T. Die Zustandsdichte ρ(E) ist aus der Vor- lesung bekannt. Nun wird ein Magnetfeld B angelegt.

(a) Gib die Energie-EigenwerteEp,σ eines Elektrons mit Impuls ~pund Spin σ=±¹₂ an (Land´e -Faktor:g= 2, Bohrsches Magneton:µ_B) und berechne die großkanonische Zustandssumme ZG des Systems.

(b) Gib das großkanonische Potential Ω bei Gegenwart des Magnetfeldes an (allgemeiner Aus- druck) und berechne dann die Tieftemperaturentwicklung von Ω (Sommerfeld-Entwicklung) bis O(T²).

(c) Berechne die Teilchenzahlen N↑ und N↓ f¨ur σ = +¹₂ , −¹₂ Elektronen (allgemeiner Aus- druck). Interpretiere das Ergebnis anhand der Abbildung.

(d) Gib die differentielle ¨Anderung des großkanonischnen Potentials bei Magnetfeld- ¨Anderung an. Bestimme insbesondere das Vorzeichen des Magnetfeld-Terms.

(e) Berechne die Magnetisierung M des Systems als thermodynamische Ableitung bei fester Temperatur und festem chemischen Potential. Bestimme dann das Tieftemperaturverhalten von M(T) bisO(T²).

(f) Berechne die magnetische Suszeptibilit¨atχ= ^∂M_∂B

T ,µ f¨urB → 0 allgemein und bei tiefen Temperaturen bisO(T²) und skizziere limB→0χ(T).

(g) Wie m¨usstest du die Rechnung ¨andern, um die Magnetisierung nicht bei festem µsondern bei fester Gesamtteilchenzahl N =N↑+N↓ zu berechnen?

H 9.4 System aus lokalisierten Spins (2+2=4) Punkte Sei ein System ausN lokalisierten Spins mits=±¹₂ gegeben, in dem die Spins nicht beweglich, d.h. unterscheidbar sind: Kanonisches Ensemble. Berechne

(a) die MagnetisierungM(B, T) und

(b) die Suszeptibilit¨atχ(B →0, T) des Systems.

Vergleiche das Tieftemperaturverhalten mit dem von Aufgabe H 9.3.

3

H 9.5 Landau-Diamagnetismus (2+3+x+3+2=10) Punkte (a) Wir betrachten zun¨achst ein klassisches Gas vonN Teilchen mit Ladung −e(kanonische Rechnung mit unterscheidbaren Teilchen, wiein der Vorlesung.). Die kinetische Energie eines Teilchens in einem angelegten ¨außeren Magnetfeld B = ∇ ×A ist dann gegeben durch

H= 1 2m

p+e

cA2

.

Zeige, dass die Zustandssumme des Systems unabh¨angig vonB ist, d.h., dass die magne- tische Suszeptibilit¨at exakt gleich Null ist (Bohr-van-Leuwen-Theorem). Dies bedeutet, dass es klassisch keinen Magnetismus geben kann.

Als Landau-Diamagnetismus bezeichnet man den Magnetismus, der sich aus der Quantisierung der Bahnbewegung der Elektronen in einem magnetischen Feld ergibt. Wir betrachten nun quan- tenmechanisch ein System von Elektronen (Fermionen!) in einem Kasten mit den Seitenl¨angen L_x,L_y,L_z in einem homogenen Magnetfeld B entlang der z-Achse. Der Elektronenspin w¨urde zum Pauli-Paramagnetismus f¨uhren (vgl. Aufgabe H 10.1) und soll hier nicht betrachtet werden.

Wir w¨ahlen die Eichung A= (0, xB,0) mitB >0 und gehen im Folgenden vom thermodyna- mischen GrenzfallL_i 1,i=x, y, z, aus.

(b) Zeige, dass die Bewegung eines Elektrons in der x-y-Ebene einem eindimensionalen har- monischen Oszillator entspricht. Gib die Einteilchen-Energieniveausε_{pz, n}an, die sich aus der Oszillatorenergie und der kinetischen Energie der freien Bewegung in z-Richtung zu- sammensetzen. Die Oszillatorniveaus im Magnetfeld heißen Landau-Niveaus. Bestimme den Entartungsgrad eines Landau-Niveaus mit Hilfe der Tatsache, dass der Impuls p_y in dem Kasten quantisiert ist.

(c^∗) Die Zustandsdichte dieses Elektronengases im Magnetfeld lautet ρ() =mω~

xp

1 +x²+ArcCsch(x) mit x = ^√mω~

2m und der inversen hyperbolischen Cosecansfunktion ArcCsch(x). Sie ist definiert durchArcCsch

1 sinh(x)

=x.

F¨ur Interessierte (ohne Punktewertung): Leite diesen Ausdruck f¨ur die Zustandsdichte mit Hilfe der in (b) berechneten Einteilchen-Energieniveaus her, wobei sowohl die Impuls- als auch die Oszillatoruantenzahlen,p_z und nals kontinuierlich angesehen werden.

(d) Schreibe nun das großkanonische Potential Ω analog zur Vorlesung mit Hilfe der Zustands- dichte als ein Energieintegral und f¨uhre hierf¨ur eine Sommerfeldentwicklung bis O(T²) durch.Anmerkung: Hierbei taucht die zweite Stammfunktion der Zustandsdichte auf. Die- se braucht nicht explizit berechnet werden, sondern darf als Parameter stehen bleiben.

(e) Berechne nun die Magnetisierung des Elektronengases bei tiefen Temperaturen bisO(T²) im Grenzfall verschwindenden Magnetfeldes.

Sch¨one Weihnachtstage!

4