Institut für Allgemeine Elektrotechnik
Volltext
Abbildung
ÄHNLICHE DOKUMENTE
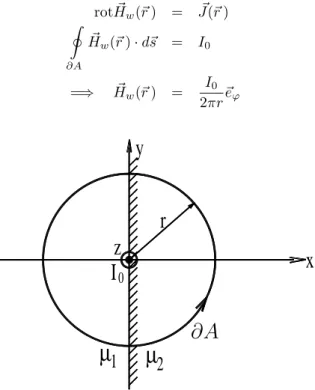
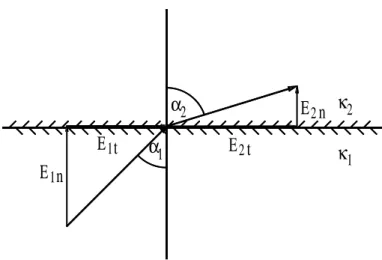
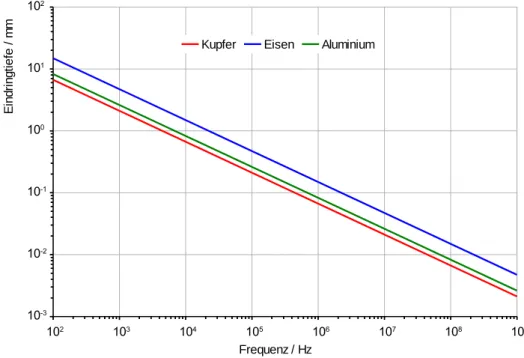
den beiden Materialien, c) den Strom, den Widerstand und die Verlustleistung des Widerstandes. Berechnen Sie d) die Flächenladungsdichte an der Grenzfläche.. Der
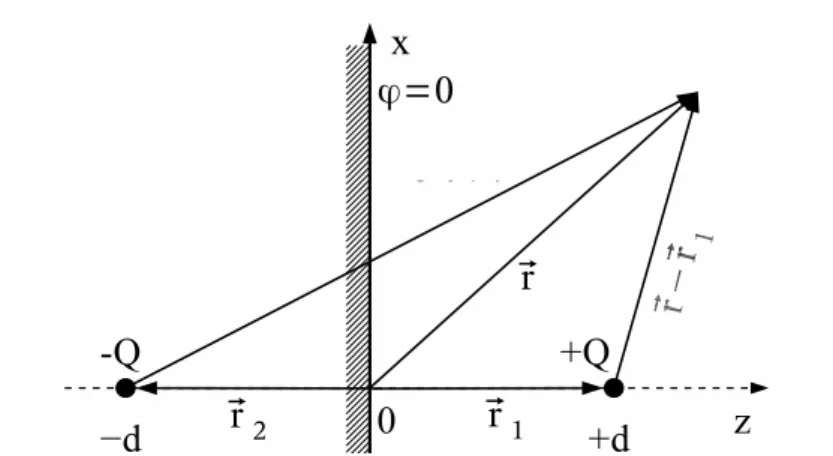
[r]
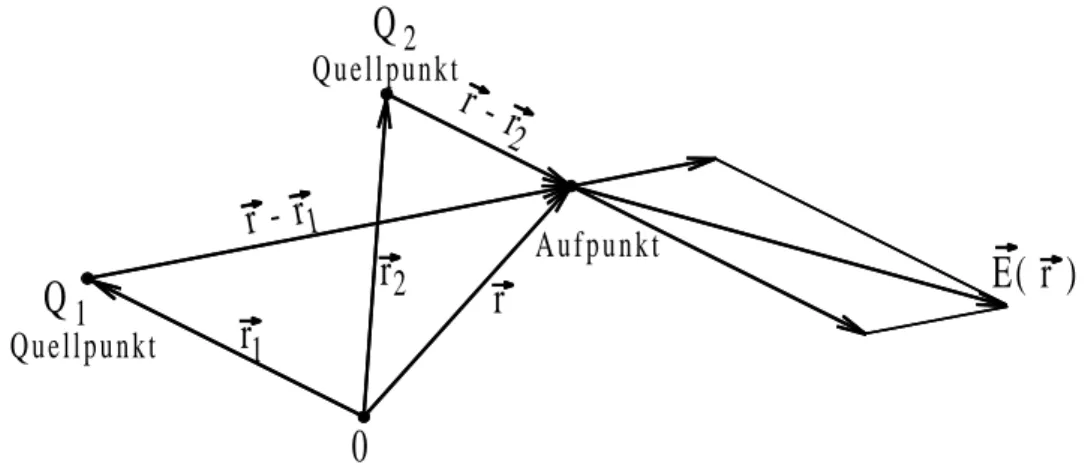
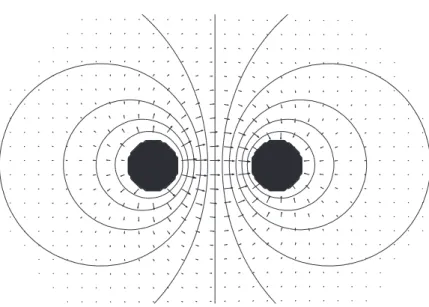
Ein elektrischer Dipol (zwei entgegengesetzt aufgeladene Metallkugeln werden in das Feld eines Plattenkondensators (homogen) und das Feld zwischen einer Platte und einer
Magnetische Felder bewirken in Materie eine Magnetisierung M, definiert als die Summe der magnetischen Dipolmomente p, geteilt durch das Volumen - ähnlich der Polarisation, die
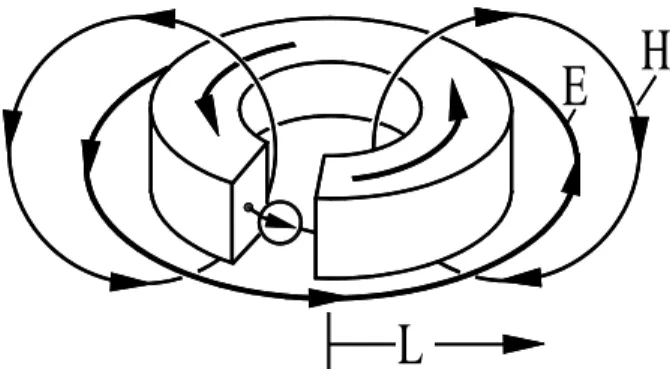
Gasentladung an Luft und lässt eine Leuchtstoffröhre leuchten. 2) Mit einer Sekundärspule sehr kleiner Windungszahl (5) wird ein hoher Strom bei niedriger Spannung erzeugt. Der
• Moleküle wandern entsprechend ihrer Ladung im elektrischen Feld.. • Das Gel behindert die Moleküle bei
[r]
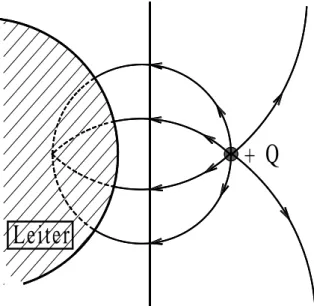
Bringt man Ladungen in ein homognes elektrisches Feld, so erfahren sie eine Kraft in Feldrichtung (positive Ladungen) bzw. entgegen der Feldrichtung