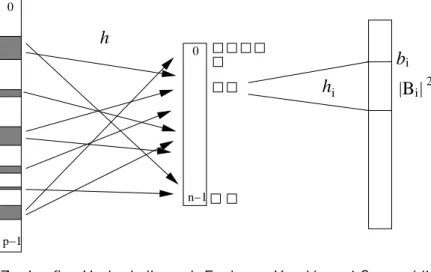
Die Struktur der perfekten Hashtabelle nach Michael L. Fredman, J´anos Koml´os, Endre Szemer´edi:

Die Struktur der perfekten Hashtabelle nach

Michael L. Fredman, J´ anos Koml´ os, Endre Szemer´ edi:

Storing a sparse table with O(1) worst case access time, Journal of the ACM 31(3), p. 538–544 (1984)

verwendet ein zweistufiges Hashverfahren.

F¨ ur einen gegebenen Schl¨ ussel x wird zun¨ achst i = h(x) berechnet, um ¨ uber den Tabellenplatz T [i], b _i , |B _i | und h i ∈ H _2,|B

_|

zu ermitteln. Dann wird im Tabellenplatz

T ⁰ [b i + h i (x)] nachgeschaut, ob x da abgespeichert ist. Falls ja, wird true ausgegeben und sonst false.

Falls

n−1

X |B _i | ² < 4n

|B | i ²

h 0

n−1 0

p−1

h _i

b i

Abbildung 2: Aufbau der zweistufigen Hashtabelle von Fredman, Komlos und Szemeredi.

• Eingabe: S ⊆ U , |S| = n

• Ausgabe: Hashtabelle nach Abb. 2

• Methode:

1. W¨ahle h ∈ H s zuf¨allig. Berechne h(x) f¨ur alle x ∈ S.

2. Falls ^P _i |B _i | ² ≥ 4n, dann wiederhole 1.

3. Kontruierte die Mengen B i f¨ur alle 0 ≤ i < s.

4. F¨ur i = 0 bis s − 1 tue

(a) W¨ahle h i ∈ H _|B

|

zuf¨allig.

(b) Falls h i | B

nicht injektiv ist, wiederhole (a).

Es ist einfach zu sehen, dass wenn der Algorithmus terminiert, er eine Hashtabelle mit O(n) Platz konstruiert. Die Frage ist also nur, wie lange der Algorithmus braucht, um zu terminieren. Schauen wir uns zun¨achst die (1-2)-Scheife an. Ein einmaliger Durchlauf dieser Schleife kostet O(n) Zeit.

Weiterhin ist nach Lemma 1.3(d) die Wahrscheinlichkeit daf¨ur, dass Schritt 1 wiederholt werden muss, h¨ochstens 1/2 f¨ur jedes neue h. Also ist

Pr[(1-2)-Scheife wird > k-mal durchlaufen] ≤

1 2

k

Da f¨ur eine Zufallsvariable X auf den nat¨urlichen Zahlen gilt

E[X] =

X ∞ i=1

i · Pr[X = i] =

X ∞ i=1

Pr[X ≥ i]

folgt

∞ 1 ⁱ

Zweistufige Hashtabelle nach Fredman, Koml´ os und Szemer´ edi

EADS 4.4 Perfektes Hashing 129/146

ľErnst W. Mayr

Algorithmus f¨ ur Hashtabelle nach FKS:

Eingabe: S ⊆ U, |S| = m ≤ n Ausgabe: Hashtabelle nach FKS

1. W¨ ahle h ∈ H _2,n zuf¨ allig. Berechne h(x) f¨ ur alle x ∈ S.

2. Falls P

i |B _i | ² ≥ 4m, dann wiederhole 1.

3. Konstruiere die Mengen B _i f¨ ur alle 0 ≤ i < n.

4. for i = 0 to n − 1 do

(a) w¨ ahle h i ∈ H _2,|B

_|

zuf¨ allig

(b) falls h _i auf B _i nicht injektiv ist, wiederhole (a)

Ein Durchlauf der Schleife bestehend aus den Schritten 1. und 2.

ben¨ otigt Zeit O(n). Gem¨ aß Lemma 34 ist die Wahrscheinlichkeit, dass Schritt 1. wiederholt werden muss, ≤ 1/2 f¨ ur jedes neue h.

Die Anzahl der Schleifendurchl¨ aufe ist also geometrisch verteilt mit Erfolgswahrscheinlichkeit ≥ 1/2, und es ergibt sich

E [# Schleifendurchl¨ aufe] ≤ 2 .

Also ist der Zeitaufwand f¨ ur diese Schleife O(n). Schritt 3. kostet

offensichtlich ebenfalls Zeit O(n).

F¨ ur jedes i ∈ {0, . . . , n − 1} gilt, ebenfalls gem¨ aß Lemma 34, dass Pr[h i ist auf B i injektiv] ≥ 1 − |B _i |(|B _i | − 1)

2|B _i | ² > 1 2 . Damit ist auch hier die erwartete Anzahl der Schleifendurchl¨ aufe

≤ 2 und damit der erwartete Zeitaufwand O(|B _i | ² ) .

Insgesamt ergibt sich damit f¨ ur Schritt 4. wie auch f¨ ur den gesamten Algorithmus ein Zeitaufwand von

O(n) .

4.4.2 Dynamisches perfektes Hashing

Sei U = {0, . . . , p − 1} f¨ ur eine Primzahl p. Zun¨ achst einige mathematische Grundlagen.

Definition 35

H _k,n bezeichne in diesem Abschnitt die Klasse aller Polynome

∈ Z p [x] vom Grad < k, wobei mit ~a = (a ₀ , . . . , a _k−1 ) ∈ U ^k

h _{~ a} (x) =









k−1

X

j=0

a j x ^j



 mod p



 mod n f¨ ur alle x ∈ U .

Definition 36

Eine Klasse H von Hashfunktionen von U nach {0, . . . , n − 1}

heißt (c, k)-universell, falls f¨ ur alle paarweise verschiedenen x 0 , x 1 , . . . , x k−1 ∈ U und f¨ ur alle i 0 , i 1 , . . . , i k−1 ∈ {0, . . . , n − 1}

gilt, dass

Pr[h(x 0 ) = i 0 ∧ · · · ∧ h(x k−1 ) = i k−1 ] ≤ c

n ^k ,

wenn h ∈ H gleichverteilt gew¨ ahlt wird.

Satz 37

H _k,n ist (c, k)-universell mit c = (1 + ⁿ _p ) ^k .

Beweis:

Da Z p ein K¨ orper ist, gibt es f¨ ur jedes Tupel (y ₀ , . . . , y k−1 ) ∈ U ^k genau ein Tupel (a ₀ , . . . , a k−1 ) ∈ Z ^k _p mit

k−1

X

j=0

a j x ^j _r = y r mod p f¨ ur alle 0 ≤ r < k.

Damit folgt, dass

|{~a; h _{~ a} (x _r ) = i _r f¨ ur alle 0 ≤ r < k}|

= |{(y ₀ , . . . , y k−1 ) ∈ U ^k ; y r = i r mod n f¨ ur alle 0 ≤ r < k}|

≤ l p n

m k

.

Beweis (Forts.):

Da es insgesamt p ^k M¨ oglichkeiten f¨ ur ~a gibt, folgt Pr[h(x _r ) = i _r f¨ ur alle 0 ≤ r < k] ≤ l p

n m k

· 1 p ^k

= l p

n m

· n p

k

· 1 n ^k

<

1 + n

p k

· 1

n ^k .

Kuckuck-Hashing f¨ ur dynamisches perfektes Hashing

Kuckuck-Hashing arbeitet mit zwei Hashtabellen, T 1 und T 2 , die je aus den Positionen {0, . . . , n − 1} bestehen. Weiterhin ben¨ otigt es zwei (1 + δ, O(log n))-universelle Hashfunktionen h ₁ und h ₂ f¨ ur ein gen¨ ugend kleines δ > 0, die die Schl¨ usselmenge U auf

{0, . . . , n − 1} abbilden.

Jeder Schl¨ ussel x ∈ S wird entweder in Position h ₁ (x) in T ₁ oder

in Position h 2 (x) in T 2 gespeichert, aber nicht beiden. Die

IsElement-Operation pr¨ uft einfach, ob x an einer der beiden

Positionen gespeichert ist.

Die Insert-Operation verwendet nun das Kuckucksprinzip, um neue Schl¨ ussel einzuf¨ ugen. Gegeben ein einzuf¨ ugender Schl¨ ussel x, wird zun¨ achst versucht, x in T ₁ [h ₁ (x)] abzulegen. Ist das erfolgreich, sind wir fertig.

Falls aber T 1 [h 1 (x)] bereits durch einen anderen Schl¨ ussel y besetzt ist, nehmen wir y heraus und f¨ ugen stattdessen x in T ₁ [h ₁ (x)] ein.

Danach versuchen wir, y in T ₂ [h ₂ (y)] unterzubringen. Gelingt das, sind wir wiederum fertig. Falls T 2 [h 2 (y)] bereits durch einen anderen Schl¨ ussel z besetzt ist, nehmen wir z heraus und f¨ ugen stattdessen y in T ₂ [h ₂ (y)] ein. Danach versuchen wir, z in

T 1 [h 1 (z)] unterzubringen, und so weiter, bis wir endlich den zuletzt

angefassten Schl¨ ussel untergebracht haben. Formal arbeitet die

Insert-Operation wie folgt:

if T ₁ [h ₁ (x)] = x then return fi repeat MaxLoop times

(a) exchange x und T 1 [h 1 (x)]

(b) if x = NIL then return fi (c) exchange x und T ₂ [h ₂ (x)]

(d) if x = NIL then return fi od

rehash(); Insert(x)

F¨ ur die Analyse der Zeitkomplexit¨ at nehmen wir an, dass die Schleife t-mal durchlaufen wird (wobei t ≤ MaxLoop).

Es gilt, die folgenden zwei F¨ alle zu betrachten:

1

Die Insert-Operation ger¨ at w¨ ahrend der ersten t Runden in eine Endlosschleife

2

Dies ist nicht der Fall

x ₁ x ₂ x ₃ x _l

x ₁ x ₂ x ₃ . . . x _j . . . x _i

. . .

x ₁ x ₂ x ₃ . . . x _j . . . x _i

. . . x _i+j+1 x _i+j+2 x _i+j+3

x _i+j+2 x _i+j+3 x _i+j+1

(a)

(b)

(c)

. . . . .

. . . . . x _l

x x

. . . . . .

. . . j’ l

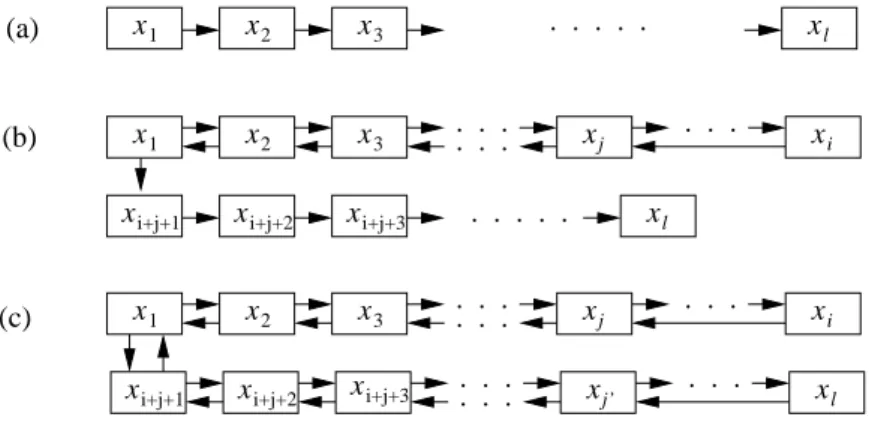
Abbildung 3: Drei F¨alle f¨ur den Ausgang der Insert Operation. (a): Es wird keine Position zweimal besucht. (b): x i besucht die Position von x j , was dazu f¨uhrt, dass alle Schl¨ussel x j , . . . , x 2 wieder in ihre Ausgangspositionen zur¨uckgeschoben werden. x 1 versucht daraufhin die andere Alternativpositi- on, und hier terminiert die Kuckucksregel in x ℓ . (c): x i besucht die Position von x j und x ℓ besucht die Position von x j

, was zu einer Endlosschleife f¨uhrt.

2. Die Insert Operation formt keine Endlosschleife w¨arend der ersten t Runden.

Wir untersuchen zun¨achst den ersten Fall. Sei v ≤ ℓ die Anzahl der verschiedenen angefassten Schl¨ussel. Dann ist die Anzahl der M¨oglichkeiten, eine Endlosscheife zu formen, h¨ochstens

v ³ · s ^v−1 · n ^v−1

da es maximal v ³ M¨oglichkeiten f¨ur die Werte i, j und ℓ in Abb. 3 gibt, s ^v−1 viele M¨oglichkeiten f¨ur die Positionen der Schl¨ussel gibt, und n ^v−1 viele M¨oglichkeiten f¨ur die Schl¨ussel außer x 1 gibt.

Angenommen, wir haben (1, v)-universelle Hashfunktionen, dann passiert jede M¨oglichkeit nur mit einer Wahrscheinlichkeit von s ^−2v . Falls nun s ≥ (1 + ǫ)n f¨ur eine Konstante ǫ > 0, dann ist die Wahrscheinlichkeit f¨ur den Fall 1 h¨ochstens

X ℓ v=3

v ³ s ^v−1 n ^v−1 s ^−2v ≤ 1 sn

X ∞ v=3

v ³ (n/s) ^v = O(1/n ² )

F¨ur den zweiten Fall ben¨otigen wir das folgende Lemma.

Lemma 1.7 Angenommen, die Insert Operation formt keine Endlosschleife nach ℓ besuchten Schl¨usseln.

Dann gibt es eine Schl¨usselfolge in der L¨ange mindestens ℓ/3 in x 1 , . . . , x ℓ , in der alle Schl¨ussel ver- schieden sind.

Beweis. Falls die Insert Operation niemals zu einer bereits besuchten Position zur¨uckkehrt, die das Lemma wahr. Nehmen wir also an, dass die Operation zu einer bereits besuchten Position zur¨uckkehrt, und seien i und j so definiert wie in Abb. 3. Falls ℓ < i+j, dann bilden die ersten j−1 ≥ (i+j −1)/2 ≥

ℓ/2 ℓ ≥ i + j x , . . . x x , . . . , x

Insert bei Kuckuck-Hashing; Endlosschleife im Fall (c)

EADS 4.4 Perfektes Hashing 141/146

ľErnst W. Mayr

Erster Fall: Sei v ≤ l die Anzahl der verschiedenen angefassten Schl¨ ussel. Dann ist die Anzahl der M¨ oglichkeiten, eine

Endlosscheife zu formen, h¨ ochstens v ³ · s ^v−1 · n ^v−1 ,

da es maximal v ³ M¨ oglichkeiten f¨ ur die Werte i, j und l gibt, s ^v−1 viele M¨ oglichkeiten f¨ ur die Positionen der Schl¨ ussel, und n ^v−1 viele M¨ ooglichkeiten f¨ ur die Schl¨ ussel außer x ₁ .

Angenommen, wir haben (1, v)-universelle Hashfunktionen, dann

passiert jede M¨ oglichkeit nur mit einer Wahrscheinlichkeit von

s ^−2v . Falls s ≥ (1 + δ)n f¨ ur eine Konstante δ > 0, dann ist die

Wahrscheinlichkeit f¨ ur den Fall 1 h¨ ochstens

Zweiter Fall:

Lemma 38

Im zweiten Fall gibt es eine Schl¨ usselfolge der L¨ ange mindestens l/3 in x ₁ , . . . , x _l , in der alle Schl¨ ussel paarweise verschieden sind.

Beweis:

Nehmen wir an, dass die Operation zu einer bereits besuchten Position zur¨ uckkehrt, und seien i und j so definiert wie in der Abbildung. Falls l ≤ i + j, dann bilden die ersten

j − 1 ≥ (i + j − 1)/2 ≥ l/2 Schl¨ ussel die gesuchte Folge.

F¨ ur l ≥ i + j muss eine der Folgen x ₁ , . . . , x j−1 und x i+j−1 , . . . , x _l

die L¨ ange mindestens l/3 haben.

Beweis (Forts.):

Sei also x ⁰ ₁ , . . . , x ⁰ _v eine solche Folge verschiedener Schl¨ ussel in x ₁ , . . . , x _2t der L¨ ange v = d(2t − 1)/3e. Dann muss entweder f¨ ur (i 1 , i 2 ) = (1, 2) oder f¨ ur (i 1 , i 2 ) = (2, 1) gelten, dass

h _i

(x ⁰ ₁ ) = h _i

(x ⁰ ₂ ), h _i

(x ⁰ ₂ ) = h _i

(x ⁰ ₃ ), h _i

(x ⁰ ₃ ) = h _i

(x ⁰ ₄ ), . . . Gegeben x ⁰ ₁ , so gibt es n ^v−1 m¨ ogliche Folgen von Schl¨ usseln x ⁰ ₂ , . . . , x ⁰ _v . F¨ ur jede solche Folge gibt es zwei M¨ oglichkeiten f¨ ur (i 1 , i 2 ). Weiterhin ist die Wahrscheinlichkeit, dass die obigen Positions¨ ubereinstimmungen gelten, h¨ ochstens s ^−(v−1) , wenn die Hashfunktionen aus einer (1, v)-universellen Familie stammen. Also ist die Wahrscheinlichkeit, dass es irgendeine Folge der L¨ ange v gibt, so dass Fall 2 eintritt, h¨ ochstens

2(n/s) ^v−1 ≤ 2(1 + δ) −(2t−1)/3t+1 .

Beweis (Forts.):

Zusammen ergibt sich f¨ ur die Laufzeit von Insert :

1 +

MaxLoop

X

t=2

(2(1 + δ) −(2t−1)/3+1 + O(1/n ² ))

≤ 1 + O

MaxLoop n ²

+ 2

∞

X

t=0

((1 + δ) ^−2/3 ) ^t

= O

1 + 1

1 − (1 + δ) ^−2/3

= O(1 + 1/δ) .

Beweis (Forts.):

Uberschreitet ¨ m irgendwann einmal die Schranke n/(1 + δ), so

wird n hochgesetzt auf (1 + δ)n und neu gehasht. Unterschreitet

auf der anderen Seite m die Schranke n/(1 + δ) ³ , so wird n

verringert auf n/(1 + δ) und neu gehasht. Auf diese Weise wird die

Tabellengr¨ oße linear zur Anzahl momentan existierender Schl¨ ussel

gehalten. Der Aufwand f¨ ur ein komplettes Rehashing ist O(n), so

dass amortisiert ¨ uber Θ(n) Einf¨ ugungen und L¨ oschungen der

Aufwand nur eine Konstante ist.