BEGRÜNDET VON P. GROTH

ZEITSCHRIFT

FÜR

KRISTALLOGRAPHIE

<KRISTALLGEOMETRIE, KRISTALLPHYSIK, KRISTALLCHEMIE)

BEGRÜNDET VON P. GROTH

H E R A U S G E B E R UND S C H R I F T L E I T E R

PROFESSOR DR. PAUL NIGGLI

ZÜRICH

*

SIEBENUNDFÜNFZIGSTER BAND

MIT 129 TEXTFIGUREN UND 1 TAFEL

VERLAG VON WILHELM ENGELMANN IN LEIPZIG

Inhaltsverzeichnis des siebenundfünfzigsten Bandes.

Seite

Heft I. (Geschlossen am 4. März 1922.)

I. L. Burmester (München), Geschichtliche .Entwicklung des kristallographi- schen Zeichnens und dessen Ausführung in schräger Projektion. Mit

1 Tafel 1 II. W. Orahmann (Giessen), Eristallstruktur und chemische Eonstitntion. Mit

8 Textfiguren 48 III. Kürzere Originalmitteilungen und Notixen.

1. Ξ. Hirschi (Braunwald), Eine neue Fluoritbildung? 94 2. H. Steinmetz (München), Isotypie, betrachtet als eine verwandt-

schaftliche Beziehung zwischen kubischer und trigonaler Struktur.

Mit 3 Textfiguren 94 IV. Auszüge. Besprechungen von P. Niggli unter Mitwirkung von K. Faesy 98

Wasserfreie Alumosilikate ein- und zweiwertiger Elemente mit ihren Ver-

wandten. (Fortsetzung) 98 (Cancrinit, Mikrosommit Davyngruppe, Nosean-Hauyn-Sodalithgruppe,

Leucit, 3CaO. AI2O3. S1O2, Gehlenit, Velardenit, Melilithgruppe, Justit- familie Grothin, Feldspate)

Anzeige eingegangener Einzelschritten 128

Heft II. (Geschlossen am 15. Mai 1922.)

V. L. Weber (Zürich), Rene Just Haüy. Zur hundertsten Wiederkehr seines

Sterbetages. Mit 2 Textfiguren 129 VI. N. Gross (Hamburg!, Die Bezugsfläehe der LOsungsgeschwindigkeit für

Gips. Mit 16 Textfignren und 8 Tabellen 145 VII. G. Aminoff (Stockholm), Über die Krietallstruktur von AgJ. Mit 2 Text-

figuren 180 VIII. P. Scherrer (Zürich), Das Raumgitter des Kadmiumoxyds 186

IX. Kürzere Originalmitteilungen und Notizen:

1. G. Wulff (Moskau), Die Struktur des Natriumchlorats. Mit 6 Text-

fignren 190 2. L. Weber (Zürich), Das viergliedrige Zonensymbol des hexagonalen

Systeme 200 3. G. Aminoff (Stockholm), Debye-Photogramm von Zinkoxyd. - Mit

2 Textfiguren 204 X. Auszüge: Besprechungen von P. Niggli unter Mitwirkung von K. Faesy 207

Wasserfreie Alnmosilikate ein- und zweiwertiger Elemente mit ihren Ver-

wandten. (Fortsetzung) 207 (Plagioklase, Skapolitbgruppe, Fluosiderit, Leifit, Beryll, Gadolinit, Granat-

gruppe).

87. Versammlung der Gesellschaft deutscher Naturforscher und Ärzte (Programm) 231

IV Inhaltsverzeichnis des siebenundfünfzigsten Bandes.

Seite

H e f t III. (Geschlossen am 1. August 1922.)

XI. H. Steinmetz (München), Krietallographische Untersuchung von Komplex-

verbindungen. 1. Mit 7 Textfiguren 233 XII. P. Niggli (Zürich), Die Kristallstruktur einiger Oxyde. I. Mit 3 Text-

figuren 253 XIII. Kürzere Originalmitteilungen und Notixen:

1. J. Beckenkamp (WUrzburg), Beziehungen der tetrakis-trigonalen zu

den übrigen Syngonien 300 2. J. Beckenkamp (Würzburg), Über Spaltbarkeit 301

3. P. J. Beger (Tübingen), Kristallographische Untersuchung einiger

organischen Verbindungen 303 4. H. Steinmetx (München), Theoretische Darstellung der Atzfiguren

an triklin-asymmetrischen Kristallen. Mit 12 Textfiguren . . . . 307 XIV. Auszüge: Besprechungen von P. Niggli unter Mitwirkung von K. Faesy.

Mit 4 Textfiguren 310 Silikate zwei- und dreiwertiger Elemente mit relativ geringem Wasser-

gehalt (Vesuvian. Staurolith, Lievrit, Cordierit, Epidot-Zoieitgruppe) . . 310

Borsilikate (Turmalin) 332 Bücherbesprechungen 343

H e f t IV. (Geschlossen am 1. November 1922.)

XV. J. Beekenkamp (Würzburg), Einteilung der Kristalle nach ihrer Flächen-

umgrenzung 345 XVI. P. Tschirtvinsky (Nowotscherkassk, Dongebiet), Von den Orthoklas-

und Mikroklinperthiten und über J. H. L. Vogts Zustandsdiagramm der

K—Na-Feldspäte. Mit 1 Textfigur 359 XVII. P. Niggli (Zürich;, Bemerkungen zu vorstehender Abhandlung von

P. T s c h i r w i n s k y 376 XVIII. L. Tokody (Budapest), Neue Beiträge zur Kenntnis der kristallographi-

schen und optischen Eigenschaften des Fassaits von Hodrusbänya.

Mit 15 Textfiguren 378 XIX. V. Zsivny (Budapest), Die chemische Zusammensetzung des Fassaites

von Hodrusbänya (Comitat Hont) 387 XX. Kürxere Originalmitteilungen und Notixen:

1. Μ. v. Schwarz (München), Ein grobkristallines Lagermetall. Mit

6 Textfiguren 394 2. L. Weber (Zürich), Die Struktur von ZnO 398

XXI. Auszüge: Besprechungen von P. Niggli unter Mitwirkung von K. Faesy. 404

Borsilikate (Fortsetzung) 404 (Axinit, Euklas, Danburit, Dumortierit, Datolith, Homilit, Caryo-

cerit, Tritomit).

Die Mineralien der Glimmergrnppe und ihre Verwandten 411 Die Sprödgliramergruppe und verwandte Mineralien 426 Die Mineralien der Chlorit-Talkgrnppe und ihre Verwandten . . . . 429

H e f t V. (Geschlossen am 1. Januar 1923.)

XXII. A. Johnsen (Berlin), Theodor Liebisch + 443 XXIII. A. Reis und L. Zimmermann (Karlsruhe^, Über Härte und Härteaniso-

tropie. Mit 8 Textfiguren und 16 Tabellen 449

Inhaltsverzeichnis des siebenundfünfzigsten Bandes. V

Seite

XXIV. K. Spangenberg (Kiel), Dichte und Lichtbrechung der Alkalihalogenide.

Mit 1 Textfigur und 14 Tabellen 494 XXV. F. Rinne (Leipzig), Über physikalisch - chemische Grundlagen der

Kristallkonstitution. Mit 8 Textfiguren 535 XXVI. Kürzere Originalmitteilungen und Notixen:

1. F. Haag (Stuttgart), Ein Beitrag zur Geometrie des kubischen

Gittere. Mit 2 Textfiguren 519 2. H. Stintxing (Gießen), Zerlegbare Raumgittermodelle. Mit 5 Text-

fignren 551 XXVII. Auszüge über Vorträge, die an Tagungen mineralogischer Gesellschaften

gehalten wurden.

1. Bericht über die 8. Jahresversammlung der »Deutschen Minera- logischen Gesellschaft« zu Leipzig (14.—16. September 1922). Mit Autoreferaten von:

L. Milch (Breslau), Übersicht über den Stand des Differentiations-

problems 555 F. Becke (Wien), Differentiation im Zentralgneis der Hohen Tauern 556

0. H. Erdmannsdoerffer (Hannover), Über Differentiation und Erz-

gan gfüllung im Harz 557 H. Steinmetz (München), Die Kristallform des Eiaes 558

W. Kunitz (Halle a. S.), Die Beziehungen zwischen der chemischen Zusammensetzung und den physikalisch-optischen Eigenschaften

in der Glimmergruppe 559 W. Mauchcr (München), Über partialorientierte Kristallgruppen . . 561

E. Lehmann (Halle), Differentiationsvorgänge in Natronmagmen. . 562 P. J. Beger (Tübingen), Die Bildung des lamprophyrischen Magmas

in der Lausitz und im Odenwald als Prüfstein für die Bowen-

sche Differentiationstheorie 564 K. Mieleitner (München), Die chemischen Verhältnisse der Peg-

matite des ostbayerischen Grenzgebirges 566 W. Eitel (Königsberg i. Pr.), CaC03 — Ca2Si04 als Beispiel kontakt-

metamorpher Systeme 567 E. Kaiser (München), Assimilations- und Differentiationserschei-

nungen an den Syeniten der Namib Südwestafrikas 568 H. Schneiderhöhn (Gießen), Erforschung der Natur- und Stabilitäts-

verhältnisse der undurchsichtigen Erzmineralien mit Hilfe der

chulkographischen Methodik 569 B. Rose und 0. Mügge (Göttingen), Das Verhalten des rhombischen

Schwefels und Quarzes bei hohen Drucken und Temperaturen 571

Q. Kalb (Berlin), Beitrag zur Erzmikroskopie 572 R. Θ. Qrimm (München), Kristallchemie und Ionenbau. Mit 1 Textfigur 574

E. Schiebold (Berlin - Neubabelsberg), Erfahrungen über Röntgeno-

graphieche Drehspektrogramme 579 M. Bereck (Wetzlar), Neue Wege zur Universalmethode 581

Κ. H. Scheumann, Über Intrusiv-, Injektions- und Assimilations- verband dee Granulits mit Derivaten der Peridotit-Gabbro- Amphibolitreihe im sächsischen Granulitgebirge , 581 2. Tagung der schweizerischen Mineralogen in Bern, anläßlich der

103. Jahresversammlung der Schweiz. Naturf. Gesellschaft (24. bis

27. August 1922) 584

VI Inhaltsverzeichnis des siebenundfiinfzigsten Bandes.

Seite XXVIII. Auszüge: Besprechungen von P. Niggli unter Mitwirkung von K. Faesy

Wasserhaltige Silikate mehr oder weniger unbestimmter Gruppenzugehörig- keit (Seladonit, Zebedassiit, Coleraine'it, Racewinit, Magnaüt, Hodgkin- sonit, Plazolith, Cebollit, Deeckeit)

Die Mineralien der Eaolingruppe und ihre Verwandten 589

Bücherbesprechungen 594

Heft VI. (Geschlossen am 15. April 1923.)

XXIX. Ralph W. G. Wyckoff (Washington), Die Kristallstruktur der Alaune.

Mit 10 Textfiguren ö9ö XXX. W. Grahmann (Frankfurt;, Die Zerreißfestigkeit der Kristalle. (Vor-

läufige Mitteilung) 610 XXXI. Β. A. Sonder (Zürich-Neapel), Zum Bau der Atomkerne. Mit δ Text-

figuren 611 XXXII. Kürzere Originalmitteilungen und. Notizen:

1. P. Niggli (Zürich), Bemerkungen zu vorstehender Arbeit von

R. Sonder 642 2. P. N. Tschiricinsky (Nowotscherkassk, Dongebiet), Von der Passi-

vität des Meteoreisens. Mit 2 Textfiguren 643 XXXIII. Auszüge. Besprechungen von P. Niggli unter Mitwirkung von K. Faesy.

Zeolithe und ihnen verwandte Mineralien 647

Berichtigungen 696 Autorenregister 696 Sachregister 700

I. Geschichtliche Entwicklung

des kristallographischen Zeichnens und dessen Ausführung in schräger Projektion.

Von

L u d w i g B u r m e s t e r in München.

Mit Tafel I.

I. Schrägbildliche Darstellungen.

1. Um die zweihundertjährige Entwicklung des kristallographischen Zeichnens zu verfolgen, ist zum Verständnis die uralte schräge Projektion1) erforderlich. Ihre Definition lautet: Parallele Projektionsstrahlen, die durch die Punkte eines Objektgebildes gehen und gegen die Bildebene schräg gerichtet sind, erzeugen auf ihr eine s c h r ä g e P r o j e k t i o n , die das S c h r ä g - b i l d und schlechthin das Bild des Objektgebildes genannt wird. Aus dieser Definition ergeben sich die folgenden hauptsächlichen Beziehungen:

Einer Objektgeraden entspricht eine Bildgerade, die sich in der Bild- ebene schneiden, und einer zur Bildebene parallelen Objektgeraden ent- spricht demnach eine parallele Bildgerade. Einer Punktreihe auf einer Objektgeraden entspricht eine ähnliche Punktreihe auf der zugehörigen Bildgeraden, und die entsprechenden Strecken sind also in gleichem Ver- hältnis. Parallelen Objektgeraden entsprechen parallele Bildgerade. Dem Verhältnis zwischen zwei parallelen Objektstrecken entspricht das gleiche Verhältnis zwischen den beiden zugehörigen Bildstrecken. Einem ebenen Objektgebilde in einer zur Bildebene parallelen Ebene entspricht ein kon- gruentes Bild.*"

Wir wollen die schräge Projektion bei den Zeichnungen der kristallo- graphischen Achsenkreuze und an vorbildlichen Beispielen erläutern, wobei die Bildebene stets in lotrechter Stellung angenommen wird.

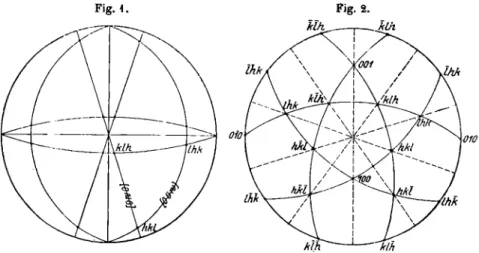
2. Um das kubische Achsenkreuz mit den drei gleichen rechtwinkeligen Achsen zu zeichnen, ziehen wir in Fig. 4 eine wagerechte Gerade und eine lotrechte Gerade, die sich in einem Punkt Ο also recht winkelig schneiden.

Zeitschr. f. Kristallographie. LVII. \

2 Ludwig Burmester.

Eine gegebene Länge der Halbachsen übertragen wir beiderseits von dem Punkt 0 auf die Wagrechte nach OB = OB und auf die Lotrechte nach OC = OC. Im Punkt Ο denken wir uns auf der Bildebene nach vorn im Raum «die Halbachse OA^r gleich jener Länge errichtet, und wählen einen durch den Punkt A^r gehenden Projektionsstrahl in beliebiger schräger Richtung gegen die Bildebene, der sie in einem Punkte Α trifft, und machen die Strecke OA entgegensetzt gleich OA. Sonach ist das Schrägbild AABBCC des kubischen Achsenkreuzes mit dem Mittelpunkte Ο gezeichnet; und OA, OB, OC werden die positiven, OA, OB, OC die negativen Halbachsen genannt.

Bei der schrägen Projektion wird theoretisch ein gedachtes unendlich fernes Auge angenommen, welches gleichsam in der Richtung A,.A auf die Bild- ebene schaut.

Betrachten wir die drei Halbachsen OA, OB, OC als die Kanten eines Würfels, dann wird dadurch dessen Schrägbild und auch das Schrägbild des Oktaeders bestimmt, dessen sechs Eckpunkte in den Mittelpunkten der Würfelseiten liegen. Die drei Diagonalen des Oktaeders bilden für den Würfel und das Oktaeder ein kubisches Achsenkreuz mit dem Mittelpunkte o.

Hinsichtlich senkrechter Projektion werden die Achseneben AOB, BOC, AOC Grundriß-, Aufriß-, Seitenrißebene genannt, und die senkrechten Pro- jektionen von dem Punkt ο auf diese Ebenen o^1} 02, o3 heißen Grundriß-, Aufriß-.und Seitenrißprojektion des Mittelpunktes 0 dieses kubischen Achsen- kreuzes.

Aus dieser schrägbildlichen Darstellung wollen wir die Beziehungen ableiten, die fürderhin zu den konstruktiven Ausführungen dienen. Wir legen das in OA auf der Bildebene senkrechte Dreieck OAA^r gedreht um OA in die Bildebene nach O A V um, indem wir die auf OA die Senk- rechte OA⁰' = OB machen, weil O B = O A , . ist. Dann ist A⁰'A.der umgelegte Projektionsstrahl A^rA und der Winkel OA⁰'A die wahre Größe des Winkels, den er mit A^rO im Raum bildet. Diesen Winkel nennen wir den R i c h t - w i n k e l der parallelen Projektionsstrahlen und bezeichnen ihn mit ρ. Däs Verhältnis OA: OA,, heißt das P r o j e k t i o n s v e r h ä l t n i s , das für jede Bild- strecke zu der ihr entsprechenden auf der Bildebene senkrechten Streckc gilt; und bezeichnen es mit 0·. Demnach wird durch tan ρ = Ö der Richt- winkel ρ bestimmt. Den Winkel BOA bezeichnen wir mit λ, und nennen ihn den L e n k w i n k e l , weil wir die Strecke OA beliebig lenken können, aber meistens ist sie bei den Schrägbildern nach links gewendet. Ein Schrägbild wird durch die Größen λ, & bestimmt, und symbolisch mit (λ, bezeichnet. Durch eine zweckmäßige Wahl dieser Größen kann nach Möglichkeit ein ästhetisch anschauliches Schrägbild erlangt werden.

Indem wir die Grundrißebene um OB nach unten gedreht in die Bild- ebene umlegen, gelangt der gedachte Punkt A,., dessen Bild Α ist, nach dem Punkt A⁰, der mit C vereint liegt. Dann ist der umgelegte Grundriß

Geschieht], Entwicklung d. kristallogr. Zeichnens α. dess. Ausf. in schräg. Projekt. 3

affin zu dem bildlichen Grundriß in bezug auf OB als Affinitätsachse, wobei die entsprechenden Punkte in parallelen Geraden liegen und die entsprechen- den Geraden sich auf der Affinitätsachse schneiden. Durch zwei ent- sprechende Punkte, wie A0, Α werden die affinen Gebilde bestimmt, wobei das Projektions verhältnis Ο Α : Ο A0 = d- ist. Sonach ergibt sich ζ. B. zu dem auf der Geraden A⁰B liegenden Punkt o⁰ der entsprechende Punkt Oj vermittelst der beziehlich zu A0O, OA, A0 Α Parallelen o0o12, o12o1( o0ol; mithin ist das Dreieck 000120! ähnlich und ähnlich liegend zu dem Drei- eck AoOA. Oder wir ziehen die Gerade AB, und zu A0A die Parallele o0o.

Indem wir die Seitenrißebene um OC nach links gedreht in die Bildebene umlegen, gelangt der gedachte Punkt A,. nach A°, der mit Β vereint liegt, und der Punkt o3 nach o°. Sonach ergeben sich die analogen affinen Beziehungen wie bei der Umlegung der Grundrißebene.

Bei dieser schrägbildlichen Darstellung ist als Beispiel der Lenkwinkel λ = 30° und das ProjektionsVerhältnis OA: OA⁰ = also (30°, ge- wählt. Demnach kann die Konstruktion ohne Halbierung der betreffenden Strecken vermittelst eines Zeichendreiecks, welches die Winkel 30° und 60°

enthält, einfach und genau ausgeführt werden, weil bei den entsprechenden Punkten A0, Α die Gerade A0A die Gerade OA rechtwinkelig schneidet;

und ebenso bei jedem Paar entsprechender Punkte. Wegen dieser Einfach- heit werden wir diese besondere schräge Projektion fernerhin meistens ver- wenden. In diesem besonderen Fall ist der Richtwinkel OA⁰'A = ρ be- stimmt durch tan ρ = O A : OA0' = £ und ρ = 26°34'. Da Α0Ό parallel A0A ist, und A0' in der Verlängerung von o12o0 liegt, so entspricht dem Punkt A⁰' der Schnittpunkt A' der Geraden Α⁰Ό , O J J O J und die ent- sprechenden Geraden OA0', OA' fallen in einer Geraden zusammen, sind also selbstentsprechende Gerade in den beiden affinen Gebilden. Demnach sind alle durch zwei entsprechende Punkte gehende Geraden selbst- entsprechende Gerade.

In dem Schrägbilde des tetragonalen Achsenkreuzes mit drei auf- einander rechtwinkeligen Achsen, von denen zwei als Nebenachsen gleiche Länge haben, sind OA, OB die halben Nebenachsen, und die Länge der halben Hauptachse wird auf der Geraden OC abgetragen. Das Schrägbild des rhombischen Achsenkreuzes mit drei ungleichen aufeinander recht- winkeligen Achsen wird durch die gegebenen Längenverhältnisse a:b: c bestimmt, wenn die Länge einer Achse gegeben ist.

Um das Schrägbild des hexagonalen Achsenkreuzes zu zeichnen, dessen drei gleiche Nebenachsen auf der Hauptachse senkrecht sind und miteinander den Winkel von 60° einschließen, machen wir, weil der Winkel BOA0' = 60° ist, in dem über Β Β beschriebenen Halbkreis die Sehne λ⁰Ή⁰ = A⁰'B, dann sind in der Umlegung OH0, OA0' zwei halbe Nebenachsen. Durch das zu A0OA parallele Dreieck EtH12S ergibt sich zu H0 der entsprechende

4 +

4 Ludwig Burmesler.

Punkt H. Demnach sind 0Ξ, OA', OB die Schrägbilder der halben Neben- achsen des hexagonalen Achsenkreuzes.

Ein Achsenkreuz, von dem eine lotrechte Achse, die als Hauptachse betrachtet wird, und eine andere in der Bildebene liegen oder beide zu ihr parallel sind, nennen wir ein r e g e l r e c h t g e s t e l l t e s Achsenkreuz.

Bei der regelrechten Feststellung eines Kristalls kann vermittelst der Ver- änderung der Projektionsrichtung jede erforderliche Ansicht zum Erlangen eines günstigen anschaulichen Schrägbildes desselben ermöglicht werden.

3. In Fig. \ a ist das Schrägbild desselben Würfels mit dem Oktaeder für den Lenkwinkel λ = 30° nach rechts gewendet gezeichnet, das sym- metrisch zu dem Schrägbild in Fig. 1 ist. Und beide Darstellungen be- wirken in größerem Maßstab als es auf der Tafel möglich ist, auch bei senkrechtem Sehen auf die Bildebene eine günstige Vorstellung von den beiden Körpern.

Ferner ist in Fig. \ b das Schrägbild Ο, X YZ von drei rechtwinkeligen Koordinatenachsen und das Schrägbild P2P von einer auf der Bildebene senkrechten Strecke P2Pr in der schrägen Projektion'(30°, gezeichnet;

dann ist in bezug auf die Koordinatenachsen die Lage des Punktes Pr im Raum und die des Bildpunktes Ρ in der Bildebene bestimmt durch das teils gestrichelt gezeichnete Schrägbild des Quaders, dessen Eckpunkte Pu P2, P3

Grundriß-, Aufriß- und Seitenrißprojektion im Bilde von dem Punkt Ρ sind.

Wenn die drei Koordinaten χ = OP^{1 3}, y = P13P1, « = P^tP , von denen

;y, χ in der wahren Größe, χ gleich der Hälfte der wahren Größe ist, ge- geben sind, so erhalten wir dadurch den Bildpunkt P. Legen wir beispiels- weise durch die Punkte P^{1 3}, P^{1 2}, P^{2 3} auf den Koordinatenachsen eine Ebene E, welche die Koordinatenebenen O X Y , O Y Z , O X Z in den hierdurch be- stimmten Geraden Ε ' , Ε", E ' " schneiden, dann heißen diese beziehlich Grundriß-, Aufriß-, Seitenrißspur; und die Strecken OP^{1 3}, OP^{1 2}, OP^{2 3} werden, bei rechtwinkeligen sowie bei schiefwinkeligen Koordinatenachsen die P a r a m e t e r der Ebene Ε genannt.

Bei dem Umlegen der Ebene Ο Χ Y in die Bildebene gelangt der Punkt P⁴ nach P ^ und die Grundrißspur E' nach E⁰'. Ebenso gelangt bei dem Umlegen der Ebene O X Z der Punkt P3 nach P3° und die Seitenriß- spur E'" nach E0"'. Durch diese Umlegungen, welche die senkrechte Projektion erfordert, wird der räumliche Zusammenhang der drei Projektions- ebenen zerstört und dadurch in der senkrechten Projektion die Anschaulich- keit und die Vorstellung der Gebilde im Raum erschwert.

4. Eine Zeichnung, die eine deutliche Vorstellung von einem Objekt- gebilde bewirkt, und es gleichsam ersetzt, wird eine a n s c h a u l i c h e Z e i c h - nung genannt. Wir erkennen in dem Bilde das wirkliche Objektgebilde, und befolgen ζ. B. die Ausdrucksweise: »der Punkt Pt gelangt bei der Drehung um die Achse OY nach P^t° « ; aber im strengen Sinne wird der

Geschieht!. Entwicklung d. kristallogr. Zeichnens u. dess. Ausf. in schräg. Projekt. 5

Punkt gedreht, dessen Schrägbild ist; ferner auch »die Strecke P1 2P ist senkrecht auf den beiden Geraden PP\, PP3«, und zwar nötigenfalls, sie ist »bildlich senkrecht«. Über diese Auffassung schreibt J. H. L a m b e r t²) schon vor 162 Jahren: »Denn es versteht sich von selbsten, daß hier durch eine zwar etwas harte Metapher dem Bild der Sache auf der Tafel zuge- eignet wird, was eigentlich der Sache selbsten zukömmt. Indessen geht der Ausdruck nothwendig an, weil nach der vorgegebenen Zeichnung in der That das Bild der Sache herauskömmt.«

Eine Zeichnung, die nach gegebenen Bestimmgrößen ausgeführt ist und zu konstruktiven Lösungen maßlicher Aufgaben dienen kann, nennen wir k o n s t r u k t i v e Z e i c h n u n g .

In der Kristallographie haben die Zeichnungen der Kristalle haupt- sächlich zu der Veranschaulichung gedient; und die wissenschaftlich not- wendige Ermittelung wahrer Größen wurde nicht beachtet.

Bei den Aufgaben, die nur zur konstruktiven Bestimmung wahrer Größen dienen, und bei denen die Anschaulichkeit der Zeichnung nicht in Betracht kommt, kann man wegen der Einfachheit und der Genauigkeit auch das Projektionsverhältnis 3- = I, also den Richtwinkel ρ = 45° annehmen. In dem Schrägbilde dieser besonderen schrägen Projektion (λ, 1) sind alle drei Achsen eines regelrecht gestellten kubischen Achsenkreuzes gleich. Sie wurde auf wagerechter Bildebene bei Festungswerken angewendet, und hat nach einem erhöhtem Stand in denselben, den man »Kavallier« nannte, die Be- nennung »Kavalierperspektive« erhalten, wobei in der Zeichnung meistens λ = 45° angenommen wird.

5. In Fig. 2 ist der Lenkwinkel λ = 90°, also OA senkrecht OB;

dann entsteht eine besondere schräge Projektion, die wir m i t t e l s c h r ä g e P r o j e k t i o n nennen, weil sie zwischen den beiden symmetrischen schrägen Projektionen in Fig. 1 und 1a gleichsam eine mittlere ist. Die mittelschräge Projektion ist geschichtlich wichtig; aber das Mittelschrägbild 0, ABC des regelrecht gestellten halben kubischen Achsenkreuzes mit den in der Bild- ebene liegenden Halbachsen OB, OC ist nicht anschaulich. Wenn wir in dem Punkt Ο auf der Bildebene die senkrechte Halbachse OAr errichten und um OB gedreht in die Bildebene nach OA⁰ umlegen, so ergibt sich zu A⁰ der affin entsprechende Punkt A, indem wir beispielsweise & = ^ annehmen, also die Strecke OA = ^OA0 machen. Der Richtwinkel OArA des nun in der Ebene AOC liegenden Projektionsstrahls Α,.Α ist hiernach gleich dem Neig-

winkel, den er mit der wagrechten Ebene AOB bildet, Nach der geschicht- lichen Annahme erhebt sich das unendlich fern gedachte Auge aus der wagrechten Ebene und schaut in der Richtung ArA auf die Bildebene.

Deshalb wurde dieser Neigwinkel E r h e b u n g s w i n k e l genannt, den wir kurz E r h e b w i n k e l nennen, und mit ε bezeichnet. Seine wahre Größe ist in der seitlichen Umlegung gleich dem Winkel Ο BA.

6 Ludwig Burmester.

Um nun ein anschauliches Mittelschrägbild des kubischen Achsenkreuzes zu erhalten, wurde es aus der regelrechten Stellung um seine Halbachse 0C gedreht. In der Umlegung ist dieser Drehwinkel δ — BOB⁰ nach der geschichtlichen Annahme durch die auf OB Senkrechte B¹²Bo = J-OB¹², also tan <$ = ^ und δ = 18° 26' bestimmt. Wir zeichnen das umgelegte Quadrat OAOD0B0, ziehen die auf OB Senkrechte A0AN und machen in ihr die Strecke A¹²A = ^A^L2A⁰, mithin ist tan ε = Zu diesem Quadrat konstruieren wir das affin entsprechenden Schrägbild OADB in bezug auf OB als Affinitätsachse vermittelst der entsprechenden Geraden Α$Β0, AB, die sich auf der Affinitätsachse im Punkt χ schneiden, und zeichnen das Parallelogramm OADB, wobei die entsprechenden Punkte in Senkrechten zur Affinitätsachse liegen. Sonach ergibt sich das Mittelschrägbild des ge- drehten kubischen Achsenkreuzes und das Mittelschrägbild des Würfels mit dem Oktaeder, welches ästhetisch anschaulicher erscheint als das einfacher konstruierbare Schrägbild derselben Körper in Fig. 1, bei denen die rechten Winkel eine herbe Straffheit bewirken. Und im Beschauen dieser Bilder empfangen wir assoziativ die Vorstellung von den in räumlicher Vertiefung erscheinenden Gebilden. Das Allereinfachste wäre, wenn man das Pro- jektionsverhältnis & = 1, also den Erhebwinkel ε = 45° annähme; denn

dann fällt OADB mit dem umgelegten Quadrat OAQD0B0 zusammen, und die obere Würfelfläche erscheint als ein zu diesem gleiches paralleles Qua- drat. Das Mittelschrägbild des Würfels und das des Oktaeders sind dann so sehr verzerrt, daß sie nicht zur Veranschaulichung dienen können.

Diese mittelschräge Projektion (90°, 1) auf eine wagrechte Bildebene wird M i l i t ä r p e r s p e k t i v e genannt³). Sie kann zur Ermittelung wahrer Größen aus der Zeichnung verwendet werden, und von der Kavalier- perspektive unterscheidet sie sich nur durch den besonderen Lenkwinkel λ — 90°.

6. Das monokline Achsenkreuz mit drei ungleichen Achsen, von denen zwei schiefwinkelig sind und die dritte auf ihnen senkrecht ist, und das trikline Achsenkreuz mit drei ungleich schiefwinkeligen ungleichen Achsen wurden zuerst von G. F. N a u m a n n4) in mittelschräge Projektion auf Grund des gedrehten kubischen Achsenkreuzes konstruiert. Wir wollen diese Achsen- kreuze in schräger Projektion und regelrechter Stellung konstruieren, um aus den affinen Beziehungen die geschichtlichen Konstruktionen füglich ab- zuleiten. Das kubische Achsenkreuz wird sich dabei als nebensächlich er- weisen. Wir setzen voraus, daß bei diesen Achsenkreuzen die drei Achsen gleich denen des kuhischen Achsenkreuzes sind; und durch gegebene Ver- hältnisse a:b: c werden die ungleichen Achsen bestimmt.

a) In Fig. 3 soll auf Grund des regelrecht gestellten kubischen Achsen- kreuzes das Schrägbild eines regelrecht gestellten monoklinen Achsenkreuzes in schräger Projektion (λ, 'ή, für die Annahme λ = 30°, & = £ in

Geschichtl. Entwicklung d. kristallogr. Zeichnens u. dess. Ausf. in schräg. Projekt. 7

der Zeichnung, konstruiert werden. Hierbei wird aber die auf den beiden schiefwinkeligen Achsen senkrechte Symmetrieachse nicht als lot- rechte Hauptachse, sondern eine der schiefwinkligen Achsen angenommen, in der die Kristalle häufiger prismatisch ausgebildet sind. Wir setzen voraus, daß die drei Achsen gleich denen des kubischen Achsenkreuzes sind, dessen Schrägbild AÄBBCC gezeichnet ist.

Von den beiden schiefwinkeligen Achsen, die einen gegebenen Winkel β einschließen, nehmen wir eine CC lotrecht und die Symmetrieachse Β Β wagrecht an, die wegen des geringen Platzes nach rechts in die benach- barte Figur hineinreicht. Die Ebene AOC legen wir um CC gedreht in die Bildebene um, dann gelangt der Punkt Α nach A° mit Β vereint, und A°, Α sind affin entsprechende P u n k t e in bezug auf CC als Affinitätsachse.

In der Umlegung machen wir den Winkel COA° = ß, fällen auf CC die Senkrechte A°A2. Zu A° ergibt sich erstens der affin entsprechende P u n k t A als Schnittpunkt der zu OA, A°A Parallelen A2A, A°A, und zweitens ohne die affine Beziehung nach dem Verhältnis A2A : A2A° = ϋ-, durch die zu OA parallele Strecke A2A = &-A2A<> = £A2A°. Sodann wird OÄ = OA gemacht, und AAEQCC ist das Schrägbild des monoklinen Achsenkreuzes.

Wenn wir uns in dem Punkt A2 auf der Bildebene nach vorn die

\

Senkrechte A2Ar = — A2A = SA2A errichtet d e n k e n , so erhalten wir V

eine Vorstellung von der nach vorn gelegenen Halbachse OA,, im Raum.

Um die N a u m a n n s c h e Konstruktion des Schrägbildes, wie sie in mittelschräger Projektion ausgeführt w i r d , abzuleiten, beachten w i r , daß dem Rechteck OA2A0J° das Parallelogramm OA2AJ affin entspricht. Da OA° — OA° = OC ist, so ergibt sich die Strecke OA2 = OC cosß, und nach dem Verhältnis OJ: OA = OJ°: OA° die Strecke OJ = OA sin ß.

Sodann wird das durch die Punkte 0 , A2, J bestimmte Parallelogramm OA2AJ gezeichnet. Dabei müssen aber die Strecken 0A2, OJ entweder konstruiert oder ihre Werte berechnet werden.

b) In Fig. & soll auf Grund des regelrecht gestellten kubischen Achsen- kreuzes das Schrägbild eines regelrecht gestellten triklinen Achsenkreuzes konstruiert werden, dessen drei Achsen die Achsenwinkel α, β, y einschließen, und dessen zwischen den Halbachsen OA, OB, OC befindliche Achsenebenen bilden die nach dem umfaßten pyramidalen Raum gelegenen Neigwinkel Α, Β, Ο, deren Supplemente in der Kristallographie »Flächenwinkel« ge- nannt werden.

Wir nehmen a, ß, G als gegebene Beslimmgrößen des triklinen Achsen- kreuzes an, und behufs der Konstruktion seines Schrägbildes verfahren wir in der nämlichen, aber zweifachen Weise wie in a). Die beiden Achsen, die den Achsenwinkel α einschließen, legen wir in die Bildebene nach

8 Ludwig Burmeeter.

CC, BB. Erstens wird die wagrechle Ebene ABB um BB gedreht in die Bildebene umgelegt; dann gelangt der Punkt Α nach A⁰ mit C vereint, und A0, Α sind affin entsprechende Punkte in bezug auf Β Β als Affinitätsachse.

In der Umlegung zeichnen wir den Winkel Β Ο Γ⁰ = G und fällen auf Β Β die Senkrechte Γ⁰Γ^ί2. Zu Γ⁰ wird der affin entsprechende Punkt Γ als Schnittpunkt der zu OA, A<,A Parallelen 1\2Γ, Γ0Γ bestimmt. Zweitens wird die Ebene FOC gedreht um CC in die Bildebene umgelegt, dann gelangt der Punkt Γ nach Γ⁰ mit Β vereint. In der Umlegung machen wir den Winkel COA° = ß, fällen auf CC die Senkrechte bestimmen zu A° den affin entsprechenden P u n k t e als Schnittpunkt der zu ΟΓ, Γ0Γ Parallelen <iA, A0A, und machen OA = OA. Sonach ist AABBCC das Schrägbild des triklinen Achsenkreuzes. Wird nun noch die zu Α Ο Parallele AA² bis an A°& gezogen, und denken wir uns in A² auf der Bildebene nach vorn die Senkrechte A2A^r = --A1 ²A = 2A²A errichtet,

Ί Λ

so erhalten wir eine Vorstellung von der nach vorn gelegenen Halbachse OA^r im Raum.

Nun aber wollen wir darlegen, wie die Konstruktion des Schrägbildes direkt ausgeführt werden kann. Wir zeichnen an OC den Achsenwirikel COA° = ß, fällen auf CC die Senkrechte Α0^, und zeichnen an deren Ver- längerung Q££ den Neigwinkel £(£Ai)'"=C; sodann machen wir den Schenkel

®AQ'" = IAO, fällen auf die Senkrechte A⁰"'A², ziehen A²A unter dem Lenkwinkel λ gegen A°A2 geneigt und machen die Strecke A2A = 4 ^••A²A^ü'". Denn, wenn wir uns den umgelegten Neigwinkel G um Α^Ξ

gedreht aufgerichtet denken, gelangt Α²Α^ΰ"' in die auf der Bildebene Senk- rechte A²A^r.

Um die Naumannsche Konstruktion des Schrägbildes, wie sie in der mittelschrägen Projektion ausgeführt wird, abzuleiten, beachten wir, daß dem Rechteck Ο Γ, ² Γ⁰ J⁰ das Parallelogramm Ο Γ¹² ΓΙ entspricht. Da die Punkte Γ0, Γ°, .40 auf dem über AoC als Durchmesser beschriebenen Halb- kreis liegen, so ergibt sich die Strecke Ο Γ^{ί 2} = ΟC cos G und nach dem Verhältnis Ol: OA = OI^t: OA⁰ die Strecke 01= OA sin Ο. Sodann wird das durch die Punkte Ο, Γ^ί2, 1 bestimmte Parallelogramm ΟΙ\²ΓΙ ge- zeichnet. Ferner beachten wir, daß dem Rechteck das Paral- lelogramm O&AJ entspricht, so ergibt sich die Strecke OS = OC cos β und nach dem Verhältnis OJ: OF=OJ°:On die Strecke OJ=OT ein ß.

Hiernach wird das durch die Punkte 0, (£, J bestimmte Parallelogramm O&AJ gezeichnet. Dabei müssen die Strecken 01\2, Ol, O S , OJ ent- weder berechnet oder konstruiert werden, und ferner ist in der mittel- schrägen Projektion auch noch die andere Halbachse ebenso durch zwei Strecken und ein Parallelogramm zu bestimmen; demnach sind sechs Strecken erforderlich.

Geschichtl. Entwicklung d. krietallogr. Zeichnens u. dess. Ausf. in schräg. Projekt. 9

Aus diesen Darlegungen ersehen wir, wie umständlich die bisher üb- lichen Naumannschen Konstruktionen sind; und in Nr. 8 werden wir in allen Fällen zu einfachen Konstruktionen gelangen.

7. Ein Dreikant, das von einer um seinen Scheitel Ο beschriebenen Kugelfläche in einem sphärischen Dreieck ABC geschnitten wird, kann als ein triklines Achsenkreuz mit gleichen Halbachsen OA, OB, 00 betrachtet werden, dessen Achsenwinkel α, β, γ die Seiten und dessen Neigwinkel Α, Β, Ο die Winkel des Dreikants und des sphärischen Dreiecks sind.

Demnach ergeben sich die verschiedenen Konstruktionen des Schrägbildes des triklinen Achsenkreuzes unabhängig von dem kubischen Achsenkreuz im einheitlichen Zusammenhang als Konstruktionen des Schrägbildes des Dreikants.

Behufs der schrägbildlichen Darstellung des Dreikants und des sphäri- schen Dreiecks nehmen wir in Fig. 5 zuvörderst die drei Seiten α, β, γ als gegeben an, legen diese Winkel in der Bildebene mit gemeinsamem Scheitel Ο so aneinander, daß der Schenkel 00 lotrecht und α der zwischen β, γ liegende Winkel ist. Wir beschreiben um Ο einen Kreisbogen Ϊ, der die Schenkel in den Punkten A0, B, G, A° schneidet, fällen auf OB die Senkrechte Λ093 und auf OG die Senkrechte Α°(ί, die beide verlängert sich im Punkt At schneiden. Der Winkel γ wird um OB nach vorn aus der Bildebene gedreht, ebenso der Winkel β um OG, bis die Schenkel OA0 und OA° sich im Raum in der gedachten Kante OAr vereinen; dem- nach ist A2 die senkrechte Projektion von dem Punkt Ar auf die Bild- ebene, und nun konstruieren wir das Schrägbild Α des Punktes Ar. Zu diesem Zweck errichten wir auf A²(& die Senkrechte A²A⁰'", die von dem um (£ mit dem Radius 0A° beschriebenen Kreisbogen im Punkt A0"' ge- schnitten wird, ziehen die gegen A²(£ unter dem Lenkwinkel λ = 30° ge- neigte Gerade A2A, und machen auf ihr die Länge A2A gleich der Hälfte von A² AQ" , denn A²A⁰"' ist gleich der auf der Bildebene Senk- rechten A2Ar. Ebenso kann man auch auf A2Sä die Senkrechte A2A0"

errichten, die von dem um SB mit dem Radius OA0 beschriebenen Kreisbogen im Punkt A^t" geschnitten wird; und A²A⁰", A²A¹⁾"' sind dann gleich. Sonach ist OA das Schrägbild .der Kante OAr, die nach vorn gelegen, aber wegen der besseren Ubersicht der Zeichnung nach oben ge- wendet ist.

An dem Schrägbilde ABC des sphärischen Dreiecks entsprechen die elliptischen Seiten AB, AC den in die Bildebene umgelegten Kreisbögen A0B, A°C. Zu dem Kreisbogen A°G ist der Ellipsenbogen AG affin in bezug auf O C als Affinitätsachse. Zieht man ζ. B. durch einen beliebigen auf A0C liegenden Punkt t° die Gerade bis sie OC in einem Punkt χ trifft, ferner die entsprechende Gerade Αχ und durch t° die zu A°A Parallele, so schneidet sie Αχ im Punkt t des Ellipeenbogens AC.

10

Die umgelegten Dreiecke A^AQ", A^&A^'" enthalten die Neigwinkel B, G, deren Schrägbilder A2%A, A2QA sind. Um das Schrägbild des Neigwinkels Α und dessen wahre Größe zu bestimmen, ist eine besondere Konstruktion erforderlich. Wir ziehen die auf OAQ Senkrechte AtiP bis an OB und die auf OA" Senkrechte A"Q bis an OG, dann ist die Ebene PA Q bildlich senkrecht auf OA, und ihre in der Bildebene befindliche Spur P Q schneidet die Gerade OA2 rechtwinkelig in einem Punkt N , weil OA2 die senkrechte Projektion von OA auf die Bildebene ist. Indem wir die Geraden AP, AQ ziehen, ergibt sich das Schrägbild PAQ des Neig- winkels A. Seine wahre Größe erhalten wir durch Drehung des Dreiecks PAQ um PQ in die Bildebene, wobei die Strecke NA nach Ν A40 in die verlängerte Gerade OA2 gelangt, und der Punkt wird bestimmt durch die Strecken PA0° = PA0, QA0° = QA° als Schnittpunkt des um Ρ mit dem Radius PAo und des um Q mit dem Radius PA0 beschriebenen Kreises. Demnach ist der Winkel PA0° Q = A.

Der Punkt A0° ergibt sich auch in anderer Weise. Die auf der Bild- ebene senkrechte Ebene OA2A, welche die um Ο beschriebene Kugelfläche in einem Großkreis schneidet, legen wir um OA2 gedreht in die Bildebene um, dann gelangt der Punkt Α nach dem Punkt A0', der auf dem Kreis- bogen ! liegt und durch die auf OA2 Senkrechte A2A0' bestimmt wird.

Da A2A0' = A2A<)" = A2A0'" ist, so schneidet der um A2 beschriebene, durch die Punkte Αϋ", A0"' gehende Kreisbogen κ den Kreisbogen I auch in dem Punkt A<,'. Sonach entsprechen OA, NA in der Umlegung die aufeinander Senkrechten ΟΑΰ', NA^; folglich ist die Strecke NAQ0 = NA0', wodurch der Punkt A0° auch bestiiqmt wird. Und alle sechs Winkel a, (J, γ, Α, Β, G liegen nun in der Bildebene.

Wie bei dem regelrecht gestellten kubischen Achsenkreuz, so bezeichnen wir auch in dem Schrägbild des regelrecht gestellten triklinen Achsenkreuzes die Halbachsen mit OA, OB, OC. Um diese nach den gegebenen Verhält- nissen a:b:e beispielsweise \ ,33:1:1,501| oder || 8 : 6 : 9 zu konstruieren, nehmen wir eine der Halbachsen, etwa OC als gegeben an, machen OB = — OC,

c ferner auf OA0' die Strecke OA0' = — OC und ziehen zu A4 Α die

c

Parallele A0'A bis an OA. Sodann fällen wir auf OA2 die Senkrechte, A0'A2, die gleich der wahren Länge der zu AA2 Parallelen AA2 ist.

Eine Fläche eines Kristalls wird nach dem Gesetz der rationalen In- dizes, wenn deren Verhältnisse h : k : l , beispielsweise 2 : 1 : 3 , gegeben sind, bestimmt durch die auf den Achsen O A , OB, OC liegenden Parameter OH, OK, OL\ demnach ist:

O S o ' = ! O A0' . O i f = j - O B , 0 L = \ 0 C ,

h ' κ ι

Geschichtl. Entwicklung d. kristallogr. Zeichnens u. dess. Auef. in schräg. Projekt. H

und der Punkt Η ergibt sich auf OA durch die zu A⁰'A Parallele H⁰' Π.

Die auf OA2 Senkrechte HQ'H2 ist gleich der wahren Länge der zu AA2

Parallelen ΗΞ². Der Punkt Κ liegt mit Β vereint, weil lc = \ ist. Wenn die durch ein Symbol (HKL) bestimmte Fläche Η KL beliebig parallel zu sich verschoben wird, dann bleiben die Verhältnisse der Indizes unverändert, und die Parameter werden dem Abstände dieser Fläche von dem Punkt Ο proportional verändert. Die durch die Achsenendpunkte A, B, C bestimmte Fläche, deren Symbol (Ή1) ist, wird die E i n h e i t s f l ä c h e und auch die G r u n d f o r m des Kristalls genannt.

Aus diesen Darlegungen der Beziehungen bei dem triklinen Achsen- kreuz gehen die analogen Beziehungen bei dem monoklinen Achsenkreuz ale besondere Fälle hervor. Wenn dessen Symmetrieachse senkrecht zur Bildfläche ist, fällt A^a mit 0 zusammen, und wenn sie, wie es üblich ist, mit der einen schiefen, lotrechten Achse in der Bildebene liegt, dann liegt der Punkt A² auf OG.

8. " In Fig. 5 sind die wahren Größen der Achsenwinkel a, β, γ und

λ Λ Λ

der Neigwinkel Α, Β, G des triklinen Achsenkreuzes enthalten; ferner sind die drei gleichen Strecken A²A⁰', A²A⁰", A²A⁰'" gleich der gedachten auf der Bildebene in A² Senkrechten A²A^R, deren Schrägbild A² Α ist, für das man den Lenkwinkel λ und das Projektionsverhältnis & zweckdienlich wählen kann, um ein günstiges Schrägbild des triklinen Achsenkreuzes zu

erlangen. . — - / N

Hiernach wollen wir, wenn drei von den Winkeln Α, Β, Γ, A, Β, C ge- geben sind, im. folgenden erstens die Konstruktionen des Schrägbildes des triklinen Achsenkreuzes mit gleichen Achsen und zweitens die Konstruk- tionen der anderen drei Winkel aus der Zeichnung Fig. 5 mit einer Aus- nahme ermitteln.

a) G e g e b e n s i n d d i e A c h s e n w i n k e l α , β , γ. Von den Punkten Λ0, A° fälle man beziehlich auf OB, OC die Senkrechten 4,99, Λ0©, die verlängert sich in dem Punkt A² schneiden, errichte auf AQA² die Senk- rechte A²A⁰", deren Länge durch 93Λ⁰" = SBAQ begrenzt wird; danach ist Β = A2^ßA(L"; und durch das Verhältnis A2A: A2A0" = & wird die Strecke A2A bestimmt. — Der um A2 beschriebene durch A0" gehende Kreisbogen κ schneidet die auf A2A° Senkrechte A2A0"' in A^" und den Kreisbogen ΐ in A⁰'; dann ergibt sich CJ= A²(£A⁰'" und durch NA⁰<> = NA⁰' auch

A = PA0°Q.

b) G e g e b e n s i n d die A c h s e n w i n k e l α , β u n d d e r z w i s c h e n - l i e g e n d e N e i g w i n k e l C~. Man fälle auf OG die Senkrechte zeichne an deren Verlängerung den Winkel A2&A<)"' = C, mache

und fälle auf A2A° die Senkrechte A0'"A2, wie in Nr. 6 , b) Fig. 4.

Danach wird durch das Verhältnis IJ A: A² A^A'" = & die Strecke A²A bestimmt. — Durch die auf OB Senkrechte die den Kreisbogen !

12 Ludwig Burmester.

in dem Punkt Λ0 trifft, ergibt sich γ = BOAQ, und durch die auf A2A0

Senkrechte A2A2", die den Kreisbogen κ in dem Punkt AQ" trifft, ergibt B= A2S&A0". Sodann wird wieder durch NA^ = NA\ auch A = PA^a° Q.

c) G e g e b e n sind der A c h e e n w i n k e l α und die b e i d e n a n - l i e g e n d e n N e i g w i n k e l B, G. Man zeichne den Winkel A⁰"A2A0"' = a, dessen Schenkel von einem um A2 mit beliebigem Radius beschriebenen Kreisbogen κ in den Punkten A0", AQ'" geschnitten werden, zeichne ferner an die Schenkel die rechtwinkeligen Dreiecke Ai^Aj', A²&A0'", in denen beziehlich die Neigwinkel Β, G enthalten sind und A²A0", A2A0"' gegen- überliegen; sodann ziehe man zu A2A0", A2A0"' die Parallelen 580, SO, die sich in einem Punkt 0 schneiden. Durch das Verhältnis A2A:A2A" = i) wird die Strecke A²A bestimmt. Da dieses so erhaltene Schrägbild von beliebiger Größe ist, so kann man für eine bestimmte Größe ein hierzu ähnliches und in bezug auf 0 als Ähnlichkeitspunkt ähnlich liegendes Schrägbild konstruieren. Die auf 0A² S e n k r e c h t e s t e ' trifft den Kreis- bogen κ in dem Punkt A⁰'; und der um 0 beschriebene durch A^ü' gehende Kreisbogen ! schneidet A2$i, beziehlich in den Punkten A0, A°, welche die Winkel γ, α bestimmen. Sodann ergibt sich wieder durch JVA0°

= NA„' auch A = PA⁰*Q.

d) G e g e b e n sind die N e i g w i n k e l Α, Β, G. Dieser Fall ist in Fig. 5 nicht enthalten und muß besonders erörtert werden. Wir betrachten

/ Ν Λ

A, B, G als die Winkel eines Dreikants, und vermittelst dessen Polardrei- kants werden dann die Achsenwinkel a, β, γ bestimmt. Zu diesem Zweck bezeichnen wir die Seiten des Polardreikants mit a', ß', /' und dessen Winkel mit Ä , i ? , demnach ist:

u' = 180° — Α, β' — \ 80° — Β , / — 180° — (J.

Aus diesen Seiten «', ß', / wird das Polardreikant konstruiert, und durch dessen Winkel ergeben sich die Seiten:

α = 180° — 2, β = 180° — Β, 7 = 180° -

Sodann wird wie in a) das Schrägbild des triklinen Achsenkreuzes konstruiert.

In der darstellenden Geometrie gibt es auch Konstruktionen, aus den Neigwinkeln direkt die Achsenwinkel zu erhalten und danach das Schräg- bild zu zeichnen; aber sie sind nicht einfach, so daß ihre Verwendung auch nicht zweckmäßig erscheint. Alle in vorherigen Darstellungen ge- gebenen Konstruktionen sind graphische Lösungen sphärisch trigonometri- scher Aufgaben, die in der Kristallographie durch Berechnung genauer ausgeführt werden als durch die konstruktiven Bestimmungenx die aber bei den bildlichen Darstellungen der Kristalle genügen und verwendet werden können.

Geschichtl. Entwicklung d. kristallogr. Zeichnens u. dess. Ausf. in schräg. Projekt. 1 3

9. In Fig. 5 a nehmen wir die ungleichen positiven Halbachsen Ο A, OB, OC eines triklinen Achsenkreuzes als gegeben an, von denen O B , OC in der Bildebene liegen und OA nach vorn geneigt ist. Um das Schräg- bild des durch diese Halbachsen bestimmten Parallelepipeds zu konstru- ieren, zeichnen wir in der Bildebene das Parallelogramm OBA'C, ziehen durch dessen Ecken A', B, C die zu OA Parallelen Α Ό ' , BC', CB', machen sie gleich OA und zeichnen das Parallelogramm O'B'AC', welches kon- gruent zu A'COB ist. In dem so erhaltenen Schrägbild des Parallelepipeds bilden die Endpunkte der von den gegenüberliegenden Ecken 0 , 0 ' aus- gehenden Kanten die Dreiecke ABC, A'B'C', deren Seiten die 0 , 0 ' gegen- überliegenden Diagonalen der benachbarten Parallelogramme sind. Aus der Zeichnung folgt, daß diese Dreiecke kongruent sind und in parallelen Ebenen liegend gegeneinander um 180° gedreht erscheinen.

Die Ebene OBO'B' schneidet AC in der Mitte b, mithin die Dreiecks- ebene ABC in der Geraden Bi>, und auf ihr liegt der Schnittpunkt P , in dem die Diagonale 0 0 ' durch diese Dreiecksebene geht; demnach ist Ρ der Schnittpunkt der drei Geraden, die in dem Dreieck ABC von den Ecken nach den Mitten der diesen Ecken gegenüberliegenden Seiten gehen. Das- selbe gilt auch von dem Punkt f , in welchem die Diagonale 0 0 ' die Drei- ecksebene A'B'C' schneidet; und durch die von B' nach der Mitte b' auf A'C' gehenden Geraden Β'b' wird der Punkt P1 bestimmt. Die Strecken Β'δ, Βb' gleich und parallel; folglich ebenso auch die Strecken B6, Β'b', von denen Bi die Strecke O P ' in dem Punkt Ρ halbiert, und ebenso halbiert B' b' die Strecke O ' P in dem Punkt P'. Demnach wird die Diago- nale 0 0 ' von ihren Schnittpunkten Ρ, P ' mit den Dreiecksebenen ABC, A'B'C' in drei gleiche Teile geteilt; und das Analoge gilt bei jeder Diago- nalen des Parallelepipeds.

Wenn wir annehmen, daß die drei von 0 ausgehenden Kanten des Parallelepipeds gleich sind, dann sind dessen zwölf Kanten alle gleich und alle sechs Seilen Rhomben. Dieses Parallelepiped wird R h o m - b o e d e r genannt, und von den Rhomben sind je zwei gegenüberliegende gleich.

Wenn insonderheit die drei gleichen von 0 ausgehenden Kanten gleiche Winkel einschließen, mithin ebenso auch die von 0 ' ausgehenden Kanten, so sind alle sechs Rhomben gleich; dann entsteht ein g l e i c h s e i t i g e s R h o m b o e d e r , in dem die Dreiecke ABC, A'B'C' gleichseitig sind. Die Diagonale 0 Cf ist senkrecht auf den Ebenen dieser Dreiecke und geht durch deren Höhenschnittpunkte Ρ, P . Diese Diagonale 0 0 ' , die dadurch aus- gezeichnet ist, daß sich an ihren Enden je drei gleiche Rhombenwinkel be- finden, heißt die H a u p t a c h s e des gleichseitigen Rhomboeders, das schlecht- hin R h o i t f b o e d e r genannt wird, weil es das einzige kristallographisch mögliche ist.

14 Ludwig Burmester.

Sind diese Rhombenwinkel 90°, dann entsieht ein Würfel. Aus der bekannten Dreiteilung einer Diagonalen des Würfels durch die Ebenen ABC, A'B'C' ergibt sich auch vermittelst der bei der thermischen Veränderung der Kristalle5) erscheinenden räumlichen Affinität verallgemeinert diese Eigen- schaft bei dem Parallelepiped.

Denken wir uns die Kanten eines Würfels in jeder Ecke gelenkig ver- bunden, dann entsteht ein affin veränderliches Rhomboid, das, je nachdem eine Diagonale gleich der doppelten Kantenlänge oder gleich Null wird, in diese Diagonale oder in ein reguläres Sechseck entartet, und dieses gilt auch für das gleichseitige Rhomboid, wenn insonderheit die von einem End- punkt einer Diagonalen ausgehenden Kanten beständig gleiche veränderliche Winkel miteinander einschließen.

Ein naiver Beschauer, der ohne Kenntnis der schrägen Projektion das Bild in Fig. 5 a auf die lotrecht gehaltene Zeichenebene aufrecht stehend betrachtet, empfängt durch das Bild eine unbestimmte Vorstellung von einem parallelepipedischen Körper, dessen von der Ecke Ο ausgehende punktiert gezeichneten Kanten unsichtbar sind. Die lotrechten Strecken erscheinen dem Beschauer auch als lotrechte Kanten; aber wie noch der Körper gegen die Bildebene gestellt ist, darüber kann er nicht urteilen. Zeichnungen dieser Art, die in allen Zeiten, zuweilen auch nur skizzenhaft ausgeführt, erfolgreich zum Erläutern und zum Erklären dienen, wollen wir p r o j e k - t i v e Z e i c h n u n g e n nennen, weil die bei der Parallelprojektion bestehen bleibenden Lagenbeziehungen und Streckenverhältnisse in den Gebilden projektive Eigenschaften der Gebilde heißen.

Wenn wir nun in das Schrägbild des Parallelepipeds, dessen hintere Fläche in der Bildebene liegt, den Punkt A2 als die gegebene senkrechte Projektion von dem Punkt Ar auf die Bildebene noch einzeichnen und uns in A2 nach vorn die auf der Bildebene senkrechte Strecke A2Ar = 2A2A errichtet denken, dann erhalten wir eine bestimmte Vorstellung von dem Parallelepiped und gelangen zu dessen Kenntnis. Die zur Bildebene paral- lelen Kanten und Winkel erscheinen in wahrer Größe, und die wahren Größen der anderen Kanten und Winkel können aus dem Bilde konstruktiv bestimmt werden. Durch den Punkt A2 und einen gegebenen Wert von Ό- wird die projektive Zeichnung in eine konstruktive Zeichnung ver- wandelt.

10. Um in Fig. 6 von dem Mittelpunkt Ο eines regelrecht gestellten triklinen Achsenkreuzes die Senkrechte auf eine zu einem Kristall gehörende Zwillingsebene zu fällen, nehmen wir a n , daß deren Parameter O K , OL in der Bildebene gegeben sind und der Parameter OH durch die Strecke HH-L bestimmt w i r d , wobei & = £ ist. Wir konstruieren zunächst den Neigwinkel der Zwillingsebene HKL gegen die Bildebene. Zu diesem Zweck fällen wir auf die Spur KL in der Bildebene die Senkrechten Η2Θ , OT,

Geechichll. Entwicklung d. kristallogr. Zeichnens u. dess. Auef. in schräg. Projekt. 1 5

errichten auf Η2Θ die Senkrechte H2H° = 2HH2 und ziehen die Gerade Η°Θ\ dann ist der Winkel H² ΘΗ^α der um H² Θ gedrehte umgelegte Neig- winkel. Ferner ziehen wir durch Τ die zu ΘΠ° Parallele und fallen auf sie die Senkrechte 0 P ° . Hiernach wird durch die auf 0 Τ Senkrechte P»P² und durch die beziehlich zu H²H, H»H Parallelen P²P , P ° P der Fuß- punkt Ρ der von Ο auf die Zwillingsebene gefällten bildlich Senkrechten be- stimmt. Sodann wird Ο Ρ um die eigene Länge PO' verlängert, und O'H, O'K, OL sind die Halbachsen des in der Zwillingsstellung befindlichen anderen Kristalls.

Um ein günstiges anschauliches Schrägbild von den Achsenkreuzen des regelrecht gestellten ersten Kristalls und des Zwillingskristalls zu erhalten, kann die Richtung der Strecke H²H und das Projektions Verhältnis d- be- liebig verändert und demnach die Projektionsrichtung zweckmäßig gewählt werden; dagegen ist es viel umständlicher, wenn zu diesem Zweck die Stellung des ersten Kristalls verändert wird, wie es von S t . J o l l es in Grundriß- und Aufrißprojektion ausgeführt wurde6).

Wenn man bedenkt, daß bei der Konstruktion zu den Geraden H°H7

Η*Θ nur die Parallelen P°P, F>T zu ziehen sind, wobei die Punkte H°, II und H°, Θ genügen, so werden diese beiden Geraden gar nicht als Hilfslinien verwendet; aber dennoch erfordert diese Konstruktion der auf die Zwil-

ingsebene gefällten Senkrechten acht Hilfslinien und eine Streckenabtragung.

Bei dem kubischen Achsenkreuz liegt der Punkt if2 und demnach fällt Η²Θ mit Ο Τ zusammen, also sind noch sieben Hilfslinien nötig. Zwar kann in diesem besonderen Fall die Konstruktion der gefällten Senkrechten

O P ohne deren Umlegung in die Bildebene, wie V. von Lang⁷) angegeben hat, ausgeführt werden. Dabei sind aber zwölf Hilfslinien erforderlich. Im allgemeinen ist bei einer Aufgabe mit maßlicher Beziehung, wie hier das Fällen einer Senkrechten auf eine Ebene, eine Umlegung erforderlich. Wenn in diesem besonderen Fall das Fällen der Senkrechten ohne Umlegung aus- geführt wird, so ist das darin begründet, daß in dem kubischen Achsen- kreuz die Achsen rechtwinkelig und gleich, also maßliche Beziehungen ent- halten sind.

11. In Fig. 7 ist in der Bildebene ein Dreieck ABC mit dem im Innern liegenden Höhenschnittpunkt 0² gegeben. Es soll das Schrägbild und die auf die Bildebene senkrechte Projektion eines kubischen Achsen- kreuzes konstruiert werden, dessen Achsen durch die Eckpunkte A, B, G gehen. Die Seiten des Dreiecks sind die Spuren der drei Achsenebenen in der Bildebene. Die senkrechten Projektionen der Achsen auf die Bild- ebene sind rechtwinkelig zu den Spuren der betreffenden Achsenebenen;

folglich liegen diese Projektionen in den Höhen des Dreiecks, und der Höhenschnittpunkt 02 ist die senkrechte Projektion des Mittelpunktes Or

des Achsenkreuzes.

16 Ludwig Burmester.

Behufs der Konstruktion des Schrägbildes legen wir die Ebene 02 OR G gedreht um die Höhe G $^c in die Bildebene um, beschreiben über £7$^c einen Halbkreis und errichten in 02 auf C!QC die Senkrechte O2O⁰, die ihn in dem umgelegten Punkt O0 trifft. Sodann wird die Richtung der Strecke O j O durch λ und deren Länge durch & bestimmt; demnach liegen die Schrägbilder der Achsen in OA, OB, OG. Auf der umgelegten Achse O0 G machen wir die Strecke O0C0 gleich der gegebenen Halbachse, ziehen die zu O0O Parallele C0C bis an OG, ferner die zu 002 Parallele C0C2

bis an 0²C oder fällen die auf 0²C Senkrechte C⁰C²; demnach ist C² die senkrechte Projektion von C. Bei der Bestimmung der Punkte Α, Β und deren senkrechten Projektionen A2, B2 verfahren wir in anderer Weise, wobei wir anstatt des Halbkreises in dem Punkt 0² auf 02A, 02B Senk- rechte gleich O²O⁰ errichten.

Sonach ist das Schrägbild OA, OB, ΟC des kubischen Achsenkreuzes und dessen senkrechte Projektion 0²A², 0² B^J( 0²C² konstruiert. Wenn wir die Strecke 0²0' entgegengesetzt gleich 0² Ο. machen, so erhalten wir das punktiert gezeichnete Schrägbild eines zweiten kubischen Achsenkreuzes, das zu dem ersten in bezug auf die Bildebene symmetrisch ist, und beiden entspricht dieselbe senkrechte Projektion auf die Bildebene. Bei dem ersten kubischen Achsenkreuz sind die Halbachsen von dem Beschauer weggewendet und bei dem zweiten nach ihn hingewendet.

Die senkrechte Projektion eines rechtwinkeligen Achsenkreuzes und eines auf ihn bezogenen Gebildes wird eine a c h s o n o m e t r i s c h e P r o j e k - t i o n genannt, und diese Darstellungsweise heißt A c h s o n o m e t r i e , die in der Kristallographie meistens verwendet wird, trotzdem daß alle drei Achsen gegen die Bildebene geneigt sind und in der Projektion verkürzt erscheinen, während in der schrägen Projektion eines regelrecht gestellten Achsen- kreuzes nur eine Achse verkürzt erscheint.

Mit dem Spurendreieck ABG ist die achsonometrische Projektion des rechtwinkeligen Achsenkreuzes gegeben. Denken wir uns auf der in 0² zur Bildebene Senkrechten nach vorn und hinten die Strecken 020^R, 0²Ο gleich O2O0 abgetragen, dann sind dadurch die beiden Achsenkreuze im Raum bestimmt. Betrachten wir nur das vordere Achsenkreuz und legen wir die in den Achsenebenen befindlichen Dreiecke gedreht in die Bild- ebene um, so gelangt der Punkt 0r nach den Punkten O0', O0", O0'", und diese sind die Schnittpunkte der verlängerten Höhen ASQu, BSQ^, C$$^c mit den nicht eingezeichneten Halbkreisen über den Dreiecks- seiten BG, CA, AB. Werden ζ. B. auf OA'B, O⁰'C die gleichen Achsen- längen O0'B0', O0'C0' abgetragen, dann ergeben sich durch die auf BG Senkrechten BÜ' B², G0' C² die Projektionen 0²B², 0²C². Zu einem Ge- bilde in dieser Umlegung ist dessen Projektion das affin entsprechende Gebilde.

Geschichtl. E n t w i c k l u n g d. kristallogr. Zeichnens u. dees. Ausf. in schräg. Projekt. 1 7

12. In Fig. 8 soll der Neigwinkel ν zweier auf den Achsen eines tri- klinen Achsenkreuzes durch die Parameter gegebenen Ebenen Ε, E ' in schräger Projektion (30°, konstruiert und seine wahre Größe bestimmt werden. Wir nehmen an, daß nach dem Verfahren in Nr. 7, Fig. 5 für gegebene Achsenwinkel die Achsen des regelrecht gestellten triklinen Achsen- kreuzes mit den Parametern OH, OK, OL und OROK', OL' der Ebenen Ε, E ' konstruiert sind. Der Parameter O H ist im Raum durch die Strecke HH² gegeben. Die in der Bildebene liegenden Spuren KL, K'L' der Ebenen Ε, Ε' schneiden sich in dem Punkt T². Die in den beiden Achsenebenen HOK, HOL liegenden Spuren HK, Η'K' und HL, H' L' schneiden sich beziehlich in dem Punkt S^it U³. Danach liegen die drei Punkte S^1} T²,U³ in der Schnittgeraden der beiden Ebenen, und <S^t T² ist die begrenzte Schnittgerade.

Die von St auf die Bildebene senkrechte Projektion S2 ist der Schnittpunkt der Geraden II2K mit der zu HII2 Parallelen S2, und S2T2 ist die Auf- rißprojektion von SⁱT². Hiernach ziehen wir durch S² die auf S²T² senk- rechte Gerade, welche die Spuren KL, K'L' beziehlich in den Punkten e, e' schneidet. Legen wir nun durch die Gerade ee' die auf S^T2 bildlich senk- rechte Ebene, so sind ihre Schnittgeraden mit den Ebenen Ε, E ' im Bilde die Schenkel des Neigwinkels v. Indem wir auf der Geraden ee' die Strecke S2S0 = 2 <S2Si machen, die Gerade S°T2 ziehen und auf sie die Senkrechte S2F° fällen, ist S2F<> die um S2T2 gedrehte Umlegung von der auf S^tT² bildlichen Senkrechten S²F, deren Fußpunkt F durch die zu S°S^t Parallele F°F bestimmt wird, und eFe' ist das Bild des Neigwinkels. Wird nun die Ebene eFe' mit dem Neigwinkel um ee' nach unten gedreht in die Bildebene umgelegt, dann gelangt der Punkt F nach F⁰ in die ver- längerte Gerade T²S², und der Punkt F⁰ wird durch S²F⁰ = S²F° be- stimmt. Somit ergibt sich der Neigwinkel v⁰= e F o e ' in der wahren Größe.

Nach dieser einfachen Konstruktion der wahren Größe des Neigwinkels zweier Ebenen, wobei dessen Schrägbild nicht nötig ist, kommt aber in Betracht, daß vorher die Konstruktion der Parameter dieser Ebenen aus- zuführen ist, wenn gegeben sind: die drei Achsenwinkel oder drei andere Bestimmgrößen des triklinen Achsenkreuzes, ferner die Verhältnisse a\b:c 'der Achsenlängen und die Verhältnisse der Indizes (h, l, k), (ti, k', ΐ ) der

beiden Ebenen. Demnach ist zwar die vollständige Konstruktion der wahren Größe des Neigwinkels umständlich; aber wie umständlich und mühsam ist doch auch deren Berechnung nach der ungeheuerlichen Formel, die vermittelst der analytischen Geometrie des Raumes abgeleitet wird⁸).

Wenn man das Schrägbild der drei Achsen und der beiden Ebenen mit ihrer Schnittgeraden für sich, abgesehen von allen anderen, betrachtet, so ist es eine projektive Zeichnung, die als solche von jeher in der Kri- stallographie zur Erklärung gedient hat, wobei zum Verständnis etwa ge- sagt wird; es sei ein kubisches oder ein triklines Achsenkreuz.

Zeitschr. f. Kristallographie. LVII. %