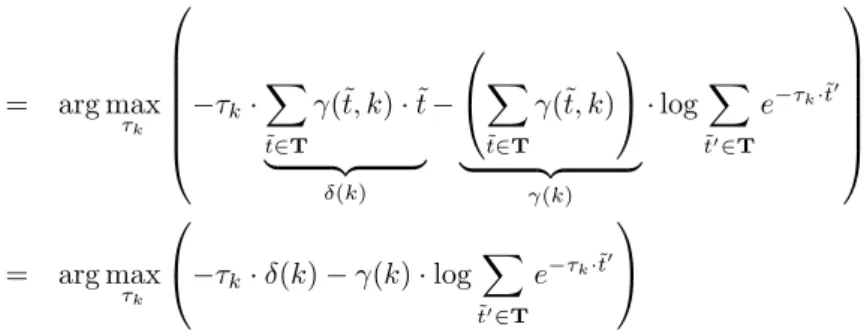Diplomarbeit Untersuchung der Ähnlichkeit von TRLFS

Untersuchung der Ähnlichkeit von TRLFS ^∗ -Spektren

von André Steinborn

14. März 2006

Hochschullehrer: Doz. Dr. rer. nat. habil. Boris Flach Technische Universität Dresden,

Institut für künstliche Intelligenz, Head of the Neural Computation Group Betreuer: Dr. rer. nat. Steffen Taut Technische Universität Dresden Strahlenschutzbevollmächtigter Leiter Sachgebiet Strahlenschutz Leiter Zentrales Radionuklidlabor Ansprechpartner: Dr. Gerhard Geipel Forschungszentrum Rossendorf Institut für Radiochemie Leiter Abteilung Aquachemie

∗TRLFS: Time Resolved Laserinduced Fluorescence Spectroscopy.

Hiermit versichere ich, die vorliegende Arbeit selbständig und unter ausschließlicher Verwendung der angegebenen Literatur und Hilfsmittel erstellt zu haben. Die Arbeit wurde bisher keiner anderen Prü- fungsbehörde vorgelegt.

Dresden, den 14. März 2006

Andrè Steinborn

Danksagung

An dieser Stelle möchte ich mich bei Doz. Dr. Flach bedanken, der die Betreuung dieser Arbeit als verantwortlicher Hochschullehrer nach der Emeritation von Professor Fuchs übernommen hat. Deswei- teren möchte ich meinem Betreuer Dr. Taut und den Mitarbeitern vom Sachgebiet Strahlenschutz der TU-Dresden meinen herzlichsten Dank für die schöne Diplomandenzeit aussprechen. Bei Dr. Geipel und Dr. Brendler vom Forschungszentrum Rossendorf bedanke ich mich für die lehrreichen Gespräche.

Dresden, den 14. März 2006

Andrè Steinborn

In dieser Arbeit wird die Ähnlichkeit von TRLFS-Spektren untersucht. Dafür werden Ähnlich- keitsmaße gesucht, welche die Ähnlichkeit der Spektren nach den Vorstellungen der TRLFS-Experten berechnen. Es wird zwischen Sichtähnlichkeitsmaßen und Parameterähnlichkeitsmaßen unterschie- den. Die Sichtähnlichkeitsmaße berechnen die Ähnlichkeit der Spektren auf Grund des gemessenen Funktionsverlaufes der Spektren und die Parameterähnlichkeitmaße berechnen die Ähnlichkeit auf Grund der physikalisch relevanten Parameter der Spektren. Der Ähnlichkeitsbegriff der Experten wurde durch Befragungen der Experten erfasst. Da der Ähnlichkeitsbegriff der Experten nicht for- mal beschrieben werden kann, wird eine empirische Untersuchung der Ähnlichkeit durchgeführt. Es wird eine formale Aufgabe für die Auswahl des besten Ähnlichkeitsmaßes formuliert. Diese Aufga- be wird sowohl für die Sichtähnlichkeitsmaße als auch für die Parameterähnlichkeitsmaße genauer spezifiziert. Es werden vier Sichtähnlicheitsmaße untersucht und das Kosinusähnlichkeitsmaß als das beste Sichtähnlichkeitsmaß ermittelt. Für die Untersuchung der Parameterähnlichkeitsmaße wird ein Parameterähnlichkeitsmaß mit freien Parametern konstruiert. Es wird untersucht, für welche Para- metrisierung das Parameterähnlichkeitsmaß am besten nach den Vorstellungen der Experten über die Ähnlichkeit der Spektren entscheidet. Weiterhin wird ein Modell für die TRLFS-Spektren vorgestellt.

Für dieses Modell wird eine Modellanpassungsaufgabe formuliert und es wird ein EM-Algorithmus als Lösung dieser Aufgabe abgeleitet. Da es sich bei dem EM-Algorithmus um einen iterativen Algo- rithmus handelt, wird auch ein Verfahren zur Schätzung initialer Startwerte vorgestellt.

Inhaltsverzeichnis

1 Einleitung 5

1.1 Aufgabenstellung . . . 5

1.2 Gliederung der zu lösenden Aufgabe . . . 6

2 TRLFS 7 3 Modellierung 9 4 Modellanpassung 14 4.1 Expectation-Maximization-Algorithmus . . . 14

4.2 Alternative Modellanpassung . . . 25

4.3 Schätzung initialer Startwerte . . . 26

4.4 Simulieren von Spektren . . . 31

4.5 Untersuchung der Verfahren . . . 32

4.5.1 Simulierte Spektren . . . 32

4.5.2 Reale Spektren . . . 39

5 Untersuchung der Ähnlichkeit 41 5.1 Erfassen des Ähnlichkeitsbegriffs . . . 44

5.2 Sichtähnlichkeitsmaße . . . 45

5.3 Parameterähnlichkeitsmaße . . . 47

5.4 Vergleich . . . 53

6 Computerprogramm 56

7 Zusammenfassung und Ausblick 56

8 CD-ROM 58

A Symbolverzeichnis 59

B Nützliche Lemmas 60

C Ähnlichkeitsbewertungen 61

Literatur 63

1 Einleitung

In dieser Arbeit soll die Ähnlichkeit von TRLFS-Spektren untersucht werden. TRLFS ist die Abkürzung von Time Resolved Laserinduced Fluorescence Spectroscopy. Dies ist ein spektroskopisches Verfahren und wird in der Chemie eingesetzt, um die Zusammensetzung von chemischen Stoffgemischen zu ana- lysieren. Durch Anwendung dieses Verfahrens auf eine chemische Probe erhält man ein für diese Probe typisches Spektrum, aus dem die Experten Informationen über die chemische Zusammensetzung der Probe erhalten. Ein TRLFS-Spektrum ist ein gemessener Funktionsverlauf über Wellenlänge und Zeit.

TRLFS ist ein sehr teures Verfahren, da aufwändige Geräte benötigt werden und sowohl die Ausmes- sung als auch die Analyse der Spektren sehr viel Zeit erfordern und meist durch Experten durchgeführt werden müssen. Um eine effektive Handhabung der „teuren” Spektren zu erreichen, sollen alle gemes- senen und bereits analysierten Spektren in einer Datenbank gespeichert werden und es soll möglich sein, auf Grund eines neu gemessenen Spektrums, ähnliche Spektren in der Datenbank zu finden. Hierfür ist es notwendig, die Ähnlichkeit der Spektren mit Computern berechnen zu können. Zur Berechnung von Ähnlichkeiten werden Ähnlichkeitsmaße verwendet. Um eine Aussage darüber treffen zu können, wel- che Ähnlichkeitsmaße für die Berechnung der Ähnlichkeit der Spektren geeignet sind, ist es notwendig, die Ähnlichkeit der Spektren zu untersuchen.

Hauptsächlich stellt sich dabei die Frage, unter welchen Bedingungen TRLFS-Spektren mehr oder we- niger ähnlich zueinander sind. In dieser Arbeit wird davon ausgegangen, dass die Spektren genau dann zueinander ähnlich sind, wenn sie von den Experten als ähnlich empfunden werden.

Die TRLFS-Experten haben durch ihre Erfahrung im Umgang mit den Spektren und durch ihr Wissen über den physikalischen Hintergrund der Entstehung der Spektren, eine bestimmte Vorstellung davon entwickelt, wann Spektren mehr oder weniger ähnlich zueinander sind. Die Aufgabe besteht nun darin, Ähnlichkeitsmaße zu finden, welche dieses Ähnlichkeitsempfinden der Experten im Computer nachbil- den.

1.1 Aufgabenstellung

Thema: Untersuchung der Ähnlichkeit von TRLF-Spektren

Beschreibung: Die chemische Analysenmethode Time Resolved Laser Fluorescence Spectroscopy (TRLFS) ist ein wichtiges Verfahren zur Analyse von Actiniden-Elementen (z. B. Uran, Americium und Curium) in umweltrelevanten chemischen Verbindungen. Ein TRLF-Spektrum ist die gemessene Fluo- reszenzintensität (Funktionswert) in Abhängigkeit der beiden unabhängigen Variablen Lichtwellenlänge und Zeit. Ziel der Diplomarbeit ist es, zu untersuchen, in welcher Art und Weise die Ähnlichkeit von TRLF-Spektren beschrieben bzw. verglichen werden kann.

Aufgabenstellung: In Fortsetzung der Arbeiten am Großen Beleg „Retrieval von Spektren” sind fol- gende Aufgaben zu lösen:

1. Untersuchung, ob die im Großen Beleg vorgestellte Sichtähnlichkeit zur Ähnlichkeitsanalyse prak- tisch geeignet ist. Dazu sind die im Großen Beleg vorgeschlagenen Sichtähnlichkeitsmaße auf mehrere TRLF-Spektrenserien anzuwenden, deren Ähnlichkeit von Chemikern vorab bewertet wurde.

2. Untersuchung, ob die im Großen Beleg vorgestellten Ähnlichkeitsmaße der Parameterähnlichkeit zur Ähnlichkeitsanalyse geeignet sind. Dazu sind diese Maße auf mehrere TRLF-Spektrenserien anzuwen- den, deren physikalische Parameter von Chemikern vorab ermittelt wurden.

3. Weiterentwicklung und Implementierung des im Großen Beleg begonnenen Modellanpassungspro- gramms. Mit seiner Hilfe sollen aus einem TRLF-Spektrum die entsprechenden physikalischen Para- meter innerhalb weniger Minuten ermittelt werden können.

1.2 Gliederung der zu lösenden Aufgabe

Aufbauend auf [Ste05] wird in dieser Arbeit die Ähnlichkeit von TRLFS-Spektren für eine größere ähnlichkeitsbewertete Spektrenmenge untersucht. Zuvor werden jedoch in Abschnitt 2 das spektrosko- pische Verfahren TRLFS und die daraus resultierenden TRLFS-Spektren vorgestellt. Um zu verstehen, welche Merkmale für die Bewertung der Ähnlichkeit der TRLFS-Spektren von Bedeutung sind, wird in Abschnitt 3 ein Wahrscheinlichkeitsmodell aufgestellt, welches die Verteilung der bei TRLFS emit- tierten Photonen über Zeit und Wellenlänge beschreibt. Da gerade diese Verteilung Aufschluss über die mit TRLFS zu untersuchende chemische Probe gibt, werden die Parameter dieses Modells als die physikalisch relevanten Parameter der Spektren bezeichnet. Aus dem Wahrscheinlichkeitsmodell der emittierten Photonen wird ein Modell für die Verteilung der gemessenen Photonen abgeleitet und es werden die TRLFS-Spektren modelliert.

Um die Spektren durch ihre physikalisch relevanten Parameter beschreiben zu können, muss es mög- lich sein, die freien Parameter des Wahrscheinlichkeitsmodells an die gemessenen Spektren anzupassen.

Dazu wird in Abschnitt 4.1 die Aufgabe formuliert, solche Modellparameter zu bestimmen, für welche die Wahrscheinlichkeit der im Spektrum beobachteten Photonen maximal wird. Als Lösung dieser Auf- gabe wird ein EM-Algorithmus abgeleitet. Zusätzlich wird in Abschnitt 4.2 ein alternativer Ansatz für die Modellierung und Modellanpassung der TRLFS-Spektren vorgestellt. Dieser Ansatz führt auf die Aufgabe, die Summe der quadratischen Abweichungen zwischem dem gemessenen Spektrum und einer Modellfunktion zu minimieren. Da es sich bei den daraus resultierenden Modellanpassungsverfahren um iterative und lokal konvergierende Algorithmen handelt, wird in Abschnitt 4.3 ein Verfahren zur Bestimmung initialer Startwerte vorgeschlagen.

Die in dieser Arbeit zu lösende Aufgabe besteht aus drei Teilaufgaben. Für die erste Teilaufgabe wer- den die in [Ste05] vorgestellten Sichtähnlichkeitsmaße anhand einer größeren Menge von ähnlichkeits- bewerteten Spektren dahingehend untersucht, ob sie sich für die Ähnlichkeitsbewertung von TRLFS- Spektren eignen. Dazu wird in Abschnitt 5 eine formale Aufgabe für die Bewertung der Ähnlichkeits- maße formuliert und darauf aufbauend werden in Abschnitt 5.2 die Sichtähnlichkeitsmaße für eine grö- ßere Menge von ähnlichkeitsbewerteten TRLFS-Spektren untersucht. Die Menge ähnlichkeitsbewerteter TRLFS-Spektren wurde aus einer Expertenbefragung erhalten. Diese Befragung und die daraus resul- tierenden Ergebnisse werden in Abschnitt 5.1 beschrieben.

Für die zweite Teilaufgabe werden in Abschnitt 5.3 die Parameterähnlichkeitsmaße untersucht. Diese Maße berechnen die Ähnlichkeit auf Grund der physikalisch relevanten Parameter der Spektren. Diese Parameter wurden von den Experten für die zu untersuchenden Spektrenserien bestimmt. Um eine Aus- sage darüber zu erhalten, ob sich die Sichtähnlichkeitsmaße oder die Parameterähnlichkeitsmaße besser für die Bewertung der Ähnlichkeit der TRLFS-Spektren eignen, werden beide Typen von Ähnlichkeits- maßen in Abschnitt 5.4 miteinander verglichen.

Zur Erfüllung der dritten Teilaufgabe werden in Abschnitt 4 Methoden aufgezeigt, mit denen die phy- sikalisch relevanten Parameter der Spektren ermittelt werden können. In Abschnitt 4.5 werden diese Methoden sowohl für simulierte als auch für reale Spektren untersucht.

Das im Rahmen dieser Arbeit entstandene Computerprogramm wird in Abschnitt 6 vorgestellt. Mit die- sem Programm ist es möglich, die Spektren zu sichten, die Algorithmen zur Modellanpassung zu testen

sowie die Ähnlichkeit der Spektren nach den in dieser Arbeit vorgestellten Verfahren zu untersuchen.

2 TRLFS

Der Messaufbau für TRLFS ist schematisch in Abbildung 1 dargestellt. Zuerst wird die zu untersu- chende Probe mit einem Laserimpuls fester Wellenlänge angeregt. Nach dieser Anregung emittiert die Probe über die Zeit Fluoreszenzlicht verschiedener Wellenlängen. Dieses austretende Licht wird mit einem Spektrograph in seine wellenlängenabhängigen Anteile zerlegt und mit einem nachgeschalteten ortsauflösenden Photodiodenarray gemessen. Durch die Ortsauflösung des Photodiodenarrays werden die Intervalle über der Wellenlänge bestimmt, in denen die einzelnen Lichtanteile gemessen werden.

Die zeitlichen Messintervalle werden durch einen Delaygenerator vorgegeben. Dieser Delaygenerator steuert den Bildverstärker an, über welchen das Photodiodenarray belichtet wird. Wie in Abbildung 1 angedeudet, sind die Messintervalle über der Wellenlänge zusammenhängend und äquidistant, wo- hingegen die Messintervalle über der Zeit im Allgemeinen weder zusammenhängend noch äquidistant sind.

Probe

Spektroskop Photodiodenarray

Delay Las

er

Probe

Zeit

Wellenlänge

Spektrum:

Bildverstärker

Probe

Spektroskop Photodiodenarray

Delay Delay Las

er Las

er Las

er

Probe

Zeit

Wellenlänge

Spektrum:

Bildverstärker

Abbildung 1: Messvorgang TRLFS.

Das von einer chemischen Probe emittierte Fluoreszenzlicht wird somit in Intervallen über Zeit und Wellenlänge gemessen und gespeichert. Als Ergebnis einer solchen TRLFS-Messung erhält man einen gemessenen Funktionsverlauf, welcher TRLFS-Spektrum genannt wird. Ganz allgemein kann man sich ein Spektrum als eine Menge von Kanälen vorstellen, wobei für jeden Kanal Ereignisse gezählt und gespeichert werden. In anderen Anwendungen, zum Beispiel in der Bildverarbeitung, werden solche Kanalmengen als Bilder oder als Histogramme bezeichnet. Ein Beispiel für ein gemessenes TRLFS- Spektrum ist in Abbildung 2 zu sehen.

Die Verteilung der Lichtintensitäten über Zeit und Wellenlänge ist von der chemischen Verbindung ab- hängig, welche das Fluoreszenzlicht emittiert. Im Allgemeinen können sich in der zu untersuchenden chemischen Probe mehrere fluoreszierende chemische Verbindungen befinden, weswegen die gemes- senen Lichtintensitäten eine Überlagerung der emittierten Lichtintensitäten verschiedener chemischer Verbindungen sind.

Im Folgenden soll der physikalische Prozess erläutert werden, der bei der Ausmessung einer chemischen Probe für genau eine chemische Verbindung stattfindet: Während der Anregung der zu untersuchenden

440 460 480 500 520 540 560 580 600

0 50000 100000 150000 200000

300 600 900 1200 1500 1800

TRLFS-Spektrum der Apatitsuspension mit Uran (VI) bei pH=5,5

Zeit in ns

Wellenlänge in nm

Intensität

Abbildung 2: Beispiel eines gemessenen TRLFS-Spektrums.

Probe werden die Elektronen, die sich in der chemischen Probe im Grundzustand befinden, auf ein hö- heres Energieniveau gehoben und fallen nach der Anregung über verschiedene Zwischenzustände in ihren Grundzustand zurück. Die dabei auftretenden Energieübergänge sind in Abbildung 3 dargestellt.

Für TRLFS sind dabei nur die Übergänge vom niedrigsten Anregungsniveau in den Grundzustand inter- essant, da nur bei diesen Übergängen das für TRLFS interessante Fluoreszenzlicht emittiert wird. Dieser Teil der Darstellung ist deshalb noch einmal in Abbildung 4 vergrößert zu sehen.

Abbildung 3: Physikalischer Prozess (aus [BB86]).

Die Energieübergänge vom niedrigsten Anregungsniveau in den Grundzustand finden unter Emission eines Photons pro Übergang statt. Auf Grund der Wellenlängen der emittierten Photonen können Rück- schlüsse auf die Energie der Energieübergänge und damit auf die in der chemischen Probe befindlichen chemischen Verbindungen gezogen werden. Speziell bei Spektren mit Uranylionen kommt noch hinzu,

Abbildung 4: Energieübergänge vom letzten Anregungszustand in den Grundzustand, wobei das bei TRLFS zu messende Fluoreszenzlicht emittiert wird (aus [BB86]).

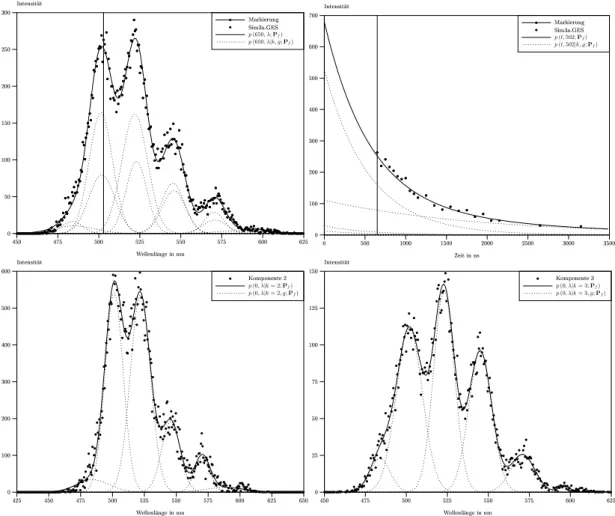
dass auf Grund der hantelförmigen Struktur zusätzliche Schwingungen auftreten, welche einen gewis- sen Teil der freigesetzten Energie verbrauchen. Deswegen existieren im Grundzustand sogenannte fünf Schwingungsniveaus. Durch den zusätzlichen Energieverbrauch sind die Energien der Photonen damit geringer und deren Wellenlänge entsprechend größer. Die einzelnen Photonen kann man somit in sechs verschiedene Klassen einteilen. Jede Klasse wird durch die mittlere Wellenlänge der Photonen dieser Klasse sowie durch die Streuung der Wellenlängen um den Mittelwert beschrieben. Die mittleren Wel- lenlängen der einzelnen Klassen sind fast äquidistant und die Streuungen sind ungefähr gleich. Die spektrale Verteilung der Photonen über der Wellenlänge wird damit durch die Verteilung der Photonen innerhalb der Klassen sowie durch die Verteilung der Photonen auf die einzelnen Klassen bestimmt. In Abbildung 4 wird ein Beispiel gezeigt, wie die Wellenlängen der Photonen der einzelnen Klassen um die mittleren Wellenlängen streuen und wie die Photonen auf die einzelnen Klassen verteilt sind.

Direkt nach der Anregung der chemischen Probe fallen sehr viele Elektronen in den Grundzustand zu- rück, wodurch sehr viele Photonen emittiert werden. Da die Energieübergänge voneinander unabhängig stattfinden, ergibt sich über der Zeit ein exponentieller Abfall des Fluoreszenzsignals.

Die Verteilung der Photonen über Zeit und Wellenlänge ist für die zu untersuchende chemische Verbin- dung charakteristisch und unterscheidet sich für verschiedene chemische Verbindungen.

3 Modellierung

Im Allgemeinen ist eine chemische Probe ein Gemisch aus mehreren chemischen Verbindungen, von denen einige nach der Anregung fluoreszieren. Die Menge der Photonen, die von genau einer dieser fluoreszierenden chemischen Verbindungen emittiert werden, wird im Folgenden als eine Komponente k∈Kbezeichnet, wobeiKdie Menge der Komponenten des Spektrums ist. In dieser Arbeit werden nur Uranylspektren betrachtet. Bei diesen werden die Wellenlängen der Photonen einer Komponente durch sechs verschiedene Schwingungsniveaus beeinflusst. Die Menge der Photonen, die von genau einem

dieser Schwingungsniveaus beeinflusst werden, wird im Folgenden als Peakg∈Gkbezeichnet, wobei G_k die Menge der Peaks der k−ten Komponente ist. Für jedes Photon wird der Ausschüttungszeit- punkt und die Wellenlänge beobachtet. Ein Photon(t, λ, k, g)kann somit durch die zwei beobachtbaren Merkmale Ausschüttungszeitpunktt∈R⁺und Wellenlängeλ∈R⁺sowie durch die zwei nichtbeob- achtbaren Merkmale Komponentenzugehörigkeitk ∈Kund Peakzugehörigkeitg ∈Gk beschrieben werden.

Die Verteilung der aus einer chemischen Probe emittierten Photonen wird als eine kontinuierliche Wahr- scheinlichkeitsverteilungp(t, λ), t ∈R⁺, λ ∈R⁺ modelliert. Diese Wahrscheinlichkeitsverteilung ist eine Mischung der Wahrscheinlichkeitsverteilungenp(t, λ|k),∀k∈Kder|K|Komponenten:

p(t, λ) = X

k∈K

p(k)·p(t, λ|k) (1)

Die Mischungskoeffizientenp(k),∀ksind die Wahrscheinlichkeiten des Auftretens der einzelnen Kom- ponenten. Für sie giltP

k∈Kp(k) = 1sowiep(k)>0,∀k∈K.

Die Wahrscheinlichkeitsverteilungp(t, λ|k)einer Komponentek ∈ K setzt sich wiederum aus einer Mischung der sechs Wahrscheinlichkeitsverteilungenp(t, λ|k, g)von sechs Peaksg∈Gk zusammen:

p(t, λ|k) = X

g∈Gk

p(g|k)·p(t, λ|k, g)

Die Mischungskoeffizientenp(g|k),∀g∈Gksind die Auftretenswahrscheinlichkeiten für die einzelnen Peaks. Für sie giltP

g∈G_kp(g|k) = 1sowiep(g|k)>0,∀g∈G_k,∀k∈K.

Die Wahrscheinlichkeitsverteilung eines Peaksp(t, λ|k, g)wird über der Wellenlänge als eine Gaußver- teilung und über der Zeit als eine Exponentialverteilung modelliert:

p(t, λ|k, g) = τ_k σ_kg·√

2·π·e

−^(λ−µkg)2

2·σ2

kg ·e^−τk·t

Die Zerfallskonstanteτ_k beschreibt dabei den exponentiellen Abfall derk−ten Komponente über der Zeit und die Parameterµkg undσkgbestimmen den Mittelwert und die Standardabweichung desg−ten Peaks derk−ten Komponente. Die Wahrscheinlichkeitsverteilungp(t, λ|k)einer Komponente

p(t, λ|k) =τk·e^−τk·t

| {z }

p(t|k)

· X

g∈G_k

p(g|k) σkg·√

2·π·e⁻

(λ−µkg)2 2·σ2

kg

| {z }

p(λ|k)

besteht aus dem Produkt der Verteilungenp(t|k)undp(λ|k). Die Verteilungp(t|k)der Photonen über der Zeit ist damit unabhängig von der Verteilungp(λ|k)der Photonen über der Wellenlänge und es gilt:

p(t, λ|k) =p(t|k)·p(λ|k) (2)

Das im Folgenden zu modellierende SpektrumSkann durch die physikalisch relevanten Parameter P = {τk, µkg, σkg, p(k), p(g|k),∀k∈K, g∈Gk}

beschrieben werden. Damit sieht die Wahrscheinlichkeitsverteilungp(t, λ;P)für die emittierten Photo-

nen folgendermaßen aus:

p(t, λ;P) = X

k∈K

p(k)· X

g∈Gk

p(g|k)· τk

σkg·√

2·π·e⁻

(λ−µkg)2 2·σ2

kg ·e^−τk·t (3)

= X

k∈K

p(k)·p(t|k;P)·p(λ|k;P) (4)

Ein gemessenes SpektrumS= (T,Λ,Φ, m, n,4_t,4_λ,P)besteht aus einer MengeTvonm=|T|

positiven reellen Zeitpunkten˜t∈Tund einer MengeΛvonn=|Λ|reellen Wellenlängenλ˜ ∈Λ. Da die Photonen in Intervallen über Zeit und Wellenlänge gemessen wurden, repräsentiert jeder Zeitpunkt

˜t ∈ Tein Intervall ˜t− 4t,˜t+4t

und jede Wellenlänge˜λ ∈ Λein Intervall h

˜λ− 4λ,λ˜+4λ

i . Desweiteren besteht ein Spektrum aus einer(m×n)−MatrixΦ = n

φ^(m×n)_˜

t,˜λ

o

, welche jedem Tupel (˜t,˜λ)∈T×Λeine Zahlφ_˜t,λ˜∈Rzuweist, welche die im Intervall

˜t− 4t,˜t+4t

×h

˜λ− 4λ,λ˜+4λ

i

gemessene Photonenanzahl beschreibt.

Die Wahrscheinlichkeitsfunktionp(t, λ), t∈R⁺, λ∈R⁺wird über diesen Intervallen integriert:

p₄

˜t,λ;˜ P

=

Z ^˜t+4t

˜t−4t

Z λ+4^˜ λ

˜λ−4_λ

p(t, λ;P)·dλ·dt

=

Z ^˜t+4t

˜t−4t

Z λ+4^˜ λ

˜λ−4_λ

X

k∈K

p(k)·p(t, λ|k;P)·dλ·dt

= X

k∈K

p(k)· Z ^˜t+4t

t−4˜ t

Z ^˜λ+4λ

λ−4˜ λ

p(t, λ|k;P)·dλ·dt

| {z }

p4(^t,˜λ|k˜ )

= X

k∈K

p(k)·p₄ t,˜˜λ|k

(5)

Die Integralep₄

˜t,˜λ|k

der komponentenbedingten Wahrscheinlichkeitenp t,˜λ|k˜

ergeben sich wie folgt:

p₄

˜t,λ|k;˜ P

=

Z ^˜t+4_t

˜t−4t

Z ^˜λ+4_λ λ−4˜ λ

p(t, λ|k;P)·dλ·dt

=

Z ^˜t+4_t

˜t−4t

Z ^˜λ+4_λ λ−4˜ λ

p(t|k;P)·p(λ|k;P)·dλ·dt

=

Z ^˜t+4t

t−4˜ t

p(t|k;P)dt

!

| {z }

p4(^˜t|k;P)

·

Z ^˜λ+4λ

λ−4˜ λ

p(λ|k;P)dλ

| {z }

p4(^˜λ|k;P)

= p₄ t|k;˜ P

·p₄

˜λ|k;P

(6)

Dabei können die Integralep₄ ˜t|k;P

undp₄ λ|k;˜ P

durch

p₄ ˜t|k;P

=

Z ^˜t+4t

p(t|k;P)dt

≈ 2· 4t·p ˜t|k;P

(7) und

p₄ λ|k;˜ P

=

Z λ+4^˜ λ

˜λ−4λ

p(λ|k;P)dλ

≈ 2· 4λ·p λ|k;˜ P

(8)

angenähert¹werden. Es ergibt sich für die Wahrscheinlichkeiten über den Integrationsintervallen p4

t,˜λ;˜ P

=X

k∈K

p(k)·p4 ˜t|k;P

·p4

λ|k;˜ P

. (9)

Die Wahrscheinlichkeitsverteilungp(t, λ;P),∀t∈R⁺, λ∈R⁺ist über einer unendlichen Unterstüt- zungsmengeR⁺×R⁺definiert. An jeder Stelle dieses Definitionsbereiches können Photonen emittiert werden. Die Photonen wurden aber, wie in Abbildung 1 angedeutet, nur über endlichen Intervallen ge- messen. Es kommt noch hinzu, dass die Integrationsintervalle über der Zeit nicht zusammenhängend sind. Somit gibt es Bereiche des Definitionsbereiches in denen Photonen zwar emittiert aber nicht ge- messen wurden. Aus diesem Grund müssen die Integralep₄

˜t,λ;˜ P

mit der Normierungskonstanten p(T,Λ;P) = X

t˜⁰∈T,λ˜⁰∈Λ

p₄

t˜⁰,˜λ⁰;P

(10)

normiert werden. Dadurch erhält man die Wahrscheinlichkeitsverteilung für die beobachteten Photonen:

˜ p

˜t,λ˜

= p₄

˜t,λ;˜ P

p(T,Λ;P) (11)

Die Zahlp(T,Λ;P)gibt an, mit welcher Wahrscheinlichkeit ein emittiertes Photon in die definierten Integrationsintervalle fällt und damit beobachtet werden kann. Für die Modellanpassung im nächsten Abschnitt erweist es sich als günstig, eine äquivalente Wahrscheinlichkeitsverteilungp˜

˜t,λ; ˜˜ P mit einer anderen ParametrisierungP˜ zu benutzen, durch welche die Wahrscheinlichkeit der beobachteten Photonen ohne Verwendung vonp(T,Λ;P)beschrieben werden kann. Dafür wird die folgende kom- ponentenbedingte Wahrscheinlichkeitsverteilung eingeführt:

˜ p

˜t,˜λ|k;P

=

p₄

˜t,˜λ|k;P P

˜t⁰∈T,˜λ⁰∈Λp₄

˜t⁰,λ˜⁰|k;P

= p₄ ˜t|k;P P

˜t⁰∈Tp₄ ˜t⁰|k;P

| {z }

˜ p(^˜t|k;P)

·

p₄

˜λ|k;P Pλ˜⁰∈Λp₄

˜λ⁰|k;P

| {z }

˜ p(^λ|k;P˜ )

= p˜ ˜t|k;P

·p˜ λ|k;˜ P

.

Die Wahrscheinlichkeitenp˜ ˜t|k;P

lassen sich folgendermaßen darstellen:

˜

p ˜t|k;P

= p4 t|k;˜ P P

t˜⁰∈Tp₄ ˜t⁰|k;P

1Im folgenden Text werden für die Annäherungen(≈)in den Gleichungen 7 und 8 Gleichheiten(=)angenommen.

= 2· 4_t·τ_k·e^−τk·˜t 2· 4t·τk·P

˜t⁰∈Te^−τk·˜t0

= e^−τk·˜t P

t˜⁰∈Te^−τk·t˜0. (12)

In Abbildung 1 ist zu sehen, dass die Integrationsbereiche über der Wellenlänge zusammenhängend sind.

Weiterhin wird angenommen, dass die Integrationsintervalle über der Wellenlänge so gewählt wurden, dass alle relevanten Wellenlängen abgedeckt werden. Damit kannP

˜λ⁰∈Λp₄

˜λ⁰|k;P

= 1angenom- men werden und es ergibt sich

˜ p

˜λ|k;P

=

p₄ λ|k;˜ P Pλ˜⁰∈Λp₄

λ˜⁰|k;P

= p₄

˜λ|k;P

= 2· 4λ·p

˜λ|k;P

. (13)

Mit Hilfe dieser Wahrscheinlichkeiten kannp˜

˜t,λ;˜ P

ohne Verwendung von p(T,Λ;P)durch die Wahrscheinlichkeitsverteilungp˜

˜t,˜λ; ˜P

mit einer etwas anderen ParametrisierungP˜ dargestellt wer- den:

˜ p

˜t,˜λ; ˜P

= X

k∈K

˜

p(k)·p˜

t,˜λ|k;˜ P

= X

k∈K

˜

p(k)·p˜ t|k;˜ P

·p˜ λ|k;˜ P

(14)

Die Komponentenwahrscheinlichkeitenp(k),˜ ∀k∈Krepräsentieren die Wahrscheinlichkeiten der Kom- ponenten im gemessenen Spektrum. Sie müssen von den Komponentenwahrscheinlichkeitenp(k),∀k∈ Kder emittierten Photonen unterschieden werden. Die Parameter des gemessenen Spektrums sind dem- nach Folgende:

P˜ = {τk, µkg, σkg,p(k), p(g|k),˜ ∀k∈K, g∈Gk}

Da der Unterschied zwischen den ParametrisierungenPundP˜ nur in den unterschiedlichen Kompo- nentengewichtenp(k)undp˜(k)liegt, gelten folgende Gleichungen²:

˜ p

˜t,˜λ|k;P

= p˜

t,˜λ|k; ˜˜ P

,∀t˜∈T,˜λ∈Λ

˜

p ˜t|k;P

= p˜ t|k; ˜˜ P

,∀˜t∈T

˜ p

˜λ|k;P

= p˜ λ|k; ˜˜ P

,∀λ˜∈Λ

Nachdem nun Wahrscheinlichkeitsmodelle für die emittierten und gemessenen Photonen erstellt wur- den, wird im folgenden Kapitel ein Algorithmus zur Bestimmung der Parameter dieser Wahrscheinlich- keitsmodelle vorgestellt.

2Es gelten noch weitere Gleichungen (Zum Beispiel gilt auchp4

˜t,λ|k;˜ P

=p4

˜t,λ|k; ˜˜ P

,∀˜t∈T,˜λ∈Λusw.). Es werden aber nur die Wichtigsten genannt.

4 Modellanpassung

4.1 Expectation-Maximization-Algorithmus

Da die bei TRLFS emittierten Photonen sowohl durch beobachtete Merkmale (Ausschüttungszeitpunkt und Wellenlänge) als auch durch nichtbeobachtbare Merkmale (Komponenten- und Peakzugehörigkeit) beschrieben werden, handelt es sich bei der Bestimmung der Modellparameter um ein Problem mit unvollständigen Daten. Für solche Probleme wird in der Statistik häufig ein Expectation-Maximization (EM) Algorithmus eingesetzt. Ein solcher Algorithmus wurde 1976 erstmalig von A. P. Dempser, N.

M. Laird und D. B. Rubin „EM-Algorithmus” genannt und unter diesem Namen in [DLR77] publiziert.

Allerdings hatte M. I. Schlesinger bereits 1968 einen äquivalenten Algorithmus in [Sch68] vorgestellt.

EM-Algorithmen sind iterativer Algorithmen und werden in der Statistik als Maximum-Likelyhood Schätzer für Probleme mit unvollständigen Daten verwendet. Es handelt es sich dabei nicht um einen bestimmten Algorithmus, sondern um eine Klasse von Algorithmen. Für ein gegebenes Problem muss ein spezieller EM-Algorithmus abgeleitet werden. In diesem Abschnitt wird ein EM-Algorithmus ab- geleitet, der die ParameterPder Wahrscheinlichkeitsfunktion 14 für ein gemessenes SpektrumSso bestimmt, dass die Wahrscheinlichkeit

˜

p(Φ;P) = Y

˜t∈T,λ∈Λ˜

˜ p

t,˜λ;˜ Pφ_˜t,λ˜

(15)

dieses Spektrums maximal wird. Dies wird auch Maximum-Likelyhood-Schätzung genannt.

Demnach muss für die Bestimmung der physikalisch relevanten ParameterP^∗folgende formale Aufga- be formuliert werden:

P^∗ = arg max

P p˜(Φ;P) (16)

= arg max

P

Y

˜t∈T,λ∈Λ˜

˜ p

t,˜λ;˜ Pφ_˜t,λ˜

Wie in Abschnitt 3 beschrieben, erfordert die Wahrscheinlichkeitsverteilungp˜

˜t,λ;˜ P

Wissen über die Wahrscheinlichkeitp(T,Λ;P)der gemessenen Photonen. Diese Wahrscheinlichkeit ist jedoch im Allgemeinen für ein gemessenes Spektrum nicht bekannt. In Abschnitt 3 wurde jedoch auch eine äqui- valente Wahrscheinlichkeitsverteilungp˜

˜t,λ; ˜˜ P

mit der ParametrisierungP˜eingeführt. Im Folgenden wird ein EM-Algorithmus zur Bestimmung der besten ParameterP˜^∗hergeleitet und danach wird be- schrieben, wie daraus die gesuchten physikalisch relevanten ParameterP^∗berechnet werden. Nebenbei ergibt sich eine Berechnungsvorschrift fürp(T,Λ;P).

Nun soll die formale Aufgabe gelöst werden, die Wahrscheinlichkeit

˜

p(Φ; ˜P) = Y

t∈T,˜ ˜λ∈Λ

˜

p(˜t,λ; ˜˜ P)^φt,˜λ˜ (17)

der beobachteten MatrixΦ=n φ^(m×n)_˜

t,˜λ

o

bezüglich des Parametersatzes P˜ = {τk, µ_kg, σ_kg,p(k), p(g|k),˜ ∀k∈K, g∈G_k}

zu maximieren:

P˜^∗ = arg max

P˜

˜ p(Φ; ˜P)

= arg max

P˜

Y

t∈T,˜ ˜λ∈Λ

˜

p(˜t,λ; ˜˜ P)^φt,˜λ˜

Da es schwierig ist, ein Produkt zu maximieren, wird im Folgenden der Logarithmus dieses Produk- tes maximiert. Dies ändert an dem gesuchten Ergebnis nichts, da die Logarithmenfunktion eine streng monoton steigende Funktion ist. Jedoch vereinfacht sich die Maximierungsaufgabe, da jetzt nur eine Summe maximiert werden muss:

P˜^∗ = arg max

P˜

log Y

˜t∈T,λ∈Λ˜

˜

p(˜t,˜λ; ˜P)^φ˜t,λ˜

= arg max

P˜

X

˜t∈T,λ∈Λ˜

φ_t,˜λ˜·log ˜p(˜t,λ; ˜˜ P)

Nun wird das nichtbeobachtbare Merkmalkeingeführt, welches die Zugehörigkeit der Photonen zu den einzelnen Komponenten beschreibt:

P˜^∗= arg max

P˜

X

˜t∈T,λ∈Λ˜

φ_˜t,λ˜·log X

k⁰∈K

˜

p(k⁰)·p(˜˜t,λ|k˜ ⁰; ˜P)

Es wird ein TermP

k∈Kα(˜t,λ, k) = 1,˜ ∀t˜∈T,∀˜λ∈Λmitα(˜t,˜λ, k)>0,∀˜t∈T,∀λ˜∈Λ,∀k∈K eingeführt, der die Photonen der einzelnen Photonenintervalle auf die Komponenten aufteilt:

P˜^∗= arg max

P˜

X

t∈T,˜ ˜λ∈Λ

φ_˜t,˜λ· X

k∈K

α(˜t,λ, k)˜

!

·log X

k⁰∈K

˜

p(k⁰)·p(˜˜t,˜λ|k⁰; ˜P)

Wegen des Distributivgesetzes in(R; +,·)gilt:

P˜^∗= arg max

P˜

X

˜t∈T,˜λ∈Λ

φ_˜t,˜λ·X

k∈K

α(˜t,λ, k)˜ ·log X

k⁰∈K

˜

p(k⁰)·p(˜˜t,˜λ|k⁰; ˜P)

Wegenlog a· ^b_c

= loga−log^c_b erhält man daraus folgende Formel:

P˜^∗ = arg max

P˜

X

˜t∈T,λ∈Λ˜

φ˜t,λ˜·X

k∈K

α(˜t,˜λ, k)·log p(k)˜ ·p(˜˜t,λ|k; ˜˜ P)· P

k⁰∈Kp(k˜ ⁰)·p(˜˜t,λ|k˜ ⁰; ˜P)

˜

p(k)·p(˜˜t,λ|k; ˜˜ P)

!

= arg max

P˜

X

˜t∈T,λ∈Λ˜

φ_˜t,λ˜·X

k∈K

α(˜t,˜λ, k)·

· log

˜

p(k)·p(˜˜t,λ|k; ˜˜ P)

−log p(k)˜ ·p(˜˜t,˜λ|k; ˜P) P

k⁰∈Kp(k˜ ⁰)·p(˜˜t,λ|k˜ ⁰; ˜P)

!

Durch Anwendung des Distributivgesetzes und Umsortieren der Summanden ergibt sich:

P˜^∗ = arg max

P˜













 X

˜t∈T,λ∈Λ˜

φ_˜t,λ˜·X

k∈K

α(˜t,˜λ, k)·log

˜

p(k)·p(˜˜t,λ|k; ˜˜ P)

| {z }

H₁

−

− X

˜t∈T,λ∈Λ˜

φ_˜t,λ˜·X

k∈K

α(˜t,˜λ, k)·log p(k)˜ ·p(˜˜t,λ|k; ˜˜ P) P

k⁰∈Kp(k˜ ⁰)·p(˜˜t,λ|k˜ ⁰; ˜P)

| {z }

H2















Wegen P˜^∗ = arg maxP˜(H1−H2) müssen der Parametersatz P˜^∗ und die Zahlen α(˜t,˜λ, k),∀˜t ∈ T,∀˜λ∈Λ,∀k∈Kso gewählt werden, dassH1möglichst groß undH2möglichst klein wird.

Die EM-Methodik sieht vor, zuerstH2bezüglich den Zahlenα(˜t,λ, k)˜ für einen gegebenen Parame- tersatzP˜ zu maximieren. Wegen Lemma 2 aus Anhang B und dem Theorem von Shannon (Lemma 1) ergibt sich:

α(˜t,λ, k) =˜ p(k)˜ ·p(˜˜t,λ|k; ˜˜ P) P

k⁰∈Kp(k˜ ⁰)·p(˜˜t,λ|k˜ ⁰; ˜P),∀˜t∈T,∀˜λ∈Λ,∀k∈K

Mit den so berechneten Zahlenα(˜t,˜λ, k) wird im Folgenden H1 bezüglich P˜ maximiert. Mit dem daraus erhaltenen ParametersatzP˜ wird TermH₁wegen der Maximierung größer und TermH₂wegen des Theorems von Shannon (Lemma 1) kleiner . Somit wird die GesamtfunktionH =H1−H2größer.

Wegen der Unabhängigkeit vonp(˜˜ t|k; ˜P)undp(˜˜λ|k; ˜P)erhält man fürH₁:

H₁ = X

˜t∈T,λ∈Λ˜

φ_t,˜λ˜·X

k∈K

α(˜t,λ, k)˜ ·log

˜

p(k)·p(˜˜ t|k; ˜P)·p(˜˜λ|k; ˜P)

= X

˜t∈T,λ∈Λ˜

φt,˜λ˜·X

k∈K

α(˜t,λ, k)˜ ·

log ˜p(k) + log ˜p(˜t|k; ˜P) + log ˜p(˜λ|k; ˜P)

= X

k∈K



 X

˜t∈T,λ∈Λ˜

φ_˜t,λ˜·α(˜t,λ, k)˜



·log ˜p(k) + (18)

+ X

k∈K

X

˜t∈T



 X

λ∈Λ˜

φ_˜t,λ˜·α(˜t,λ, k)˜



·log ˜p(˜t|k; ˜P) + (19)

+ X

k∈K

X

˜λ∈Λ



 X

˜t∈T

φ_˜t,λ˜·α(˜t,λ, k)˜



·log ˜p(˜λ|k; ˜P) (20)

Term 18 wird wegen dem Theorem von Shannon (Lemma 1) bezüglichp(k),˜ ∀k∈Kmaximal, wenn

˜ p(k) =

P

˜t∈T,˜λ∈Λφ_t,˜λ˜·α(˜t,˜λ, k) P

˜t∈T,˜λ∈Λφ_˜t,λ˜

,∀k∈K.

Term 19 wird nach Lemma 2 bezüglichτk,∀k∈Kmaximal mit

τ_k^∗ = arg max

τ_k

X

˜t∈T



 X

˜λ∈Λ

φ_˜t,˜λ·α(˜t,˜λ, k)





| {z }

γ(˜t,k)

·log ˜p(˜t|k;τk),∀k∈K

= arg max

τ_k

X

˜t∈T

γ(˜t, k)·log e^−τk·˜t P

˜t⁰∈Te^−τk·t˜0

= arg max

τk

X

˜t∈T

γ(˜t, k)·



−τk·˜t−logX

˜t⁰∈T

e^−τk·˜t0





= arg max

τ_k















−τk·X

t∈T˜

γ(˜t, k)·˜t

| {z }

δ(k)

−



 X

t∈T˜

γ(˜t, k)





| {z }

γ(k)

·logX

˜t⁰∈T

e^−τk·˜t0















= arg max

τ_k



−τk·δ(k)−γ(k)·logX

˜t⁰∈T

e^−τk·˜t0





Um die gesuchte Extremstelle bezüglich τ_k zu finden, wird die Ableitung der Zielfunktion auf Null gesetzt:

−δ(k) +γ(k)· P

˜t⁰∈T˜t⁰·e^−τk·t˜0 P

˜t⁰∈Te^−τk·t˜0 = 0 f_a(τ_k) = X

t˜⁰∈T

˜t⁰−δ(k) γ(k)

·e^−τk·t˜0 = 0

τk

fa(τk)

τk

fb(τk)

Abbildung 5: Funktionenf_a(τ_k)(links) undf_b(τ_k)(rechts) zur Bestimmung derτ_k.

In Abbildung 5 wird links die Funktionf_a(τ_k)gezeigt. Die Lösung der Gleichungf_a(τ_k) = 0kann mit dem Newton-Verfahren

τ_k⁽ⁱ⁺¹⁾=τ_k⁽ⁱ⁾− f_a

τ_k⁽ⁱ⁾ f_a⁰

τ_k⁽ⁱ⁾

iterativ bestimmt werden. Problematisch ist jedoch, dass die Funktionf_a(τ_k)nicht monoton ist und das Newton-Verfahren mit einem zu groß gewählten Startwertτ_k⁽⁰⁾divergiert. Deshalb werden weitere Umformungen vorgenommen:

X

t˜⁰∈T

˜t⁰−δ(k) γ(k)

·e^{−τk·δ(k)γ(k)} e^{−τk·δ(k)γ(k)}

e^−τk·˜t0 = 0

1 e^−τk·

δ(k) γ(k)

·X

˜t⁰∈T

˜t⁰−δ(k) γ(k)

· e^−τk·˜t0 e^−τk·

δ(k) γ(k)

= 0

1 e^{−τk·γ(k)δ(k)}

·X

˜t⁰∈T

˜t⁰−δ(k) γ(k)

·e^−τk·(^˜t0−^δ(k)_γ(k)) = 0

fb(τk) = X

˜t⁰∈T

˜t⁰−δ(k) γ(k)

·e^−τk·(^t˜0−_γ(k)^δ(k)) = 0

Die Funktionf_b(τ_k)ist in Abbildung 5 rechts zu sehen. Sie ist im Intervallτ_k ∈[0,∞)stetig und die Ableitung

f_b⁰(τk) = −X

˜t⁰∈T

˜t⁰− δ(k) γ(k)

²

·e^−τk·(^t˜0−_γ(k)^δ(k))

besitzt keine Nullstellen. Daraus folgt, dassf_b(τ_k) eine monotone Funktion ist. Bestimmt man die Lösung der Gleichungfb(τk) = 0mit dem Newton-Verfahren

τ_k⁽ⁱ⁺¹⁾=τ_k⁽ⁱ⁾− fb

τ_k⁽ⁱ⁾ f_b⁰

τ_k⁽ⁱ⁾,

erhält man theoretisch für beliebige Startwerteτ_k⁽⁰⁾die gesuchte Lösungτ^∗. Bei der praktischen Berech- nung tritt jedoch das Problem auf, dassfb(τk)mit zunehmendemτk stark abfällt, so dass der Funkti- onswertf_b(τ_k)für ein zu groß gewähltesτ_k⁽⁰⁾nicht mehr berechnet werden kann. Aus diesem Grund wird als Startwertτ_k⁽⁰⁾= ^γ(k)_δ(k)gewählt. Dies ist sinnvoll, da sichτ_k^∗durchτ_k^∗= ^γ(k)_δ(k) berechnen würde, falls alle emittierten Photonen im Spektrum gemessen werden. Damit liegtτ_k⁽⁰⁾ in der unmittelbaren Nähe des gesuchtenτ_k^∗.

Term 20 auf Seite 16 wird nach Lemma 2 bezüglichµ_kgundσ_kg,∀k∈K, g∈G_kmaximal mit

µ^∗_kg, σ_kg^∗

= arg max

(µ_kg,σ_kg)

X

λ∈Λ˜



 X

t∈T˜

φ˜t,˜λ·α(˜t,˜λ, k)





| {z }

(˜λ,k)

·log ˜p(˜λ|k; ˜P)

= arg max

(µ_kg,σ_kg)

X

λ∈Λ˜

(˜λ, k)·log

2· 4λ·p

λ|k; ˜˜ P

= arg max

(µ_kg,σ_kg)

X

λ∈Λ˜

(˜λ, k)·

log (2· 4λ) + logp

λ|k; ˜˜ P

= arg max

(µkg,σkg)











 X

λ∈Λ˜

(˜λ, k)·log (2· 4_λ)

| {z }

konstant

+X

˜λ∈Λ

(˜λ, k)·logp

˜λ|k; ˜P













= arg max

(µ_kg,σ_kg)

X

λ∈Λ˜

(˜λ, k)·logp(˜λ|k; ˜P)

= arg max

(µkg,σkg)

X

λ∈Λ˜

(˜λ, k)·log X

g⁰∈Gk

p(g⁰|k)·p(˜λ|k, g⁰;µ_kg⁰, σ_kg⁰)

Es wird ein TermP

g∈Gkβ(˜λ, g, k) = 1,∀λ˜ ∈Λ, k∈Kmitβ(˜λ, g, k)>0,∀˜λ∈Λ, g∈Gk, k∈K eingeführt:

(µ^∗_kg, σ_kg^∗ ) = arg max

(µ_kg,σ_kg)

X

λ∈Λ˜



 X

g∈Gk

β(˜λ, g, k)



·(˜λ, k)·log X

g⁰∈Gk

p(g⁰|k)·p(˜λ|k, g⁰;µkg⁰, σkg⁰)

= arg max

(µ_kg,σ_kg)

X

λ∈Λ˜

X

g∈Gk

β(˜λ, g, k)·(˜λ, k)·log X

g⁰∈Gk

p(g⁰|k)·p(˜λ|k, g⁰;µkg⁰, σkg⁰)

= arg max

(µkg,σkg)

X

λ∈Λ˜

X

g∈G_k

β(˜λ, g, k)·(˜λ, k)·

· log p(g|k)·p(˜˜λ|k, g;µkg, σkg)· P

g⁰∈Gkp(g⁰|k)·p(˜λ|k, g⁰;µkg⁰, σkg⁰) p(g|k)·p(˜λ|k, g;µ_kg, σ_kg)

!

= arg max

(µ_kg,σ_kg)













 X

λ∈Λ˜

X

g∈Gk

β(˜λ, g, k)·(˜λ, k)·log

p(g|k)·p(˜λ|k, g;µkg, σkg)

| {z }

B₁

−

− X

λ∈Λ˜

X

g∈G_k

β(˜λ, g, k)·(˜λ, k)·log p(g|k)·p(˜λ|k, g;µkg, σkg) P

g⁰∈G_kp(g⁰|k)·p(˜λ|k, g⁰;µ_kg⁰, σ_kg⁰)

| {z }

B₂















UmB =B1−B2 zu maximieren, mussB1größer undB2kleiner werden. Nach der EM-Methodik wird zunächstB2bezüglich den Zahlenβ(˜λ, g, k)maximiert:

B2 = X

˜λ∈Λ

(˜λ, k)· X

g∈G_k

β(˜λ, g, k)·log p(g|k)·p(˜λ|k, g;µkg, σkg) P

g⁰∈Gkp(g⁰|k)·p(˜λ|k, g⁰;µ_kg⁰, σ_kg⁰) → max

β(˜λ,g,k)

Nach dem Theorem von Shannon (Lemma 1) berechnen sich die Zahlenβ(˜λ, g, k)aus β(˜λ, g, k) = p(g|k)·p(˜λ|k, g;µkg, σkg)

P

g⁰∈Gkp(g⁰|k)·p(˜λ|k, g⁰;µkg⁰, σkg⁰)

Mit diesen Zahlenβ(˜λ, g, k)wird nunB1bezüglich der Parameter(p(g|k), µkg, σkg,∀g∈Gk),∀k∈ Kmaximiert, wodurchB₂kleiner wird:

B1 = X

λ∈Λ˜

X

g∈G_k

β(˜λ, g, k)·(˜λ, k)·log

p(g|k)·p(˜λ|k, g;µ_kg, σ_kg)

→ max

(^p(g|k),µkg,σ_kg)

= X

λ∈Λ˜

X

g∈G_k

β(˜λ, g, k)·(˜λ, k)·

logp(g|k) + logp(˜λ|k, g;µ_kg, σ_kg)

→ max

(^p(g|k),µkg,σ_kg)

= X

g∈G_k

0

@X

˜λ∈Λ

β(˜λ, g, k)·(˜λ, k) 1

A·logp(g|k) + (21)

+ X

g∈G_k

0

@X

˜λ∈Λ

β(˜λ, g, k)·(˜λ, k)·logp(˜λ|k, g;µkg, σkg) 1

A→ max

(^p(g|k),µkg,σ_kg) (22)

Term 21 kann mit dem Theorem von Shannon (Lemma 1) bezüglichp(g|k)folgendermaßen maximiert werden:

p(g|k) = P

λ∈Λ˜ β(˜λ, g, k)·(˜λ, k) Pλ∈Λ˜ (˜λ, k)

= P

λ∈Λ˜ β(˜λ, g, k)·(˜λ, k) P

t∈T,˜ λ∈Λ˜ φ_˜t,˜λ·α(˜t,˜λ, k)

= P

λ∈Λ˜ β(˜λ, g, k)·(˜λ, k)

˜ p(k)·P

˜t∈T,λ∈Λ˜ φ_˜tλ˜