Datenstrukturen Theorie (L)

Datenstrukturen

Theorie (L)

Inhaltsverzeichnis

1 Datentypen 3

1.1 Einfache Datentypen . . . 3

1.2 Zusammengesetzte Datentypen . . . 3

1.3 Abstrakte Datentypen . . . 5

2 Lineare Datenstrukturen 7 2.1 Stacks (Stapel) . . . 7

2.2 Queues (Warteschlangen) . . . 9

2.3 Deques (zweiseitige Warteschlangen) . . . 11

2.4 Linked Lists (einfach verkettete Listen) . . . 13

3 B¨aume (Trees) 17 3.1 Beispiele . . . 17

3.2 Begriffe . . . 18

3.3 Typologie . . . 19

3.4 Darstellung bin¨arer B¨aume als verschachtelte Listen . . . 21

3.5 Darstellung bin¨arer B¨aume durch Knoten und Referenzen . . . 21

3.6 Darstellung vollst¨andiger Bin¨arb¨aume als Heap . . . 24

4 Graphen 28 4.1 Begriffe . . . 28

4.2 Eigenschaften von Graphen . . . 30

4.3 S¨atze ¨uber Graphen . . . 33

4.4 Repr¨asentation von Graphen . . . 35

4.5 Graphentheoretische Fragestellungen . . . 38

Version vom 22. Juni 2021

1 Datentypen

Der Datentyp besagt . . .

• welchen Wertebereich die Daten haben,

• welche Operationen auf den Daten zul¨assig sind.

1.1 Einfache Datentypen

Ein einfacher Datentyp (Synonyme: elementarer oder primitiver Datentyp) besteht aus einem einzelnen Wert.

In Python sind das (unter anderem):

• ganze Zahlen (integer): +, -, *, //, . . .

• Gleitkommazahlen (float): +, -, *, /, . . .

• Wahrheitswerte (boolean): not, and, or

1.2 Zusammengesetzte Datentypen

Zusammengesetzte Datentypen sind Zusammenfassungen (Datenstrukturen) aus einfa- chen Datentypen.

Im folgenden werden einige der in Python bereits vorhandenen zusammengesetzten Da- tentypen wiederholt.

Listen

Eine Liste ist eine geordnete Menge von null oder mehr Referenzen auf Python-Daten.

0 1 2 . . . . . . . . . . . . n−1

Abbildung 1.1: Modell einer Liste

Operation Effizienz

L[i] O(1)

L[3]=25 O(1)

L.append(item) O(1)

L.pop() O(1)

L.pop(i) O(n)

L[i:j] O(k)

L1+L2 O(k)

L.del(i) O(n)

L.insert(i,item) O(n)

x in L O(n)

for item in L O(n)

L.reverse O(n)

L.sort() O(nlogn)

Tabelle 1.1: Effizienz einiger Funktionen und Methoden f¨ur Listen

Tupel

Tupel sind unver¨anderliche Listen. Das heisst, dass von den Listenmethoden nur diejenigen anwendbar sind, welche das Tupel und ihre Elemente nicht modifizieren.

Bei der literalen Eingabe werden Tupel durch runde anstelle von eckigen Klammern de- finiert.

Zeichenketten

Zeichenketten (strings) sind Folgen aus null oder mehr Symbolen (Zeichen).

Bei der literalen Eingabe werden Zeichenketten durch einfache oder doppelte Anf¨uhrungszeichen gekennzeichnet.

Strings verhalten sich wie Tupel, deren Elemente die einzelnen Symbole sind. Die Metho- den zum Sortieren, L¨oschen oder Einf¨ugen sind daher nicht unmittelbar anwendbar.

Sets

Eine Menge ist eine ungeordnete Sammlung unver¨anderlicher Python-Objekte ohne Du- plikate. Die Mengen werden literal als komma-separierte Listen dargestellt, die von ge- schweiften Klammern eingeschlossen sind.

A = {1, ’Hallo’, 3.14, True}

B = set() (die leere Menge)

Beispiel Erkl¨arung

x in M Ist x ein Element von M?

len(M) Anzahl der Elemente in der Menge M A | B Vereinigungsmenge A∪B

A & B Schnittmenge A∩B A - B Mengendifferenz A\B A <= B Teilmenge A⊂B?

Tabelle 1.2: Operationen f¨ur Sets

Beispiel Erkl¨arung

A.union(B) A∪B A.intersection(B) A∩B A.difference(B) A\B A.issubset(B) A⊂B

A.add(item) F¨uge item zur Menge A hinzu.

A.remove(item) Entferneitem aus MengeA.

A.pop() Entferne beliebiges Element aus MengeA.

A.clear() Entferne alle Element aus Menge A.

Tabelle 1.3: Methoden f¨ur Sets Dictionaries (Assoziative Listen)

Eine Dictionary ist eine ungeordnete Sammlung von Schl¨ussel-Wert Paaren (key-value pair).

Dictionaries werden literal als komma-separierte Listen der Schl¨ussel-Wert-Paare darge- stellt, die von geschweiften Klammern eingeschlossen sind. Die Schl¨ussel-Wert Paare selbst werden durch einen Doppelpunkt getrennt.

Operation Effizienz

D[key] O(1)

D[key]=25 O(1) D.del(key) O(1) key in D O(1) for key in D O(n) D.copy() O(n)

Tabelle 1.4: Effizienz einiger Funktionen und Methoden f¨ur Dictionaries

1.3 Abstrakte Datentypen

Schnittstellen

Ahnlich verh¨¨ alt es sich beim Informatikanwender. Er muss nichts ¨uber Variablen, Schleifen oder Unicode wissen, um Dokumente zu schreiben, Mails zu verschicken oder im Web zu surfen (auch wenn es hilfreich ist).

In beiden Beispielen muss der Benutzer (Client) einer Abstraktion nichts von den darunter liegenden Details wissen, so lange er die Schnittstelle (Steuerrad, Bremspedal, Browser, Textverarbeitungsprogramm) versteht und bedienen kann.

Im Zusammenhang mit Datentypen wollen wir den Begriff der Schnittstelle noch weiter einschr¨anken:

Unter einer Schnittstelle versteht man eine Beschreibung aller Operationen (Methoden), mit denen auf eine Sammlung von Daten zugegriffen werden kann.

In vielen F¨allen w¨unschen sich Programmierer f¨ur eine Aufgabe eine massgeschneiderte Datenstruktur, die das L¨osen der Aufgabe m¨oglichst einfach macht.

Daher schafft man sogenannte Abstrakte Datentypen (abstract data type, ADT), welche eine logische Sicht auf die Daten erlaubt, die nicht unbedingt mit der physikalischen Darstellung der Daten ¨ubereinstimmen muss.

Ein abstrakter Datentyp (ADT) ist eine Sammlung von Objekten sowie eine Beschreibung der zul¨assigen Operationen, die darauf zugreifen.

Kapselung und Information Hiding

Bei der Beschreibung der Operationen eines abstrakten Datentyps sind zwei Dinge we- sentlich:

• Kapselung:Der Zugriff auf die Operation darf nur ¨uber die Abstraktion der Schnitt- stelle erfolgen.

• Information Hiding: Die Details der Implementierung (Variablen) m¨ussen vor dem Client verborgen werden. Bei einer ¨Anderung der Implementierung k¨onnten diesese Details nicht mehr g¨ultig sein und zu Fehlern f¨uhren.

Durch stabile Schnittstellen k¨onnen komplexe Softwaresysteme verbessert werden, ohne das gesamte System ver¨andern zu m¨ussen.

Implementation Client Schnittstelle

Operationen

Abbildung 1.2: Abstrakter Datentyp

2 Lineare Datenstrukturen

Uberblick¨

In linearen Datenstrukturen lassen sich die Daten in einer Weise repr¨asentieren, dass, ausgenommen vom letzten Element, jedes Element einen eindeutiger Nachfolger besitzt.

Element 1 Element 2 . . . Elementn

Die jeweils m¨oglichen Operationen definieren den spezifischen Typ.

2.1 Stacks (Stapel)

• Last In First Out (LIFO)

• Hinzuf¨ugen (push) und Entfernen (pop) erfolgen von derselben Seite

• Anwendung: Browser-History; Undo-Funktion von Anwendungsprogammen; Aus- wertung von Postifix-Ausdr¨ucken und ¨Ubersetzung von Infix-Ausdr¨ucken in Postfix- Form; Backtracking-Algorithmen; Verwaltung des Arbeitsspeichers von Computern

pushpop

Basis

Abbildung 2.1: Modell eines Stacks

Python-Implementation eines Stacks

Die Klasse Stack wird als Python-Liste implementiert. Die Methoden sind:

• Der Konstruktor Stack()erzeugt einen leeren Stack.

• push(item) legt item auf den Stack ab.

• pop() entfernt das oberste Element vom Stack und liefert es als Wert zur¨uck.

• peek()liefert das oberste Element des Stacks als Wert zur¨uck ohne es zu entfernen.

• isEmpty()liefertTruebzw.Falseals R¨uckgabewert, wenn der Stack leer bzw. nicht-

Der Quellcode

1 class Stack:

2

3 def __init__(self):

4 self.items = []

5

6 def push(self, item):

7 self.items.append(item)

8

9 def pop(self):

10 return self.items.pop()

11

12 def peek(self):

13 return self.items[-1]

14

15 def size(self):

16 return len(self.items)

Anwendung

Schreibe eine Funktion check(string), das einen String als Argument entgegen nimmt und ¨uberpr¨uft, ob die (runden) Klammern in diesem String korrekt gesetzt sind.

L¨osungsidee: Erzeuge einen leeren Stack s. Durchlaufe die Zeichenkette zeichenweise. Ist das Symbol eine ¨offnende Klammer, kommt es auf den Stack. Ist das Symbol eine schlies- senden Klammer, so entferne das oberste Stackelement. ¨Uberpr¨ufe, ob diese Operation auf einem leeren Stack ausgef¨uhrt wird. Wenn ja, gibt es mehr schliessende als ¨offende Klammern und der Ausdruck ist falsch. Nachdem der gesamte String verarbeitet wurde, ist noch zu pr¨ufen, ob noch Klammern auf dem Stack liegen. Wenn ja, dann gibt es mehr

¨offnende als schliessende Klammern und der Ausdruck ist falsch.

1 from stack import Stack

2

3 def check(string):

4

5 s = Stack()

6

7 for symbol in string:

8 if symbol == ’(’:

9 s.push(symbol)

10 elif symbol == ’)’:

11 if s.isEmpty():

12 return False

13 else:

14 s.pop()

15 else: # andere Symbole ignorieren

16 pass

17

18 return s.size() == 0 # True, falls Stack leer

2.2 Queues (Warteschlangen)

• First In First Out (FIFO)

• Hinzuf¨ugen (enqueue) und Entfernen (dequeue) erfolgen an entgegengesetzten Seiten

• Beispiele: Druckerwarteschlangen; Warteschlange von Computerprozessen, Simula- tionen (Strassenverkehr, Supermarkt, . . . )

enqueue dequeue

Abbildung 2.2: Modell einer Queue

Python-Implementation einer Queue

Die Klasse Queue soll als Python-Liste implementiert werden. Die Methoden sind:

• Der Konstruktor Queue()erzeugt eine leere Queue.

• enqueue(item) f¨ugt item am Ende der Queue ein.

• dequeue() entfernt das vorderste Element der Queue.

• isEmpty()liefertTruebzw.Falseals R¨uckgabewert, wenn die Queue leer bzw. nicht- leer ist.

• s.size() liefert die Anzahl Elemente der Queue zur¨uck.

Anwendung: Gesellschaftsspiel-Simulation

Bei dem in den USA verbreiteten KinderspielHot Potato geht es darum, dass die im Kreis sitzenden Teilnehmer einen Gegenstand (die heisse Kartoffel) weiterreichen. Derjenige, der nach Ablauf einer (zuf¨alligen) Frist, den Gegenstand in der Hand h¨alt, scheidet aus.

Schreibe eine FunktionhotPotatoe(namelist, k) mit einer Namensliste und einer gan- zen Zahl k als Argument.

Die Namen werden in eine Warteschlange eingef¨ullt. In jeder Runde wird die Warteschlan- ge um k Positionen zyklisch vertauscht und derjenige Name, der danach ganz vorne in der Schlange steht, entfernt. Am Ende gibt das Programm den Namen der Person aus, die alle Runden ¨uberstanden hat.

1 from random import randint

2 from myqueue import Queue

3

4 L = [’Bill’, ’Sue’, ’Kent’, ’Jane’, ’Brad’, ’Kim’]

5 q = Queue()

6

7 for name in L:

8 q.enqueue(name)

9

10 while q.size() > 1:

11 n = q.size()-1

12 # Elemente zyklisch verschieben

13 for i in range(0, randint(0, n)):

14 q.enqueue(q.dequeue())

15

16 q.dequeue()

17

18 print(q)

2.3 Deques (zweiseitige Warteschlangen)

Deque [ausgesprochen

”Deck“] steht f¨ur Double-ended queue.

addRear removeFront

removeRear addFront

Abbildung 2.3: Modell einer Deque

• Hinzuf¨ugen (add) und Entfernen (remove) erfolgen jeweils an beiden Seiten

• Anwendungen: Textsuche mittels regul¨arer Ausdr¨ucke, nichtdeterministische endli- che Automaten

Python-Implementation einer Deque

Die KlasseDeque soll auf der Basis einer Python-Liste implementiert werden. Die Metho- den sind:

• Der Konstruktor Deque()erzeugt eine leere Deque.

• addFront(item) f¨ugt itemam vorderen Ende ein.

• addRear(item) f¨ugt item am hinteren Ende ein.

• removeFront() entfernt das Element vom vorderen Ende.

• removeRear(item)entfernt das Element vom hinteren Ende.

• isEmpty() liefert True bzw. False, wenn die Deque leer bzw. nichtleer ist.

• s.size() liefert die Anzahl Elemente der Queue zur¨uck.

Anwendung: Palindrome erkennen

• Ein Palindrom-Kandidat wird zeichenweise in eine Deque

”geschoben“.

• So lange die Deque mehr als ein Element besitzt, wird von beiden Seiten jeweils ein Element entfernt. Sind die beiden Elemente verschieden, liefert die Funktion den Wert False zur¨uck.

• Hat die Deque nur noch ein Element oder ist sie leer, muss es sich um ein Palindrom handeln und die Funktion liefert True zur¨uck.

1 from deque import Deque

2

3 def palinChecker(text):

4

5 d = Deque()

6

7 for character in text:

8 d.addFront(character)

9

10 while d.size() > 1:

11 if d.removeFront() != d.removeRear():

12 return False

13

14 return True

15

16 # Pr¨ufe, ob 11**0, 11**1, 11**2, ... 11**6 Palindrome sind:

17 for i in range(0, 6):

18 print(11**i, palinChecker(str(11**i)))

2.4 Linked Lists (einfach verkettete Listen)

7 9 5 8 2 9

Abbildung 2.4: Modell einer Linked List

• Die einfach verkettete Liste wird durch den ersten Zeiger links repr¨asentiert.

• Dieser Zeiger zeigt auf den ersten Knoten, der wiederum aus einer Zeigevariablen (Punkt) und einem Datenfeld besteht.

• Der Zeiger eines Knotens zeigt entweder auf einen weiteren Knoten oder auf den Nullwert, der das Ende der Liste kennzeichnet (Quadrat mit Kreuz).

Die Klasse Node

Die Knoten werden als Objekte der Klasse Node implementiert.

Node

data: <any>

next: Node

Node(data: <any>) getData(): <any>

getNext(): Node

setData(newData: <any>) getNext(newNext: Node)

1 class Node:

2

3 def __init__(self, data):

4 self.data = data

5 self.next = None

6

7 def getData(self):

8 return self.data

9

10 def getNext(self):

11 return self.next

12

13 def setData(self, newData):

14 self.data = newData

15

16 def setNext(self, newNext):

17 self.next = newNext

Die Klasse Linkedlist

Linkedlist head: Node

add(item: <any>) isEmpty(): bool length(): int

search(item: <any>) bool remove(item: <any>)

Der Konstruktor

Es wird eine Instanzvariable head erzeugt der mit None initialisiert wird. Sobald sp¨ater der erste Knoten hinzugef¨ugt wird, ersetzt man Node durch die Adresse des Knotens.

head

1 from node import Node

2

3 class Linkedlist:

4

5 def __init__(self):

6 self.head = None

Die Methode isEmpty()

1 def isEmpty(self):

2 return self.head == None

Die Methode add(item)

M¨ochte man einer einfach verketteten Liste das Element

”5“ hinzuf¨ugen, so erfolgt dies effizient am Listenkopf.

(1) Erzeuge einen neuen

”isolierten“ Knoten mit dem Wert 5.

(2) Kopiere den Wert dernext-Variable des Listenkopfs in dienext-Variable des neuen Knotens.

(3) Der Variablenextdes Listenkopfs wird die Adresse des neuen Knotens zugewiesen.

head

(1)

8 2 9

(2) (2)

5

(3)

1 def add(self, data):

2 temp = Node(data)

3 temp.setNext(self.head)

4 self.head = temp

Die Methode length()

Man beginnt bei head und geht dann mit einerwhile-Schleife von Referenz zu Referenz, bis man mit Nonedas Ende der Liste erreicht hat.

Erh¨oht man bei jeder Iteration einen Z¨ahler um 1, so erh¨alt man am Ende die L¨ange der Datenstruktur.

1 def length(self):

2 count = 0

3 node = self.head

4 while node != None:

5 count += 1

6 node = node.getNext()

7 return count

Die Methode search(item)

Diese Methode ist ¨ahnlich wie length aufgebaut. Zus¨atzlich ¨uberpr¨uft man bei jedem Schleifendurchlauf, ob sich item im Knoten befindet. Wenn ja, liefert die MethodeTrue als R¨uckgabewert.

Erricht die Schleife das Ende der einfach verketteten Liste, ohneitemgefunden zu haben, so liefert die Methode False zur¨uck.

1 def search(self, item):

2 node = self.head

3 while node != None:

4 if node.getData() == item:

5 return True

6 node = node.getNext()

7 return False

Die Methode remove(item)

Um den Knoten mit dem Datenwert item aus der Linkedlist zu entfernen muss man ihn wie in search(item) zuerst finden. Das Problem dabei ist, dass die Referenz auf den zu l¨oschenden Knoten beim Erreichen des gesuchten Knotes bereits ¨ubersprungen wurde;

also nicht mehr zur Verf¨ugung steht, um auf den (allf¨alligen) ¨ubern¨achsten Knoten zu zeigen.

current previous

Die L¨osung besteht darin, beim Durchlaufen der einfach verketteten Liste jeweils eine Referenz auf den aktuellenund den davor liegenden Knoten zu speichern.

Man beachte, dass der Listenkopf head keinen Vorg¨anger hat, weshalb man seinen Vor- g¨angerknoten mit None initialisieren sollte.

Weiter gilt es zu beachten, dass das Entfernen des ersten Knotens getrennt von dem Entfernen eines

”inneren“ Knotens behandelt werden muss.

Muss man auch das Entfernen des letzten Knotens separat behandeln?

1 def remove(self, item):

2 prevNode = None

3 currNode = self.head

4 while currNode != None:

5 if currNode.getData() == item:

6 if prevNode == None:

7 head = currNode.getNext()

8 else:

9 prevNode.setNext(currNode.getNext())

10

11 prevNode = currNode

12 currNode = currNode.getNext()

13 return False

Bemerkung

Das Entfernen eines Elements, hinterl¨asst einen verwaisten Knoten. In vielen Program- miersprachen muss der Programmierer dieses Objekt explizit mit einem sogenannten De- struktor l¨oschen, wenn er nicht Speicherplatz verschwenden will.

Auch Python kennt einedel() Methode f¨ur Objekte. Diese wird in der Regel aber nicht ben¨otigt, da ein spezieller Mechanismus, der Garbage Collection genannt wird, von Zeit zu Zeit daf¨ur sorgt, dass nicht mehr verwendete Speicherbereiche freigegeben werden.

3 B¨ aume (Trees)

Uberblick¨

B¨aume stellen eine fundamentale Abstraktion in der Informatik dar und eignen sich dazu, hierachische Strukturen abzubilden.

Informatiker stellen die Wurzel eines Baums oben und die Bl¨atter unten dar!

3.1 Beispiele

Unix-Dateisystem

/

bin dev etc home lib mnt proc root sbin tmp usr

cp ksh ls pwd passwd bin

Andere Betriebssysteme haben ebenfalls eine mehr oder weniger feste Verzeichnisstruktur.

HTML-Dokumente

1 <html>

2 <head>

3 <title>Simple HTML-Document</title>

4 </head>

5 <body>

6 <h1>Caption</h1>

7 <p>Paragraph</p>

8 <ul>

9 <li>Item 1</li>

10 <li>Item 2</li>

11 </ul>

12 </body>

13 </html>

html

head

title

body

h1 p ul

Syntaxb¨aume (Parse Trees)

+

∗ 3

2 7

3.2 Begriffe

Knoten (node): Baustein eines Baums, der die Daten enth¨alt.

Kante (edge): Eine Kante verbindet zwei Knoten.

Wurzel (root): Der oberste Knoten eines Baums.

Kind (child): Ein Knoten, der durch eine Kante mit dem unmittelbar dar¨uber liegenden Knoten verbunden ist.

Eltern (parent): Ein Knoten, der durch eine Kante mit einem unmittelbar darunter lie- genden Knoten verbunden ist.

Geschwister (sibling): Menge der Knoten, die Kinder des gleichen Elternknotens sind.

Pfad (path): Eine geordnete Folge von Knoten, die durch Kanten verbunden sind.

Blatt (leaf node): Ein Knoten, der keine Kindknoten hat.

Innerer Knoten (interior node): Ein Knoten, der mindestens ein Kind hat.

Teilbaum (subtree): Die Menge der Knoten und Kanten, die aus einem Elternknoten und all seinen Kindern und Kindeskindern besteht.

Tiefe eines Knotens (depth, level):Die Anzahl der Kanten auf dem Pfad vom Wurzelkno- ten zum betreffenden Knoten. Der Wurzelknoten hat die Tiefe 0.

H¨ohe eines Baums (height): Das Maximum der Menge aller Knotenlevels.

Bin¨arbaum (binary tree): Ein Baum, dessen Knoten maximal zwei Kinder haben.

Wald (forest): Eine Menge von B¨aumen.

Definition eines Baums (rekursiv)

Ein Baum ist entweder leer oder besteht aus einer Wurzel und null oder mehr Teilb¨aumen, die jeweils selber ein Baum sind. Die Wurzel jedes Teilbaums ist mit der Wurzel des Elternbaums durch eine Kante verbunden.

Bemerkung

In der Informatik haben B¨aume normalerweise gerichtete Kanten. In der Graphentheorie (einem Teilgebiet der Mathematik) k¨onnen B¨aume aber auch ungerichtet sein.

3.3 Typologie

Bin¨arbaum (binary tree)

A

B C

D E

F G

H

Ein Baum, bei dem jeder innere Knoten maximal zwei Bl¨atter hat.

Entarteter Bin¨arbaum (degenerated binary tree)

A

B

C

D

Bei einem entarteteten Baum hat jeder innere Knoten genau ein Kind. Also handelt es sich um einen

”Un¨arbaum“; d. h. um eine lineare Datenstruktur.

Voller Bin¨arbaum (full binary tree)

A

B C

D E

F G

H I

Jeder innere Knoten hat entweder null oder zwei Bl¨atter. Das Adjektiv

”voll“ bezieht sich darauf, dass alle inneren Knoten mit zwei Knoten oder Bl¨attern aufgef¨ullt“ sind.

Balancierter Bin¨arbaum (balanced binary tree)

A

B C

D E F G

H I J K

Ein balancierter Bin¨arbaum ist ein Bin¨arbaum, bei dem sich die Tiefe der Bl¨atter h¨ochstens um 1 unterscheiden.

Vollst¨andiger Bin¨arbaum (complete binary tree)

A

B C

D E F G

H I J K L

Ein vollst¨andiger Bin¨arbaum ist ein balancierter Bin¨arbaum, bei dem alle Bl¨atter mit der Tiefen links von denjenigen mit der Tiefe n−1 stehen.

Perfekter Bin¨arbaum (perfect binary tree)

A

B C

D E F G

H I J K L M N O

Ein perfekter Bin¨arbaum ist ein voller Bin¨arbaum, dessen Bl¨atter dieselbe Tiefe haben.

n-¨are B¨aume

Entsprechende Baumstrukturen k¨onnen auch f¨ur mehr als zwei Verzweigungen definiert werden. Im Fall von drei Verzweigungen spricht man von terner¨aren B¨aumen (ternary trees); im Fall von n Verzweigungen spricht man von n-¨aren B¨aumen (n-ary trees).

M

T F P

3.4 Darstellung bin¨ arer B¨ aume als verschachtelte Listen

tree=[’U’,[’X’,[’A’,[],[’S’,[],[]]],[]],[’M’,[],[]]]

Repr¨asentation als Baum:

U

X M

A S

• Jeder Subbaum besteht aus drei Teilen:

[Wurzel, linker Knoten, rechter Knoten]

• Fehlende Kinder werden durch leere Listen gekennzeichnet.

3.5 Darstellung bin¨ arer B¨ aume durch Knoten und Referenzen

Die Datenstuktur wird analog zur einfach verketteten Liste definiert. Dabei gehen von der Wurzel eines (Sub)Baums jeweils zwei Referenzen aus. Diese Referenzen k¨onnen ins Nichts (None) oder auf weitere (Sub)B¨aume verweisen.

1 class BinaryTree:

2

3 def __init__(self, value):

4 self.value = value

5 self.leftChild = None

6 self.rightChild = None

Speichertechnisch l¨asst sich dies so visualisieren:

Bei Adresse 07 (Zeile/Kolonne) beginnt eine Bin¨arbaumstruktur aus drei aufeinanderfol- genden Zellen: key,leftChild,rightChild.

Die Speicherzelle00wird nicht verwendet, damit dieser Adresswert als leerer Zeiger (NULL oder None) verwendet werden kann. Grau hinterlegte Zellen sind besetzt.

0 1 2 3 4 5 6 7 8 9 A B C D E F 0

1 2 3

’B’ 2C 11

’W’ 00 03

’C’ 00 00

’Q’ 00 00

Knoten einf¨ugen

1 def insertLeft(self, value):

2 if self.leftChild == None:

3 self.leftChild = BinaryTree(value)

4 else:

5 tmp = BinaryTree(value)

6 tmp.leftChild = self.leftChild

7 self.leftChild = tmp

8

9 def insertRight(self, value):

10 if self.rightChild == None:

11 self.rightChild = BinaryTree(value)

12 else:

13 tmp = BinaryTree(value)

14 tmp.rightChild = self.rightChild

15 self.rightChild = tmp

Knoten abfragen und ver¨andern

1 def getRootVal(self):

2 return self.value

3

4 def setRootVal(self, value):

5 self.value = value

6

7 def getLeftChild(self):

8 return self.leftChild

9

10 def getRightChild(self):

11 return self.rightChild

Maximale Tiefe eines Baumes bestimmen

1 def maxDepth(self):

2 if self.leftChild == None and self.rightChild == None:

3 return 1

4 elif self.leftChild == None:

5 return 1 + self.rightChild.maxDepth()

6 elif self.rightChild == None:

7 return 1 + self.leftChild.maxDepth()

8 else:

9 return 1 + max(self.leftChild.maxDepth(),

10 self.rightChild.maxDepth())

Traversierung eines Baumes

Traversierung: systematisches Durchlaufen aller Knoten eines Baumes

U

Y M

A E J

S C P

Preorder

1 def preorder(self):

2 yield self.value

3 if self.leftChild != None:

4 yield from self.leftChild.preorder()

5 if self.rightChild != None:

6 yield from self.rightChild.preorder()

Inorder

1 def inorder(self):

2 if self.leftChild != None:

3 yield from self.leftChild.inorder()

4 yield self.value

5 if self.rightChild != None:

6 yield from self.rightChild.inorder()

Postorder

1 def postorder(self):

2 if self.leftChild != None:

3 yield from self.leftChild.postorder()

4 if self.rightChild != None:

5 yield from self.rightChild.postorder()

6 yield self.value

3.6 Darstellung vollst¨ andiger Bin¨ arb¨ aume als Heap

Heap:Darstellung eines vollst¨andigen Bin¨arbaums als Liste M D T Z Q B W K N E U L

0 1 2 3 4 5 6 7 8 9 10 11 12

M

D T

Z Q B W

K N E U L

Elternknoten des Kindknotens mit Indexi: bi/2c linker Kindknoten des Elternknotens mit Index i: 2i rechter Kindknoten des Elternknotens mit Index i: 2i+ 1 Min- und Max-Heaps

Ein Min-Heap ist ein Heap, bei dem jeder Kindknoten einen Schl¨ussel hat, der gr¨osser (oder gleich) wie der seines Vaters ist. Max-Heaps werden analog definiert.

5

9 7

11 18 10 13

21 19 25 31 14

Min-Heap-Eigeschaft: Der kleinste Schl¨ussel ist in der Wurzel.

1 class MinHeap:

2

3 def __init__(self):

4 self.heap = [None]

5 self.size = 0

6

7 def __str__(self):

8 return str(self.heap)

9

10 def swap(self, i, j):

11 self.heap[j],self.heap[i] \

12 = self.heap[i],self.heap[j]

Schl¨ussel hinzuf¨ugen

Ein neuer Schl¨ussel (3) wird an die letzte Position des Heaps gesetzt und so lange

”hoch- getrieben“ (swim), bis die Min-Heap-Eigenschaft wieder hergestellt ist.

5

9 7

11 18 10 13

21 19 25 31 14

1 def insert(self, item):

2 self.heap.append(item)

3 self.size += 1

4 self.swim(self.size)

5

6 def swim(self, i):

7 while i // 2 > 0:

8 if self.heap[i] < self.heap[i//2]:

9 self.swap(i, i//2)

10 i = i // 2

Schl¨ussel an der Wurzel entfernen

Wird ein Schl¨ussel an der Wurzel des Baums entfernt, so r¨uckt der letzte Schl¨ussel im Baum (Heap) an diese Position nach. Danach wird dieser Schl¨ussel so lange

”herunterge- trieben“ (sink), bis die Min-Heap-Eigenschaft wieder hergestellt ist.

5

9 7

11 18 10 13

21 19 25 31 14

1 def delMin(self):

2 top = self.heap[1]

3 self.heap[1] = self.heap.pop()

4 self.size -= 1

5 self.sink(1)

6 return top

7

8 def sink(self, i):

9 while 2*i <= self.size:

10 j = self.minChild(i)

11 if self.heap[i] > self.heap[j]:

12 self.swap(i, j)

13 i = j

1 def minChild(self, i):

2 # falls der letzte Elternknoten nur ein Kind hat:

3 if 2*i+1 > self.size:

4 return 2*i

5 else:

6 if self.heap[2*i] < self.heap[2*i+1]:

7 return 2*i

8 else:

9 return 2*i+1

Einen Heap in einen Min-Heap verwandeln

Es gen¨ugt, alle Schl¨ussel mit einem Index kleiner als bn/2c (innere Knoten) so weit wie n¨otig

”sinken“ zu lassen.

25

21 31

18 19 10 11

14 7 5 13 9

1 def buildHeap(self, L):

2 self.heap = [None] + L[:]

3 self.size = len(L)

4 i = self.size//2

5 while i > 0:

6 self.sink(i)

7 i = i-1

4 Graphen

4.1 Begriffe

Einleitung

Graphen stellen eine Verallgemeinerung von B¨aumen dar. Die bei B¨aumen existierende Einschr¨ankung, dass – ausgenommen vom Wurzelknoten – jeder Kindknoten genau einen Elternknoten hat, entf¨allt bei den Graphen. Bei Graphen kann grunds¨atzlich jedes Objekt Beziehungen (Links, Kanten) zu jedem anderen Objekt haben. Damit lassen sich komplexe Strukturen wie Verkehrswege oder Beziehungen zwischen Personen modellieren.

Graph, Knoten, Kanten

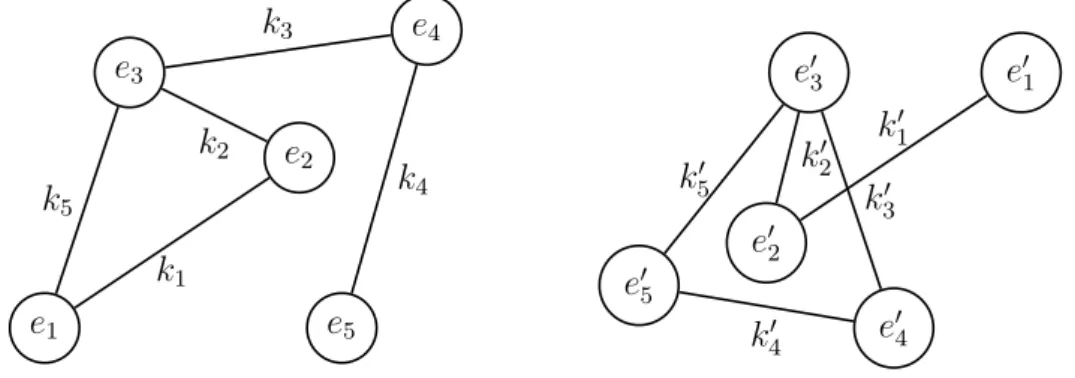
Ein GraphGist ein Diagramm, das aus einer endlichen Menge von Punkten besteht, von denen einige durch Kurvensegmente verbunden sind. Die Punkte nennt man Knoten, die Kurvensegmente Kanten.

e₁

e₂

e₃

e₄

e₅

k₁ k₂

k3

k4 k₅

Abbildung 4.1: Graph G₁

Schlinge

Eine Schlinge ist eine Kante, die einen Knoten mit sich selbst verbindet.

In G₁ istk₁ eine Schlinge.

Inzident

Eine Kante und ein Knoten sind inzident, wenn der Knoten ein Endpunkt der Kante ist.

In G₁ sind z. B. e₂ und k₄ inzident.

Isolierte Knoten

Ein Knoten heisst isoliert, wenn sie mit keiner Kante inzident ist.

In G₁ iste₅ isoliert.

Adjazent oder benachbart

Zwei Knoten heissen adjazent, wenn sie mit einer gemeinsamen Kante inzidieren. Zwei Kanten sind adjazent, wenn sie mit einem gemeinsamen Knoten inzidieren.

In G₁ sind z. B. die Kanten k₁ und k₂ adjazent (via e₂) oder die Knoten e₂ und e₄ (via k₄).

Kantenzug

In einem Graphen G mit den Knoten e₀ und e_n ist ein Kantenzug von e₀ nach e_n eine endliche, alternierende Folge von benachbarten Knoten und Kanten. Ein Kantenzug ist also von der Form e0k1e1k2. . . en−1knen.

e1

e₂

e₃

e4

e₅ k₁

k₂

k₃

k₄ k₅

k6

k₇

k₈

Abbildung 4.2: Graph G₂ In G2 iste1k1e2k2e3k7e5k6e2k2e3k3e4 ein Kantenzug.

Weg

In einem GraphenGmit den Knotene₀ und e_nist ein Weg vone₀ nache_n ein Kantenzug, der keine Kante mehrfach enth¨alt. Ein Weg hat also die Forme₀k₁e₁k₂. . . en−1k_ne_n, wobei alle k_j verschieden sind.

In G₂ iste₁k₅e₅k₇e₃k₂e₂k₆e₅k₈e₄ ein Weg.

Pfad

In einem Graphen G mit den Knoten e₀ und e_n ist ein Pfad von e₀ nach e_n ein Weg, der keinen Knoten wiederholt enth¨alt. Ein Pfad hat also die Form e₀k₁e₁k₂. . . en−1k_ne_n, wobei alle e_i und k_j verschieden sind.

Achtung: Der hier eingf¨uhrte Begriff des Pfades wird in der Literatur manchmal auchWeg genannt.

In G2 iste1k5e5k7e3k3e4 ein Pfad.

Zyklus

Ein Zyklus ist ein geschlossener Weg. Er hat also die Form e₀k₁e₁k₂. . . en−1k_ne₀, wobei alle kj verschieden sind.

In G₂ iste₁k₅e₅k₇e₃k₂e₂k₆e₅k₈e₄k₄e₁ ein Zyklus.

Kreis

Ein Kreis ist ein Zyklus, der keinen Knoten wiederholt aufweist, d. h. ein geschlossener Pfad. Er ist also von der Form e₀k₁e₁k₂e₂. . . en−1k_ne₀ wobei alle e_i und k_j verschieden sind.

In G₂ iste₁k₅e₅k₇e₃k₃e₄k₄e₁ ein Kreis.

Hinweis: Wenn es zwischen zwei Knoten nicht mehr als eine Kante gibt, dann gen¨ugt es zur Beschreibung von Kantenz¨ugen, Wegen, usw. die Folge der Knoten anzugeben.

4.2 Eigenschaften von Graphen

Isomorphe Graphen

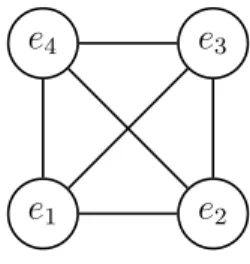
Zwei Graphen heissen zueinander isomorph, wenn eine kantentreue Bijektion zwischen den Knotenmengen existiert, d. h., dass zwei Knoten genau dann durch eine Kante miteinander verbunden sind, wenn dies auch f¨ur die Bildecken gilt.

e₁

e₂ e₃

e₄

e₅ k₁

k₂ k₃

k₄ k₅

e⁰₁

e⁰₂ e⁰₃

e⁰₄ e⁰₅

k⁰₁ k₂⁰

k₃⁰

k⁰₄ k₅⁰

Abbildung 4.3: Isomorphe Graphen G₃ und G⁰₃ kantentreue Bijektion G₃ →G⁰₃:

e₁ → e⁰₅, e₂ → e⁰₄, e₃ → e⁰₃, e₄ →e⁰₂,e₅ → e⁰₁

Ebener Graph

Ein Graph heisst eben, wenn die Knoten und Kanten in einer Ebene liegen und sich je zwei Kanten h¨ochstens in einem Knoten schneiden.

Der Graph G₃ ist eben, der Graph G⁰₃ nicht.

Ein Graph heisst pl¨attbar, wenn er isomorph zu einem ebenen Graphen ist.

Der Graph G⁰₃ ist pl¨attbar.

Zusammenh¨angender Graph

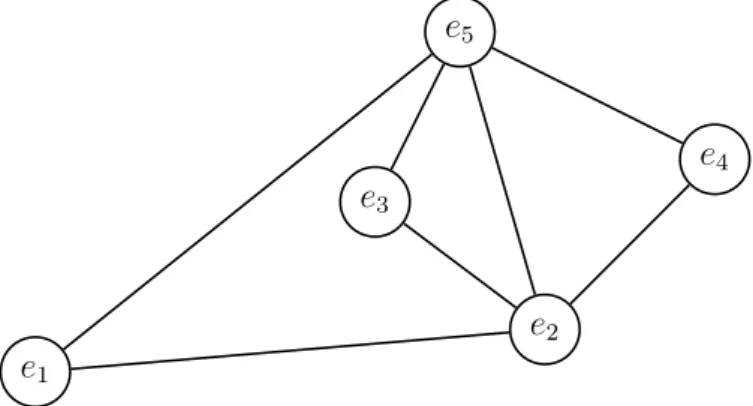
Ein Graph heisst zusammenh¨angend, wenn es zwischen je zwei Knoten e_i und e_j einen Weg gibt.

Die Graphen G₂, G₃, G⁰₃ sind zusammenh¨angend. G₁ ist es nicht.

Baum

Ein zusammenh¨angender Graph G heisst Baum, wenn er keine Zyklen enth¨alt. Knoten, die genau eine Kante haben, werden Bl¨atter des Baumes genannt. Alle anderen Knoten heissen innere Knoten.

e₁ e₂

e₃

e₄

e₅

e₆

k₁ k₂ k₃

k₄

k5

Abbildung 4.4: Baum G₄

• Es seien e_i und e_j zwei verschiedene Knoten eines Baumes B. Dann gibt es genau einen Weg von e_i nache_j.

• G sei ein Graph ohne Schlingen. Wenn es f¨ur jedes Paar von verschiedenen Knoten e_i und e_j von G genau einen Weg vone_i nach e_j gibt, dann ist Gein Baum.

• Wenn B ein Baum mit n Knoten ist, dann hat er genau n−1 Kanten.

Der Baum G₄ hat 6 Knoten und 5 Kanten

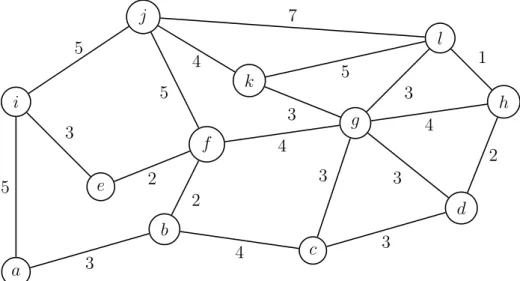
Vollst¨andiger Graph

Ein Graph heisstvollst¨andig, wenn jeder Knoten mit jedem anderen Knoten des Graphen durch eine Kante verbunden ist, also alle Knoten paarweise benachbart sind.

e₁ e₂

e₃ e₄

Abbildung 4.5: Vollst¨andiger Graph G₅ der Isomorphieklasse K₄

Knotenbewerteter Graph

Ein eckenbewerteter Graph ist ein Graph, bei dem jeder Knoten eine reelle Zahl zugeord- net ist.

Interpretiert man die Bewertung als Code f¨ur verschiedene Farben, dann wird ein eckenbewer- teter Graph zu einem eckengef¨arbten Graphen.

1

2

1

2 2

1

3

1 3

2

1

2

Abbildung 4.6: Knotenbewerteter Graph G₆

Kantenbewerteter Graph (gewichteter Graph)

Ein kantenbewerteter Graph ist ein Graph, bei dem jeder Kante eine reelle Zahl zugeordnet ist.

Kantenbewertungen treten h¨aufig in Optimierungsproblemen auf und werden dort meist als Kosten interpretiert (z. B. Fahrzeit oder Transportkosten in einem Strassennetz).

a

b

c

d e

f

g

h i

j

k

l

3 5

4 2

3

3 3

2 2

3 4

5

3 4

3 5 1

4

7

5

Abbildung 4.7: Kantenbewerteter Graph G₇

L¨ange eines Weges

In einem kantenbewerteten Graph bezeichnet man die Summe der Kantenbewertungen als L¨ange des Weges. Ohne Kantenbewertungen setzt man f¨ur jede Kante den Wert 1.

len(a, i, j, k) = 5 + 5 + 4 = 14

K¨urzester Weg vona nach k: len(a, b, f, g, k) = 12

4.3 S¨ atze ¨ uber Graphen

Grad (Inzidenzzahl)

Der Grad deg(e) oder dieInzidenzzahl eines Knotens e ist die Anzahl der Kanten, die zu e inzident sind. Isolierte Knoten haben den Grad 0.

e₁

e2

e₃

e₄

e5

Abbildung 4.8: Graph G₈ deg(e₃) = 1, deg(e₄) = 4, . . .

Grad eines Graphen

Der Grad eines Graphen ist die Summe der Grade aller seiner Knoten.

deg(G₈) = deg(e₁) + deg(e₂) +· · ·+ deg(e₅) = 2 + 3 + 1 + 4 + 2 = 12

Satz ¨uber den Grad eines Graphen

Ein GraphG mit den Knotene1, . . . ,en und den Kantenk1, . . . ,km hat einen Grad, der doppelt so gross ist wie die Anzahl m der Kanten:

deg(G) = deg(e₁) +· · ·+ deg(e_n) = 2m Folgerungen:

• Der Grad eines Graphen ist geradzahlig.

• Die Anzahl der Knoten von ungeradem Grad ist gerade.

Eulerzyklus

Ein Eulerzyklus in einem Graphen G ist ein Zyklus, der jede Kante vonG enth¨alt.

e₁

e₂ e₃

e₄ e₅

Abbildung 4.9: Graph G₉ mit Eulerzyklus In G₉ ist z. B. e₁e₂e₃e₅e₂e₄e₁ ein Eulerzyklus.

Satz vom Eulerzyklus

Ein Graph enth¨alt genau dann einen Eulerzyklus, wenn er zusammenh¨angend ist und jeder Knoten von geradem Grad ist.

Vergleiche mit dem Graphen G₉:

deg(e₁) = 2, deg(e₂) = 4, deg(e₃) = 2, deg(e₄) = 2, deg(e₅) = 4

Hamiltonkreis

Ein Hamiltonkreis in einem Graphen G ist ein Kreis, der jeden Knoten von Genth¨alt.

e₁ e₂

e3 e4

e₁ e₅

e3

e6

e₂ e₄

e₁ e₂

e3

e₄

e5

Abbildung 4.10: Graphen G₁₀, G₁₁ und G₁₂ G10 und G12 besitzen einen Hamilton-Kreis; G11 nicht.

Satz vom Hamiltonkreis

Hat in einem zusammenh¨angenden Graphen mit n > 2 Knoten jeder Knoten den Grad

≥ ⁿ₂, dann enth¨alt der Graph einen Hamiltonkreis.

Es handelt sich um eine hinreichende Bedingung.G₁₂erf¨ullt die Bedingung nicht, enth¨alt aber trotzdem einen Hamiltonkreis.

4.4 Repr¨ asentation von Graphen

Adjazenzmatrix

Ein Graph G mit den nummerierten Knoten e₁, e₂, . . . , e_n hat die Adjazenzmatrix A = (aij), aij ∈ R, i, j = 1, . . . , n, wenn aij gleich der Anzahl der Kanten ist, die ei mit ej

verbinden odera_ij das Gewicht der Kante k= (e_i, e_j) ist.

Adjazenzliste

Eine Adjazenzliste ist eine assoziative Liste, in der jedem Knoten (key) die Menge seiner Kanten (value) zugeordnet wird.

e1 e2

e₃ e₄

e5

Abbildung 4.11: Graph G₁₃ Adjazenzmatrix vonG₁₃:

e1 e2e3 e4 e5

e₁ e₂ e₃ e₄ e₅













0 1 1 0 0 1 0 1 0 0 1 1 0 1 0 0 0 1 1 0 0 0 0 0 0













Adjazenzliste von G₁₃: e₁:{e₂, e₃}

e₂:{e₁, e₃} e₃:{e₁, e₂} e₄:{e₃, e₄} e₅:{ }

Fl¨ache

Ein ebener Graph G teilt eine Ebene in endlich viele Gebiete auf, die als Fl¨achen vonG bezeichnet werden.

e₁

e2

e₃ e₄

e₅

e₆

f₁

f2

f₃

f₄

f₅

k1

k₂

k3

k₄ k₅

k₆

k7

k₈

k₉

Abbildung 4.12: Graph G₁₄

• Benachbarte Fl¨achen haben mindestens eine gemeinsame Randkante.

¨aussere Fl¨ache:f₅; innere Fl¨achen: f₁ bisf₄ k₇ ist Randkante von f₂ und f₃

k₉ ist Randkante von f₄ und f₅

Die Eulersche Polyederformel

Ist G ein zusammenh¨angender ebener Graph und bezeichnen e, k und f die Anzahl der Knoten (Ecken), Kanten bzw. Fl¨achen vonG, so gilte−k+f = 2.

Beweisskizze e−k+f =. . .

F¨uge xKanten ein, so dass jede innere Fl¨ache durch ein Dreieck begrenzt ist.

· · ·=e−(k+x) + (f +x) = e−k+f =. . .

Entferne von aussen sukzessive y Kanten, bis nur noch ein Baum ¨ubrig ist.

· · ·=e−(k−y) + (f−y) = e−k+f =. . .

Entferne von aussen sukzessive z Bl¨atter mit ihren Kanten, bis nur noch eine Ecke ¨ubrig ist.

· · ·= 1−0 + 1 = 2

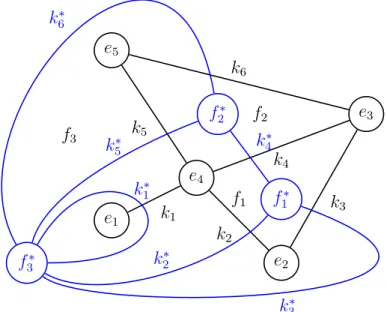
Dualer Graph

Es sei G ein ebener Graph. Der Graph G^∗ heisst zu G dual, wenn es zu jeder Fl¨ache f von Geinen entsprechenden Knotenf^∗ vonG^∗ und es zu jeder Kante k von Geinen ent- sprechenden Knoten k^∗ von G^∗ gibt, sodass die Kante k^∗ genau dann die entsprechenden Knotenf^∗ und g^∗ inG^∗ verbindet, wenn die Kantek zu den R¨andern der zwei Fl¨achen f und g geh¨ort.

e₁

e₂

e₃

e₄ e₅

f₁ f₂ f₃

k1

k₃ k₂

k₄ k6

k5

f₃^∗

f₁^∗ f₂^∗

k^∗₄ k₁^∗

k₂^∗

k₃^∗ k₅^∗

k₆^∗

Abbildung 4.13: Graph G₁₅ und der dazu duale Graph G^∗₁₅

p-partiter Graph

Es sei G ein Graph. Eine Zerlegung (Partition) der Knotenmenge E in p disjunkte Teil- mengen E₁, . . .E_p heisst p-partiter Graph, falls keine benachbarten Knoten in einem ge- meinsamen E_i liegen. (Anschaulich heisst das: Alle Kanten verlaufen zwischen diesen Teilmengen, keine innerhalb einer der Teilmengen.)

e₁ e₂ e₃ e₄

e₅ e₆ e₇

Abbildung 4.14: Der 2-partite Graph G₁₆

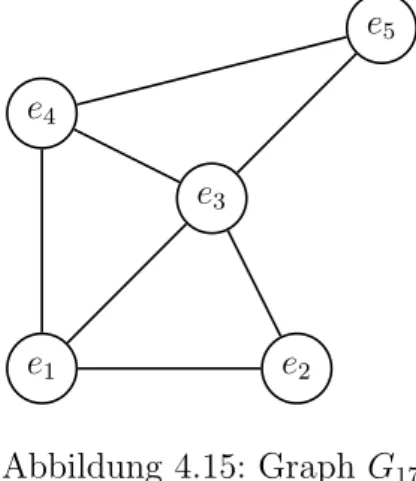
p-eckenf¨arbbar

Ein Graph G heisst p-eckenf¨arbbar, wenn seine Knoten mit h¨ochstens p Farben gef¨arbt werden k¨onnen, wobei benachbarte Knoten verschiedene Farben haben.

e₁ e₂

e₃ e₄

e₅

Abbildung 4.15: Graph G₁₇ G₁₇ ist 5-f¨arbbar (trivial)

G₁₇ ist 4-f¨arbbar G17 ist 3-f¨arbbar G₁₇ ist nicht 2-f¨arbbar

Chromatische Zahl

Die chromatische Zahl eines Graphen ist die kleinste Zahlp, f¨ur die der Graphp-eckenf¨arbbar ist.

Die chromatische Zahl von G₁₇ istp= 3.

Vierfarbensatz

Jeder planare Graph hat die chromatische Zahl ≤4. Folgerung: Jede Landkarte kann mit vier oder weniger Farben gef¨arbt werden.

4.5 Graphentheoretische Fragestellungen

Problem des Handlungsreisenden

Das ist die Aufgabe, in einem kantenbewerteten Graphen einen Hamiltonkreis zu finden, der die k¨urzeste L¨ange unter allen solchen Kreisen aufweist. (Man beachte: wenn der Graph nicht vollst¨andig ist, muss es keinen Hamiltonkreis geben.)

Chinesisches Brieftr¨agerproblem

Das ist die Aufgabe, in einem kantenbewerteten Graphen einen Kantenzug zu finden, der jede Kante des Graphen mindestens einmal enth¨alt, zum Anfangspunkt zur¨uckkehrt und die k¨urzeste L¨ange unter allen solchen Kantenz¨ugen aufweist. (Man beachte: wenn alle Knotengrade gerade sind, so ist der gesuchte Kantenzug ein Eulerzyklus.)

Tiefensuche

Die Tiefensuche (edepth-first search, DFS) ist ein Verfahren zum Suchen von Knoten in einem Graphen.

Die Suche beginnt in einem vorgegegenen Knoten. Handelt es sich um den gesuchten Knoten, so sind wir fertig.

Wenn nicht, markiere den Knoten als

”besucht“ und lege alle Knoten, die zu diesem Knoten adjazent sind, auf einem Stack ab.

Solange dieser Stack nicht leer ist, wird ein Element vom Stack entfernt und als

”be- sucht“ markiert. Ist es der gesuchte Knoten, sind wir fertig. Andernfalls werden alle zu diesem Knoten adjazenten und noch nicht als

”besucht“ markierten Knoten auf dem Stack abgelegt.

Sollte der Stack leer sein, bevor der Knoten gefunden wurde, befindet sich der Knoten nicht im Graphen oder er liegt nicht in der Zusammenhangskomponente des Startknotens.

Breitensuche

Die Breitensuche(breadh-first search, BFS) ist ein Verfahren zum Suchen von Knoten in einem Graphen.

Die Suche beginnt in einem vorgegegenen Knoten. Dieser wird in eine Warteschlange eingef¨ugt.

Danach wird ein Knoten der Warteschlange entnommen und als

”besucht“ markiert.

Wenn es der gesuchte Knoten ist, liefert der Algorithmus

”gefunden“ zur¨uck.

Wenn nicht, werden alle nocht nicht als

”besucht“ markierten Knoten der Warteschlange hinzugef¨ugt.

Auf diese Weise f¨ahrt man fort, bis der gesuchte Knoten gefunden worde oder die Warte- schlange leer ist. In diesem Fall befindet sich der Knoten nicht im Graphen oder er liegt nicht in der Zusammenhangskomponente des Startknotens.

Minimaler Spannbaum

Ein Spannbaum (spanning tree ist ein Teilgraph eines ungerichteten Graphen, der ein Baum ist und alle Knoten dieses Graphen enth¨alt.

Sind die Kanten des GraphenG= (V, E) gewichtet, so ist ein Spannbaumminimal, wenn es keinen anderen Spannbaum in G mit einer kleineren Kantensumme gibt.

Minimale Spannb¨aume lassen sich z. B. mit dem Algorithmus von Prim oder dem Algo- rithmus von Kruskal berechnen.

Matchingprobleme

Ein Graph bestehe aus einer Menge von Objekten (Knoten) und Informationen dar¨uber welche Objekte welchen anderen Objekten zugeordnet werden k¨onnen (Kanten).

Ein Matching ist eine Menge m¨oglicher Zuordnungen, die kein Objekt mehr als einmal enth¨alt.

• Wie findet man ein Matching mit einer maximalen Anzahl von Zuordnungen oder einem maximalen Gewicht, wenn die Zuordnungen durch Zahlen gewichtet werden.

• Gibt es ein Matching, das alle Objekte enth¨alt? (ein sogenanntperfektes Matching).

Maximale Fl¨usse

Ein Netzwerk N = (G, s, t, u) besteht aus einem gerichteten Graphen G = (V, E), einer Quelle s∈V, einer Senke t∈V (target) sowie einer Kapazit¨atsfunktion u:E →R⁺, die jeder Kante e∈E eine nichtnegative Kapazit¨at zuweist.

EinFlussist eine Funktionf, die jeder Kantene∈Eeines Netzwerks einen nichtnegativen Flusswertf(e) zuordnet und die Kapazit¨aten des Netzwerks nicht ¨ubersteigt:

• F¨ur alle e∈E gilt: f(e)≤u(e)

Maximale Clique

Ist G = (V, E) ein ungerichteter Graph ohne Mehrfachkanten, dann ist eine Clique ein Teilmengen von V⁰ ⊂ V, so dass es f¨ur alle v, w ∈ V⁰ eine Kante gibt, die v und w verbindet.

Eine Clique mit der Knotenmenge V⁰ ist maximalwenn es keine andere Clique mit einer gr¨osseren Knotenmenge gibt.

Das Entscheidungsproblem, ob ein Graph G eine maximale Clique mit mit mindestens k Knoten enth¨alt ist ein NP-schweres Problem. Es gibt als nach heutigem Wissensstand keinen polynomiellen Algorithmus um das Cliquenproblem zu l¨osen.

K¨urzeste Wege

Ist G = (V, E) ein kantengewichteter Graph und sind v, w ∈V, dann wird ein Pfad von u nachv gesucht, so dass die Summe der Kantengwichte ¨uber diesem Pfad minimal ist.

Eine L¨osung dieses Problems wird im Thema

”Netzwerke“ behandelt.