e ≈ 2 . 718281828 exp: → x 7→ e 4.5.1Exponentialfunktion e y e e e 4.5Exponential-undLogarithmusfunktion =0 =1 =( = e e x ) · e →−∞ e =( e )

4.5

4.5 Exponential- und Logarithmusfunktion

Eine der wichtigsten wenn nicht sogar die wichtigste Funktion in der Physik ist die Exponentialfunktion. Wir werden die Exponentialfunktion zusammen mit ihrer Umkehr- funktion, der Logarithmusfunktion, vorstellen und deren wichtigsten Eigenschaften dis- kutieren.

4.5.1 Exponentialfunktion

Die zur Beschreibung naturwissenschaftlicher Ph¨anomene wichtigste Funktion ist die Exponentialfunktion:

Definition:Die Funktion

exp :IR→IR mit x7→e^x

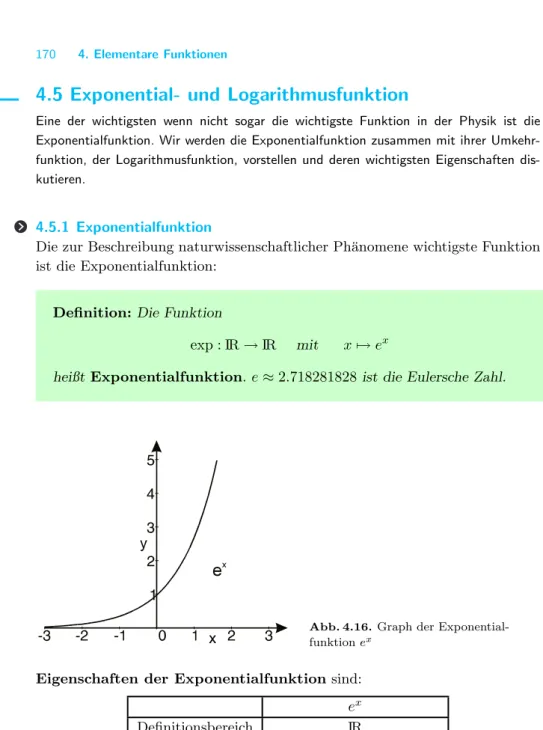
heißtExponentialfunktion.e≈2.718281828 ist die Eulersche Zahl.

Abb. 4.16.Graph der Exponential- funktione^x

Eigenschaften der Exponentialfunktionsind:

e^x Definitionsbereich IR

Wertebereich IR>0

Monotonie streng monoton wachsend Asymptote y= 0f¨urx→ −∞

F¨ur die Exponentialfunktion gelten dieRegeln:

(1) e⁰= 1 (2) e^x+y =e^x·e^y

(3) e^−x= (e^x)⁻¹, e^{n x}= (e^x)ⁿ

Beispiele 4.35:

1 Die Funktionen fa(x) = e^{a x} verhalten sich f¨ur a > 0 qualitativ wie die Exponentialfunktione^x: F¨ur x→ ∞ gehen sie gegen Unendlich und f¨ur x→ −∞gegen Null.

2 Die Funktionen f_a(x) = e^{−a x} verhalten sich f¨ur a > 0 qualitativ wie die Exponentialfunktion e^−x: F¨ur x→ ∞ gehen sie gegen Null und f¨ur x→ −∞gegen Unendlich.

Abb. 4.17. Graphen der Exponential- funktionen

Anwendungsbeispiel 4.36 (Auftreten der Exponentialfunktion).

1 Radioaktiver Zerfall: Beim Zerfall radioaktiver Atomkerne wird die Zahln(t)der zur Zeitt noch nicht zerfallenen Kerne durch das Zerfalls- gesetz

n(t) =n0e^{−λ t}

beschrieben. Dabei istn0 die Anzahl der zu Beginn (t= 0)vorhandenen Atomkerne undλ >0 die f¨ur den Zerfall typische Zerfallskonstante.

2 Entladung eines Plattenkondensators:Beim Entladen eines Platten- kondensators ist die Spannung am Kondensator U(t) zum Zeitpunkt t gegeben durch

U(t) =U0e^{−RC1 t}.

Dabei istU0die Kondensatorspannung zur Zeitt= 0undCdie Kapazit¨at, Rder Ohmsche Widerstand der Schaltung.

1 Anzahl der Atomkernen(t) 2 Spannung am KondensatorU(t)

4.5.2 Logarithmusfunktion

Die Exponentialfunktionexp :IR →IR>0 mit x7→ e^x ist auf dem gesamten Definitionsbereich streng monoton wachsend. Folglich existiert auf dem Wer- tebereich IR>0 die Umkehrfunktion.

Definition:Die Umkehrfunktion zur Exponentialfunktion wirdnat¨urli- cher Logarithmusgenannt:

ln :IR>0→IR mit x7→lnx.

Abb. 4.18. Graph der Logarithmusfunk- tionln(x)

Eigenschaften der Logarithmusfunktionsind:

ln(x) Definitionsbereich IR>0

Wertebereich IR

Nullstellen x0= 1

Monotonie streng monoton wachsend

Asymptoten x= 0

Rechenregeln f¨ur die Logarithmusfunktion. Die Rechenregeln ergeben sich direkt aus den Regeln der Exponentialfunktion. F¨urx, y∈IR>0 gilt

(1) ln(1) = 0

(2) ln (x·y) = lnx+ lny (3) ln(xⁿ) =nlnx

(4) ln(e^x) =x bzw. e^lnx=x

Anwendungsbeispiel 4.37 (Auftreten der Logarithmusfunktion).

1 Halbwertszeitτ einer radioaktiven Substanz:Unter der Halbwerts- zeit τ einer radioaktiven Substanz versteht man die Zeit, nach der die H¨alfte der radioaktiven Kerne zerfallen ist: n(τ) = ¹₂n0. Nach Beispiel 4.36¹ istn(t) =n₀e^{−λ t},also gilt f¨urt=τ :

1

2n0=n0e^{−λ τ}

Wir dividieren durch n0, wenden den Logarithmus an und l¨osen nach τ auf

ln1

2 = ln e^{−λ τ}

=−λ τ

,→τ =−1 λln1

2 =−1

λ(ln 1−ln 2). Die Halbwertszeitτ ergibt sich somit zu

τ= ¹_λln 2.

2 Abklingzeit eines Kondensators:Unter der Abklingzeitτa eines Kon- densators versteht man die Zeit, nach der die Spannung am Kondensator auf z.B. ¹_e-tel des maximalen Spannungswertes abgefallen ist: U(τa) =

1

eU₀. Nach Beispiel 4.36² istU(t) =U₀e^{−RC1 t}, also gilt f¨urt=τ_a: 1

eU0=U0e^{−RC1 τa} ,→ ln1

e = ln(e^{−RC1 τa}) =− 1 RCτa

Die Abklingzeit am Kondensatorτa ergibt sich somit zu τ_a=−RCln(¹_e) =RC.

1 Halbwertszeitτ 2 Abklingzeit am Kondensator

Beispiel 4.38.Wie lautet die Umkehrfunktion von

f :IR→IR_>0 mit x7→f(x) = 3e^2x−1?

Die Funktionf ist auf ihrem gesamten Definitionsbereich streng monoton wachsend, also existiert auf dem Wertebereich IR>0die Umkehrfunktion.

Wir setzen

y= 3e^2x−1 und l¨osen nach xauf:

1

3y=e^2x−1,→ln1

3y= 2x−1,→x=1 2(ln1

3y+ 1).

Nach Vertauschen der Variablen erhalten wir die Umkehrfunktion g:IR>0→IR mit x7→g(x) =1

2(ln1 3x+ 1).

Allgemeine Potenz- und Exponentialfunktion

Mit der Exponential- und Logarithmusfunktion ist man in der Lage, die allge- meine Potenz- und Exponentialfunktion zu definieren.

Definition:

(1) Die Funktion

f :IR>0→IR mit x7→f(x) =x^α:=e^αlnx heißt allgemeine Potenzfunktion.

(2) Die Funktion

f :IR→IR>0 mit x7→f(x) =a^x:=e^xlna (a >0) heißt allgemeine Exponentialfunktion.