Eliminating Dummy Elimination
JurgenGiesl 1
andAartMiddeldorp 2
1
ComputerSieneDepartment
UniversityofNewMexio,Albuquerque,NM87131,USA
giesls.unm.edu
2
InstituteofInformationSienesandEletronis
UniversityofTsukuba,Tsukuba305-8573,Japan
amiis.tsukuba.a.jp
Abstrat. This paperis onerned with methods that automatially
proveterminationoftermrewritesystems.Theaimofdummyelimina-
tion,amethodtoproveterminationintroduedbyFerreiraandZantema,
istotransformagivenrewritesystemintoarewritesystemwhosetermi-
nationiseasiertoprove.Weshowthatdummyeliminationissubsumed
bythemorereentdependenypairmethodofArtsandGiesl.Morepre-
isely,if dummyeliminationsueedsintransforminga rewritesystem
into aso-alled simplyterminatingrewrite system thenterminationof
thegivenrewritesystemanbediretlyprovedbythedependenypair
tehnique. Evenstronger, usingdummy elimination as apreproessing
step to the dependeny pair tehniquedoes not have any advantages
either. We show that to a large extent these results also hold for the
argumentlteringtransformationofKusakarietal.
1 Introdution
Traditional methods to prove termination of term rewrite systems are based
onsimpliationorders,likepolynomialinterpretations[6,12,17℄, thereursive
pathorder [7,14℄, andtheKnuth-Bendixorder [9,15℄. However,therestrition
tosimpliationordersrepresentsasigniantlimitationonthelassofrewrite
systemsthatanbeprovedterminating.Indeed,there arenumerousimportant
andinterestingrewritesystemswhiharenotsimply terminating,i.e.,theirter-
mination annot be proved by simpliation orders. Transformation methods
(e.g. [5,10,11,16,18,20{22℄)aim toprovetermination bytransformingagiven
term rewritesysteminto aterm rewritesystem whosetermination is easier to
prove.Thesuessofsuh methodshasbeenmeasuredbyhowwelltheytrans-
form non-simply terminating rewrite systems into simply terminating rewrite
systems,sinesimplyterminatingsystemsweretheonlyoneswheretermination
ouldbeestablishedautomatially.
Inreentyears,thedependenypairtehniqueofArtsandGiesl[1,2℄emerged
as themostpowerfulautomatimethodforprovingterminationofrewritesys-
tems.Foranygivenrewritesystem,thistehniquegeneratesasetofonstraints
?
Proeedings ofthe17thInternationalConfereneonAutomated Dedution(CADE-
17),Pittsburgh,PA,USA,LNAI1831,pages309-323,Springer-Verlag,2000.
power of traditional termination proving methods has been inreased signi-
antly,i.e., thelass ofsystemswhere termination isprovablemehaniallyby
thedependenypairtehniqueismuhlargerthanthelassofsimplyterminat-
ing systems. Inlight of this development,it is no longer suÆient to base the
laim that apartiulartransformation method is suessfulonthe fat that it
maytransformnon-simplyterminatingrewritesystemsintosimplyterminating
ones.Inthispaperweomparetwotransformationmethods,dummyelimination
[11℄ and the argument ltering transformation [16℄,with the dependeny pair
tehnique.Withrespetto dummyeliminationweobtainthefollowingresults:
1. If dummy elimination transforms a given rewrite system R into a simply
terminatingrewritesystemR 0
,thentheterminationofRanalsobeproved
bythemostbasiversionofthedependenypairtehnique.
2. IfdummyeliminationtransformsagivenrewritesystemRintoaDPsimply
terminating rewritesystemR 0
,i.e., theterminationofR 0
anbeprovedby
asimpliation order in ombination with thedependeny pairtehnique,
thenRisalsoDPsimplyterminating.
These resultsareonstrutivein thesense that theonstrutionsin theproofs
aresolelybasedontheterminationproofofR 0
.Thisshowsthatprovingtermi-
nation of R diretlyby dependeny pairsis nevermore diÆult than proving
terminationof R 0
. Theseond result statesthat dummy elimination is useless
asapreproessingsteptothedependenypairtehnique.Not surprisingly,the
reversestatementsdonothold.Inotherwords,asfarasautomatitermination
proofsareonerned,dummyeliminationisnolongerneeded.
The reent argument ltering transformation of Kusakari, Nakamura, and
Toyama[16℄anbeviewedasanimprovementofdummyelimination byinor-
poratingideasofthe dependeny pairtehnique.Weshow that therstresult
above also holds for the argument ltering transformation. The seond result
doesnotextendinitsfullgenerality,but weshowthatunderasuitablerestri-
tion on the argument ltering applied in the transformation of R to R 0
, DP
simpleterminationofR 0
alsoimpliesDPsimpleterminationofR.
Theremainder of thepaperis organizedasfollows.In the nextsetion we
briey reall somedenitions and results pertaining to termination of rewrite
systemsandinpartiular,thedependenypairtehnique.InSetion3werelate
the dependeny pair tehniqueto dummy elimination. Setion 4is devoted to
the omparison of the dependeny pair tehnique and the argument ltering
transformation.Weonludein Setion5.
2 Preliminaries
Anintrodutiontotermrewritesystems(TRSs)anbefoundin[4℄,forexample.
We rst introdue the dependeny pair tehnique. Our presentation ombines
features of [2,13,16℄. Apartfrom thepresentation, allresultsstated beloware
due to Arts and Giesl. We refer to [2,3℄ for motivations and proofs. Let R
sides ofrewriterules arealled dened, whereasallotherfuntion symbolsare
onstrutors.LetF
℄
denotetheunionofFandff
℄
jf isadened symbolofRg
wheref
℄
hasthesamearityasf.Givenatermt=f(t
1
;:::;t
n
)2T(F;V)with
f dened,wewritet
℄
forthetermf
℄
(t
1
;:::;t
n
).Ifl!r2Randtisasubterm
ofrwithdenedrootsymbolthentherewriterulel
℄
!t
℄
isalledadependeny
pair ofR.ThesetofalldependenypairsofRisdenotedbyDP(R).Inexamples
weoftenwriteF forf
℄
.
Forinstane, onsiderthefollowingwell-knownone-ruleTRSRfrom[8℄:
f(f(x))!f(e(f(x))) (1)
Heref isdened,eisaonstrutor,andDP(R)onsistsofthetwodependeny
pairs
F(f(x))!F(e(f(x))) F(f(x))!F(x)
Anargumentltering[2℄forasignatureFisamappingthatassoiateswith
everyn-aryfuntion symbolanargumentpositioni2f1;:::;ngora(possibly
empty) list [i
1
;:::;i
m
℄ of argument positions with 1 6 i
1
< < i
m 6 n.
ThesignatureF
onsists ofallfuntion symbolsf suhthat (f)issomelist
[i
1
;:::;i
m
℄,where inF
thearityof fism. Everyargumentltering indues
amappingfromT(F;V)toT(F
;V),alsodenotedby:
(t) = 8
>
<
>
:
t ift isavariable;
(t
i
) ift=f(t
1
;:::;t
n
)and(f)=i;
f((t
i1
);:::;(t
im
)) ift=f(t
1
;:::;t
n
)and(f)=[i
1
;:::;i
m
℄:
Thus,anargumentlteringisusedto replaefuntion symbolsbyoneoftheir
argumentsortoeliminateertainargumentsoffuntionsymbols.Forexample,if
(f)=(F)=[1℄and(e)=1,thenwehave(F(e(f(x))))=F(f(x)).However,
ifwehange(e)to [℄,thenweobtain(F(e(f(x))))=F(e).
A preorder (or quasi-order) is atransitive andreexiverelation. A rewrite
preorderisapreorder%ontermsthatislosedunderontextsandsubstitutions.
A redution pair [16℄ onsists of arewrite preorder % and a ompatible well-
foundedorder>whihislosedunder substitutions.Here ompatibilitymeans
that the inlusion %> > or the inlusion >% > holds. In pratie,
> is often hosen to be the strit part of % (or the order where s > t i
s t for all ground substitutions ). The following theorem presents the
(basi)dependenypairapproahofArtsand Giesl.
Theorem1. A TRS R overa signature F isterminating if and only if there
exists an argument ltering for F
℄
and a redution pair (%;>) suh that
(R)%and(DP (R))>.
Beause rewriterules are just pairsof terms, (R) %is ashorthand for
(l) % (r) for every rewrite rule l ! r 2 R. In our example, when using
(e) = [℄, the inequalities f(f(x)) % f(e), F(f(x)) > F(e), and F(f(x)) > F(x)
order,forinstane. Hene,terminationofthisTRSisproved.
Ratherthan onsidering alldependeny pairsat the sametime, likein the
abovetheorem,itisadvantageoustotreatgroupsofdependenypairsseparately.
These groupsorrespond to lusters in the dependeny graph ofR. Thenodes
of thedependenygraphare thedependenypairsof Rand there isan arrow
from node l
℄
1
! t
℄
1 to l
℄
2
! t
℄
2
if there exist substitutions
1 and
2
suh that
t
℄
1
1
!
R l
℄
2
2
. (By renamingvariables in dierent ourrenesof dependeny
pairswemayassumethat
1
=
2
.)Thedependenygraphof Ris denotedby
DG (R). Weall anon-emptysubset C ofdependenypairsofDP(R)aluster
if foreverytwo(not neessarilydistint)pairs l
℄
1
! t
℄
1 and l
℄
2
!t
℄
2
in C there
existsanon-emptypathin C froml
℄
1
!t
℄
1 to l
℄
2
!t
℄
2 .
Theorem2. A TRS R is terminating if and only if for every luster C in
DG (R) there exists an argument ltering and a redution pair (%;>) suh
that (R)%,(C)%[>,and(C)\>6=?.
Notethat(C)\>6=?denotes thesituation that(l
℄
)>(t
℄
)foratleast
onedependenypairl
℄
!t
℄
2C.
Inthe above example, the dependeny graph only ontainsan arrowfrom
F(f(x))! F(x) to itself and thusfF(f(x))! F(x)gis the onlyluster.Hene,
withtherenementofTheorem2theinequalityF(f(x))>F(e)isnolongerne-
essary.See[3℄forfurtherexampleswhihillustratetheadvantagesofregarding
lustersseparately.
Note that while in generalthe dependeny graph annot be omputed au-
tomatially (sine it is undeidable whether t
℄
1
!
R l
℄
2
holds for some ),
oneanneverthelessapproximatethisgraphautomatially,f. [1{3,\estimated
dependenygraph"℄.Inthisway,theriterionofTheorem2anbemehanized.
Most lassial methods for automated termination proofs are restrited to
simpliation (pre)orders, i.e., to (pre)orders satisfying the subterm property
f(:::t:::) t or f(:::t:::) % t, respetively. Hene, these methods annot
proveterminationofTRSslike(1),astheleft-handsideofitsruleisembedded
in theright-hand side (so the TRS is not simply terminating). However, with
the development of the dependeny pair tehnique now the TRSs where an
automated termination proof is potentially possible are those systems where
the inequalities generated by the dependeny pair tehnique are satised by
simpliation(pre)orders.
A straightforwardway to generate asimpliation preorder from asim-
pliation order is to dene s t if s t or s = t, where = denotes syn-
tati equality. Suh relations are partiularly relevant,sine manyexisting
tehniquesgenerate simpliation orders rather than preorders. Byrestriting
ourselves to this lass of simpliation preorders, we obtainthe notion of DP
simpletermination.
Denition1. ATRS Risalled DPsimplyterminating iffor everylusterC
inDG (R)thereexistsanargumentltering andasimpliationordersuh
that (R[C)and(C)\6=?.
example,theTRS(1)isDPsimplyterminating,butnotsimplyterminating.The
abovedenition oinides with theonein [13℄ exept that we usethe real de-
pendenygraphinsteadoftheestimated dependenygraphof[1{3℄.Thereason
forthis isthat wedonotwantto restritourselvesto apartiularomputable
approximation of the dependeny graph, for the same reason that we do not
insistonapartiular simpliationordertomaketheonditionseetive.
3 Dummy Elimination
In [11℄, Ferreira and Zantema dened an automati transformation tehnique
whih transformsaTRSRinto anew TRSdummy (R) suhthat termination
of dummy (R) implies terminationof R.The advantageof this transformation
isthatnon-simplyterminatingsystemslike(1)maybetransformedintosimply
terminatingones. Thus, after thetransformation, standardtehniques may be
usedto provetermination.
BelowwedeneFerreiraandZantema'sdummyeliminationtransformation.
Whileourformulationofdummy (R)isdierentfromtheonein[11℄,itiseasily
seentobeequivalent.
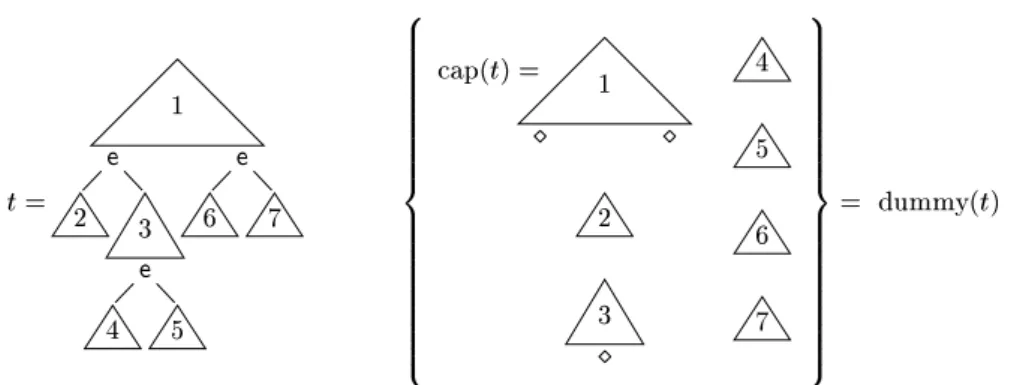
Denition2. Let R be a TRS over a signature F. Let e be a distinguished
funtion symbol in F of arity m >1 and let be a fresh onstant. We write
F
for (Fnfeg)[fg. The mapping ap: T(F;V) ! T(F
;V) is indutively
denedasfollows:
ap(t)= 8
>
<
>
:
t ift2V;
ift=e(t
1
;:::;t
m );
f(ap(t
1
);:::;ap(t
n
)) ift=f(t
1
;:::;t
n
)with f 6=e:
Themappingdummy assignstoeveryterm inT(F;V)asubsetofT(F
;V),as
follows:
dummy (t)=fap(t)g[fap(s)js isanargumentofan esymbol intg:
Finally, wedene
dummy (R)=fap(l)!r 0
jl!r2Randr 0
2dummy (r) g:
Themappingsap anddummy areillustratedinFigure1,whereweassume
that the numberedontexts do notontain any ourrenesof e. Ferreira and
Zantema[11℄showedthatdummyeliminationissound.
Theorem3. Let Rbe a TRS.If dummy (R) is terminating then R is termi-
nating.
Fortheone-ruleTRS (1), dummy eliminationyields theTRS onsisting of
thetworewriterules
f(f(x))!f() f(f(x))!f(x)
1
e
2
3
e
4 5
e
6 7
t=
1
ap(t)=
2
3
4
5
6
7
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
;
= dummy(t)
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
:
Fig.1.Themappingsapanddummy.
Inontrasttotheoriginalsystem,thenewTRSissimplyterminatinganditster-
minationiseasilyshownautomatiallybystandardtehniqueslikethereursive
path order. Hene, dummy elimination an transform non-simply terminating
TRSs intosimply terminatingones.However,asindiatedin theintrodution,
nowadaystherightquestionto askis whetheritantransformnon-DPsimply
terminatingTRSsintoDPsimplyterminatingones.Beforeansweringthisques-
tionweshowthatifdummyeliminationsueedsintransformingaTRSintoa
simplyterminatingTRSthentheoriginalTRSisDPsimplyterminating.Even
stronger,wheneverterminationofdummy (R)anbeprovedbyasimpliation
order,thenthesame simpliationorder satisestheonstraintsofthedepen-
denypairapproah.Thus,theterminationproofusingdependenypairsisnot
morediÆultormoreomplexthantheonewithdummyelimination.
Theorem4. Let Rbe a TRS. If dummy(R) is simply terminating then R is
DP simply terminating.
Proof. LetF bethesignatureofR.WeshowthatRisDPsimplyterminating
even without onsidering the dependeny graph renement. So we dene an
argumentltering forF
℄
andasimpliation orderonT(F
℄
;V)suh that
(R) and (DP (R)) .The argumentltering isdened asfollows:
(e)=[℄and(f)=[1;:::;n℄foreveryn-arysymbolf 2(Fnfeg)
℄
.Moreover,
ifeisadenedsymbol,wedene(e
℄
)=[℄.Let=beanysimpliation order
that showsthe simpleterminationof dummy (R). Wedene the simpliation
orderonT(F
℄
;V)asfollows:stifandonlyifs 0
=t 0
where() 0
denotesthe
mappingfromT(F
℄
;V)toT(F
;V)that rstreplaeseverymarkedsymbolF
byfandafterwardsreplaeseveryourreneoftheonstanteby.Notethat
and=areessentiallythesame.Itisveryeasytoshowthat(t) 0
=(t
℄
) 0
=ap(t)
foreverytermt2T(F;V).Letl!r2R.Beauseap(l)!ap(r)isarewrite
ruleindummy (R),weget(l) 0
=ap(l)=ap(r)=(r) 0
andthus(l)(r).
Hene(R)andthusertainly(R).Nowletl
℄
!t
℄
beadependeny
pairof R,originatingfromthe rewriterulel!r2R.FromtEr (E denotes
the subterm relation) we easily infer the existene of a term u 2 dummy(r)
suhthatap(t)Eu.Sineap(l)!uisarewriterulein dummy (R),wehave
(l ) =ap(l)=u.Thesubtermpropertyof=yieldsuwap(t)=(t ).Hene
(l
℄
) 0
=(t
℄
) 0
andthus(l
℄
)(t
℄
).Weonludethat(DP (R)). ut
Thepreviousresultstatesthatdummyeliminationoersnoadvantageom-
paredto thedependenypairtehnique.Onthe otherhand,dependenypairs
sueed for manysystems where dummyelimination fails [1,2℄(anexample is
given in the next setion). One ould imagine that dummy elimination may
nevertheless be helpful in ombination with dependeny pairs. Then to show
terminationofaTRSonewouldrstapplydummyelimination andafterwards
proveterminationofthetransformedTRSwiththedependenypairtehnique.
In the remainder of this setion we show that suh a senario annot handle
TRSs whih annot already be handled by the dependeny pair tehniquedi-
retly.Inshort,dummyeliminationisuselessforautomatedterminationproofs.
Weproeedinastepwisemanner.FirstwerelatethedependenypairsofRto
thoseofdummy (R).
Lemma1. If l
℄
!t
℄
2DP(R) thenap(l)
℄
!ap(t)
℄
2DP(dummy (R)).
Proof. In theproof of Theorem 4 we observedthat there exists arewrite rule
ap(l)!uindummy (R)withap(t)Eu.Sineroot(ap(t))isadenedsymbol
in dummy (R),ap(l)
℄
!ap(t)
℄
isadependenypairofdummy(R). ut
Nowweprovethatreduibilityin Rimpliesreduibilityindummy (R).
Denition3. Givenasubstitution,the substitution
ap
isdenedasapÆ
(i.e., the omposition ofapand where isapplied rst).
Lemma2. Foralltermst andsubstitutions, wehaveap(t)=ap(t)
ap .
Proof. Easyindution onthestrutureoft. ut
Lemma3. If s!
R
t thenap(s)!
dummy(R) ap(t).
Proof. It is suÆient to show that s !
R
t implies ap(s) !
dummy(R)
ap(t).
There must be a rule l ! r 2 R and a position p suh that sj
= l and
t = s[r℄
p
. If p is below the position of an ourrene of e, then we have
ap(s)=ap(t).Otherwise,ap(s)j
p
=ap(l)=ap(l)
ap
byLemma2.Thus,
ap(s)!
dummy(R)
ap(s)[ap(r)
ap
℄
p
=ap(s)[ap(r)℄
p
=ap(t). ut
Next we show that if there is an arrow between two dependeny pairs in
the dependeny graphof Rthen there is an arrow betweenthe orresponding
dependenypairsin thedependenygraphofdummy (R).
Lemma4. Lets,t betermswith denedrootsymbols.Ifs
℄
!
R t
℄
for some
substitution ,thenap(s)
℄
ap
!
dummy(R) ap(t)
℄
ap .
Proof. Let s = f(s
1
;:::;s
n
). We have s
℄
= f
℄
(s
1
;:::;s
n
). Sine f
℄
is a
onstrutor,nostepinthesequenes
℄
!
R t
℄
takesplaeattherootposition
and thus t
℄
= f
℄
(t
1
;:::;t
n
) with s
i
!
R t
i
for all 1 6 i 6 n. We obtain
ap(s
i )
ap
=ap(s
i )!
dummy(R) ap(t
i
) =ap(t
i )
ap
for all16i 6nby
Lemmata2and3.Heneap(s)
℄
ap
!
dummy(R) ap(t)
℄
ap
. ut
Theorem5. LetRbeaTRS.If dummy(R) isDPsimply terminatingthenR
isDP simply terminating.
Proof. LetCbealusterinthedependenygraphofR.FromLemmata1and4
we infer the existene of a orresponding luster, denoted by dummy (C), in
thedependenygraphofdummy (R). Byassumption, thereexistsanargument
ltering 0
andasimpliationorder=suhthat 0
(dummy (R)[dummy(C))
w and 0
(dummy(C))\= 6= ?. Let F be the signature of R. We dene an
argument ltering forF
℄
as follows: (f)= 0
(f)for every f 2 (Fnfeg)
℄
,
(e)=[℄ and,if eis adened symbolof R,(e
℄
)=[℄. Slightlydierentfrom
the proof of Theorem 4, let () 0
denote the mapping that just replaes every
ourreneoftheonstantebyandeveryourreneofe
℄
by
℄
.Itiseasyto
showthat(t) 0
= 0
(ap(t))foreverytermt2T(F;V)and(t
℄
) 0
= 0
(ap(t)
℄
)
for everytermt 2T(F;V)with adened root symbol. SimilartoTheorem 4,
we dene the simpliation order on F
as s t if and only if s 0
= t 0
.
We laim that and satisfy the onstraints for C, i.e., (R[C) and
(dummy(C))\6=?.Ifl!r2R,then ap(l)!ap(r)2dummy (R) and
thus(l) 0
= 0
(ap(l))w 0
(ap(r))=(r) 0
.Hene (l)(r). Ifl
℄
!t
℄
2C,
thenap(l)
℄
!ap(t)
℄
2dummy (C)byLemma1andthus(l
℄
) 0
= 0
(ap(l)
℄
)w
0
(ap(t)
℄
)=(t
℄
) 0
. Hene (l
℄
)(t
℄
)and if 0
(ap(l)
℄
)= 0
(ap(t)
℄
), then
(l
℄
)(t
℄
). ut
WestressthattheproofisonstrutiveinthesensethataDPsimpletermi-
nationproofofdummy (R) anbeautomatiallytransformedintoaDPsimple
terminationproofofR(i.e.,theordersandargumentlteringsrequiredforthe
DP simple terminationproofs of dummy (R) and R are essentially thesame).
Thus,theterminationproofofdummy (R)isnotsimplerthanadiretprooffor
R.
Theorem 5also holds if oneuses the estimated dependenygraph of [1{3℄
insteadof thereal dependenygraph.As mentionedin Setion 2,suh aom-
putable approximationof the dependenygraph mustbe used in implementa-
tions, sine onstruting the real dependeny graph is undeidable in general.
TheproofissimilartotheoneofTheorem5,sineagainforeverylusterinthe
estimateddependenygraphofRthereisaorrespondingoneintheestimated
dependenygraphofdummy (R).
4 Argument Filtering Transformation
By inorporatingargumentlterings, a key ingredient of the dependeny pair
tehnique,into dummy elimination, Kusakari, Nakamura, andToyama[16℄ re-
ently developed the argument ltering transformation. In their paper they
provedthesoundnessof theirtransformationandtheyshowedthatitimproves
upon dummy elimination. In this setion we ompare their transformation to
thedependenypairtehnique.Weproeedasintheprevioussetion.Firstwe
reallthedenitionoftheargumentlteringtransformation.
arity(f). Wewrite f ?
i if neitheri2(f)nor i=(f). Given two termss
andt, wesay that sisa preservedsubterm oft with respetto andwewrite
sE
t,if sEtandeithers=t ort=f(t
1
;:::;t
n
),sisapreservedsubterm of
t
i
,andf 6?
i.
Denition5. Givenanargumentltering,theargumentlteringisdened
asfollows:
(f)=
(
(f) if(f)=[i
1
;:::;i
m
℄,
[(f)℄ if(f)=i.
The mapping AFT
assigns toevery term inT(F;V) asubset of T(F
;V), as
follows:
AFT
(t)=f(t)j(t) ontainsadenedsymbol g[ [
s2S AFT
(s)
with S denoting the set of outermost non-preserved subterms of t. Finally, we
dene
AFT
(R)=f(l)!r 0
jl!r2Randr 0
2AFT
(r)[f(r)g g:
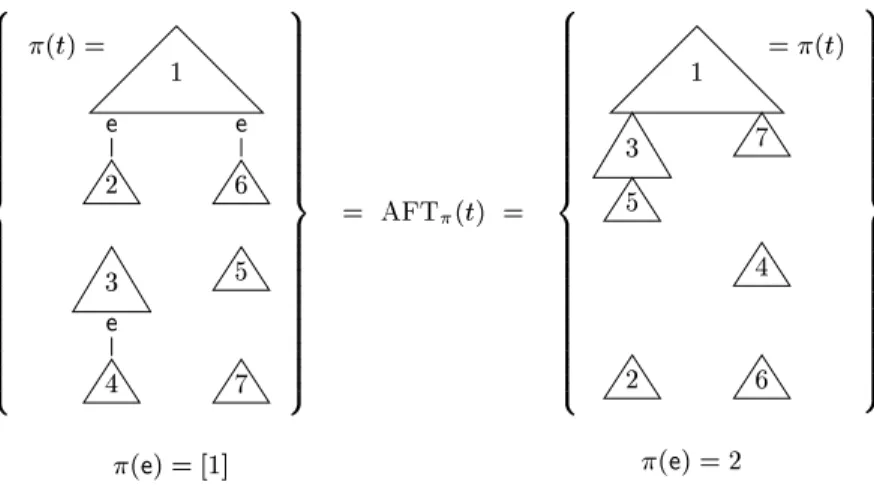
ConsiderthetermtofFigure1.Figure2showsAFT
(t)forthetwoargument
lterings with (e) =[1℄ and (e) = 2, respetively, and (f) =[1;:::;n℄ for
everyothern-aryfuntionsymbolf.Hereweassumethatallnumberedontexts
ontaindenedsymbols,butnoourreneofe.
1
e
2
e
6 (t)=
3
e
4
5
7 9
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
;
= AFT(t) = 8
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
: 8
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
:
1
3
5
7
=(t)
2
4
6
9
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
;
(e)=[1℄
(e)=2
Fig.2.ThemappingsandAFT
.
Soessentially, AFT
(t) ontains(s) for s =t and for all (maximal)sub-
terms s of t whih are eliminated if the argument ltering is applied to t.
symbol outside eliminated arguments (otherwise the original subterm s an-
nothavebeenresponsibleforapotentialnon-termination).Kusakariet al.[11℄
provedthesoundness oftheargumentlteringtransformation.
Theorem6. If AFT
(R)isterminatingthen Risterminating.
WeshowthatifAFT
(R)issimplyterminatingthenRisDPsimplytermi-
natingandagain,aterminationproofbydependenypairsworkswiththesame
argumentlteringandthesimpliationorderusedtoorientAFT
(R).Thus,
theargumentlteringtransformationhasnoadvantageomparedtodependeny
pairs.Westartwithtwoeasylemmata.
1
Lemma5. Letsandt beterms. IfsE
t then(s)E(t).
Proof. Byindution on thedenition of E
. If s=t then theresultis trivial.
Supposet=f(t
1
;:::;t
n ),sE
t
i
,andf 6?
i.Theindution hypothesis yields
(s)E(t
i
).Beausef 6?
i,(t
i
)isasubtermof(t)andthus(s)E(t)as
desired. ut
Lemma6. Letrbeaterm.Foreverysubtermtofrwithadenedrootsymbol
thereexistsaterm u2AFT
(r) suhthat(t)Eu.
Proof. We useindution onthe struture of r. Inthe base ase we musthave
t =r and we takeu=(r). Note that (r)2 AFT
(r) beauseroot((r))=
root(r)isdened.Intheindutionstepwedistinguishtwoases.IftE
rthen
wealsohavetE
randhene(t) E(r)byLemma5.Asroot((t))=root(t)
is dened,theterm(r) ontainsadened symbol.Hene (r)2AFT
(r)by
denition andthusweantakeu=(r). Intheother aset isnotapreserved
subtermofr.ThisimpliesthattEsforsomeoutermostnon-preservedsubterm
s ofr. Theindution hypothesis, applied to tEs, yieldsaterm u2AFT
(s)
suh that (t) E u. We have AFT
(s) AFT
(r) and hene u satises the
requirements. ut
Theorem7. LetRbeaTRSandanargumentltering.IfAFT
(R)issimply
terminatingthenR isDPsimply terminating.
Proof. LikeintheproofofTheorem4thereisnoneedtoonsiderthedependeny
graph. Let bea simpliation order that shows the(simple) termination of
AFT
(R).Welaimthatthedependenypaironstraintsaresatisedby and
,whereandareextendedtoF
℄
bytreatingeahmarkedsymbolF inthe
samewayastheorrespondingunmarkedf.Forrewriterulesl!r2Rwehave
(l)(r)as(l)!(r)2AFT
(R).Letl
℄
!t
℄
beadependenypairofR,
originating from therewrite rule l! r. We show that (l)(t) and hene,
1
ArgumentationssimilartotheproofsofLemma6andTheorem7analsobefound
in [16, Lemma 4.3 and Theorem 4.4℄. However, [16℄ ontains neither Theorem 7
norourmain Theorem8,sinetheauthors donotomparetheargument ltering
transformationwiththedependenypairapproah.
(l )(t )aswell.WehavetEr. Sineroot(t)is adened funtion symbol
bythedenitionofdependenypairs,weanapplyLemma6.Thisyieldsaterm
u2AFT
(r) suh that (t) Eu. Thesubterm propertyof yields u(t).
By denition,(l)! u2 AFT
(R) and thus (l) uby ompatibilityof
withAFT
(R).Hene (l)(t)asdesired. ut
Notethatintheaboveproofwedidnotmakeuseofthepossibilitytotreat
marked symbols dierently from unmarked ones. This learly shows why the
dependenypair tehniqueis muh more powerfulthan theargumentltering
transformation;there arenumerousDPsimplyterminating TRSswhihareno
longer DP simply terminating if we are fored to interpret a dened funtion
symbolanditsmarkedversionin thesameway.Asasimpleexample,onsider
R
1
= 8
<
:
x 0 !x 0s(y)!0
x s(y)!p(x y) s(x)s(y)!s((x y)s(y))
p(s(x))!x
9
=
; :
Note that R
1
is not simply terminating as the rewrite step s(x)s(s(x)) !
s((x s(x))s(s(x)))isself-embedding.ToobtainaterminatingTRSAFT
(R
1 ),
therulep(s(x))!xenforesp6?
1ands6?
1.Fromp6?
1andtherulesfor
weinferthat( )=[1;2℄.Butthen,forallhoiesof(),therules(x)s(y)!
s((x y)s(y))istransformedintoonethatisinompatiblewithasimpliation
order. So AFT
(R
1
) is not simply terminating for any . (Similarly, dummy
eliminationannottransformthisTRSintoasimplyterminatingoneeither.)On
theother hand,DPsimpleterminationof R
1
is easily shownby theargument
ltering (p) = 1, ( ) = 1, (
℄
) = [1;2℄, and (f) = [1;:::;arity(f)℄ for
every other funtion symbol f in ombination with the reursive path order.
Thisexampleillustratesthattreatingdenedsymbolsandtheirmarkedversions
dierentlyisoftenrequiredinordertobenetfromthefatthatthedependeny
pairapproahonlyrequiresweak dereasingness fortherulesofR
1 .
Thenextquestionweaddressiswhethertheargumentlteringtransforma-
tion an be useful as a preproessing step for the dependeny pair tehnique.
Surprisingly,theanswertothisquestionisyes.ConsidertheTRS
R
2
= 8
<
:
f(a) !f((a)) f(a) !f(d(a)) e(g (x))!e(x)
f((x))!x f(d(x))!x
f((a))!f(d(b)) f((b)) !f(d(a))
9
=
; :
This TRS is not DP simply terminating whih an be seen as follows. The
dependenypairE(g (x))!E(x)onstitutesalusterin thedependenygraph
of R
2
. Hene,ifR
2
wereDPsimply terminating,there would be anargument
ltering andasimpliation ordersuhthat(amongstothers)
(f(a)) (f((a))) (f(a)) (f(d(a)))
(f((x)))x (f(d(x)))x
(f((a))) (f(d(b))) (f((b))) (f(d(a)))
From (f((x))) x and (f(d(x))) x we infer that f 6?
1, 6?
1, and
d6?
1.Hene(f(a))(f((a)))and(f(a))(f(d(a)))anonlybesatised
amountto eitherf(a)f(b) andf(b)f(a)(if (f)=[1℄)oraband ba
(if (f)=1).Sine f(a)6=f(b) anda6=btherequiredsimpliation orderdoes
notexist.
Ontheotherhand,if(e)=1thenAFT
(R
2
)onsistsoftherstsixrewrite
rulesofRtogetherwithg (x)!x.Oneeasilyveriesthattherearenolusters
in DG(AFT
(R
2
))andheneAFT
(R
2
)istriviallyDPsimplyterminating.
Denition6. Anargumentltering isalled ollapsingif (f)=ifor some
denedfuntionsymbol f.
Theargumentlteringinthepreviousexampleisollapsing.Intheremainder
ofthissetionweshowthatfornon-ollapsingargumentlteringstheimpliation
\AFT
(R) is DPsimplyterminating)Ris DPsimplyterminating"is valid.
Thus,using theargumentlteringtransformationwithanon-ollapsing asa
preproessingsteptothedependenypairtehniquehasnoadvantages.
FirstweprovealemmatorelatethedependenypairsofRandAFT
(R).
Lemma7. Let be a non-ollapsing argumentltering. If l
℄
! t
℄
2 DP(R)
then(l)
℄
!(t)
℄
2DP(AFT
(R)).
Proof. Bydenition thereisarewriterulel!r2RandasubtermtErwith
dened root symbol.Aording to Lemma 6there exists aterm u2AFT
(r)
suh that (t) E u. Thus, (l) ! u 2 AFT
(R). Sine is non-ollapsing,
root((t))=root(t).Hene,asroot(t)isdened,(l)
℄
!(t)
℄
isadependeny
pairofAFT
(R). ut
ExampleR
2
showsthattheabovelemmaisnottrueforarbitraryargument
lterings. The reasonis that e(g (x))
℄
! e(x)
℄
is a dependeny pair of R,but
with(e)=1thereisnoorrespondingdependenypairinAFT
(R).
Thenextthreelemmatawillbeused toshowthatlustersin DG(R)orre-
spondtolustersin DG (AFT
(R)).
Denition7. Givenanargumentltering andasubstitution,thesubstitu-
tion
isdenedas Æ (i.e., isapplied rst).
Lemma8. Foralltermst,argumentlterings ,andsubstitutions,(t)=
(t)
.
Proof. Easyindution onthestrutureoft. ut
Lemma9. LetRbeaTRSandanon-ollapsingargumentltering.Ifs!
R t
then(s)!
AFT
(R)
(t).
Proof. ItsuÆestoshowthat (s)!
AFT
(R)
(t)whenevers!
R
tonsistsof
asinglerewrite step.Lets=C[l℄and t=C[r℄ forsomeontext C, rewrite
rule l!r2R, andsubstitution . Weuseindution onC. IfC is theempty
ontext, then (s)= (l) =(l)
and (t)= (r) =(r)
aordingto
AFT
(R)
C = f(s
1
;:::;C 0
;:::;s
n
)where C 0
is the i-th argumentof C. If f ?
i then
(s) = (t). If (f) = i (whih is possible for onstrutors f) then (s) =
(C 0
[l℄)and(t)=(C 0
[r℄),andthusweobtain(s)!
AFT
(R)
(t)fromthe
indutionhypothesis.Intheremainingasewehave(f)=[i
1
;:::;i
m
℄withi
j
=
i for somej and hene(s) = f((s
i1
);:::;(C 0
[l℄);:::;(s
im
)) and (t) =
f((s
i1
);:::;(C 0
[r℄);:::;(s
im
)).Inthisaseweobtain(s)!
AFT
(R)
(t)
fromtheindution hypothesisaswell. ut
ThefollowinglemmastatesthatiftwodependenypairsareonnetedinR's
dependenygraph,thentheorrespondingpairsareonnetedinthedependeny
graphof AFT
(R) aswell.
Lemma10. Let R be a TRS, a non-ollapsing argument ltering, and s, t
be termswith denedrootsymbols.If s
℄
!
R t
℄
for somesubstitution then
(s)
℄
!
AFT(R) (t)
℄
.
Proof. We haves=f(s
1
;:::;s
n
) andt =f(t
1
;:::;t
n
)for somen-ary dened
funtion symbolf with s
i
!
R t
i
forall 16i6n. Let (f)=[i
1
;:::;i
m
℄.
This implies (s)
℄
= f
℄
((s
i1
);:::;(s
im
)) and (t)
℄
= f
℄
((t
i1 );:::;
(t
im
)). From the preeding lemma weknowthat (s
ij ) !
AFT(R) (t
ij )
forall16j6m.Hene,usingLemma8,(s)
℄
=(s)
℄
!
AFT
(R)
(t)
℄
=
(t)
℄
. ut
Nowweannallyprovethemain theoremofthissetion.
Theorem 8. Let R be a TRS and a non-ollapsing argument ltering. If
AFT
(R) isDPsimply terminating thenRisDP simply terminating.
Proof. LetC bealusterinDG (R).AordingtoLemmata7and10,thereisa
orrespondinglusterin DG(AFT
(R)),whih wedenoteby(C).Byassump-
tion,thereexistanargumentltering 0
andasimpliationordersuh that
0
(AFT
(R)[(C))and 0
((C))\6=?.Wedeneanargumentltering
00
forR as theomposition of and 0
. Fora preise denition,let[ denote
theunmarking operation,i.e.,f [
=f and(f
℄
) [
=f forallf 2F. Thenforall
f 2F
℄
wedene
00
(f)= 8
>
<
>
: [i
j1
;:::;i
j
k
℄ if(f [
)=[i
1
;:::;i
m
℄and 0
(f)=[j
1
;:::;j
k
℄;
i
j
if(f [
)=[i
1
;:::;i
m
℄and 0
(f)=j;
i if(f)=i:
It is notdiÆult to show that 00
(t) = 0
((t)) and 0 0
(t
℄
) = 0
((t)
℄
) for all
termstwithoutmarkedsymbols.Welaimthat 0 0
andsatisfytheonstraints
forC,i.e., 00
(R [ C)and 0 0
(C) \ 6=?.Thesetwopropertiesfollowfromthe
twoassumptions 0
(AFT
(R)[(C))and 0
((C))\6=?inonjuntion
withtheobviousinlusion(R)AFT
(R). ut
Theorem8alsoholdsfortheestimateddependenygraphinsteadofthereal
dependenygraph.
Inthispaper,wehaveomparedtwotransformationaltehniquesfortermination
proofs, viz. dummy elimination[11℄ and the argument lteringtransformation
[16℄,withthedependenypairtehniqueofArtsandGiesl[1{3℄.Essentially,all
thesetehniquestransformagivenTRSintonewinequalitiesorrewritesystems
whihthenhavetobeorientedbysuitablewell-foundedorders.Virtuallyallwell-
foundedorders whih anbegeneratedautomatially aresimpliation orders.
Asourfouswasonautomated terminationproofs,wethereforeinvestigatedthe
strengthsofthesethree tehniques whenombinedwithsimpliationorders.
To that end, we showedthat whenever anautomated termination proof is
possibleusingdummyeliminationortheargumentlteringtransformation,then
a orresponding termination proof an also be obtainedby dependeny pairs.
Thus,thedependenypairtehniqueismorepowerfulthandummyelimination
ortheargumentlteringtransformationontheirown.
Moreover, we examined whether dummy elimination or the argument l-
tering transformation would at least be helpful as apreproessing step to the
dependenypairtehnique.We provedthat fordummyelimination and foran
argumentlteringtransformationwithanon-ollapsingargumentltering,this
isnotthease.Infat,wheneverthereisa(pre)ordersatisfyingthedependeny
pair onstraints forthe rewritesystemresulting from dummy eliminationora
non-ollapsingargumentlteringtransformation,thenthesame (pre)orderalso
satisesthedependenypaironstraintsfortheoriginalTRS.
As an be seen from the proofs of our main theorems, this latter result
evenholdsforarbitrary(i.e.,non-simpliation)(pre)orders.Thus,inpartiular,
Theorems 5and8 alsohold forDP quasi-simpletermination [13℄.Thisnotion
aptures those TRSs where the dependeny pair onstraints are satised by
an arbitrarysimpliation preorder %(instead of just apreorder where the
equivalenerelationissyntatiequalityasin DP simpletermination).
Futureworkwillinlude afurtherinvestigationontheusefulnessofollaps-
ing argument ltering transformations as a preproessing step to dependeny
pairs.NotethatourounterexampleR
2
isDPquasi-simplyterminating(butnot
DPsimply terminating). Inother words,at present itis notlearwhether the
argumentlteringtransformationisusefulasapreproessingsteptothedepen-
denypairtehniqueifoneadmitsarbitrarysimpliationpreorderstosolvethe
generatedonstraints.However,anextension ofTheorem8toDPquasi-simple
terminationandtoollapsing argumentlterings isnotstraightforward,sine
lusters of dependeny pairs in R maydisappear in AFT
(R) (i.e., Lemma 7
doesnotholdforollapsingargumentlterings).Wealsointendtoexaminethe
relationshipbetweendependenypairsandothertransformationtehniquessuh
as\freezing"[20℄.
Aknowledgements.JurgenGieslissupportedbytheDFGundergrantGI274/4-1.
Aart Middeldorp is partially supportedby the Grant-in-Aid for Sienti Researh
C(2)11680338oftheMinistryofEduation,Siene,SportsandCultureofJapan.
1. T. Arts and J. Giesl, Automatially Proving Termination where Simpliation
OrderingsFail,Pro.7thTAPSOFT,Lille,Frane,LNCS1214,pp.261{273,1997.
2. T.ArtsandJ.Giesl,TerminationofTermRewritingUsingDependenyPairs,The-
oretialComputerSiene236, pp.133{178,2000.Longversionavailableatwww.
inferenzsysteme.informatik.tu-d arms tadt .de/~ repo rts/ ibn-9 7-46 .ps.
3. T.Artsand J.Giesl, Modularity ofTerminationUsing DependenyPairs, Pro.
9thRTA,Tsukuba,Japan,LNCS1379,pp.226{240,1998.
4. F. BaaderandT. Nipkow,Term Rewriting andAll That,CambridgeUniversity
Press, 1998.
5. F.BellegardeandP.Lesanne,TerminationbyCompletion,AppliableAlgebrain
Engineering,CommuniationandComputing1,pp.79{96,1990.
6. A. Ben Cherifa and P. Lesanne,Termination of Rewriting Systems by Polyno-
mial Interpretationsand itsImplementation,SieneofComputerProgramming
9,pp.137{159,1987.
7. N.Dershowitz,OrderingsforTerm-RewritingSystems,TheoretialComputerSi-
ene17,pp.279{301,1982.
8. N. Dershowitz, Termination of Rewriting, Journal of Symboli Computation 3,
pp.69{116,1987.
9. J.Dik,J.Kalmus,andU.Martin,AutomatingtheKnuthBendixOrdering,Ata
Informatia28,pp.95{119,1990.
10. M.C.F. Ferreira,Termination ofTermRewriting:Well-foundedness,Totality and
Transformations,Ph.D.thesis,UtrehtUniversity,TheNetherlands,1995.
11. M.C.F.FerreiraandH.Zantema,DummyElimination:MakingTerminationEas-
ier,Pro.10thFCT,Dresden,Germany,LNCS965,pp.243{252,1995.
12. J.Giesl,GeneratingPolynomialOrderingsforTerminationProofs,Pro.6thRTA,
Kaiserslautern,Germany,LNCS914,pp.426{431,1995.
13. J.Giesl andE.Ohlebush,PushingtheFrontiers ofCombiningRewriteSystems
FartherOutwards,Pro.2ndFROCOS,1998,Amsterdam,TheNetherlands,Stud-
iesinLogiandComputation7,ResearhStudiesPress,Wiley,pp.141{160,2000.
14. S. Kamin and J.J. Levy, Two Generalizations of the Reursive Path Ordering,
unpublishedmanusript,UniversityofIllinois,USA,1980.
15. D.E.KnuthandP.Bendix,SimpleWordProblemsinUniversalAlgebras,in:Com-
putationalProblemsinAbstratAlgebra(ed.J.Leeh),PergamonPress,pp.263{
297,1970.
16. K.Kusakari,M.Nakamura,andY.Toyama,ArgumentFilteringTransformation,
Pro.1stPPDP,Paris, Frane,LNCS1702, pp.48{62,1999.
17. D.Lankford,OnProvingTermRewritingSystemsareNoetherian,ReportMTP-3,
LouisianaTehnialUniversity,Ruston,USA,1979.
18. A. Middeldorp, H. Ohsaki, and H.Zantema, TransformingTermination by Self-
Labelling, Pro. 13th CADE, New Brunswik (New Jersey), USA, LNAI1104,
pp.373{387,1996.
19. J.Steinbah,SimpliationOrderings:HistoryofResults,FundamentaInformat-
iae24,pp.47{87,1995.
20. H. Xi, Towards Automated Termination Proofs Through \Freezing", Pro. 9th
RTA,Tsukuba,Japan,LNCS1379,pp.271{285,1998.
21. H.Zantema,TerminationofTermRewriting:InterpretationandTypeElimination,
JournalofSymboliComputation17,pp.23{50,1994.
22. H.Zantema,TerminationofTermRewriting bySemantiLabelling,Fundamenta
Informatiae24,pp.89{105,1995.