7. Reglerentwurf im Frequenzbereich

In diesem Kapitel werden zwei unterschiedliche Reglerentwurfsverfahren im Frequenzbe- reich diskutiert. Das so genannte Frequenzkennlinienverfahren ist auf Regelkreise mit ei- nem Freiheitsgrad nach Abbildung 6.8 zugeschnitten. Der Reglerentwurf erfolgt dabei auf Grund von Anforderungen an das Einschwingverhalten der Antworten des geschlossenen Regelkreises auf gewisse ausgew¨ahlte Testfunktionen, die dann in Anforderungen an das Bode-Diagramm des offenen Kreises ¨ubertragen werden. Im Gegensatz dazu ist die Metho- de derPolvorgabe eine algebraische Methode, bei der zu einer gegebenen Strecken¨ubertra- gungsfunktion ein Regler so entworfen wird, dass der geschlossene Kreis ein gew¨unschtes Verhalten der F¨uhrungs¨ubertragungsfunktion aufweist. Dieses Verfahren kann sowohl f¨ur Regelkreise mit einem Freiheitsgrad nach Abbildung 6.8 als auch f¨ur Regelkreise mit zwei Freiheitsgraden nach Abbildung 6.12 formuliert werden.

7.1. Das Frequenzkennlinienverfahren

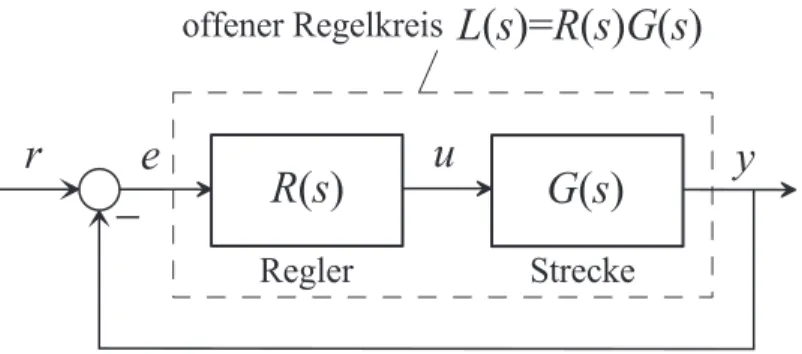
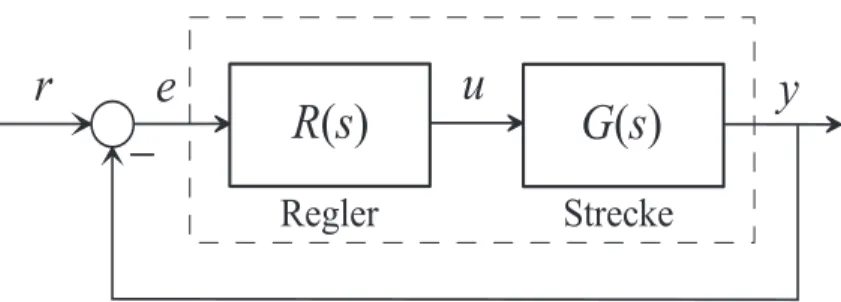
Dem Frequenzkennlinienverfahren liegt der Regelkreis von Abbildung 7.1 mit der F¨uh- rungsgr¨oße r(t), der Stellgr¨oße u(t), dem Regelfehler e(t) und der Ausgangsgr¨oße y(t) zu Grunde.

G ( s )

r R ( s ) u y e

R e g l e r S t r e c k e

o f f e n e r R e g e l k r e i s

L ( s ) = R ( s ) G ( s )

Abbildung 7.1: Regelkreis mit einem Freiheitsgrad als Basis f¨ur das Frequenzkennlinien- verfahren.

Ausgangspunkt f¨ur das Frequenzkennlinienverfahren ist die Vorgabe von Kenngr¨oßen zur Charakterisierung des Einschwingverhaltens des geschlossenen Kreises mit der ¨Ubertra- gungsfunktion

Tr,y(s) = yˆ ˆ

r = R(s)G(s)

1 +R(s)G(s) = L(s)

1 +L(s) (7.1)

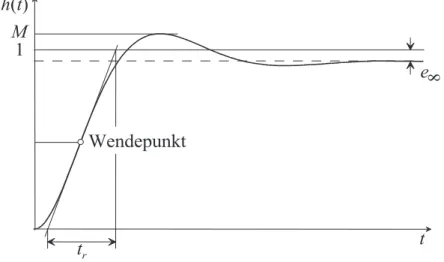
als Antwort auf gewisse Testsignale. Dazu betrachte man den in Abbildung 7.2 dargestell- ten typischen Verlauf der Sprungantwort h(t) des geschlossenen Kreises f¨ur r(t) =σ(t).

h ( t ) tt r

M e 8

1

W e n d e p u n k t

Abbildung 7.2: Kenngr¨oßen der Sprungantwort des geschlossenen Kreises.

Das Einschwingverhalten des geschlossenen Kreises wird nun an Hand der drei nachfol- genden Kenngr¨oßen beurteilt:

(1) Die Anstiegszeit tr als Maß f¨ur die Schnelligkeit (Dynamik),

(2) dieUberschwingweite¨ M oder das prozentuelle ¨Uberschwingen u¨= (M −1) 100 als Maß f¨ur den D¨ampfungsgrad (Dynamik) sowie

(3) diebleibende Regelabweichung e∞ als Maß f¨ur die station¨are Genauigkeit.

DieseKenngr¨oßen des zeitlichen Verhaltens der Sprungantwort des geschlossenen Kreises k¨onnen nun ¨uber empirische N¨aherungsbeziehungen mit dem Frequenzgang des offenen Kreises L(Iω) in Zusammenhang gebracht werden. Dazu wird vorausgesetzt, dass die Ubertragungsfunktion des offenen Kreises¨ L(s) gem¨aß Definition 6.3 vom einfachen Typ ist.

(1) Die Anstiegszeit tr h¨angt mit der Durchtrittsfrequenz ωC ¨uber die N¨aherungsbezie- hung

ωCtr ≈1.5 (7.2)

zusammen. Da vorausgesetzt wurde, dass die ¨Ubertragungsfunktion L(s) vom ein- fachen Typ ist und damit der Betragsgang vonL(s) nur einen Schnittpunkt mit der 0-dB-Linie hat, trennt die DurchtrittsfrequenzωC jene Frequenzen, die vom offenen Regelkreis verst¨arkt werden, von jenen, die vom offenen Regelkreis abgeschw¨acht werden (zur Erl¨auterung siehe auch Abbildung 6.10). Damit ist, wie bereits im vori- gen Kapitel besprochen, die DurchtrittsfrequenzωC ein Maß f¨ur die Bandbreite des offenen Kreises und bei steigendem ωC wird dementsprechend auch die Dynamik des geschlossenen Kreises schneller.

(2) Das prozentuelle ¨Uberschwingen u¨ kann ¨uber die empirische N¨aherungsbeziehung

Φ[^◦] + ¨u[%]≈70 (7.3)

mit der Phasenreserve Φ von (6.58) in Verbindung gebracht werden (siehe auch Abbildung 6.19). Nach dem vereinfachten Schnittpunktkriterium von Satz 6.6 f¨ur Ubertragungsfunktionen¨ L(s) des offenen Kreises vom einfachen Typ ist die Phasen- reserve Φ ein Maß f¨ur den Abstand zur Stabilit¨atsgrenze. Dies hat zur Konsequenz, dass eine Verminderung der Phasenreserve Φ eine Zunahme der Schwingneigung bzw. des ¨Uberschwingens mit sich bringt.

Um diese Argumentation zu unterstreichen, berechne man den Betrag der F¨uhrungs-

¨

ubertragungsfunktion Tr,y(s) von (7.1) an der Stelle s=IωC

|Tr,y(IωC)|= |L(IωC)|

|1 +L(IωC)| = |−cos (Φ)−Isin (Φ)|

|1−cos (Φ)−Isin (Φ)| = 1 2

sin ^Φ₂

. (7.4) Man erkennt, dass wegen

Φlim→0|Tr,y(IωC)|=∞ (7.5) der geschlossene KreisTr,y(s) f¨ur Φ = 0 ein konjugiert komplexes Polpaar bei ±IωC

aufweist und damit die Sprungantwort unged¨ampft schwingt.

Aufgabe 7.1. Zeigen Sie, dass die Beziehung

L(IωC) =−cos (Φ)−Isin (Φ) mit der Durchtrittsfrequenz ωC und der Phasenreserve Φ gilt.

(3) Die bleibende Regelabweichung e∞= lim

t→∞

e(t) = lim

t→∞

(r(t)−y(t)) (7.6)

steht nun direkt mit dem Verst¨arkungsfaktor V der ¨Ubertragungsfunktion des of- fenen Kreises L(s) in Verbindung. Unter der Voraussetzung, dass der geschlosse- ne Regelkreis stabil ist, kann f¨ur (7.6) unmittelbar der Endwertsatz der Laplace- Transformation angewandt werden, und man erh¨alt f¨ur e^∞ die Beziehung

e∞ = lim

t→∞

e(t) = lim

s→0sˆe(s) = lim

s→0s 1

1 +L(s)rˆ(s) . (7.7) Setzt man f¨urL(s) in (7.7) die Beziehung (6.54)

L(s) = V s^ρ

zL(s)

nL(s) , zL(0) =nL(0) = 1 und ρ∈ {0,1} (7.8) ein, dann folgte∞ zu

e∞= lim

s→0s s^ρnL(s)

s^ρnL(s) +V zL(s)rˆ(s) . (7.9)

Die bleibende Regelabweichunge∞f¨ur die beiden Testsignaler(t) =σ(t) undr(t) = t jeweils f¨urρ∈ {0,1} sind nachfolgender Tabelle

r(t) =σ(t) bzw. rˆ(s) = 1 s :







ρ= 0 ⇒ e∞ = 1 1 +V ρ= 1 ⇒ 0

r(t) =t bzw. ˆr(s) = 1 s² :







ρ= 0 ⇒ e∞ =∞ ρ= 1 ⇒ e∞ = 1

V

(7.10)

zu entnehmen. Man erkennt also aus (7.9) und (7.10), dass die ¨Ubertragungsfunktion des offenen Kreises L(s) mindestens eine einfache Polstelle bei s = 0 (ρ ≥ 1) haben muss, damit die bleibende Regelabweichung zufolge eines Eingangssprunges r(t) =σ(t) Null ist.

Analog dazu muss L(s) mindestens eine doppelte Polstelle bei s = 0 (ρ ≥ 2) ha- ben, damit die bleibende Regelabweichung bei einer rampenf¨ormigen Eingangsgr¨oße r(t) =t Null wird. Man beachte aber, dass im Fallρ≥2 die ¨Ubertragungsfunktion L(s) nicht mehr vom einfachen Typ ist und somit die Stabilit¨atspr¨ufung auch nicht mit dem vereinfachten Schnittpunktkriterium erfolgen kann, sondern das Nyquist- kriterium nach Satz 6.5 herangezogen werden muss.

Man beachte, dass die empirischen N¨aherungsbeziehungen (7.2) und (7.3) f¨ur eine ¨Uber- tragungsfunktion des geschlossenen Kreises vom Typ

Tr,y(s) = 1

1 + 2ξ(sT) + (sT)² , T > 0 und 0< ξ <1 (7.11) mit der zugeh¨origen ¨Ubertragungsfunktion des offenen Kreises

L(s) = 1

sT(2ξ+sT) (7.12)

auch exakt hergeleitet werden k¨onnen.

L¨osen Sie dazu nachfolgende Aufgaben:

Aufgabe 7.2. Berechnen Sie die Steigung ∆tW der Sprungantwort des geschlossenen Kreises (7.11) am Wendepunkt (siehe Abbildung 7.2).

Ergebnis:

∆tW = 1 T exp







−arctan √

1−ξ² ξ

ξ p1−ξ²







Zeigen Sie, dass in diesem Fall f¨ur die Anstiegszeit tr gilt tr = 1/∆tW. Berechnen Sie weiters allgemein die Durchtrittsfrequenz ωC f¨ur L(s) von (7.12).

Ergebnis:

ωC = 1 T

qp

4ξ⁴+ 1−2ξ²

Zeichnen Sie das Produkt ωCtr als Funktion des D¨ampfungsgrades ξ im Bereich 0.5 ≤ ξ≤0.8.

Aufgabe 7.3. Berechnen Sie das Maximum M der Sprungantwort des geschlossenen Kreises (7.11) (siehe Abbildung 7.2).

Ergebnis:

M = 1 + exp − ξπ p1−ξ²

!

Bestimmen Sie weiters allgemein die Phasenreserve Φ f¨ur L(s)von (7.12).

Ergebnis:

Φ = arctan



 2ξ qp

4ξ⁴+ 1−2ξ²



 Zeichnen Sie den Ausdruck

(M −1) 100

| {z }

¨ u[%]

+ Φ[^◦]

als Funktion des D¨ampfungsgrades ξ im Bereich 0.5≤ξ≤0.8.

Es hat sich nun gezeigt, dass die empirischen N¨aherungsbeziehungen (7.2) und (7.3) auch f¨ur Systeme h¨oherer Ordnung sinnvoll sind, insbesondere dann, wenn die Sprungantwort des geschlossenen Kreises in erster N¨aherung durch ein konjugiert komplexes Polpaar bestimmt ist.

Damit l¨asst sich die Vorgangsweise beim Reglerentwurf nach dem Frequenzkennlinienver- fahren wie folgt angeben:

(A) Zu einer gegebenen Strecken¨ubertragungsfunktionG(s) m¨ussen die Kenngr¨oßen des Einschwingverhaltens des geschlossenen Kreises (tr, M oder ¨u und e^∞) spezifiziert werden.

(B) Die Kenngr¨oßentr,M oder ¨u unde^∞ werden mit Hilfe der Beziehungen (7.2), (7.3) und (7.9) in Vorgaben an den Frequenzgang des offenen Kreises L(Iω) ¨ubersetzt.

(C) Ein Regler R(s) muss so gew¨ahlt werden, dass der geschlossene Kreis BIBO-stabil ist und die Forderungen von (B) erf¨ullt werden. Ist die ¨UbertragungsfunktionL(s) = R(s)G(s) vom einfachen Typ, dann folgt automatisch aus dem vereinfachten Schnitt- punktkriterium die Stabilit¨at des geschlossenen Kreises. Sehr oft f¨uhrt das Frequenz- kennlinienverfahren auch bei ¨Ubertragungsfunktionen L(s) des offenen Kreises, die nicht vom einfachen Typ sind, zu brauchbaren Ergebnissen, doch muss dann die Stabilit¨at des geschlossenen Kreises mit Hilfe des Nyquistkriteriums nach Satz 6.5 untersucht werden.

(D) Um ein kriechendes Einlaufen der Sprungantwort in den station¨aren Endwert zu vermeiden, soll in (C) der Regler R(s) so entworfen werden, dass ca. 1 Dekade um die Durchtrittsfrequenz ωC die Betragskennlinie von L(s) mit mindestens 20 dB/Dekade abf¨allt.

(E) Die Qualit¨at des Entwurfes ist immer durch Simulation zu ¨uberpr¨ufen, insbeson- dere auch deshalb, weil das Verfahren sich auf empirische Formeln st¨utzt. Sind die Ergebnisse nicht zufriedenstellend, dann muss man sich die Frage stellen, ob die An- forderungen von (A) ¨uberhaupt prinzipiell erf¨ullbar sind, oder ob ein anderer Regler R(s) von (C) die Situation verbessern w¨urde.

(F) Die Begrenzung der Stellgr¨oße u(t), die bei jedem technisch relevanten Prozess vor- handen ist, kann im Rahmen dieses einfachen Entwurfsverfahrens nicht systematisch ber¨ucksichtigt werden. Sollte sich bei der Simulation herausstellen, dass man zu viel Stellgr¨oße ben¨otigt, dann muss man die Anforderungen in (A) entsprechend den Uberlegungen von Abschnitt 6.3 ver¨andern, also die Anstiegszeit¨ tr vergr¨oßern. Im Rahmen einer F¨uhrungsregelung sollte auf keinen Fall ein Sprung sondern immer ein hinreichend glattes Signal als F¨uhrungsgr¨oße verwendet werden (man wiederhole dazu auch die ¨Uberlegungen von Abschnitt 6.3).

Beispiel: PI-Reglerentwurf (A) Strecken¨ubertragungsfunktion:

G(s) = 5

1 + 2×0.707s+s² (7.13)

Entwurfsvorgaben: tr= 3 s, ¨u= 10 % und e∞|r(t)=σ(t) = 0

(B) Vorgaben an den Frequenzgang des offenen KreisesL(Iω):ωC = 0.5 rads⁻¹, Φ = 60^◦ und der offene Kreis muss mindestens eine einfache Polstelle bei s= 0 haben.

(C) Als Regler wird ein PI-Regler der Form

R(s) = VI(1 +sTI)

s (7.14)

gew¨ahlt. Im ersten Schritt wird das Bode-Diagramm aller bekannten Terme des offenen KreisesL(s) =R(s)G(s), also

L1(s) = 5

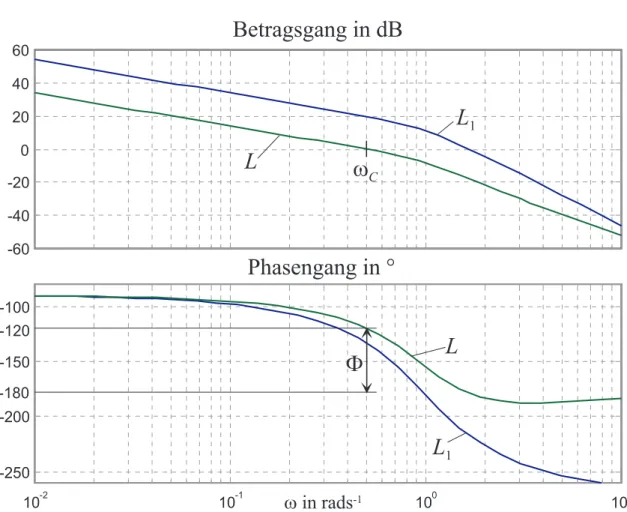
s(1 + 2×0.707s+s²) (7.15) gezeichnet, siehe Abbildung 7.3. An der Durchtrittsfrequenz ωC = 0.5 errechnet sich das Argument von L1(IωC) zu arg (L1(IωC)) = −133.3^◦. Damit muss wegen Φ = 60^◦ mit Hilfe des Linearterms im Z¨ahler des PI-Reglers (1 +sTI) die Phase um 13.3^◦ angehoben werden. Aus dieser Bedingung

arg (1 +IωCTI) = arctan (ωCTI) = 13.3 π

180 (7.16)

folgtTI zu TI = 0.47.

In einem zweiten Schritt wird V so berechnet, dass der Betragsgang bei ωC die 0-dB-Linie schneidet, also die Bedingung

VI

5 (1 + 0.47IωC)

IωC(1−w²_C+I2×0.707ωC)

= 1 (7.17)

erf¨ullt ist. Aus (7.17) erh¨alt man sofortVI = 0.1. Der PI-Regler lautet daher R(s) = 0.1 (1 + 0.47s)

s . (7.18)

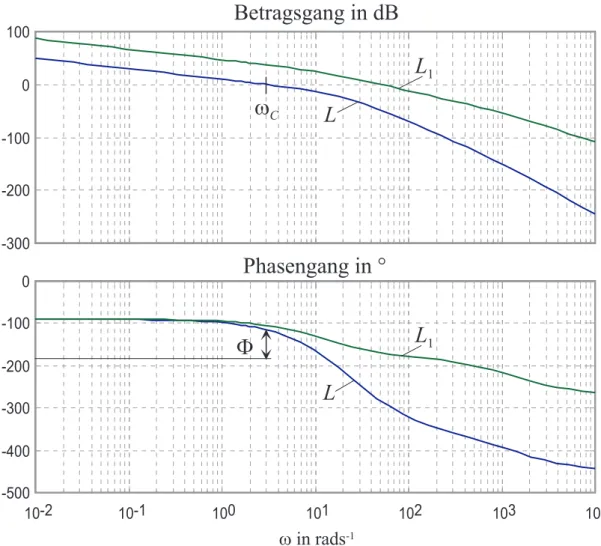
(D) Aus dem Bode-Diagramm des offenen KreisesL(s) von Abbildung 7.3 erkennt man, dass einerseits die Bedingungen von (B) erf¨ullt sind und andererseits die Betrags- kennlinie von L(s) um die Durchtrittsfrequenz ωC mit mindestens 20 dB/Dekade abf¨allt.

- 6 0 - 4 0 - 2 0

0

2 0 4 0 6 0

1 0 ^{- 2} 1 0 ^{- 1} 1 0 ⁰ 1 0 ¹

- 2 5 0 - 2 0 0 - 1 5 0 - 1 0 0

B e t r a g s g a n g i n d B

P h a s e n g a n g i n °

w i n r a d s ^{- 1}

L

L

L L

w

F

- 1 8 0 - 1 2 0

Abbildung 7.3: Bode-Diagramme des offenen Kreises L1(s) undL(s).

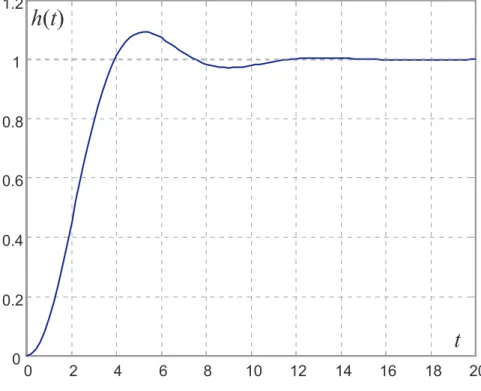
(E) Die zugeh¨orige Sprungantwort des geschlossenen Kreises von Abbildung 7.4 zeigt, dass die Entwurfsanforderungen recht gut erf¨ullt werden.

(F) In diesem Beispiel wurden an die Stellgr¨oße keine Anforderungen gestellt.

Es sei noch anzumerken, dass die Vorgangsweise, zuerst die Phase an der Durchtritts- frequenz ωC mit dem Linearterm des PI-Reglers (1 +sTI) einzustellen und anschließend mit VI den Betrag zu korrigieren, insofern Sinn macht, als der Verst¨arkungsfaktor VI des PI-Reglers zwar den Betrag aber nicht die Phase ¨andert.

0 2 4 6 8 1 0 1 2 1 4 1 6 1 8 2 0

0

0 . 2 0 . 4 0 . 6 0 . 8

1

1 . 2

t

h ( t )

Abbildung 7.4: Sprungantwort des geschlossenen Kreises.

Beispiel: Lead-Lag-Reglerentwurf

(A) Strecken¨ubertragungsfunktion:

G(s) = 1.8 _1.8^s + 1 s

1 + 2×0.8_2.8^s + _2.8^s 2 (7.19) Entwurfsvorgaben: tr= 0.1 s, ¨u= 20 % und e∞|r(t)=t = 0.01

(B) Vorgaben an den Frequenzgang des offenen KreisesL(Iω):ωC = 15 rads⁻¹, Φ = 50^◦ und der Verst¨arkungsfaktor VL des offenen Kreises muss nach (7.10) den Wert

VL = 1

e^∞ = 100 (7.20)

annehmen. Damit errechnet sich unmittelbar der Verst¨arkungsfaktor des Reglers zu

VR=VL/1.8 = 55.56 . (7.21)

(C) Berechnet man nun Betrag und Phase vonL1(Iω) =VRG(Iω) an der Stelleω=ωC, dann erh¨alt man

|L1(IωC)|= 1.93 und arg (L1(IωC)) = −169.65^◦ . (7.22) Man erkennt also, dass der Betrag gesenkt und die Phase angehoben werden muss.

Da der Verst¨arkungsfaktor VL durch die Forderung an die bleibende Regelabwei- chung fixiert ist, kann nicht die gleiche Vorgangsweise wie im vorigen Abschnitt beim

PI-Reglerentwurf gew¨ahlt werden, sondern man muss in diesem Fall einen Lead-Lag- Regler entwerfen. Dazu wird in einem ersten Schritt ein Lead-Regler so bestimmt, dass die Phase an der Durchtrittsfrequenz um ∆ϕ = 39.65^◦+ 10^◦ angehoben wird.

Die Phase wird deshalb um zus¨atzliche 10^◦ angehoben, da bei der nachfolgenden Betragsabsenkung durch ein Lag-Glied auch die Phase wieder abgesenkt wird.

Das Lead-Glied mit der ¨Ubertragungsfunktion (siehe auch 5.60) RLead(s) = 1 +sT

1 +sηT , 0< η <1 (7.23) hat nach Abschnitt 5.4 an der Stelle

ωmax = 1

√ηT (7.24)

die maximale Phasenanhebung ϕmax von ϕmax= arg (RLead(Iωmax)) = arctan

1

√η

−arctan (√η) . (7.25) Legt man nun die Durchtrittsfrequenz genau an die Stelle der maximalen Phasenan- hebung, alsoωmax=ωC, dann folgt aus (7.25)

η= 1 + 2 tan (∆ϕ)

tan (∆ϕ)− q

tan (∆ϕ)²+ 1

= 0.135 (7.26) bzw. mit (7.24) gilt

T = 1

√ηωC

= 0.1814 . (7.27)

Das Lead-Glied hat demnach die ¨Ubertragungsfunktion RLead(s) = 1 + 0.1814s

1 + 0.0245s . (7.28)

Eine erneute Berechnung des offenen Kreises f¨uhrt zu der ¨Ubertragungsfunktion L2(s) =VRG(s)RLead(s) = 55.56 1.8 _1.8^s + 1

s

1 + 2×0.8_2.8^s + _2.8^s 21 + 0.1814s

1 + 0.0245s . (7.29) Der Betrag und die Phase vonL₂(Iω) an der Stelle ω=ωC ergibt sich zu

|L2(IωC)|= 5.252 und arg (L2(IωC)) =−120^◦ . (7.30) Im n¨achsten Schritt muss nun an der Durchtrittsfrequenz ωC der Betrag um ∆a = 1/5.252 = 0.19 und die Phase um ∆ϕ=−10^◦ gesenkt werden. Dazu w¨ahle man ein Lag-Glied mit der ¨Ubertragungsfunktion

RLag(s) = 1 +sT

1 +sηT , η >1 . (7.31)

Aus den Bedingungen

arg (RLag(IωC)) = arctan (ωCT)−arctan (ωCηT) =

= arctan

ωCT −ηωCT 1 +ηω_C²T²

= ∆ϕ (7.32)

und

|RLag(IωC)|=

p1 +ω_C²T²

p1 +η²ω_C²T² = ∆a (7.33) folgen f¨ur T und η die allgemeinen Beziehungen

T = ∆a q

1 + tan (∆ϕ)²−1

ωCtan (∆ϕ) und η = ωCT −tan (∆ϕ)

ωCT (1 +ωCT tan (∆ϕ)) (7.34) bzw. f¨ur obiges Beispiel T = 0.305 und η = 5.37.

Damit lautet die ¨Ubertragungsfunktion des Lag-Reglers RLag(s) = 1 + 0.305s

1 + 1.638s . (7.35)

Fasst man (7.21), (7.28) und (7.35) zusammen, dann ergibt sich die Regler¨ubertra- gungsfunktion zu

R(s) =VRRLead(s)RLag(s) = 55.56

1 + 0.1814s 1 + 0.0245s

1 + 0.305s 1 + 1.638s

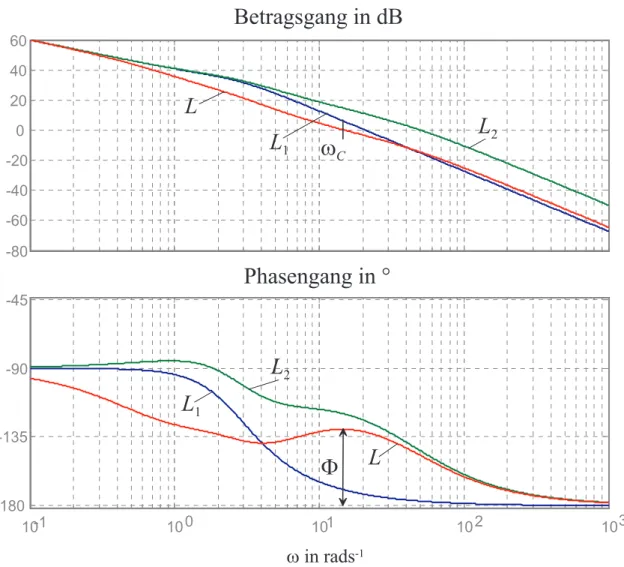
. (7.36) (D) Aus dem Bode-Diagramm des offenen KreisesL(s) von Abbildung 7.5 erkennt man, dass einerseits die Bedingungen von (B) erf¨ullt sind und andererseits die Betrags- kennlinie von L(s) um die Durchtrittsfrequenz ωC mit mindestens 20 dB/Dekade abf¨allt.

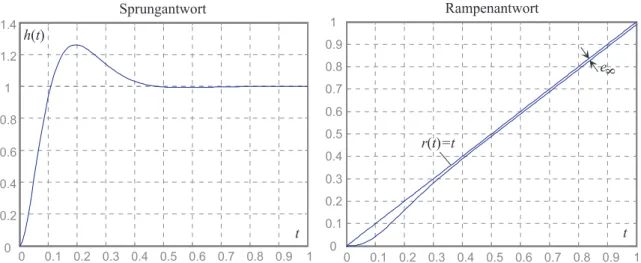
(E) Die Sprung- sowie die Rampenantwort des geschlossenen Kreises sind Abbildung 7.6 zu entnehmen.

(F) In diesem Beispiel wurden an die Stellgr¨oße keine Anforderungen gestellt.

Aufgabe 7.4. Berechnen Sie die Beziehungen f¨ur T und η von (7.34).

Beispiel: Kompensationsreglerentwurf

(A) Als Strecken¨ubertragungsfunktion betrachte man die Antriebsregelstrecke von Ab- bildung 6.2 mit der ¨Ubertragungsfunktion (siehe auch (6.8))

GuT ,n,ω2(s)∼= 222.22 1 + _11.17^s

1 + _1321.66^s 1 + 2×0.138 _1.82^s

+ _1.82^s 2 . (7.37) Entwurfsvorgaben: tr = 0.5 s, ¨u = 5 %, e^∞|r(t)=σ(t) = 0 und |uT,n| ≤ 1 f¨ur r(t) = 100σ(t)

P h a s e n g a n g i n °

1 0 - 1 1 0 0 1 0 1 1 0 2 1 0 3

- 1 8 0 - 1 3 5

- 9 0 - 4 5 - 8 0 - 6 0 - 4 0 - 2 0

0

2 0 4 0 6 0

w i n r a d s ^{- 1}

B e t r a g s g a n g i n d B

L

L

L

L

L L

w

F

Abbildung 7.5: Bode-Diagramme des offenen Kreises L1(s), L2(s) und L(s).

(B) Vorgaben an den Frequenzgang des offenen Kreises L(Iω):ωC = 3 rads⁻¹, Φ = 65^◦ und der offene Kreis muss mindestens eine einfache Polstelle bei s= 0 haben (C) Als Regler wird in diesem Fall ein so genannter Kompensationsregler der Form

R(s) = VR

1 + 2×0.138 _1.82^s

+ _1.82^s 2

s(1 +sTR)² (7.38)

gew¨ahlt. Im ersten Schritt wird das Bode-Diagramm aller bekannten Terme des offenen KreisesL(s) =R(s)GuT ,n,ω2(s), also

L1(s) = 222.22 s 1 + _11.17^s

1 + _1321.66^s (7.39)

gezeichnet, siehe Abbildung 7.7. An der Durchtrittsfrequenz ωC = 3 errechnet sich das Argument von L1(IωC) zu arg (L1(IωC)) = −104.5^◦. Daher muss wegen Φ =

0 0 . 1 0 . 2 0 . 3 0 . 4 0 . 5 0 . 6 0 . 7 0 . 8 0 . 9 1

0

0 . 2 0 . 4 0 . 6 0 . 8

1

1 . 2 1 . 4

0 0 . 1 0 . 2 0 . 3 0 . 4 0 . 5 0 . 6 0 . 7 0 . 8 0 . 9 1

0

0 . 1 0 . 2 0 . 3 0 . 4 0 . 5 0 . 6 0 . 7 0 . 8 0 . 9

1 te 8

r (t)= t

R a m p e n a n t w o r t S p r u n g a n t w o r t

t

h (t)

Abbildung 7.6: Sprung- und Rampenantwort des geschlossenen Kreises.

65^◦ mit Hilfe der verbleibenden Terme im Nenner des Reglers (1 +sTR)² die Phase um 10.5^◦ abgesenkt werden. Aus dieser Bedingung errechnet sich TR zu

TR= tan ^10.5_{2 180}^π ωC

= 0.0306 . (7.40)

Die Betragskorrektur an der Durchtrittsfrequenz ωC = 3 erfolgt mit Hilfe des Ver- st¨arkungsfaktors VR

VR = 1

|L2(IωC)| = 0.0141 mit L₂(s) = 222.22 s 1 + _11.17^s

1 + _1321.66^s

(1 + 0.0306s)² (7.41) und somit lautet die gesamte Regler¨ubertragungsfunktion

R(s) =

0.0141

1 + 2×0.138 _1.82^s

+ _1.82^s 2

s(1 + 0.0306s)² . (7.42)

(D) Aus dem Bode-Diagramm des offenen KreisesL(s) von Abbildung 7.7 erkennt man, dass einerseits die Bedingungen von (B) erf¨ullt sind und andererseits die Betrags- kennlinie von L(s) um die Durchtrittsfrequenz ωC mit mindestens 20 dB/Dekade abf¨allt.

(E) Die Sprungantwort des geschlossenen Kreises ist dem linken Bild von Abbildung 7.8 zu entnehmen.

(F) Zur ¨Uberpr¨ufung der Betragsbeschr¨ankung der Stellgr¨oße |uT,n| ≤ 1 f¨ur r(t) = 100σ(t) wird die ¨Ubertragungsfunktion

Gr,uT ,n(s) = R(s)

1 +R(s)GuT ,n,ω2(s) (7.43)

P h a s e n g a n g i n ° B e t r a g s g a n g i n d B

- 3 0 0 - 2 0 0 - 1 0 0

0

1 0 0

1 0 - 2 1 0 - 1 1 0 0 1 0 1 1 0 2 1 0 3 1 0 4

- 5 0 0 - 4 0 0 - 3 0 0 - 2 0 0 - 1 0 0

0 w i n r a d s ^{- 1}

L

L L L

w

F

Abbildung 7.7: Bode-Diagramme des offenen Kreises L1(s) undL(s).

berechnet und die Sprungantwort f¨urr(t) = 100σ(t) aufgezeichnet. Im rechten Bild von Abbildung 7.8 erkennt man, dass diese Forderung nicht eingehalten wird. Den Ausf¨uhrungen von Abschnitt 6.3 folgend wird deshalb dem Regelkreis ein Vorfilter der Form

F (s) = rˆ ˆ ω2,soll

= 1

1 + 2×0.92 ^s₅

+ ₅^s2 (7.44)

vorgeschaltet.

Wie man sich an Hand von Abbildung 7.8 selbst ¨uberzeugen kann, bedingt diese Maßnahme eine drastische Verringerung der Stellgr¨oße ohne dabei wesentlich die Dynamik der F¨uhrungsregelung zu verringern.

Es sei an dieser Stelle erw¨ahnt, dass schwach ged¨ampfte quadratische Terme der Form 1 + 2ξsT + (sT)²

mit T >0, 0< ξ <0.7 wie der Term

1 + 2×0.138 _1.82^s

+ _1.82^s 2 von (7.37) typischer Weise bei der Regelung mechanischer Systeme auftreten. Man be- achte, dass obige Vorgangsweise eines Kompensationsreglerentwurfes dann bei prakti- schen Implementationen nicht zum Ziel f¨uhrt, wenn die tats¨achlichen Streckenparame- ter vom Modell zu weit abweichen. In diesem Fall empfiehlt es sich, den quadratischen

0 0 . 5 1 1 . 5 2 2 . 5 3

0

0 . 2 0 . 4 0 . 6 0 . 8

1

1 . 2 1 . 4

t

h (t)

S p r u n g a n t w o r t d e r F ü h r u n g s ü b e r t r a g u n g s f u n k t i o n f ü r r (t) = s (t)

m i t V o r f i l t e r o h n e V o r f i l t e r

0 0 . 5 1 1 . 5 2 2 . 5 3

- 1

0123456

S p r u n g a n t w o r t d e r S t e l l g r ö ß e n ü b e r t r a g u n g s f u n k t i o n

f ü r r(t) = 1 0 0 s (t) t

m i t V o r f i l t e r o h n e V o r f i l t e r

Abbildung 7.8: Sprungantworten der F¨uhrungs- und Stellgr¨oßen¨ubertragungsfunktion mit und ohne Vorfilter.

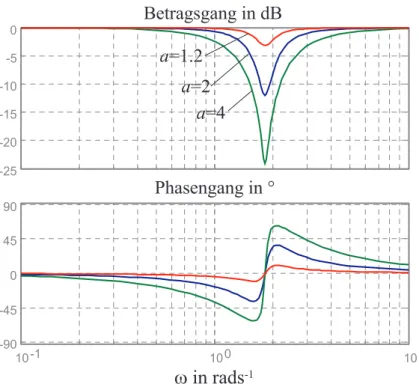
Term nicht exakt zu kompensieren, sondern ein so genanntes Notchfilter zu entwer- fen. Abbildung 7.9 zeigt das Bode-Diagramm eines m¨oglichen Notchfilters f¨ur den Term 1 + 2×0.138 _1.82^s

+ _1.82^s 2

der Form

RN(s) = 1 + 2×0.138/a _1.82^s

+ _1.82^s 2

1 + 2×0.138a _1.82^s

+ _1.82^s 2 (7.45)

f¨ur verschiedene Werte vona >0.

Man erkennt, dass gr¨oßere Werte von a ein breitbandigeres Kompensieren der st¨orenden Resonanzfrequenz bedingen und somit der Regelkreis robuster gegen¨uber Schankungen des Wertes der Resonanzfrequenz wird, sich gleichzeitig aber die Phase vor der Resonanz- frequenz entsprechend verschlechtert.

Aufgabe 7.5. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = yˆ

ˆ

u = 50

1 + ₁₇₁^s

1 + ₂₃₃₀^s

einen PI-Regler so, dass die Sprungantwort des geschlossenen Kreises folgende Spezifika- tionen tr = 0.01s, u¨ = 10 %, e∞|r(t)=σ(t) = 0 und |u| ≤ 15 f¨ur r(t) = 500σ(t) erf¨ullt.

Uberpr¨ufen Sie das Entwurfsergebnis durch Simulation in¨ Matlab/Simulink.

Ergebnis: Ein m¨oglicher PI-Regler, der diese Anforderung erf¨ullt, lautet R(s) = 3.91 + _567.3^s

s .

Aufgabe 7.6. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = 0.5

s ₂^s + 1

w i n r a d s ^{- 1}

- 2 5 - 2 0 - 1 5 - 1 0 - 5

0

1 0 - 1 1 0 0 1 0 1

- 9 0 - 4 5

0

4 5

9 0 P h a s e n g a n g i n °

B e t r a g s g a n g i n d B a = 1 . 2

a = 2

a = 4

Abbildung 7.9: Bode-Diagramm eines Notchfilters zur Kompensation der Resonanzfre- quenz.

einen Regler so, dass die Sprungantwort des geschlossenen Kreises folgenden Spezifikatio- nen tr = 1s,u¨= 10 % und e^∞|r(t)=σ(t) = 0 gen¨ugt.

Hinweis: Benutzen Sie einen Regler der Form R(s) =VR

1 + ₂^s 1 +sTR

und ¨uberpr¨ufen Sie das Entwurfsergebnis durch Simulation in Matlab/Simulink.

Aufgabe 7.7. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion

G(s) = 0.759

1 + _0.196^s 1 + 2×0.152 _5.945^s

+ _5.945^s 2

einen Regler so, dass die Sprungantwort des geschlossenen Kreises folgenden Spezifikatio- nen tr = 2s,u¨= 0 % und e^∞|r(t)=σ(t) = 0 gen¨ugt.

Hinweis:Entwerfen Sie in einem ersten Schritt einen PI-Regler. Falls bei der ¨Uberpr¨ufung des Entwurfsergebnisses durch Simulation inMatlab/Simulinkkein zufriedenstellendes Resultat erzielt wird, erweitern Sie den PI-Regler um ein geeignetes Notchfilter.

Aufgabe 7.8. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion

G(s) = 1

2 + 2s+s²

einen Regler so, dass die Sprungantwort des geschlossenen Kreises folgenden Spezifikatio- nen tr = 1s,u¨= 20 % und e∞|r(t)=σ(t) = 0 gen¨ugt.

Hinweis: Benutzen Sie einen PI-Regler und ¨uberpr¨ufen Sie das Entwurfsergebnis durch Simulation inMatlab/Simulink.

Aufgabe 7.9. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion

G(s) = 5

s

2 + 2 ^s₅

+ ₅^s2

einen Regler so, dass die Sprungantwort des geschlossenen Kreises folgenden Spezifikatio- nen tr = 0.25s, u¨= 20 % und e∞|r(t)=σ(t) = 0gen¨ugt.

Hinweis:Uberpr¨ufen Sie das Entwurfsergebnis durch Simulation in¨ Matlab/Simulink.

Aufgabe 7.10. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion

G(s) = 1

2 + 2 ^s₂

+ ^s₂2

einen Regler so, dass die Anstiegszeit der Sprungantwort des geschlossenen Kreises fol- gender Spezifikation tr = 0.75s gen¨ugt.

Hinweis: Da außer an die Anstiegszeit tr keine weiteren Anforderungen gestellt sind, versuchen Sie den Entwurf mit Hilfe eines einfachen P-ReglersR(s) = VRdurchzuf¨uhren.

Aufgabe 7.11. Entwerfen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = 2 1 + _1.2^s

s

1 + 2×0.6 _0.8^s

+ _0.8^s 2

einen Regler so, dass die Sprungantwort des geschlossenen Kreises folgenden Spezifikatio- nen tr = 0.625s,u¨= 10 % und e∞|r(t)=t= 0.25 gen¨ugt.

Hinweis:Uberpr¨ufen Sie das Entwurfsergebnis durch Simulation in¨ Matlab/Simulink.

7.2. Polvorgabe im Frequenzbereich

Die Methode der Polvorgabe ist eine algebraische Reglerentwurfsmethode, bei der zu ei- ner gegebenen Strecken¨ubertragungsfunktionG(s) ein Regler so entworfen wird, dass der geschlossene Kreis von der F¨uhrungsgr¨oße r(t) zur Ausgangsgr¨oße y(t) ein gew¨unschtes Verhalten der F¨uhrungs¨ubertragungsfunktion Tr,y(s) aufweist. Nat¨urlich kann die F¨uh- rungs¨ubertragungsfunktion Tr,y(s) nicht beliebig vorgegeben werden, sondern muss in Abh¨angigkeit von der Strecken¨ubertragungsfunktion G(s) gewissen Einschr¨ankungen ge- n¨ugen.

Dazu nachfolgende Definition:

Definition 7.1. (Implementierbarkeit) Man nennt eine F¨uhrungs¨ubertragungsfunk- tionTr,y(s)zu einer Strecken¨ubertragungsfunktionG(s) implementierbar, wenn die nach- folgenden Bedingungen erf¨ullt sind:

(1) Das Regelgesetz ist realisierbar (siehe Satz 4.4), (2) der Regelkreis ist intern stabil (siehe Satz 6.1) und

(3) der Regelkreis ist nicht degeneriert, d.h. s¨amtliche ¨Ubertragungsfunktionen des ge- schlossenen Kreises sind realisierbar.

Die Implementierbarkeit einer F¨uhrungs¨ubertragungsfunktion kann nun sehr einfach ¨uber- pr¨uft werden, es gilt n¨amlich folgender Satz:

Satz 7.1. (Implementierbarkeit) Eine F¨uhrungs¨ubertragungsfunktion Tr,y(s) zu ei- ner realisierbaren Strecken¨ubertragungsfunktion G(s) ist genau dann implementierbar, wenn

(1) die F¨uhrungs¨ubertragungsfunktionTr,y(s)BIBO-stabil und (2) die Stellgr¨oßen¨ubertragungsfunktion

Tr,u(s) = Tr,y(s)

G(s) (7.46)

realisierbar und BIBO-stabil ist.

Beweis:F¨uhrungs¨ubertragungsfunktion ist implementierbar⇒Bedingungen (1) und (2):

Da der Regelkreis gem¨aß Definition 7.1 Bedingung (2) intern stabil sein muss, sind die F¨uhrungs- und die Stellgr¨oßen¨ubertragungsfunktionTr,y(s) undTr,u(s) BIBO-stabil. Aus der Bedingung (3) von Definition 7.1 folgt, dassTr,y(s) und Tr,u(s) realisierbar sein m¨us- sen. WennG(s) realisierbar ist, dann folgt aus der Realisierbarkeit vonTr,u(s) nach (7.46) automatisch die Realisierbarkeit von Tr,y(s).

Bedingungen (1) und (2) ⇒ F¨uhrungs¨ubertragungsfunktion ist implementierbar: Dieser Teil des Beweises erfolgt konstruktiv an Hand der n¨achsten beiden Kapitel.

Polvorgabe mit einem Freiheitsgrad

Den weiteren Betrachtungen liegt ein Regelkreis mit einem Freiheitsgrad nach Abbildung 7.10 zugrunde.

G ( s )

r R ( s ) u y e

R e g l e r S t r e c k e

Abbildung 7.10: Regelkreis mit einem Freiheitsgrad.

F¨ur die realisierbaren ¨Ubertragungsfunktionen G(s) und R(s) gelte G(s) = a(s)

b(s) = Pn

j=0ajs^j Pn

j=0bjs^j, bn6= 0 und R(s) = x(s) y(s) =

Pm j=0xjs^j Pm

j=0yjs^j, ym 6= 0 (7.47) mit den teilerfremden Z¨ahler- und Nennerpolynomen a(s), b(s) sowie x(s), y(s). Die F¨uhrungs¨ubertragungsfunktion Tr,y(s) errechnet sich dann in der Form

Tr,y(s) = a(s)x(s)

a(s)x(s) +b(s)y(s) . (7.48) Im Rahmen derPolvorgabe mit einem Freiheitsgrad wird eine realisierbare ¨Ubertragungs- funktion R(s) so entworfen, dass die Pole von Tr,y(s) eine gew¨unschte Lage aufweisen.

Nach (7.48) ist diese Aufgabe aber ¨aquivalent dazu, die so genannte Diophantische Glei- chung

a(s)x(s) +b(s)y(s) =d(s) (7.49) f¨ur die gegebenen teilerfremden Polynome a(s) und b(s) der Strecken¨ubertragungsfunk- tion G(s) und das gew¨unschte Nennerpolynom d(s) der F¨uhrungs¨ubertragungsfunktion Tr,y(s) nach den Polynomenx(s) undy(s) der Regler¨ubertragungsfunktionR(s) zu l¨osen.

Das Ergebnis l¨asst sich im nachfolgenden Satz formulieren:

Satz 7.2. (Polvorgabe mit einem Freiheitsgrad) Gegeben ist der Regelkreis mit ei- nem Freiheitsgrad nach Abbildung 7.10 mit der Strecken¨ubertragungsfunktionn-ter Ord- nung

G(s) = a(s)

b(s) , grad(a(s))< grad(b(s)) =n (7.50) und den teilerfremden Polynomena(s)und b(s). Dann existiert zu jedem Polynomd(s) mit grad(d(s)) = 2n−1 eine L¨osung x(s)und y(s) der Diophantischen Gleichung

a(s)x(s) +b(s)y(s) =d(s) (7.51) so, dass f¨ur die Regler¨ubertragungsfunktion gilt

R(s) = x(s)

y(s) , grad(x(s))≤grad(y(s)) =n−1 . (7.52) Beweis: Setzt man in der Diophantischen Gleichung (7.51) f¨ur die Polynome die Aus- dr¨ucke von (7.47) ein und w¨ahlt f¨urd(s) ein Polynom der Ordnung p, dann erh¨alt man

Xn j=0

ajs^j Xm

j=0

xjs^j + Xn

j=0

bjs^j Xm

j=0

yjs^j = Xp

j=0

djs^j , dp 6= 0 . (7.53) Durch Ausmultiplikation der Ausdr¨ucke in (7.53) ergibt sich

(ansⁿ+an−1sⁿ⁻¹+. . .+a0) (xms^m+xm−1s^m−1+. . .+x0) +

(bnsⁿ+bn−1sⁿ⁻¹+. . .+b0) (yms^m+ym−1s^m−1+. . .+y0) =dps^p+. . .+d0

(7.54)

bzw.

(anxm+bnym)s^n+m+ (an−1xm+anxm−1+bn−1ym+bnym−1)s^n+m−1+. . .

+ (a₀x₀+b₀y₀) =dps^p+dp−1s^p−1+. . .+d₀ . (7.55) Aus (7.55) erkennt man durch Koeffizientenvergleich, dass einerseits die Beziehungn+m = p gelten muss und dass andererseits p+ 1 Gleichungen in 2m+ 2 Unbekannten zu l¨osen sind. Daraus errechnen sich die Ordnungen m und p der Regler- und der F¨uhrungs¨uber- tragungsfunktion zu

m =n−1 und p= 2n−1 . (7.56)

Schreibt man nun die Gleichungen des Koeffizientenvergleiches von (7.55) in Matrixform an, dann erh¨alt man















a0 b0 0 0 . . . 0 0 a1 b1 a0 b0 . . . ... ...

... ... ... ... ... ... a0 b0

an bn an−1 bn−1 . . . a1 b1

... ... an bn . . . a2 b2

... ... ... ... ... ... ... ... 0 0 0 0 . . . an bn















| {z }

R











 x0

y0

x₁ y1

...

xn−1

yn−1













=











 d0

d1

d2

... ... d2n−2

d_2n−1













. (7.57)

Die MatrixR, die aus den Koeffizienten der Polynomea(s) undb(s) gebildet wird, nennt man auchResultante.

Wie noch gezeigt wird, ist die ResultanteR zweier Polynome a(s) und b(s) genau dann regul¨ar, wenn a(s) und b(s) teilerfremd sind. Da aber in Satz 7.2 vorausgesetzt wurde, dass a(s) und b(s) teilerfremd sind, ist damit das Gleichungssystem (7.57) eindeutig l¨osbar. Weiters folgt aus der letzten Gleichung von (7.57) wegen an = 0, bn 6= 0 (siehe (7.50)) und d2n−1 6= 0 sofort die Beziehung yn−1 6= 0 und damit die Realisierbarkeit von R(s). Dies beendet auch den Beweis.

Im Beweis von Satz 7.2 wurde noch nachfolgender Satz verwendet, der im Weiteren auch bewiesen werden soll:

Satz 7.3. (Sylvester-Kriterium) Die Resultante R zu den Polynomen a(s) und b(s) ist genau dann regul¨ar, wenn die Polynome a(s) und b(s) teilerfremd sind.

Beweis: a(s) und b(s) sind teilerfremd ⇒ R ist regul¨ar oder ¨aquivalent dazu R ist singul¨ar⇒a(s) undb(s) sind nicht teilerfremd: Unter der Annahme, dassRsingul¨ar ist, existiert f¨ur das Gleichungssystem

Rz=0 mit z^T = [x0, y0, x1, y1, . . . , xn−1, yn−1] (7.58) eine nichttriviale L¨osung z6=0. Damit gibt es eine nichttriviale Regler¨ubertragungsfunk- tion (7.52) so, dass gilt

a(s)x(s) +b(s)y(s) = 0 (7.59)

bzw.

a(s)

b(s) =−y(s)

x(s) mit grad(b(s)) =n und grad(x(s))≤n−1 . (7.60) Daraus erkennt man unmittelbar, dassa(s) undb(s) nicht teilerfremd sein k¨onnen.

Aufgabe 7.12. Beweisen Sie die Umkehrung, dass die Regularit¨at vonRdie Teilerfremd- heit der Polynome a(s)und b(s) impliziert.

Es sei an dieser Stelle angemerkt, dass die Einschr¨ankung der betrachteten Strecken¨uber- tragungsfunktionenG(s) in (7.50) auf jene mit Z¨ahlergrad kleiner als Nennergrad (strictly proper) nicht unbedingt notwendig ist. Man muss im Falle von ¨Ubertragungsfunktionen G(s) mit Z¨ahlergrad gleich Nennergrad lediglich zus¨atzlich ¨uberpr¨ufen, ob der Regelkreis nicht degeneriert ist.

Tafelbeispiel: Berechnen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = s−1

s(s−2) (7.61)

einen Regler R(s) durch Polvorgabe mit einem Freiheitsgrad so, dass alle Pole des ge- schlossenen Kreises bei −1 liegen.

Ergebnis: Die Regler¨ubertragungsfunktion lautet R(s) = 14s−1

s−9 . (7.62)

Aufgabe 7.13. Schreiben Sie ein Programm in Matlab, das aus der Strecken¨ubertra- gungsfunktionG(s)und dem gew¨unschten Nennerpolynom des geschlossenen Kreisesd(s) die Regler¨ubertragungsfunktionR(s)berechnet.

Aufgabe 7.14. Berechnen Sie f¨ur die Strecken¨ubertragungsfunktion

G(s) = 4s

(s+ 3) (s−10)

einen Regler R(s) durch Polvorgabe mit einem Freiheitsgrad so, dass alle Pole des ge- schlossenen Kreises bei −1liegen.

Ergebnis: Die Regler¨ubertragungsfunktion lautet R(s) = 2.508s+ 8.192

s−0.0333 .

Aufgabe 7.15. Berechnen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = s+ 2

s(s²−1)

einen Regler R(s) durch Polvorgabe mit einem Freiheitsgrad so, dass die Pole des ge- schlossenen Kreises bei −1, −2±3I und −4±5I liegen.

Ergebnis: Die Regler¨ubertragungsfunktion lautet

R(s) = 33.5s²+ 300s+ 266.5 s²+ 13s+ 65.5 .

Polvorgabe mit zwei Freiheitsgraden

Wie man aus (7.48) unmittelbar erkennt, kann durch die Methode der Polvorgabe mit einem Freiheitsgrad das Z¨ahlerpolynom der F¨uhrungs¨ubertragungsfunktion Tr,y(s) nicht gezielt beeinflusst werden. Dieser Nachteil kann nun mit Hilfe der Polvorgabe mit zwei Freiheitsgraden beseitigt werden. Man betrachte dazu den Regelkreis mit zwei Freiheits- graden von Abbildung 7.11.

G ( s ) y

r u R ( s )

V ( s )

Abbildung 7.11: Regelkreis mit zwei Freiheitsgraden.

F¨ur den Regler sei angenommen, dass V (s) und R(s) das gleiche Nennerpolynom y(s) besitzen (siehe auch Aufgabe 6.4). Man sagt dann auch, V (s) und R(s) bilden ein dy- namisches System. Wie wir im Folgenden noch sehen werden, hat dies essentielle Konse- quenzen bei der Realisierung des Reglers. Die ¨Ubertragungsfunktionen G(s), R(s) und V (s) angeschrieben in Form ihrer Z¨ahler- und Nennerpolynome lauten dann

G(s) = a(s) b(s) =

Pn j=0ajs^j Pn

j=0bjs^j,R(s) = x(s) y(s) =

Pm j=0xjs^j Pm

j=0yjs^j und V (s) = z(s)

y(s) = Pm

j=0zjs^j Pm

j=0yjs^j

(7.63)

mit bn 6= 0 und ym 6= 0. Ohne Einschr¨ankung der Allgemeinheit wird auch hier wieder vorausgesetzt, dass f¨ur die Strecken¨ubertragungsfunktion giltgrad(a(s))< grad(b(s)) = n und dass die Polynome a(s) und b(s) teilerfremd sind.

Nach Satz 7.1 ist eine F¨uhrungs¨ubertragungsfunktion Tr,y(s) genau dann implementier- bar, wenn Tr,y(s) BIBO-stabil und die Stellgr¨oßen¨ubertragungsfunktion Tr,u(s) = ^T_G(s)^r,y(s) realisierbar und BIBO-stabil ist. Um diesen Satz auf den Regelkreis mit zwei Freiheits- graden von Abbildung 7.11 anwenden zu k¨onnen, berechne man in einem ersten Schritt die zugeh¨orige F¨uhrungs- und Stellgr¨oßen¨ubertragungsfunktion

Tr,y(s) = V (s)G(s)

1 +R(s)G(s) = a(s)z(s)

a(s)x(s) +b(s)y(s) = zT (s)

nT (s) (7.64)

und

Tr,u(s) = Tr,y(s)

G(s) = zT (s) nT (s)

b(s)

a(s) . (7.65)

Damit ergibt sich als unmittelbare Konsequenz von Satz 7.1 folgender Satz:

Satz 7.4. (Implementierbarkeit f¨ur einen Regelkreis mit zwei Freiheitsgra- den) Eine F¨uhrungs¨ubertragungsfunktion Tr,y(s) = _n^zT(s)

T(s) (zT(s) und nT (s) teilerfremd) zu einer realisierbaren Strecken¨ubertragungsfunktion G(s) = ^a(s)_b(s) (a(s) und b(s) teiler- fremd) ist f¨ur den Regelkreis mit zwei Freiheitsgraden von Abbildung 7.11 genau dann implementierbar, wenn nachfolgende Bedingungen erf¨ullt sind:

(1) Das Polynom nT (s)ist ein Hurwitzpolynom,

(2) die Graddifferenz vonTr,y(s), also grad(nT (s))−grad(zT (s)), ist gr¨oßer gleich der Graddifferenz von G(s), also grad(b(s))−grad(a(s)), und

(3) alle Nullstellensj von G(s) mit Re(sj)≥0sind auch Nullstellen von Tr,y(s).

Aufgabe 7.16. Beweisen Sie Satz 7.4.

Hinweis:Verwenden Sie Satz 7.1 und wenden Sie diesen auf die Beziehungen (7.64) und (7.65) an.

Die Vorgangsweise bei der Polvorgabe mit zwei Freiheitsgraden sieht nun wie folgt aus:

(A) Zu einer gegebenen Strecken¨ubertragungsfunktion G(s) = ^a(s)_b(s) w¨ahle man eine im- plementierbare F¨uhrungs¨ubertragungsfunktionTr,y(s) = ^z_n^T(s)

T(s), die die Bedingungen (1) - (3) von Satz 7.4 erf¨ullt.

(B) Danach berechne man die Stellgr¨oßen¨ubertragungsfunktion Tr,u(s) gem¨aß (7.65) und f¨uhre s¨amtliche K¨urzungen zwischenzT(s) unda(s) durch (eingerahmte Poly- nome in (7.65)). Bezeichnet man mit ˜zT (s) und ˜a(s) die gek¨urzten Polynome, dann ergibt sich Tr,u(s) zu

Tr,u(s) = z˜T (s) nT(s)

b(s)

˜

a(s) . (7.66)

Man unterscheidet nun drei F¨alle:

(a) grad(nT(s) ˜a(s)) = 2n−1: Es kann sofort die Diophantische Gleichung a(s)x(s) +b(s)y(s) = d(s) =nT (s) ˜a(s) (7.67) f¨urx(s) und y(s) gel¨ost werden.

(b) grad(nT(s) ˜a(s)) < 2n −1: Um nun die Diophantische Gleichung l¨osen zu k¨onnen, wirdTr,u(s) im Z¨ahler und Nenner um ein Hurwitzpolynom ˜r(s), auch Realisierungspolynom genannt, mit grad(˜r(s)) = 2n−1−grad(nT (s) ˜a(s)) in der Form

Tr,u(s) = z˜T (s) nT (s)

b(s)

˜ a(s)

˜ r(s)

˜

r(s) (7.68)

erweitert. Anschließend kann die Diophantischen Gleichung

a(s)x(s) +b(s)y(s) = d(s) =nT (s) ˜a(s) ˜r(s) (7.69) f¨urx(s) und y(s) gel¨ost werden.

(c) grad(nT(s) ˜a(s))>2n−1: Die gew¨ahlte ¨Ubertragungsfunktion Tr,y(s) muss in zwei BIBO-stabile jeweils f¨ur sich realisierbare Teil¨ubertragungsfunktionen Tr,y(s) = T1(s)T2(s) so zerlegt werden, dass man f¨ur T2(s) die Implementie- rungsaufgabe l¨osen kann. In einem zweiten Schritt wird vor die Regler¨uber- tragungsfunktion V (s) die ¨Ubertragungsfunktion T1(s) geschaltet und damit ergibt die Serienschaltung vonT1(s) und T2(s) die gew¨unschte F¨uhrungs¨uber- tragungsfunktionTr,y(s).

(C) Im letzten Schritt muss noch das Z¨ahlerpolynom z(s) der ¨Ubertragungsfunktion V (s) berechnet werden. Dazu vergleiche man die Z¨ahlerpolynome von

Tr,y(s) = a(s)z(s)

a(s)x(s) +b(s)y(s) und Tr,y(s) =Tr,u(s)G(s) = z˜T(s)a(s) ˜r(s) d(s)

(7.70) und daraus erh¨alt man die Beziehung

z(s) = ˜zT (s) ˜r(s) . (7.71) Reglerrealisierung

Da die Regler¨ubertragungsfunktionen V (s) und R(s) ein dynamisches System bilden (V (s) und R(s) haben das gleiche Nennerpolynomy(s)),muss der Regler auch als sol- cher implementiert werden, insbesondere dann, wenny(s) kein Hurwitzpolynom ist. Eine geeignete Realisierung der ¨Ubertragungsfunktionen V (s) und R(s) eines dynamischen Systems der Form

V (s) = bV,0+bV,1s+. . .+bV,n−1sⁿ⁻¹+bV,nsⁿ a0+a1s+. . .+an−1sⁿ⁻¹+sⁿ R(s) = bR,0 +bR,1s+. . .+bR,n−1sⁿ⁻¹+bR,nsⁿ

a0+a1s+. . .+an−1sⁿ⁻¹+sⁿ

(7.72)

ist durch die so genannte erweiterte 2-te Standardform von (4.61)

d dt







 x1

x2

...

xn−1

xn









| {z }

x

=









0 . . . 0 −a0

1 0 . . .0 −a1

... 1 ... ... ...

0 0 . .. 0 −an−2

0 0 . . .1 −an−1









| {z }

A







 x1

x2

...

xn−1

xn









| {z }

x

+









˜bV,0 −˜bR,0

˜bV,1 −˜bR,1

... ...

˜bV,n−2 −˜bR,n−2

˜bV,n−1 −˜bR,n−1









| {z }

B

r y

u =

0 0. . . 0 1

| {z }

c^T







 x1

x₂ ...

xn−1

xn









| {z }

x

+

bV,n −bR,n

| {z }

D

r y

(7.73)

mit

˜bV,j =bV,j−bV,naj und ˜bR,j =bR,j −bR,naj f¨ur j = 0,1, . . . , n−1 (7.74) gegeben.

Asymptotisches Verhalten

Abgesehen davon, dass die F¨uhrungs¨ubertragungsfunktion Tr,y(s) implementierbar sein muss, also den Bedingungen von Satz 7.4 gen¨ugt, w¨unscht man sich oft ein definier- tes asymptotisches Verhalten. Man fordert beispielsweise, dass der station¨are Regelfehler e(t) =y(t)−r(t) f¨ur einen Einheitssprung r(t) =σ(t) Null wird, also der Bedingung

tlim→∞

e(t) = lim

s→0sˆe(s) = lim

s→0s(ˆr(s)−yˆ(s)) = lim

s→0s 1

s − 1

sTr,y(s)

= 0 (7.75) gen¨ugt. Aus (7.75) erkennt man, dass in diesem Fall f¨ur die F¨uhrungs¨ubertragungsfunktion Tr,y(s) die Beziehung lims→0Tr,y(s) = 1 gelten muss. Diese ¨Uberlegung kann nun nat¨urlich auf allgemeinere Eingangssignale r(t) erweitert werden.

Als zweites Beispiel betrachte man jenen Fall, dass der Fehler e(t) f¨ur ein harmonisches Referenzsignal der Formr(t) =Asin (ω0t) im eingeschwungenen Zustand zu Null gemacht werden soll. Dies bedeutet also, dass man die BedingungTr,e(Iω0) = 0 bzw.

Tr,e(Iω0) = 1−Tr,y(Iω0) = 0 (7.76) einhalten muss.

Simulationsbeispiel:

F¨ur die Strecken¨ubertragungsfunktion

G(s) = (s−2) (s+ 3)

(s−3)³ (7.77)

ist ein Regler durch Polvorgabe mit zwei Freiheitsgraden so zu entwerfen, dass die F¨uh- rungs¨ubertragungsfunktion Tr,y(s) implementierbar ist und das asymptotische Verhalten limt→∞e(t) = 0 f¨ur r(t) =σ(t) aufweist. S¨amtliche Pole eines eventuell ben¨otigten Rea- lisierungspolynoms ˜r(s) sind auf -2 zu legen.

(A) Man ¨uberzeugt sich leicht, dass mit

Tr,y(s) =−1 2

s−2

(s+ 1)² (7.78)

eine geeignete implementierbare F¨uhrungs¨ubertragungsfunktion gegeben ist.

(B) Die zugeh¨orige Stellgr¨oßen¨ubertragungsfunktionTr,u(s) lautet Tr,u(s) = Tr,y(s)

G(s) = ⁻

1

2(s−2) (s+ 1)²

(s−3)³

(s−2) (s+ 3) (7.79) bzw. nach K¨urzung der gerahmten Terme erh¨alt man

Tr,u(s) = −¹₂(s−3)³

(s+ 1)²(s+ 3) ^. (7.80)

Da der Grad des Nennerpolynoms von Tr,u(s) gleich 3 und die Streckenordnung n= 3 ist, muss Tr,u(s) um ein Realisierungspolynom 2-ter Ordnung der Form

Tr,u(s) = −¹2(s−3)³ (s+ 1)²(s+ 3)

˜ r(s)

z }| { (s+ 2)² (s+ 2)²

| {z }

˜ r(s)

(7.81)

erweitert werden.

Damit ergibt sich die zu l¨osende Diophantische Gleichung zu (s−2) (s+ 3)

| {z }

a(s)

x0+x1s+x2s²

| {z }

x(s)

+ (s−3)³

| {z }

b(s)

y0+y1s+y2s²

| {z }

y(s)

= (s+ 1)²(s+ 3) (s+ 2)²

| {z }

d(s)

(7.82)

und man erh¨alt als Ergebnis

x(s) = 161s²−1006s+ 1969 und y(s) =s²−143s−438 . (7.83) (C) Das Z¨ahlerpolynom z(s) der ¨Ubertragungsfunktion V (s) folgt unmittelbar aus

(7.71) zu

z(s) = ˜zT (s) ˜r(s) =−1

2(s+ 2)² =−1

2s²−2s−2 . (7.84)

Die Realisierung der Regler¨ubertragungsfunktionen V (s) = −¹2s²−2s−2

s²−143s−438 R(s) = 161s²−1006s+ 1969

s²−143s−438

(7.85)

in der erweiterten 2-ten Standardform von (7.73) lautet d

dt x1

x2

| {z }

x

=

0 438 1 143

| {z }

A

x1

x2

| {z }

x

+

−221 −72487

−73.5 −22017

| {z }

B

r y

u =

0 1

| {z }

c^T

x1

x2

| {z }

x

+

−0.5 −161

| {z }

D

r y

.

(7.86)

Integralanteil im Regler

Es zeigt sich nun, dass dieser Regler eine sprungf¨ormige St¨orungd(t) =σ(t) am Ausgang station¨ar nicht unterdr¨ucken kann. Um dies zu zeigen, berechne man die St¨or¨ubertra- gungsfunktion

Td,y(s) = 1

1 +R(s)G(s) = b(s)y(s)

a(s)x(s) +b(s)y(s) (7.87) und wende den Endwertsatz der Laplace-Transformation an

tlim→∞

y(t) = lim

s→0sTd,y(s)1 s = lim

s→0Td,y(s) = 0 . (7.88) Man sieht unmittelbar, dass (7.88) nur dann erf¨ullt werden kann, wenn entweder die Stre- cken¨ubertragungsfunktionG(s) oder die Regler¨ubertragungsfunktion R(s) eine Polstelle bei s = 0 hat. Um nun in den Regler systematisch einen Integralanteil (Pol bei s = 0) einzubauen, wird folgender Trick angewandt.

Man entwirft den Regler f¨ur die um einen Integrator erweiterte Strecke G˜(s) = 1

sG(s) (7.89)

und realisiert anschließend diesen Integrator im Regler. Abbildung 7.12 veranschaulicht diese Vorgangsweise.

Simulationsbeispiel:

F¨ur das Beispiel mit der Strecken¨ubertragungsfunktion (7.77) und der F¨uhrungs¨ubertra- gungsfunktion (7.78) erh¨alt man in diesem Fall mit allen Realisierungspolen bei -2

V (s) = −¹₂s³−3s²−6s−4 s³+ 21s²−850s−2712

1 s R(s) = 1072s³−6388s²+ 12180s−4

s³+ 21s²−850s−2712 1 s

(7.90)

G ( s ) y

r R ( s )

V ( s ) s 1 G ( s ) ~ d

Abbildung 7.12: Zum Einbau eines Integralanteils bei der Polvorgabe mit zwei Freiheits- graden.

bzw. in erweiterter zweiter Standardform d

dt





 x1

x2

x₃ x4





 =







0 0 0 0 1 0 0 2712 0 1 0 850 0 0 1 −21











 x1

x2

x₃ x4





 +







−4 4

−6 −12184

−3 6388

−0.5 −1072





 r

y

u =

0 0 0 1





 x1

x₂ x3

x4





 + 0 0

r y

.

(7.91)

St¨orverhalten

Das Realisierungspolynom hat auf die F¨uhrungs¨ubertragungsfunktion keine Auswirkung und ist daher, abgesehen davon, dass es stabil zu w¨ahlen ist, willk¨urlich. Berechnet man hingegen die St¨or¨ubertragungsfunktion und verwendet die Beziehung (7.69)

Td,y(s) = 1

1 +R(s)G(s) = b(s)y(s)

a(s)x(s) +b(s)y(s) = b(s)y(s)

nT (s) ˜a(s) ˜r(s), (7.92) so erkennt man, dass das Realisierungspolynom sich im Allgemeinen nicht herausk¨urzt und somit das St¨orverhalten sehr wohl beeinflusst.

Simulationsbeispiel:

Man kann f¨ur das Beispiel mit der Strecken¨ubertragungsfunktion (7.77) und der F¨uh- rungs¨ubertragungsfunktion (7.78) zeigen, dass durch Verschieben der Realisierungspole von -2 auf -20 die Dynamik des St¨orverhaltens wesentlich verbessert wird.

Aufgabe 7.17. Schreiben Sie ein Programm in Matlab, das aus der Strecken¨ubertra- gungsfunktion G(s) und der gew¨unschten F¨uhrungs¨ubertragungsfunktion Tr,y(s) sowie

der eventuell ben¨otigten Realisierungspole die Regler¨ubertragungsfunktionen V (s) und R(s)berechnet.

Aufgabe 7.18. Schreiben Sie ein Programm inMatlab, das f¨ur die Regler¨ubertragungs- funktionenV (s)und R(s)die Matrizen A,B,c^T undD der erweiterten 2-ten Standard- form von (7.73) berechnet.

Aufgabe 7.19. Geben Sie f¨ur die Strecken¨ubertragungsfunktion G(s) von (7.77) eine implementierbare F¨uhrungs¨ubertragungsfunktion Tr,y(s) so vor, dass gilt

(1) limt→∞y(t) = 0f¨ur einen Einheitssprung der St¨orung am Ausgang d(t) =σ(t)und (2) der Fehler e(t) f¨ur ein harmonisches Referenzsignal der Form r(t) =Asin (ω₀t) im

eingeschwungenen Zustand ist Null.

Ergebnis: Um die Forderung (1) zu erf¨ullen, muss man im Regler einen Integralanteil einbauen und die Forderung (2) kann durch eine F¨uhrungs¨ubertragungsfunktion der Form

Tr,y(s) =−1 2

(s−2) (α₀+α₁s) (s+ 1)⁴ mit

α0 = 43ω⁴₀−8ω₀²+ 1 ω₀²+ 4 α1 = 2ω₀⁴−14ω₀²+ 9

ω₀²+ 4 ber¨ucksichtigt werden.

Entwerfen Sie nun f¨ur ω0 = 4 einen Regler durch Polvorgabe mit zwei Freiheitsgraden und legen Sie s¨amtliche Realisierungspole auf -20.

Ergebnis: Die Regler¨ubertragungsfunktionen lauten

V (s) = −2.05s³−146.1s²−3384s−25640 s³+ 56s²−19550s−59140

1 s R(s) = 20730s³−135500s²+ 265200s−200

s³+ 56s²−19550s−59140 1 s . Simulieren Sie den Regelkreis in Matlab/Simulink.

Aufgabe 7.20. Berechnen Sie f¨ur die Strecken¨ubertragungsfunktion G(s) = s−4

s(s+ 2)²

einen Regler nach der Methode der Polvorgabe mit zwei Freiheitsgraden. W¨ahlen Sie aus den nachfolgenden F¨uhrungs¨ubertragungsfunktionen

Tr,y(s) =−1 4

s−4

(s+ 1)², Tr,y(s) =−1 4

s−4

(s+ 1)³, Tr,y(s) =−1 4

s−4 s(s+ 1)², die implementierbare aus und legen Sie eventuelle Realisierungspole auf −1.

Ergebnis: Die erweiterte zweite Standardform des Reglers lautet d

dt x1

x2

=

0 −1.701 1 −1

x1

x2

+

0.175 0.758

−0.25 −0.09 r y

u =

0 1 x1

x2

+

−0.25 −0.298 r y

.