Logistic Regression
Volltext
Abbildung
ÄHNLICHE DOKUMENTE
Our contributions are: (1) accumulating a dataset for pun detection; (2) utilizing a logistic regression model to show the relations with straightforward features on both sentence
In Section 4.3.1 we analyzed weights and expression values of the genes and exons selected by group ` 1 and elastic net.. In the following we consider publications about
The Logistic Regression will implement both ideas: It is a model of a posterior class distribution for classification and can be interpreted as a probabilistic linear classifier.
The Logistic Regression will implement both ideas: It is a model of a posterior class distribution for classification and can be interpreted as a probabilistic linear classifier..
One approach that has been used in the literature is to estimate marginal effects by comparing point estimates of the expected probability of various characteristics (Pohlmann
example, the LPC of the impact of female gender on the probability of unemployment can be derived from the results of a logistic regression by estimating the female and male
■ Assume effect of either independent variable is the same, regardless of the value of the other variable (additivity, parallel regression lines).. ■ Usual assumptions on
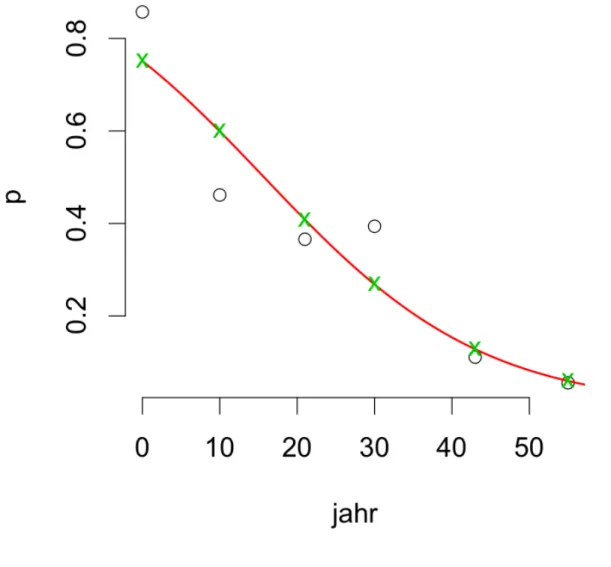
Outside this range we get fitted values that are smaller than zero or larger than one.. ◆ Nonparametric regression shows S-shaped fit, not a