Skript zur Vorlesung
Logik, Berechenbarkeit und Komplexit¨ at
Sommersemester 2008
Prof. Dr. Steffen Reith reith@informatik.fh-wiesbaden.de
Fachhochschule Wiesbaden
Fachbereich Design Informatik Medien
Erstellt von: Steffen Reith Zuletzt ¨uberarbeitet von: Steffen Reith
Email: reith@informatik.fh-wiesbaden.de Erste Version vollendet: Juli 2006
Version: 1072 Date: 2009-01-01
Durch nichts zeigt sich mathematischer Unverstand deutlicher als durch ein ¨Ubermaß an Genauigkeit im Zahlenrechnen.
Carl Friedrich Gauß
Dieses Skript ist aus der Vorlesung
”Logik, Berechenbarkeit und Komplexit¨at“ des Master- Studiengangs
”Informatik“ an der Fachhochschule Wiesbaden hervorgegangen. Ich danke allen H¨oreren dieser Vorlesung f¨ur konstruktive Anmerkungen und Verbesserungen. Naturgem¨aß ist ein Skript nie fehlerfrei (ganz im Gegenteil!) und es ¨andert (mit Sicherheit!) sich im Laufe der Zeit. Deshalb bin ich auf weitere Verbesserungvorschl¨age angewiesen und freue mich auch ¨uber weitere Anregungen durch die H¨orer.
Inhaltsverzeichnis
1. Logik 1
1.1. Aussagenlogik . . . 1
1.1.1. Syntax und Semantik der Aussagenlogik . . . 1
1.1.2. Einige grundlegende Eigenschaften von aussagenlogischen Formeln . . . . 5
1.1.3. Normalformen . . . 7
1.1.4. Hornformeln . . . 10
1.1.5. Resolution . . . 13
1.2. Pr¨adikatenlogik der ersten Stufe (PL1) . . . 17
1.2.1. Syntax und Semantik . . . 17
1.2.2. Einige grundlegende Eigenschaften von Formeln der PL1 . . . 23
1.2.3. Die Pr¨anexnormalform . . . 24
2. Berechenbarkeit 26 2.1. Die Unentscheidbarkeit der PL1 . . . 26
2.2. Berechenbarkeit und die Churchsche These . . . 30
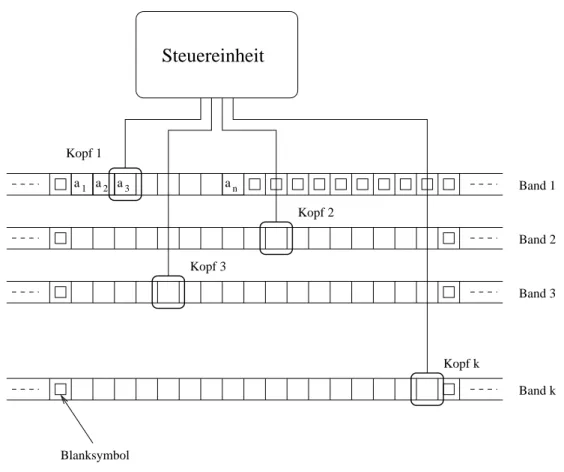
2.2.1. Turingmaschinen und Turingberechenbarkeit . . . 30
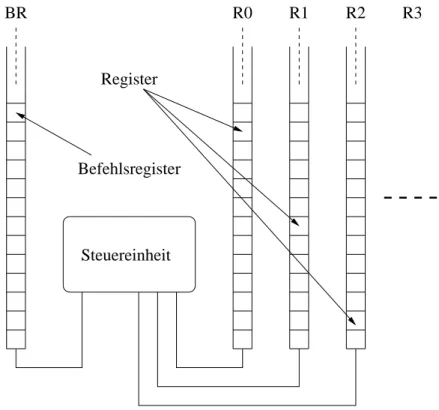
2.2.2. RAMs und RAM-Berechenbarkeit . . . 32
2.2.3. Die Churchsche These . . . 34
2.3. Entscheidbarkeit, das Halteproblem und der Satz von Rice . . . 35
3. Komplexit¨at 40 3.1. Effizient l¨osbare Probleme: die Klasse P . . . 40
3.1.1. Das Problem der 2-F¨arbbarkeit . . . 42
3.2. Effizient ¨uberpr¨ufbare Probleme: die Klasse NP . . . 46
3.3. Schwierigste Probleme inNP: der Begriff derNP-Vollst¨andigkeit . . . 49
3.3.1. Traveling Salesperson ist NP-vollst¨andig . . . 51
3.4. Die Auswirkungen der NP-Vollst¨andigkeit . . . 52
3.5. Der Umgang mitNP-vollst¨andigen Problemen in der Praxis . . . 54
A. Grundlagen und Schreibweisen 59 A.1. Mengen . . . 59
A.1.1. Die Elementbeziehung und die Enthaltenseinsrelation . . . 59
A.1.2. Definition spezieller Mengen . . . 59
A.1.3. Operationen auf Mengen . . . 60
A.1.4. Gesetze f¨ur Mengenoperationen . . . 60
A.1.5. Tupel (Vektoren) und das Kreuzprodukt . . . 61
A.1.6. Die Anzahl von Elementen in Mengen . . . 61
A.2. Relationen und Funktionen . . . 62
A.2.1. Eigenschaften von Relationen . . . 62
A.2.2. Eigenschaften von Funktionen . . . 62
A.2.3. Permutationen . . . 63
A.3. Summen und Produkte . . . 64
A.3.1. Summen . . . 64
A.3.2. Produkte . . . 65
A.4. Gebr¨auchliche griechische Buchstaben . . . 65
B. Einige formale Grundlagen von Beweistechniken 66 B.1. Direkte Beweise . . . 66
B.1.1. Die Kontraposition . . . 67
B.2. Widerspruchsbeweise . . . 67
B.5. Induktionsbeweise und das Induktionsprinzip . . . 68
B.5.1. Die vollst¨andige Induktion . . . 69
B.5.2. Induktive Definitionen . . . 69
B.5.3. Die strukturelle Induktion . . . 70
Index 71
Literaturverzeichnis 75
1
1. Logik
1.1. Aussagenlogik
Die Aussagenlogik studiert die Verkn¨upfung von Aussagen (, sprachliche atomare Gebilde).
Dabei interessiert nur der Wahrheitswert (kurz: WW) einer Aussage:
i) Wahrheitswert 1 ,Aussage wahr ii) Wahrheitswert 0 ,Aussage falsch Damit sind die Aussagen
”Wiesbaden liegt am Rhein“ und
”2 + 5 = 7“
logisch gleichwertig. Aber auch die Aussagen
”Wiesbaden liegt am Mittelmeer“ und
”2 + 5 = 6“
sind gleichwertig, da sie beide falsch sind.
Im weiteren verwenden wir f¨ur solche Aussagen spezielle Variablen, so genannteWahrheitswer- tevariablen (kurz: WW-Variable), die nur die Werte 0 oder 1 annehmen k¨onnen.
Beliebige Aussagenverkn¨upfen wir durchKonnektoren:
Umgangssprachlicher Name Symbol Name in der Logik
und ∧ Konjunktion
oder ∨ Alternative, Disjunktion
nicht ¬ Negation
wenn . . . so (dann) → Implikation
genau dann, wenn ↔ Aquivalenz¨
Wie wollen wir nun die Verkn¨upfungen von Aussagen konstruieren?
Beispiel 1 Seien A, B und C Aussagenvariablen f¨ur drei beliebige Aussagen. Ist die folgende Gesamtaussage wahr (unabh¨angig vom Wahrheitsgehalt der Einzelaussagen A, B und C)?
Genau dann, wenn ausCfolgt, dassAnicht gilt und wenn ausAund dem Nichtgelten von B folgt, dass B gilt oder C nicht gilt, k¨onnen nicht gleichzeitig A und C gelten.
Dies kann man mit den oben eingef¨uhrten Konnektoren als
(((C→ ¬A)∧((A∧ ¬B)→(B∨ ¬C)))↔ ¬(A∧C)) schreiben.
1.1.1. Syntax und Semantik der Aussagenlogik
Obwohl die Syntax von Formeln der Aussagenlogik anschaulich klar ist, brauchen wir pr¨azise Definitionen von Syntax und Semantik, um sp¨ater mathematische Beweise f¨uhren zu k¨onnen:
Definition 2 (Syntax der Aussagenlogik) Die Menge der Formeln der Aussagenlogik ist induktiv wie folgt definiert:
(IA) Atomare Formeln: Das sind die Aussagenvariablenx1, x2, x3, . . . (oft auch x, y und z)
(IS) Zusammengesetzte Formeln:
• Ist H eine Formel, so auch ¬H.
• Sind H1 und H2 Formeln, so auch (H1∧H2), (H1∨H2), (H1→H2) und (H1 ↔H2).
LAL =def {H|H ist eine aussagenlogische Formel} Bemerkung 3
• Bis jetzt haben aussagenlogische Formeln keinerlei Bedeutung, sondern sind rein syntakti- sche Gebilde (
”Strings“).
• Treten in einer Formel H die Variablen x1, . . . , xn auf, so soll dies durch H(x1, . . . , xn) notiert werden.
Zur Definition der Bedeutung / Semantik von Formeln der Aussagenlogik ben¨otigen wir Boo- lesche Funktionen:
Definition 4 Eine Funktionf:{0,1}n→ {0,1} heißt (n-stellige) Boolesche Funktion.
Da der Definitionsbereich einer Booleschen Funktion endlich ist, k¨onnen sie durch Wahrheits- wertetabellen (kurz: WW-Tabelle) angegeben werden:
Definition 5 Einstellige Boolesche Funktionen:
x id(x) not(x)
0 0 1
1 1 0
Zweistellige Boolesche Funktionen (Auswahl):
x y and(x, y) or(x, y) imp(x, y) aeq(x, y) xor(x, y)
0 0 0 0 1 1 0
0 1 0 1 1 0 1
1 0 0 1 0 0 1
1 1 1 1 1 1 0
Lemma 6 Es gibt22n n-stellige Boolesche Funktionen.
Beweis: ¨Ubung. #
Nun k¨onnen wir die Semantik / Bedeutung der aussagenlogischen Formeln festlegen:
Definition 7 (Semantik der Aussagenlogik) Die Funktion I:LAL → {0,1} (
”Interpreta- tionsfunktion“) ist induktiv wie folgt definiert:
(IA) I(x1), I(x2), I(x3), . . . ist gegeben (Belegung der Aussagenvariablen).
1.1 Aussagenlogik 3 (IS) Seien H, H1, H2∈LAL, dann
• I(¬H) =def not(I(H))
• I(H1∧H2) =def and(I(H1), I(H2))
• I(H1∨H2) =def or(I(H1), I(H2))
• I(H1→H2) =def imp(I(H1), I(H2))
• I(H1↔H2) =def aeq(I(H1), I(H2))
• I(H1⊕H2) =def xor(I(H1), I(H2))
Mit Hilfe einer InterpretationsfunktionI (,Belegung der Wahrheitswertevariablen) wird einer Formel H(x1, . . . , xn) ein Wahrheitswert zugeordnet, d.h. jede aussagenlogische FormelH legt eine Boolesche Funktion fH fest:
fH(a1, . . . , an) =def I(H(x1, . . . , xn)), wobei I(xi) =ai∈ {0,1}f¨ur 1≤i≤n
Beispiel 8 BestimmefH1 f¨urH1 =¬(¬x∨¬y). Es gilt alsoI(H1) =I(¬(¬x∨¬y)) = not(I(¬x∨
¬y)) = not(or(I(¬x), I(¬y))) = not(or(not(I(x)),not(I(y)))).
I(x) I(y) not(I(x)) not(I(y)) or(. . .) not(. . .)
0 0 1 1 1 0
0 1 1 0 1 0
1 0 0 1 1 0
1 1 0 0 0 1
Also gilt fH1(x, y) = and(x, y) =fx∧y(x, y), d.h. syntaktisch verschiedene Formeln k¨onnen se- mantisch gleich sein.
Bemerkung 9
• Oft werden die Spalten einer WW-Tabelle aus Bequemlichkeitsgr¨unden mit den entspre- chenden (Sub)formeln benannt (statt der dazugeh¨origen Booleschen Funktion).
• Abweichend von der Definition der Syntax lassen wir aus ¨Ubersichtlichkeits- oder Bequem- lichkeitsgr¨unden manchmal Klammern weg, wenn die vollst¨andige Klammerung durch den Kontext klar ist.
Beispiel 10 Der Fachbereichsrat einer hessischen Informatikfakult¨at beschloss eine neue Pr¨u- fungsordnung, in der auch die erlaubten F¨acherkombinationen geregelt wurden. Zur Auswahl stehen die F¨acher Theologik, Praxologie und Schaltkreisl¨oten, sowie ein Appelwoipraktikum.¨ Es wurde festgelegt, dass eine g¨ultige F¨acherkombination alle folgenden Bedingungen erf¨ullen muss:
i) Wurde das ¨Appelwoipraktikum nicht erfolgreich absolviert, so muss die Praxologiepr¨ufung bestanden werden.
ii) War ein Student in der Praxologie- oder Schaltkreispr¨ufung nicht erfolgreich, so muss Theo- logik und das ¨Appelwoipraktikum bestanden werden.
iii) Hat ein Kandidat weder die Pr¨ufung in Theologik noch in Praxologie bestanden, so muss die Schaltkreisvorlesung und das ¨Appelwoipraktikum bestanden werden.
Obwohl diese Pr¨ufungsordnung das Ergebnis eines sehr schwierigen Abstimmungsprozesses war, lehnte das Ministerium die Pr¨ufungsordnung wegen
”undurchsichtigen Formulierungen“ ab. Die Fakult¨at wurde aufgefordert, die Pr¨ufungsbedingungen ¨aquivalent so umzuformen, dass m¨oglichst wenige, einfache Alternativen entstehen. Helfen Sie dem Dekan bei dieser schweren Arbeit.
Zur L¨osung f¨uhren wir folgende WW-Variablen ein:
• t , ”Hat Theologik bestanden“
• p , ”Hat Praxologie bestanden“
• s, ”Hat Schaltkreisl¨oten bestanden“
• a, ”Hat ¨Appelwoipraktikum bestanden“
und formalisieren die Aussagen zu:
i) (¬a→p)≡a∨p ii) (¬p∨ ¬s)→(t∧a) iii) (¬t∧ ¬p)→(s∧a)
Nun stellen wir folgende WW-Tabelle auf:
t p s a (b) (c) (d) (e) (f) (g) (h) (i)
0 0 0 0 0 1 0 0 1 0 0 0
0 0 0 1 1 1 0 0 1 0 0 0
0 0 1 0 0 1 0 0 1 0 0 0
0 0 1 1 1 1 0 0 1 1 1 0
0 1 0 0 1 1 0 0 0 0 1 0
0 1 0 1 1 1 0 0 0 0 1 0
0 1 1 0 1 0 0 1 0 0 1 1
0 1 1 1 1 0 0 1 0 1 1 1
1 0 0 0 0 1 0 0 0 0 1 0
1 0 0 1 1 1 1 1 0 0 1 1
1 0 1 0 0 1 0 0 0 0 1 0
1 0 1 1 1 1 1 1 0 1 1 1
1 1 0 0 1 1 0 0 0 0 1 0
1 1 0 1 1 1 1 1 0 0 1 1
1 1 1 0 1 0 0 1 0 0 1 1
1 1 1 1 1 0 1 1 0 1 1 1
Wobei die Bezeichnungen der Spalten gegeben sind durch:
• (b) ,¬a→p
• (c) ,(¬p∨ ¬s)
• (d) , (t∧a)
• (e) , (¬p∨ ¬s)→(t∧a)
• (f) , (¬t∧ ¬p)
• (g) ,(s∧a)
• (h) ,(¬t∧ ¬p)→(s∧a)
• (i) , (a)∧(d)∧(g)
Also kann man die Anweisungen vereinfachen zu: Es m¨ussen das ¨Appelwoipraktikum und die Theologik bestanden werden oder Praxologie und Schaltkreisl¨oten muss erfolgreich absolviert wer- den.
Beispiel 11 Folgende Aussagen sind gegeben:
i) Jeder, der ein gutes Geh¨or hat, kann richtig singen.
ii) Niemand ist ein wahrhafter Musiker, wenn er nicht seine Zuh¨orer begeistern kann.
iii) Niemand, der kein gutes Geh¨or hat, kann seine Zuh¨orerschaft begeistern.
iv) Niemand, außer einem wahrhaften Musiker, kann eine Sinfonie schreiben.
1.1 Aussagenlogik 5 Nun stellt sich die Frage: Welche Eigenschaften muss jemand notwendigerweise besitzen, wenn er eine Sinfonie geschrieben hat?
Zur L¨osung f¨uhren wir folgende WW-Variablen ein:
• xG , ”Hat ein gutes Geh¨or“
• xS ,”Kann richtig singen“
• xZ ,”Kann seine Zuh¨orer begeistern“
• xM , ”Ist ein wahrhafter Musiker“
• xI , ”Kann Sinfonie schreiben“
und formalisieren die Aussagen zu:
(i) xG→xS (ii) xM →xZ
(iii) xZ →xG (iv) xI →xM
Nun sind erf¨ullende Belegungen gesucht mit I(xI) = 1. Folgende Idee vereinfacht die Aufgabe:
SeienH1, H2aussagenlogische Formeln, dannI(H1→H2) = 1gdw.I(H1)≤I(H2). DaI(xI) = 1 muss auch I(xM) = I(xZ) = I(xG) = I(xS) = 1 gelten. D.h. jemand der eine Sinfonie geschrieben hat, muss alle anderen angesprochenen Eigenschaften haben.
1.1.2. Einige grundlegende Eigenschaften von aussagenlogischen Formeln Definition 12
i) Zwei aussagenlogische FormelnH1, H2 heißen (logisch)¨aquivalent(Schreibweise: H1 ≡H2) genau dann wenn (kurz gdw. ) f¨ur jede Interpretation I gilt I(H1) =I(H2).
ii) Eine aussagenlogische Formel H heißt erf¨ullbar gdw. es eine Interpretation I gibt mit I(H) = 1.
iii) Eine aussagenlogische Formel H heißt allgemeing¨ultig(Tautologie) gdw. f¨ur alle Interpre- tationen I gilt I(H) = 1.
iv) Gilt f¨ur eine InterpretationI und eine aussagenlogische Formel H I(H) = 1, dann heißt I Modellvon H (Schreibweise: I |=H). Ist I ein Modell von H, so vereinbaren wir auch die Sprechweise: H gilt unter der BelegungI.
Damit ergibt sich die folgende Eigenschaft:
H erf¨ullbar gdw.¬H nicht allgemeing¨ultig Eigenschaft 13 Die folgenden Eigenschaften sind ¨aquivalent:
(i) H1≡H2
(ii) fH1 =fH2
(iii) (H1 ↔H2) ist allgemeing¨ultig
Beweis: ¨Ubung #
Es gelten die folgenden ¨Aquivalenzen, die durch Aufstellen der WW-Tabelle gezeigt werden k¨onnen:
Satz 14 Er gelten die folgenden ¨Aquivalenzen:
H1∧H2 ≡ H2∧H1 Kommutativgesetz
H1∨H2 ≡ H2∨H1 Kommutativgesetz
H1∧(H2∧H3) ≡ (H1∧H2)∧H3 Assoziativit¨atsgesetz H1∨(H2∨H3) ≡ (H1∨H2)∨H3 Assoziativit¨atsgesetz H1∧(H2∨H3) ≡ (H1∧H2)∨(H1∧H3) Distributivgesetz H1∨(H2∧H3) ≡ (H1∨H2)∧(H1∨H3) Distributivgesetz
H1∨H1 ≡ H1 Duplizit¨atsgesetz
H1∧H1 ≡ H1 Duplizit¨atsgesetz
H1∧(H1∨H2) ≡ H1 Absorptionsgesetz
H1∨(H1∧H2) ≡ H1 Absorptionsgesetz
¬(H1∧H2) ≡ ¬H1∨ ¬H2 de-Morgansche Regel
¬(H1∨H2) ≡ ¬H1∧ ¬H2 de-Morgansche Regel
¬¬H ≡ H doppelte Verneinung
H1 →H2 ≡ ¬H1∨H2 Aufl¨osung der Implikation H1 ↔H2 ≡ ((H1∧H2)∨(¬H1∧ ¬H2)) Aufl¨osung der ¨Aquivalenz H1 →H2 ≡ ¬H2→ ¬H1 Kontraposition
Bemerkung 15
• Man kann beobachten, dass die ¨Aquivalenzen aus Theorem 14 analog auch f¨ur die Men- genoperationen Schnitt (∩,∧), Vereinigung (∪,∨) und Komplement ( ,¬) gelten.
• Die Konnektoren
”→“ und
”↔“ k¨onnen durch die Konnektoren
”∧“,
”∨“ und
”¬“ ¨aquiva- lent ersetzt werden.
Damit k¨onnen die Definitionen von Syntax und Semantik der Aussagenlogik
”abgespeckt“
werden (die F¨alle f¨ur
”→“ und
”↔“ bzw.
”imp“ und
”aeq“ einfach entfernen).
D.h. wir verwenden H1 → H2 als Abk¨urzung f¨ur ¬H1∨H2 und H1 ↔ H2 als Abk¨urzung von ((H1∧H2)∨(¬H1∧ ¬H2)).
• Da ∧ (bzw. ∨) kommutativ und assoziativ sind, k¨onnen wir uns im folgenden Fall die Klammerung sparen und vereinfachen wie folgt:
∧n i=1
Hi =def (H1∧H2∧. . .∧Hn) =def (H1∧(H2∧(H3∧. . .(Hn−1∧Hn). . .)))
bzw.
∨n i=1
Hi =def (H1∨H2∨. . .∨Hn) =def (H1∨(H2∨(H3∨. . .(Hn−1∨Hn). . .)))
1.1 Aussagenlogik 7 Beispiel 16 Mit Hilfe dieser Regeln k¨onnen wir Beispiel 10 nun auch durch Umformungen l¨osen:
(¬a→p)∧((¬p∨ ¬s)→(t∧a))∧((¬t∧ ¬p)→(s∧a))
≡ (a∨p)∧((p∧s)∨(t∧a))∧((t∨p)∨(s∧a))
≡ (a∨p)∧((p∧s)∨(t∧a))∧(t∨p∨s)∧(t∨p∨a)
Absorb.
≡ (a∨p)∧((p∧s)∨(t∧a))∧(t∨p∨s)
≡ (a∨p)∧((p∧s)∨t)∧((p∧s)∨a)∧(t∨p∨s)
≡ (a∨p)∧(p∨t)∧(s∨t)∧(p∨a)∧(s∨a)∧(t∨p∨s)
Absorb.+Dupl.
≡ (a∨p)∧(p∨t)∧(s∨t)∧(s∨a)
2×Distr.
≡ (a∨(p∧s))∧(t∨(p∧s))
Distr.
≡ (a∧t)∨(p∧s)
Wodurch sich die schon bekannten Regeln der Pr¨ufungsordnung ergeben: Es m¨ussen das Ap- pelwoipraktikum und die Theologik bestanden werden oder Praxologie und Schaltkreisl¨oten muss erfolgreich absolviert werden.
Wir definieren die folgenden weiteren Abk¨urzungen: H1=def H und H0=def ¬H.
Lemma 17 F¨ur jede InterpretationI gilt:
(i) I(Hσ) = 1 gdw.I(H) =σ f¨urσ ∈ {0,1}
(ii) I(∧n
i=1Hi) = 1 gdw. f¨ur alle i∈ {1, . . . , n} gilt I(Hi) = 1 (iii) I(∨n
i=1Hi) = 1 gdw. es gibt eini∈ {1, . . . , n} mit I(Hi) = 1
Beweis: ¨Ubung #
1.1.3. Normalformen Definition 18
• Ein Literal ist eine WW-Variable oder eine negierte WW-Variable. Dabei wird eine un- negierte WW-Variable als positives und eine negierte WW-Variable als negatives Literal bezeichnet.
• Eine Disjunktion von Literalen heißt Klausel, d.h. eine Klausel ist von der Form∨m
i=1Li = (L1∨L2∨. . .∨Lm), wobei m∈Nist und L1, . . . , Lm Literale sind.
• Eine Formel H ist in konjunktiver Normalform (kurz: KNF), falls sie eine Konjunktion von Klauseln ist:
H= (
∧n i=1
(
mi
∨
j=1
Li,j)), wobei n, m1, . . . , mn∈N und Li,j Literale
• Eine Formel H ist in disjunktiver (alternativer) Normalform (kurz: DNF), falls sie eine Disjunktion von Konjunktionen von Literalen ist:
H= (
∨n i=1
(
mi
∧
j=1
Li,j)),wobei n, m1, . . . , mn∈N und Li,j Literale
Beispiel 19
• KNF-Formeln: ((x∨y∨z)∧(¬x∨ ¬y∨ ¬z)),x∨y, x
• DNF-Formeln: ((x∧y∧ ¬z)∨(¬x∧ ¬y∧ ¬z)), x∨y, x
Satz 20 Jede FormelH ist ¨aquivalent zu einer Formel in disjunktiver Normalform. Es gilt:
H(x1, . . . , xn) = ∨
fH(a1,...,an)=1
∧n j=1
xajj
Beispiel 21
H(x1, x2, x3) = x1∧(x2∨x3)
≡ ∨
fH(a1,a2,a3)=1(xa11 ∧xa22 ∧xa33)
≡ (x1∧ ¬x2∧x3)∨(x1∧x2∧ ¬x3)∨(x1∧x2∧x3) D.h. die DNF von H kann man aus der WW-Tabelle
”ablesen“.
Beweis: F¨ur jede Interpretation I gilt:
I(∨
fH(a1,...,an)=1
∧n
j=1xajj) = 1 gdw. es gibt einn-Tupel (a1, . . . , an) mitfH(a1, . . . , an) = 1 und I(∧n
j=1xajj) = 1
gdw. es gibt einn-Tupel (a1, . . . , an) mitfH(a1, . . . , an) = 1 und I(xajj) = 1 f¨ur alle 1≤j ≤n
gdw. es gibt einn-Tupel (a1, . . . , an) mitfH(a1, . . . , an) = 1 und I(xj) =aj f¨ur alle 1≤j≤n
gdw. fH(I(x1), . . . , I(xn)) = 1 gdw. I(H(x1, . . . , xn)) = 1 D.h.I |=H gdw.I |=∨
fH(a1,...,an)=1
∧n
j=1xajj, alsoH(x1, . . . , xn)≡∨
fH(a1,...,an)=1
∧n
j=1xajj. # Bemerkung 22
• Der Beweis von Satz 20 liefert einen Algorithmus, der zu einer beliebigen aussagenlogischen Formel H eine ¨aquivalente DNF-Formel berechnet: H −→ Wahrheitswertetabelle von H berechnen −→ DNF-Formel ablesen.
• Zu einer Formel H kann es verschiedene ¨aquivalente DNF-Formeln geben:
x∨y≡(x∧ ¬y)∨(¬x∧y)∨(x∧y)
• Die mit Hilfe von Satz 20 konstruierte Formel hat eine besondere Eigenschaft: In jedem Disjunkt kommt jede Variable (negiert oder unnegiert) genau einmalvor. Eine solche DNF- Formel heißt in kanonisch disjunktiver Normalform (kurz: kDNF).
Satz 23 Jede FormelH ist ¨aquivalent zu einer Formel in konjunktiver Normalform. Es gilt:
H(x1, . . . , xn) = ∧
fH(a1,...,an)=0
∨n j=1
x1j−aj
Beispiel 24
H(x1, x2, x3) = x1∨(x2∧x3)
≡ (x1∨x2∨x3)∧(x1∨x2∨ ¬x3)∧(x1∨ ¬x2∨x3) D.h. die KNF von H kann man aus der WW-Tabelle
”ablesen“.
1.1 Aussagenlogik 9 Beweis:
H ≡ ¬¬H ≡ ¬( ∨
f¬H(a1,...,an)=1
∧n
j=1xajj) (vgl. Satz 20 f¨ur¬H)
≡ ( ∧
f¬H(a1,...,an)=1
¬∧n
j=1xajj) (via Regel von de-Morgan)
≡ ( ∧
f¬H(a1,...,an)=1
∨n
j=1¬xajj) (via Regel von de-Morgan)
≡ ( ∧
fH(a1,...,an)=0
∨n
j=1x1j−aj)
Die letzte Zeile gilt, da ¬xσ ≡x1−σ, denn¬x0≡ ¬¬x≡x≡x1 bzw.¬x1 ≡ ¬x≡x0. # Bemerkung 25
• Der Beweis von Satz 23 liefert einen Algorithmus, der zu einer beliebigen aussagenlogischen Formel H eine ¨aquivalente KNF-Formel berechnet: H −→ Wahrheitswertetabelle von H berechnen −→ KNF-Formel ablesen.
• Zu einer Formel H kann es verschiedene ¨aquivalente KNF-Formeln geben:
(x∨y)∧(¬x∨z)≡(x∨y∨z)∧(x∨y∨ ¬z)∧(¬x∨y∨z)∧(¬x∨ ¬y∨z)
• Der oben skizzierte Algorithmus liefert eine KNF-Formel mit der Eigenschaft, dass in jeder Klausel jede Variable (negiert oder unnegiert) genau einmal vorkommt. Eine solche KNF-Formel heißt in kanonisch konjunktiver Normalform (kurz: kKNF).
Ein sehr wichtiges (Berechnungs-) Problem, das in der Theoretischen Informatik h¨aufig be- nutzt wird und dessen Varianten auch von großer praktischer Relevanz sind, ist das so genannte Erf¨ullbarkeitsproblem (engl.
”satisfiability problem“):
Problem: SAT
Eingabe: Aussagenlogische FormelH Frage: HatH eine erf¨ullende Belegung?
F¨ur dieses Problem ist kein effizienter Algorithmus bekannt1, d.h. man muss im schlimmsten Fall alle 2n Belegungen von H(x1, . . . , xn) durchprobieren. SAT ist ein typisches Problem f¨ur eine ganze Klasse von (schweren) Problemen f¨ur die kein praktisch brauchbarer Algorithmus bekannt ist (Stichwort:NP-Vollst¨andigkeit, siehe z.B. Abschnitt 3 oder [RV01b]).
Sogar die Einschr¨ankung auf KNF-Formeln mit drei Variablen pro Klausel (3 -SAT) ist noch ein schweres Problem und von gleicher Schwierigkeit wie SAT. ¨Ahnlich schwer ist TAUT, ein Problem bei dem gefragt wird, ob eine Formel eine Tautologie ist.
Problem: 3-SAT
Eingabe: Aussagenlogische FormelH in KNF mit max. 3 Literalen pro Klausel Frage: HatH eine erf¨ullende Belegung?
Damit ist offensichtlich Problem: KNF-SAT
Eingabe: Aussagenlogische FormelH in KNF Frage: HatH eine erf¨ullende Belegung?
1D.h. man kennt keinen Algorithmus, der f¨ur eine gegebene FormelH(x1, . . . , xn) das Erf¨ullbarkeitsproblem in h¨ochstensp(n) Schritten l¨ost, wobeipein festes Polynom ist (Polynomialzeit).
auch eine schweres Problem.
Beispiel 26 Eine Formel H legt die gegebene WW-Tabelle fest:
x1 x2 x3 H
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 0
Damit ergibt sich die folgende kanonische DNF:
H≡ (¬x1∧ ¬x2∧ ¬x3)∨(x1∧ ¬x2∧ ¬x3)∨
(x1∧ ¬x2∧x3) und die kanonische KNF:
H≡ (x1∨x2∨ ¬x3)∧(x1∨ ¬x2∨x3)∧
(x1∨ ¬x2∨ ¬x3)∧(¬x1∨ ¬x2∨x3)∧ (¬x1∨ ¬x2∨ ¬x3)
Bemerkung 27
• Die Umformung in eine DNF- oder KNF-Formel kannzu einer sehr langen Formel f¨uhren (Wenn die Ausgangsformel die L¨angenhat, kann eine Formel der L¨angeO(2n) entstehen.
Stichwort: Die Anwendung der Distributivgesetze kann in einem Umformungsschritt die L¨ange etwa verdoppeln).
• Oft hat eine kurze Formel in DNF eine lange Darstellung in KNF (und umgekehrt).
1.1.4. Hornformeln
Wir haben gesehen, dass das Erf¨ullbarkeitsproblem f¨ur aussagenlogische Formeln sehr schwer ist.
F¨ur einen in der Praxis wichtigen Spezialfall ist das nicht so. Diese speziellen aussagenlogischen Formeln heißen Hornformeln (nach dem MathematikerAlfred Horn)2.
Definition 28 Eine KNF-Formel heißt Hornformel, wenn jede ihrer Klauseln h¨ochstens eine unnegierte Variable (, positives Literal) enth¨alt.
Beispiel 29 Die Formel H(x1, . . . , x5) ist eine Hornformel:
H≡ (¬x1∨ ¬x2∨x5)∧(x2∨ ¬x3∨ ¬x4∨ ¬x6)∧(¬x5∨ ¬x6)∧(x4)∧
(¬x1∨x3∨ ¬x4)∧(x1∨ ¬x4)∧(x1∨ ¬x5)
Hornformeln sind deshalb so wichtig, weil man ihre Klauseln wie folgt umformen kann:
(¬x1∨ ¬x2∨. . .∨ ¬xm∨xk) ≡ (¬(x1∧x2∧. . .∧xm)∨xk)
≡ (x1∧x2∧. . .∧xm)→xk
Solche Bedingungsmengen haben große Bedeutung f¨ur Datenbanken und in der k¨unstlichen Intelligenz (z.B. bedeutet die PROLOG-Anweisung
”spass :- witz,lustig“ eigentlich: Wenn
”Witz“
und ”Lustig“, dann
”Spass“).
Beispiel 30 Wir verwenden hier zus¨atzlich die Konstanten 0und 1(also Abk¨urzungen f¨ur eine unerf¨ullbare Formel und eine Tautologie). F¨ur jede Interpretation gilt: I(0) =def 0 und I(1) =def
1. Dann kann man die Hornformel aus Beispiel 29 schreiben als:
H≡ ((x1∧x2)→x5)∧((x3∧x4∧x6)→x2)∧((x5∧x6)→0)∧(1→x4)∧ ((x1∧x4)→x3)∧(x4 →x1)∧(x5→x1)
2*1918 Lower East Side, Manhattan (USA) -†2001 in Pacific Palisades (USA)
1.1 Aussagenlogik 11 Definition 31 Die Klausel, die kein Literal enth¨alt, nennen wir leere Klausel (Schreibweise:
()). F¨ur jede Interpretation I gilt I(()) = 0, d.h. die leere Klausel ist unerf¨ullbar.
Wir betrachten nun folgenden Algorithmus, der die Erf¨ullbarkeit von Hornformeln effizient testet:
Algorithmus 1: Hornalgorithmus Eingabe : HornformelH(x1, . . . , xn)
Ergebnis:true, wenn H erf¨ullbar,false sonst
while (es gibt eini, so dass die Klausel(xi) in H vorkommt) { nimm das kleinste solche i;
eliminiere alle Klauseln in denenxi unnegiert vorkommt;
/* Nur hier kann die leere Klausel entstehen */
eliminiere¬xi aus allen Klauseln;
}
if (Klausel () entstanden){ return false;
}else{
return true;
}
Beispiel 32 Sei die folgende FormelH(x1, . . . , x5) als Eingabe f¨ur Algorithmus 1 gegeben:
H≡ (¬x1∨ ¬x2∨x5)∧(x2∨ ¬x3∨ ¬x4∨ ¬x6)∧(¬x5∨ ¬x6)∧(x4)∧ (¬x1∨x3∨ ¬x4)∧(x1∨ ¬x4)∧(x1∨ ¬x5)
Nach Ausf¨uhrung des 1. Durchlaufs der while-Schleife(i= 4):
(¬x1∨ ¬x2∨x5)∧(x2∨ ¬x3∨ ¬x6)∧(¬x5∨ ¬x6)∧(¬x1∨x3)∧(x1)∧(x1∨ ¬x5) Nach Ausf¨uhrung des 2. Durchlaufs der while-Schleife(i= 1):
(¬x2∨x5)∧(x2∨ ¬x3∨ ¬x6)∧(¬x5∨ ¬x6)∧(x3) Nach Ausf¨uhrung des 3. Durchlaufs der while-Schleife(i= 3):
(¬x2∨x5)∧(x2∨ ¬x6)∧(¬x5∨ ¬x6)
Nach diesem Schritt bricht die while-Schleife ab, da keine Klausel der Form (xi) vorhanden ist. Auch die Klausel () kommt nach dem 3. Durchlauf nicht vor, deshalb ist die Hornformel H erf¨ullbar.
Zum jetzigen Zeitpunkt ist nicht klar, warum Algorithmus 1 korrekt ist. Dies wollen wir nun kl¨aren.
Lemma 33 (Schleifeninvariante) Entsteht bei einem Durchlauf der while-Schleife des Hor- nalgorithmus (Algorithmus 1) aus einer Formel H die Formel H′ durch das Eliminieren der Variablen xi, so gilt f¨ur jede Interpretation I:
I(H) = 1 gdw. (I(H′) = 1 und I(xi) = 1) Beweis:
”⇒“ SeiI(H) = 1, dann auchI(K) = 1 f¨ur jede KlauselK vonH. Insbesondere f¨ur die Klausel (xi) gilt I((xi)) = 1, also I(xi) = 1. Sei nunK eine beliebige Klausel inH′:
Fall 1: (K∨ ¬xi) ist Klausel inH, dann I(K) =or(I(K),0) =I(K∨ ¬xi) = 1.
Fall 2: K ist Klausel inH, dann ist sowieso I(K) = 1.
Also ist I(K) = 1 f¨ur alle KlauselnK von H′ und damitI(H′) = 1.
”⇐“ Sei I(H′) = 1 undI(xi) = 1, also I(K′) = 1 f¨ur alle Klauseln K′ von H′. Sei K nun eine beliebige Klausel in H:
Fall 1: Wenn K = (K′∨xi), dannI(K)≥I(xi) = 1.
Fall 2: Wenn K = (K′∨ ¬xi), dann istK′ Klausel inH′ und damitI(K)≥I(K′) = 1.
Fall 3: Wederxinoch¬xikommen inKvor, dann istKauch Klausel inH′, alsoI(K) = 1.
Zusammen: F¨ur alle KlauselnK von H giltI(K) = 1, also ergibt sich I(H) = 1. # Folgerung 34 Ist aus der HornformelHnach Verlassen der while-Schleife des Hornalgorithmus (Algorithmus 1) die Formel H′ entstanden, dann gilt f¨ur jede Interpretation I:
I(H) = 1 gdw. (I(H′) = 1 und I(xi) = 1)
Beweis: Direkte Folge von Lemma 33 #
Lemma 35 Ist aus der Hornformel H nach Verlassen der while-Schleife des Hornalgorithmus (Algorithmus 1) die Formel H′ entstanden, so gilt:
i) Kommt die Klausel() in H′ vor, so giltI(H) = 0 f¨ur jede Interpretation I.
ii) Kommt die Klausel()inH′nicht vor, so giltI(H) = 1f¨ur die InterpretationI mitI(xi) = 1 gdw.(xi wurde durch den Hornalgorithmus eliminiert).
Beweis:
Aussage i): Die leere Klausel () kommt in H′ vor, dann gilt I(H′) = 0 f¨ur jede Interpretation I. Also muss aufgrund von Folgerung 34I(H) = 0 gelten.
Bem.: () ist entstanden, weil negative Literale¬xigestrichen wurden, aber es giltI(xi) = 1 laut Folgerung 34.
Aussage ii): Die Klausel () kommt inH′ nicht vor, dann muss in jeder Klausel K′ mindestens ein negatives Literal existieren. Wir w¨ahlen
I(xi) =
{ I(xi) = 1 , falls xi durch den Hornalgorithmus eliminiert wurde I(xi) = 0 , sonst
Dann gilt I(K′) = 1 f¨ur jede Klausel K′ von H′, also I(H′) = 1. Mit Folgerung 34 gilt
dann I(H) = 1. #
Bemerkung 36
• Die von uns konstruierte Belegung ist die, die kleinstm¨ogliche Wahrheitswerte zuordnet.
• Es kann noch weitere erf¨ullende Belegungen geben, denn wurdexi nicht eliminiert, so muss nicht immer I(xi) = 0 gew¨ahlt werden.
Beispiel 37 Im Beispiel 32 wurdenx1, x3 undx4eliminiert. Also istI0(x1) =I0(x3) =I0(x4) = 1 und I0(x2) =I0(x5) =I0(x6) = 0 eine erf¨ullende Belegung. Aber auchI1 und I2
x1 x2 x3 x4 x5 x6
I0 1 0 1 1 0 0
I1 1 0 1 1 1 0
I2 1 1 1 1 1 0
sind erf¨ullende Belegungen.
1.1 Aussagenlogik 13 Satz 38 Der Hornalgorithmus (Algorithmus 1) ist korrekt und ben¨otigt O(|H|4) Schritte.
Beweis:
• Die Korrektheit folgt direkt aus Lemma 35.
• Mit |H| =def
”Anzahl der Buchstaben von H“ bezeichnen wir die L¨ange der Formel3 H.
Sei H(x1, . . . , xn) die Eingabe des Hornalgorithmus:
– Da in jedem Durchlauf genau eine Variable eliminiert wird, haben wir maximal n Schleifendurchl¨aufe.
– Bei einem Durchlauf muss jede Klausel betrachtet (suchen) und evtl. ge¨andert werden.
Laufzeit: O(|K|2).
Gesamte Laufzeit: |{z}n
#Schleifendurchl¨aufe
·
# der Klauseln
z}|{m ·O(|K|2)≤n· |H| ·O(|H|2) =O(|H|4).
Diese Absch¨atzung ist extrem grob, zeigt aber, dass der Hornalgorithmus in Polynomialzeit arbeitet.
1.1.5. Resolution
Wir wissen schon: F¨ur SAT und 3 -SAT gibt es vermutlich keine Algorithmen, die in der Praxis ausreichend schnell sind und f¨uralle aussagenlogischen Formeln die Erf¨ullbarkeit testen. D.h. wir k¨onnen nicht hoffen, dass ein Algorithmus Af¨ur SAT oder 3 -SAT existiert mit:
• Wenn H erf¨ullbar, dann stopptA mit dem Ergebnis
”erf¨ullbar“
• Wenn H unerf¨ullbar, dann stopptA mit dem Ergebnis
”unerf¨ullbar“
• A arbeitet max. O(|H|k) Schritte f¨ur ein festesk∈N (
”Polynomialzeit“) Ein einfacher, aber nicht schneller Algorithmus f¨ur SAT ist
Algorithmus 2: Erf¨ullbarkeit von aussagenlogischen Formeln Eingabe : Formel H(x1, . . . , xn)
Ergebnis:true, wenn H erf¨ullbar,false sonst stelle die WW-Tabelle von H auf;
pr¨ufe alle Eintr¨age der WW-Tabelle;
if (eine Zeile der WW-Tabelle hat eine 1 in der Spalte H){ return true;
} else{
return false;
}
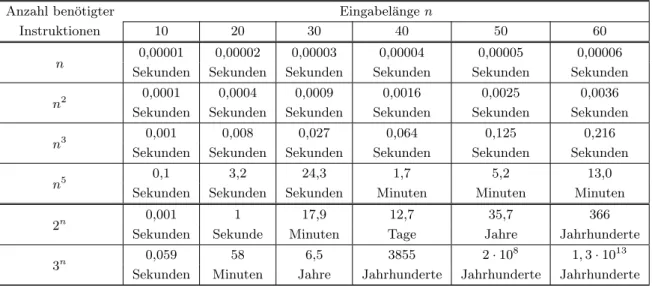
Eine Formel H hat maximal |H|Variablen, d.h. die WW-Tabelle kann maximal 2|H| Eintr¨age haben und damit ist die Rechenzeit des obigen Algorithmus mindestens O(2|H|) (kein Poly- nom!). Damit ist dieser Algorithmus f¨ur die Praxis unbrauchbar (vgl. Abbildung 7 auf Seite 45).
Wesentlich bessere Algorithmen sind f¨ur SAT und 3 -SAT aber nicht bekannt.
Hoffnung: Wir k¨onnen das Erf¨ullbarkeitsproblem wenigstens f¨ur einen (m¨oglichst großen) Teil der Formeln schnell l¨osen. Der Resolutionsalgorithmus f¨ur KNF-SAT soll dies leisten.
Wir legen fest: Klauseln enthalten nie eine Variable negiert und unnegiert (solche Klauseln k¨onnte man sowieso streichen, denn sie sind allgemeing¨ultig).
3z.B.|(x∨y)|= 5 und|((x∧y)→z)|= 9
Definition 39 Sind(C1∨x)und (C2∨ ¬x)Klauseln und kommt in der Klausel(C1∨C2) keine Variable negiert und unnegiert vor, so heißt (C1∨C2) Resolvent von (C1∨x) und (C2∨ ¬x).
Beispiel 40 Sei H = (x∨y)
| {z }
=K1
∧(¬y)
|{z}
=K2
∧(¬x∨z)
| {z }
=K3
∧(x∨ ¬y∨z)
| {z }
=K4
∧(y∨ ¬z)
| {z }
=K5
, dann sind die Resol- venten der Klauseln von H:
• K6 = (x) ist Resolvent von K1 und K2,
• K7 = (y∨z) ist Resolvent von K1 und K3,
• K8 = (x∨z) ist Resolvent von K1 und K4,
• K9 = (¬z) ist Resolvent von K2 und K5,
• K10= (¬y∨z) ist Resolvent von K3 und K4 und
• K11= (¬x∨y) ist Resolvent von K3 und K5.
Der Resolvent von (x) und (¬x) ist die leere Klausel (). F¨ur jede Interpretation I gilt wieder I(()) = 0.
Definition 41 Sei H eine KNF-Formel und R1, . . . , Rm alle Resolventen von Klauseln in H, die nicht schon Klauseln in H sind, dann ist
Res(H) =def H∧R1∧R2∧. . .∧Rm.
Beispiel 42 Mit Beispiel 40 gilt deshalb Res(H) =H∧K6∧K7∧. . .∧K11. Definition 43 Sei H eine KNF-Formel, dann definieren wir induktiv f¨urk∈N:
• Res0(H) =def H
• Resk+1(H) =def Res(Resk(H))
Beispiel 44 Mit Bezug auf Beispiel 40 ergibt sich:
• Res0(H) =H,
• Res1(H) =H∧K6∧. . .∧K11,
• Res2(H) = Res1(H)∧K12∧. . .∧K15, wobei – K12= (y) ist Resolvent von K1 und K11, – K13= (z) ist Resolvent von K2 und K7, – K14= (¬x) ist Resolvent von K2 und K11 und – K15= (x∨ ¬y) ist Resolvent von K4 und K9,
• Res3(H) = Res2(H)∧K16∧K17, wobei
– K16= () ist Resolvent von K2 und K12 und – K17= (x∨ ¬z) ist Resolvent von K5 und K15,
• Res4(H) = Res3(H),
• Res5(H) = Res4(H) und deshalb
• Resn(H) = Res3(H) f¨ur n≥3.
1.1 Aussagenlogik 15 Im Beispiel 44 zeigte es sich, dass nach 3 Schritten keine neuen Resolventen mehr gebildet wer- den k¨onnen. Das n¨achste Lemma zeigt, dass f¨ur jede KNF-Formel dieser Zustand nach endlich vielen Schritten erreicht ist. Diese Eigenschaft werden wir sp¨ater dazu benutzen, einen Algorith- mus zu formulieren, der berechnet, ob eine KNF-Formel unerf¨ullbar ist.
Lemma 45 F¨ur jede KNF-FormelH gilt:
i) Es gibt eink≥0 mit Resk(H) = Resk+1(H) (
”Fixpunkt von Res(·)(·)“) ii) Aus Resk(H) = Resk+1(H) folgtResk+i(H) = Resk(H) f¨ur alle i≥0.
Beweis:
i): Bei jedem Schritt von Resk(H) nach Resk+1(H) kommen h¨ochstens Klauseln dazu. Bei n Variablen gibt es h¨ochstens 3n verschiedene Klauseln, denn jede dern Variablen kann in einer Klausel nicht vorkommen, unnegiert vorkommen oder negiert vorkommen. Also gibt es maximal 3n verschiedene k mit Resk(H) ̸= Resk+1(H) und deshalb muss es ein k ∈ N mit Resk(H) = Resk+1(H) geben.
ii): Wir zeigen die Aussage via Induktion ¨uber i:
(IA) Seii= 0, dann gilt Resk+0(H) = Resk(H).
(IV) Es gibt eink, so dass f¨ur alle i≥0 gilt Resk+i(H) = Resk(H).
(IS) i → i+ 1: Es gilt Resk+(i+1)(H) = Res(Resk+i(H)) (IV)= Res(Resk(H)) = Resk+1(H) (IV)=
Resk(H). #
Definition 46 F¨ur die KNF-Formel H sei kH das kleinste k mit Resk(H) = Resk+1(H). Wir legen fest:
Res∗(H) =def ReskH(H)
Mit Hilfe des folgenden Lemmas zeigen wir, dass die Hinzunahme der Resolventen zu einer logisch ¨aquivalenten Formel f¨uhrt. Damit ver¨andert die Resolventenbildung die Eigenschaft der Unerf¨ullbarkeit einer KNF-Formel nicht.
Lemma 47 Seien H, K1 und K2 Formeln und ist x eine Aussagenvariable, dann gilt:
H∧(K1∨x)∧(K2∨ ¬x)≡H∧(K1∨x)∧(K2∨ ¬x)∧(K1∨K2)
Beweis: Wir m¨ussen zeigen, dass f¨ur alle I giltI(H∧(K1∨x)∧(K2∨ ¬x)) =I(H∧(K1∨x)∧ (K2∨ ¬x)∧(K1∨K2)).
”⇒“ Sei I(H∧(K1∨x)∧(K2∨ ¬x)) = 1, dannI(H) =I(K1∨x) =I(K2∨ ¬x) = 1.
Fall 1: Wenn I(x) = 1, dannI(K2∨ ¬x) =I(K2) = 1 und damitI(K1∨K2) = 1.
Fall 2: Wenn I(x) = 0, dannI(K1∨x) =I(K1) = 1 und damitI(K1∨K2) = 1.
In beiden F¨allen ergibt sichI(H∧(K1∨x)∧(K2∨ ¬x)) = 1
”⇐“ Sei I(H∧(K1∨x)∧(K2∨ ¬x)∧(K1∨K2)) = 1, dann sicherlich auchI(H∧(K1∨x)∧
(K2∨ ¬x)) = 1. #
Lemma 48 F¨ur jede KNF-FormelH gilt:
i) H≡Res(H)
ii) H≡Resk(H) f¨ur jedes k≥0 iii) H≡Res∗(H)
Beweis: Aussage i) ist eine direkte Folge von Lemma 47, Aussage ii) folgt aus Aussage i) und
Punkt iii) ergibt sich mitii). #
Der n¨achste Satz zeigt die Korrektheit des Resolutionsmethode, mit der wir entscheiden k¨onnen, ob eine gegebene KNF-Formel erf¨ullbar ist.
Satz 49 Eine KNF-Formel H ist genau dann erf¨ullbar, wenn die leere Klausel () nicht in Res∗(H) enthalten ist.
Beweis:
”⇒“ SeiH erf¨ullbar. Es gilt mit Lemma 48 auchH≡Res∗(H). DaH erf¨ullbar ist, existiert ein I mit I(H) =I(Res∗(H)) = 1. Dann kann () keine Klausel von Res∗(H) sein, da f¨ur alle I gilt: I(()) = 0.
”⇐“ Wir zeigen diese Aussage durch Kontraposition (siehe Abschnitt B.1.1 auf Seite 67) und Induktion ¨uber die Anzahln der Variablen in der Formel H.
(IA) Sein= 0, dann istH= () die einzig m¨ogliche Formel und damit ()∈Res∗(H).
(IV) SeiH(x1, . . . , xn) nicht erf¨ullbar, dann gilt ()∈Res∗(H).
(IS) n→n+ 1:H(x1, . . . , xn+1) sei nicht erf¨ullbar und habe die Form
xn+1kommt nicht vor
z }| {
H1∧H2∧. . .∧Hk ∧
alle Klauseln mitxn+1
z }| {
(H1′ ∨xn+1)∧(H2′ ∨xn+1)∧. . .∧(Hl′∨xn+1)
∧ (H1′′∨ ¬xn+1)∧(H2′′∨ ¬xn+1)∧. . .∧(Hm′′ ∨ ¬xn+1)
| {z }
alle Klauseln mit¬xn+1
D.h. inH1, . . . , Hk,H1′, . . . , Hl′undH1′′, . . . , Hm′′ kommen sowohlxn+1als auch¬xn+1nicht vor.
Wir definieren
• F0(x1, . . . , xn) =def H1∧. . . Hk∧H1′. . .∧Hl′ und
• F1(x1, . . . , xn) =def H1∧. . . Hk∧H1′′. . .∧Hm′′
Beh. F0 und F1 sind nicht erf¨ullbar.
Ann. F0 w¨are erf¨ullbar, dann existiert ein I mit I |= F0, d.h. I(H1) = · · · = I(Hk) = I(H1′) =. . . I(Hl′) = 1. Da xx+1 in F0 nicht vorkommt, k¨onnen wir I(xn+1) = 0 w¨ahlen.
Dann gilt:
• I(Hi) = 1 f¨ur 1≤i≤k,
• I(Hi′∨xn+1) = or(I(Hi′), I(xn+1)) = or(I(Hi′),0) =I(Hi′) = 1 f¨ur 1≤i≤lund
• I(Hi′′∨ ¬xn+1) = or(I(Hi′′), I(¬xn+1)) = or(I(Hi′),not(I(xn+1))) = or(I(Hi′),1) = 1 f¨ur 1≤i≤m.
Damit ist I(H) = 1, d.h. H w¨are erf¨ullbar. Widerspruch. Also war die Annahme falsch und damit ist F0 unerf¨ullbar.
Analog: F1 nicht erf¨ullbar.
Die Formeln F0 und F1 haben nur n Variablen und sind unerf¨ullbar, also gilt mit der Induktionsvoraussetzung, dass die leere Klausel in Res∗(F0) und Res∗(F1) vorkommt. Nun unterscheiden wir f¨urF0 zwei F¨alle: