0 Intensität [I ]

UNIVERSITÄT HEIDELBERG Physikalisches Praktikum PAP 2

für Studierende der Physik

Mechanik und Thermodynamik

Praktikumsvorbereitung 211 Gekoppelte Pendel

212 Zähigkeit von Flüssigkeiten 213 Kreisel

221 Adiabatenkoeffizient  cp/cv 222 Heißluftmotor

223 Messung der Boltzmannkonstante Teil I Brownsche Bewegung

Elektrizität und Radioaktivität

241 Wechselstromeigenschaften von RCL-Gliedern (2-Tages-Versuch) 242 Spannungsverstärkung

243 Messung der Boltzmannkonstante Teil II Thermisches Rauschen 245 Induktion

Grundlagen zu den Versuchen der Radioaktivität 251 Statistik

252 Aktivierung mit thermischen Neutronen 253 Absorption von und Strahlen 255 Röntgenspektrometer

256 Röntgenfluoreszenz

Ausgabe 04_2010

Optik

232 Michelson-Interferometer 233 Fourieroptik (2-Tages-Versuch)

234 Lichtquellen und Gitterspektroskopie

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

Versuch 232

Michelson-Interferometer

Abbildung 1: Versuchsaufbau.

I Messaufbau

• Michelson Interferometer

• Verschiedene Lichtquellen: Quecksilberdampflampe, Halogenlampe, Gl¨ uhlampe

• Thermometer

• Vakuumpumpe

• CCD-Kamera mit Monitor

• Antriebsmotor

II Literatur

• Bergmann- Sch¨afer, Lehrbuch der Experimentalphysik, Band III, de Gruy- ter Berlin.

• R. P. Pohl, Optik und Atomphysik, Springer Verlag.

• W. Demtr¨oder, Experimentalphysik 2, Springer Verlag.

• Homepage des Praktikums (http://www.physikpraktika.uni-hd.de).

III Vorbereitung

Bereiten Sie sich auf die Beantwortung von Fragen zu folgenden Themen vor:

Grundlagen der Wellenoptik (Hyugens’sches Prinzip, Interferenz, Superpo- sitionsprinzip, Koh¨arenz). Interferenz gleicher Neigung, Interferenz gleicher Dicke. Aufbau eines Michelson-Interferometers.

Verst¨andnisfragen:

1. Was ist Interferenz? Was besagt das Superpositionsprinzip?

2. Was sind Interferenzmuster und wie kommen sie zustande? Nennen Sie die Bedingungen f¨ ur die Phasenverschiebung bzw. f¨ ur den Gangunterschied zweier Wellen, damit die ¨ uberlagerte Welle eine maximale bzw. eine ver- schwindene Intensit¨at besitzt. Was ist zu beachten, wenn eine Teilwelle ein Medium mit einem anderem Brechungsindex durchl¨auft als die andere Teilwelle?

3. Warum kann man bei nat¨ urlichem Licht in der Regel keine Inter- ferenzerscheinugen beobachten? Erl¨autern Sie die Begriffe Koh¨arenz, Koh¨arenzzeit und Koh¨arenzl¨ange. Wie groß sind die Gr¨oßenordnungen der Koh¨arenzl¨angen einer Gl¨ uhlampe bzw. eines Lasers?

4. Wie groß ist gem¨aß Gleichung (8) die Intensit¨at der ¨ uberlagerten Welle, wenn die interferierenden Wellen inkoh¨arent sind?

5. Was versteht man unter Interferenz gleicher Neigung und Interferenz glei- cher Dicke?

6. Beschreiben Sie den Aufbau eines Michelson-Interferometers. Welche Auf- gabe hat die Kompensationsplatte? Erkl¨aren Sie das Zustandekommen der verschiedenen Interferenzmuster (Kreissystem, Streifensystem).

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

7. Wie l¨asst sich mit einem Michelson-Interferometer die Wellenl¨ange der Lichtquelle bzw. der Brechungsindex eines Mediums bestimmen?

8. Wie muss der bewegliche Spiegel des Interferometers justiert sein, um Interferenzen mit Licht einer sehr kleinen Koh¨arenzl¨ange beobachten zu k¨onnen (Weißlichtinterferenz)?

9. Warum erscheint das an einer rauhen Oberfl¨ache reflektierte Licht eines Lasers granuliert (Stichwort: Speckle-Muster)?

IV Aufgaben

1. Messen Sie die Wellenl¨ange der gr¨ unen Linie einer Quecksilberdampflampe.

2. Bestimmen Sie den Brechungsindex von Luft.

3. Messen Sie die Koh¨arenzl¨ange einer Halogenlampe als Funktion der spek- tralen Bandbreite.

4. Bestimmen Sie die K¨oh¨arenzl¨ange einer Gl¨ uhbirne.

V Grundlagen

Interferenz bezeichnet allgemein die ¨ Uberlagerung von Wellen. Sie haben dieses Ph¨anomen sicherlich schon anhand von Wasserwellen an einem See oder bei Ex- perimenten mit der Wellenwanne in der Vorlesung kennengelernt. Treffen z.B.

zwei Wasserwellen aufeinander, so ¨ uberlagern sich diese zu einer neuen Wel- le. Die Amplitude der resultierenden Welle h¨angt von der Phasenverschiebung der beiden Teilwellen ab. Trifft in einem bestimmten Punkt (Abbildung 2) ein

” Wellenberg“ der einen Welle auf einen

” Wellenberg“ der anderen Welle, so vergr¨oßert sich die Amplitude der resultierenden Welle (konstruktive Interfe- renz). Trifft dagegen ein

” Wellenberg“ auf ein

” Wellental“, so verringert sich die Amplitude. Sind die Amplituden gar gleich groß, so l¨oscht sich im letzten Fall die Amplitude der resultierenden Welle aus.

Auch Licht l¨asst sich durch eine Welle beschreiben. Betrachten wir zwei ebene monochromatische Lichtwellen E ~ 1 , ~ E 2 :

E ~ 1 (~r, t) = E ~ 01 e ^{i(ωt− k ~}

^{~ r+φ}

⁾ (1) E ~ 2 (~r, t) = E ~ 02 e ^{i(ωt− k ~}

^{~ r+φ}

⁾

Abbildung 2: Interferenz zweier Wasserwellen.

Dabei bezeichnen E ~ 0i die Amplituden, k ~ i die Wellenvektoren, ω die Frequenz und φ i die Phasen der jeweiligen Wellen. Treffen diese aufeinander, so ¨ uberla- gern sie sich gem¨aß des Superpositionsprinzips, d.h. die Wellen addieren sich vektoriell zu einer resultierenden Welle E ~ S (~r, t):

E ~ S (~r, t) = E ~ 1 (~r, t) + E ~ 2 (~r, t). (2) Bei Licht ist aufgrund der hohen Frequenz nicht die Amplitude der Welle beob- achtbar, sondern nur die Intensit¨at I, d.h. der zeitliche Energiemittelwert, der auf eine bestimmte Fl¨ache trifft. Dieser ist proportional zum Betragsquadrat der Amplitude:

I S (~r, t) ∝ | E ~ S (~r, t) | ² . (3) In der hier verwendeten komplexen Notation l¨asst sich das Betragsquadrat sehr einfach berechnen. Wir m¨ ussen lediglich E ~ S mit dem komplex konjugierten E ~ _S ^∗ multiplizieren:

I S ∝ | E ~ S | ² = E ~ S E ~ _S ^∗ = ( E ~ 1 + E ~ 2 )( E ~ 1 ^∗ + E ~ 2 ^∗ ) (4)

= E ~ 1 E ~ 1 ^∗ + E ~ 2 E ~ 2 ^∗ + E ~ 1 E ~ 2 ^∗ + E ~ 2 E ~ ^∗ 1

= | E ~ 1 | ² + | E ~ 2 | ² + E ~ 1 E ~ 2 ^∗ + E ~ 2 E ~ 1 ^∗ .

Die ersten beiden Summanden sind die Betragsquadrate der Einzelwellen. F¨ ur

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

die beiden anderen Summanden berechnen wir durch Einsetzen von Glei- chung (1)

E ~ 1 E ~ 2 ^∗ + E ~ 2 E ~ 1 ^∗ = E ~ 01 E ~ 02 (e ^iϕ + e ^−iϕ ), (5) wobei wir hier die Phasenverschiebung

ϕ = ( ~k 1 − ~k 2 ) ~r + φ 1 − φ 2 (6) definiert haben. Mit Hilfe der Euler’schen Gleichung

e ^iϕ = cos ϕ + i sin ϕ (7)

erhalten wir schließlich f¨ ur die Intensit¨at der ¨ uberlagerten Welle:

I S ∝ | E ~ 1 | ² + | E ~ 2 | ² + 2 E ~ 01 E ~ 02 cos ϕ

| {z }

Interferenzterm

. (8)

Die Intensit¨at der ¨ uberlagerten Welle entspricht demnach nicht der Summe der Intensit¨aten der Einzelwellen. Es tritt zus¨atzlich ein Interferenzterm auf, der dazu f¨ uhrt, dass die Intensit¨at der ¨ uberlagerten Wellen gr¨oßer (konstruk- tive Interferenz) oder kleiner (destruktive Interferenz) ist als die Summe der Einzelintensit¨aten.

Beispiel: Interferenz zweier linear polarisierten, ebener Wellen gleicher Fre- quenz und Amplitude, die sich in z-Richtung ausbreiten und gleiche Polari- sationsrichtungen (z.B. in x-Richtung) besitzen. F¨ ur die x-Komponente der elektrischen Feldst¨arke gilt:

E 1 (z, t) = E 0 e ^{i(ωt−kz+φ}

⁾ (9) E 2 (z, t) = E 0 e ^{i(ωt−kz+φ}

⁾ ,

und f¨ ur die Intensit¨at I S der ¨ uberlagerten Welle E S = E 1 + E 2 :

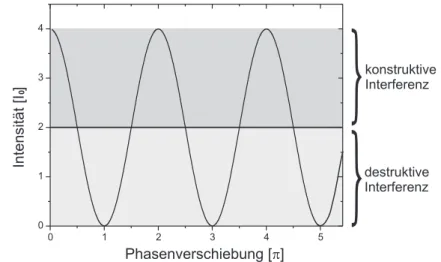
I S ∝ E S ² ∝ 2I 0 (1 + cos ϕ), (10) wobei I 0 proportional zur Intensit¨at der Einzelwelle ist und ϕ = φ 1 − φ 2 die Phasenverschiebung der beiden Wellen darstellt. In Abbildung 3 ist die Inten- sit¨at als Funktion der Phasenverschiebung ϕ aufgetragen. Maximale Intensit¨at ergibt sich, wenn die Phasenverschiebung ein Vielfaches von 2π betr¨agt. F¨ ur ein ungerades Vielfaches von π verschwindet dagegen die Intensit¨at der ¨ uber- lagerten Welle:

0 1 2 3 4 5

0 1 2 3 4

Intensität[I]

Phasenverschiebung [ ] p

konstruktive Interferenz

destruktive Interferenz

Abbildung 3: Intensit¨at der ¨uberlagerten Welle nach Gleichung (10) in Einhei- ten von I 0 als Funktion der Phasenverschiebung in Einheiten von π.

Maximale Intensit¨at f¨ ur ϕ = 2mπ , (m ∈ Z) (11) Minimale Intensit¨at f¨ ur ϕ = (2m + 1)π , (m ∈ Z) (12)

Bei vielen Interferenzversuchen kommt die Phasenverschiebung dadurch zu- stande, dass die sich ¨ uberlagernden Wellen zuvor unterschiedliche Wegl¨angen durchlaufen haben. Ein Beispiel ist in Abbildung 4a) dargestellt. Nehmen wir an, dass die beiden Lichtquellen punktf¨ormig sind und Licht mit gleicher Fre- quenz, Amplitude, Polarisationsrichtung und konstanter Phase aussenden. Die Intensit¨at der ¨ uberlagerten Welle im Punkt P h¨angt dann von der Phasenver- schiebung ab, die durch den Gangunterschied ∆ = s 1 − s 2 der beiden Wellen hervorgerufen wird. Dabei bezeichnen s 1 und s 2 die Wegl¨angen der jeweiligen Teilwellen. Da eine Phasenverschiebung von 2π einem Wegunterschied von λ entspricht, besteht zwischen der Phasenverschiebung ϕ und dem Gangunter- schied ∆ die Beziehung:

ϕ = 2π

λ ∆, (13)

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

wobei λ die Wellenl¨ange der Teilwellen beschreibt.

Breitet sich ein Wellenzug nicht im Vakuum aus, sondern durchl¨auft ein Medi- um mit dem Brechungsindex n (Abbildung 4b), so tritt eine zus¨atzliche Pha- senverschiebung auf. Da die Wellenl¨ange im Medium um das n-fache der Va- kuumlichtgeschwindigkeit kleiner ist, darf man bei der Berechnung des Gang- unterschieds nicht die geometrischen Wegl¨angen s verwenden, sondern muss die optischen Wegl¨angen Λ ber¨ ucksichtigen. Diese entspricht dem Produkt des Brechungsindex des Mediums, in dem sich die Welle ausbreitet und der geome- trischen Wegl¨ange s, die die Welle in dem Medium zur¨ ucklegt:

Λ = n s. (14)

Mit Hilfe des Gangunterschieds lassen sich die Gleichungen (11) und (12) auch wie folgt formulieren:

Maximale Intensit¨at f¨ ur ∆ = mλ , (m ∈ Z) (15)

Minimale Intensit¨at f¨ ur ∆ = (2m + 1) λ

2 , (m ∈ Z) (16) Koh¨ arenz

Voraussetzung f¨ ur die Beobachtung von Interferenzerscheinungen ist die Koh¨arenz der Lichtquellen. Damit ist gemeint, dass die interferierenden Wellen eine konstante Phasenbeziehung aufweisen m¨ ussen. Bei inkoh¨arentem Licht ist die Phasenverschiebung ϕ in Gleichung (8) statistisch verteilt, so dass der Interferenzterm verschwindet und man daher keine Interfenzen beobachtet kann.

Die meisten Lichtquellen, wie z.B. das Licht der Sonne oder einer Gl¨ uhbirne, erzeugen inkoh¨arentes Licht. Die Atome dieser Lichtquellen senden innerhalb eines sehr kurzen Zeitraums τ unabh¨angig voneinander Wellenz¨ uge aus, deren einzelnen Phasen statistisch verteilt sind. Das in Abbildung 4a) dargestellte Experiment w¨ urde daher bei Verwendung von nat¨ urlichem Licht nicht funk- tionieren. Um dennoch mit nat¨ urlichen Lichtquellen Interferenzen beobachten zu k¨onnen, muss man das Licht einer einzigen Lichtquelle verwenden und die- ses in Teilwellen aufspalten. Abbildung 4c) zeigt ein Beispiel, welches auch bei der Verwendung von nat¨ urlichem Licht, die Beobachtung von Interferenzer- scheinungen erm¨oglicht. Anstatt zwei Lichtquellen, die statistisch unabh¨angig

Abbildung 4: a) Gangunterschied ∆ zweier Teilwellen nach dem Durchlaufen unterschiedlicher Wegl¨angen. b) Breitet sich eine Teilwelle in einem Medium mit dem Brechungsindex n aus, tritt eine zus¨atzliche Phasenverschiebung auf.

c) Erzeugung von koh¨arentem Licht durch Teilung der Wellenfront mit einer

Doppellochblende.

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

voneinader emittieren, verwenden wir hier eine Lichquelle, deren Wellenfront mit Hilfe einer Doppellochblende in zwei Teilwellen aufgespalten wird. Da bei- de ¨ Offnungen von der gleichen Prim¨arwelle angeregt werden, emittieren diese nach dem Hyugens’schen Prinzip Sekund¨arwellen, die die gleiche Phase aufwei- sen und daher

” interferenzf¨ahig“ sind.

Es gibt noch weitere Eigenschaften, die bei der Beobachtung von Interferenz- erscheinungen erf¨ ullt sein m¨ ussen. So darf der Gangunterschied der Wellen nicht beliebig groß sein. Wie bereits erw¨ahnt wurde, erfolgt die atomare Emis- sion eines Wellenzugs bei nat¨ urlichem Licht in einem sehr kurzem Zeitraum τ (Koh¨arenzzeit). Diese kurze Emissionszeit bedingt schließlich, dass die ausge- sendeten Wellenz¨ uge auch nur eine kleine L¨ange ¹ besitzen. Ist c die Lichtge- schwindigkeit, so ergibt sich f¨ ur die L¨ange L des emittierten Wellenzugs

L = cτ. (17)

Die L¨ange L wird als Koh¨arenzl¨ange bezeichnet. Bei Interferenzversuchen ist darauf zu achten, dass der Gangunterschied nicht gr¨oßer als die Koh¨arenzl¨ange wird. Andernfalls stammen die interferierenden Teilwellen nicht aus dem selben

” Emisionsakt“ und besitzen daher keine konstante Phasenbeziehung.

Die Koh¨arenzl¨angen von Temperaturstrahlern wie z.B. einer Gl¨ uhlampe oder der Sonne sind sehr klein (einige Wellenl¨angen ≈ 10 µm). Bei Gasentladungs- lampen liegt die Koh¨arenzl¨ange bei einigen Millimetern bis Metern und kann sich bei Lasern gar im Bereich von vielen Kilometern bewegen.

Koh¨ arenzl¨ ange und spektrale Bandbreite

Bei unseren bisherigen Betrachtungen sind wir immer davon ausgegan- gen, dass die Lichtquelle monochromatisch ist. Die Koh¨arenzbedingung besagt, dass nur dann Interferenzen beobachtbar sind, wenn die sich ¨ uberlagernden Wellen eine konstante Phasenbeziehung aufweisen. Dies ist aber nur dann m¨oglich, wenn die Lichtquelle monochromatisches Licht aussendet. Solch eine Lichtquelle gibt es aber nicht! Auch eine reale, extrem schmalbandige Lichtquelle wie z.B. ein Laser, emittiert nur Licht einer bestimmten Frequenz ω 0 mit einer endlichen spektralen Bandbreite ² ∆ω. Damit ist gemeint, dass das Licht Frequenzanteile im Bereich von ω 0 ± ∆ω/2 enth¨alt.

1

Achtung: Hier ist die geometrische L¨ ange des Wellenzugs gemeint und nicht die Wel- lenl¨ ange!

2

Dies folgt z.B. aus der Heisenberg’schen Energie-Zeit Unsch¨ arfe.

w Dw

w

z Spektrum

FT g( ) w

4 c p Dw

g

Blende

E s

z

Abbildung 5: Links: Polychromatisches Licht mit rechteckf¨ormigen Speektrum der spektralen Breite ∆ω. Rechts: Resultierende Wellenform. Der Pfeil mit der Abk¨urzung FT steht f¨ur Fouriertransformation.

Betrachten wir eine Lichtquelle mit einem rechteckigen Frequenzspektrum, wie es links in Abbildung 5 dargestellt ist. Solch ein Spektrum kann z.B. durch Aus- blenden eines bestimmten Spektralbereichs eines kontinuierlichen Spektrums erzeugt werden. Die Amplitude g(ω) bei der Frequenz ω sei gegeben durch:

g(ω) =

( g 0 , | ω − ω 0 | ≤ ∆ω/2

0, | ω − ω 0 | > ∆ω/2. (18) Das von solch einer Lichtquelle ausgesandte Licht entspricht einer ¨ Uberlagerung von Wellen mit Frequenzen im Bereich von ω 0 − ∆ω/2 bis ω 0 + ∆ω/2:

E S = Z ∞

−∞

g(ω) e ^i(ωt−kz) dω = Z ∆ω/2

−∆ω/2

g 0 e ^iω(t−z/c) dω, (19) wobei c die Lichtgeschwindigkeit bezeichnet. F¨ ur die Phase nehmen wir an, dass diese am Ort z = ct f¨ ur alle Frequenzen Null ist. Verwenden wir der Ubersichtlichkeit wegen die Abk¨ ¨ urzungen σ = ω − ω 0 , dσ = dω und ρ = t − z/c, so folgt:

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

E S = Z ∆ω/2

− ∆ω/2

g 0 e ^iρ(ω

^+σ) dσ (20)

= g 0 e ^iρω

Z ^∆ω/2

−∆ω/2

e ^iρσ dσ. (21)

= g 0

iρ e ^iρω

e ^iρ∆ω/2 − e ^{−iρ∆ω/2}

(22)

= 2g 0

ρ e ^iρω

sin ρ∆ω/2. (23)

Ersetzen wir nun wieder σ und ρ durch die urspr¨ unglichen Gr¨oßen, so erhalten wir schließlich:

E S = E 0

sin ∆ω/2(t − z/c)

∆ω/2(t − z/c) e ^iω

^(t−z/c) , (24) wobei hier E 0 = g 0 ∆ω definiert wurde. Die Form dieser Welle ist in Abbil- dung 5 rechts dargestellt. Die von einer Lichtquelle mit einem rechteckigen Frequenzspektrum ausgehende Welle ist amplitudenmoduliert. Die Amplitude ist an der Stelle z 0 maximal. Zudem besitzt der Wellenzug noch weitere Neben- maxima, deren Amplituden aber schnell abfallen. Man bezeichnet solch einen Wellenzug auch als Wellenpaket.

Die Intensit¨at des Wellenpakets berechnet sich aus dem Quadrat der Amplitu- de. Eine Rechnung zeigt, dass die Intensit¨at des ersten Nebenmaximums nur 4,7 % der Intensit¨at des Hauptmaximums betr¨agt. Die Intensit¨aten der wei- teren Nebenmaxima betragen gar nur 1,7 %, 0,8 %, 0,5 % u.s.w. Nahezu die gesamte Intensit¨at des Wellenpakets steckt im Hauptmaximum. Wir k¨onnen daher annehmen, dass das Wellenpaket eine endliche Breite besitzt, welches der Breite des Hauptmaximums von 4πc/∆ω entspricht.

Uberlagern sich zwei solcher Wellenpakete mit einer relativen Verschiebung von ¨

∆z = 2πc/∆ω, so f¨allt die Maximalamplitude des einen auf die erste Nullstel- le des anderen Wellenpakets. Man kann also f¨ ur Wellenpakete dieser Art die Koh¨arenzl¨ange L definieren durch:

Koh¨arenzl¨ange: L = 2πc

∆ω . (25)

Je schmalbandiger die Lichtquelle, desto gr¨oßer ist die Koh¨arenzl¨ange. Damit wird nun auch verst¨andlich, warum die Koh¨arenzl¨angen von Temperaturstrah-

lern so klein sind. Nur streng monochromatisches Licht (d.h. ∆ω → 0) hat unendlich lange Wellenz¨ uge und damit eine unendliche Koh¨arenzl¨ange.

Anstatt die Koh¨arenzl¨ange durch die Frequenz auszudr¨ ucken, k¨onnen wir die- se auch durch die Angabe der Wellenl¨ange beschreiben. Mit ∆ω = 2π∆ν = 2πc∆λ/λ ² schreibt sich die Koh¨arenzl¨ange

Koh¨arenzl¨ange: L = λ ²

∆λ . (26)

Es soll noch angemerkt werden, dass zwischen der Amplitude E S und dem Fre- quenzspektrum g(ω) in Gleichung (19) ein wichtiger Zusammenhang besteht:

g(ω) ist die Fouriertransformierte von E S . Im n¨achsten Praktikumsversuch Fou- rieroptik werden Sie sich mit dieser Thematik noch genauer besch¨aftigen.

Im Versuchsteil 3 werden wir den Zusammenhang der spektralen Bandbreite und der Koh¨arenzl¨ange genauer untersuchen. Hierbei zerlegen wir das Licht einer Halogenlampe (kontinuierliches Spektrum) mit Hilfe eines Prismas und blenden mit einem Spalt einen bestimmten Spektralbereich aus. Je gr¨oßer die Spaltbreite, desto gr¨oßer ist die spektrale Bandbreite des Lichts und damit umso kleiner die Koh¨arenzl¨ange.

Interferenzen an d¨ unnen Schichten

In den beiden folgenden Abschnitten, werden zwei Spezialf¨alle, die In- terferenzen gleicher Neigung und die Interferenzen gleicher Dicke behandelt, die f¨ ur das Verst¨andnis des Michelson-Interferometers sehr wichtig sind.

Interferenzen gleicher Neigung

Interferenzen gleicher Neigung treten dann auf, wenn ein Lichtb¨ undel auf eine transparente, planparallele Platte trifft. Abbildung 6a) verdeutlicht das Prinzip. Das von einer Lichtquelle ausgehende Lichtb¨ undel f¨allt unter dem Winkel α auf eine Platte der Dicke d und mit dem Brechungsindex n.

Ein Teil der Intensit¨at wird an der Oberfl¨ache reflektiert, der andere Teil wird im Medium nach dem Snellius’schen Brechungsgesetz gebrochen. Beim Austritt des Lichtb¨ undels aus dem Medium tritt erneut eine Reflexion bzw.

Transmission auf.

Durch die Platte wird das einfallende Lichtb¨ undel in mehrere reflektierte und

transmittierte Lichtb¨ undel aufgespaltet, wobei benachbarte Teilb¨ undel einen

Gangunterschied entsprechend des optischen Wegunterschieds besitzen. In Ab-

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

Abbildung 6: a) Interferenz gleicher Neigung. b) Berechnung des Gangunter- schieds benachbarter Teilb¨undel. c) Strahlengang f¨ur zwei Lichtb¨undel mit un- terschiedlichem Einfallswinkel. d) Interferenzmuster: Haidinger’sche Ringe.

bildung 6b) ist dies f¨ ur zwei benachbarte reflektierte Teilb¨ undel dargestellt. F¨ ur den Gangunterschied ∆ berechnen wir:

∆ =n(AB + BC) − AD (27)

= 2nd

cos β − 2d tan β sin α.

Mit Hilfe des Snellius’schen Brechungsgesetzes ergibt sich:

∆ = 2nd

cos β − 2nd sin ² β

cos β (28)

=2nd cos β (29)

=2d p

n ² − sin ² α.

Ber¨ ucksichtigen wir noch zus¨atzlich, dass bei Reflexion am optisch dichteren Medium ein Phasensprung von π (bzw. ein Gangunterschied von λ/2) auftritt, so erhalten wir schließlich f¨ ur den Gangunterschied:

∆ = 2d p

n ² − sin ² α − λ

2 . (30)

Bringt man in den Strahlengang eine Sammellinse, so interferieren die Teilb¨ undel im Punkt P in der Brennebene der Linse. Dabei tritt maximale Intensit¨at auf, wenn der Gangunterschied ein Vielfaches der Wellenl¨ange be- tr¨agt. F¨ ur den Fall, dass der Gangunterschied ein ungeradzahliges Vielfaches der halben Wellenl¨ange betr¨agt, l¨oschen sich die Teilwellen aus.

Der Gangunterschied benachbarter Teilb¨ undel h¨angt vom Einfallswinkel α (Neigungswinkel) des einfallenden Lichts ab. Ist das einfallende Licht nicht parallel, so dass mehrere Lichtb¨ undel mit unterschiedlichen Einfallswinkel auf die Platte treffen (Abbildung 6c), so interferieren alle Teilb¨ undel, die unter dem gleichen Neigungswinkel einfallen im selben Punkt. Daher spricht man von Interferenz gleicher Neigung.

Abbildung 6c) zeigt nur einen zweidimensionlen Spezialfall, bei dem die

Wellenb¨ undel in der gleichen Einfallsebene auf die Platte treffen. Im Dreidi-

mensionalen, bei dem die Wellenb¨ undel auch unter unterschiedlichen Winkel

ψ zum Einfallslot einfallen, interferieren alle Teilwellen, die den gleichen

Neigungswinkel α besitzen, nicht in einem Punkt, sondern innerhalb eines

Kreisrings in der Brennebene der Linse. Als Interferenzmuster beobachtet man

daher ein konzentrisches Ringsystem, die als Haidinger’sche Ringe bezeichnet

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

e

x d(x) a

Interferenzmuster

1 1a 1b

Abbildung 7: Interferenz gleicher Dicke.

werden (Abbildung 6d).

Interferenzen gleicher Dicke

F¨allt paralleles Licht auf eine keilf¨ormige Platte, so verlaufen die reflektierten Lichtb¨ undel nicht mehr parallel zueinander (Abbildung 7). Falls der Keilwinkel ǫ sehr klein ist, gilt f¨ ur den Gangunterschied der Teilb¨ undel 1a und 1b

∆ ≈ 2d(x) p

n ² − sin ² α − λ

2 . (31)

F¨allt das Licht zudem fast senkrecht auf den Keil, so gilt sin α ≈ 0 und somit

∆ ≈ 2d(x)n − λ

2 . (32)

Der Gangunterschied ¨andert sich mit der Keildicke d(x). Nur in einem Streifen parallel zur Keilkante, d.h. f¨ ur d(x) = konstant, ist der Gangunterschied gleich groß. Blickt man von oben auf den Keil, so beobachtet man daher ein Streifenmuster (Fizeau- Streifen).

Das Michelson-Interferometer

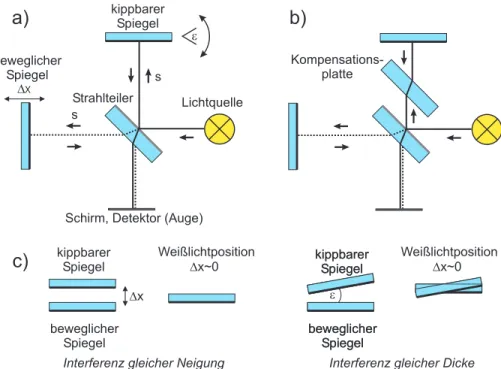
Der Aufbau eines Michelson-Interferometers ist in Abbildung 8a) skiz- ziert. Die von einer Lichtquelle ausgehenden Wellenz¨ uge treffen auf einen Strahlteiler, der das einfallende Licht in zwei Teilwellen gleicher Intensit¨at auf- teilt. Der eine Teil wird senkrecht zur Einfallsrichtung ” nach oben“ abgelenkt,

der andere Teil wird nicht abgelenkt und l¨auft weiter in den ” linken“ Schenkel.

Nach dem Durchlaufen einer Wegstrecke s treffen die Teilwellen jeweils auf einen weiteren Endspiegel, der das Licht zur¨ uckreflektiert. Der Endspiegel im linken Schenkel des Interferometers (beweglicher Spiegel) ist zudem um eine kleine Distanz ∆x verschiebbar. Der kippbare Spiegel im oberen Schenkel l¨asst sich um einen kleinen Winkel ǫ verkippen. Die reflektierten Wellenb¨ undel treffen wieder auf den Strahlteiler und verlassen diesen in gleicher Richtung.

Schließlich treffen beide Wellenb¨ undel auf einem Schirm oder Detektor (Auge), an dem sich die entstehenden Interferenzmuster beobachten lassen.

Abbildung 8: a) Aufbau eines Michelson-Interferometers. b) Strahlengang mit zus¨atzlicher Kompensationsplatte. c) Die beiden Endspiegel bilden eine ” Luft- platte“, so dass je nach Spiegelstellung entweder Interferenz gleicher Neigung oder Interferenz gleicher Dicke auftritt.

Wenn Sie Abbildung 8a) genau angeschaut haben, ist Ihnen sicherlich aufge-

fallen, dass das Lichtb¨ undel im linken Schenkel, auch bei gleichen geometri-

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

schen Wegl¨angen s, eine gr¨oßere optische Wegl¨ange durchlaufen hat als das Lichtb¨ undel im oberen Schenkel. Der Grund daf¨ ur liegt im Aufbau des Strahl- teilers. Dieser besteht aus einer planparallelen Glasplatte, bei der eine Stirn- fl¨ache mit einer d¨ unnen, ” halbreflektierenden“ Schicht bedampft wurde. Die optische Wegl¨ange des nach links abgelenkten Lichts ist dadurch innerhalb des Strahlteilers doppelt so groß, wie die optische Wegl¨ange des nach oben laufen- den Lichts. Um diesen zus¨atzlichen Gangunterschied auszugleichen, wird gem¨aß Abbildung 8b) in den oberen Schenkel eine zus¨atzliche Glasplatte (Kompensa- tionsplatte) eingebaut, die die gleiche Dicke, die gleiche Orientierung und aus dem gleichen Material besteht, wie der Strahlteiler. Dadurch wird sichergestellt, dass die optischen Lichtwege bei gleichen geometrischen Lichtwegen gleich groß sind. Dies ist besonders dann wichtig, wenn das Michelson-Interferometer von

” weißem“ bzw. breitbandigem Licht beleuchtet wird. Ohne Kompensationsplat- te w¨ urde die Dispersion des Glasmaterials dazu f¨ uhren, dass der Gangunter- schied, abh¨angig von der Wellenl¨ange, in den beiden Schenkeln unterschiedlich groß w¨are.

Abbildung 9: Interenzmuster bei unterschiedlichen Spiegelabst¨anden.

Die optischen Lichtwege in den jeweiligen Schenkeln sind je nach Position des beweglichen Spiegels unterschiedlich groß. Zum besseren Verst¨andnis k¨onnen wir uns die jeweiligen Lichtwege in der gleichen Richtung vorstellen, indem wir uns z.B. den linken Schenkel um 90 ^◦ auf den oberen Schenkel geklappt denken.

Dadurch ¨andern sich nicht die tats¨achlich durchlaufenen Lichtwege. Es wird aber ersichtlich, dass die beiden Spiegel eine Luftplatte der Dicke ∆x bilden und je nach Orientierung des kippbaren Spiegels, entweder Interferenz gleicher Neigung oder Interfernz gleicher Dicke auftritt (Abbildung 8c).

Bei parallelen Spiegeln (Interferenz gleicher Neigung) betr¨agt der Gangunter- schied in Richtung des Winkels α gem¨aß Gleichung (30):

∆ = 2∆x cos α − λ

2 , (33)

wobei wir hier f¨ ur den Brechungsindex n = 1 angenommen haben. Als In- terferenzmuster beobachtet man ein Ringsystem wie es in Abbildung 9 f¨ ur unterschiedliche Spiegelabst¨ande ∆x dargestellt ist. Die Interpretation dieses Musters ist besonders einfach, wenn wir uns nur auf das Zentrum, d.h. α = 0, beschr¨anken. Hierf¨ ur folgt aus (33):

∆ | ^α=0 = 2∆x − λ

2 . (34)

F¨ ur ∆x = λ/2 betr¨agt der Gangunterschied λ/2, so dass im Zentrum das Mini- mum 0-ter Ordnung liegt. Sind die Spiegel um ∆x = 3λ/4 verschoben, betr¨agt der Gangunterschied λ. Im Zentrum liegt dann das Maximum 1-ter Ordnung.

Ver¨andert man den Spiegelabstand kontinuierlich, so quillt bei jeder Weg¨ande- rung um λ/2 eine neue Interferenzordnung aus dem Zentrum hervor und die niedrigeren Ordnungen bewegen sich radial nach außen.

Wird der kippbare Spiegel um einen kleinen Winkel geneigt, so geht das kreisf¨ormige Interferenzmuster in ein Streifenmuster ¨ uber (Interferenz gleicher Dicke). Auch in diesem Fall f¨ uhrt eine Vergr¨oßerung von ∆x um λ/2 dazu, dass eine neue Interferenzordnung entsteht. Wird der bewegliche Spiegel kon- tinuierlich verschoben, so wandern die Interferenzstreifen gleichm¨aßig in eine bestimmte Richtung.

Dieses Prinzip l¨asst sich zur Bestimmung der Wellenl¨ange der Lichtquelle

verwenden. Der bewegliche Spiegel kann mit Hilfe einer Mikrometerschraube

messbar verschoben werden. Wird der Spiegel um die Strecke ∆x verschoben,

so wandern ∆m Interferenzstreifen an einer Markierung im Gesichtsfeld vorbei

(Abbildung 10a). Durch Messung von ∆x und Z¨ahlung der dabei vorbeige-

laufenen Interferenzstreifen ∆m kann die Wellenl¨ange berechnet werden. Da

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

Abbildung 10: a) Gesichtsfeld des Michelson-Interferometers bei der Wel- lenl¨angenmessung. b) Aufbau der evakuierbaren K¨uvette zur Messung des Bre- chungsindex von Luft.

jeder gez¨ahlte Streifen einer ¨ Anderung von ∆x um λ/2 entspricht, folgt f¨ ur die Wellenl¨ange:

λ = 2 ∆x

∆m . (35)

Des Weiteren sollen Sie im Praktikum interferometrisch den Brechungsindex von Luft bestimmen. Dazu befindet sich in einem Interferometerschenkel eine Glask¨ uvette. Der Luftdruck in der K¨ uvette kann mit Hilfe einer Pumpe und einem Nadelvenil variiert werden (Abbildung 10b). ¨ Andert sich der Druck in der K¨ uvette, so ¨andert sich der Brechungsindex ∆n und damit die optische Wegl¨ange. Im Gesichtsfeld sieht man dann wieder ∆m Interferenzstreifen an der Markierung vorbeilaufen. Ist a die L¨ange der K¨ uvette, so folgt f¨ ur die Anderung des Gangunterschieds ¨

∆ = 2a∆n. (36)

Die Zwei ber¨ ucksichtigt, dass die K¨ uvette von dem Lichtb¨ undel zweimal durch- laufen wird. Mit ∆ = λ∆m folgt:

∆m = ∆

λ = 2a ∆n

λ → ∆n = λ

2a ∆m. (37)

Der Brechungsindex wird ¨ uber den ganzen verf¨ ugbaren Bereich ∆n = n(Luft) − n(Vakuum) = n −1 variiert, indem der Druck in der K¨ uvette von p = 0 bis p = b (b: Luftdruck) ver¨andert wird und man dabei die am Marker vorbeilaufenden Interferenzstreifen ∆m z¨ahlt. Dann ist

n(λ, T, b) − 1 = λ

2a ∆m(b). (38)

Mit dem Michelson-Interferometer lassen sich auch Interferenzen mit Licht- quellen beobachten, die eine sehr kleine Koh¨arenzl¨ange besitzen (z.B. ” Weiß- licht“ einer Gl¨ uhlampe). Voraussetzung daf¨ ur ist, dass der Gangunterschied in den beiden Interferometern nicht gr¨oßer ist als die Koh¨arenzl¨ange. Daher m¨ ussen zur Beobachtung dieser sogenannten

” Weißlichtinterferenzen“die Licht- wege in den beiden Schenkeln nahezu gleich groß sein. Diese Einstellung, bei der der bewegliche Spiegel so justiert ist, dass ∆x ≈ 0 gilt, bezeichnet man als Weißlichtposition (Abbildung 8c).

VI Durchf¨ uhrung des Versuchs

VI.1 Justierung des Interferometers

Der Aufbau des im Praktikum verwendeten Michelson-Interferometers ist in Abbildung 11 dargestellt. Der Aufbau entspricht im wesentlichen der Skizze in Abbildung 8b). Im linken Schenkel befindet sich zur Messung des Brechungs- index von Luft, noch eine evakuierbare Glask¨ uvette. Da das Glasmaterial der K¨ uvette einen zus¨atzlichen wellenl¨angenabh¨angigen Gangunterschied hervor- ruft, wird dieser durch zus¨atzliche Kompensationsplatten im oberen Schenkel ausgeglichen. Die Position des beweglichen Endspiegels im linken Interferome- terschenkel kann mit Hilfe einer Mikrometerschraube eingestellt werden. Zur Erh¨ohung der Aufl¨osung wird der bewegliche Spiegel ¨ uber eine Hebelunter- setzung von 1:5 angesteuert. Eine Drehung der Mikrometerschraube um die Strecke ∆s verschiebt den Spiegel daher nur um 1/5 ∆s.

Zur Justierung des Interferometers k¨onnen zwei Zeiger in den Strahlengang eingeschwenkt werden.

Es stehen drei verschiedene Lichtquellen zur Verf¨ ugung. Eine Quecksil-

berdampflampe und eine Gl¨ uhlampe befinden sich in einem gemeinsamen

Geh¨ause (Doppellichtquelle), das auf einer optischen Schiene direkt vor der

Mattscheibe des Interferometers platziert werden kann. An der Austritts¨off-

nung der Doppellichtquelle l¨asst sich ein Gr¨ unfilter anbringen. Dadurch wird

bei Betrieb mit der Quecksilberdampflampe das Interferometer nur mit der

gr¨ unen Quecksilberlinie (λ = 546, 07 nm) beleuchtet. Des Weiteren kann das

Interferometer noch von einer Halogenlampe mit einem nachgeschalteteten

Prismen-Monochromator beleuchtet werden. Zur Variierung der spektralen

Bandbreite stehen vier Austrittsspalte unterschiedlicher Spaltbreite zur

Verf¨ ugung. Die Spaltbreiten sind auf den jeweiligen Tr¨agern angegeben.

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

Lichtquelle kippbarer

Spiegel

beweglicher Spiegel

Strahlteiler

Detektor (Auge) Kompensationsplatten

evakuierbare Küvette Mikrometerschraube

Halogenlampe

Prisma Austrittsspalt

Linse Linse

Zeiger 1

auswechselbare Spalte unterschiedlicher Breite

Zeiger 2

Mattscheibe Hebel

Abbildung 11: Oben: Aufbau des im Praktikum verwendeten Michelson- Interferometers. Unten: Aufbau des Monochromators.

Abbildung 12: Justage: Parallelstellen der Spiegel.

Parallelstellen der Spiegel:

Beleuchten Sie die Mattscheibe mit der Quecksilberdampflampe aus der Doppellichtquelle und schwenken Sie den Zeiger 1 auf die Mattscheibe. Der Zeiger 2 vor dem kippbaren Spiegel ist vorher aus dem Strahlengang herauszu- drehen. Wenn Sie in den Strahlengang blicken, sehen Sie drei Spiegelbilder des Zeigers 1 (Abbildung 12 a). Der kippbare Spiegel hat eine Dreipunktlagerung mit zwei Justierschrauben, die sich so einstellen lassen, dass zwei der Bilder des Zeigers 1 zusammenfallen (Abbildung 12 b). Es wird dann ein Ausschnitt aus dem Ringsystem mit im allgemeinen sehr vielen eng beisammen liegenden Ringsegmenten sichtbar. Durch vorsichtiges Nachjustieren l¨asst sich unter allm¨ahlicher Vergr¨oßerung der Ringabst¨ande das Zentrum des Ringsystems ins Gesichtsfeld bringen (Abbildung 12 c). Damit ist die Parallelstellung der Spiegel erreicht. Der Zeiger 1 wird wieder beiseite geschoben.

Einstellen gleicher optischer Wegl¨ angen (Weißlichtinterferenz):

Achtung: Bei diesem Einstellvorgang muss das Nadelventil an der eva- kuierbaren K¨ uvette ge¨offnet sein, d.h. in der Zelle muss Barometerdruck herrschen, sonst ist die Einstellung nicht reproduzierbar!

Uberzeugen Sie sich, dass der Elektromotor nicht an der Mikrometerschraube ¨ anliegt. Falls dies doch der Fall ist, h¨angen Sie die Feder aus der Halterung aus und schwenken die Motoreinheit zur Seite Abbildung 13. Zus¨atzlich muss auch die CCD-Kamera nach rechts weggeschwenkt werden, so dass Sie das Interferenzmuster mit dem Auge erkennen k¨onnen.

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

Der bewegliche Spiegel wird mittels der Mikrometerschraube so verschoben, dass die Lichtwege in beiden Schenkeln gleich groß sind. Eine Verg¨oßerung des Lichtwegs ist daran zu erkennen, dass aus dem Zentrum des Interferenzmusters neue Ordnungen herausquellen und sich radial nach außen bewegen. Bei einer Verkleinerung des Lichweges laufen die Interferenzringe nach innen und verschwinden im Zentrum. Dabei ver¨andert sich das Bild allm¨ahlich in der Weise, dass der jeweils innerste Ring einen immer gr¨oßeren Raum des Gesichtsfeldes einnimmt (Abbildung 9). Wenn praktisch nur noch ein bis zwei Ringe sichtbar sind, wird der kippbare Spiegel mittels der Justierschrauben um einen kleinen Winkel verkippt, so dass anstelle der Ringe gleicher Neigung Streifen gleicher Dicke erscheinen. Stellen Sie den Keilwinkel und damit den Streifenabstand so ein, dass etwa 8 bis 10 Streifen sichtbar sind, die am besten schr¨ag stehen sollten. Schwenken Sie den Zeiger 2 vor dem kippbaren Spiegel in den Strahlengang. Wenn Sie jetzt von Hg-Licht auf Gl¨ uhlicht umschalten, verschwindet das Interferenzbild, bis nach langsamem Weiterdrehen an der Mikrometerschraube im vorherigen Drehsinn die bunte Streifenschar der Weiß- lichtinterferenzen sichtbar wird. Bringen Sie den mittleren dunklen Streifen mit dem Zeiger zur Deckung und notieren Sie f¨ ur diese Spiegelstellung den an der Mikrometerschraube eingestellten Wert s 0 . Sollte Ihnen die Einstellung der Weißlichtinterferenz nicht gelingen, gehen Sie wie folgt vor:

Hilfe zum Auffinden der Weißlichtinterferenz:

Entfernen Sie die Doppellichtquelle und beleuchten Sie die Mattscheibe mit der Lampe des Monochromators. W¨ahlen Sie f¨ ur den Austrittsspalt die Blende mit der Spaltbreite 0,2 mm. Dadurch hat man noch einigermaßen monochromatisches Licht. Drehen Sie nun die Mikrometerschraube in die Richtung, in der die Interferenzringe im Zentrum verschwinden. Lesen Sie am Mikrometer den Wert ab, bei dem die Interferenzstreifen erscheinen und bei dem Sie verschwinden. Der Mittelwert wird eingestellt, dann der 1,5 mm Spalt im Monochromator eingesetzt und erneut die Mitte des interferenzf¨ahigen Bereichs eingestellt. Wenn Sie nun die Mattscheibe des Interferometers mit der Gl¨ uhlampe der Doppellichtquelle beleuchten, sollten Sie die Weißlichtin- terferenz erkennen k¨onnen. Notieren Sie den an der Mikrometerschraube eingestellten Wert s 0 .

Federhalterung

Abbildung 13: Motorantrieb der Mikrometerschraube.

VI.2 Messung der Wellenl¨ ange

Benutzen Sie zur Beleuchtung die Hg-Lampe mit dem Gr¨ unfilter. Schwenken Sie Zeiger 2 so in den Strahlengang, dass dieser am Spiegel aufliegt. Drehen Sie den Elektromotor in Richtung Mikrometerschraube und h¨angen Sie die Feder in die Halterung ein (Abbildung 13). Das Interferenzmuster k¨onnen Sie mit einer CCD-Kamera filmen und auf dem Monitor beobachten. Erh¨ohen Sie langsam die Motordrehzahl bis der Zeiger auf irgendeinen Streifen zeigt. Schalten Sie den Motor aus und notieren Sie die Einstellung der Mikrometerschraube (s 0 ).

Drehen Sie nun mit Hilfe des Motors die Mikrometerschraube langsam weiter und z¨ahlen Sie mindestens 200 vorbeilaufende Streifen ab. Diese Messung ist insgesamt dreimal mit jeweils anderen Werten f¨ ur s 0 durchzuf¨ uhren. Bei der Berechnung der Wellenl¨ange gem¨aß Gleichung (35) ist zu ber¨ ucksichtigen, dass die Mikrometerverschiebung ∆s = s 200 − s 0 durch einen Hebel im Verh¨altnis 5:1 untersetzt wird. Die Spiegelverschiebung ist daher ∆x = ∆s/5. Somit folgt f¨ ur die Wellenl¨ange

λ = 2 5

∆s

∆m . (39)

Hinweis zur Messgenauigkeit: Die Skala der Mikrometerschraube besitzt ein

Teilstrichabstand von 10 µm. Bei der Ablesung l¨asst sich der Wert noch auf

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum IIA Versuch 232 Michelson-Interferometer

etwa 1/5 eines Teilstrichabstands sch¨atzen, so dass die Messgenauigkeit etwa 2 µm betr¨agt. F¨ ur den Fehler des Spiegelabstands ∆x bedeutet dies wegen der 1:5 Untersetzung eine Ablesegenauigkeit von 2 µm und eine Sch¨atzm¨oglichkeit von 400 nm ≈ 0, 8 λ. Da der Gangunterschied 2∆x betr¨agt, ergibt sich hierf¨ ur ein Fehler von 1,6 λ. Der Fehler des Gangunterschieds entspricht demnach das 1,6-fache der Wellenl¨ange. Um λ auf 1% genau zu bestimmen, muss der Gang- unterschied mindestens 160 λ betragen. Durch das Abz¨ahlen von 200 Streifen sollte die Genauigkeit besser als 1% sein.

VI.3 Messung des Brechungsindex von Luft

Als Lichtquelle ist wieder die Quecksilberdampflampe mit vorgesetztem Gr¨ unfilter zu benutzen. Schließen Sie das Nadelventil indem Sie den Einstell- knopf ganz nach rechts drehen. Schalten Sie die Vakuumpumpe ein und ¨offnen Sie den Absperrhebel solange, bis sich der Druck in der K¨ uvette nicht mehr

¨ andert.

Mittels des Nadelventils l¨asst man in die evakuierte Gaszelle langsam Luft einstr¨omen und liest nach je 5 oder 10 Streifenverschiebungen das Manometer ab (p 0 , p 5 , p 10 ,...). Falls Sie allein arbeiten, m¨ ussen Sie bei der Ablesung des Manometerwertes das Nadelventil schließen und anschließend wieder ¨offnen.

F¨ uhren Sie die Messung dreimal durch und notieren Sie die Zimmertemperatur.

VI.4 Messung der Koh¨ arenzl¨ angen verschieden breiter Rechteckspektren

Offnen Sie das Nadelventil, so dass in der K¨ ¨ uvette wieder Atmosph¨arendruck herrscht. Verfahren Sie den beweglichen Spiegel auf die Weißlichtposition s 0 und schalten Sie von Quecksilberlicht auf die Gl¨ uhlampe der Doppellichtquelle um.

Im Gesichtsfeld sollte die Weißlichtinterferenz zu beobachten sein. Falls nicht, m¨ ussen Sie die Spiegelposition s 0 vorsichtig nachjustieren. Entfernen Sie nun die Doppellichtquelle aus dem Strahlengang und schalten Sie die Halogenlampe des Monochromators ein. Vorsicht, die Lampe wird sehr heiß. Lampengeh¨ause nicht ber¨ uhren!

Der Monochromator ist fest auf λ=546 nm eingestellt. Nur bei dieser Wel- lenl¨ange gelten die auf den vier austauschbaren Austrittsspalten angegebe- nen Bandbreiten. Die Spaltbreiten sind in Klammern angegeben. Zwecks Gew¨ahrleistung gleicher Beobachtungsbedingungen, sind die vier Austrittsspal- te fl¨achengleich.

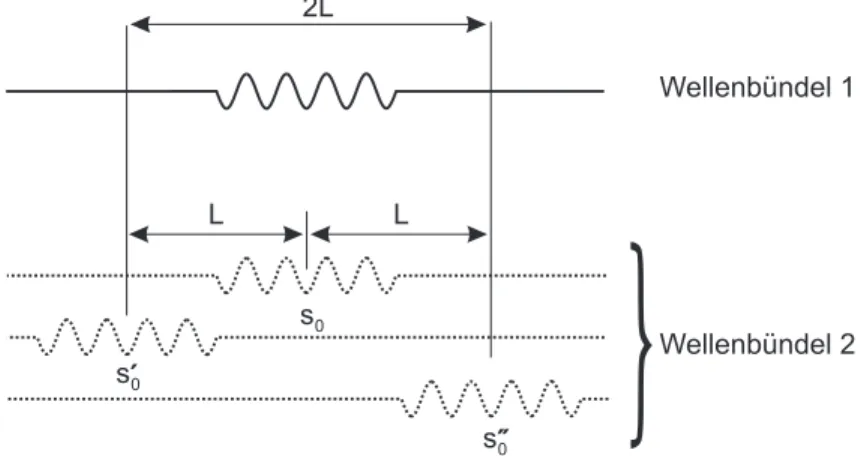
Abbildung 14: Messprinzip zur Bestimmung der Koh¨arenzl¨ange.

Um die Koh¨arenzl¨ange zu bestimmen, wird gem¨aß Abbildung 14 der bewegliche Spiegel ausgehend von s 0 solange verschoben, bis die Interferenzen gerade ver- schwinden (Position s ^′ 0 bzw. s ^′′ 0 ). In diesem Fall entspricht der Gangunterschied der beiden Teilwellen gerade der Koh¨arenzl¨ange. Zur Erh¨ohung der Messgenau- igkeit wird 2L statt L bestimmt. Man misst nicht gegen s 0 , sondern bestimmt den Abstand der symmetrisch zum Optimum bei s 0 liegenden ersten Sichtbar- keitsminima gegeneinander. Bestimmen Sie die Positionen s ^′ 0 und s ^′′ 0 f¨ ur die vier Austrittsspalte. Achtung: beim schmalsten Spalt ist das erste Minimum sehr breit, beim breitesten Spalt liegen die Minima dagegen so dicht, dass das erste ¨ ubersehen werden kann.

VII Auswertung

zu 2.

Berechnen Sie die Wellenl¨ange der gr¨ unen Qeucksilberlinie.

zu 3.

Berechnen Sie den Brechungsindex von Luft f¨ ur Normalbedingungen. Ist n 0

der Brechungsindex bei Normalbedingungen, dann gilt:

n 0 − 1

n(p) − 1 = p 0 T pT 0

. (40)

c Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 0.9 B.Sc. Stand 03/2009

Mit Hilfe von Gleichung (38) folgt dann:

(n 0 − 1) = (n − 1) p 0

p T T 0

= λ 2a

∆m p

p 0 T T 0

, (41)

wobei T die Temperatur w¨ahrend der Messung ist und die mit 0 indizierte Gr¨oßen sich auf Normalbedingungen beziehen (T ⁰ =273,15 K, p 0 =101325 Pa).

Tragen Sie in einem Diagramm ∆m uber den Druck ¨ p auf und bestimmen Sie Steigung ∆m/p. Damit k¨onnen Sie aus Gleichung (41) n 0 bestimmen. F¨ ur die Wellenl¨ange setzen Sie entweder den Literaturwert ein oder den von Ihnen zuvor bestimmten Wert. Das Innenmaß der K¨ uvette betr¨agt a = (50 ± 0, 05) mm.

Das Manometer besitzt eine G¨ uteklasse von 0,6. Eine beliebige Ablesung kann um maximal 0,6% vom Skalenendwert (800 Torr) falsch sein, also um knapp 5 Torr. Dieser systematische Fehler der Absolutanzeige sollte sich bei Diffe- renzmessungen zwar weitgehend herausheben, es muss jedoch damit gerechnet werden, dass auch die relative Teilungsgenauigkeit der Skala nicht viel besser als 0,6% ist (d.h. 1 Teilstrich 5 Torr ± 0,6%).

Vergleichen Sie Ihr Ergebnis mit dem Literaturwert (n 0 =1,00028).

zu 4.

Unter Ber¨ ucksichtigung von ∆s = ∆x/5 folgt L = 1/5 (s ^′′ 0 − s ^′ 0 ). Tragen Sie

L gegen λ ² /∆λ auf. Theoretisch sollte sich eine Gerade mit der Steigung 1

ergeben. Wie groß ist die Diskrepanz?

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum II Versuch 233 Fourieroptik

Versuch 233 Fourieroptik

Diodenlaser

Objekt

Analysierspalt

Strahlteiler- Würfel

Abbildung 1: Versuchsaufbau: optische Bank.

I Messaufbau

• Singlemode Glasfaser-gekoppelter Diodenlaser mit regelbarer Stromversor- gung und Justieroptik f¨ur einen Parallelstrahl

• Ein Satz Beugungsobjekte: Spalte (fest/mit ver¨anderlicher Breite), Dop- pelspalt, Gitter, Kreuzgitter, Spalt mit gaussf¨ormigem Transmissionsprofil

• Verschiedene sph¨arische und Zylinder-Linsen

• Strahlteiler

Abbildung 2: Versuchsaufbau: Zeilenkamera mit Zylinderlinse.

• Graufilter

• Spiegel

• Verschiedene Fest-Reiter

• Feinjustierbare Verschiebereiter

• Symmetrisch ¨offnender Analysierspalt

• Verschiedene schmale Metallstreifen als Modenblende

• SCCD-Zeilenkamera mit PC und Monitor zur Aufnahme von Beugungs- bildern und

” Objektbildern“, sowie Drucker

II Literatur

• Hecht,

” Optics“, Addison-Wesley Publishing Company

• Klein-Furtak,

” Optik“, Springer Verlag

• Demtr¨oder, ” Experimentalphysik 2“, Springer Verlag

• Homepage des Praktikums

http://www.physi.uni-heidelberg.de/Einrichtungen/AP/info/Software.php

c Dr. J. Kowalski, Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 1.0 Stand 03/2010

III Motivation

Der vorliegende Versuch soll zu einem vertieften Verst¨andnis der Theorie der optischen Abbildung beitragen. Es wird dabei die Rolle der Beugung am Ob- jekt, also des abzubildenden Gegenstandes, beim Zustandekommen des Objekt- bildes untersucht. Das Beugungsbild des Objektes entsteht zum ersten Mal in der Brennebene einer Linse, die hinter dem Objekt aufgestellt ist. Es heißt–

aus Gr¨ unden, die im Lauf der Lekt¨ure verst¨andlich werden sollen– auch ” Fou- rierbild“, die Brennebene, in der es entsteht, nennt man ” Fourierebene“. Ernst Abbe, der Jenaer Physiker, der sich 1873 mit den Fragen der prinzipiellen Aufl¨osung eines Mikroskopes befaßte, nannte das Beugungsbild das ” prim¨are Bild“ und das ¨ ubliche Bild des Objektes das

” sekund¨are Bild“. In der Betrach- tungsweise der Fourieroptik ist ein Bild, das von einer Linse entworfen wird, die Summe– das Integral– aller am Objekt gebeugten Teillichtb¨ undel. Die Linse erf¨ullt dabei nur die Funktion, diese Teilb¨undel im Endlichen– der Bildebene–

zusammenzuf¨uhren. Um zu untersuchen, welchen Beitrag die verschiedenen Beugungsordnungen zum entstehenden Bild liefern– also dessen Helligkeits- verteilung, Bildsch¨arfe– erlaubt es der Aufbau, u.a. gezielt in der Fourierebene einzelne Beugungsordnungen auszublenden bzw. zuzulassen und am Bild zu verfolgen, wie sich dabei dessen Struktur ¨andert.

An dem formal besonders einfach zu behandelnden aber auch als Modell be- sonders wichtigen Objekt ” Spalt“ wird zun¨achst die Intensit¨atsverteilung ¨ uber die Spaltbreite bei Zulassung einer zunehmenden Zahl von Beugungsordnun- gen zum Spaltbild mit einer empfindlichen CCD-Zeilenkamera gemessen. Die jeweils beobachtbaren charakteristischen Bildstrukturen k¨onnen mit den Ergeb- nissen einer theoretischen Analyse verglichen werden, in welcher das Bild aus den jeweils zur Abbildung zugelassenen Beugungsordnungen wieder mehr oder minder vollst¨andig zusammengesetzt wird. Diese theoretische Analyse wird mit Hilfe des Programms “Mathematica“ auf einem PC durchgef¨ uhrt, wobei mit we- nigen Programmzeilen Fourierintegrale bestimmt und damit errechnete Spalt- bilder geplottet werden k¨onnen. An dem etwas komplexeren aber immer noch mathematisch genau und einfach zu behandelnden Doppelspalt werden analo- ge Untersuchungen durchgef¨uhrt. Dar¨uberhinaus wird an diesem Modellobjekt das Problem der Aufl¨osung der Doppelstruktur experimentell sowie durch Si- mulationsrechnungen mit Mathematica untersucht.

IV Vorbereitung

Machen Sie sich vertraut mit den Themen der geometrischen Optik, der opti- schen Abbildung (Linsenformel, Abbildungsmaßstab), der Fraunhoferbeugung und den mathematischen Regeln der Fouriertransformation. Schauen Sie sich auch nochmals den Versuch

” Optische Abbildung“ an, den Sie im Praktikum I durchgef¨ uhrt haben.

V Aufgaben

Ein einfacher optischer Aufbau mit wenigen Linsen, einem Strahlteiler sowie einem kleinen Diodenlaser als spektral schmale, intensive Parallellichtquelle erm¨oglicht es, simultan sowohl das Beugungsbild des Objektes (hier Spalte, Gitter, Kreuzgitter etc.) als auch das ¨ ubliche Bild des Objektes selbst darzu- stellen. Durch Eingriffe in der

” Fourierebene“– das ist die Ebene, in der die Beugungsstruktur erstmals auftritt– werden gezielt die Beitr¨age der einzelnen Beugungsordnungen zum Objektbild sichtbar gemacht und k¨onnen quantitativ verfolgt werden.

Folgende Aufgaben sollen bearbeitet werden:

1. Aufbau der ben¨otigten optischen Anordnung.

2. Registrierung und Ausmessung der Beugungsfigur eines Einfachspaltes mit einer CCD-Kamera.

3. Registrierung und Ausmessung des Spaltbildes mit der CCD-Kamera bei gezielten Manipulationen (Ausblenden/Zulassen verschiedener Beugungs- maxima) in der

” Fourier-Ebene“ (Fouriersynthese).

4. Zu Aufgabe 2 und 3 analoge Untersuchungen an einem Doppelspalt. Auf- suchen von Beugungsfigur und Objektbild, zun¨achst mit dem Auge, dann mit der Kamera. Messungen zur Grenze der Aufl¨osung der Doppelstruktur.

5. Quantitativer Vergleich der bei 2.) bis 4.) gemessenen Strukturen mit den theoretisch zu erwartenden Intensit¨atsprofilen (u.a. Verwendung des Pro- grammes Mathematica). Simulation des Grenzfalles

” Verschwinden der

Doppelstruktur“ beim Doppelspalt mit Hilfe von Mathematica und Ver-

gleich mit dem Experiment.

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum II Versuch 233 Fourieroptik

6. Qualitative Beobachtung verschiedener Beugungsobjekte bei Manipu- lationen in der Fourierebene (Liniengitter, Kreuzgitter, beugungsfreier Spalt,...).

VI Grundlagen

Die ” klassische“ Theorie der Beugung

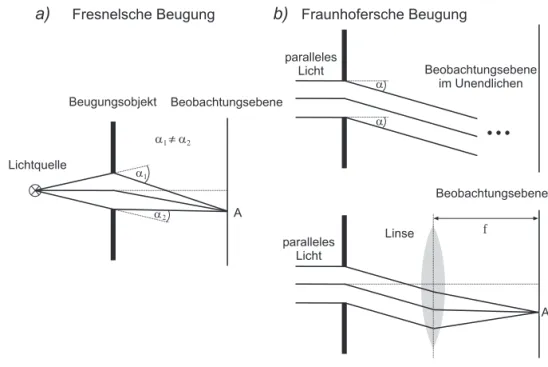
Prinzipiell gibt es zwei Versuchsanordnungen, mit denen sich Beugungserschei- nungen untersuchen lassen. Bei der Fresnelschen Beugung (Abbildung 3a), die den allgemeinen Fall der Beugung beschreibt, befinden sich die Lichtquelle und die Beobachtungsebene in einem endlichen Abstand zum beugenden Objekt.

Diese Anordnung f¨uhrt dazu, dass die im Punkt A interferierende Lichtb¨ undel unter verschiedenen Winkeln gebeugt werden. Die mathematische Behandlung dieser Beugungserscheinung ist daher ¨außerst kompliziert. Einfacher gestaltet sich der Fall, wenn nur parallele Lichtb¨undel vorhanden sind. Bei dieser sogenannten Fraunhoferschen Beugung (Abbildung 3b) befindet sich die Lichtquelle im Unendlichen, so dass das beugende Objekt von parallelem Licht beleuchtet wird. Da alle Lichtb¨undel parallel sind, interferieren diese im Unendlichen. Will man die Intensit¨atsverteilung in einem endlichen Abstand beobachten, so ist dies mit einer Sammellinse hinter dem beugenden Objekt m¨oglich. Die Beugungsstrukturen lassen sich dann in der Brennebene der Linse beobachten (Denken Sie an die elementaren Linsengesetze: Parallelstrahlen werden zu Brennpunktstrahlen). ¨ Uberlegen Sie sich, dass die Gr¨oße der Beugungsstruktur von der Brennweite der verwendeten Linse abh¨angt.

Wir wollen hier nur auf die Fraunhofersche Beugung eingehen und als Beispiel die Beugung an einem Spalt untersuchen.

Ein Spalt (Abbildung 4) wird von einem parallelen und monochromatischen Lichtstrahl der Wellenl¨ange λ beleuchtet. Wir k¨onnen infolgedessen sagen, dass alle Punkte des Spaltes mit gleicher Amplitude E 0 und Phase ϕ = ωt erregt werden:

E(Spalt) = E(y) = E 0 e ^iωt (1) Die Breite des Spaltes d werde in y-Richtung gemessen, der Nullpunkt liege in der Mitte des Spaltes. Zudem soll die L¨ange sehr groß gegen¨ uber der Breite sein, so dass das einfallende Lichtb¨undel nur in einer Dimension begrenzt wird.

Gem¨aß dem Huygens- Fermat’schen Prinzip geht von jedem Punkt des Spaltes eine Elementarwelle aus, deren ¨ Uberlagerung zu einer bestimmten Intensit¨ats-

Beobachtungsebene

f paralleles

Licht

Linse a paralleles

Licht

a

Beobachtungsebene im Unendlichen Beugungsobjekt

Lichtquelle a

a

Beobachtungsebene

a) b)

a

= a

Fresnelsche Beugung Fraunhofersche Beugung

A

A

Abbildung 3: a) Fresnelsche Beugung. b) Fraunhofersche Beugung. Die Beob- achtungsebene l¨asst sich mit Hilfe einer Linse aus dem Unendlichen auf einen endlichen Abstand verlegen.

verteilung im Unendlichen, bzw. in der Brennebene einer Linse, f¨ uhrt. Wir m¨ ussen dazu alle Teilb¨ undel untersuchen, die parallel zueinander in einer be- stimmten Richtung α laufen. Mathematisch bedeutet dies die Aufintegration ebener Wellen aus den Quellpunkten des Spaltes:

E ∞ (α) =

+d/ 2

Z

− d/ 2

E 0 e ^{i(ωt − kl)} dy. (2)

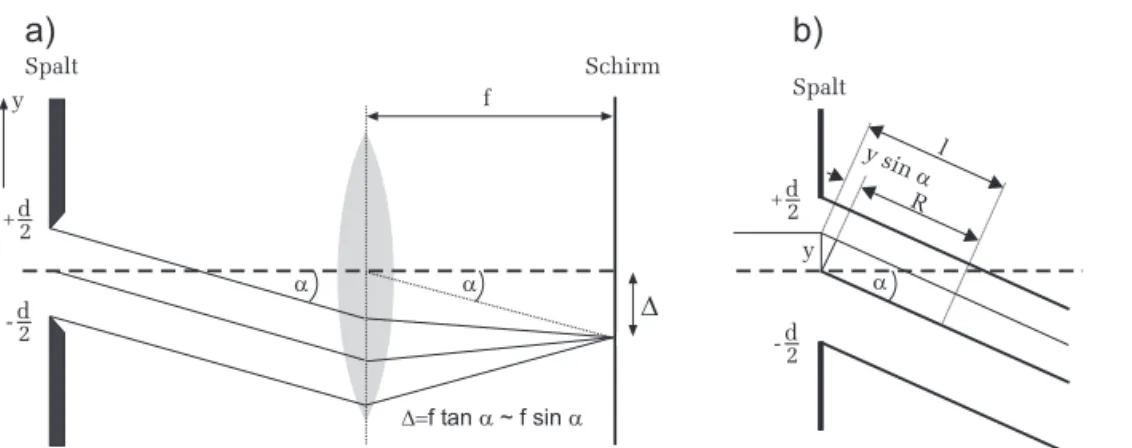
Hierbei ist k = 2π/λ der Betrag des Wellenvektors. Aus Abbildung 4b ist zu erkennen, dass ein bei y ausgehendes Lichtb¨undel gegen¨ uber einem vom Mittelpunkt des Spalts ausgehenden Lichtb¨ undel einen Gangunterschied von y sin α aufweist. F¨ ur die Wegl¨ange l gilt dann:

l = R + y sin α. (3)

c Dr. J. Kowalski, Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 1.0 Stand 03/2010

d 2

d 2 -

Spalt

d

2

d 2 -

l Spalt

R

y a a

y sin a Schirm

a) b)

a y f

D

D= f tan a ~ f sin a

Abbildung 4: a) Fraunhofersche Beugung am Spalt. Das in Richtung α gebeug- te Parallellichtb¨undel wird auf einen Punkt in der Brennebene der Linse, im Abstand ∆ von der optischen Achse abgebildet. b) Detailansicht zur Ermittlung des Gangunterschiedes eines von y ausgehenden Lichtb¨undels.

Einsetzen dieses Ausdrucks in Gleichung (2) und Ausf¨ uhren des Integrals ergibt:

E ∞ (α) =E 0 e ^i(ωt−kR) e ^{− ik sin α d/2} − e ^{ik sinα d/2}

−ik sin α (4)

=E 0 e ^i(ωt−kR) sin πd sin α/λ

π sin α/λ , (5)

wobei wir die Beziehung

e ^±iδ = cos δ ± i sin δ (6)

benutzt haben. Setzen wir zur Abk¨urzung x = d

λ π sin α (7)

so erhalten wir

E ∞ (x) = E 0 e ^{i(ωt − kR)} sin x

x d. (8)

Zur Bestimmung der Intensit¨at muss Gleichung (8) noch quadriert werden:

I ∞ (x) ∝ sin ² x

x ² d ² ∝ I 0 sin ² x

x ² , (9)

Spalt Linse Brennebene

der Linse

f ^x

I(x)

Abbildung 5: Intensit¨atsverteilung I(x) = I 0 sin ² (x)/x ² der Beugungsstruktur eines Spalts in der Brennebene der Linse (Fourier- Ebene).

wobei I 0 ∝ d ² ist.

Die Intensit¨atsverteilung ist in Abbildung 5 dargestellt.

Exkurs: Fourierreihen und Fourierintegrale

Aus der linearen Algebra ist Ihnen bekannt, dass ein Vektor durch eine Linearkombination von Basisvektoren dargestellt werden kann. ¨ Ahnliches ist Ihnen sicherlich auch schon in der Analysis begegnet. Auch hier gibt es Basissysteme, in denen sich Funktionen durch Linearkombination von

” Basisfunktionen“ darstellen lassen. Am bekanntesten ist wohl die Taylorreihe.

Dabei handelt es sich um eine Potenzreihe, die eine Funktion f (x) um einen bestimmten x-Wert approximiert. Die Basisfunktionen sind in diesem Fall die Potenzfunktionen x ⁿ .

Ein weiteres Basissystem stellen die trigonometrischen Funktionen Sinus und Kosinus dar. Nach dem Fourier-Theorem lassen sich periodische Funktio- nen durch eine Linearkombination dieser trigonometrischen Basisfunktionen in einer Fourierreihe entwickeln. Man bezeichnet dies als Fourierzerlegung, Fou- rieranalyse oder auch als harmonische Analyse.

Sei f (x)eine periodische Funktion mit der Periode L, d.h. f (x +L) = f (x). F¨ur

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum II Versuch 233 Fourieroptik

f(x)

-L/2 x - /2 l

L/2 l /2

-0,5 0,0 0,5

-0,8 -0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8

f( x)

x [L]

a = 1/2

n=1, Amplitude: 2/p

n=5, Amplitude: 2/5p

n=3, Amplitude: -2/3p

-0,5 0,0 0,5

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

a)

b)

c)

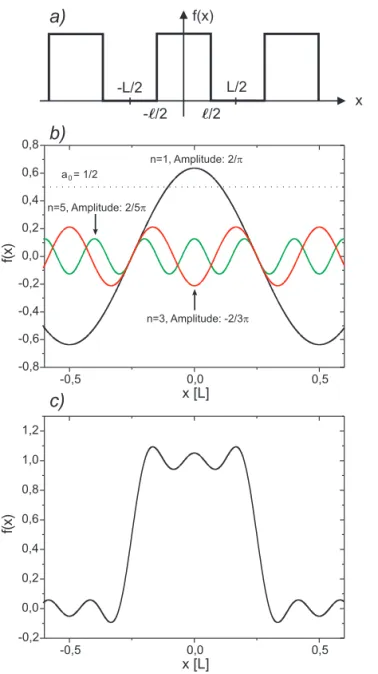
Abbildung 6: a): Rechteckfunktion mit der Periode L. b): Gleichanteil a 0 /2, sowie die ersten drei Fourierterme. c): Summe aus Gleichanteil und den ersten drei Gliedern.

die Fourierdarstellung dieser Funktion gilt:

f (x) = a 0

2 +

∞

X

n=1

a n cos 2πn

L x

+ b n sin 2πn

L x

(10) mit den Fourierkoeffizienten

a n = 2 L

Z L/2

−L/2

f (x) cos 2πn

L x

dx (11)

und

b n = 2 L

Z L/2

− L/2

f (x) sin 2πn

L x

dx. (12)

Wir wollen hier nicht auf die Herleitung dieser Gleichungen eingehen, sondern deren Aussagen an einem konkreten Beispiel diskutieren. Betrachten wir dazu eine Rechteckfunktion mit der Periode L, wie sie in Abbildung 6 a) dargestellt ist. Die Funktion f (x) ist definiert durch:

f (x) =

( 1, −l/2 < x < l/2

0, l/2 > |x| < L/2. (13) Um diese Funktion in einer Fourierreihe gem¨aß Gleichung (10) darzustellen, m¨ussen wir die Fourierkoeffizienten berechnen. Da die Rechteckfunktion gerade ist, d.h. f (x) = f (−x), verschwinden, wie Sie leicht nachrechnen k¨onnen, alle Koeffizienten b n . Wir m¨ ussen daher nur die Koeffizienten a n bestimmen. F¨ur a 0 berechnen wir:

a 0 = 2 L

Z l/2

− l/2

dx = 2l

L . (14)

F¨ ur die restlichen Koeffizienten a n gilt:

a n = 2 L

Z l/2

− l/2

cos 2πn

L x

dx = 1 πn sin

2πn L x

l/2

− l/2

= 2 πn sin

πn l

L

(15) Betrachten wir als konkretes Beispiel eine Rechteckfunktion mit einem Tast- verh¨altnis von L : l = 2 : 1 (Abbildung 6 a). Aus Gleichung (10) und den oben berechneten Koeffizienten folgt dann f¨ur die Fourierreihe:

f (x) = 1 2 + 2

π cos 2π

L x

− 2 3π cos

6π L x

+ 2

5π cos 10π

L x

− ... (16)

c Dr. J. Kowalski, Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 1.0 Stand 03/2010

In Abbildung 6 b) sind die ersten drei Glieder der Fourierreihe sowie der Gleich- anteil a 0 /2 grafisch dargestellt, darunter im Teilbild 6 c) die Summe dieser Ter- me. Zus¨atzlich zeigt Abbildung 7 noch die Fourierreihen bis hin zu n = 27. Je mehr Summanden (Ordnungen) in der Fourierreihe ” mitgenommen“ werden, desto genauer n¨ahert sich die Reihe der Rechteckfunktion an.

Die Fourieranalyse ist von außerordentlicher Bedeutung in vielen Bereichen der Physik. Ein anschauliches Beispiel findet sich f¨ur Funktionen, die ein zeitperi- odisches Signal beschreiben, z.B. einen akustischen Ton oder ein elektrisches Signal. Ersetzen wir in Gleichung (10) die Variable x durch die Zeit t und w¨ahlen f¨ur die Periode L, die Periodendauer T , wobei gilt:

T = 2π

ω , (17)

so ergibt sich f¨ ur die Fourierreihe einer periodischen, zeitabh¨angigen Funktion:

f (t) = a 0

2 +

∞

X

n=1

a n cos(nωt) + b n sin(nωt). (18) Dieser Ausdruck stellt eine ¨ Uberlagerung von Sinus- und Kosinusfunktionen mit unterschiedlichen Frequenzen und Amplituden dar. Die Fourieranalyse gibt somit Auskunft ¨ uber das Frequenzspektrum, aus dem sich ein zeitperiodisches Signal zusammensetzt. In Abbildung 8 ist das Spektrum eines zeitperiodischen Rechtecksignals dargestellt. Entlang der Abszisse ist die Frequenz aufgetragen.

Die jeweiligen Amplituden entsprechen den Koeffizienten a n .

Das Spektrum eines periodischen Signals ist stets diskret. Neben der Grund- frequenz ω (Grundton) treten auch Vielfache nω auf, die als Obert¨one oder n-te Harmonische bezeichnet werden.

In einer Fourierreihe lassen sich nur periodische Funktionen entwickeln. Aber auch nichtperiodische Funktionen lassen sich mit Hilfe der trigonometrischen Funktionen darstellen. Eine nichtperiodische Funktion erh¨alt man aus einer periodischen Funktion f¨ur den Grenzfall, dass die Periode gegen unendlich geht.

In Abbildung 9 ist dies f¨ ur einen Rechteckpuls, der sich aus einer periodischen Rechteckfunktion ableiten l¨asst, dargestellt. Bild a) zeigt das Spektrum bei einem Tastverh¨altnis von L : l = 2 : 1. Vergr¨oßert man die Periode L bei gleich bleibender Pulsbreite l, so treten im Spektrum zus¨atzliche Moden auf.

Die Teilbilder b) und c) zeigen dies f¨ur ein Tastverh¨altnis von 4 : 1 bzw. 8 : 1.

F¨ur den Grenzfall L → ∞ geht die Anzahl der Moden gegen unendlich und sind unendlich dicht gepackt (Abbildung 9 d). Es ist einleuchtend, dass in diesem

n=1

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

-1,0 -0,5 0,0 0,5 1,0

-0,2 0,0 0,2 0,4 0,6 0,8 1,0 1,2

f( x)

x [L]

n=3

n=5 n=7

n=19 n=27

Abbildung 7: Fourierentwicklung eines Rechtecksignals.

Physikalisches Anf¨ angerpraktikum der Universit¨ at Heidelberg - Praktikum II Versuch 233 Fourieroptik

0 2 4 6 8 10 12 14 16 18 20 22 24

-0,2 0,0 0,2 0,4 0,6 0,8

A m p lit u d e

Frequenz w w

3w 5w

7w 9w

11w p

2

3p

-2 7p

-2 11p -2 5p

2

9p 2

Abbildung 8: Frequenzspektrum eines Rechtecksignals. Bei den ersten sechs Mo- den sind die Frequenzen und Amplituden mit angegeben.

Fall die Fourierreihe in ein Integral ¨ ubergeht und die Fourierkoeffizienten nicht mehr diskret sind, sondern durch eine kontinuierliche Funktion beschrieben wer- den. Dies f¨ uhrt zur sogenannten Fouriertransformation eines nichtperiodischen Signals.

Die kontinuierliche Fouriertransformation ¹ ist definiert durch:

f (x) = Z ^∞

−∞

F(k) e ^ikx dk. (19)

Wegen

e ^ikx = cos(kx) + i sin(kx) (20)

stellt auch die Fouriertransformation die Entwicklung einer Funktion nach tri- gonometrischen Funktionen dar. F (k) heißt Fouriertransformierte der Funk- tion f (x).

1

In der Literatur finden sich verschiedene Definitionen der Fouriertransformation, die sich durch einen Normierungsfaktor unterscheiden.

0 10 20 30 40 50 60 70 80

-0,10 -0,05 0,00 0,05 0,10 0,15 0,20 0,25

Amplitude

L = 8l

x

0 10 20 30 40 50 60 70 80

-0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7

Amplitude

x

L

l

L = 2 l

0 10 20 30 40 50 60 70 80

-0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

Amplitude

x

L = 4 l

0 20 40 60 80

Amplitude

L

10 30 50 70

a)

c)

b)

d)

x

L

2p

L 2p

L 2p

L 2p

-0,02 -0,01 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07

Abbildung 9: Verdeutlichung des ¨ Ubergang zur Fouriertransformation einer nichtperiodischen Funktion.

F¨ ur die R¨ ucktransformation gilt:

F (k) = 1 2π

Z ^∞

−∞

f (x) e ^{− ikx} dx. (21)

Handelt es sich bei f (t) um eine Funktion, die von der Zeit abh¨angt, so stellt die Fouriertransformierte F (ω) (wir schreiben nun ω anstatt k) das kontinuierliche Frequenzspektrum dieser Funktion dar. F¨ ur den Fall, dass x eine Ortsvaria- ble ist, schreiben wir f¨ ur die Fouriertransformierte F (k) und bezeichnen k als Raumfrequenz (Ortsfrequenz). Wir werden im n¨achsten Abschnitt ausf¨ uhrlich darauf eingehen.

c Dr. J. Kowalski, Dr. J.Wagner - Physikalisches Anf¨angerpraktikum - V. 1.0 Stand 03/2010

VI.1 Herleitung der Fourierdarstellung der Fraunhofer- schen Beugung

Wir wollen im Folgenden das Thema der Fraunhoferschen Beugung in etwas all- gemeinerer Gestalt formulieren, um den ¨ Ubergang zu der hier interessierenden Beschreibung mit Hilfe der Fouriertheorie vorzubereiten.

Wir betrachten nach Abbildung 10 eine ¨ Offnung S von willk¨ urlicher Gestalt in der yz - Ebene, die mit monochromatischem Licht bestrahlt werde und wollen die elektrische Feldst¨arke im Aufpunkt P bestimmen.

y

z

0 dS

P(X,Y,Z) x

r R

Y

Z

X

Abbildung 10: Zur Geometrie bei der Beugung an einer beliebigen ¨ Offnung.

Dazu greifen wir ein differentielles Fl¨achenelement dS(x = 0, y, z) heraus und betrachten eine davon ausgehende Kugelwelle (Elementarwelle) e ^ikr /r. Mit ǫ als Quellst¨arke pro Einheitsfl¨ache, die zun¨achst als konstant ¨ uber der Fl¨ache S angenommen wird, ist die elektrische Feldst¨arke am Ort P durch

dE = ǫ e ^ikr

r dS (22)

gegeben.

F¨ ur den Abstand von dS zu P(X,Y,Z) erhalten wir r = q

X ² + (Y − y) ² + (Z − z) ²

. (23)

Wenn die beugende ¨ Offnung klein gegen¨uber dem Abstand OP ist, so kann man im Amplitudenterm ǫ A /r statt r den Abstand OP=R verwenden. Diese N¨aherung f¨ur r darf im Phasenterm hingegen nicht ohne weiteres angewendet werden, da kr = (2π/λ)r eine große Zahl darstellt. (Sie entspricht dem Abstand OP in Wellenl¨angen ausgedr¨uckt). Mit Hilfe von

R = q

X ² + Y ² + Z ²

(24) erhalten wir durch Einsetzen in Gleichung (23) und einigen Umformungen:

r = R q

1 + (y ² + z ² )/R ² − 2(Y y + Zz)/R ²

. (25)

Im Fernfeld ist R groß gegen¨ uber den Dimensionen der ¨ Offnung, so daß der Term

(y ² + z ² )/R ² ≪ 1 (26)

vernachl¨assigbar wird. Es verbleibt:

r = R q

1 − 2(Y y + Zz)/R ²

. (27)

Auch der Ausdruck in der eckigen Klammer kann mit Hilfe der Relation p 1 − ξ = 1 − ξ/2. (28) f¨ ur ξ ≪ 1 vereinfacht werden:

r = R

1 − (Y y + Zz)/R ²

. (29)

Setzen wir nun diese N¨aherung f¨ur r in den Phasenterm in Gleichung (22) ein und integrieren ¨uber die gesamte ¨ Offnung S, so erhalten wir f¨ ur die elektrische Feldst¨arke am Ort P:

E(R) = ǫ e ^ikR R

Z Z

e ⁻

^{(Y y+Zz)} dy dz. (30)

Beschr¨anken wir nun unsere Betrachtung auf einen kleinen Bereich um R. Wir

k¨onnen dann davon ausgehen, dass der Term e ^ikR /R vor dem Integral eine