Kapitel 1 Grundlagen
Volltext
Abbildung



ÄHNLICHE DOKUMENTE
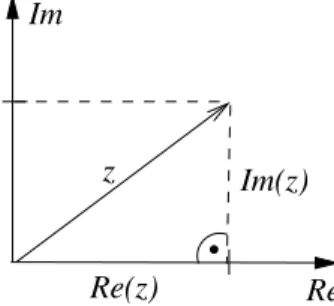
Der Betrag einer komplexen Zahl erf¨ullt die Eigenschaften einer Norm, und daraus kann durch d(z, w) = |z − w| ein Abstandsbegriff (Metrik) gewonnen werden.. C ist dadurch
Tutorien Höhere Mathematik I, WS
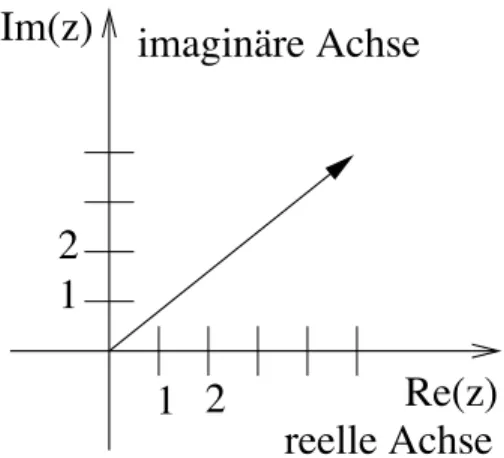
Da die Addition zweier komplexer Zahlen darin besteht, dass Real- und Imaginärteile jeweils für sich addiert werden (siehe oben), kann man diese Addition auch einfach
Die komplexen Zahlen sind der umfassendeste Zahlenbereich, der die reellen Zahlen enthält und für den alle diese Rechengesetze gelten. In der Robotik ver- wendet man
Zeichne ein xy-Koordinantensystem für x=-4 bis x=4 (L.E.=1cm). a) Trage dort die Werte der Quadrate für die x-Werte aus Aufgabe 3 ein. b) Versuche, die eingetragen Punkte
Es stellt sich heraus, dass diese gr¨oßere Menge gerade die Menge der komplexen Zahlen ist..
[r]
Anstelle der Vektoren treten Funktionen und anstelle der Matri- zen treten lineare Operatoren, welche Funktionen auf Funktionen abbilden. Ein Beispiel f¨ ur einen solchen Operator
![Abbildung 1.8: x ∈ ]1, 3[ und x ∈ [3, 5[](https://thumb-eu.123doks.com/thumbv2/1library_info/3900854.1524310/7.918.111.671.205.546/abbildung-x-x.webp)