Statistische Analyseverfahren Abschnitt 7: Multidimensionale Skalierung

Statistische Analyseverfahren

Abschnitt 7: Multidimensionale Skalierung

Dr. Andreas W¨ unsche

TU Bergakademie Freiberg Institut f¨ ur Stochastik

Januar 2020

7 Multidimensionale Skalierung

I Die multidimensionale Skalierung (auch mehrdimensionale Skalierung, MDS) hat das Ziel, n Untersuchungsobjekte durch Punkte in einem niedrigdimensionalen Raum (h¨ aufig 2-dimensional oder 3-dimensional) so darzustellen, dass die Abst¨ ande zwischen den Objekten m¨ oglichst exakt oder gut reproduziert werden.

I Diese Darstellung durch Punkte nennt man eine Konfiguration.

I Ausgangspunkt sind Daten ¨ uber die Abst¨ ande zwischen den Objekten oder ¨ uber die Rangfolge dieser Abst¨ ande. Merkmalswerte selber liegen in der Regel oft nicht vor bzw. sind nicht quantitativ, so dass eine Hauptkomponentenanalyse nicht direkt anwendbar ist.

I Bei einer metrischen multidimensionalen Skalierung geht man von einer Distanzmatrix aus. Bei einer nichtmetrischen

multidimensionalen Skalierung ist man an der Reihenfolge der

Distanzen und nicht an den Distanzen selber interessiert.

7.1 Metrische multidimensionale Skalierung

Einfache geometrische Fakten sind:

I Sind n Datenpunkte (Datenvektoren) im Raum R ^p gegeben, dann findet man Konfigurationen von n Punkten im Raum der Dimension min{n − 1, p} , die dieselben Abst¨ ande zwischen den Punkten wie die Datenpunkte besitzen.

I

Zwei unterschiedliche Punkte liegen auf einer Geraden, die man durch die Menge R

beschreiben kann.

I

Drei unterschiedliche Punkte liegen auf einer Geraden oder in einer zweidimensionalen Ebene.

I

. . .

I Sind umgekehrt (euklidische) Abst¨ ande von n Punkten (in einem Raum unbekannter Dimension) gegeben und nicht die Punkte selber, dann kann man

I

im Fall n = 2 zwei Punkte in R

mit dem selben Abstand finden;

I

im Fall n = 3 drei Punkte in R

oder in R

mit den selben

Abst¨ anden zueinander finden, usw.

Nichteindeutigkeit der Konfigurationen

I Ist eine Konfiguration von n Punkten in einem Raum R ^k gegeben, dann f¨ uhren Verschiebungen (Translationen) aller Punkte um einen festen Vektor, Drehungen aller Punkte um einen festen Winkel und Spiegelungen aller Punkte an einer Geraden zu Konfigurationen von Punkten, bei denen die Abst¨ ande zwischen den transformierten Punkten und zwischen den urspr¨ unglichen Punkten ¨ ubereinstimmen.

I Bsp. 7.1

I

3 Punkte im R

in Datenmatrix : x

=

1 5 1 1 1 4

;

I

−1.33 2.66 −1.33

−1 −1 2

um Mittelwertvektor verschobene Punkte;

I

−1 −1 −4

1 5 1

um 90 Grad gegen den Uhrzeigersinn gedrehte Punkte;

I

an der Abszisse gespiegelte Punkte :

1 5 1

−1 −1 −4

.

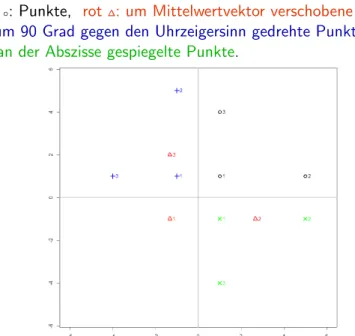
Grafik der Punkte und Distanzmatrix Beispiel 7.1

Schwarz

: Punkte, rot

: um Mittelwertvektor verschobene Punkte,

blau

: um 90 Grad gegen den Uhrzeigersinn gedrehte Punkte,

gr¨ un

: an der Abszisse gespiegelte Punkte.

Ausgangspunkt Distanzmatrix

I F¨ ur alle oben angegebenen Konfigurationen des Beispiels 7.1 lauten die Distanzmatrizen f¨ ur euklidische Abst¨ ande (bei entsprechender Nummerierung der Punkte)

d =





0 4 3 4 0 5 3 5 0



 .

I Ist nur eine Distanzmatrix gegeben, kann man versuchen, eine Konfiguration im R ² konstruktiv zu bestimmen. Dazu kann man zwei Punkte im richtigen Abstand zeichnen und dann um diese Punkte Kreise mit den entsprechenden Abst¨ anden aus der Distanzmatrix.

I Dabei gibt es 3 M¨ oglichkeiten:

I

2 Schnittpunkte (zwei m¨ ogliche ¨ aquivalente Konfigurationen),

I

1 Schnittpunkt (eine eindeutig bestimmte Konfiguration) oder

I

kein Schnittpunkt (keine m¨ ogliche Konfiguration).

Geometrische Konstruktion - zwei M¨ oglichkeiten

Fortsetzung Bsp. 7.1 Distanzmatrix d =





0 4 3 4 0 5 3 5 0



 .

Geometrische Konstruktion - genau eine M¨ oglichkeit

Bsp. 7.2 Distanzmatrix d =





0 4 1 4 0 3 1 3 0



 .

(Hier gibt es sogar eine Konfiguration im Raum R ¹ .)

Geometrische Konstruktion - keine M¨ oglichkeit

Bsp. 7.3 Distanzmatrix d =





0 4 1 4 0 2 1 2 0



 .

(d 12 > d 13 + d 23 , d.h. die Dreiecksungleichung ist verletzt.)

Bemerkungen und Fragestellungen

I Das letzte Beispiel zeigt, dass auch Distanzmatrizen auftreten k¨ onnen, f¨ ur die es keine m¨ ogliche Konfiguration in irgendeinem Raum R ^k geben kann. Derartige F¨ alle treten auch oft in den Anwendungen auf, z.B. wenn

” Distanzen“ aus nichtmetrischen Merkmalen berechnet werden.

I Dies f¨ uhrt auf folgende Fragestellungen:

1. Ist ¨ uberhaupt eine Darstellung der Distanzen durch eine Punktekonfiguration m¨ oglich und wenn ja, in welchem Raum ? 2. Wie kann man bei Distanzmatrizen eine Konfiguration von Punkten

im Raum R

finden, sodass die Abst¨ ande zwischen den Punkten mit denen in der Distanzmatrix ¨ ubereinstimmen ?

I Hier soll zuerst eine M¨ oglichkeit vorgestellt werden, aus einer Datenmatrix mit reellen Werten eine Distanzmatrix zu berechnen.

I Danach wird auf dieser Grundlage ein Algorithmus angegeben, mit

dessen Hilfe man aus einer Distanzmatrix eine Punktekonfiguration

bestimmen kann (falls eine solche existiert).

Berechnung Distanzmatrix

I Datenmatrix x =











x ₁₁ x ₁₂ . . . x _1p x ₂₁ x ₂₂ . . . x _2p .. . .. . . .. .. . x _n1 x _n2 . . . x _np











=







 x ^T ₁ x ^T ₂ . . . x ^T _n







 .

I Mit b = (b rs ) _{r ,s=1,...,n} := x x ^T und d = (d rs ) r,s=1,...,n gilt

d _rs ² = d _L ²

(x _r , x _s ) = b _rr + b _ss − 2b _rs , r, s ∈ {1, 2, . . . , n} . (1)

I Fortsetzung Bsp. 7.1 F¨ ur x ^T =

1 5 1 1 1 4

erh¨ alt man

b = x x ^T =





2 6 5

6 26 9 5 9 17



 und daraus d =





0 4 3 4 0 5 3 5 0



 .

Berechnung einer Konfiguration mit der Matrix b

I Eine reelle n × n-Matrix b , die wie oben aus einer Datenmatrix x durch b = x x ^T berechnet wird, ist immer symmetrisch und nichtnegativ definit.

I Die Spektralzerlegung (Satz 5.1) liefert die Darstellung b = u Λ u ^T

mit der Diagonalmatrix Λ = diag(λ ₁ , . . . , λ _n ) der nichtnegativen Eigenwerte und der orthogonalen Matrix u , welche spaltenweise die normierten Eigenvektoren von b enth¨ alt.

I Im Fall n > p ist mindestens ein Eigenwert gleich 0.

I Mit Λ ^0.5 = diag( √

λ 1 , . . . , √

λ n ) liefert dann x := u Λ ^0.5

eine geeignete Konfiguration, da b = x x ^T gilt. Ist k die Anzahl

der Eigenwerte echt gr¨ oßer als Null, dann liegt die Konfiguration in

einem k −dimensionalen Raum.

Berechnungen f¨ ur das Bsp. 7.1

I Wir erhielten b =





2 6 5

6 26 9 5 9 17



 .

I Die Eigenwerte der Matrix b und deren Quadratwurzeln sind λ 1 = 33.466 , p

λ 1 = 5.785 ; λ 2 = 11.534 , p

λ 2 = 3.396 ; λ 3 = 0 .

I Eine Matrix der normierten Eigenvektoren ist u =





0.239 0.087 0.967 0.820 −0.552 −0.153 0.521 0.829 −0.204



 .

I Eine Punktekonfiguration im Raum R ² erh¨ alt man durch x = u Λ ^0.5 =





1.383 0.297 0 4.742 −1.875 0 3.012 2.816 0



 .

Gefundene Konfiguration aus der Matrix b im Bsp. 7.1

Berechnung der Matrix b aus der Distanzmatrix

I Um f¨ ur eine gegebene Distanzmatrix d eine Punktekonfiguration berechnen zu k¨ onnen, reicht es also aus, die dazu entsprechende Matrix b zu berechnen. Dies bedeutet, dass das Gleichungssystem (1) d _rs ² = b rr + b ss − 2b rs nach den Gr¨ oßen b rs , r, s ∈ {1, . . . , n} , aufgel¨ ost werden muss.

I Dazu kann man als erstes die Matrix a = (a rs ) r,s=1,...,n mit a _rs := −0.5d _rs ² berechnen.

I Dann gilt b _rs = a _rs − a _r • − a •s + a •• f¨ ur r , s ∈ {1, . . . , n} mit

I

a

= 1 n

n

X

s=1

a

(Zeilenmittel);

I

a

= 1 n

n

X

r=1

a

(Spaltenmittel);

I

a

= 1 n

n

X

r=1 n

X

s=1

a

(Gesamtmittel).

Algorithmus 7.4 der metrischen MDS

Ausgangspunkt ist die Distanzmatrix d = (d rs ) _{r ,s=1,...,n} . 1. Bilde die Matrix a = (a rs ) _{r ,s=1,...,n} mit a rs = −0.5d _rs ² .

2. Bilde die Matrix b = (b _rs ) _{r ,s=1,...,n} mit b _rs = a _rs − a _r • − a •s + a ••

I

a

= 1 n

n

X

s=1

a

(Zeilenmittel);

I

a

= 1 n

n

X

r=1

a

(Spaltenmittel);

I

a

= 1 n

n

X

r=1 n

X

s=1

a

(Gesamtmittel).

3. Bestimme die Eigenwerte λ 1 ≥ λ 2 ≥ . . . ≥ λ n und die zugeh¨ origen Eigenvektoren u ₁ , u ₂ . . . ,u _n der Matrix b .

4. Bestimme die Koordinaten der Konfiguration ˆ x _ij = u _ij p λ _j ,

i = 1, . . . , n (n Objekte) , j = 1, . . . , k f¨ ur eine geeignete Anzahl k

der Dimensionen (ˆ x = (u ₁ . . . u _k ) · diag(λ 1 , . . . , λ k )).

1. m¨ oglicher Fall f¨ ur Eigenwerte

I Angenommen mit einem k ≤ n gilt λ 1 ≥ λ 2 ≥ . . . ≥ λ k > 0 und im Fall k < n zus¨ atzlich λ _{k +1} = λ _k+2 = . . . = λ n = 0 , dann gibt es eine exakte Konfiguration (mit euklidischen Abst¨ anden wie in der Distanzmatrix d) im Raum R ^k .

I Falls k < n gibt es nat¨ urlich auch exakte Konfigurationen in den R¨ aumen R ^{k +1} , R ^{k +2} , . . . , R ⁿ .

I Es gibt aber keine exakten Konfigurationen in den R¨ aumen

R ^k−1 , R ^k−2 , . . . , R ¹ mit euklidischen Abst¨ anden wie in d .

Die in diesen R¨ aumen genutzten Konfigurationen besitzen nur

n¨ aherungsweise dieselben euklidischen Abst¨ ande wie in der

Distanzmatrix d .

2. m¨ oglicher Fall f¨ ur Eigenwerte

I Ist der kleinste Eigenwert λ n der Matrix b echt kleiner als 0, dann gibt es in keinem Raum R ^k mit k ∈ N eine exakte Konfiguration mit Abst¨ anden wie in der gegebenen Distanzmatrix d .

I Gilt in dieser Situation mit einem k < n

λ ₁ ≥ λ ₂ ≥ . . . λ _k > 0 ≥ λ _k+1 ≥ . . . ≥ λ _n , λ _n < 0 , (d.h. k ist der gr¨ oßte Index mit einem Eigenwert echt gr¨ oßer als 0) und berechnet die Koordinaten von Punkten im Raum R ^k nach den Formeln im Algorithmus 7.4 4., dann erh¨ alt man eine Konfiguration mit n¨ aherungsweise denselben Abst¨ anden wie in der Distanzmatrix.

I Man kann sich auch f¨ ur eine noch kleinere Dimension entscheiden.

Wahl der Dimension

I Nutzt man eine Konfiguration mit nur n¨ aherungsweise denselben Abst¨ anden wie in der Distanzmatrix kann man die G¨ ute mit Hilfe der Summe der quadrierten Distanzen bewerten. Es gilt

n

X

r =1 n

X

s=1

d _rs ² = 2n

n

X

r=1

b rr = 2n sp b = 2n

n

X

i =1

λ i

f¨ ur die Werte der gegebenen Distanzmatrix und f¨ ur die N¨ aherungskonfiguration im k −dimensionalen Raum 2n

k

X

i=1

λ _i .

I Kriterien zur Wahl von k ( Mardia , 1978):

W¨ ahle f¨ ur α = 0.75 (oder 0.8 oder 0.85) das minimale k < n mit λ _k > 0 und

P k i=1 λ _i P n

i=1 |λ _i | ≥ α oder P k

i=1 λ ² _i P n

i=1 λ ² _i ≥ α .

Bemerkungen

I Im Algorithmus 7.4 wird die Matrix b durch doppelte Zentrierung (zuerst Zentrierung der Spalten und dann Zentrierung der Zeilen oder umgekehrt) aus der Matrix a berechnet. In Matrixschreibweise bedeutet dies mit der symmetrischen n × n-Zentrierungsmatrix m := I _n − ¹ _n 1 _n 1 ^T _n die Berechnung von b = m a m .

I Wegen m 1 _n = 0 _n ist der Vektor 1 _n immer ein Eigenvektor von b zum Eigenwert 0 .

I Ist d (und damit a) symmetrisch, dann ist auch b symmetrisch.

I Ist f¨ ur eine Distanzmatrix mindestens eine Dreiecksungleichung verletzt, kann man zu allen Elementen außerhalb der

Hauptdiagonalen ein und dieselbe hinreichend große Zahl dazu addieren, so dass die Dreiecksungleichung immer erf¨ ullt wird.

I Wird die euklidische Distanzmatrix f¨ ur eine Datenmatrix genutzt,

liefern die metrische MDS und die Hauptkomponentenanalyse auf

Basis der Datenmatrix ¨ ubereinstimmende Konfigurationen.

Fortsetzung Bsp. 7.1 mit euklidischem Abstand

I Distanzmatrix d =





0 4 3 4 0 5 3 5 0



 .

I Matrix a =





0 −8 −4.5

−8 0 −12.5

−4.5 −12.5 0



 .

I Matrix b =





2.778 −2.556 −0.222

−2.556 8.111 −5.556

−0.222 −5.556 5.778



 (gerundete Werte) .

I Eigenwerte von b und Quadratwurzeln (gerundet) λ ₁ = 12.964 , p

λ ₁ = 3.601 , λ ₂ = 3.703 , p

λ ₂ = 1.924 , λ ₃ = 0.

Fortsetzung Bsp. 7.1 mit euklidischem Abstand

I Zugeh¨ orige Eigenvektoren von b (gerundet)

u ₁ =





0.183

−0.781 0.598



 , u ₂ =





0.796

−0.240

−0.556



 , u ₃ =



 0.577 0.577 0.577



 .

I Konfiguration (gerundet) ˆ x ₁ =

0.658 1.531

, ˆ x ₂ =

−2.810

−0.461

, ˆ x ₃ =

2.152

−1.070

.

I Euklidische Distanzmatrix f¨ ur Konfiguration





0 4 3 4 0 5 3 5 0



 .

Fortsetzung Bsp. 7.1 mit euklidischem Abstand

Fortsetzung Bsp. 7.1 mit Maximumsabstand

I Distanzmatrix d =





0 4 3 4 0 4 3 4 0



 .

I Matrix a =





0 −8 −4.5

−8 0 −8

−4.5 −8 0



 .

I Matrix b =





3.778 −3.056 −0.722

−3.056 6.111 −3.056

−0.722 −3.056 3.778



 .

I Eigenwerte von b und Quadratwurzeln (gerundet) λ ₁ = 9.167 , p

λ ₁ = 3.028 , λ ₂ = 4.500 , p

λ ₂ = 2.121 , λ ₃ = 0.

Fortsetzung Bsp. 7.1 mit Maximumsabstand

I Zugeh¨ orige Eigenvektoren von b (gerundet)

u ₁ =





0.408

−0.816 0.408



 , u ₂ =





0.707 0

−0.707



 , u ₃ =



 0.577 0.577 0.577



 .

I Konfiguration (gerundet)

˜ x ₁ =

1.236 1.5

, ˜ x ₂ =

−2.472 0

, ˜ x ₃ =

1.236

−1.5

.

I Euklidische Distanzmatrix f¨ ur Konfiguration





0 4 3 4 0 4 3 4 0



 6=





0 4 3 4 0 5 3 5 0



 .

Fortsetzung Bsp. 7.1 mit Maximumsabstand

Fortsetzung Bsp. 7.2

I Distanzmatrix d =





0 4 1 4 0 3 1 3 0



 .

I Matrix a =





0 −8 −0.5

−8 0 −4.5

−0.5 −4.5 0



 .

I Matrix b =





2.778 −3.889 1.111

−3.889 5.444 −1.556 1.111 −1.556 0.444



 .

I Eigenwerte von b und Quadratwurzeln (gerundet) λ ₁ = 8.667 , p

λ ₁ = 2.944 , λ ₂ = 0 , p

λ ₂ = 0 , λ ₃ = 0.

Fortsetzung Bsp. 7.2

I Zugeh¨ orige Eigenvektoren von b (gerundet)

u ₁ =





0.566

−0.793 0.226



 , u ₂ =





0.824 0.544

−0.156



 , u ₃ =



 0 0.275 0.962



 .

I Konfiguration (gerundet)

˜ x ₁ =

1.667 0

, ˜ x ₂ =

−2.333 0

, ˜ x ₃ =

0.667 0

.

I Euklidische Distanzmatrix f¨ ur Konfiguration





0 4 1 4 0 3 1 3 0



 .

Fortsetzung Bsp. 7.2

Fortsetzung Bsp. 7.3

I Distanzmatrix d =





0 4 1 4 0 2 1 2 0



 .

I Matrix a =





0 −8 −0.5

−8 0 −2

−0.5 −2 0



 .

I Matrix b =





3.333 −4.167 0.833

−4.167 4.333 −0.167 0.833 −0.167 −0.667



 .

I Eigenwerte von b und Quadratwurzeln (gerundet) λ ₁ = 8.083 , p

λ ₁ = 2.843 , λ ₂ = 0 , p

λ ₂ = 0 , λ ₃ = −1.083.

Fortsetzung Bsp. 7.3

I Zugeh¨ orige Eigenvektoren von b (gerundet)

u ₁ =





0.665

−0.743 0.078



 , u ₂ =



 0.577 0.577 0.577



 , u ₃ =





0.474 0.339

−0.813



 .

I Konfiguration (gerundet)

˜ x ₁ =

1.891 0

, ˜ x ₂ =

−2.111 0

, ˜ x ₃ =

0.220 0

.

I Euklidische Distanzmatrix f¨ ur Konfiguration





0 4.002 1.671 4.002 0 2.332 1.671 2.332 0



 6=





0 4 1 4 0 3 1 3 0



 .

Fortsetzung Bsp. 7.3

Metrische multivariate Skalierung mit R

I In R kann man den Befehl cmdscale zur Realisierung einer metrischen multivariate Skalierung nutzen.

I Bsp. 7.5 Luftlinienentfernungen zwischen 5 St¨ adten

(Quelle: Handl, Kuhlenkasper , Multivariate Analysemethoden, Springer 2017, Bsp. 1.5, S. 8)

HH B K F M

HH 0 250 361 406 614

B 250 0 475 432 503

K 361 475 0 152 456

F 406 432 152 0 305

M 614 503 456 305 0

Die Berechnung der metrischen MDS mit R ergibt folgende

Konfiguration, die noch gedreht werden kann um eine f¨ ur Landkarten

¨ ubliche Ausrichtung zu bekommen.

Fortsetzung Bsp. 7.5

7.2 Nichtmetrische multidimensionale Skalierung

I Bei der nichtmetrischen mehrdimensionalen Skalierung sucht man eine Konfiguration von Punkten, so dass die Reihenfolge der Distanzen zwischen den Punkten der Konfiguration der Reihenfolge der Distanzen in der Distanzmatrix (Un¨ ahnlichkeitsmatrix)

entspricht.

I Wie im Abschnitt 7.1 folgen wir weitgehend den Ausf¨ uhrungen in Handl, Kuhlenkasper , Multivariate Analysemethoden, Springer 2017, Kap. 6.

I Bsp. 7.6 Das Vorgehen wird anhand eines Datenbeispiels aus diesem Buch illustriert (vgl. Bsp. 32, S. 185). Dabei geht es um die Einsch¨ atzung der ¨ Ahnlichkeiten der Politiker Putin, Trump, Merkel, Obama und Trudeau. Benutzt man Indizes in der angegebenen Reihenfolge und bezeichnet mit δ ij den Rang der ¨ Ahnlichkeit des Paares (i, j ) (je kleiner, desto ¨ ahnlicher) erh¨ alt man

δ 21 < δ 54 < δ 43 < δ 53 < δ 31 < δ 41 < δ 42 < δ 52 < δ 32 < δ 51 . (2)

Fortsetzung Bsp. 7.6

I Dies ergibt die folgende Distanzmatrix (Un¨ ahnlichkeitsmatrix)

∆ =













0 1 5 6 10

1 0 9 7 8

5 9 0 3 4

6 7 3 0 2

10 8 4 2 0











 .

I Eine solche Matrix hat nichtnegative Elemente, die Zahlen auf der Hauptdiagonale sind Null und sie ist symmetrisch.

I Die Dreiecksungleichung muss allerdings hier nicht gelten, da die Elemente Rangzahlen sind und nicht tats¨ achliche Abst¨ ande zwischen Punkten im Raum R ² darstellen.

In obiger Matrix gilt z.B. (im Widerspruch zur Dreiecksungleichung) 10 = δ ₅₁ > δ ₅₂ + δ ₂₁ = 8 + 1 .

I Gesucht ist eine Konfiguration von 5 Punkten im Raum R ² mit

derselben Rangfolge der Abst¨ ande wie in (2).

Ein Algorithmus der nichtmetrischen MDS

Algorithmus 7.7 ( Kruskal , 1964)

1. Bestimmung der Monotoniebedingung auf Basis der gegebenen Distanzmatrix (Un¨ ahnlichkeitsmatrix).

2. Erzeugung einer Startkonfiguration von Punkten im Raum R ² mit einer metrischen MDS auf Basis der gegebenen Distanzmatrix (Un¨ ahnlichkeitsmatrix).

3. Berechnung euklidische Distanzmatrix f¨ ur die Startkonfiguration.

4. Uberpr¨ ¨ ufung der Monotoniebedingung f¨ ur die Startkonfiguration.

5. Bestimmung der Disparit¨ aten mit Hilfe des PAV-Algorithmus.

6. Iterative Bestimmung neuer Punktekonfigurationen, bis das G¨ utemaß STRESS1 hinreichend klein ist.

7. Ausgabe und Grafik der Endkonfiguration.

8. Interpretation der Endkonfiguration falls m¨ oglich.

Anfang Kruskal -Algorithmus im Bsp. 7.6

I Gegebene Distanzmatrix (Un¨ ahnlichkeitsmatrix)

∆ =













0 1 5 6 10

1 0 9 7 8

5 9 0 3 4

6 7 3 0 2

10 8 4 2 0











 .

und Monotoniebedingung (2)

δ ₂₁ < δ ₅₄ < δ ₄₃ < δ ₅₃ < δ ₃₁ < δ ₄₁ < δ ₄₂ < δ ₅₂ < δ ₃₂ < δ ₅₁ .

I Anfangskonfiguration (gerundete Werte) in R ² mit metrischer multidimensionaler Skalierung

4.49 4.46 −2.36 −2.06 −4.53

−2.05 2.79 −3.08 0.05 2.29

.

Grafik Anfangskonfiguration Bsp. 7.6

Fortsetzung Kruskal -Algorithmus im Bsp. 7.6

I Euklidische Distanzmatrix (gerundete Werte) f¨ ur Startkonfiguration

d (0) = (d _ij ) _{i ,j =1,...,5} =













0.00 4.84 6.93 6.88 10.01 4.84 0.00 9.00 7.07 9.01 6.93 9.00 0.00 3.15 5.80 6.88 7.07 3.15 0.00 3.34 10.01 9.01 5.80 3.34 0.00











 .

I Uberpr¨ ¨ ufung der Monotoniebedingung

δ 21 < δ 54 < δ 43 < δ 53 < δ 31 < δ 41 < δ 42 < δ 52 < δ 32 < δ 51

d 21 > d 54 > d 43 < d 53 < d 31 > d 41 < d 42 < d 52 > d 32 < d 51

da

4.84 > 3.34 > 3.15 < 5.80 < 6.93 > 6.88 < 7.07 < 9.01 > 9.00 < 10.01 .

Bestimmung der Disparit¨ aten

I Die Disparit¨ aten sind Werte ˆ d _ij , die m¨ oglichst nahe an den Punktabst¨ anden d _ij der Startkonfiguration liegen und die Monotoniebedingung erf¨ ullen.

I Minimiert man X

i>j

(d ij − d ˆ ij ) ²

unter der Nebenbedingung, dass die Werte ˆ d _ij die

Monotoniebedingung erf¨ ullen, kann man diese mit Hilfe des

PAV-Algorithmus (”Pool Adjacent Violators algorithm”) bestimmen.

I Bei diesem findet man iterativ beim Durchlaufen der Folge von links nach rechts Bl¨ ocke aufeinanderfolgender Distanzen, in denen die Monotoniebedingung verletzt ist. Die Werte in diesen Bl¨ ocken werden dann durch deren arithmetischen Mittelwert ersetzt.

I Die Disparit¨ aten bilden die Elemente der Disparit¨ atsmatrix ˆ d =

d ˆ _ij

i,j=1,...,n .

Das G¨ utemaß STRESS1

I Kruskal (1964) hat folgendes G¨ utemaß f¨ ur die St¨ arke der Verletzung der Monotoniebedingung bei einer gegebenen Punktekonfiguration mit Abst¨ anden d ij vorgeschlagen.

STRESS1 = v u u u u u t

P

i>j

d _ij − d ˆ _ij 2

P

i >j

d _ij ² = v u u u u u u t

n

P

i,j=1

d _ij − d ˆ _ij 2 n

P

i,j =1

d _ij ² .

I Die Bewertung einer Konfiguration mit Hilfe von STRESS1 kann wie folgt erfolgen.

Wert von STRESS1 G¨ ute der Konfiguration 0.00 ≤ STRESS1 < 0.05 hervorragend

0.05 ≤ STRESS1 < 0.10 gut

0.10 ≤ STRESS1 < 0.15 zufriedenstellend

0.15 ≤ STRESS1 nicht gut

PAV-Algorithmus Bsp. 7.6 (gerundete Werte)

I Erster Block mit Verletzung der Monotoniebedingung:

4.84 > 3.34 > 3.15 mit Mittelwert 3.78 ⇒ neue Folge

3.78 ≤ 3.78 ≤ 3.78 < 5.80 < 6.93 > 6.88 < 7.07 < 9.01 > 9.00 < 10.01 .

I Zweiter Block mit Verletzung der Monotoniebedingung:

6.93 > 6.88 mit Mittelwert 6.90 ⇒ neue Folge

3.78 ≤ 3.78 ≤ 3.78 < 5.80 < 6.90 ≤ 6.90 < 7.07 < 9.01 > 9.00 < 10.01 .

I Dritter Block mit Verletzung der Monotoniebedingung:

9.01 > 9.00 mit Mittelwert 9.00 ⇒ neue Folge

3.78 ≤ 3.78 ≤ 3.78 < 5.80 < 6.90 ≤ 6.90 < 7.07 < 9.00 ≤ 9.00 < 10.01 . f¨ ur

d ˆ 21 ≤ d ˆ 54 ≤ d ˆ 43 < d ˆ 53 < d ˆ 31 ≤ d ˆ 41 < d ˆ 42 < d ˆ 52 ≤ d ˆ 32 < d ˆ 51 .

Disparit¨ atsmatrix und STRESS1 f¨ ur Bsp. 7.6

I Die Disparit¨ atsmatrix ist

d ˆ = d ˆ ij

i ,j =1,...,5 =













0.00 3.78 6.90 6.90 10.01 3.78 0.00 9.00 7.07 9.00 6.90 9.00 0.00 3.78 5.80 6.90 7.07 3.78 0.00 3.78 10.01 9.00 5.80 3.78 0.00











 .

I Der Wert von STRESS1 betr¨ agt f¨ ur die Startkonfiguration STRESS1 = 0.05974568 ,

damit ist also eine gute Konfiguration gefunden, bei der aber noch

die Monotoniebedingung verletzt ist.

Verbesserung einer Punktkonfiguration

I Erf¨ ullen die Punktabst¨ ande einer Konfiguration noch nicht der Monotoniebedingung, kann man in einem iterativen Verfahren eine andere Konfiguration finden, die die Monotoniebedingung erf¨ ullt (monotone Regression).

I Dabei k¨ onnen die Punkte so verschoben werden, dass die Abst¨ ande m¨ oglichst den Disparit¨ aten entsprechen, wobei die Verschiebung nur eines Punktes in der Regel dessen Abst¨ ande zu allen anderen Punkten ¨ andert.

I Bezeichnen x _j , j = 1, . . . , n , die Koordinaten der Punkte einer gegebenen Konfiguration und x ^∗ _j , j = 1, . . . , n die Koordinaten der Punkte der verbesserten Konfiguration, dann kann folgende Formel genutzt werden

x ^∗ _j = x _j + 1 n − 1

X

k6=j

d jk − d ˆ jk

d _jk x _k − x _j

. (3)

Bemerkungen

I Die Formel (3) ergibt sich daraus, dass der Punkt x ^∗ _{j (k)} := x _j + d _jk − d ˆ _jk

d _jk x _k − x _j

auf der Geraden durch x _k und x _j liegt und genau einen Abstand von ˆ d jk zum Punkt x _k hat. Da sich bei einer solchen Verschiebung auch andere Abst¨ ande ¨ andern, erfolgt die Mittelwertbildung.

I Im Allgemeinen wird es auch zur Disparit¨ atsmatrix keine Konfiguration mit diesen Distanzen im Raum R ² geben.

I Im Bsp. 7.6 ergibt z.B. eine metrische multidimensionale Skalierung mit der Disparit¨ atsmatrix als Distanzmatrix die Eigenwerte

(gerundet) der entsprechenden Matrix b

λ 1 = 72.30 , λ 2 = 25.11 , λ 3 = 2.28 , λ 4 = 0.00 , λ 5 = −2.87 .

Fortsetzung Bsp. 7.6

Mit gerundeten Werten erh¨ alt man x

:= x

+ d

− d ˆ

d

x

− x

x

=

4.46 2.79

+ 4.84 − 3.78 4.84

4.49

−2.05

− 4.46

2.79

= 4.47

1.72

x

= 4.46

2.79

+ 9.00 − 9.00 9.00

−2.36

−3.08

− 4.46

2.79

= 4.46

2.79

x

= 4.46

2.79

+ 7.07 − 7.07 7.07

−2.06 0.05

− 4.46

2.79

= 4.46

2.79

x

= 4.46

2.79

+ 9.01 − 9.00 9.00

−4.53 2.29

− 4.46

2.79

= 4.46

2.79

Dies ergibt einen neuen Vektor x ^∗ ₂ nach der 1. Iteration x ^∗ ₂ = 1

4 X

k6=2

x ^∗ _{2(k )} =

4.46 2.52

.

Fortsetzung Bsp. 7.6

I Analog erh¨ alt man verschobene Vektoren x ^∗ ₁ , x ^∗ ₃ , x ^∗ ₄ und x ^∗ ₅ , so dass sich folgende Konfiguration nach der ersten Iteration ergibt:

4.49 4.46 −2.37 −1.97 −4.61

−1.79 2.52 −3.24 0.13 2.36

.

I Der Wert von STRESS1 betr¨ agt f¨ ur diese Konfiguration 0.5158158 < 0.05974568 .

I F¨ ur diese Konfiguration ergibt eine metrische multidimensionale Skalierung die Eigenwerte (gerundet) der entsprechenden Matrix b

λ ₁ = 70.80 , λ ₂ = 25.63 , λ ₃ = 0.00 , λ ₄ = 0.00 , λ ₅ = 0.00 ,

die entsprechende Distanzmatrix stammt ja auch schon von einer

Konfiguration im Raum R ² .

Fortsetzung Bsp. 7.6

Anfangskonfiguration (blau) und neue (gr¨ un) Konfiguration

Fortgesetzte Iterationen

I Die Verbesserungen k¨ onnen iterativ wiederholt werden, bis ein hinreichend kleiner Wert f¨ ur STRESS1 erzielt wird oder eine vorher festgelegte maximale Anzahl von Iterationen erreicht ist.

I In R kann man dazu den Befehl isoMDS() aus dem Paket MASS nutzen (siehe R-Skript zu diesem Kapitel).

I Der Aufruf dieses Befehls f¨ ur die Distanzmatrix der Startkonfiguration im Bsp. 7.6 ergibt mit einem Wert STRESS1 = 1.94 · 10 ⁻¹⁴ die folgende Endkonfiguration

4.44 4.85 −2.15 −2.91 −4.22

−0.84 1.88 −4.25 0.35 2.86

.

Fortsetzung Bsp. 7.6

Endkonfiguration Bsp. 7.6

Fortsetzung Bsp. 7.6

Anfangs- (blau) und Endkonfiguration (rot)

Fortsetzung Bsp. 7.6

Anfangs- (blau), neue (gr¨ un) und Endkonfiguration (rot)

Bemerkungen

I Neben dem vorgestellen Algorithmus von Kruskal sind weitere m¨ ogliche Algorithmen in der Literatur zu finden.

I Eine Variante bei der Verbesserung der Konfigurationen besteht darin, bei der Verschiebung in (3) einen weiteren Parameter α > 0 einzuf¨ uhren und geeignet auszuw¨ ahlen. Die modifizierten Formeln sind dann

x ^∗ _j = x _j + α n − 1

X

k6=j

d jk − d ˆ jk

d _jk x _k − x _j

.