Statistische Analyseverfahren Abschnitt 3: Diskriminanzanalyse

Statistische Analyseverfahren Abschnitt 3: Diskriminanzanalyse

Dr. Andreas W¨ unsche

TU Bergakademie Freiberg Institut f¨ur Stochastik

Oktober/November 2019

3 Diskriminanzanalyse 3.1 Einf¨ uhrung

I

Zielstellung einer Diskriminanzanalyse ist es, einen Merkmalstr¨ ager (ein Objekt) mit Hilfe der beobachteten Messwerte zu einer von mehreren Klassen (Gruppen, Populationen, . . . ) zuzuordnen, wobei in der Regel keine eindeutige deterministische Zuordnung mittels einfacher Entscheidungsregeln m¨ oglich ist.

I

Zuerst soll der Fall behandelt werden, dass die unterschiedlichen Klassen durch jeweils bekannte Wahrscheinlichkeitsverteilungen der Merkmalszufallsvektoren charakterisiert werden.

I

Danach wird auf den praktisch relevanteren Fall eingegangen, dass die unterschiedlichen Wahrscheinlichkeitsverteilungen der Merkmalszufallsvektoren nicht vollst¨ andig bekannt sind.

I

Außerdem soll die lineare Diskriminanzanalyse von

vorgestellt werden, bei der keine speziellen Verteilungen der

Merkmalszufallsvektoren genutzt werden.

Beispiele

I

Kredit-Scoring: Beurteilung der Kreditw¨ urdigkeit f¨ ur (z.B.) Neukunden, wobei ein Kunde anhand von bestimmten erhobenen Daten, wie z.B. Familienstand, Alter, Verm¨ ogen, Status als Arbeitsnehmer, Besch¨ aftigungsdauer, etc. in die Klasse der kreditw¨ urdigen oder kreditunw¨ urdigen Kunden eingestuft werden soll.

I

Im Zusammenhang mit dem R-Beispieldatensatz

” Iris“ kann man das Problem betrachten, eine Schwertlilienpflanze anhand der gemessenen Gr¨ oßen L¨ ange des Kelchblattes, Breite des Kelchblattes, L¨ ange des Bl¨ utenblattes und Breite des Bl¨ utenblattes zu einer der drei Blumenarten

” Iris setosa“ (Borsten-Schwertlilie),

” Iris versicolor“ (Verschiedenfarbige Schwertlilie) und

” Iris virginica“

(Virginische Schwertlilie) zuzuordnen.

Formales Vorgehen

I

Aufgabenstellung: Klassifikation (Klassierung), Zuordnung eines Merkmalstr¨ agers zu einer von g

2 Klassen Π

, . . . , Π

auf der Grundlage von

” Messwerten“ x als Realisierungen von zuf¨ alligen p−dimensionalen Merkmalsvektoren X

.

I

Ziel: Die Zuordnung soll zu m¨ oglichst wenigen Fehlklassifikationen f¨ uhren.

I

Formales Vorgehen: Der Merkmalsraum (oft

) wird in g disjunkte Regionen R

, . . . , R

eingeteilt (zerlegt).

I

Diskriminanzregel: Der Merkmalstr¨ ager mit Merkmalsvektor x ( ” der Merkmalsvektor x“) wird der Population Π

(i

g

genau dann zugeordnet, wenn x

R

gilt.

I

H¨ aufige Annahme: Die Verteilung des Merkmalsvektors f¨ ur jede

Klasse besitze eine Dichtefunktion f

, j = 1, . . . , g , bzgl. eines

Maßes auf dem Merkmalsraum (oft die ¨ ubliche Verteilungsdichte).

Beispiel f¨ ur die Maximum-Likelihood-Diskriminanzregel

I

1 Merkmal, 2 Klassen, Normalverteilungen.

I

Geg. p = 1 , g = 2 , Π

=

, σ

) , Π

=

, σ

) , µ

< µ

; µ

, µ

, σ

bekannt.

I

Maximum-Likelihood-Diskriminanzregel:

Ordne dem Merkmalstr¨ ager mit Merkmalswert x

diejenige Klasse zu, deren Dichtefunktion im Punkt x maximal wird, bei Gleichheit kann man beliebig (messbar) zuordnen.

I

Da hier f¨ ur alle x < µ

+ µ

2 gilt f

(x) > f

(x) , lautet die (oder besser: eine) Diskriminanzregel

x < µ

+ µ

2

Π

, Zuordnung zu Klasse 1 ; x

µ

+ µ

2

Π

, Zuordnung zu Klasse 2 .

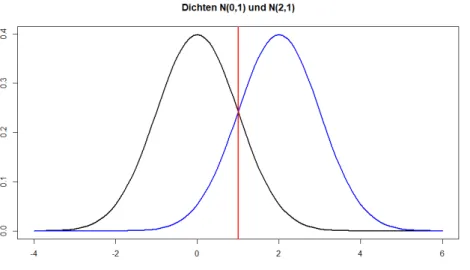
Grafik Dichtefunktionen mit µ

= 0, µ

= 2, σ

= 1

Simulationsstudie Maximum-Likelihood-Diskriminanzregel

I

In einer Simulationsstudie wurden jeweils 1000 Realisierungen des Merkmals der Klasse 1 mit der Verteilung

1) und

erzeugt.

I

Mit der Maximum-Likelihood-Diskriminanzregel werden

Realisierungwerte <

der Klasse 1 zugeordnet, die anderen (d.h.

≥1) der Klasse 2. Die theoretische Wahrscheinlichkeit f¨

ur eine Fehlklassifikation (eine Realisierung aus der Klasse 1 wird der

zugeordnet bzw. eine Realisierung aus der

wird der Klasse 1 zugeordnet) betr¨ agt jeweils 1

Φ(1)

0.159 .

I

In der erzeugten Stichprobe werden 148 Realisierungen aus der Klasse 1 der

zugeordnet und 161 Realisierungen aus der

der Klasse 1 zugeordnet, also fehlerhaft klassifiziert.

I

Bei einer Trenngrenze von

statt

zum Beispiel w¨ urden 74

Realisierungen aus Klasse 1 und 324 Realisierungen aus

fehlerhaft klassifiziert.

Histogramme Simulationsstudie

Beispiel f¨ ur die Bayes sche Diskriminanzregel

I

Geg. p = 1 , g = 2 , Π

=

, σ

) , Π

=

, σ

) , µ

< µ

; µ

, µ

, σ

bekannt, π

, π

a-priori-Wahrscheinlichkeiten f¨ ur die 1. bzw. 2. Klasse.

I Bayes

sche Diskriminanzregel: Ordne dem Merkmalstr¨ ager mit Merkmalswert x

diejenige Klasse zu, deren a-posteriori- Wahrscheinlichkeit π(j

beliebig (messbar) zuordnen.

I

Es gelten

π(j

f

(x)π

f

(x)π

+ f

(x)π

∝

f

(x )π

, j = 1, 2 ; π(1|x) > π(2|x)

x < 1

2 (µ

+ µ

) + σ

µ

µ

ln π

π

.

Simulationsstudie Bayes sche Diskriminanzregel

I

In einer Simulationsstudie wurden 2000 Realisierungen des Merkmals der Klasse 1 mit der Verteilung

1) und 1000 Realisierungen der

erzeugt. Dies entspricht der Situation mit a-priori-Wahrscheinlichkeiten π

=

, π

=

.

I

Mit der

schen Diskriminanzregel werden Realisierungwerte

<

der Klasse 1 zugeordnet, die anderen der

I

In der erzeugten Stichprobe werden 177 Realisierungen aus der Klasse 1 der

zugeordnet und 255 Realisierungen aus der

der Klasse 1 zugeordnet (also fehlerhaft klassifiziert), dies entspricht einer relativen H¨ aufigkeit von 0.144.

I

Bei einer Trenngrenze von

statt

zum Beispiel w¨ urden 314

Realisierungen aus Klasse 1 und 154 Realisierungen aus

fehlerhaft klassifiziert, dies entspricht einer relativen H¨ aufigkeit von

0.156.

Histogramme Simulationsstudie

3.2 Diskrimination bei bekannten Verteilungen

I

Allgemeine Maximum-Likelihood-Diskriminanzregel (ML-Diskriminanzregel) bei bekannten Verteilungen:

x

R

, falls L(i; x) = max

j=1,...,g

L(j ; x) mit

L(j ; x) := f

(x) , j = 1, . . . , g , (Likelihood-Funktion) mit speziellen Vereinbarungen im Fall mehrfacher Maxima, so dass eine messbare Zuordnung realisiert wird.

I

Beispiel Π

=

0 1 0.5

, Π

=

0 1

;

x = 0 : L(1; 0) = 0.5 >

= L(2; 0) , Zuordnung zu Π

;

x = 1 : L(1; 1) =

<

= L(2; 1) , Zuordnung zu Π

.

ML-Diskrimination f¨ ur Normalverteilungen mit identischen regul¨ aren Kovarianzmatrizen

I

Satz 3.2.1 Geg. Π

=

(µ

, Σ) , Σ regul¨ ar, j = 1, . . . , g . Die ML-Diskriminanzregel ist dann gegeben durch: x

R

(x

µ

)

Σ

(x

µ

) = min

j=1,...,g

(x

µ

)

Σ

(x

µ

) und eine geeignete Vereinbarung im Fall mehrfacher Minima.

I

Def. 3.2.2 Die Zahl d

(x, µ

) :=

(x

µ

)

Σ

(x

µ

)

ist der

-Abstand von x zum Erwartungswertvektor µ

(oft wird auch keine Quadratwurzel gezogen) .

I

Bem. Nimmt der

-Abstand zwischen dem Merkmalsvektor x und dem Erwartungswertvektor µ

i

der i−ten Klasse das Minimum unter allen

-Abst¨ anden

zwischen x und µ

(j = 1, . . . , g ) an, so wird der Merkmalstr¨ ager

mit dem Merkmalsvektor x der i

Allgemeiner Fall von 2 Klassen: Diskriminanzfunktion

I

Bem.

Im Fall mit g = 2 gilt: x

R

, falls L(1; x) > L(2; x) , d.h. falls ln L(1; x)

L(2; x) = ln L(1; x)

ln L(2; x) > 0 .

I

Def. 3.2.3 Die Funktion

h(x) := ln L(1; x)

L(2; x) = ln L(1; x)

ln L(2; x) , x

, wird Diskriminanzfunktion genannt.

I

Bem.

Die Diskriminanzfunktion teilt

in zwei Teilmengen. Mit der

ML-Diskriminanzregel liegt x in R

, wenn h(x) > 0 gilt.

Zwei Normalverteilungen mit gleichen Kovarianzmatrizen

I

Satz 3.2.4

Geg. Π

=

(µ

, Σ) , Σ regul¨ ar, j = 1, 2 . Dann gelten

x

R

h(x) = (µ

µ

)

Σ

x

1

2 (µ

+ µ

)

> 0 . x

R

h(x)

0 .

Folglich ist die Diskriminanzfunktion h(x) (affin) linear, ihre Nullstellenmenge

: h(x) = 0} beschreibt eine Hyperebene (die Trennebene) im Raum

, die durch den Schwerpunkt (den Mittelpunkt) der beiden Erwartungswertvektoren (µ

1

+ µ

2

)/2 geht.

I

Bem.

Wird eine affin lineare Diskriminanzfunktion zur Klassifizierung genutzt, spricht man auch von

” linearer Diskriminanzanalyse

(LDA)“.

Zwei Normalverteilungen mit regul¨ aren Kovarianzmatrizen

Bem.

Besitzen die Normalverteilungen unterschiedliche Kovarianzmatrizen, f¨ uhrt die Maximum-Likelihood-Diskriminanzregel zu einer quadratischen Diskriminanzfunktion. Das entsprechende Verfahren wird auch

” quadratische Diskriminanzanalyse (QDA)“ genannt.

Im univariaten Fall (p = 1) gilt dann x

R

x

1 σ

1

σ

−2x

µ

σ

µ

σ

+ µ

σ

µ

σ

< 2 ln σ

σ

.

Beispiel 3.2.5

Geg. Π

=

(µ

, Σ) ; j = 1, 2 ; Σ =

1 0 0 2

; µ

=

1

1

; µ

=

0

0

.

Merkmalstr¨ ager mit Merkmalsvektor x = 1

2 , 1

.

Bayes sche Diskriminanzregel

I

Wenn man bereits

” Vorurteile“ bzw. Vorinformationen ¨ uber die Zugeh¨ origkeiten zu den g Klassen hat, kann man diese mit in die Diskriminanzregel aufnehmen.

I

Geg. zus¨ atzlich a-priori-Wahrscheinlichkeiten π

0, . . . , π

0 mit

g

X

j=1

π

= 1 f¨ ur die Klassen Π

, . . . , Π

.

⇒

a-posteriori-Wahrscheinlichkeiten π(i|x) = L(i ; x)π

Pg

j=1

L(j; x)π

L(i; x)π

, i = 1, . . . , g .

I Bayes

sche Diskriminanzregel: Ordne den Merkmalsvektor x zur Klasse i zu, d.h. x

R

, falls

π

L(i; x) = max

j=1,...,g

π

L(j ; x)

(mit speziellen Vereinbarungen im Fall mehrfacher Maxima).

Bemerkungen zur Bayes schen Diskriminanzregel

I

Die Maximum-Likelihood-Diskriminanzregel erh¨ alt man im Fall π

= . . . = π

=

.

I

Im Spezialfall g = 2 f¨ uhrt das auf eine Verschiebung des kritischen Wertes der Diskriminanzfunktion: x

R

h(x) > ln(π

/π

) .

I

Insbesondere lautet die

sche Diskriminanzregel bei 2 Klassen von p-dimensional normalverteilten Merkmalsvektoren mit gleichen Kovarianzmatrizen Σ = Σ

= Σ

(vgl. Satz 3.2.4)

x

R

h(x) = (µ

µ

)

Σ

x

1

2 (µ

+ µ

)

> ln π

π

; x

R

h(x)

ln

π

π

;

bzw. mit der Diskriminanzfunktion h

(x) := h(x)

ln π

π

:

Zuordnung zu Π

falls h

(x) > 0 , sonst zu Π

.

Fortsetzung Beispiel 3.2.5

Zus¨ atzlich geg.

π

= 2

3 , π

= 1

3 .

3.3 Diskrimination, wenn Verteilungen bis auf Parameter bekannt sind

I

Sind die Verteilungen der zuf¨ alligen Merkmalsvektoren f¨ ur die einzelnen Klassen nicht bekannt, ben¨ otigt man eine Lernstichprobe (Trainingsstichprobe) von Merkmalstr¨ agern mit beobachteten Merkmalsvektoren, f¨ ur die die Zugeh¨ origkeit zu einer Klasse bekannt sein muss. Dann kann man f¨ ur weitere Merkmalstr¨ ager die

Diskrimination z.B. mit Hilfe gesch¨ atzter Parameter durchf¨ uhren.

I

Vor. 3.3.1

Es liegt eine Datenmatrix x vor, mit jeweils n

Realisierungen der Population Π

, j = 1, . . . , g , d.h.

x = (x

, . . . , x

)

, x

, x

= (x

, . . . , x

)

.

Mit diesen Daten soll eine passende Diskriminanzregel gelernt

werden.

Prinzip der Stichproben-ML-Diskriminanzregel

Prinzip 3.3.2

(i)

Die unbekannten Parameter von Π

werden mit x

j

gesch¨ atzt.

(ii)

Danach benutzt man die ML-Diskriminanzregel zur Zuordnung mit

gesch¨ atzten statt theoretischen Parametern.

Univariates Beispiel Stichproben-ML-Diskriminanzregel

3.3.3 Bsp.

Geg. p = 1 , g = 2 , Π

=

, σ

) , Π

=

, σ

) , µ

< µ

; µ

, µ

, σ

unbekannt;

Lernstichproben x

= (x

, . . . , x

)

, x

= (x

, . . . , x

)

; Sch¨ atzwerte µ

µ ˆ

= x

= (x

+ . . . + x

)/n

, j = 1, 2 .

Diskriminanzregel (Fall x

< x

) : x

R

falls x <

(x

+ x

) . Zahlenbeispiel:

x

= (4.09, 1.11, 3.73, 5.21, 2.99, 4.36, 3.46, 2.01, 1.72, 3.38)

, x

= (4.57, 5.41, 3.82, 4.12, 5.20, 4.91, 6.12, 3.72, 2.93, 4.85)

, x

= 3.21 , x

= 4.57 ,

1

2 (x

+ x

) = 3.89 . x

R

falls x < 3.89 ,

sonst x

R

.

Sch¨ atzung der Parameter der Klassenverteilungen

I

Vor. 3.3.4

Neben Vor. 3.3.1 sind die Daten in den g Klassen p-dimensional normalverteilt mit den Erwartungswertvektoren µ

1

, . . . , µ

g

und

¨

ubereinstimmenden Kovarianzmatrizen Σ = Σ

= . . . = Σ

, d.h.

X

(µ

, Σ) , j = 1, . . . , g ; µ

und Σ sind unbekannt.

I

Beh. 3.3.5

Sch¨ atzwerte aus erwartungstreuen Sch¨ atzfunktionen aus den Datenmatrizen x

sind unter Vor. 3.3.4

I f¨ur die Erwartungswertvektoren ˆ

µj =x_j = 1 nj

nj

X

k=1

x_jk, j= 1, . . . ,g;

I f¨ur die Kovarianzmatrizen Σˆ

j=s

j = 1

n_j−1

nj

X

k=1

(x_jk−x_j)(x_jk−x_j)^T, j = 1, . . . ,g.

Sch¨ atzung der gemeinsamen Kovarianzmatrix

Beh. 3.3.6

Eine geeignete Sch¨ atzmatrix (mit einer erwartungstreuen Sch¨ atzung) der gemeinsamen Kovarianzmatrix Σ ist unter Vor. 3.3.4 und mit

n = n

+ . . . + n

gegeben durch Σ ˆ = ˜ s = 1

n

g

g

X

j=1

(n

1)s

= 1

n

g

g

X

j=1 n_j

X

k=1

(x

x

)(x

x

)

=: 1

n

g w .

Beispiel 3.3.7 (Simulation f¨ ur Beispiel 3.2.5)

Lernstichprobe Klasse 1 k x

x

1 1.83 -0.41 2 0.72 -0.57 3 0.64 0.92 4 1.09 2.66 5 3.25 2.49 6 1.83 1.08 7 2.31 -0.04 8 3.50 2.32 9 2.17 3.36 10 0.57 1.79 x

= 1.791 1.360 s

= 1.102 1.907 r

= 0.336

Lernstichprobe Klasse 2 k x

x

1 -0.75 -0.60 2 1.26 0.02 3 0.04 1.00 4 0.19 1.37 5 0.46 -0.88 x

= 0.240 0.182 s

= 0.528 0.962

r

= 0.053

⇒

˜ s =

0.925 0.348 0.348 1.616

˜ s

=

1.176

−0.254

0.673

Streudiagramm Beispiel 3.3.7

blau: Merkmalsvektoren Klasse 1 ,

Stichproben-ML-Diskriminanzregel

Beh. 3.3.8

Unter obigen Voraussetzungen 3.3.4 gilt

I

die folgende Stichproben-ML-Diskriminanzregel: x

R

x

R

(x

µ ˆ

i

)

Σ ˆ

(x

µ ˆ

i

) = min

j=1,...,g

(x

µ ˆ

j

)

Σ ˆ

(x

µ ˆ

j

) und eine geeignete Vereinbarung im Fall mehrfacher Minima.

I

Im Spezialfall von 2 Klassen erh¨ alt man mit der aus der Lernstichprobe gesch¨ atzten (

” gelernten“) Diskriminanzfunktion h(x) = (x ˆ

x

)

˜ s

x

1

2 (x

+ x

)

die (oder besser: eine) Zuordnungsregel

x

R

ˆ h(x) > 0 , x

R

h(x) ˆ

0 .

Streudiagramm Beispiel 3.3.7 mit Trenngerade

blau: Merkmalsvektoren Klasse 1 ,

Rauten: Mittelwertvektoren.

Bayes sche Stichprobendiskriminanzregel (2 Klassen)

I

Beh. 3.3.9

Unter obigen Voraussetzungen 3.3.4 f¨ ur 2 Klassen gilt mit a-priori-Wahrscheinlichkeiten π

, π

mit der angepassten gesch¨ atzten Diskriminanzfunktion

h ˆ

(x) = ˆ h(x)

ln π

π

die

sche Stichprobendiskriminanzregel

x

R

h ˆ

(x) > 0 , x

R

h ˆ

(x)

0 .

I

Bem.

M¨ oglicherweise werden die a-priori-Wahrscheinlichkeiten π

, π

auch aus der Stichprobe gesch¨ atzt (und in der gesch¨ atzten Diskriminanzfunktion statt π

, π

genutzt):

ˆ

π

= n

n

+ n

, π ˆ

= n

n

+ n

.

Streudiagramm Bsp. 3.3.7 mit Bayes scher Trenngerade

blau: Merkmalsvektoren Klasse 1 ,

gestrichelt: Trenngerade

sche Diskriminanzregel;

gr¨un: Erwartungswertvektoren, Trenngeraden theoretische Verteilungen.

3.4 Einige relevante statistische Tests 3.4.1 Test auf Normalverteilung

I

Verschiedene Apassungstests k¨ onnen f¨ ur multivariate Daten verallgemeinert werden. Dies trifft auch auf die Fragestellung der Uberpr¨ ¨ ufung einer vorliegenden Normalverteilung zu.

I

Eine Variante einer Verallgemeinerung f¨ ur multivariate Daten des

-Testes auf Normalverteilung kann mit dem R-Paket

mvnormtest (Befehl mshapiro.test()) realisiert werden.

Testergebnisse f¨ ur Beispiel 3.3.7

I

1. Lernstichprobe (vgl. R-Skript f¨ ur Bezeichnungen)

> mshapiro.test(t(bsp3 3 7 lk1)) Shapiro-Wilk normality test data: Z

W = 0.9108, p-value = 0.2865

I

2. Lernstichprobe

> mshapiro.test(t(bsp3 3 7 lk2)) Shapiro-Wilk normality test data: Z

W = 0.95874, p-value = 0.7992

I

Zusammengefasste Lernstichprobe

> mshapiro.test(t(bsp3 3 7 lg)) Shapiro-Wilk normality test data: Z

W = 0.96272, p-value = 0.7395

3.4.2 Test auf Kovarianzhomogenit¨ at

I

Voraussetzung zur Anwendung der MANOVA (siehe 3.4.3) und der Nutzung der oben angegebenen Diskriminanzfunktionen ist die Gleichheit (Homogenit¨ at) der Kovarianzmatrizen. Ein m¨ oglicher Test dazu f¨ ur normalverteilte Daten ist der M-Test von

.

I

Voraussetzung Die Daten sind p-dimensional normalverteilt.

I

Hypothesen

I Die Kovarianzmatrizen sind in alleng Klassen gleich, H₀ : Σ

1=. . .=Σ

g =Σ.

I Es gibt unterschiedliche Kovarianzmatrizen in deng Klassen, HA : es gibt j 6=l : Σ

j 6=Σ

l.

I

Sch¨ atzer f¨ ur Teilstichproben µ ˆ

:= X

= 1 n

n_j

X

k=1

X

; f¨ ur Kovarianzmatrix S

:= 1

n

1

nj

X

(X

X

)(X

X

)

.

Fortsetzung M-Test von Box

I

Gepoolte Kovarianzmatrix

˜ S := 1 n

g

g

X

k=1

(n

1)S

=: 1 n

g W , W ist die Inner-Gruppen-Streumatrix, auch Inner-Gruppen- SPP-Matrix (within groups

I

Testgr¨ oße

T = (1

c)

"

(n

g ) ln det ˜ S

g

X

k=1

(n

1) ln det S

#

= (1

c)

g

X

k=1

(n

1) ln det

S

S ˜

mit c = 2p

+ 3p

1 6(p + 1)(g

1)

g

X

k=1

1

n

1

1 n

g

!

.

Fortsetzung M-Test von Box

I

Asymptotische Verteilung

T

χ

Die Approximation ist gut, falls n

> 20 , g

5 , p

5 .

I

Kritischer Bereich K =

t

: t > χ

o

.

Testergebnisse f¨ ur Beispiel 3.3.7

(vgl. R-Skript f¨ ur Berechnungen)

I

p(p + 1)(g

1)/2 = 3 ;

I

χ

7.82 f¨ ur α = 0.05 ;

I

c

0.205 ;

I

s

1.102 0.486 0.486 1.907

, s

0.528 0.038 0.038 0.962

,

˜ s

0.925 0.348 0.348 1.616

;

I

det S ˜

1.374 , det S

1 ≈

1.865 , det S

2≈

0.506 ;

I

Realisierungswert der Testgr¨ oße t

0.990

⇒

t < χ

, t

K ,

wird nicht abgelehnt, es gibt

keine signifikanten Unterschiede zwischen den Kovarianzmatrizen.

3.4.3 Test auf Gleichheit der Erwartungswertvektoren

I

Bem.

Dies ist eine Aufgabenstellug der multivariaten Varianzanalyse (MANOVA). Analog zum univariaten Fall wird die Streuung innerhalb der Klassen verglichen mit der Streuung zwischen den Klassen.

I

Voraussetzungen

I Die Daten sindp-dimensional normalverteilt.

I Die Kovarianzmatrizen in deng Klassen stimmen ¨uberein, d.h.

Σ1=Σ

2=. . .=Σ

g=Σ.

I

Hypothesen

I Die Erwartungswertvektoren sind in alleng Klassen gleich (in diesem Fall ist die Diskriminanzanalyse nicht sinvoll),

H0 : µ₁=. . .=µ_g.

I Es gibt unterschiedliche Erwartungswertvektoren in deng Klassen (in diesem Fall ist die Diskriminanzanalyse sinvoll),

H : es gibt j 6=l :µ 6=µ .

Forts. Test auf Gleichheit der Erwartungswertvektoren

I

Streuungsmatrix innerhalb der Klassen W :=

g

X

j=1

(n

1)S

=

g

X

j=1 nj

X

k=1

(X

X

)(X

X

)

;

I

Streuungsmatrix zwischen den Klassen B :=

g

X

j=1

n

(X

X)(X

X)

mit X = 1 n

g

X

j=1 nj

X

k=1

X

;

I

totale Streuungsmatrix S

:=

g

X

j=1 nj

X

k=1

(X

X)(X

X)

;

I

Streuungszerlegung

S

= W + B ;

Forts. Test auf Gleichheit der Erwartungswertvektoren

I

Testgr¨ oßen basieren z.B. auf der Spur der Matrix W

B oder auf Λ = det W

det B + W = det

+ W

B

.

I

Testgr¨ oße im Zweigruppenfall (g = 2) T = (n

p

1)n

n

pn(n

2) (X

X

)

S ˜

(X

X

) .

I

Kritischer Bereich

K =

: t > F

.

Testergebnisse f¨ ur Beispiel 3.3.7

(vgl. R-Skript f¨ ur Berechnungen)

I

F

3.89 f¨ ur α = 0.05 .

I

Realisierungswert der Testgr¨ oße t

4.364 .

⇒

t

K ,

wird abgelehnt, es gibt signifikante Unterschiede

zwischen den Erwartungswertvektoren.

3.5 Wahrscheinlichkeit f¨ ur Fehlklassifikation

I

Bei bekannten Verteilungen kann man Wahrscheinlichkeiten f¨ ur eine Fehlklassifikation (theoretisch) berechnen.

I

Ist

p

:=

Z

Ri

L(j ; x)

=

Ri

f

(x)

die Wahrscheinlichkeit daf¨ ur, dass ein Merkmalstr¨ ager aus der j -ten Klasse der i -ten Klasse zugeordnet wird, dann ist p

f¨ ur i

j eine Fehlklassifikationswahrscheinlichkeit .

I

Die Fehlklassifikationswahrscheinlichkeiten sollten m¨ oglichst klein sein.

I

Sind die Verteilungen der Populationen Π

, . . . , Π

nicht bekannt, k¨ onnen verschiedene Ans¨ atze zur Sch¨ atzung dieser

Wahrscheinlichkeiten genutzt werden.

3.5.1 Nutzung gesch¨ atzter Parameter

I

Bsp. Geg. g = 2 , Π

=

(µ

, Σ) , i = 1, 2 .

I

Die Diskriminanzfunktion (bei bekannten Parametern) lautet dann h(x) = (µ

1−

µ

2

)

Σ

x

1 2 (µ

1

+ µ

2

)

, x

.

I

F¨ ur einen Zufallsvektor X aus Π

gilt h(X)

1

2 ∆

, ∆

, ist X aus Π

gilt h(X)

−

1 2 ∆

, ∆

, mit

∆

:= (µ

µ

)

Σ

(µ

µ

)

(Quadrat des

-Abstandes zwischen µ

und µ

) .

Fortsetzung Beispiel

I

Hieraus folgt

p

=

> 0|Π

) = Φ

−

∆ 2

= p

=

< 0|Π

) .

I

Mit gesch¨ atzten Parametern erh¨ alt man mit

∆ ˆ

= (x

x

)

˜ s

(x

x

) und

˜ s = 1 n

+ n

2

(n

1)s

+ (n

1)s

: ˆ

p

= ˆ p

= Φ

∆ ˆ 2

!

.

I

F¨ ur Beispiel 3.2.5 bzw. 3.3.7 p

= Φ

√

1.5 2

!

= 0.2701 , p ˆ

= Φ

−

1.684 2

= 0.1998 .

3.5.2 Resubstitutionsmethode

I

Prinzip Man wendet die aus einer Lernstichprobe konstruierte Diskriminanzregel auf die Lernstichprobe selber an und bestimmt die relative H¨ aufigkeit von Fehlklassifikationen.

I

Sei n

die Anzahl der n

Individuen von Π

, deren Merkmalsvektor x in R

liegt, die also zu Π

zugeordnet werden m¨ ussen.

I

Dann ist eine Sch¨ atzung der indivuellen Fehlerraten gegeben durch ˆ

p

= n

n

, i

j .

I

F¨ ur Beispiel 3.3.7 (ML-Diskriminanzregel, siehe Streudiagramm Folie 31)

n

= 1 , n

= 3 , p ˆ

= 1

5 = 0.2 , p ˆ

= 3

10 = 0.3 .

3.5.3 Cross-Validation-Prinzip (

” jack-knifing“)

I

Ausgangspunkt Die in 3.5.1 und 3.5.2 vorgestellten Methoden sind oft zu optimistisch, da diesselben Daten, die die

Diskriminanzregel definieren, zu deren Bewertung herangezogen werden.

I

Cross-Validation (Kreuzvalidierung) ist eine Methode zur Bewertung von statistischen Verfahren, bei der Teile des (bekannten)

Datenmaterials nicht zur Konstruktion des Verfahrens, sondern zu seiner Kontrolle genutzt werden.

I

Wird jede einzelne Beobachtung einmal zur Kontrolle genutzt,

spricht man auch von einer Leave-One-Out-Methode oder

Leave-One-Out-Kreuzvalidierung.

Leave-One-Out-Methode

I

Geg. x

= (x

, . . . , x

, . . . , x

) .

I

Vorgehen

(i) Streiche r−tes Datum x_jr aus x

j.

(ii) Bestimme die Diskriminanzregel mit den verbleibenden n−1 Daten, das Ergebnis sind die Regionen R₁^(jr), . . . ,Rg^(jr).

(iii) Wende die Diskriminanzregel auf das gestrichene Datum x_jr an;

mache dies nj mal, d.h. f¨ur r= 1, . . . ,nj.

(iv) Sei n^∗_ij die Anzahl der F¨alle, bei denen x_jr aus Πj in R_i^(jr) liegt, d.h. Πi zugeordnet werden w¨urde.

(v) Die gesuchten Sch¨atzungen sind ˆ p_ij =n^∗_ij

n_j .

3.6 Fisher s lineare Diskriminanzfunktion

I

Bem. Bei dieser Methode wird der Verteilungstyp der Populationen Π

, . . . , Π

nicht vorausgesetzt.

I

Prinzip Man finde eine lineare Funktion der Datenmatrix, d.h.

einen Vektor a

mit

z :=







x

a

.. . x

a







=







z

.. . z







(z

) , so dass in z

Streuung zwischen den Gruppen Streuung innerhalb der Gruppen

= max

.

Dann ist die Variation zwischen den Gruppen so groß wie m¨ oglich

und die Variation innerhalb der Gruppen so klein wie m¨ oglich und

Fisher s lineare Diskriminanzfunktion

I

Man kann zeigen, dass diese Aufgabenstellung ¨ aquivalent ist zu a

b a

a

w a

= max

.

(b und w sind die entsprechenden Ausdr¨ ucke f¨ ur die Variation zwischen (between) und innerhalb (within) der Gruppen, siehe 3.4.3.) Man kann weiterhin zeigen, dass die L¨ osung dieses Problems folgendermaßen bestimmt werden kann.

I

Def.

Sei a

0

ein Eigenvektor zum gr¨ oßten Eigenwert von w

b .

Die Funktion

x

(a

)

x

heißt

s lineare

Diskriminanzfunktion.

Diskriminanzregel

Diskriminanzregel

x wird der Klasse i zugeordnet, d.h. x

R

, falls f¨ ur alle j

i gilt

|(a^∗

)

x

(a

)

x

<

)

x

(a

)

x

,

d.h. der transformierte Vektor zu x kommt dem transformierten

Zentrum der Gruppe i am n¨ achsten.